Metrology for Measuring Bumps in a Protection Layer Based on Phase Shifting Fringe Projection
Abstract
:1. Introduction
2. Fringe Projection System and Sample Details
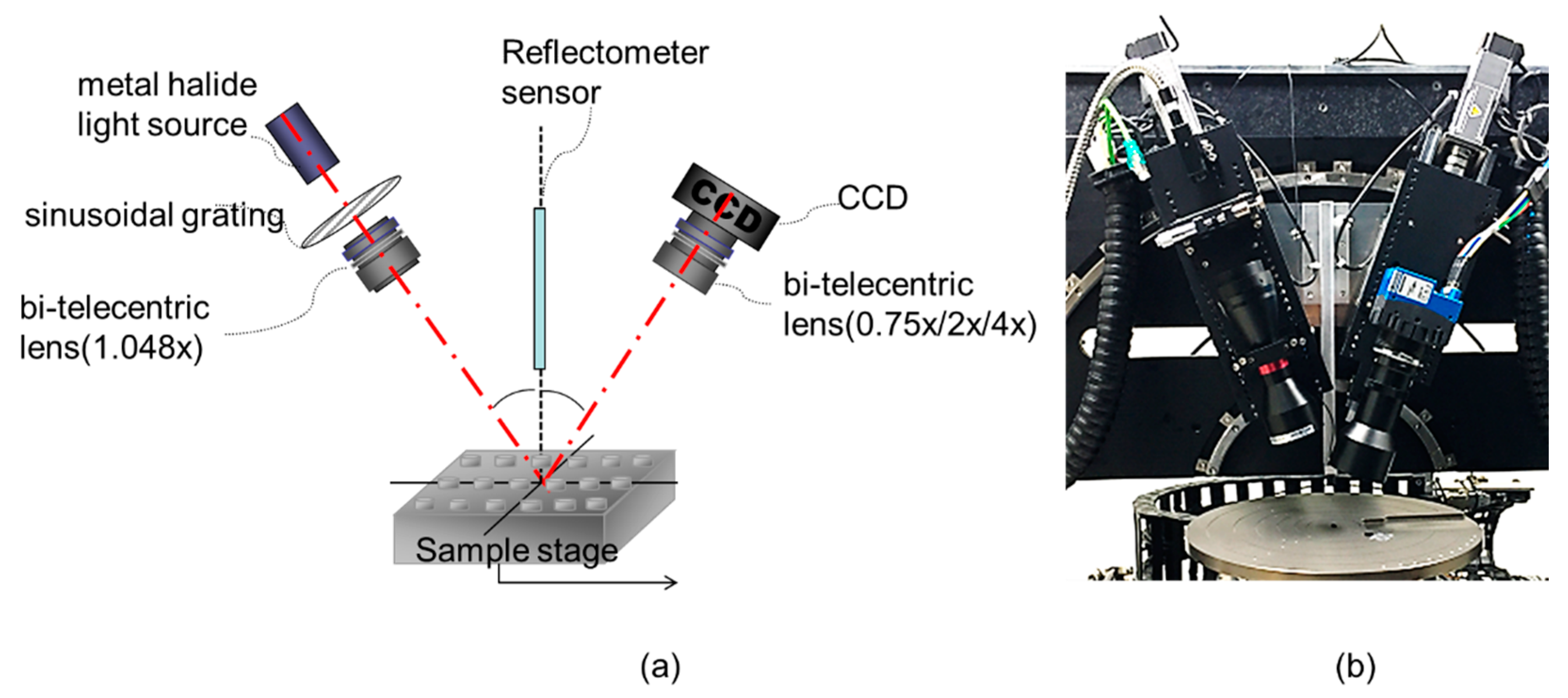
2.1. System Setup
2.2. System Design
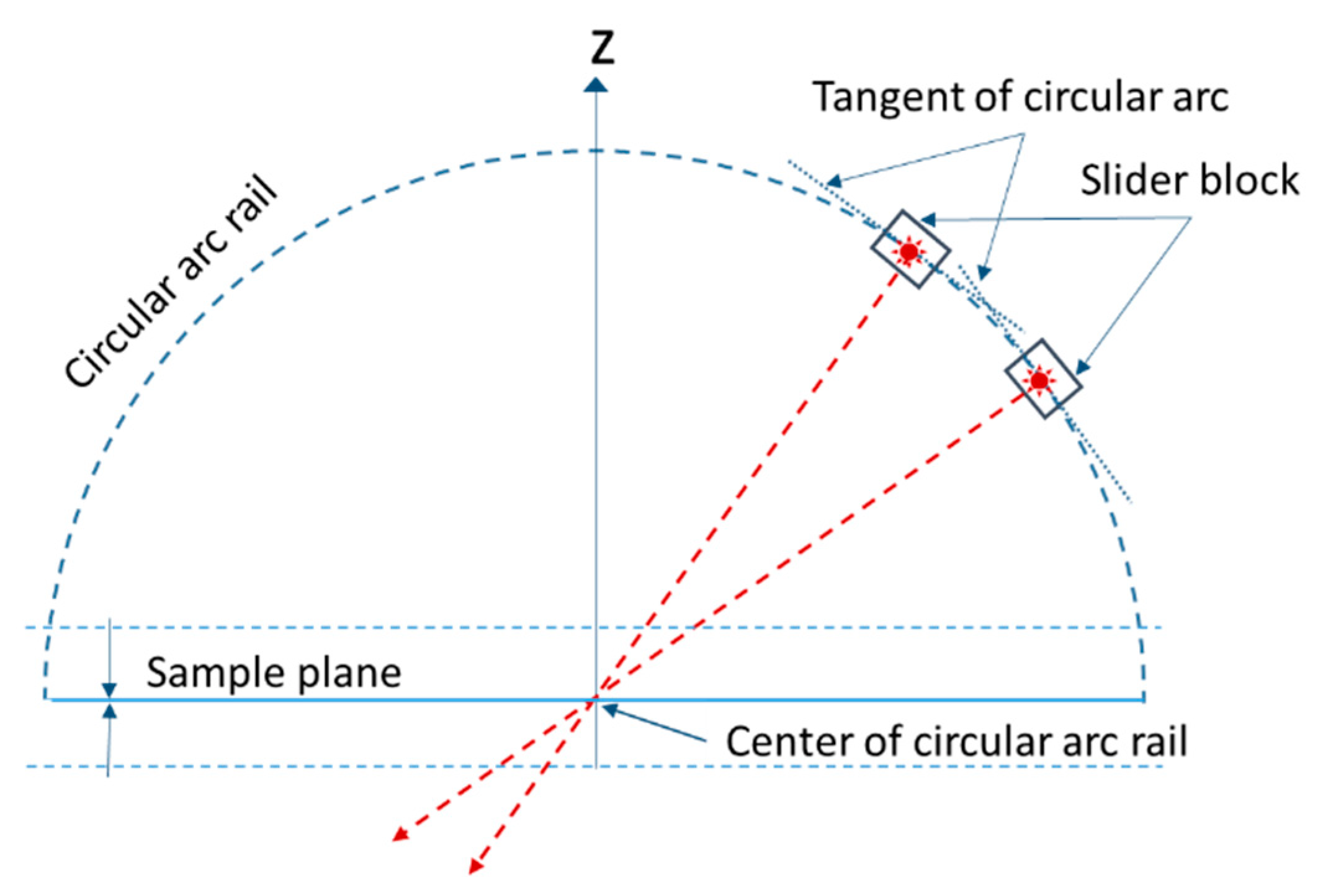
2.3. Reference Plane Identification and Rotation Center Calibration
2.4. Sample Details
3. Theoretical Model of Fringe Projection Profilometry
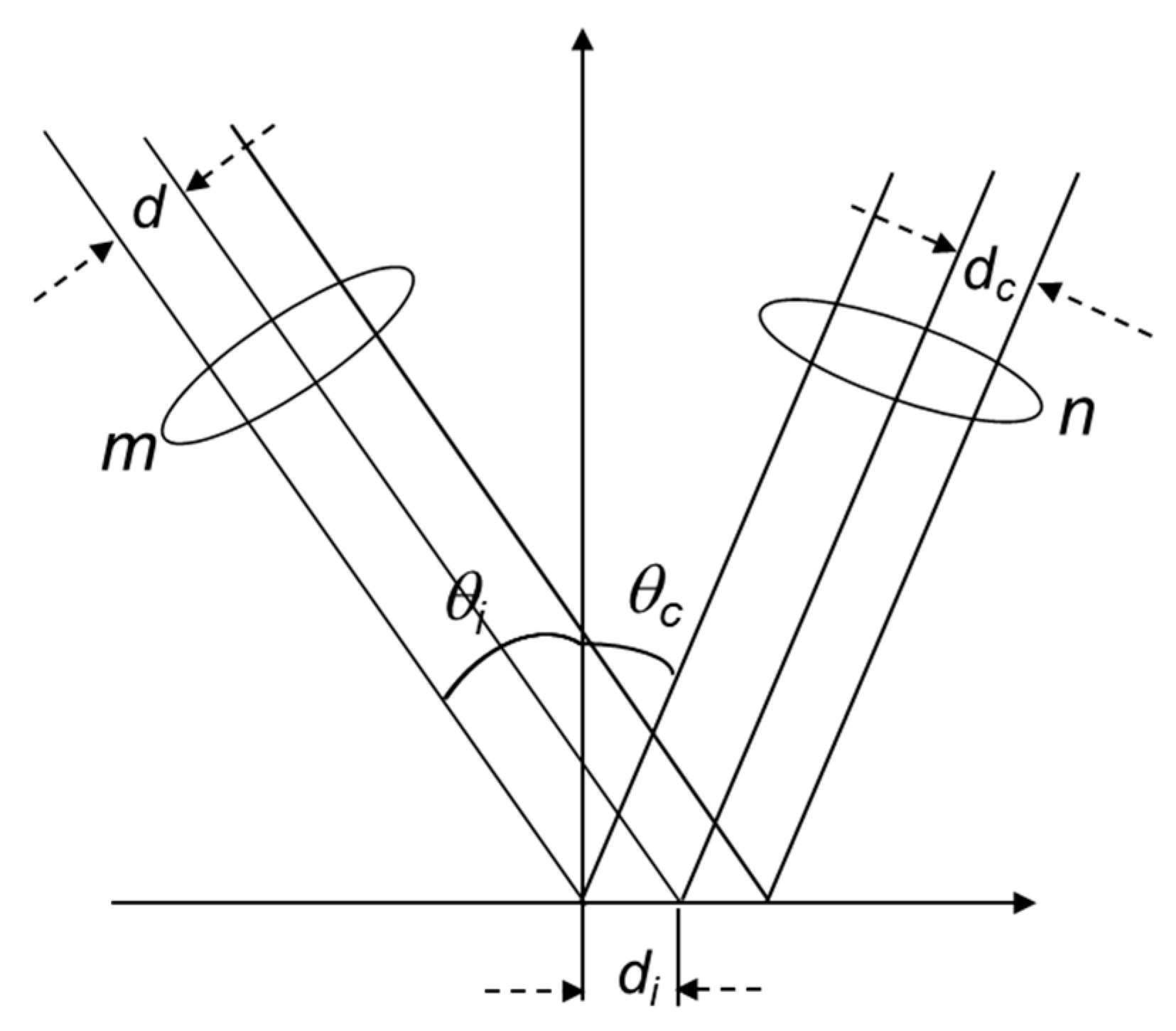
3.1. Basic Theoretical Model for Fringe Projection Profilometry
3.2. Three-Step Phase-Shifting Technique
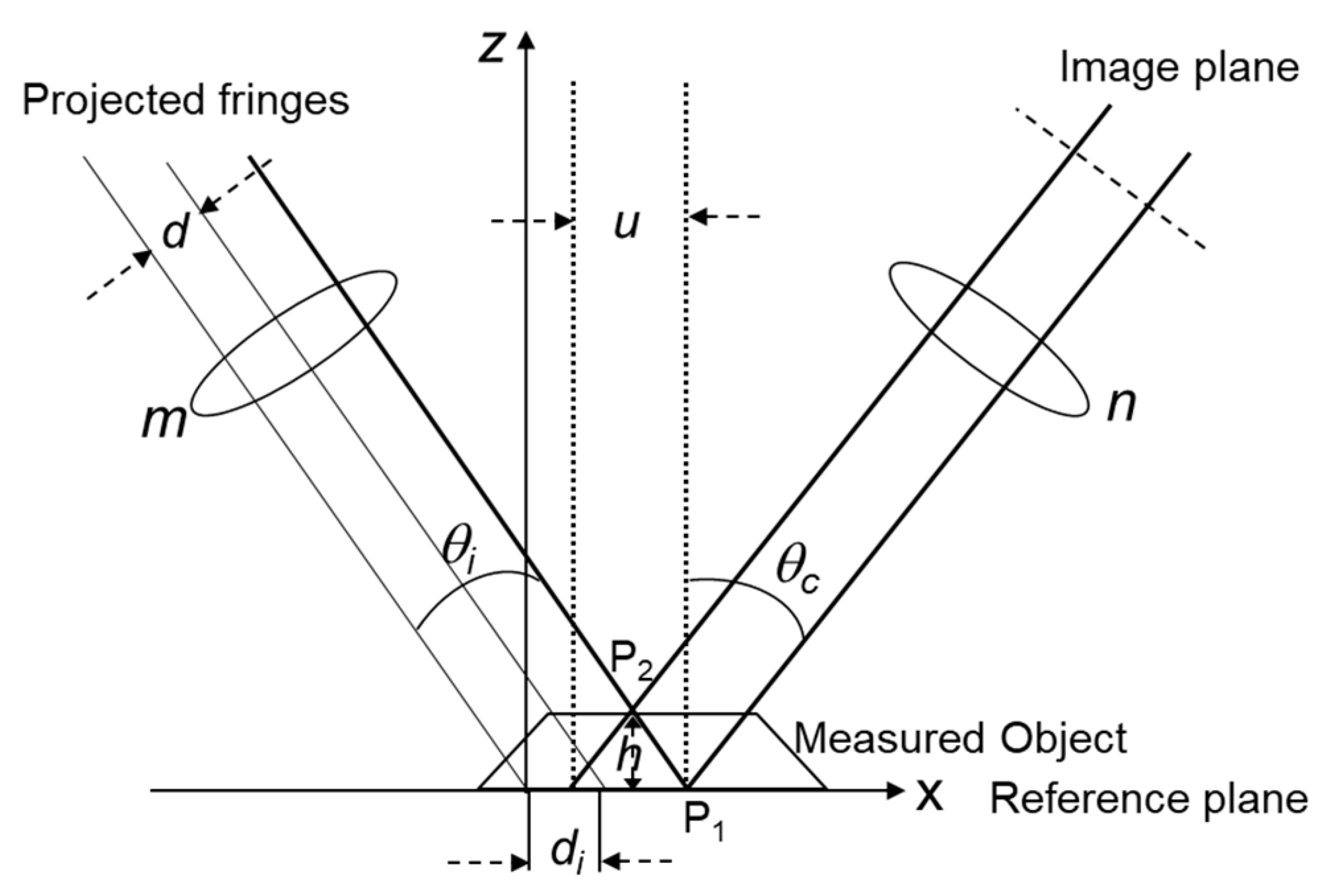
3.3. Phase-Height Conversion
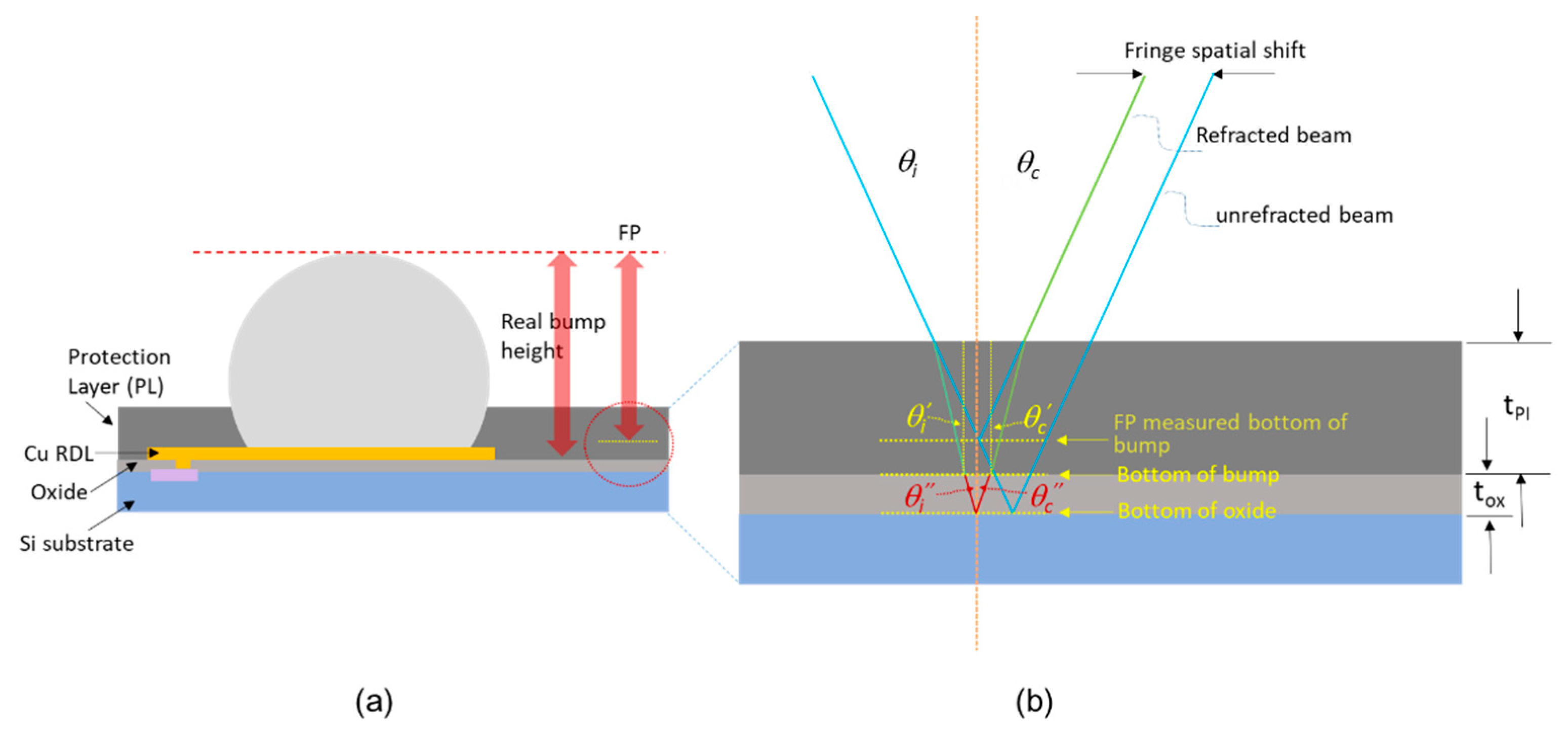
3.4. Bump Height Correction in Polymer Layers
4. Measurement Algorithm and System Calibration
5. Experimental Results and Discussion
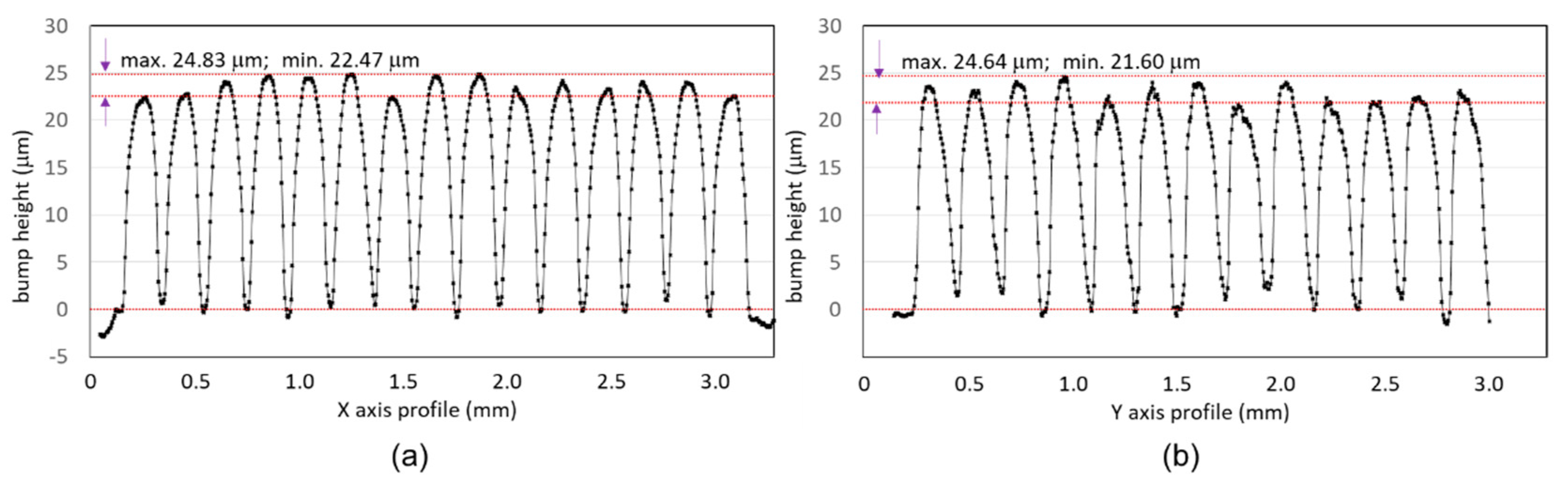
5.1. Measurement of Double Peripheral Solder Bumps
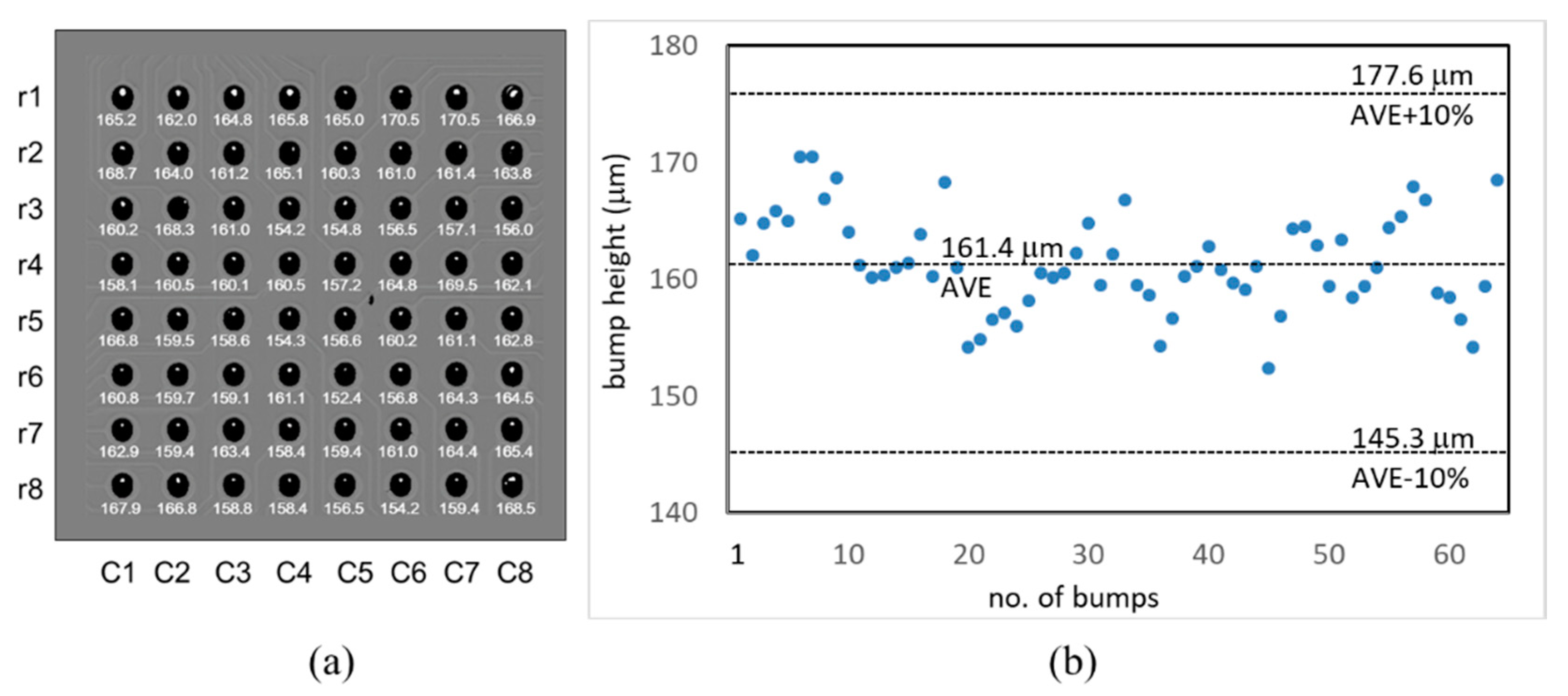
5.2. Height Measurement of Bumps in a Polymer
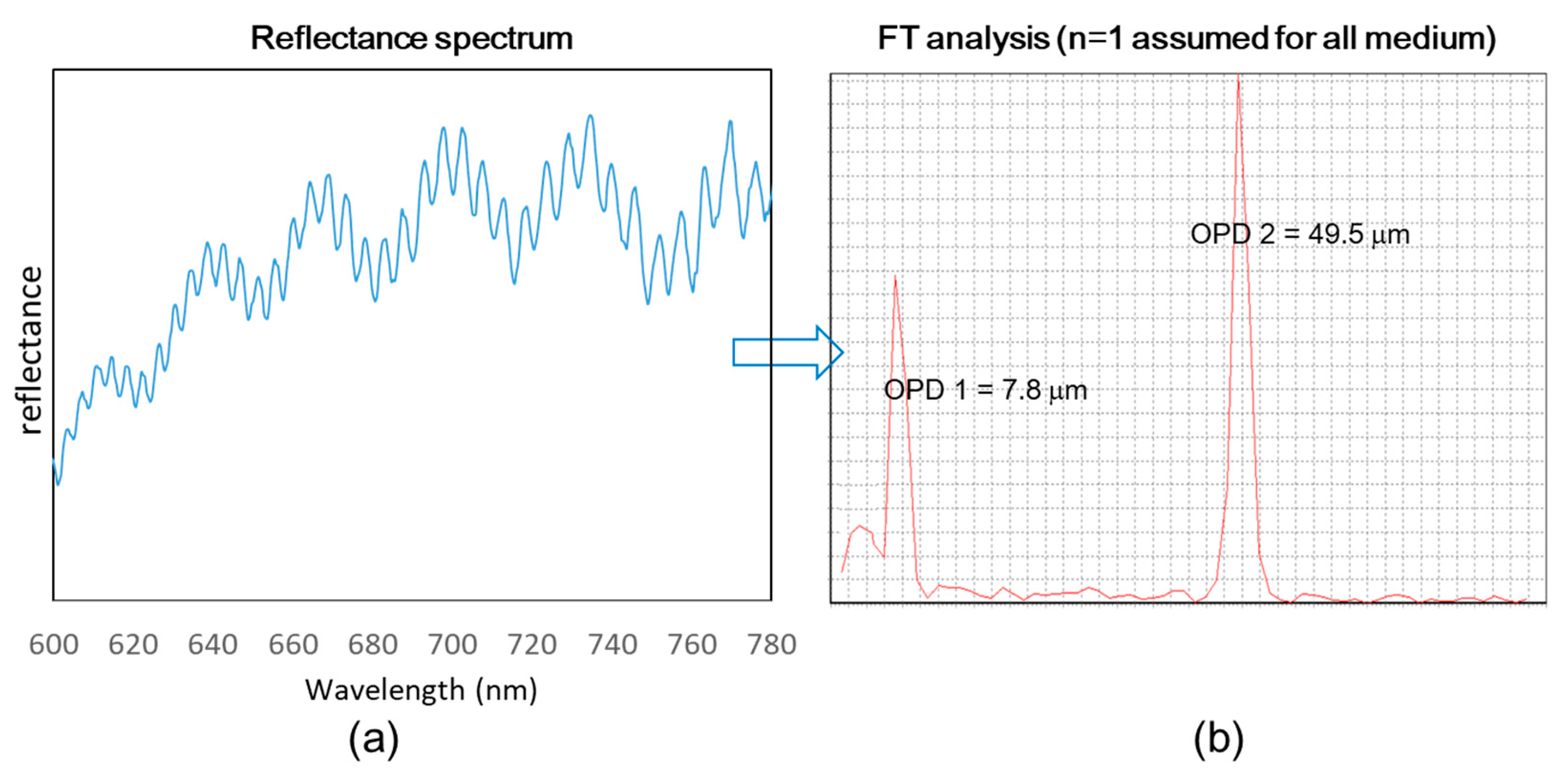
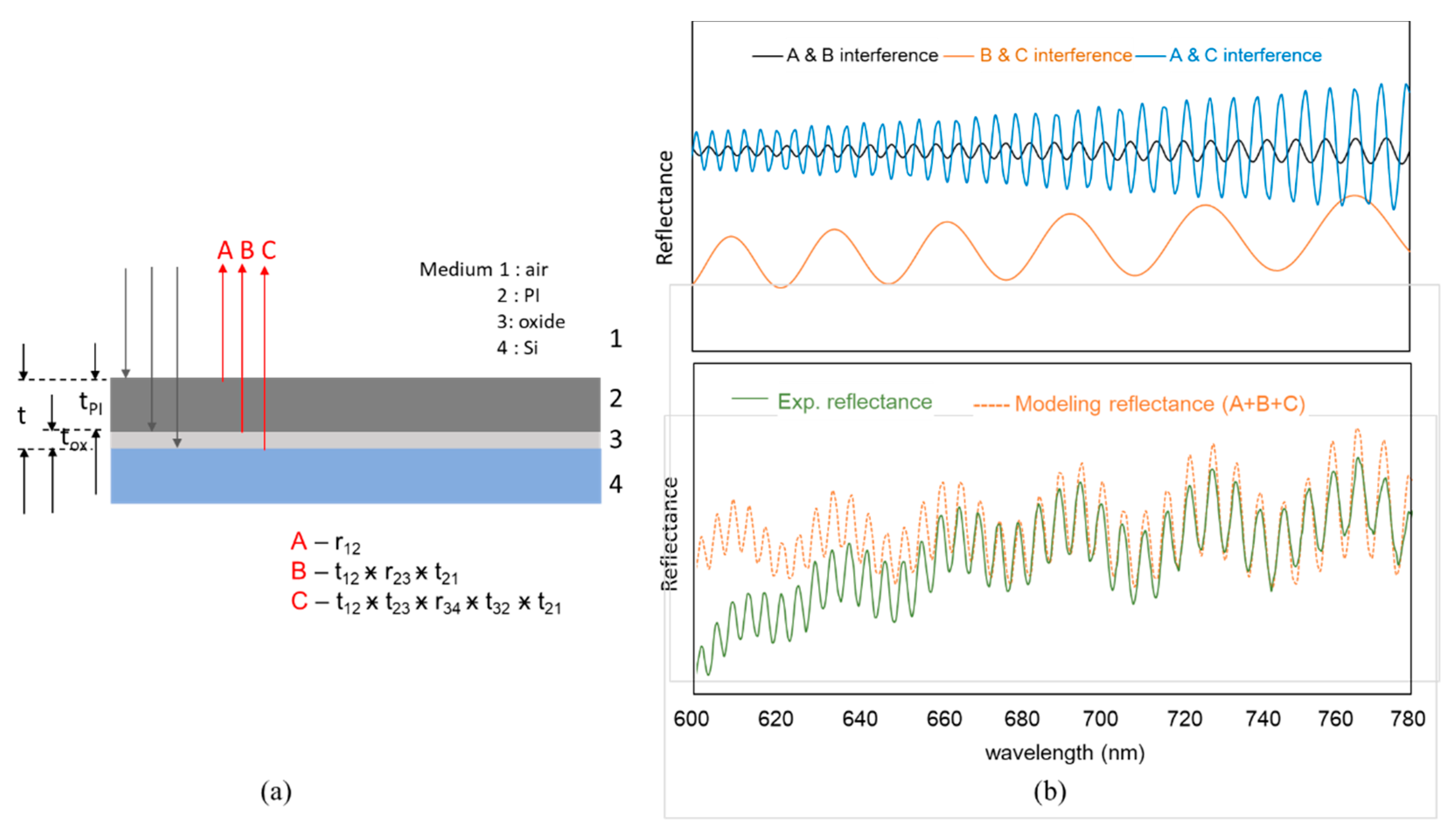
5.2.1. Reflectrometric Spectrum Model Fit
5.2.2. Comparison of PL Measurement with Scanning White Light Interferometry
5.2.3. Bump Height Correction for Polymer Layers
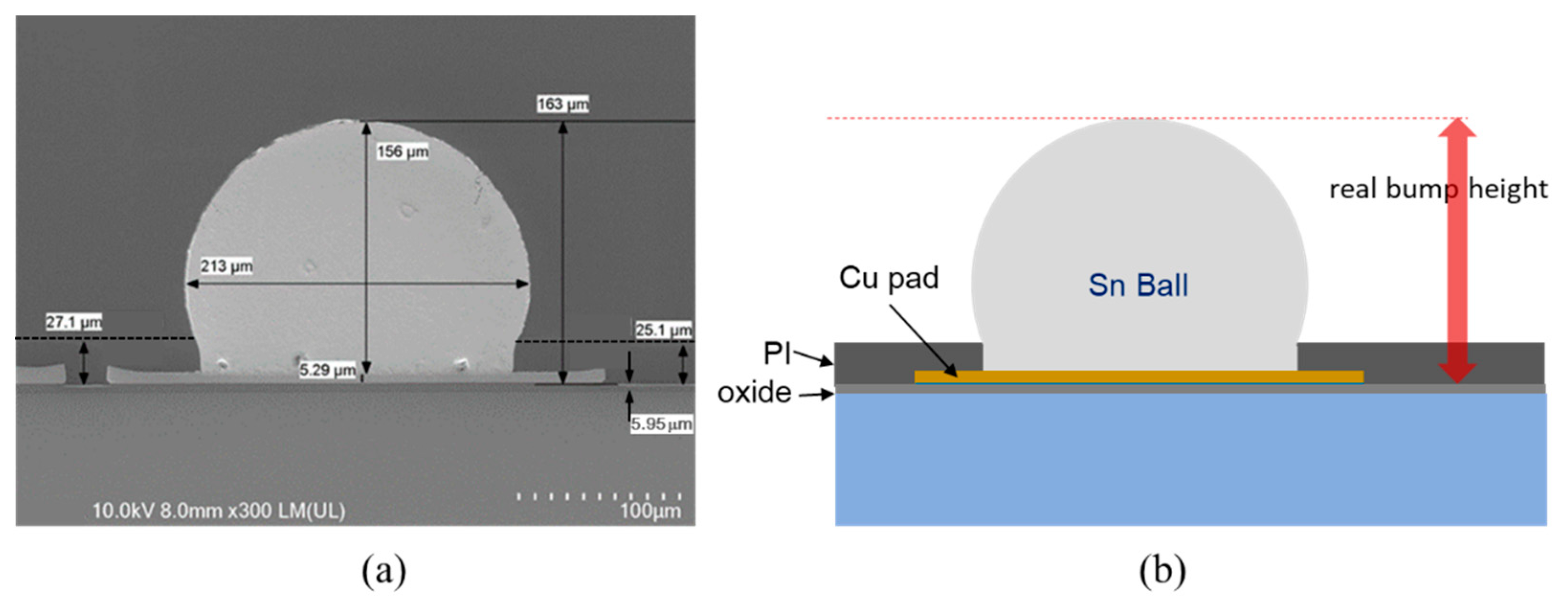
5.2.4. Comparison of 3D Measurement with Scanning Electron Microscopy
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Su, X.; Zhang, Q. Dynamic 3D shape measurement method: A review. Opt. Lasers Eng. 2010, 48, 191–204. [Google Scholar] [CrossRef]
- Wang, Z.; Du, H.; Park, S.; Xie, H. Three-dimensional shape measurement with a fast and accurate approach. Appl. Opt. 2009, 48, 1052–1061. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Brown, G.M.; Song, M. Overview of three-dimensional shape measurement using optical methods. Opt. Eng. 2000, 39, 10–22. [Google Scholar]
- Fratz, M.; Seyler, T.; Bertz, A.; Carl, D. Digital holography in production: An overview. Light Adv. Manuf. 2021, 2, 134–146. [Google Scholar] [CrossRef]
- Jecić, S.; Drvar, N. The assessment of structured light and laser scanning methods in 3D shape measurements. In Proceedings of the 4th International Congress of Croatian Society of Mechanics (CSM), Bizovac, Croatia, 18–20 September 2003; pp. 237–244. [Google Scholar]
- Tsukahara, H.; Nishiyama, Y.; Takahashi, F.; Fuse, T. High-speed solder bump inspection system using a laser scanner and camera. Syst. Comput. Jpn. 2000, 31, 2556–2564. [Google Scholar] [CrossRef]
- Zong, S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques. Opt. Lasers Eng. 2010, 48, 149–158. [Google Scholar] [CrossRef]
- Múnera, N.; Lora, G.J.; Sucerquia, J.G. Evaluation of fringe projection and laser scanning for 3D reconstruction of dental pieces. DYNA 2012, 79, 65–73. [Google Scholar]
- Hayashi, T.; Murata, Y.; Fujigaki, M. 3D shape measurement using inclined small pitch fringe projection method with Talbot effect and phase shifting method with linear fiber arrays. IEEJ Trans. Electron. Inf. Syst. 2016, 136, 1063–1070. [Google Scholar]
- Silva, A.; Legarda-Saenz, R.; García-Torales, G.; Balderas-Meta, S.; Flores, J.L. 3D shape measurement with binary phase-shifted technique and digital filters. Proc. SPIE 2014, 9219, 92190L. [Google Scholar]
- Yu, M.; Zhang, Y.; Zhang, D. Review of 3D shape measurement using fringe projection techniques. Adv. Mater. Res. 2012, 503–504, 1437–1440. [Google Scholar] [CrossRef]
- Liu, H.; Lin, H.; Yao, L. Calibration method for projector-camera-based telecentric fringe projection profilometry system. Opt. Express 2017, 25, 31492. [Google Scholar] [CrossRef]
- Li, D.; Liu, C.; Tian, J. Telecentric 3D profilometry based on phase-shifting fringe projection. Opt. Express 2014, 22, 31826. [Google Scholar] [CrossRef] [PubMed]
- Quan, C.; Tay, C.J.; Huang, Y.H. 3D deformation measurement using fringe projection and digital image correlation. Optik 2004, 115, 164–168. [Google Scholar] [CrossRef]
- Chen, T.; Tian, J.; Tian, Y.; Wu, J.; Li, D. A flexible, simple telecentric three dimensional measurement system. Proc. SPIE 2017, 10330, 103300H. [Google Scholar]
- Li, D.; Tian, J. An accurate calibration method for a camera with telecentric lenses. Opt. Lasers Eng. 2013, 51, 538–541. [Google Scholar] [CrossRef]
- Espino, J.G.R.; Gonzalez-Barbosa, J.J.; Loenzo, R.A.G. Vision system for 3D reconstruction with telecentric lens. Proc. MCPR 2012, 7329, 127–136. [Google Scholar]
- Yao, L.; Liu, H. A flexible calibration approach for camera with double-sided telecentric lenses. Int. J. Adv. Robot Syst. 2016, 13, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Mikš, A.; Novák, J. Design of a double-sided telecentric zoom lens. Appl. Opt. 2012, 51, 5928–5935. [Google Scholar] [CrossRef]
- Balak, S. Improving the accuracy of bump height and co-planarity measurement. Solid State Technol. 2016, 13, 12–14. [Google Scholar]
- Ku, Y.S.; Yang, F.S. Reflectometer-based metrology for high-aspect ratio via measurement. Opt. Express 2010, 18, 7269. [Google Scholar] [CrossRef]
- Ku, Y.S.; Huang, K.C.; Hsu, W. Characterization of high density through silicon vias with spectral reflectometry. Opt. Express 2011, 19, 5993. [Google Scholar] [CrossRef] [PubMed]

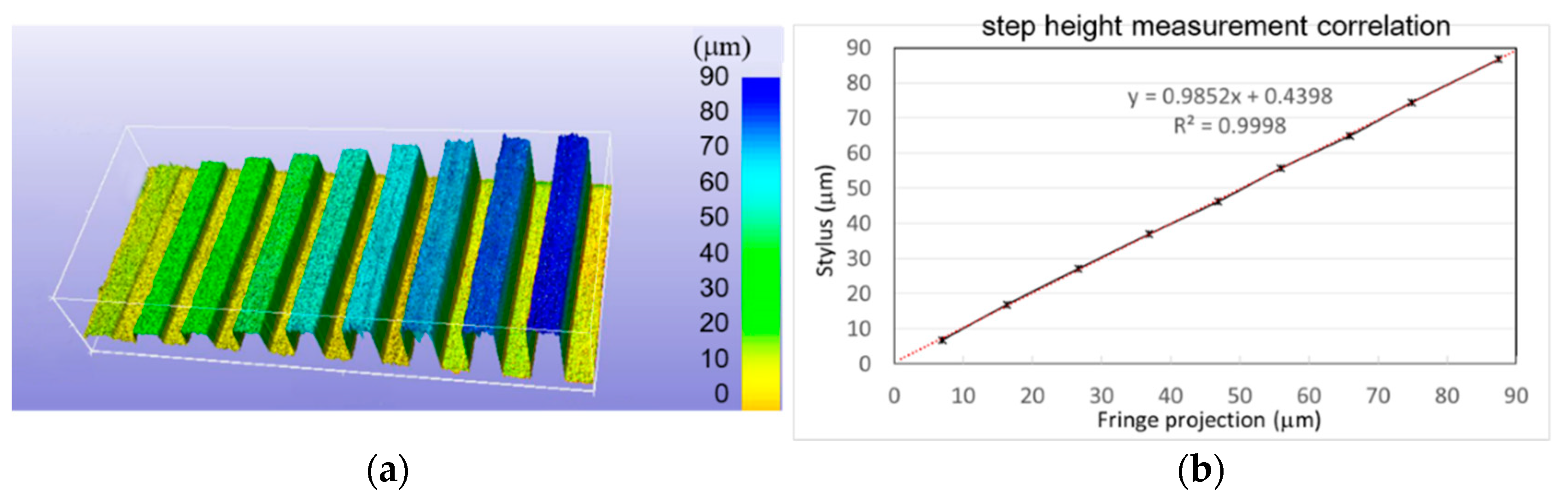



| Site | Nominal (μm) | Calibrated(μm) Stylus | Measured(μm) Fringe Projection | Discrepancy(μm) % |
|---|---|---|---|---|
| 1 | 5 | 6.76 | 6.94 | −0.19 (2.75) |
| 2 | 15 | 16.92 | 16.36 | 0.57 (3.36) |
| 3 | 25 | 27.16 | 26.70 | 0.46 (1.69) |
| 4 | 35 | 37.01 | 36.92 | 0.09 (0.24) |
| 5 | 45 | 46.20 | 46.86 | −0.66 (1.42) |
| 6 | 55 | 55.69 | 55.95 | −0.26 (0.47) |
| 7 | 65 | 64.98 | 65.97 | −0.99 (1.52) |
| 8 | 75 | 74.39 | 74.86 | −0.47 (0.63) |
| 9 | 85 | 86.66 | 87.46 | −0.79 (0.92) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, Y.-S.; Chang, P.-Y.; Lee, H.-W.; Lo, C.-W.; Chen, Y.-C.; Cho, C.-H. Metrology for Measuring Bumps in a Protection Layer Based on Phase Shifting Fringe Projection. Appl. Sci. 2022, 12, 898. https://doi.org/10.3390/app12020898
Ku Y-S, Chang P-Y, Lee H-W, Lo C-W, Chen Y-C, Cho C-H. Metrology for Measuring Bumps in a Protection Layer Based on Phase Shifting Fringe Projection. Applied Sciences. 2022; 12(2):898. https://doi.org/10.3390/app12020898
Chicago/Turabian StyleKu, Yi-Sha, Po-Yi Chang, Han-Wen Lee, Chun-Wei Lo, Yi-Chang Chen, and Chia-Hung Cho. 2022. "Metrology for Measuring Bumps in a Protection Layer Based on Phase Shifting Fringe Projection" Applied Sciences 12, no. 2: 898. https://doi.org/10.3390/app12020898
APA StyleKu, Y.-S., Chang, P.-Y., Lee, H.-W., Lo, C.-W., Chen, Y.-C., & Cho, C.-H. (2022). Metrology for Measuring Bumps in a Protection Layer Based on Phase Shifting Fringe Projection. Applied Sciences, 12(2), 898. https://doi.org/10.3390/app12020898





