3D FEM Analysis of the Subsoil-Building Interaction
Abstract
:1. Introduction
2. Materials and Methods
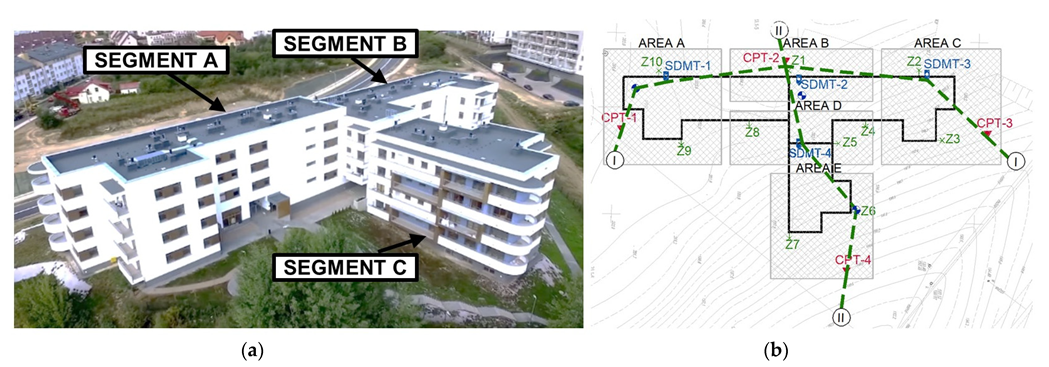
2.1. Tests on a Real Building
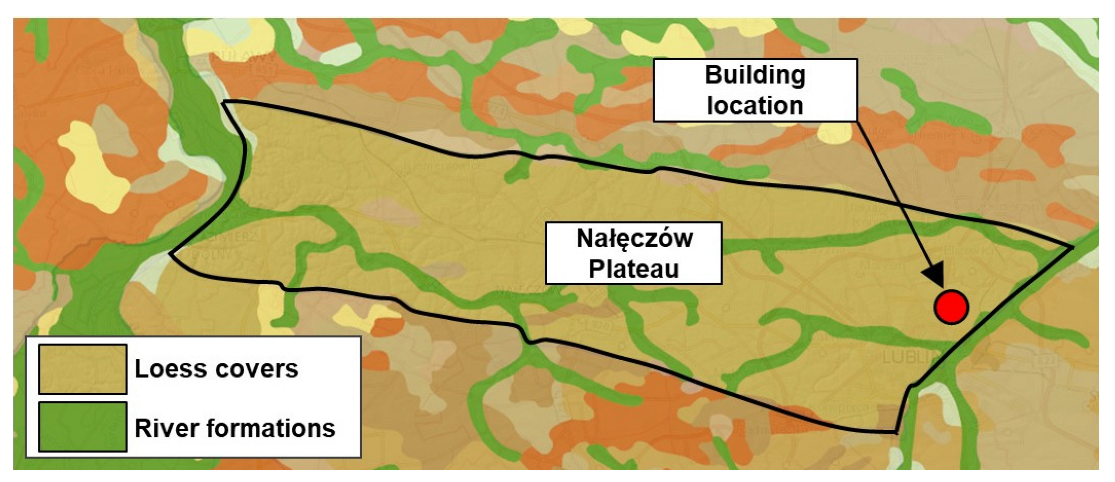
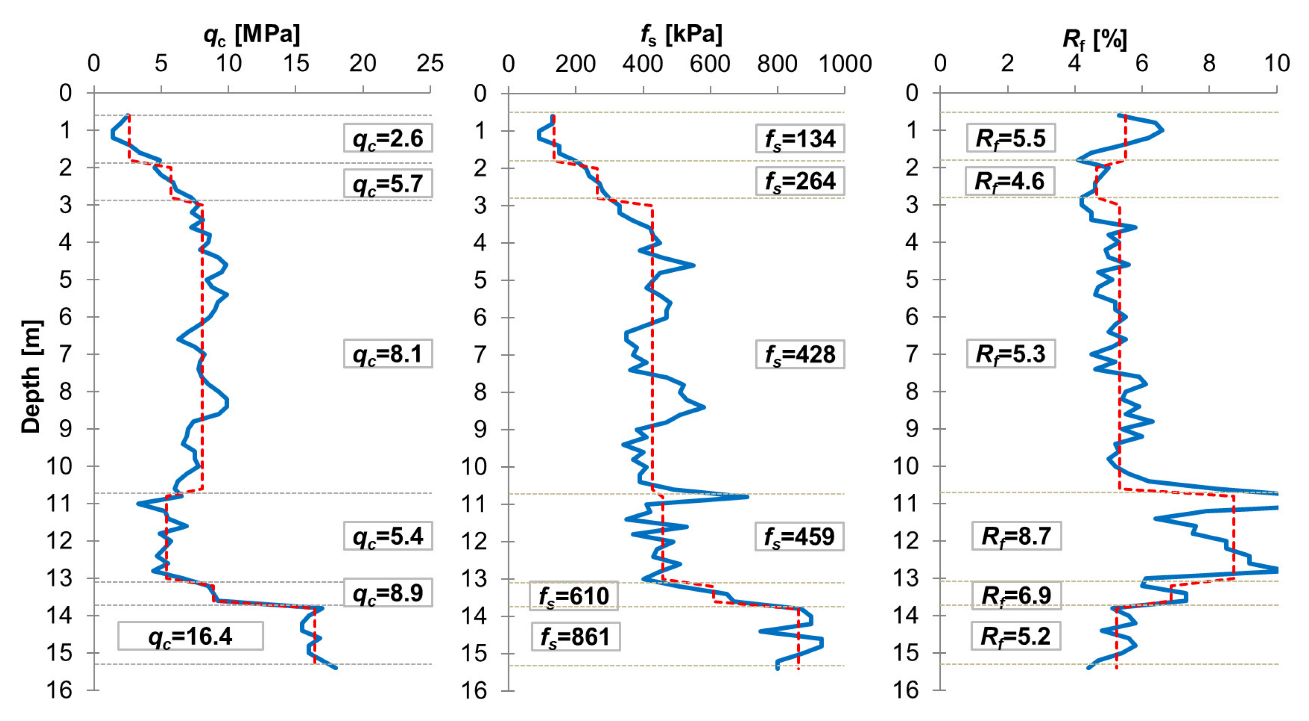
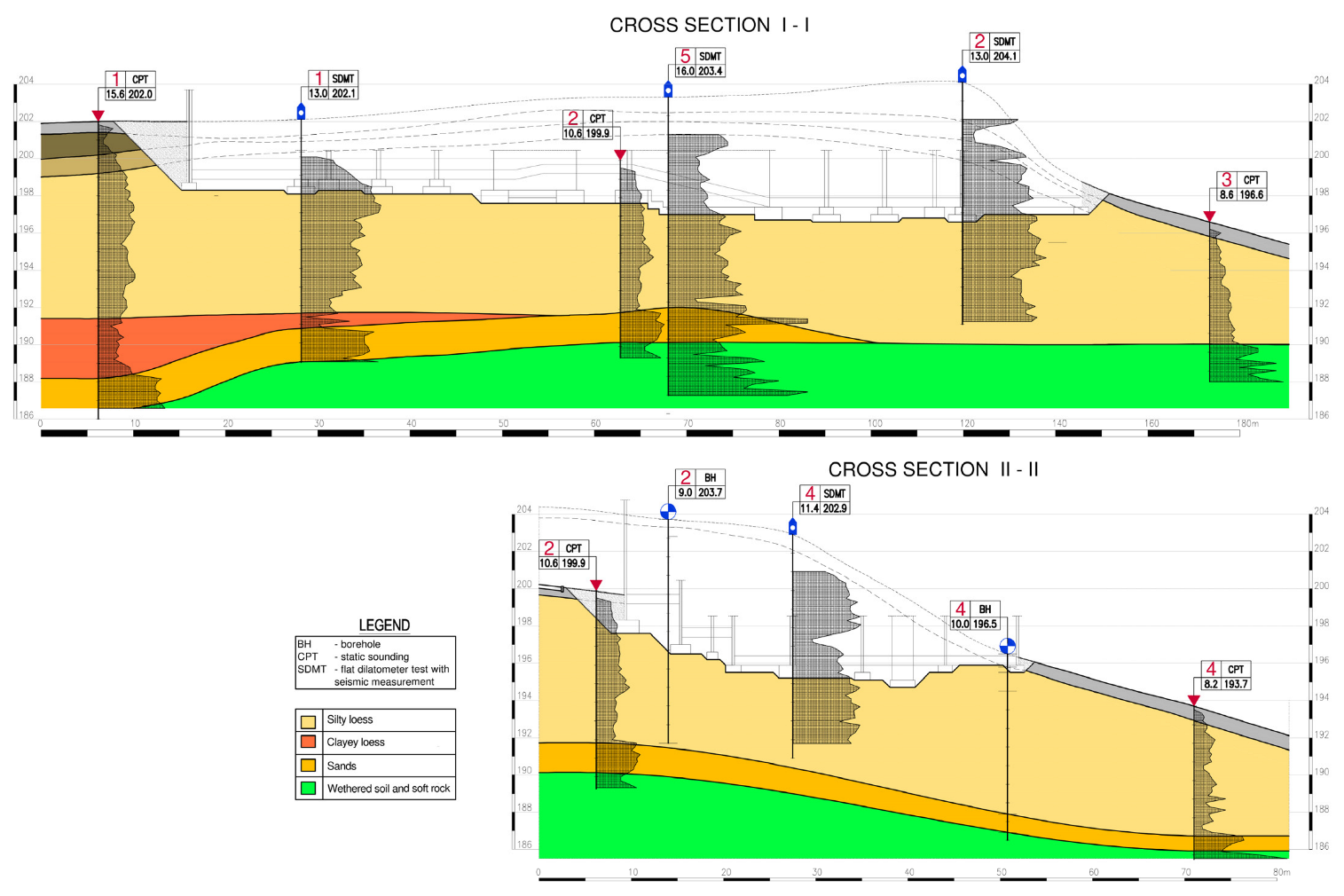
2.1.1. Subsoil Examination
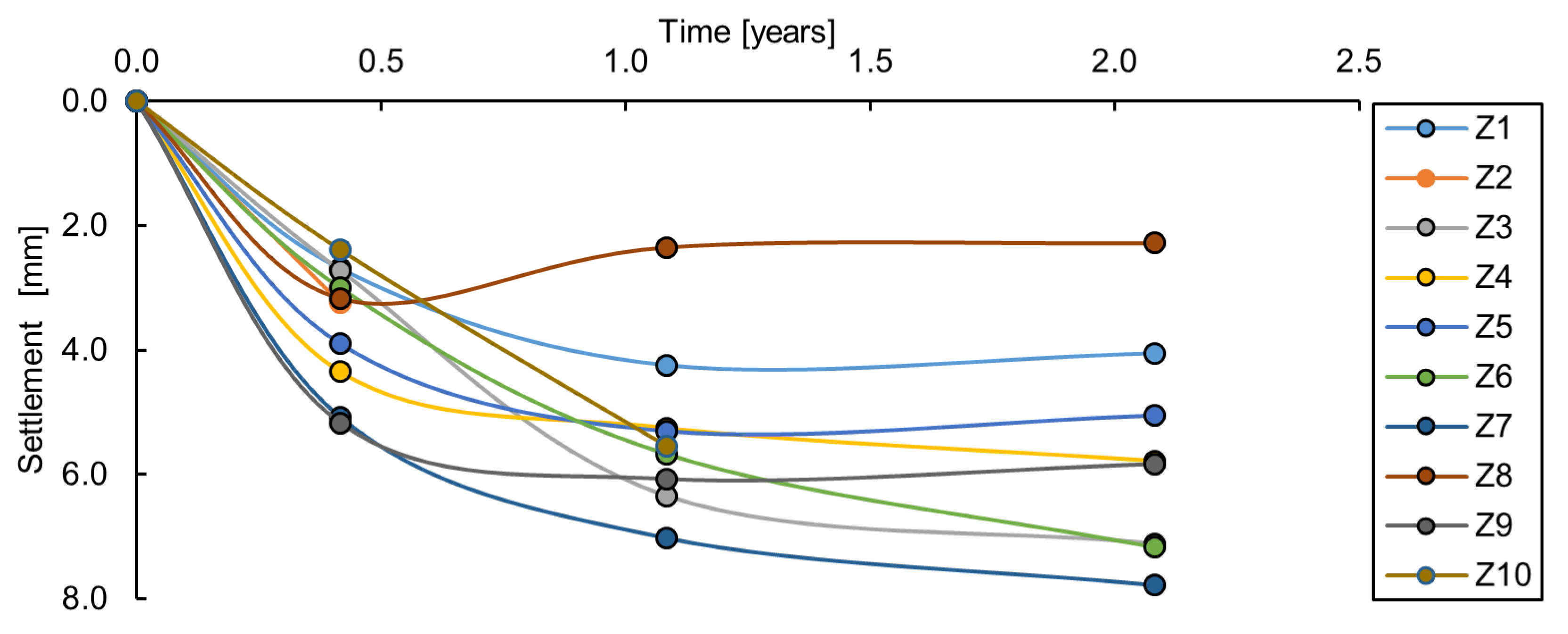
2.1.2. Building Settlement Measurements
2.1.3. Building Vibration Measurements
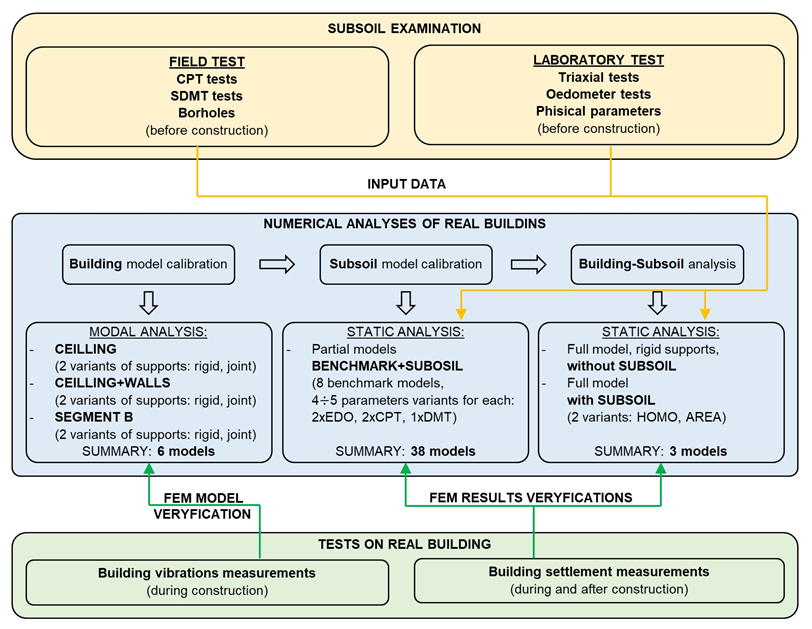
2.2. Numerical Analyses of Real Buildings
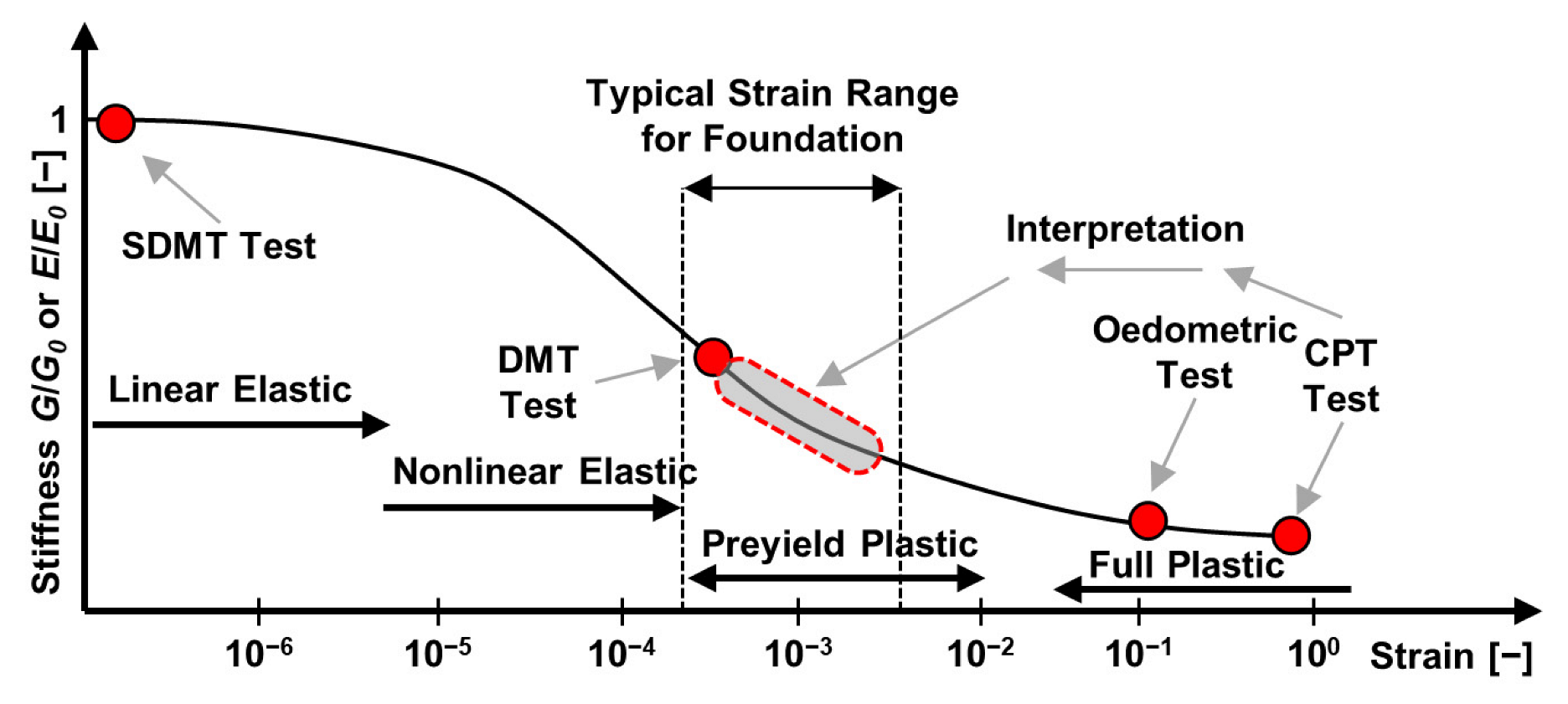
2.2.1. Subsoil Model
2.2.2. The Process of Building FEM Models and Their Assumptions
2.2.3. FEM Numerical Model of the Building
2.2.4. FEM Numerical Model of the Subsoil
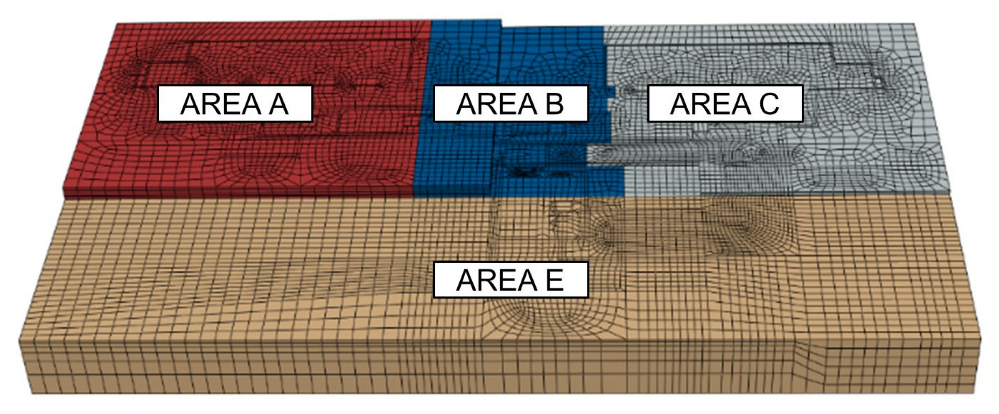
2.2.5. Calibration of the Subsoil Numerical Model—Partial Models
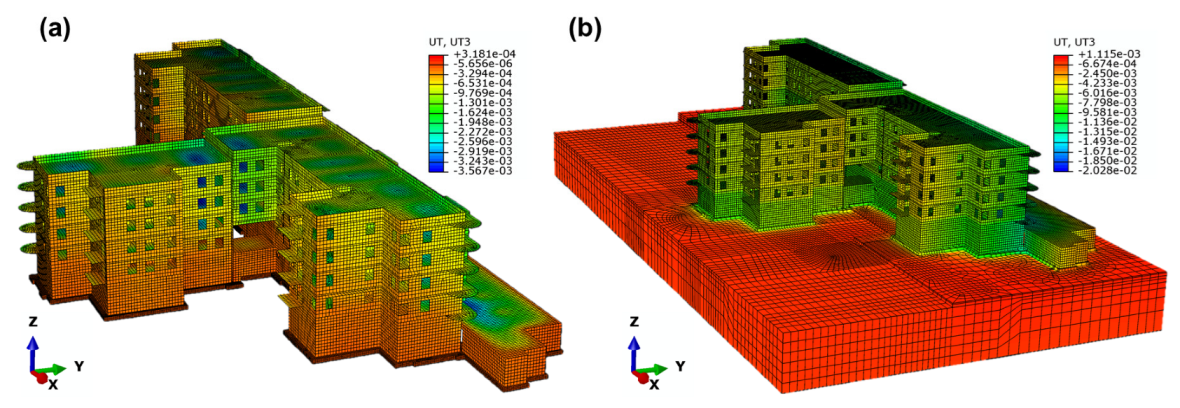
2.2.6. Numerical Analysis of the Full “Building-Subsoil” Model
3. Results
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chai, J.; Shen, S.; Ding, W.; Zhu, H.; Carter, J. Numerical investigation of the failure of a building in Shanghai, China. Comput. Geotech. 2014, 55, 482–493. [Google Scholar] [CrossRef]
- Grodecki, M. Numerical Modelling of a Sheet Pile and Diaphragm Walls. Ph.D. Thesis, Cracow University of Technology, Kraków, Poland, 2007. (In Polish). [Google Scholar]
- Lechowicz, Z.; Kiziewicz, D.; Wrzesiński, G. Bearing capacity assessment of subsoil in undrained conditions under pad foundation subjected to inclined load according to Eurocode 7. Acta Archit 2013, 12, 51–60. (In Polish) [Google Scholar]
- Biały, M. Application of FC + MCC model in numerical analysis of cooling tower with subsoil. Czas. Tech. 2008, 3-Ś, 21–29. (In Polish) [Google Scholar]
- Kowalska, A. Analysis of the Influence of Non-Structural Elements on the Dynamic Characteristics of Buildings. Ph.D. Thesis, Cracow University of Technology, Kraków, Poland, 2007. (In Polish). [Google Scholar]
- Mrozek, D.; Mrozek, M.; Fedorowicz, J. The protection of masonry buildings in a mining area. Procedia Eng. 2017, 193, 184–191. [Google Scholar] [CrossRef]
- Mrozek, D. Nonlinear Numerical Analysis of the Dynamic Response of Damaged Buildings. Ph.D. Thesis, The Silesian Technical University in Gliwice, Gliwice, Poland, 2010. (In Polish). [Google Scholar]
- Przewlocki, J.; Zielinska, M. Analysis of the behavior of foundations of historical buildings. Procedia Eng. 2016, 161, 362–367. [Google Scholar] [CrossRef] [Green Version]
- Nepelski, K. The verification of subsoil parameters based on back analysis of a bridge. Bud. i Archit. 2014, 13, 39–48. (In Polish) [Google Scholar] [CrossRef]
- Comodromos, E.M.; Papadopoulou, M.C.; Konstantinidis, G.K. Effects from diaphragm wall installation to surrounding soil and adjacent buildings. Comput. Geotech. 2013, 53, 106–121. [Google Scholar] [CrossRef]
- Ko, J.; Cho, J.; Jeong, S. Nonlinear 3D interactive analysis of superstructure and piled raft foundation. Eng. Struct. 2017, 143, 204–218. [Google Scholar] [CrossRef]
- Słowik, L. The Influence of the Slope of the Land Caused by Underground Mining on the Inclination of Buildings. Ph.D. Thesis, Instytut Techniki Budowlanej, Warsaw, Poland, 2015. (In Polish). [Google Scholar]
- Michalak, H.; Przybysz, P. The Use of 3D Numerical Modeling in Conceptual Design: A Case Study. Energies 2021, 14, 5003. [Google Scholar] [CrossRef]
- Bovolenta, R.; Bianchi, D. Geotechnical Analysis and 3D Fem Modeling of Ville San Pietro (Italy). Geosciences 2020, 10, 473. [Google Scholar] [CrossRef]
- Labudkova, J.; Cajka, R. Experimental Measurements of Subsoil–Structure Interaction and 3D Numerical Models. Perspect. Sci. 2016, 7, 240–246. [Google Scholar] [CrossRef] [Green Version]
- Labudkova, J.; Cajka, R. 3D Numerical Model in Nonlinear Analysis of the Interaction between Subsoil and Sfcr Slab. Int. J. GEOMATE 2017, 13, 120–127. [Google Scholar] [CrossRef]
- Milovic, D.; Djogo, M. Differential Settlement of Foundations on Loess. In Proceedings of the International Conference on Case Histories in Geotechnical Engineering, Chicago, IL, USA, 2 May 2013; pp. 1–10. [Google Scholar]
- Nepelski, K. A FEM Analysis of the Settlement of a Tall Building Situated on Loess Subsoil. Open Eng. 2020, 10, 519–526. [Google Scholar] [CrossRef]
- Godlewski, T.; Kotlicki, W.; Wysokiński, L. Geotechnical Design According Eurocode 7; Wyd. ITB: Warsaw, Poland, 2011. (In Polish) [Google Scholar]
- Wszędyrówny-Nast, M. Estimation of the modulus of elasticity determination methods for the displacements analysis of the diaphragm wall. Geologos 2007, 11, 303–310. (In Polish) [Google Scholar]
- Młynarek, Z. Site investigation and mapping in urban area. In Proceedings of the XIV European Conference on Soil Mechanics and Geotechnical Engineering, Madrid, Spain, 24–27 September 2007; Volume 1. [Google Scholar]
- Atkinson, J.; Sallfors, G. Experimental determination of soil properties. In Proceedings of the 10th ECSMFE, Florence, Italy, 26–30 May 1991. [Google Scholar]
- Mair, R. Developments in geotechnical engineering research: Application to tunnels and deep excavations. Proc. Inst. Civ. Eng. Civ. Eng. 1993, 93, 27–41. [Google Scholar]
- Frankowski, Z.; Pietrzykowski, P. Displacement parameters of loesslike soils from southeastern Poland. Przegląd Geol. 2017, 65, 832–839. (In Polish) [Google Scholar]
- Truty, A. Small strain stiffness of soils. Numerical modeling aspects. Czas. Tech. 2008, 3, 107–126. (In Polish) [Google Scholar]
- Superczyńska, M. Values of elasticity parameters in the field of small and medium deformation range for Warsaw clays of the Poznań Formation. Inżynieria Morska i Geotech. 2015, 3, 207–211. (In Polish) [Google Scholar]
- Sas, W.; Gabrys, K.; Szymański, A. Analysis of stiffness of cohesive soils with use of resonant column. Inżynieria Morska Geotech. 2012, 4, 370–376. (In Polish) [Google Scholar]
- Lipiński, M. Criteria for Determining Geotechnical Parameters; SGGW: Warsaw, Poland, 2013. (In Polish) [Google Scholar]
- Borowczyk, M.; Frankowski, Z. Variability in geotechnic properties of loesses in the light of modern studies. Kwart. Geol. 1977, 23, 447–461. (In Polish) [Google Scholar]
- Szulborski, K.; Wysokiński, L. Assessment of the interaction of the structure with the subsoil in the diagnosis of building damage. In Proceedings of the VIII Conference Construction Appraisal Problems, Cedzyna, Poland, 2004. (In Polish). [Google Scholar]
- Godlewski, T.; Szczepański, T. Non-linear soil stiffness characteristic (Go)—Methods of determination, examples of application. Górnictwo i Geoinżynieria 2011, 2, 243–250. (In Polish) [Google Scholar]
- Gryczmański, M. An attempt of classification of constitutive models for soils. Zesz Nauk Politech Śląskiej 1995, 81, 433–446. (In Polish) [Google Scholar]
- Available online: www.asa-architekci.eu (accessed on 10 February 2018).
- Nepelski, K. Interpretation of CPT and SDMT tests for Lublin loess soils exemplified by Cyprysowa research site. Bud. I Archit. 2019, 18, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Sanglerat, G. The Penetrometer and Soil Exploration; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Senneset, K.; Janbu, N.; Svano, G. Strenght and deformation parameters from cone penetration tests. In Proceedings of the 2nd European Symposium on Penetration Testing, Amsterdam, The Netherlands, 1982. [Google Scholar]
- Ciloglu, F.; Cetin, K.O.; Erol, A.O. CPT-based compressibility assessment of soils. In Proceedings of the International Symposium on Cone Penetration Testing, Las Vegas, USA, 2014; pp. 629–636. [Google Scholar]
- Kulhawy, F.H.; Mayne, P.H. Manual on Estimating Soil Properties for Foundation Design; Electric Power Research Institute: New York, NY, USA, 1990. [Google Scholar]
- Młynarek, Z.; Wierzbicki, J.; Mańka, M. Geotechnical parameters of loess soils from CPTU and SDMT. In Proceedings of the International Conference on the Flat Dilatometer DMT, Roma, Italy, 2015; pp. 481–489. [Google Scholar]
- Młynarek, Z.; Wierzbicki, J.; Mańka, M. Constrained deformation and shear moduli of loesses from CPTU and SDMT tests. Inżynieria Morska i Geotech. 2015, 36, 193–199. (In Polish) [Google Scholar]
- Marchetti, S. In situ tests by flat dilatometer. J. Geotech. Eng. Div. 1980, 105, 299–321. [Google Scholar] [CrossRef]
- Marchetti, S. Some 2015 Updates to the TC16 DMT Report 2001. In Proceedings of the 3rd International Conference on the Flat Dilatometer, Rome, Italy, 2015; pp. 43–65. [Google Scholar]
- Lechowicz, Z.; Szymański, A. Deformation and Stability of Embankments on Organic Soils Part I. Research Methodology; SGGW: Warsaw, Poland, 2002. (In Polish) [Google Scholar]
- Jamiolkowski, M.; Ladd, C.C.; Germaine, J.T.; Lancellotta, R. New developments in field and laboratory testing of soils. In Proceedings of the 11th International Conference on Soil Mechanics and Foundation Engineering, San Francisco, CA, USA, 1985; pp. 57–154. [Google Scholar]
- Fedorowicz, L.; Fedorowicz, J. Preservation of pre-consolidated soils loaded with construction—Numerical modeling. Geoinżynieria Drog Most Tunele 2010, 25, 22–27. (In Polish) [Google Scholar]
- Nepelski, K.; Rudko, M. Identification of geotechnical parameters of Lublin loess subsoil based on CPT tests. Przegląd Nauk. Inżynieria I Kształtowanie Sr. 2018, 27, 186–198. (In Polish) [Google Scholar] [CrossRef]
- Nepelski, K.; Lal, A. CPT parameters of loess subsoil in Lublin area. Appl. Sci. 2021, 11, 6020. [Google Scholar] [CrossRef]
- Nepelski, K. Characteristics of the Lublin loess as a building subsoil. Prz. Geol. 2021, 69, 835–849. (In Polish) [Google Scholar] [CrossRef]
- Nepelski, K.; Błazik-Borowa, E.; Lipecki, T.; Bęc, J. Verification of the building FEM model on the basis of natural vibrations measurements. In Proceedings of the 3rd Polish Congress on Mechanics and 21st International Conference on Computer Methods in Mechanics, Gdańsk, Poland, 2015; Volume 1. [Google Scholar]
- Miller, H.; Djerbib, Y.; Jefferson, I.; Smalley, I. Collapse Behaviour of Loess Soils; ISRM Int. Symp., International Society for Rock Mechanics and Rock Engineering: Melbourne, VIC, Australia, 2000. [Google Scholar]
- Abed, A. Numerical Modeling of Expansive Soil Behavior. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2008. [Google Scholar]
- Helwany, S. Applied Soil Mechanics with ABAQUS Applications; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Deng, G.-H.; Shao, S.-J.; She, F.-T. Modified Cam-clay model of structured loess. Yantu Gongcheng Xuebao/Chin. J. Geotech. Eng. 2012, 34, 834–841. [Google Scholar]
- MAšíN, D. Hypoplastic Cam-Clay model. Géotechnique 2012, 62, 549–553. [Google Scholar] [CrossRef] [Green Version]
- Roscoe, K.H.; Burland, J.B. On the generalized stress-strain behaviour of ’wet’ clay. Eng. Plast Cambridge Univ. 1968, 535–609. [Google Scholar]
- Burland, J.B. Deformation of Soft Clay; University of Cambridge: Cambridge, UK, 1967. [Google Scholar]
- Schofield, A.; Wroth, P. Critical State Soil Mechanics; McGraw-Hill: London, UK; New York, NY, USA, 1968. [Google Scholar] [CrossRef]
- Lechowicz, Z.; Szymański, A. Deformation and Stability of Embankments on Organic Soils Part II. Calculation Methodology; SGGW: Warsaw, Poland, 2002. (In Polish) [Google Scholar]
- PN-EN 1992-1-1:2008/NA:2010; Eurocode 2, Design of concrete structures—Part 1-1: General rules and rules for buildings. European Standard; Polski Komitet Normalizacyjny: Warsaw, Poland, 2010.
- EN 1996-1-1; Eurocode 6: Design of masonry structures—Part 1-1: General rules for reinforced and unreinforced masonry structures. Polski Komitet Normalizacyjny: Warsaw, Poland, 2010.
- Fedorowicz, L. Building Structure—Subsoil Contact Task Part I Criteria for Modeling-Process and Analyses Carried out for the Basic Contact Tasks Building Structure—Subsoil; Zeszyty naukowe Politechniki Śląskiej: Gliwice, Poland, 2006. (In Polish) [Google Scholar]
- Nepelski, K. Selection of Cam-clay model parameters for loess subsoil as exemplified by a FEM 3D analysis of a wide building. ACTA Sci. Pol.—Archit. Bud. 2020, 19, 67–81. (In Polish) [Google Scholar] [CrossRef]
- PN-EN 1997-1; Eurokod 7 Geotechnical Design. General Rules. Polski Komitet Normalizacyjny: Warsaw, Poland, 2008.
- Grabowska-Olszewska, B. Physical and mechanical properties of loess deposits of the northern and north-eastern part of the Świętokrzyskie loess zone against the background of their lithology and stratigraphy and conditions of occurrence. Biul. Geol. 1963, 3, 68–183. (In Polish) [Google Scholar]
- Kolano, M.; Cała, M. Loess from Sandomierz area in the light of engineering-geological research. Górnictwo i Geoinżynieria 2011, 2, 349–358. (In Polish) [Google Scholar]
- Malinowski, J. Results of geotechnical investigations of loess between Kazimierz Dolny and Nałęczów (Lublin upland). Kwart Geol. 1959, 3, 425–456. (In Polish) [Google Scholar]
- Malinowski, J. Engineering-Geological Loess Research; Wydawnictwo Geologiczne: Warsaw, Poland, 1971. (In Polish) [Google Scholar]
- Frankowski, Z.; Majer, E.; Pietrzykowski, P. Geological and geotechnical problems of loess deposits from south-eastern Poland. In Proceedings of the International Geotechnical Conference Geotechnical Challenges Megacities, Moscow, Poland, 2010; Volume 2, pp. 546–553. [Google Scholar]
- Frankowski, Z.; Grabowski, D. Engineering-geological and geomorphological conditions of gully erosion in loess deposits in the Kazimierz Dolny area (Opolska Droga Gully). Przegląd Geol. 2006, 54, 777–783. (In Polish) [Google Scholar]
- Santrač, P.; Bajić, Ž.; Grković, S.; Kukaras, D.; Hegediš, I. Analysis of Calculated and Observed Settlements Od the Silo on Loess. Teh. Vjesn. 2015, 22, 539–545. [Google Scholar] [CrossRef]
- Luo, L.; Wang, X.; Xue, C.; Wang, D.; Lian, B. Laboratory Experiments and Numerical Simulation Study of Composite-Material-Modified Loess Improving High-Speed Railway Subgrade. Polymers 2022, 14, 3215. [Google Scholar] [CrossRef]



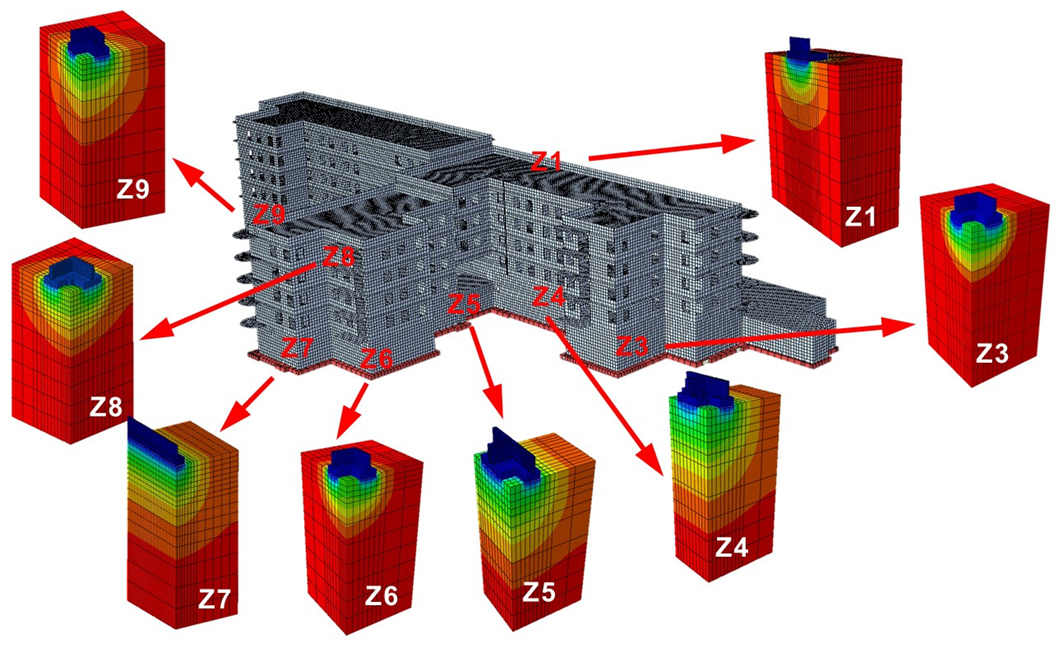
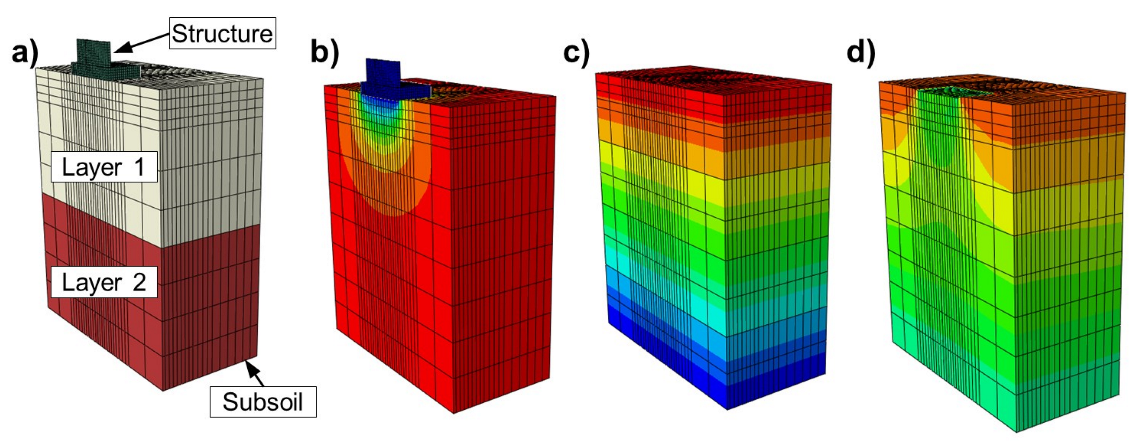

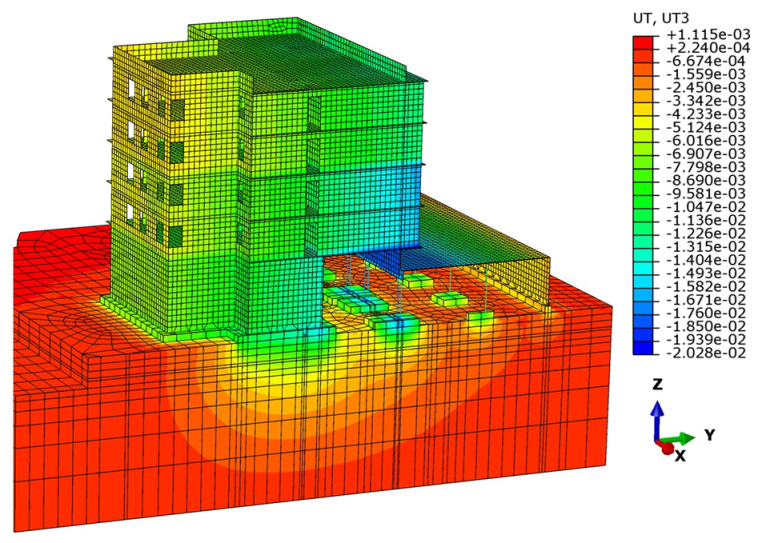
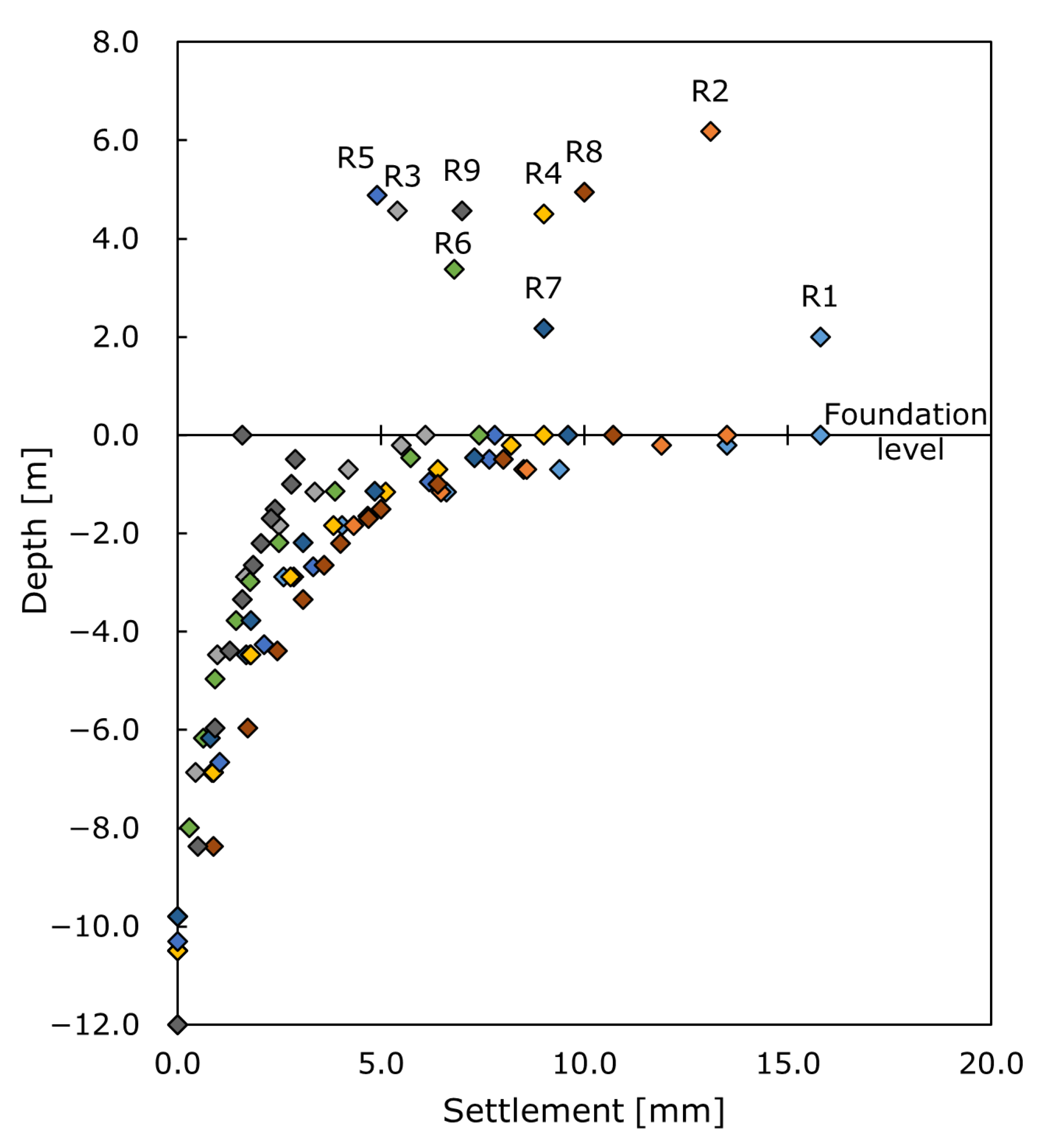
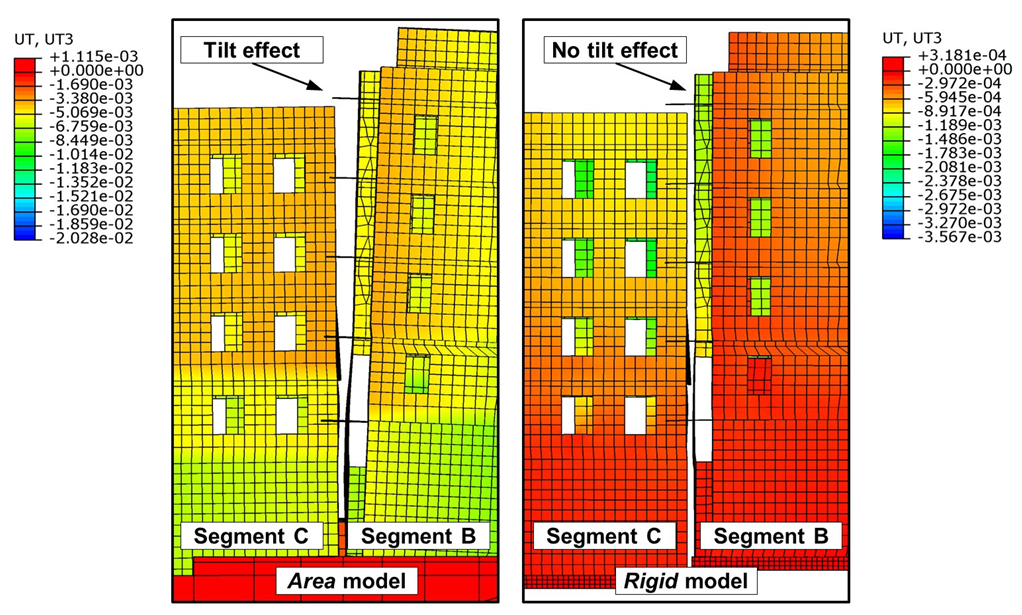
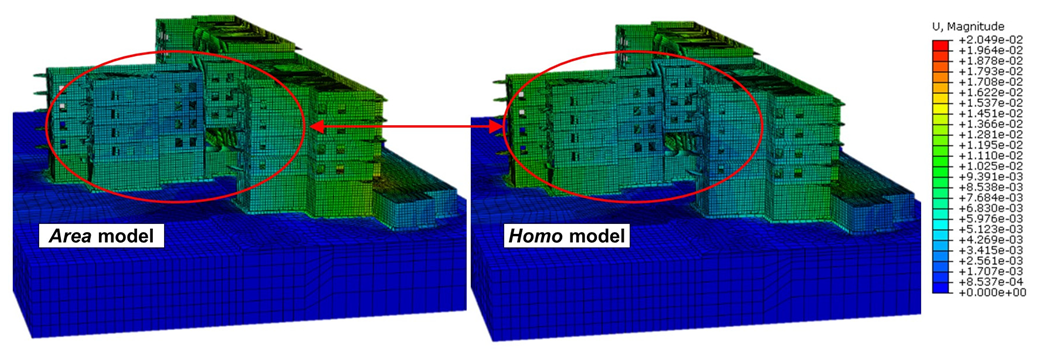
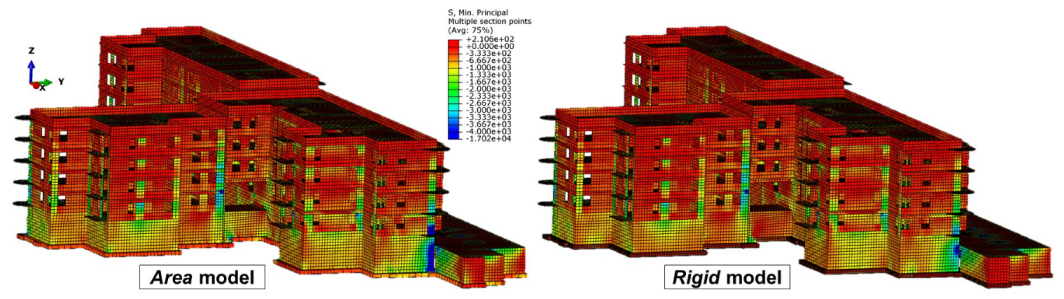

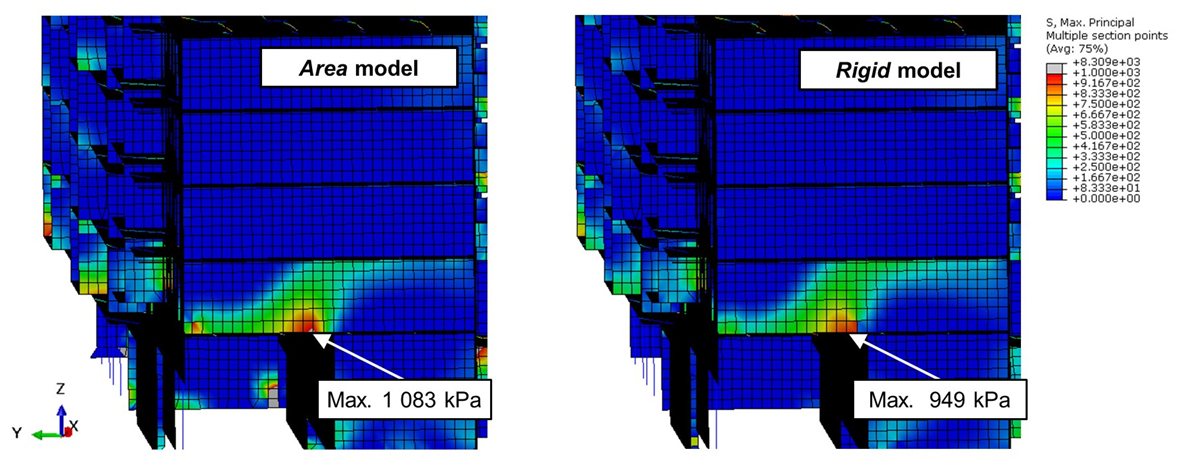
| Phase | Date of the Measurement | Period Since the “Zero” Measurement | Stage of Construction | Description of Loads for the Numerical Model | ||
|---|---|---|---|---|---|---|
| 0 | 05.2014 | 0 | SEGMENT A ceiling above the first floor | SEGMENT B ceiling above the ground floor | SEGMENT C ceiling above the ground floor and walls of the floor | Dead load,
|
| 1 | 10.2014 | 5 months | Construction works finished | Dead load,
| ||
| 2 | 07.2015 | 14 months | The building completed and commissioned | Dead load, load on internal ceilings:
| ||
| 3 | 07.2016 | 26 months | Building used for 1 year | Dead load, load on internal ceilings:
| ||
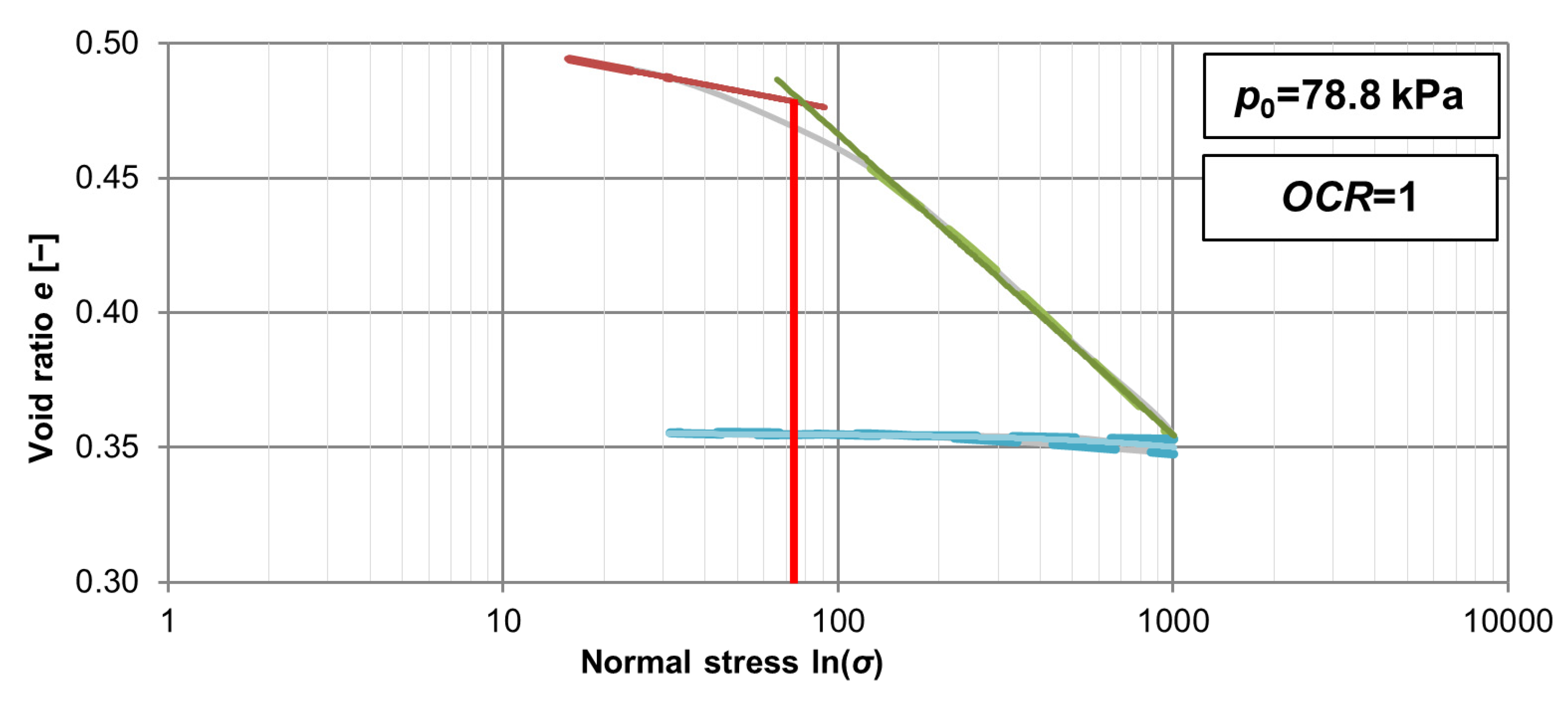
| Parameter | λ | κ | M | a0 | p0 | e1 | e0 |
|---|---|---|---|---|---|---|---|
| Sample 1 | 0.0586 | 0.0017 | 1.495 | 37.0 | 84.4 | 0.638 | 0.378 |
| Sample 2 | 0.0607 | 0.0012 | 1.495 | 33.1 | 72.1 | 0.538 | 0.278 |
| Sample 3 | 0.0485 | 0.0015 | 1.495 | 34.4 | 78.8 | 0.567 | 0.356 |
| Mean: | 0.0561 | 0.0015 | 1.495 | 34.5 | 77.4 | 0.584 | 0.340 |
| Variant | Description |
|---|---|
| EDO1 | Compressibility parameters from oedometric tests. Homogeneous subsoil. |
| EDO2 | Compressibility parameters from oedometric tests—modified. Homogeneous subsoil. |
| CPT1 | Initial compressibility parameters from CPT tests. Homogeneous subsoil. |
| CPT2 | Initial compressibility parameters from CPT tests. Layered subsoil. |
| DMT | Initial compressibility parameters from SDMT tests. Homogeneous subsoil. |
| Partial Model | Variant | Subsoil Layer | Cam-Clay Model Parameters | ||||||
|---|---|---|---|---|---|---|---|---|---|
| λ | κ | M | a0 | p0 | e1 | e0 | |||
| Z1 | EDO1 | 1 | 0.0561 | 0.0014 | 1.495 | 34.5 | 95 | 0.584 | 0.340 |
| EDO2 | 1 | 0.0512 | 0.0004 | 1.495 | 39.1 | 95 | 0.567 | 0.342 | |
| CPT1 | 1 | 0.0071 | 0.0014 | 1.495 | 19.3 | 95 | 0.584 | 0.552 | |
| CPT2 | 1 | 0.0071 | 0.0014 | 1.495 | 19.3 | 95 | 0.584 | 0.552 | |
| 2 | 0.0040 | 0.0014 | 1.495 | 13.1 | 209 | 0.584 | 0.565 | ||
| DMT | 1 | 0.0078 | 0.0014 | 1.495 | 20.9 | 95 | 0.584 | 0.548 | |
| Z3 | EDO1 | 1 | 0.0561 | 0.0014 | 1.495 | 35.3 | 38 | 0.584 | 0.340 |
| EDO2 | 1 | 0.0512 | 0.0004 | 1.495 | 39.4 | 38 | 0.567 | 0.342 | |
| CPT1 | 1 | 0.0075 | 0.0014 | 1.495 | 9.9 | 38 | 0.584 | 0.556 | |
| CPT2 | 1 | 0.0112 | 0.0014 | 1.495 | 9.9 | 38 | 0.584 | 0.556 | |
| 2 | 0.0075 | 0.0014 | 1.495 | 16.1 | 78 | 0.584 | 0.554 | ||
| 3 | 0.0034 | 0.0014 | 1.495 | 8.6 | 98 | 0.584 | 0.567 | ||
| DMT | 1 | 0.0052 | 0.0014 | 1.495 | 7.1 | 38 | 0.584 | 0.565 | |
| Z4 | EDO1 | 1 | 0.0561 | 0.0014 | 1.495 | 34.4 | 114 | 0.584 | 0.340 |
| EDO2 | 1 | 0.0512 | 0.0004 | 1.495 | 39.0 | 114 | 0.567 | 0.342 | |
| CPT1 | 1 | 0.0071 | 0.0014 | 1.495 | 25.1 | 114 | 0.584 | 0.546 | |
| CPT2 | 1 | 0.0071 | 0.0014 | 1.495 | 25.1 | 114 | 0.584 | 0.546 | |
| 2 | 0.0040 | 0.0014 | 1.495 | 10.8 | 152 | 0.584 | 0.566 | ||
| 3 | 0.0034 | 0.0014 | 1.495 | 25.4 | 182 | 0.584 | 0.554 | ||
| DMT | 1 | 0.0064 | 0.0014 | 1.495 | 20.2 | 114 | 0.584 | 0.554 | |
| Z5 | EDO1 | 1 | 0.0561 | 0.0014 | 1.495 | 34.7 | 76 | 0.584 | 0.340 |
| EDO2 | 1 | 0.0512 | 0.0004 | 1.495 | 39.1 | 76 | 0.567 | 0.342 | |
| CPT1 | 1 | 0.0071 | 0.0014 | 1.495 | 18.0 | 76 | 0.584 | 0.549 | |
| CPT2 | 1 | 0.0071 | 0.0014 | 1.495 | 18.0 | 76 | 0.584 | 0.549 | |
| 2 | 0.0040 | 0.0014 | 1.495 | 9.0 | 114 | 0.584 | 0.567 | ||
| DMT | 1 | 0.0064 | 0.0014 | 1.495 | 14.7 | 76 | 0.584 | 0.556 | |
| Z6 | EDO1 | 1 | 0.0561 | 0.0014 | 1.495 | 35.9 | 19 | 0.584 | 0.340 |
| EDO2 | 1 | 0.0512 | 0.0004 | 1.495 | 39.6 | 19 | 0.567 | 0.342 | |
| CPT1 | 1 | 0.0095 | 0.0014 | 1.495 | 6.0 | 19 | 0.584 | 0.558 | |
| CPT2 | 1 | 0.0095 | 0.0014 | 1.495 | 6.0 | 19 | 0.584 | 0.558 | |
| 2 | 0.0037 | 0.0014 | 1.495 | 9.9 | 133 | 0.584 | 0.566 | ||
| Z7 | EDO1 | 1 | 0.0561 | 0.0014 | 1.495 | 35.9 | 19 | 0.584 | 0.340 |
| EDO2 | 1 | 0.0512 | 0.0004 | 1.495 | 39.6 | 19 | 0.567 | 0.342 | |
| CPT1 | 1 | 0.0095 | 0.0014 | 1.495 | 6.0 | 19 | 0.584 | 0.558 | |
| CPT2 | 1 | 0.0095 | 0.0014 | 1.495 | 6.0 | 19 | 0.584 | 0.558 | |
| 2 | 0.0037 | 0.0014 | 1.495 | 9.9 | 133 | 0.584 | 0.566 | ||
| Z8 | EDO1 | 1 | 0.0561 | 0.0014 | 1.495 | 34.5 | 95 | 0.584 | 0.340 |
| EDO2 | 1 | 0.0512 | 0.0004 | 1.495 | 39.1 | 95 | 0.567 | 0.342 | |
| CPT1 | 1 | 0.0071 | 0.0014 | 1.495 | 20.9 | 95 | 0.584 | 0.548 | |
| CPT2 | 1 | 0.0071 | 0.0014 | 1.495 | 20.9 | 95 | 0.584 | 0.548 | |
| 2 | 0.0040 | 0.0014 | 1.495 | 24.6 | 133 | 0.584 | 0.550 | ||
| DMT | 1 | 0.0064 | 0.0014 | 1.495 | 17.5 | 95 | 0.584 | 0.555 | |
| Z9 | EDO1 | 1 | 0.0561 | 0.0014 | 1.495 | 34.7 | 76 | 0.584 | 0.340 |
| EDO2 | 1 | 0.0512 | 0.0004 | 1.495 | 39.1 | 76 | 0.567 | 0.342 | |
| CPT1 | 1 | 0.0052 | 0.0014 | 1.495 | 12.3 | 76 | 0.584 | 0.561 | |
| CPT2 | 1 | 0.0052 | 0.0014 | 1.495 | 12.3 | 76 | 0.584 | 0.561 | |
| 2 | 0.0080 | 0.0014 | 1.495 | 33.0 | 209 | 0.584 | 0.549 | ||
| DMT | 1 | 0.0064 | 0.0014 | 1.495 | 14.7 | 76 | 0.584 | 0.556 | |
| Partial Model (Benchmark) | Mean | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Z1 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 | Z9 | ||||
| Actual settlement | 4.0 | 7.1 | 5.8 | 5.1 | 7.2 | 7.8 | 2.3 | 5.8 | |||
| Calculated settlement | s [mm] | EDO1 | 42.9 | 45.5 | 19.7 | 10.6 | 38.3 | 49.4 | 7.1 | 28.1 | |
| EDO2 | 39.4 | 24.7 | 15.7 | 6.4 | 21.9 | 32.5 | 6.6 | 12.9 | |||
| CPT1 | 6.9 | 13.8 | 5.1 | 3.3 | 14.7 | 16.7 | 2.0 | 2.8 | |||
| CPT2 | 6.9 | 9.8 | 5.1 | 3.2 | 14.7 | 16.2 | 2.0 | 2.8 | |||
| DMT | 7.3 | 6.6 | 4.6 | 3.0 | - | - | 1.8 | 3.1 | |||
| Absolute calculation error | Δs [mm] | EDO1 | 38.9 | 38.4 | 13.9 | 5.6 | 31.1 | 41.6 | 4.8 | 22.3 | |
| EDO2 | 35.4 | 17.6 | 9.9 | 1.4 | 14.7 | 24.7 | 4.3 | 7.1 | |||
| CPT1 | 2.9 | 6.7 | −0.7 | −1.8 | 7.5 | 8.9 | −0.3 | −3.0 | |||
| CPT2 | 2.9 | 2.7 | −0.7 | −1.9 | 7.5 | 8.4 | −0.3 | −3.0 | |||
| DMT | 3.3 | −0.5 | −1.2 | −2.1 | - | - | −0.5 | −2.7 | |||
| Relative error | δ [%] | EDO1 | 77.7 | 76.8 | 27.8 | 11.1 | 62.3 | 83.2 | 9.6 | 44.5 | 49.1 |
| EDO2 | 70.7 | 35.2 | 19.8 | 2.7 | 29.5 | 49.4 | 8.6 | 14.1 | 28.8 | ||
| CPT1 | 5.7 | 13.4 | −1.4 | −3.5 | 15.1 | 17.8 | −0.6 | −6.1 | 7.9 | ||
| CPT2 | 5.7 | 5.4 | −1.4 | −3.7 | 15.1 | 16.8 | −0.6 | −6.1 | 6.8 | ||
| DMT | 6.5 | −1.0 | −2.4 | −4.1 | - | - | −1.0 | −5.5 | 3.4 | ||
| Variant | λ | κ | M | a0 | p0 | e1 | e0 | |
|---|---|---|---|---|---|---|---|---|
| HOMO | 0.0069 | 0.0014 | 1.495 | 12.0 | 59.0 | 0.584 | 0.557 | |
| AREA | AREA A | 0.0054 | 0.0014 | 1.495 | 12.3 | 76.0 | 0.584 | 0.561 |
| AREA B + D | 0.0071 | 0.0014 | 1.495 | 19.3 | 95.0 | 0.584 | 0.552 | |
| AREA C | 0.0078 | 0.0014 | 1.495 | 9.9 | 38.0 | 0.584 | 0.556 | |
| AREA E | 0.0090 | 0.0014 | 1.495 | 6.0 | 19.0 | 0.584 | 0.558 | |
| FULL MODEL OF THE BUILDING + SUBSOIL (HOMO) | ||||||||||
| Phase | Z1 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 | Z9 | Mean | |
| 1 | 4.1 | 2.3 | 4.5 | 2.5 | 1.7 | 2.4 | 4.9 | 3.5 | 3.2 | |
| 2 | 7.7 | 4.0 | 8.2 | 3.8 | 2.1 | 3.3 | 8.9 | 6.0 | 5.5 | |
| 3 | 8.8 | 4.6 | 9.3 | 4.2 | 2.2 | 3.5 | 10.2 | 6.8 | 6.2 | |
| FULL MODEL OF THE BUILDING + SUBSOIL (AREA) | ||||||||||
| Phase | Z1 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 | Z9 | Mean | |
| 1 | 4.9 | 2.0 | 5.7 | 3.0 | 2.0 | 2.8 | 2.8 | 2.3 | 3.2 | |
| 2 | 9.3 | 3.3 | 10.7 | 5.1 | 2.9 | 4.0 | 5.1 | 3.9 | 5.5 | |
| 3 | 10.5 | 3.7 | 12.1 | 5.7 | 3.2 | 4.4 | 6.0 | 4.4 | 6.2 | |
| ACTUAL SETTLEMENT | ||||||||||
| Phase | Z1 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 | Z9 | Mean | |
| 1 | 2.7 | 2.7 | 4.3 | 3.9 | 3.0 | 5.1 | 3.2 | 5.2 | 3.6 | |
| 2 | 4.2 | 6.3 | 5.2 | 5.3 | 5.7 | 7.0 | 2.3 | 6.1 | 5.3 | |
| 3 | 4.0 | 7.1 | 5.8 | 5.1 | 7.2 | 7.8 | 2.3 | 5.8 | 5.6 | |
| CALCULATION ERROR | ||||||||||
| Z1 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 | Z9 | Mean | ||
| Absolute error [mm] | HOMO | 4.8 | −2.5 | 3.5 | −0.9 | −5.0 | −4.3 | 7.9 | 1.0 | 3.74 |
| AREA | 6.5 | −3.4 | 6.3 | 0.6 | −4.0 | −3.4 | 3.7 | −1.4 | 3.66 | |
| Relative error [%] | HOMO | 9.6 | −5.0 | 7.0 | −1.8 | −10.0 | −8.6 | 15.8 | 2.0 | 7.48 |
| AREA | 13.1 | −6.8 | 12.5 | 1.2 | −8.0 | −6.9 | 7.4 | −2.8 | 7.34 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nepelski, K. 3D FEM Analysis of the Subsoil-Building Interaction. Appl. Sci. 2022, 12, 10700. https://doi.org/10.3390/app122110700
Nepelski K. 3D FEM Analysis of the Subsoil-Building Interaction. Applied Sciences. 2022; 12(21):10700. https://doi.org/10.3390/app122110700
Chicago/Turabian StyleNepelski, Krzysztof. 2022. "3D FEM Analysis of the Subsoil-Building Interaction" Applied Sciences 12, no. 21: 10700. https://doi.org/10.3390/app122110700





