GPR Data Augmentation Methods by Incorporating Domain Knowledge
Abstract
:1. Introduction
2. Methods
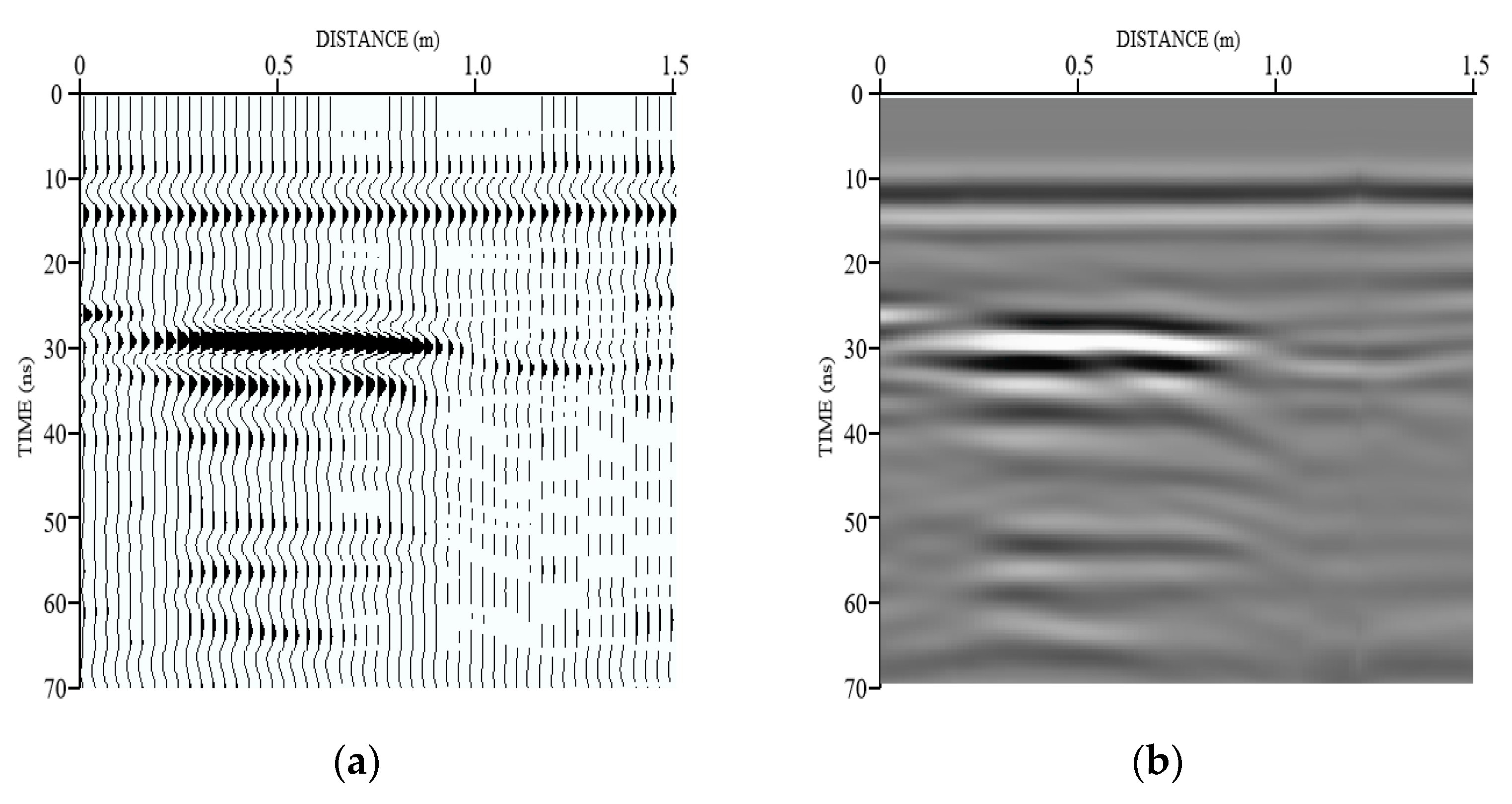
2.1. Image Brightness Transformation Based on Gain Compensation
2.2. Image Resolution Transformations Based on Station Spacing
2.3. Color Space Transformations Based on Radar Signal Mapping Rules
2.4. Deep Learning Model
3. Data Description
3.1. Field Data Collection
3.2. Data Augmentation
4. Result and Discussion
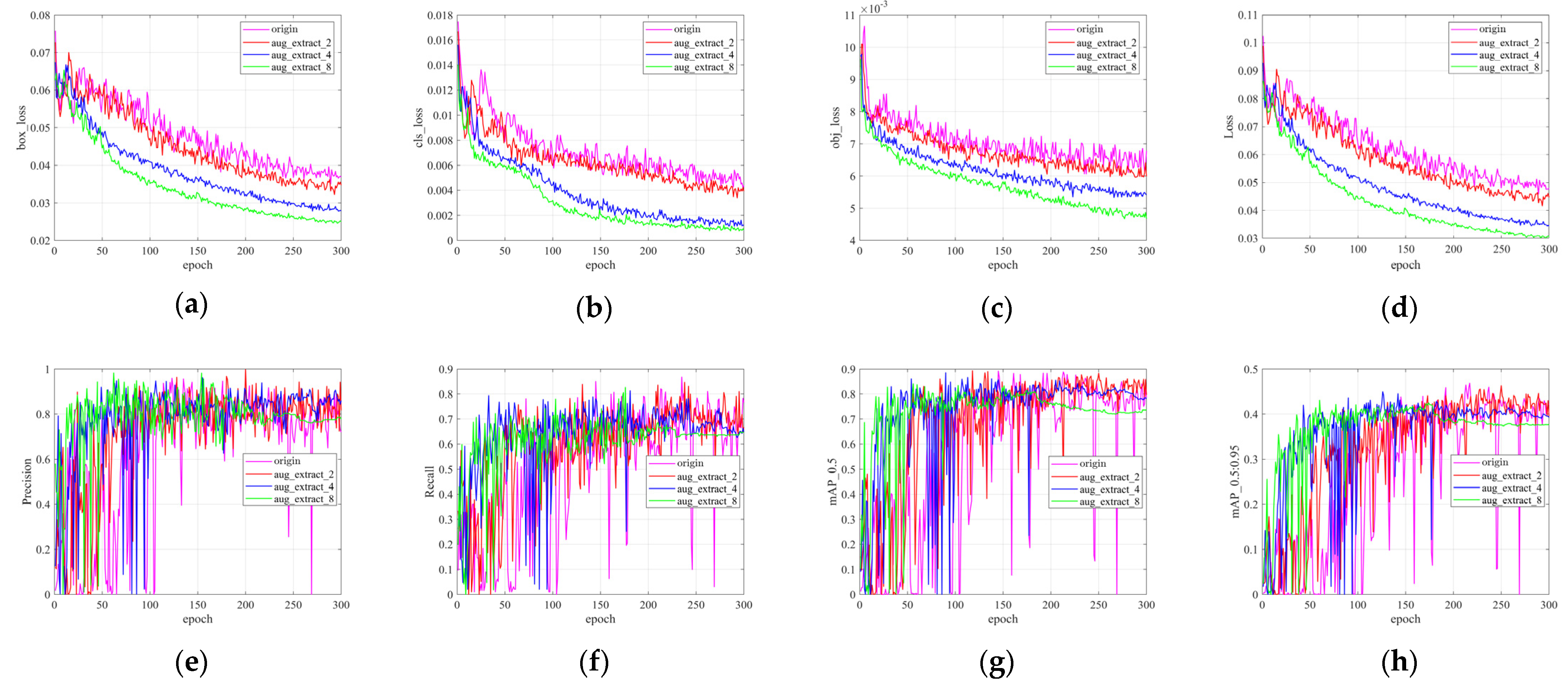
4.1. Evaluation Metrics
4.2. Training Details
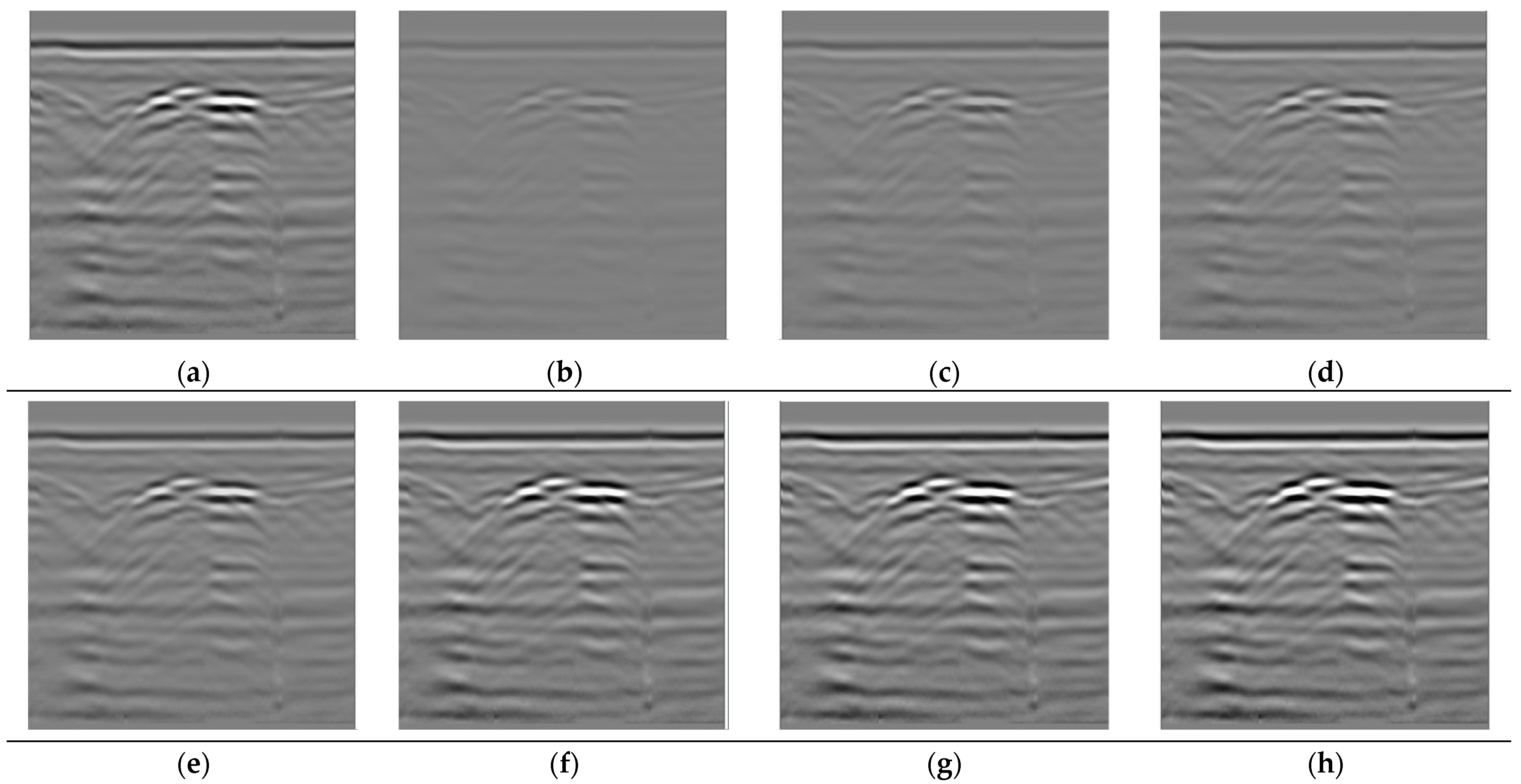
4.2.1. Image Brightness Transformation Based on Gain Compensation
4.2.2. Image Resolution Transformations Based on Station Spacing
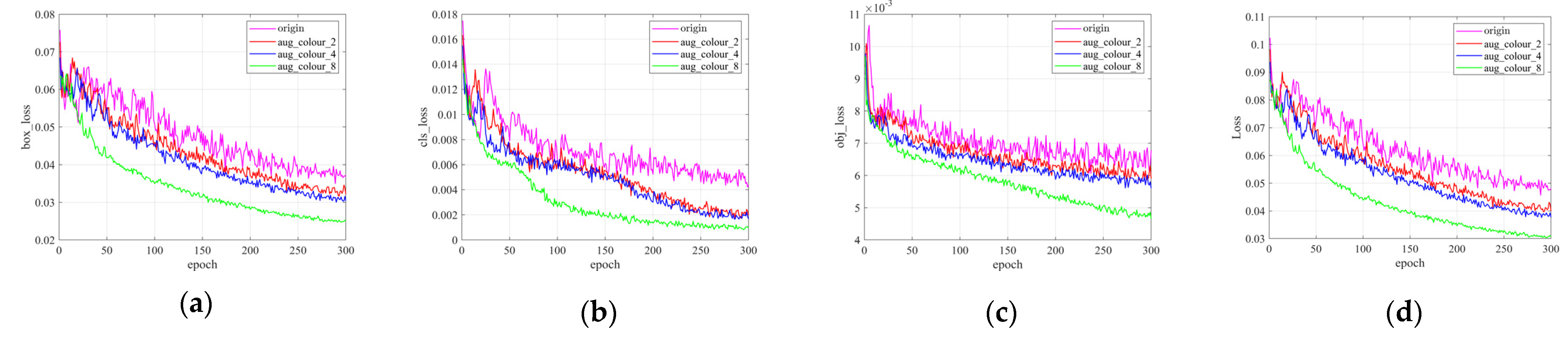
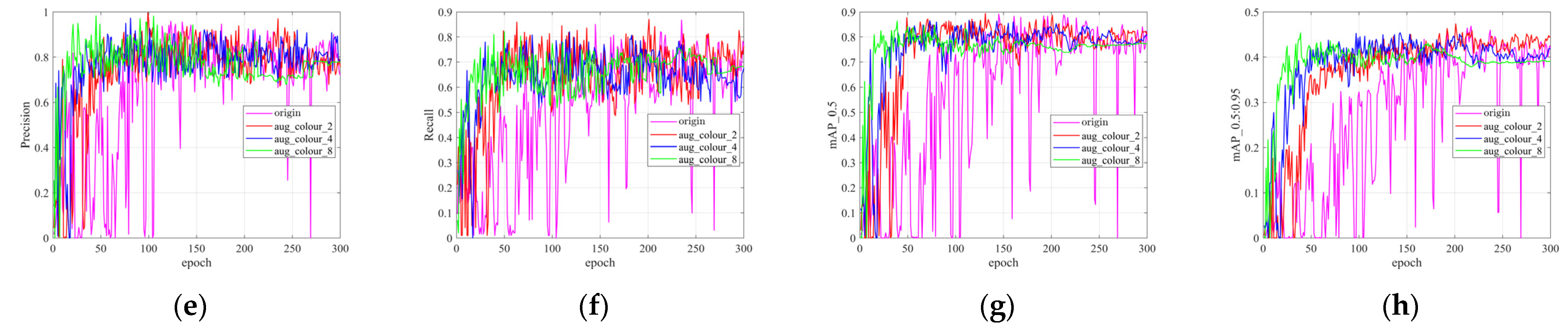
4.2.3. Color Space Transformations Based on Radar Signal Mapping Rules
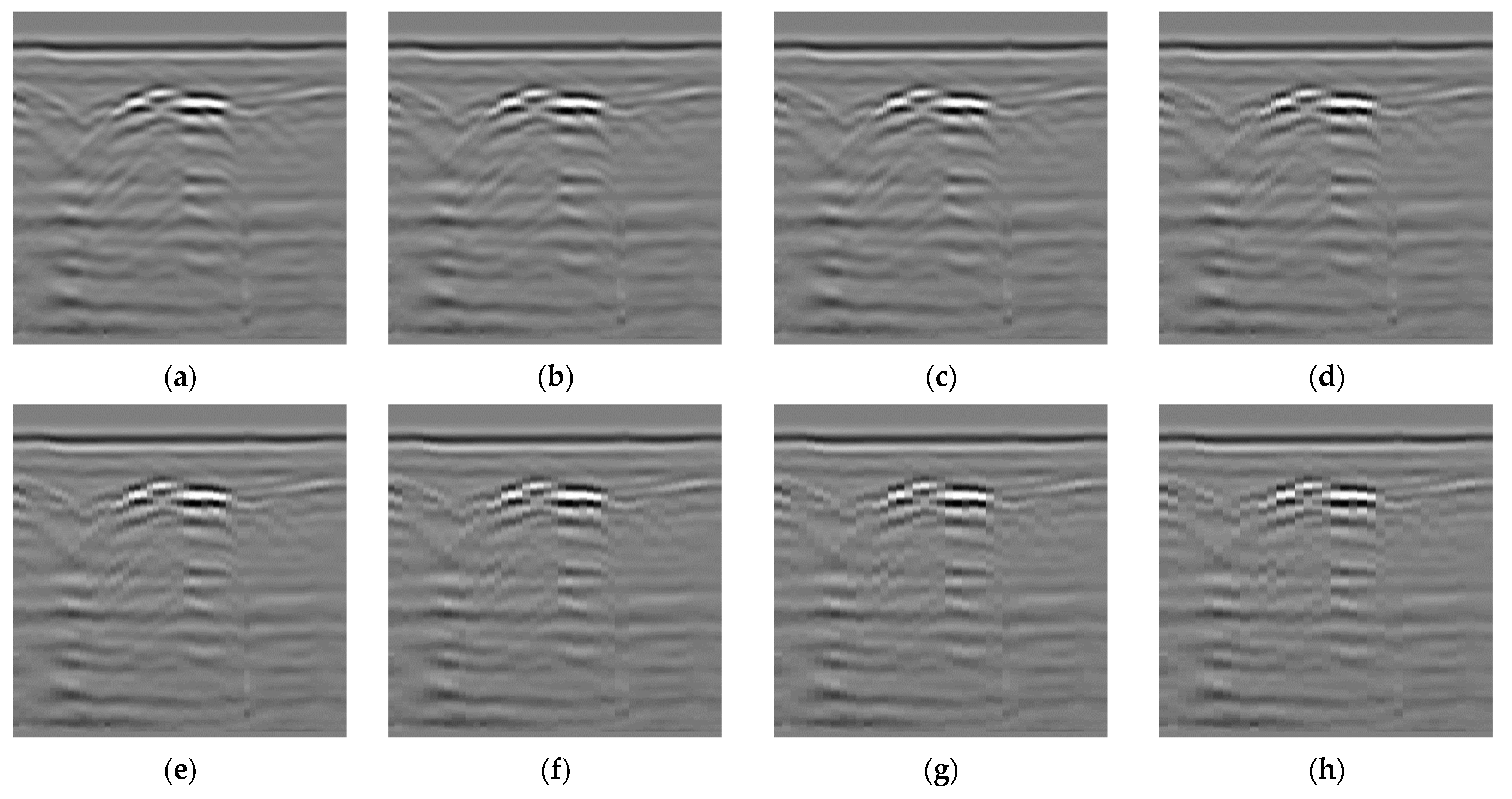
4.3. Comparative Study
4.3.1. Traditional Data Augmentation Methods
4.3.2. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Wu, D.; Li, Y.; Du, Y. Large-scale pavement roughness measurements with vehicle crowdsourced data using semi-supervised learning. Transp. Res. Part C Emerg. Technol. 2021, 125, 103048. [Google Scholar] [CrossRef]
- Du, Y.; Weng, Z.; Li, F.; Ablat, G.; Wu, D.; Liu, C. A novel approach for pavement texture characterisation using 2D-wavelet decomposition. Int. J. Pavement Eng. 2022, 23, 1851–1866. [Google Scholar] [CrossRef]
- Liu, C.; Nie, T.; Du, Y.; Cao, J.; Wu, D.; Li, F. A Response-Type Road Anomaly Detection and Evaluation Method for Steady Driving of Automated Vehicles. IEEE T. Intell. Transp. 2022, 1–12. [Google Scholar] [CrossRef]
- Yue, G.; Du, Y.; Liu, C.; Guo, S.; Li, Y.; Gao, Q. Road subsurface distress recognition method using multiattribute feature fusion with ground penetratin gradar. Int. J. Pavement Eng. 2022, 1–13. [Google Scholar] [CrossRef]
- Peng, M.; Wang, D.; Liu, L.; Shi, Z.; Shen, J.; Ma, F. Recent Advances in the GPR Detection of Grouting Defects behind Shield Tunnel Segments. Remote Sens. 2021, 13, 4596. [Google Scholar] [CrossRef]
- Guo, S.; Xu, Z.; Li, X.; Zhu, P. Detection and Characterization of Cracks in Highway Pavement with the Amplitude Variation of GPR Diffracted Waves: Insights from Forward Modeling and Field Data. Remote Sens. 2022, 14, 976. [Google Scholar] [CrossRef]
- Benedetto, A.; Tosti, F.; Bianchini Ciampoli, L.; D Amico, F. An overview of ground-penetrating radar signal processing techniques for road inspections. Signal Process. 2017, 132, 201–209. [Google Scholar] [CrossRef]
- Lei, W.; Hou, F.; Xi, J.; Tan, Q.; Xu, M.; Jiang, X.; Liu, G.; Gu, Q. Automatic hyperbola detection and fitting in GPR B-scan image. Automat. Constr. 2019, 106, 102839. [Google Scholar] [CrossRef]
- Hwang, J.; Kim, D.; Li, X.; Min, D. Polarity Change Extraction of GPR Data for Under-road Cavity Detection: Application on Sudeoksa Testbed Data. J. Environ. Eng. Geoph. 2019, 24, 419–431. [Google Scholar] [CrossRef]
- Frigui, H.; Gader, P. Detection and Discrimination of Land Mines in Ground-Penetrating Radar Based on Edge Histogram Descriptors and a Possibilistic K-Nearest Neighbor Classifier. IEEE Trans. Fuzzy Syst. 2009, 17, 185–199. [Google Scholar] [CrossRef]
- Todkar, S.S.; Le Bastard, C.; Baltazart, V.; Ihamouten, A.; Dérobert, X. Performance assessment of SVM-based classification techniques for the detection of artificial debondings within pavement structures from stepped-frequency A-scan radar data. NDT E Int. 2019, 107, 102128. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, J.; Sun, W. Recognition of the Typical Distress in Concrete Pavement Based on GPR and 1D-CNN. Remote Sens. 2021, 13, 2375. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Yuan, D.; Tong, Z.; Yang, J.; Yu, D. Autonomous pavement distress detection using ground penetrating radar and region-based deep learning. Measurement 2020, 164, 108077. [Google Scholar] [CrossRef]
- Hou, F.; Lei, W.; Li, S.; Xi, J.; Xu, M.; Luo, J. Improved Mask R-CNN with distance guided intersection over union for GPR signature detection and segmentation. Automat. Constr. 2021, 121, 103414. [Google Scholar] [CrossRef]
- Chen, S.; Wang, L.; Fang, Z.; Shi, Z.; Zhang, A. A Ground-penetrating Radar Object Detection Method Based on Deep Learning. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 18–20 August 2021; pp. 110–113. [Google Scholar] [CrossRef]
- Li, X.; Liu, H.; Zhou, F.; Chen, Z.; Giannakis, I.; Slob, E. Deep learning-based nondestructive evaluation of reinforcement bars using ground penetrating radar and electromagnetic induction data. Comput. Aided Civ. Inf. 2021. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot Multi Box Detector. In Proceedings of European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Berlin, Germany, 2016; pp. 21–37. [Google Scholar] [CrossRef] [Green Version]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Duan, K.; Bai, S.; Xie, L.; Qi, H.; Huang, Q.; Tian, Q. CenterNet: Keypoint Triplets for Object Detection. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 6568–6577. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.B.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 318–327. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Bochkovskiy, A.; Liao, H.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. arXiv 2022, arXiv:2207.02696. [Google Scholar]
- Li, Y.; Che, P.; Liu, C.; Wu, D.; Du, Y. Cross-scene pavement distress detection by a novel transfer learning framework. Comput. Aided Civ. Inf. 2021, 36, 1398–1415. [Google Scholar] [CrossRef]
- Bralich, J.; Reichman, D.; Collins, L.; Malof, J. Improving convolutional neural networks for buried target detection in ground penetrating radar using transfer learning via pretraining. In Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XXII; International Society for Optics and Photonics: Anaheim, CA, USA, 2017; p. 101820X. [Google Scholar] [CrossRef]
- Ozkaya, U.; Ozturk, S.; Melgani, F.; Seyfi, L. Residual CNN plus Bi-LSTM model to analyze GPR B scan images. Automat. Constr. 2021, 123, 103525. [Google Scholar] [CrossRef]
- Qin, H.; Zhang, D.; Tang, Y.; Wang, Y. Automatic recognition of tunnel lining elements from GPR images using deep convolutional networks with data augmentation. Automat. Constr. 2021, 130, 103830. [Google Scholar] [CrossRef]
- Perez, L.; Wang, J. The Effectiveness of Data Augmentation in Image Classification using Deep Learning. arXiv 2017, arXiv:1712.04621. [Google Scholar]
- Liu, H.; Lin, C.; Cui, J.; Fan, L.; Xie, X.; Spencer, B.F. Detection and localization of rebar in concrete by deep learning using ground penetrating radar. Automat. Constr. 2020, 118, 103279. [Google Scholar] [CrossRef]
- Buslaev, A.; Iglovikov, V.I.; Khvedchenya, E.; Parinov, A.; Druzhinin, M.; Kalinin, A.A. Albumentations: Fast and Flexible Image Augmentations. Information 2020, 11, 125. [Google Scholar] [CrossRef] [Green Version]
- Zong, Z.; Chen, C.; Mi, X.; Sun, W.; Song, Y.; Li, J.; Dong, Z.; Huang, R.; Yang, B. A Deep Learning Approach for Urban Underground Objects Detection from Vehicle-Borne Ground Penetrating Radar Data in Real-Time. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Munich, Germany, 18–20 September 2019; Volume 42, pp. 293–299. [Google Scholar] [CrossRef] [Green Version]
- Sonoda, J.; Kimoto, T. Object Identification form GPR Images by Deep Learning. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), Kyoto, Japan, 6–9 November 2018; pp. 1298–1300. [Google Scholar] [CrossRef]
- Veal, C.; Dowdy, J.; Brockner, B.; Anderson, D.T.; Ball, J.E.; Scott, G. Generative adversarial networks for ground penetrating radar in hand held explosive hazard detection. In Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XXIII; SPIE: Orlando, FL, USA, 2018; p. 106280T. [Google Scholar] [CrossRef]
- Li, J.; Madry, A.; Peebles, J.; Schmidt, L. On the Limitations of First-Order Approximation in GAN Dynamics. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 3005–3013. [Google Scholar]
- Chen, G.; Bai, X.; Wang, G.; Wang, L.; Luo, X.; Ji, M.; Feng, P.; Zhang, Y. Subsurface Voids Detection from Limited Ground Penetrating Radar Data Using Generative Adversarial Network and YOLOV5. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 12 October 2021; pp. 8600–8603. [Google Scholar] [CrossRef]
- Bianchini Ciampoli, L.; Tosti, F.; Economou, N.; Benedetto, F. Signal Processing of GPR Data for Road Surveys. Geosciences 2019, 9, 96. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Yue, G.; Gao, Q.; Du, Y. Deep learning-based pavement subsurface distress detection via ground penetrating radar data. Automat. Constr. 2022, 142, 104516. [Google Scholar] [CrossRef]
- Verdonck, L.; Taelman, D.; Vermeulen, F.; Docter, R. The Impact of Spatial Sampling and Migration on the Interpretation of Complex Archaeological Ground-penetrating Radar Data. Archaeol. Prospect. 2015, 22, 91–103. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, H.; Guo, S.; Zhang, L. Efficient Long Range Attention Network for Image Super resolution. arXiv 2022, arXiv:2203.06697. [Google Scholar]
- Kasper-Eulaers, M.; Hahn, N.; Berger, S.; Sebulonsen, T.; Myrland, Ø.; Kummervold, P.E. Short Communication: Detecting Heavy Goods Vehicles in Rest Areas in Winter Conditions Using YOLOv5. Algorithms 2021, 14, 114. [Google Scholar] [CrossRef]
- Reichman, D.; Collins, L.M.; Malof, J.M. Some good practices for applying convolutional neural networks to buried threat detection in Ground Penetrating Radar. In Proceedings of the 2017 9th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Edinburgh, UK, 28–30 June 2017; pp. 1–5. [Google Scholar] [CrossRef]





| Roads | Urban Road | Highway | |||||
|---|---|---|---|---|---|---|---|
| Location | Zhengzhou Henan | Kaifeng Henan | Xi’an Shaanxi | Huainan Anhui | Anyang Henan | Ningbo Zhejiang | |
| Surfaces | Upper layers | 4 cm AC-16C | 4 cm AC-13C | 4 cm AC-13C | 4 cm AC-13C | 4 cm AC-13C | 4 cm SMA-13 |
| Middle layers | / | / | / | / | 6 cm AC-16C | 6 cm AC-16C | |
| Lower layers | 6 cm AC-20C | 6 cm AC-16C | 6 cm AC-16C | 6 cm AC-16C | 9 cm AC-20C | 10 cm ATB-25 | |
| Bases | Upper bases | 18 cm Cement stabilized gavels | 18 cm Cement stabilized gavels | 20 cm Cement stabilized gavels | 8 cm Cement stabilized gavels | 18 cm Cement stabilized gavels | 20 cm Cement stabilized gavels |
| Lower Bases | 18 cm cement stabilized gavels | 18 cm cement stabilized gavels | 20 cm cement stabilized gavels | 20 cm Granular | 18 cm cement stabilized gavels | 20 cm cement stabilized gavels | |
| Training Set | Validation Set | Testing Set | |
|---|---|---|---|
| The number of cavities | 312 | 48 | 48 |
| The number of cracks | 271 | 63 | 63 |
| The number of images | 547 | 108 | 108 |
| Augmentations | Gain Compensation | Station Spacing | Radar Signal Imaging | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 Times | 4 Times | 8 Times | 2 Times | 4 Times | 8 Times | 2 Times | 4 Times | 8 Times | |
| The number of cavities | 624 | 1248 | 2496 | 624 | 1248 | 2496 | 624 | 1248 | 2496 |
| The number of cracks | 542 | 1084 | 2168 | 542 | 1084 | 2168 | 542 | 1084 | 2168 |
| The number of images | 1094 | 2188 | 4376 | 1094 | 2188 | 4376 | 1094 | 2188 | 4376 |
| Parameters | Configuration |
|---|---|
| System environment | Linux |
| GPU | NVIDIA GTX 1080Ti |
| GPU acceleration | CUDA 10.1 |
| Training framework | Pytorch 1.12.1 |
| Language | Python 3.9.12 |
| Augmentations | Original | Gain Compensation | Station Spacing | Radar Signal Mapping Rules | Traditional Method | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cavity | Crack | All | Cavity | Crack | All | Cavity | Crack | All | Cavity | Crack | All | Cavity | Crack | All | |
| precision | 0.584 | 0.912 | 0.748 | 0.747 | 0.922 | 0.835 | 0.769 | 0.879 | 0.824 | 0.763 | 0.899 | 0.831 | 0.663 | 0.849 | 0.756 |
| recall | 0.791 | 0.619 | 0.705 | 0.854 | 0.713 | 0.784 | 0.833 | 0.623 | 0.728 | 0.821 | 0.652 | 0.737 | 0.778 | 0.649 | 0.714 |
| F1_score | 0.672 | 0.737 | 0.726 | 0.797 | 0.804 | 0.809 | 0.800 | 0.729 | 0.773 | 0.791 | 0.756 | 0.781 | 0.716 | 0.736 | 0.734 |
| mAP_0.5 | 0.731 | 0.820 | 0.776 | 0.796 | 0.827 | 0.811 | 0.811 | 0.781 | 0.796 | 0.797 | 0.819 | 0.808 | 0.815 | 0.749 | 0.782 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, G.; Liu, C.; Li, Y.; Du, Y.; Guo, S. GPR Data Augmentation Methods by Incorporating Domain Knowledge. Appl. Sci. 2022, 12, 10896. https://doi.org/10.3390/app122110896
Yue G, Liu C, Li Y, Du Y, Guo S. GPR Data Augmentation Methods by Incorporating Domain Knowledge. Applied Sciences. 2022; 12(21):10896. https://doi.org/10.3390/app122110896
Chicago/Turabian StyleYue, Guanghua, Chenglong Liu, Yishun Li, Yuchuan Du, and Shili Guo. 2022. "GPR Data Augmentation Methods by Incorporating Domain Knowledge" Applied Sciences 12, no. 21: 10896. https://doi.org/10.3390/app122110896
APA StyleYue, G., Liu, C., Li, Y., Du, Y., & Guo, S. (2022). GPR Data Augmentation Methods by Incorporating Domain Knowledge. Applied Sciences, 12(21), 10896. https://doi.org/10.3390/app122110896






