Topology Optimization Based Material Design for 3D Domains Using MATLAB
Abstract
:1. Introduction
2. Design of Materials by Means of STO
3. Model Order Reduction in Material Design Optimization
3.1. Proper Orthogonal Decomposition
3.2. On-the-Fly Reduced Order Model Construction
3.3. Approximate Reanalysis
4. The MATLAB Code Implementation
4.1. The Seven Components of the UCOpt3D Function
4.1.1. Initialization Section



4.1.2. Interpolation Section

4.1.3. Homogenization Section


 where Young’s modulus is used to compute instead of the lame parameters. In order to specify the active degrees of freedom, 58 of the original function is modified as follows:
where Young’s modulus is used to compute instead of the lame parameters. In order to specify the active degrees of freedom, 58 of the original function is modified as follows:  where a small value for Young’s modulus is utilized instead of the matrix. Finally, for implementing the calculation part of the derivative for the homogenized elasticity tensor , a cell array of the unit cell dimensions is created first and then initialized as follows:
where a small value for Young’s modulus is utilized instead of the matrix. Finally, for implementing the calculation part of the derivative for the homogenized elasticity tensor , a cell array of the unit cell dimensions is created first and then initialized as follows: 

4.1.4. Finite Element Analysis Section
 where a, b, and c are the element dimensions and C is the elasticity tensor. The homogenized elasticity tensor provided by the homogenization formulation is provided as the input argument for the hexahedronElem function as follows:
where a, b, and c are the element dimensions and C is the elasticity tensor. The homogenized elasticity tensor provided by the homogenization formulation is provided as the input argument for the hexahedronElem function as follows: 
4.1.5. Objective Function—Sensitivity Analysis, Filtering, and Update Scheme Sections



 where a, b, and c are the half dimensions of the element in the x, y, and z dimensions. During the creation of the class through its constructor, i.e., the class method called initialize is called, and its results is then stored inside the class as follows:
where a, b, and c are the half dimensions of the element in the x, y, and z dimensions. During the creation of the class through its constructor, i.e., the class method called initialize is called, and its results is then stored inside the class as follows:  where variables and B are the weight and strain-displacement matrix of each Gauss point as computed in 102 to 139 of the hexahedron function of the original homo3D code. Thus, class method initialize contains the implementation of these . Two instances of the hexahedron class are utilized in this formulation, one for the topology optimization part and one for the homogenization one. The creation of these instances is performed in the initialization stage and they are replacing 24 of the UCOpt3D function as follows:
where variables and B are the weight and strain-displacement matrix of each Gauss point as computed in 102 to 139 of the hexahedron function of the original homo3D code. Thus, class method initialize contains the implementation of these . Two instances of the hexahedron class are utilized in this formulation, one for the topology optimization part and one for the homogenization one. The creation of these instances is performed in the initialization stage and they are replacing 24 of the UCOpt3D function as follows: 





 where is the instance of the hexahedron class. To compute the element stiffness matrix using the class instance inside the homo3D function, 12 has to be replaced, as follows:
where is the instance of the hexahedron class. To compute the element stiffness matrix using the class instance inside the homo3D function, 12 has to be replaced, as follows: 
 where the following section is implemented inside the update scheme as follows:
where the following section is implemented inside the update scheme as follows: 
4.2. Model Order Reduction: Code Implementation



 where defines the MOR model used in the finite element analysis on the macro scale and denotes which MOR model is used inside the homogenization method, i.e., on the micro scale. Next 87 of the UCOpt3D function is replaced with the following , applying MOR for performing the finite element analysis part:
where defines the MOR model used in the finite element analysis on the macro scale and denotes which MOR model is used inside the homogenization method, i.e., on the micro scale. Next 87 of the UCOpt3D function is replaced with the following , applying MOR for performing the finite element analysis part: 


 where is the number of active degrees of freedom and is the reduced basis matrix of the MOR model. The second method called reinitialize basically resets the MOR model without the need to recreate the model class. For the case of the Approximate Reanalysis model, this is achieved as follows:
where is the number of active degrees of freedom and is the reduced basis matrix of the MOR model. The second method called reinitialize basically resets the MOR model without the need to recreate the model class. For the case of the Approximate Reanalysis model, this is achieved as follows: 
 whereas for the on-the-fly approach, the implementation of the reinitialize method is as follows:
whereas for the on-the-fly approach, the implementation of the reinitialize method is as follows: 


5. Test Examples
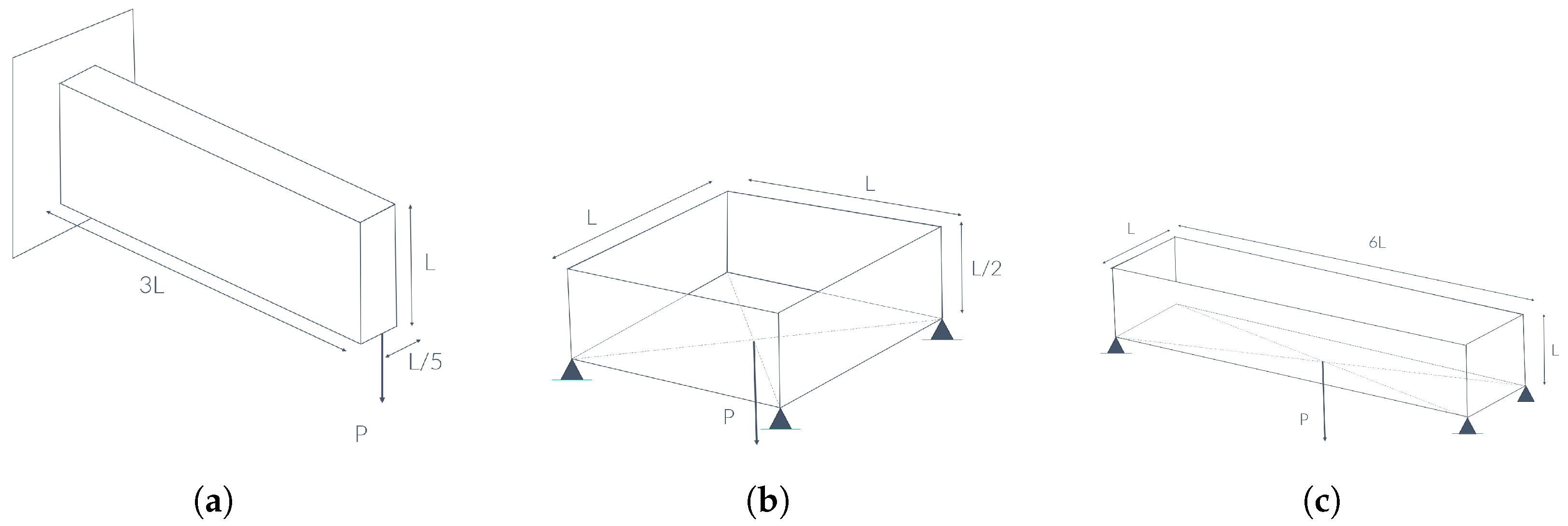
5.1. 3D Cantilever Test Example

 whereas for the implementation of the approximate reanalysis approach, 1 and 2 of the above script have to be replaced, as follows:
whereas for the implementation of the approximate reanalysis approach, 1 and 2 of the above script have to be replaced, as follows: 
 whereas for the boundary conditions, 14 to 17 of the UCOpt3D function are set as follows:
whereas for the boundary conditions, 14 to 17 of the UCOpt3D function are set as follows: 
5.2. 3D Wheel Test Example

5.3. MBB Beam Test Example

6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FE | Finite Element |
| FEA | Finite Element Analysis |
| MOR | Model Order Reduction |
| POD | Proper Orthogonal Decomposition |
| SIMP | Solid Isotropic Material with Penalization |
| STO | Structural Topology Optimization |
| SVD | Singular Value Decomposition |
References
- Sigmund, O. A 99 line topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, F.; Sigmund, O. A new generation 99 line Matlab code for compliance topology optimization and its extension to 3D. Struct. Multidiscip. Optim. 2020, 62, 2211–2228. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y. A futher review of ESO type methods for topology optimization. Struct. Multidiscip. Optim. 2010, 41, 671–683. [Google Scholar] [CrossRef]
- Challis, V.J. A discrete level-set topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2010, 41, 453–464. [Google Scholar] [CrossRef]
- Wang, M.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Otomori, M.; Yamada, T.; Izui, K.; Nishiwaki, S. Matlab code for a level-set based topology optimization method using a reaction diffusion equation. Struct. Multidiscip. Optim. 2014, 51, 1159–1172. [Google Scholar] [CrossRef] [Green Version]
- Wei, P.; Li, Z.; Li, X.; Wang, M.Y. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions. Struct. Multidiscip. Optim. 2018, 58, 831–849. [Google Scholar] [CrossRef]
- Talischi, C.; Paulino, G.H.; Pereira, A.; Menezes, I.F.M. PolyTop: A Matlab implementation of a general topology optimization framework using unstructured polygonal finite element meshes. Struct. Multidiscip. Optim. 2012, 45, 329–357. [Google Scholar] [CrossRef]
- Chi, H.; Pereira, A.; Meneze, I.F.M.; Paulino, G.H. Virtual element method (VEM)-based topology optimization: An intergrated framework. Struct. Multidiscip. Optim. 2020, 62, 1089–1114. [Google Scholar] [CrossRef]
- Andreassen, E.; Andreasen, C.S. How to determine composite material properties using numerical homogenization. Comput. Mater. Sci. 2014, 83, 488–495. [Google Scholar] [CrossRef] [Green Version]
- Guoying, D.; Yunlong, T.; Yaoyao, F.Z. A 149 Line Homogenization Code for Three-Dimensional Cellular Materials Written in Matlab. J. Eng. Mater. Technol. 2018, 141, 488–495. [Google Scholar] [CrossRef]
- Gao, J.; Luo, Z.; Xia, L.; Gao, L. Concurrent topology optimization of multiscale composite structures in Matlab. Struct. Multidiscip. Optim. 2019, 60, 2621–2651. [Google Scholar] [CrossRef]
- Amir, O.; Aage, N.; Lazarov, B.S. On multigrid-CG for efficient topology optimization. Struct. Multidiscip. Optim. 2014, 419, 815–829. [Google Scholar] [CrossRef]
- Amir, O. Revisiting approximate reanalysis in topology optimization: On the advantages of recycled preconditioning in a minimum weight procedure. Struct. Multidiscip. Optim. 2014, 51, 41–57. [Google Scholar] [CrossRef]
- Kazakis, G.; Lagaros, N.D. A Simple Matlab Code for Material Design Optimization Using Reduced Order Models. Materials 2022, 15, 4972. [Google Scholar] [CrossRef]
- Kazakis, G.; Kanellopoulos, I.; Sotiropoulos, S.; Lagaros, N.D. Topology optimization aided structural design: Interpretation, computational aspects and 3D printing. Heliyon 2017, 3, e00431. [Google Scholar] [CrossRef]
- Rogkas, N.; Vakouftsis, C.; Spitas, V.; Lagaros, N.D.; Georgantzinos, S.K. Design Aspects of Additive Manufacturing at Microscale: A Review. Micromachines 2022, 13, 775. [Google Scholar] [CrossRef]
- Sigmund, O. Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef]
- Trefethen, L.N.L.N. Numerical Linear Algebra; Trefethen, L.N., Bau, D., Eds.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997. [Google Scholar]
- Amir, O.; Bendsøe, M.P.; Sigmund, O. Approximate reanalysis in topology optimization. Int. J. Numer. Methods Eng. 2008, 78, 1474–1491. [Google Scholar] [CrossRef]
- Kazakis, G.; Lagaros, N.D. Sensitivity Analysis of Model Order Reduction Parameters Applied in Topology Optimization; Technical Report; National Technical University of Athens: Athens, Greece, 2022. [Google Scholar]
- Tovar, A.; Liu, K. Top3dSTL. Version: 3.0. Available online: https://www.top3d.app/ (accessed on 30 August 2022).



| Approach | Total Optimization Loops | Full Optimization Loops | Compliance |
|---|---|---|---|
| FEA | 24 | 24 | 879.40 |
| POD | 21 | 11 | 918.18 |
| on-the-fly | 21 | 10 | 918.18 |
| AR | 24 | 13 | 879.40 |
| Approach | Total Optimization Loops | Full Optimization Loops | Compliance |
|---|---|---|---|
| FEA | 32 | 32 | 429,740 |
| POD | 26 | 24 | 500,120 |
| on-the-fly | 26 | 24 | 500,120 |
| AR | 32 | 10 | 429,740 |
| Approach | Total Optimization Loops | Full Optimization Loops | Compliance |
|---|---|---|---|
| FEA | 49 | 49 | 8762 |
| POD | 26 | 19 | 9206 |
| on-the-fly | 26 | 20 | 9206 |
| AR | 50 | 13 | 8762 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazakis, G.; Lagaros, N.D. Topology Optimization Based Material Design for 3D Domains Using MATLAB. Appl. Sci. 2022, 12, 10902. https://doi.org/10.3390/app122110902
Kazakis G, Lagaros ND. Topology Optimization Based Material Design for 3D Domains Using MATLAB. Applied Sciences. 2022; 12(21):10902. https://doi.org/10.3390/app122110902
Chicago/Turabian StyleKazakis, George, and Nikos D. Lagaros. 2022. "Topology Optimization Based Material Design for 3D Domains Using MATLAB" Applied Sciences 12, no. 21: 10902. https://doi.org/10.3390/app122110902





