On Ghost Imaging Studies for Information Optical Imaging
Abstract
:1. Introduction
- (1)
- Multiple-dimensional light-field information is degenerated into the 2-D domain;
- (2)
- Resolution analysis is also restricted to the 2-D spatial domain;
- (3)
- Detection signals usually contain unnecessary redundant image information;
- (4)
- For specific tasks where the whole image information is not necessary, (over)sampling on the full-resolution image is still performed first;
- (5)
- For diffraction imaging systems, it is hard to achieve a resolution at the order of the wavelength without highly bright coherent sources since methods for weak signal detection developed in modern information science cannot be applied.
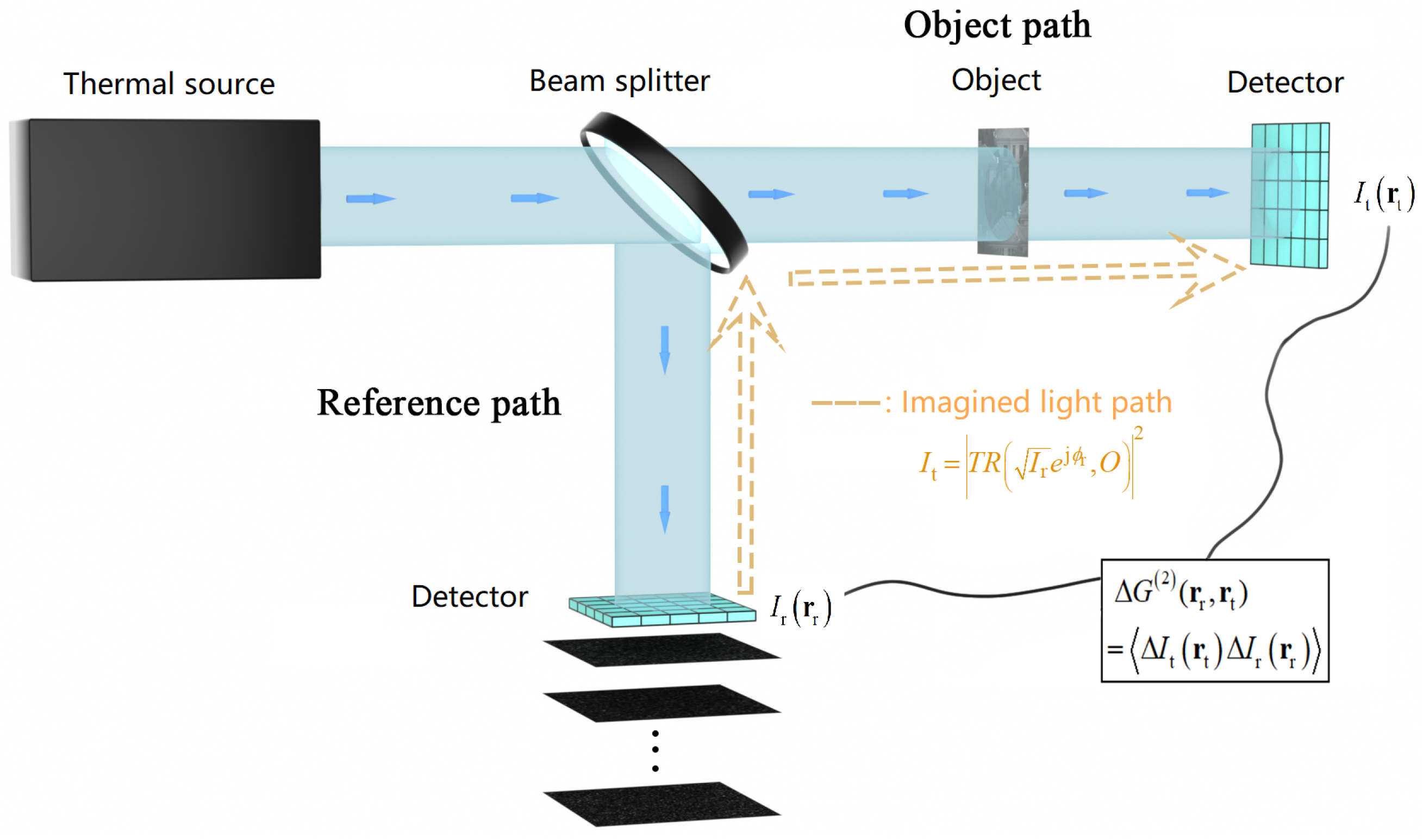
2. Optical Imaging from the Viewpoint of Optical Coherence Theory and the Connection between Ghost Imaging and Information Optical Imaging
3. Ghost Imaging Studies for Information Optical Imaging
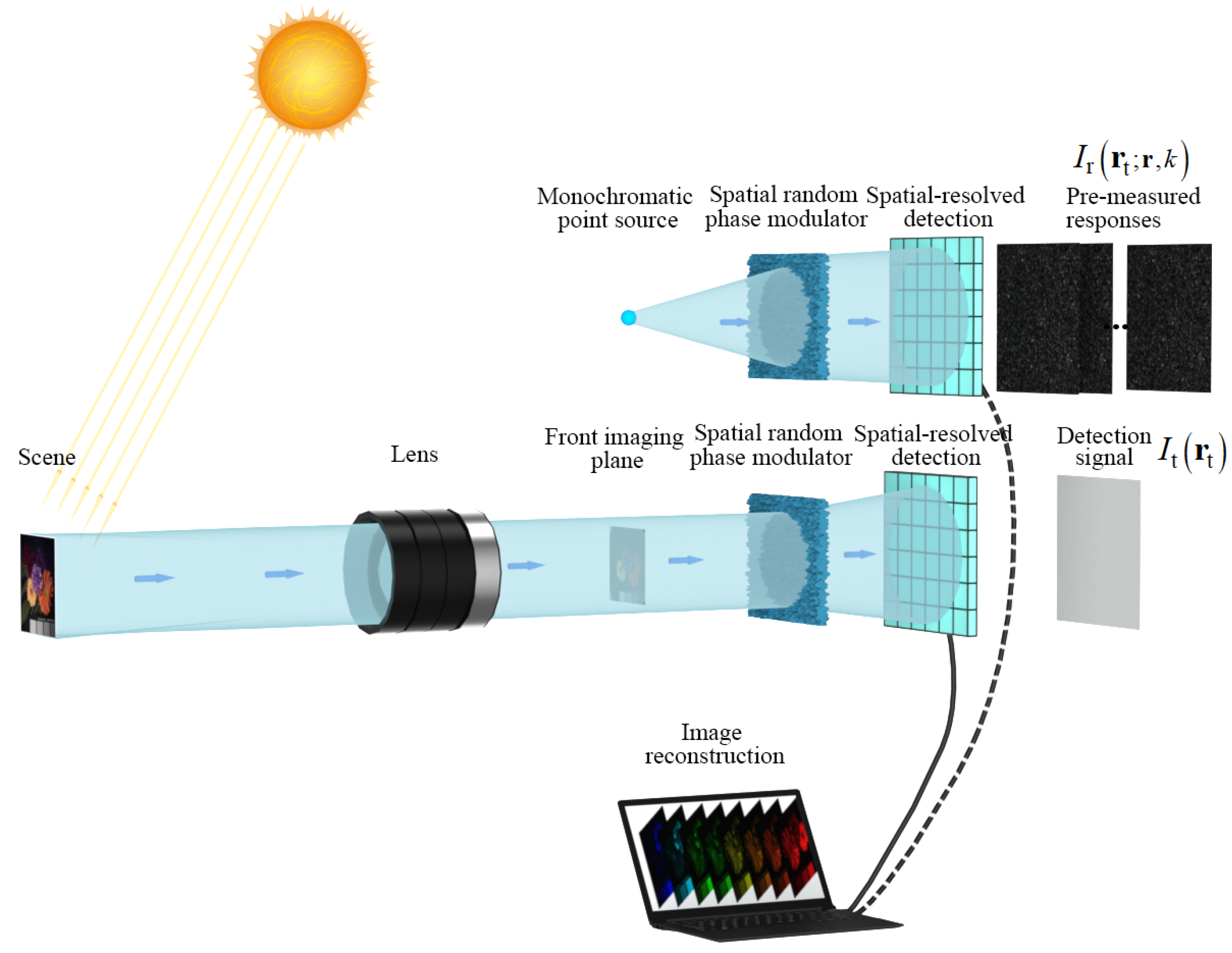
3.1. Mapping Higher-Dimensional Light-Field Information into Lower-Dimensional Domain
3.2. Resolution Analysis in the High-Dimensional Light-Field Domain
3.3. Optimizing the Encoding Mode to Reduce Unnecessary Sampling Redundancy
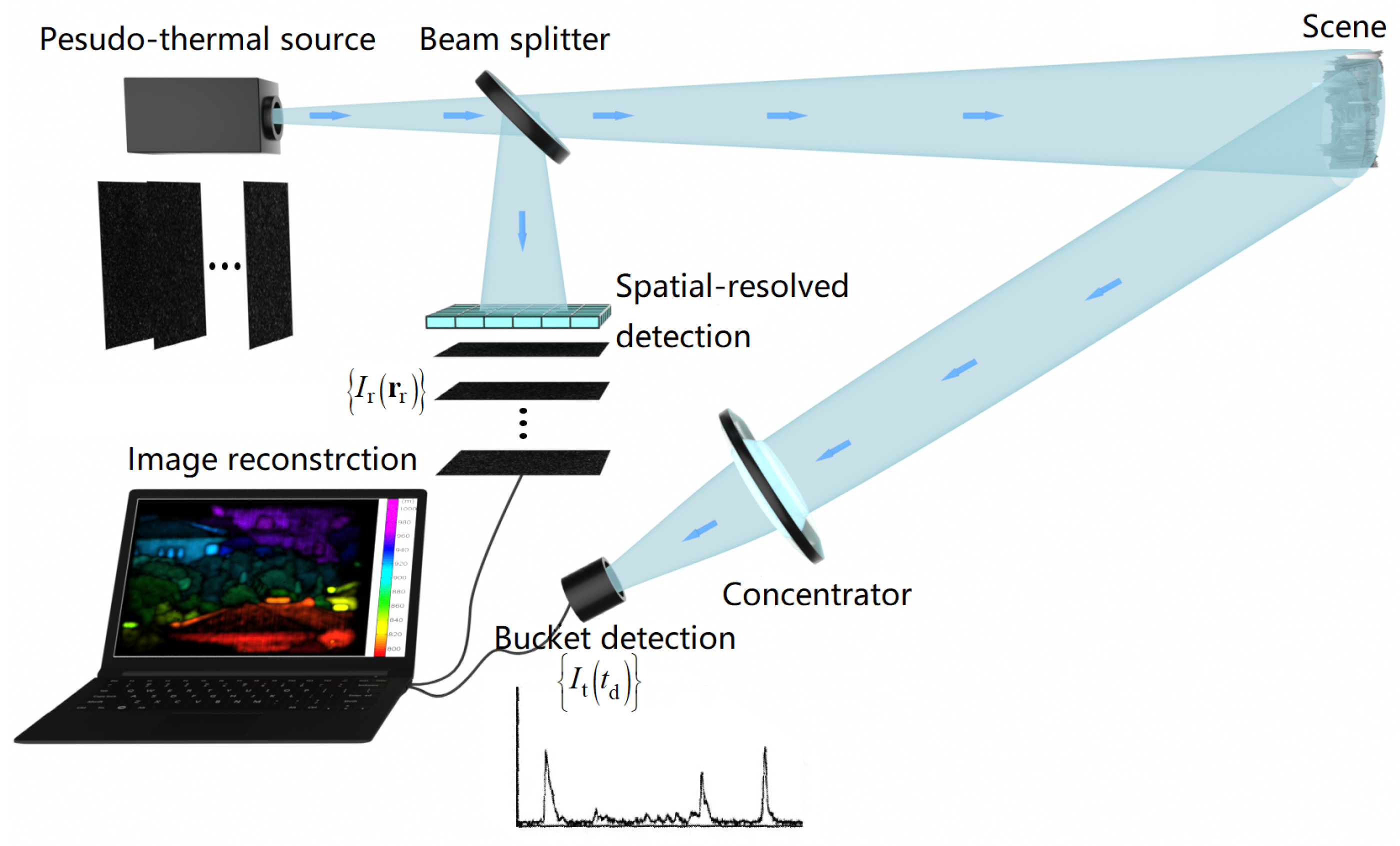
3.4. Task-Oriented Gi System Design
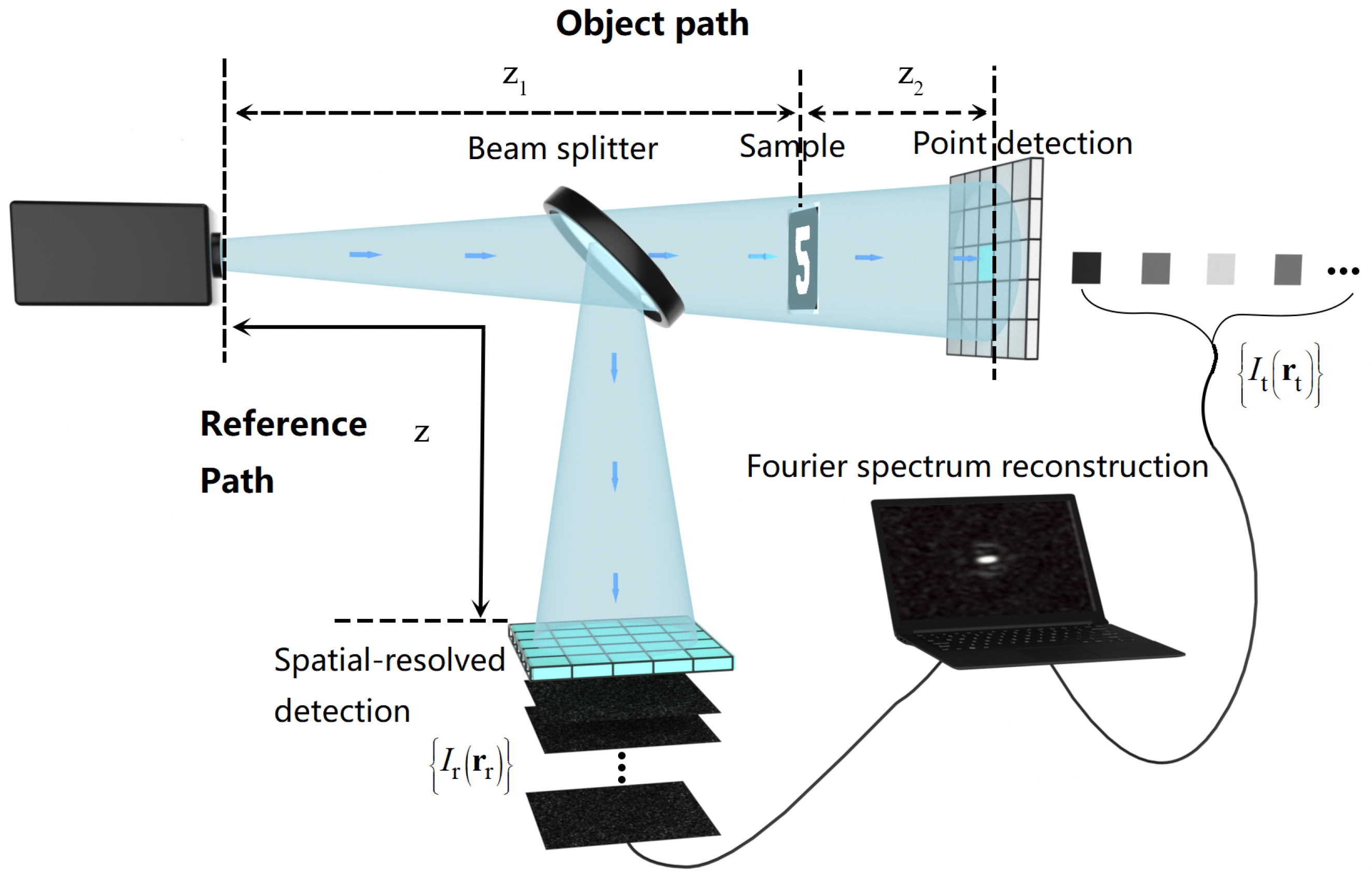
3.5. X-ray Diffraction Gi
4. Outlook
4.1. Further Utilizing High-Dimensional Light-Field Information Capacity
4.2. Task-Oriented System
4.3. X-ray Diffraction Gi
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2-D | two-dimensional |
| 3-D | three-dimensional |
| DOF | degree of freedom |
| CDI | coherent diffraction imaging |
| GI | ghost imaging |
| CTF | coherent transfer function |
| HB-T | Hanbury Brown-Twiss |
| SRPM | spatial random phase modulator |
| CS | compressed sensing |
| probability distribution function |
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Blahut, R.E. Principles and Practice of Information Theory; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1987. [Google Scholar]
- Di Francia, G.T. Resolving power and information. JOSA 1955, 45, 497–501. [Google Scholar] [CrossRef]
- Gabor, D. IV Light and Information. In Progress in Optics; Elsevier: Amsterdam, The Netherlands, 1961; Volume 1, pp. 109–153. [Google Scholar]
- Di Francia, G.T. Degrees of freedom of an image. JOSA 1969, 59, 799–804. [Google Scholar] [CrossRef] [PubMed]
- Tao, C.; Tao, C. Optical Information Theory; Science Press: Beijing, China, 1999; pp. 121–129. (In Chinese) [Google Scholar]
- Stern, A.; Javidi, B. Shannon number and information capacity of three-dimensional integral imaging. JOSA A 2004, 21, 1602–1612. [Google Scholar] [CrossRef] [Green Version]
- De Micheli, E.; Viano, G.A. Inverse optical imaging viewed as a backward channel communication problem. JOSA A 2009, 26, 1393–1402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lukosz, W. Optical systems with resolving powers exceeding the classical limit. JOSA 1966, 56, 1463–1471. [Google Scholar] [CrossRef]
- Cox, I.J.; Sheppard, C.J.R. Information capacity and resolution in an optical system. JOSA A 1986, 3, 1152–1158. [Google Scholar] [CrossRef]
- Bershad, N.J. Resolution, optical-channel capacity and information theory. JOSA 1969, 59, 157–163. [Google Scholar] [CrossRef]
- Kosarev, E. Shannon’s superresolution limit for signal recovery. Inverse Probl. 1990, 6, 55. [Google Scholar] [CrossRef]
- Helstrom, C. The detection and resolution of optical signals. IEEE Trans. Inf. Theory 1964, 10, 275–287. [Google Scholar] [CrossRef]
- Helstrom, C.W. Resolvability of objects from the standpoint of statistical parameter estimation. JOSA 1970, 60, 659–666. [Google Scholar] [CrossRef]
- Lucy, L.B. Statistical limits to super resolution. Astron. Astrophys. 1992, 261, 706. [Google Scholar]
- Bettens, E.; Van Dyck, D.; Den Dekker, A.; Sijbers, J.; Van den Bos, A. Model-based two-object resolution from observations having counting statistics. Ultramicroscopy 1999, 77, 37–48. [Google Scholar] [CrossRef]
- Smith, S.T. Statistical resolution limits and the complexified crame/spl acute/r-rao bound. IEEE Trans. Signal Process. 2005, 53, 1597–1609. [Google Scholar] [CrossRef]
- Chao, J.; Ward, E.S.; Ober, R.J. Fisher information theory for parameter estimation in single molecule microscopy: Tutorial. JOSA A 2016, 33, B36–B57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Narimanov, E. Resolution limit of label-free far-field microscopy. Adv. Photonics 2019, 1, 056003. [Google Scholar] [CrossRef] [Green Version]
- Zheltikov, A.M. Imaging through a scattering medium: The Fisher information and the generalized Abbe limit. Opt. Lett. 2021, 46, 5902–5905. [Google Scholar] [CrossRef] [PubMed]
- Lewis, A.S.; Knowles, G. Image compression using the 2-D wavelet transform. IEEE Trans. Image Process. 1992, 1, 244–250. [Google Scholar] [CrossRef]
- David, S.T.; Michael, W.M. JPEG2000: Image Compression Fundamentals, Standards and Practice; Springer: Berlin, Germany, 2002; ISBN 978-079-237-519-7. [Google Scholar]
- Hyvärinen, A.; Hurri, J.; Hoyer, P.O. Natural Image Statistics: A Probabilistic Approach to Early Computational Vision; Springer Science & Business Media: Berlin, Germany, 2009; pp. 13–14. [Google Scholar]
- Neifeld, M.A.; Ashok, A.; Baheti, P.K. Task-specific information for imaging system analysis. JOSA A 2007, 24, B25–B41. [Google Scholar] [CrossRef] [PubMed]
- Fales, C.L.; Huck, F.O.; Samms, R.W. Imaging system design for improved information capacity. Appl. Opt. 1984, 23, 872–888. [Google Scholar] [CrossRef] [PubMed]
- Huck, F.O.; Fales, C.L.; Halyo, N.; Samms, R.W.; Stacy, K. Image gathering and processing: Information and fidelity. JOSA A 1985, 2, 1644–1666. [Google Scholar] [CrossRef] [PubMed]
- Carretero, L.; Fimia, A.; Beléndez, A. Entropy-based study of imaging quality in holographic optical elements. Opt. Lett. 1994, 19, 1355–1357. [Google Scholar] [CrossRef] [Green Version]
- Alter-Gartenberg, R. Information metric as a design tool for optoelectronic imaging systems. Appl. Opt. 2000, 39, 1743–1760. [Google Scholar] [CrossRef] [PubMed]
- Miao, J.; Charalambous, P.; Kirz, J.; Sayre, D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Chapman, H.N.; Barty, A.; Bogan, M.J.; Boutet, S.; Frank, M.; Hau-Riege, S.P.; Marchesini, S.; Woods, B.W.; Bajt, S.; Benner, W.H.; et al. Femtosecond diffractive imaging with a soft-X-ray free-electron laser. Nat. Phys. 2006, 2, 839–843. [Google Scholar] [CrossRef] [Green Version]
- Robinson, I.; Harder, R. Coherent X-ray diffraction imaging of strain at the nanoscale. Nat. Mater. 2009, 8, 291–298. [Google Scholar] [CrossRef] [PubMed]
- Howells, M.R.; Beetz, T.; Chapman, H.N.; Cui, C.; Holton, J.; Jacobsen, C.; Kirz, J.; Lima, E.; Marchesini, S.; Miao, H.; et al. An assessment of the resolution limitation due to radiation-damage in x-ray diffraction microscopy. J. Electron Spectrosc. Relat. Phenom. 2009, 170, 4–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barrett, H.H.; Myers, K.J. Foundations of Image Science; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995; Chapter 8. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics, 2nd ed.; The McGraw-Hill Companies, Inc.: New York, NY, USA, 1996; Chapters 5, 6. [Google Scholar]
- Han, S.; Hu, C. Review, current status and prospect of researches on information optical imaging. Infrared Laser Eng. 2022, 51, 20220017. [Google Scholar]
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shirai, T. Modern aspects of intensity interferometry with classical light. In Progress in Optics; Elsevier: Amsterdam, The Netherlands, 2017; Volume 62, pp. 1–72. [Google Scholar]
- Brown, R.H.; Twiss, R.Q. Correlation between photons in two coherent beams of light. Nature 1956, 177, 27–29. [Google Scholar] [CrossRef]
- Shapiro, J.H.; Boyd, R.W. The physics of ghost imaging. Quantum Inf. Process. 2012, 11, 949–993. [Google Scholar] [CrossRef]
- Shih, Y. The physics of ghost imaging. In Classical, Semi-classical and Quantum Noise; Springer: Berlin, Germany, 2012; pp. 169–222. [Google Scholar]
- Moreau, P.A.; Toninelli, E.; Gregory, T.; Padgett, M.J. Ghost imaging using optical correlations. Laser Photonics Rev. 2018, 12, 1700143. [Google Scholar] [CrossRef]
- Cheng, J.; Han, S. Incoherent coincidence imaging and its applicability in X-ray diffraction. Phys. Rev. Lett. 2004, 92, 093903. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; He, X.; Meng, Q.; Liu, B.; Wang, D. Microwave staring correlated imaging and resolution analysis. In Geo-Informatics in Resource Management and Sustainable Ecosystem; Springer: Berlin, Germany, 2013; pp. 737–747. [Google Scholar]
- Li, D.; Li, X.; Qin, Y.; Cheng, Y.; Wang, H. Radar coincidence imaging: An instantaneous imaging technique with stochastic signals. IEEE Trans. Geosci. Remote. Sens. 2013, 52, 2261–2277. [Google Scholar]
- Cheng, Y.; Zhou, X.; Xu, X.; Qin, Y.; Wang, H. Radar coincidence imaging with stochastic frequency modulated array. IEEE J. Sel. Top. Signal Process. 2016, 11, 414–427. [Google Scholar] [CrossRef]
- Meyers, R.; Deacon, K.S.; Shih, Y. Ghost-imaging experiment by measuring reflected photons. Phys. Rev. 2008, 77, 041801. [Google Scholar] [CrossRef]
- Edgar, M.P.; Gibson, G.M.; Padgett, M.J. Principles and prospects for single-pixel imaging. Nat. Photonics 2019, 13, 13–20. [Google Scholar] [CrossRef]
- Gibson, G.M.; Johnson, S.D.; Padgett, M.J. Single-pixel imaging 12 years on: A review. Opt. Express 2020, 28, 28190–28208. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wei, Q.; Shen, X.; Liu, Y.; Liu, H.; Cheng, J.; Han, S. Lensless Fourier-transform ghost imaging with classical incoherent light. Phys. Rev. 2007, 75, 021803. [Google Scholar] [CrossRef] [Green Version]
- Gong, W.; Han, S. Phase-retrieval ghost imaging of complex-valued objects. Phys. Rev. 2010, 82, 023828. [Google Scholar] [CrossRef]
- Zhang, D.J.; Tang, Q.; Wu, T.F.; Qiu, H.C.; Xu, D.Q.; Li, H.G.; Wang, H.B.; Xiong, J.; Wang, K. Lensless ghost imaging of a phase object with pseudo-thermal light. Appl. Phys. Lett. 2014, 104, 121113. [Google Scholar] [CrossRef]
- Song, X.B.; Xu, D.Q.; Wang, H.B.; Xiong, J.; Zhang, X.; Cao, D.Z.; Wang, K. Experimental observation of one-dimensional quantum holographic imaging. Appl. Phys. Lett. 2013, 103, 131111. [Google Scholar] [CrossRef]
- Mandel, L.; Sudarshan, E.G.; Wolf, E. Theory of photoelectric detection of light fluctuations. Proc. Phys. Soc. (1958–1967) 1964, 84, 435. [Google Scholar] [CrossRef]
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University Press: Cambridge, UK, 2007; Chapter 7.5. [Google Scholar]
- Martienssen, W.; Spiller, E. Coherence and fluctuations in light beams. Am. J. Phys. 1964, 32, 919–926. [Google Scholar] [CrossRef]
- Han, S.; Yu, H.; Shen, X.; Liu, H.; Gong, W.; Liu, Z. A review of ghost imaging via sparsity constraints. Appl. Sci. 2018, 8, 1379. [Google Scholar] [CrossRef] [Green Version]
- Shechtman, Y.; Eldar, Y.C.; Cohen, O.; Chapman, H.N.; Miao, J.; Segev, M. Phase retrieval with application to optical imaging: A contemporary overview. IEEE Signal Process. Mag. 2015, 32, 87–109. [Google Scholar] [CrossRef] [Green Version]
- Jaganathan, K.; Eldar, Y.C.; Hassibi, B. Phase retrieval: An overview of recent developments. In Optical Compressive Imaging; Stern, A., Ed.; CRC Press Inc.: Boca Raton, FC, USA, 2016; pp. 279–312. [Google Scholar]
- Xu, M.; Dong, D.; Wang, J. Subspace Phase Retrieval. arXiv 2022, arXiv:2206.02480. [Google Scholar]
- Wang, H.; Han, S. Coherent ghost imaging based on sparsity constraint without phase-sensitive detection. EPL (Europhys. Lett.) 2012, 98, 24003. [Google Scholar] [CrossRef]
- Hu, C. Study on Several Theoretical Problems in Information Optical Imaging based on Ghost Imaing Systems. Ph.D. Thesis, Shanghai Institute of Optics and Fine Mechanics, Universtiy of Chinese Academy of Sciences, Shanghai, China, 2021. [Google Scholar]
- Liu, Z.; Hu, C.; Tong, Z.; Chu, C.; Han, S. Some research progress on the theoretical study of ghost imaging in Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences. Infrared Laser Eng. 2021, 50, 20211059. [Google Scholar]
- Scarcelli, G.; Berardi, V.; Shih, Y. Phase-conjugate mirror via two-photon thermal light imaging. Appl. Phys. Lett. 2006, 88, 061106. [Google Scholar] [CrossRef]
- Zhang, M. Experimental Investigation on Non-local Lensless Fourier-transfrom imaging with Cassical Incoherent Light. Ph.D. Thesis, Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai, China, 2007. [Google Scholar]
- Zhao, C.; Gong, W.; Chen, M.; Li, E.; Wang, H.; Xu, W.; Han, S. Ghost imaging lidar via sparsity constraints. Appl. Phys. Lett. 2012, 101, 141123. [Google Scholar] [CrossRef] [Green Version]
- Gong, W. Theoretical and Experimental Investigation On Ghost Imaging Radar with Thermal Light. Ph.D. Thesis, Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai, China, 2011. [Google Scholar]
- Gong, W.; Zhao, C.; Yu, H.; Chen, M.; Xu, W.; Han, S. Three-dimensional ghost imaging lidar via sparsity constraint. Sci. Rep. 2016, 6, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Mei, X.; Pan, L.; Wang, P.; Li, W.; Gao, X.; Bo, Z.; Chen, M.; Gong, W.; Han, S. Airborne near infrared three-dimensional ghost imaging lidar via sparsity constraint. Remote. Sens. 2018, 10, 732. [Google Scholar] [CrossRef] [Green Version]
- Kikuchi, K. Fundamentals of coherent optical fiber communications. J. Light. Technol. 2015, 34, 157–179. [Google Scholar] [CrossRef]
- Secondini, M.; Foggi, T.; Fresi, F.; Meloni, G.; Cavaliere, F.; Colavolpe, G.; Forestieri, E.; Poti, L.; Sabella, R.; Prati, G. Optical time–frequency packing: Principles, design, implementation, and experimental demonstration. J. Light. Technol. 2015, 33, 3558–3570. [Google Scholar] [CrossRef]
- Deng, C.; Gong, W.; Han, S. Pulse-compression ghost imaging lidar via coherent detection. Opt. Express 2016, 24, 25983–25994. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Wang, Y.; Deng, C.; Gong, W.; Bo, Z.; Han, S. Micro-Doppler effect based vibrating object imaging of coherent detection GISC lidar. Opt. Express 2021, 29, 43022–43031. [Google Scholar] [CrossRef]
- Gong, W.; Sun, J.; Deng, C.; Lu, Z.; Zhou, Y.; Han, S. Research progress on single-pixel imaging lidar via coherent detection. Laser Optoelectron. Prog. 2021, 58, 1011003. [Google Scholar]
- Liu, Z.; Tan, S.; Wu, J.; Li, E.; Shen, X.; Han, S. Spectral camera based on ghost imaging via sparsity constraints. Sci. Rep. 2016, 6, 25718. [Google Scholar] [CrossRef] [Green Version]
- Giglio, M.; Carpineti, M.; Vailati, A. Space intensity correlations in the near field of the scattered light: A direct measurement of the density correlation function g (r). Phys. Rev. Lett. 2000, 85, 1416. [Google Scholar] [CrossRef] [Green Version]
- Cerbino, R.; Peverini, L.; Potenza, M.; Robert, A.; Bösecke, P.; Giglio, M. X-ray-scattering information obtained from near-field speckle. Nat. Phys. 2008, 4, 238–243. [Google Scholar] [CrossRef]
- Chu, C.; Liu, S.; Liu, Z.; Hu, C.; Zhao, Y.; Han, S. Spectral polarization camera based on ghost imaging via sparsity constraints. Appl. Opt. 2021, 60, 4632–4638. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Z.; Hu, C.; Li, E.; Shen, X.; Han, S. Spectral ghost imaging camera with super-Rayleigh modulator. Opt. Commun. 2020, 472, 126017. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Liu, Z.; Wu, J.; Shen, X.; Han, S. Dispersion control of broadband super-Rayleigh speckles for snapshot spectral ghost imaging. Chin. Opt. Lett. 2022, 20, 091102. [Google Scholar] [CrossRef]
- Tong, Z.; Liu, Z.; Wang, J. Spatial resolution limit of ghost imaging camera via sparsity constraints-break Rayleigh’s criterion based on the discernibility in high-dimensional light field space. arXiv 2020, arXiv:2004.00135. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Tropp, J.A. Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory 2004, 50, 2231–2242. [Google Scholar] [CrossRef] [Green Version]
- Sekko, E.; Thomas, G.; Boukrouche, A. A deconvolution technique using optimal Wiener filtering and regularization. Signal Process. 1999, 72, 23–32. [Google Scholar] [CrossRef]
- Orieux, F.; Giovannelli, J.F.; Rodet, T. Bayesian estimation of regularization and point spread function parameters for Wiener–Hunt deconvolution. JOSA A 2010, 27, 1593–1607. [Google Scholar] [CrossRef] [Green Version]
- Jin, A.; Yazici, B.; Ale, A.; Ntziachristos, V. Preconditioning of the fluorescence diffuse optical tomography sensing matrix based on compressive sensing. Opt. Lett. 2012, 37, 4326–4328. [Google Scholar] [CrossRef]
- Yao, R.; Pian, Q.; Intes, X. Wide-field fluorescence molecular tomography with compressive sensing based preconditioning. Biomed. Opt. Express 2015, 6, 4887–4898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tong, Z.; Wang, F.; Hu, C.; Wang, J.; Han, S. Preconditioned generalized orthogonal matching pursuit. EURASIP J. Adv. Signal Process. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Tong, Z.; Liu, Z.; Hu, C.; Wang, J.; Han, S. Preconditioned deconvolution method for high-resolution ghost imaging. Photonics Res. 2021, 9, 1069–1077. [Google Scholar] [CrossRef]
- Li, E.; Chen, M.; Gong, W.; Yu, H.; Han, S. Mutual information of ghost imaging systems. Acta Opt. Sin. 2013, 33, 1211003. [Google Scholar]
- Xu, X.; Li, E.; Shen, X.; Han, S. Optimization of speckle patterns in ghost imaging via sparse constraints by mutual coherence minimization. Chin. Opt. Lett. 2015, 13, 071101. [Google Scholar]
- Candès, E.J.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Probl. 2007, 23, 969. [Google Scholar] [CrossRef] [Green Version]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Sulam, J.; Ophir, B.; Zibulevsky, M.; Elad, M. Trainlets: Dictionary learning in high dimensions. IEEE Trans. Signal Process. 2016, 64, 3180–3193. [Google Scholar] [CrossRef]
- Hu, C.; Tong, Z.; Liu, Z.; Huang, Z.; Wang, J.; Han, S. Optimization of light fields in ghost imaging using dictionary learning. Opt. Express 2019, 27, 28734–28749. [Google Scholar] [CrossRef]
- Aβmann, M.; Bayer, M. Compressive adaptive computational ghost imaging. Sci. Rep. 2013, 3, 1545. [Google Scholar]
- Yu, W.K.; Li, M.F.; Yao, X.R.; Liu, X.F.; Wu, L.A.; Zhai, G.J. Adaptive compressive ghost imaging based on wavelet trees and sparse representation. Opt. Express 2014, 22, 7133–7144. [Google Scholar] [CrossRef]
- Li, Z.; Suo, J.; Hu, X.; Dai, Q. Content-adaptive ghost imaging of dynamic scenes. Opt. Express 2016, 24, 7328–7336. [Google Scholar] [CrossRef]
- Liu, B.; Wang, F.; Chen, C.; Dong, F.; McGloin, D. Self-evolving ghost imaging. Optica 2021, 8, 1340–1349. [Google Scholar] [CrossRef]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. London. Ser. Contain. Pap. Math. Phys. Character 1922, 222, 309–368. [Google Scholar]
- Hu, C.; Zhu, R.; Yu, H.; Han, S. Correspondence Fourier-transform ghost imaging. Phys. Rev. 2021, 103, 043717. [Google Scholar] [CrossRef]
- Luo, K.H.; Huang, B.Q.; Zheng, W.M.; Wu, L.A. Nonlocal imaging by conditional averaging of random reference measurements. Chin. Phys. Lett. 2012, 29, 074216. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.J.; Meng, L.T.; Edgar, M.P.; Padgett, M.J.; Radwell, N. A Russian Dolls ordering of the Hadamard basis for compressive single-pixel imaging. Sci. Rep. 2017, 7, 3464. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.K. Super sub-Nyquist single-pixel imaging by means of cake-cutting Hadamard basis sort. Sensors 2019, 19, 4122. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.K.; Liu, Y.M. Single-pixel imaging with origami pattern construction. Sensors 2019, 19, 5135. [Google Scholar] [CrossRef] [Green Version]
- Buzzi, S.; Lops, M.; Venturino, L. Track-before-detect procedures for early detection of moving target from airborne radars. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 937–954. [Google Scholar] [CrossRef]
- Zhai, X.; Cheng, Z.; Wei, Y.; Liang, Z.; Chen, Y. Compressive sensing ghost imaging object detection using generative adversarial networks. Opt. Eng. 2019, 58, 013108. [Google Scholar] [CrossRef]
- Chen, H.; Shi, J.; Liu, X.; Niu, Z.; Zeng, G. Single-pixel non-imaging object recognition by means of Fourier spectrum acquisition. Opt. Commun. 2018, 413, 269–275. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Zheng, S.; Yao, M.; Zheng, G.; Zhong, J. Image-free classification of fast-moving objects using “learned” structured illumination and single-pixel detection. Opt. Express 2020, 28, 13269–13278. [Google Scholar] [CrossRef]
- Liu, X.F.; Yao, X.R.; Lan, R.M.; Wang, C.; Zhai, G.J. Edge detection based on gradient ghost imaging. Opt. Express 2015, 23, 33802–33811. [Google Scholar] [CrossRef]
- Wang, L.; Zou, L.; Zhao, S. Edge detection based on subpixel-speckle-shifting ghost imaging. Opt. Commun. 2018, 407, 181–185. [Google Scholar] [CrossRef]
- Yang, D.; Chang, C.; Wu, G.; Luo, B.; Yin, L. Compressive ghost imaging of the moving object using the low-order moments. Appl. Sci. 2020, 10, 7941. [Google Scholar] [CrossRef]
- Sun, S.; Gu, J.H.; Lin, H.Z.; Jiang, L.; Liu, W.T. Gradual ghost imaging of moving objects by tracking based on cross correlation. Opt. Lett. 2019, 44, 5594–5597. [Google Scholar] [CrossRef]
- Yu, H.; Lu, R.; Han, S.; Xie, H.; Du, G.; Xiao, T.; Zhu, D. Fourier-transform ghost imaging with hard X rays. Phys. Rev. Lett. 2016, 117, 113901. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Cheng, J.; Han, S. Ghost imaging in Fourier space. J. Appl. Phys. 2007, 102, 103102. [Google Scholar] [CrossRef]
- Tan, Z.; Yu, H.; Lu, R.; Zhu, R.; Han, S. Non-locally coded Fourier-transform ghost imaging. Opt. Express 2019, 27, 2937–2948. [Google Scholar] [CrossRef]
- Zhu, R.; Yu, H.; Tan, Z.; Lu, R.; Han, S.; Huang, Z.; Wang, J. Ghost imaging based on Y-net: A dynamic coding and decoding approach. Opt. Express 2020, 28, 17556–17569. [Google Scholar] [CrossRef]
- Géradin, M.; Rixen, D.J. Mechanical Vibrations: Theory and Application to Structural Dynamics; John Wiley & Sons: Hoboken, NJ, USA, 2015; Chapter 4. [Google Scholar]
- Liu, S.; Deng, C.; Wang, C.; Zunwang, B.; Han, S.; Lin, Z. Micro-vibration modes reconstruction based on Micro-Doppler coincidence imaing. arXiv 2022, arXiv:2208.13952. [Google Scholar]
- Stoica, P.; Ng, B.C. On the Cramér-Rao bound under parametric constraints. IEEE Signal Process. Lett. 1998, 5, 177–179. [Google Scholar] [CrossRef]
- Prévost, C.; Chaumette, E.; Usevich, K.; Brie, D.; Comon, P. On Cramér-Rao lower bounds with random equality constraints. In Proceedings of the ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 5355–5359. [Google Scholar]
- Prévost, C.; Usevich, K.; Haardt, M.; Comon, P.; Brie, D. Constrained Cramér-Rao lower bounds for CP-based hyperspectral super-resolution. Available online: https://hal.archives-ouvertes.fr/hal-03083709 (accessed on 19 December 2020).
- Li, W.; Tong, Z.; Xiao, K.; Liu, Z.; Gao, Q.; Sun, J.; Liu, S.; Han, S.; Wang, Z. Single-frame wide-field nanoscopy based on ghost imaging via sparsity constraints. Optica 2019, 6, 1515–1523. [Google Scholar] [CrossRef]
- Bobin, J.; Starck, J.L.; Ottensamer, R. Compressed sensing in astronomy. IEEE J. Sel. Top. Signal Process. 2008, 2, 718–726. [Google Scholar] [CrossRef] [Green Version]
- Xin, L.; Li, F.; Yang, X.; Sun, S.; Zhou, Y.; Liu, Z. A Huber function based restoration algorithm for astronomy image compression. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–5. [Google Scholar]
- Jiao, S.; Sun, M.; Gao, Y.; Lei, T.; Xie, Z.; Yuan, X. Motion estimation and quality enhancement for a single image in dynamic single-pixel imaging. Opt. Express 2019, 27, 12841–12854. [Google Scholar] [CrossRef]
- Liu, W.; Sun, S.; Hu, H.; Lin, H. Progress and prospect for ghost imaging of moving objects. Laser Optoelectron. Prog. 2021, 58, 1011001. [Google Scholar]
- Long, T.; Liang, Z.; Liu, Q. Advanced technology of high-resolution radar: Target detection, tracking, imaging, and recognition. Sci. China Inf. Sci. 2019, 62, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Kwan, C.; Chou, B.; Yang, J.; Tran, T. Target tracking and classification directly in compressive measurement for low quality videos. In Pattern Recognition and Tracking XXX; Alam, M.S., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2019; Volume 10995, p. 1099505. [Google Scholar] [CrossRef]
- Yi, W.; Morelande, M.R.; Kong, L.; Yang, J. An efficient multi-frame track-before-detect algorithm for multi-target tracking. IEEE J. Sel. Top. Signal Process. 2013, 7, 421–434. [Google Scholar] [CrossRef]
- Garcia, F.J.I.; Mandal, P.K.; Bocquel, M.; Marques, A.G. Riemann–Langevin particle filtering in track-before-detect. IEEE Signal Process. Lett. 2018, 25, 1039–1043. [Google Scholar] [CrossRef] [Green Version]
- Guerraou, Z.; Khenchaf, A.; Comblet, F.; Leouffre, M.; Lacrouts, O. Particle filter track-before-detect for target detection and tracking from marine radar data. In Proceedings of the 2019 IEEE Conference on Antenna Measurements & Applications (CAMA), Kuta, Bali, Indonesia, 23–25 October 2019; pp. 1–4. [Google Scholar]
- Nguyen, H.; Nguyen, D.; Wang, Z.; Kieu, H.; Le, M. Real-time, high-accuracy 3D imaging and shape measurement. Appl. Opt. 2015, 54, A9–A17. [Google Scholar] [CrossRef]
- Gu, Z.; Lai, J.; Wang, C.; Yan, W.; Ji, Y.; Li, Z. Theoretical range precision obtained by maximum likelihood estimation in laser radar compared with the Cramer–Rao bound. Appl. Opt. 2018, 57, 9951–9957. [Google Scholar] [CrossRef] [PubMed]
- Bouchet, D.; Dong, J.; Maestre, D.; Juffmann, T. Fundamental bounds on the precision of classical phase microscopes. Phys. Rev. Appl. 2021, 15, 024047. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Li, S.; Driver, T.; Alexander, O.; Cooper, B.; Garratt, D.; Marinelli, A.; Cryan, J.P.; Marangos, J.P. Time-resolved pump–probe spectroscopy with spectral domain ghost imaging. Faraday Discuss. 2021, 228, 488–501. [Google Scholar] [CrossRef]
- Defazio, A.; Tygert, M.; Ward, R.; Zbontar, J. Compressed sensing with a jackknife, a bootstrap, and visualization. J. Data Sci. Stat. Vis. 2022, 4, 1–29. [Google Scholar]
- Van Trees, H.L. Detection, Estimation, and Modulation theory, Part I: Detection, Estimation, and Linear Modulation Theory; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Kitanidis, P.K. An information inequality for Bayesian analysis in imaging problems. Gem-Int. J. Geomathematics 2021, 12, 1–19. [Google Scholar] [CrossRef]
- Katz, O.; Bromberg, Y.; Silberberg, Y. Compressive ghost imaging. Appl. Phys. Lett. 2009, 95, 131110. [Google Scholar] [CrossRef] [Green Version]
- Katkovnik, V.; Astola, J. Compressive sensing computational ghost imaging. JOSA A 2012, 29, 1556–1567. [Google Scholar] [CrossRef] [Green Version]
- Lyu, M.; Wang, W.; Wang, H.; Wang, H.; Li, G.; Chen, N.; Situ, G. Deep-learning-based ghost imaging. Sci. Rep. 2017, 7, 17865. [Google Scholar] [CrossRef] [Green Version]
- Higham, C.F.; Murray-Smith, R.; Padgett, M.J.; Edgar, M.P. Deep learning for real-time single-pixel video. Sci. Rep. 2018, 8, 2369. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, F.; Wang, H.; Wang, H.; Li, G.; Situ, G. Learning from simulation: An end-to-end deep-learning approach for computational ghost imaging. Opt. Express 2019, 27, 25560–25572. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Wang, C.; Chen, M.; Gong, W.; Zhang, Y.; Han, S.; Situ, G. Far-field super-resolution ghost imaging with a deep neural network constraint. Light. Sci. Appl. 2022, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter: Particle Filters for Tracking Applications; Artech House: Norwood, MA, USA, 2004; Chapters 1–4. [Google Scholar]
- Afshari, H.H.; Gadsden, S.A.; Habibi, S. Gaussian filters for parameter and state estimation: A general review of theory and recent trends. Signal Process. 2017, 135, 218–238. [Google Scholar] [CrossRef]
- Bao, Z.; Jiang, Q.; Liu, F. A PHD-based particle filter for detecting and tracking multiple weak targets. IEEE Access 2019, 7, 145843–145850. [Google Scholar] [CrossRef]
- Bourque, A.E.; Bedwani, S.; Filion, É.; Carrier, J.F. A particle filter based autocontouring algorithm for lung tumor tracking using dynamic magnetic resonance imaging. Med Phys. 2016, 43, 5161–5169. [Google Scholar] [CrossRef]
- Kyriakides, I. Multiple target tracking using thermal imaging and radar sensors. In Proceedings of the 2016 4th International Workshop on Compressed Sensing Theory and Its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Aachen, Germany, 19–22 September 2016; pp. 158–162. [Google Scholar]
- Kaltiokallio, O.; Hostettler, R.; Patwari, N. A novel Bayesian filter for RSS-based device-free localization and tracking. IEEE Trans. Mob. Comput. 2019, 20, 780–795. [Google Scholar] [CrossRef]
- Pittman, T.B.; Shih, Y.; Strekalov, D.; Sergienko, A.V. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. 1995, 52, R3429. [Google Scholar] [CrossRef]
- Strekalov, D.; Sergienko, A.; Klyshko, D.; Shih, Y. Observation of two-photon “ghost” interference and diffraction. Phys. Rev. Lett. 1995, 74, 3600. [Google Scholar] [CrossRef]
- Bennink, R.S.; Bentley, S.J.; Boyd, R.W.; Howell, J.C. Quantum and classical coincidence imaging. Phys. Rev. Lett. 2004, 92, 033601. [Google Scholar] [CrossRef]
- Gatti, A.; Brambilla, E.; Bache, M.; Lugiato, L.A. Ghost imaging with thermal light: Comparing entanglement and classicalcorrelation. Phys. Rev. Lett. 2004, 93, 093602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreau, P.A.; Toninelli, E.; Gregory, T.; Padgett, M.J. Imaging with quantum states of light. Nat. Rev. Phys. 2019, 1, 367–380. [Google Scholar] [CrossRef] [Green Version]
- Gatti, A.; Brambilla, E.; Bache, M.; Lugiato, L.A. Correlated imaging, quantum and classical. Phys. Rev. 2004, 70, 013802. [Google Scholar] [CrossRef]
- Xie, X.; Chen, Y.; Yang, K.; Zhou, J. Harnessing the point-spread function for high-resolution far-field optical microscopy. Phys. Rev. Lett. 2014, 113, 263901. [Google Scholar] [CrossRef] [PubMed]
- Litchinitser, N.M. Structured light meets structured matter. Science 2012, 337, 1054–1055. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Han, S. On Ghost Imaging Studies for Information Optical Imaging. Appl. Sci. 2022, 12, 10981. https://doi.org/10.3390/app122110981
Hu C, Han S. On Ghost Imaging Studies for Information Optical Imaging. Applied Sciences. 2022; 12(21):10981. https://doi.org/10.3390/app122110981
Chicago/Turabian StyleHu, Chenyu, and Shensheng Han. 2022. "On Ghost Imaging Studies for Information Optical Imaging" Applied Sciences 12, no. 21: 10981. https://doi.org/10.3390/app122110981
APA StyleHu, C., & Han, S. (2022). On Ghost Imaging Studies for Information Optical Imaging. Applied Sciences, 12(21), 10981. https://doi.org/10.3390/app122110981





