Numerical Simulation and Experimental Research on Multi-Channel Laser Directional Energy Deposition of IN718

Abstract

In this paper, the deposition layer calculation model is proposed for laser-directed energy deposition (DED) with coaxial powder feeding by combining the powder feeding equation with the volume of fluid (VOF) method, and the single-channel IN718 forming process is simulated in real-time with moving boundary conditions in a fixed coordinate system and experimentally validated. Under single-layer single-channel deposition processing, the deposition height and width decreased by 57.1% and 21.6%, respectively, as the scanning speed increased from 8 mm/s to 14 mm/s. The calculated deposition height, width, and melt pool depth were in good agreement with the experimental results. Calculating the temperature field distribution of the single-layer double-channel deposition at an overlapping-rate of 30% yielded the temperature fluctuation pattern of the deposition at various lap moments. Under the influence of the thermal accumulation of the first deposition channel, the latent heat effect of the melt pool will cause the maximum surface temperature during overlap processing to be slightly lower than the maximum surface temperature during single channel processing; at the same time, under the influence of the high-temperature state of the overlap deposition channel during the scanning process, the first deposition channel will exhibit rewarming during the overlap scanning process. The deposition layer and temperature field of single-layer multi-channel laser deposition are modelled using this information. It has been proved that the model may be used to forecast deposition and temperature fields for intricate processing procedures. The study findings are significant for understanding the process mechanism of coaxial powder feeding laser-directed energy deposition in detail and optimizing the process.

1. Introduction

Coaxial powder-fed metal laser 3D printing technology is one of the additive manufacturing technologies that have broad application prospects in many fields, including aerospace, equipment manufacturing, and biomedical, due to its advantages such as large forming size, high efficiency, and excellent part performance [1,2,3]. The mass transfer, heat transfer, and flow within the melt pool during coaxially fed powder laser-directed energy deposition (DED) are closely related to the intrinsic and surface quality of the formed part [4,5,6], and numerical simulation techniques can be used to study this complex series of interdependent physical phenomena. Dongyun Zhang [7] and other authors used a three-dimensional transient model to simulate the temperature field of the melt pool during the fabrication of straight-walled walls by the coaxial powder-fed laser metal deposition forming technique and to reproduce the changes in the shape of the melt pool and the instability of the forming process during the forming process. For single-channel laser cladding, Zhonghe Ren [8] and other authors created a heat transfer model for single-channel laser cladding using the ANSYS parametric design language (APDL), generated the stress field for single-channel laser cladding based on the temperature field, and experimentally validated it. Caiazzo [9] and other authors created a non-stationary mathematical model based on the morphology of the deposited layer during single-channel and overlap laser deposition forming tests on aluminium alloy materials to simulate the temperature field during single-channel and overlap. Chen Wenzhi [10] and other authors analyzed the temperature field of multi-channel laser cladding of nickel-based alloy surfaces at different pause times using finite element calculations and experimental verification, which revealed that the flatness of the cladding was better and the quality of the cladding was higher when the pause between passes was 1.5 s. In recent years, the numerical modeling of powder-fed laser deposition as a whole has made substantial strides. Nevertheless, the majority of the deposition layer morphology computation in the numerical calculation is predefined. The formation and growth of the morphology of a deposition layer are the consequence of the interaction of many phenomena, including powder feeding, melting, and solidification. In anticipation of precise control of laser deposited layer shape and size for precision manufacturing, the establishment of coupled mathematical models that can accurately describe the development of deposited layer formation and physical processes within the melt pool and perform simultaneous calculations is essential for a deeper understanding of the intrinsic mechanism of laser deposition manufacturing and for enhancing the intrinsic and surface quality of molded parts.

In this paper, a mathematical model of coaxial powder feeding laser directed energy deposition is developed, and the real-time computation of deposition layer generation is implemented in ANSYS Fluent software using the VOF method and the powder feeding equation. Simultaneously, the lap rate of single-layer double-channel was simulated and compared to experimental results in order to obtain the temperature field and temperature gradient during double-lap processing and analyze the mutual temperature effect of the first deposition channel and the lap deposition channel during double-lap processing. The model proposed in this paper was used to simulate and compute the single-layer multi-channel process by adjusting the simulation parameters to accomplish the prediction of deposition layers and temperature fields for a variety of processes, some of which were quite complicated.

2. Numerical Modeling

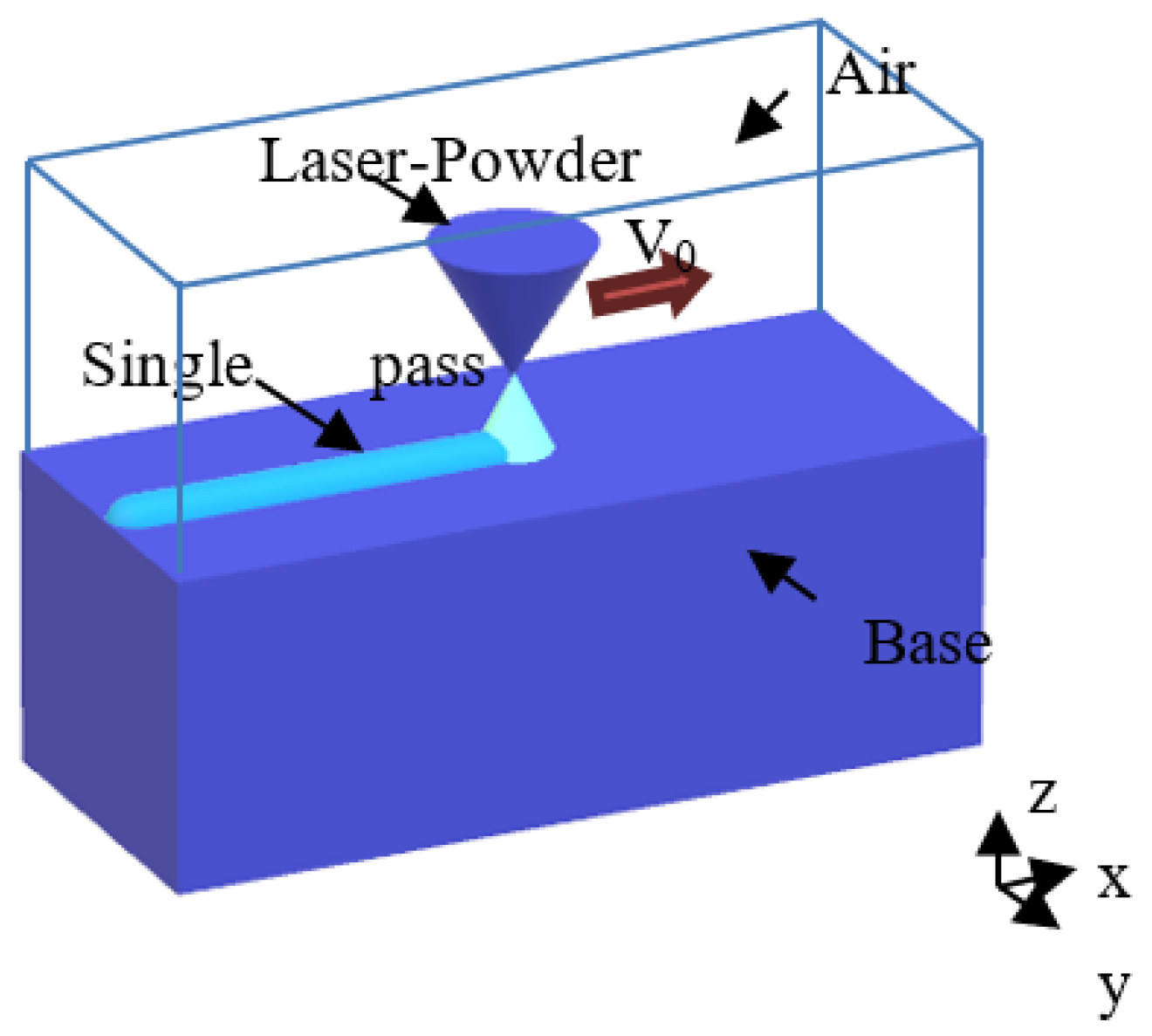
2.1. Geometric and Physical Models

Figure 1 shows the processes of coaxial powder feeding laser-directed energy deposition. The one-piece powder-feeding laser head advances above the substrate toward the x-axis at a constant velocity of V₀, and the laser beam with constant power P melts the supplied IN718 powder and the substrate material to create a molten pool. At the same time, argon gas is expelled for protection. As the laser beam travels, the pool of molten material quickly cools and solidifies, resulting in the deposition on the surface of the substrate material.

Figure 2 depicts the computational domain for this paper, where the blue region represents air and the red area represents the IN718 substrate. (0.005, 0.005, 0.005) (m) in the picture represents the original position of the spot in the center of the computational area. The discretization of the computational simulation uses a cubic structured grid with the size of 0.1 mm × 0.1 mm × 0.1 mm, and the number of nodes is 1030301. Finally, the residuals converge to 2.1153 × 10⁻⁷.

2.2. Mathematical Model

2.2.1. Control Equations

During laser-directed energy deposition, the melting and solidification process of the powder and substrate material includes a change in mass, momentum, energy, and solid-liquid phase transition in the melt pool. The control equations consist of the following expressions for the continuity equation, momentum equation, and energy equation [11]:

Continuity equation

$$\frac{\partial \rho }{\partial t}+div\left(\rho \mathit{U}\right)=0$$

(1)

Momentum equation in x, y and z directions

$$\frac{\partial }{\partial t}\left(\rho u\right)+div\left(\rho \mathit{U}u\right)=\frac{\partial }{\partial x}\left(\mu \frac{\partial u}{\partial x}\right)+\frac{\partial }{\partial y}\left(\mu \frac{\partial u}{\partial y}\right)+\frac{\partial }{\partial z}\left(\mu \frac{\partial u}{\partial z}\right)-\frac{\partial p}{\partial x}+S_u$$

(2)

$$\frac{\partial }{\partial t}\left(\rho v\right)+div\left(\rho \mathit{U}v\right)=\frac{\partial }{\partial x}\left(\mu \frac{\partial v}{\partial x}\right)+\frac{\partial }{\partial y}\left(\mu \frac{\partial v}{\partial y}\right)+\frac{\partial }{\partial z}\left(\mu \frac{\partial v}{\partial z}\right)-\frac{\partial p}{\partial y}+S_v$$

(3)

$$\frac{\partial }{\partial t}\left(\rho w\right)+div\left(\rho \mathit{U}w\right)=\frac{\partial }{\partial x}\left(\mu \frac{\partial w}{\partial x}\right)+\frac{\partial }{\partial y}\left(\mu \frac{\partial w}{\partial y}\right)+\frac{\partial }{\partial z}\left(\mu \frac{\partial w}{\partial z}\right)-\frac{\partial p}{\partial z}+S_w$$

(4)

Energy Equation

$$\frac{\partial }{\partial t}\left(\rho h\right)+div\left(\rho \mathit{U}h\right)=div\left(\frac{k}{c_p}gradh\right)+S_h$$

(5)

$$S_h=\frac{\partial }{\partial t}\left(\rho \Delta H\right)+div\left(\rho u_i\Delta H\right)$$

(6)

where $\rho$ represents the mixing density, $t$ represents the time, $u$, $v$ and $w$ represent the components of the mixing velocity vector $\mathit{U}$ in the $x$, $y$ and $z$ directions, respectively, $p$ represents the pressure, $\mu$ represents the dynamic viscosity coefficient of the fluid, $S_u,S_v$ and $S_w$ represent the additional source terms of the momentum equation in the $x$, $y$, and $z$ directions, respectively. The deposition process can be regarded as an isobaric open system process in which heat transfer results in an enthalpy change and an isobaric specific heat is used. In the energy equation, $h$ represents the sensible enthalpy, $\Delta H$ is the latent heat, and the latent heat is a function of temperature, which can be expressed by Equation (7) [12]:

$$\Delta H=L{f}_l$$

(7)

$f_l$ is the mass fraction of the liquid phase, and $L$ is the value of the latent heat of solidification. This paper treats the liquid phase fraction as a linear relationship with temperature [12].

$$f_l=\{\begin{array}{l}0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}T<T_s\\ \frac{T-T_s}{T_l-T_s}\hspace{1em}\hspace{1em}{T}_s\le T\le T_l\hspace{1em}\\ 1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}T>T_l\end{array}$$

(8)

where $T_s$ represents the solidus, and $T_l$ represents the liquidus.

2.2.2. Deposition Shape Calculation Model

In this study, we present a computational model for the morphology of the deposition by integrating the VOF technique with the powder feeding equation, whose model equation form is as follows:

$$\frac{\partial \left(\rho \varphi \right)}{\partial t}+div\left(\rho \mathit{U}\varphi \right)=m_p$$

(9)

where $\varphi$ is the VOF value in the calculation unit, $m_p$ is the powder feeding flow rate (kg/s/m³), and the first term on the left-hand side of the equation reflects the non-stationary component for the time-dependent change in the VOF value of the cell. The second component is the convection term that influences the unit’s VOF value; the right end of the equation is the additional source term caused by the powder feed.

The powder spatial concentration distribution in the powder convergence space is nearly Gaussian; therefore the powder feeding flow rate $m_p$ fulfills the equation.

$$m_p=3v_p/\left(\pi r_p^2\Delta z\right)\mathit{exp}(\frac{-3d_p^2}{r_p^2})$$

(10)

where $v_p$ represents the powder feeding rate (kg/s), $r_p$ represents the powder feeding radius (m), $d_p$ represents the distance from the current unit to the center of the powder feeding laser head (m), and $\mathsf{\Delta }z\mathrm{represents}$ the unit height (m).

2.2.3. Moving Gaussian Heat Sources and Other Boundary Conditions

Within the circular spot of the fiber laser used in this study, the energy follows a Gaussian distribution, and the heat flow density $Q\left(r\right)$ meets the equation [13]:

$$Q\left(r\right)=3P\eta /\left(\pi r_l^2\right)\mathit{exp}(\frac{-3d_l^2}{r_l^2})$$

(11)

where P represents the laser power (W), η represents the laser absorption rate, $r_l$ represents the laser spot radius (m), and $d_l$ represents the distance (m) from the current unit to the center axis of the spot. This research does not examine the interaction between the laser beam and the powder stream in space, i.e., the heating of the powder particles by the laser beam and the dissipation of the laser energy by the powder stream. There is also convection and radiation heat dissipation $Q_l$ at the surface of the deposited (at the interface between the substrate material and the air) and at the surrounding surface of the substrate, which is accounted for by the equation:

$$Q_l=h_c\left(T-T_r\right)+\epsilon \sigma \left(T^4-T_r^4\right)$$

(12)

where $h_c$ represents the convective heat transfer coefficient between the substrate surface and the air (W/m²/K), $\epsilon$ represents the emissivity of the substrate surface, and $\sigma$ represents the Stephen Boltzmann constant. Therefore, the heat source term Q added to the surface can be expressed as:

$$Q=Q\left(r\right)-Q_l$$

(13)

The surface tension resulting from a temperature gradient also occurs on the surface of the melt pool; therefore the momentum boundary condition of the solid-liquid phase junction cell is [14]:

$$\mu \frac{\partial vel}{\partial l_n}=-\frac{\partial \gamma }{\partial T}\frac{\partial T}{\partial l_r}$$

(14)

The left side of the equation represents the tangential stress, while the right side represents the surface tension gradient; $\mu$ represents the dynamic viscosity coefficient, $\frac{\partial vel}{\partial l_n}$ represents the normal velocity gradient of the molten pool surface, $\frac{\partial \gamma }{\partial T}$ represents the temperature coefficient of surface tension; and $\frac{\partial T}{\partial l_r}$ represents the tangential temperature gradient of the molten pool surface. The parameters used for calculation are shown in

Table 1. Data used in the simulation.

Parameter	Value
Powder feeding radius rp (m)	$1.5\times {10}^{-3}$
$\mathrm{Time}\mathrm{step}\Delta t$$\left(\mathrm{s}\right)$	$1\times {10}^{-5}$
Laser absorptivity η	70%
$\mathrm{Laser}\mathrm{spot}\mathrm{radius}{r}_l\left(\mathrm{m}\right)$	$0.55\times {10}^{-3}$
$\mathrm{Convective}\mathrm{heat}\mathrm{transfer}\mathrm{coefficient}{h}_c$ (W/m2/K)	350
Ambient temperature Tr (K)	300
Surface emissivity of substrate ε	0.4

. The crystallization latent heat value of IN718 alloy is 2.5 × ${10}^5$ J/kg. The liquid and solidus temperatures are 1609 K and 1533 K, respectively. Other thermophysical characteristics are temperature-dependent, as described in detail in reference [15].

3. Experimental Method

Figure 3 depicts the coaxially supplied powder laser deposition setup. A 1000 W fiber laser is used to deposit and create IN718 powder on an IN718 substrate, which is sandblasted before usage to remove the oxide layer. By controlling the laser power and powder feeding rate for different parameters of single pass processing, after forming, the metal specimen is cut along the perpendicular to the scanning direction, ground and polished and then mounted, and etched with aqua regia for 45~60 s.

The specimen was then examined with an ultra-deep field microscope (Keyence VHX-5000), and three measurements were taken at each of the three positions of the stable section on the sedimentary layer. The final average value was used to characterize the morphological dimensions of the single-channel deposited and the laser melt pool.

4. Results Analysis and Discussion

4.1. Single-Channel Deposition

4.1.1. Influence of Powder Feeding Rate on the Shape of Single-Channel Deposition

For the simulation calculation of single-layer single-channel deposition molding, 500 W of laser power, 10 mm/s of scanning speed, and feeding rates of 9.6 g/min, 12.0 g/min, 14.4 g/min, and 16.8 g/min of powder were employed. Figure 4 depicts the simulation results when the geometry of the sedimentary layer achieves a steady state after a length of time. It can be observed that the deposited height and breadth grow with increasing powder feeding rate when the laser power and scanning speed are constant.

The specimens of the above single-channel forming experiments were measured under an ultra-deep field microscope. Shape and dimensions of the sedimentary layer under different powder feeding rates were obtained, as shown in Figure 5. Figure 6 compares the simulation findings to the experimental measurement data, and it can be observed that the estimated values for the breadth and height of the deposition corresponding to various powder feeding rates are greater than the experimental results. This implies that the simulation findings of the sediment layer shape include a certain amount of systematic inaccuracy, which is mostly attributable to the departure of the proposed powder feeding equation based on the normal distribution from the experimental powder flow concentration distribution. Through calculation, the relative error in height increased from 3.67% to 6.80% as the powder feeding rate increased; while the relative error in width was 7.29% at the highest when the powder feeding rate was 16.8 g/min and 5.40% at the lowest when the powder feeding rate was 14.4 g/min. The maximum relative error in height and width is less than 8%, and the numerical simulation results of the deposition channel height and width values are essentially comparable with the experimental data, demonstrating the validity of the numerical model developed in this paper.

4.1.2. Effect of Laser Power on the Shape of the Single-Channel Deposition

Simulation calculations for single-layer, single-channel deposition forming were performed using scanning speeds of 10 mm/s, powder feeding rates of 12.0 g/min, and laser powers of 400 W, 500 W, 600 W, and 700 W, respectively. Figure 7 depicts the simulation results when the deposited form achieves a stable state after 0.4 s. The deposited height and breadth decrease with increasing laser power when the scanning speed and powder feeding rate remain constant. Other process parameters were held constant, and when the laser power was increased from 400 W to 700 W, or by 75%, the deposition height and width increased by 30.67% and 25.31%, respectively, demonstrating that the effect of laser power change on the deposition height and width is similar.

The specimens of the aforementioned single-channel forming experiments were measured using an ultra-deep field microscope, and Figure 8 depicts the shape and size of the deposited layers at various laser powers. Figure 9 depicts a comparison between simulation and experimental measurement outcomes. Since the laser power is a parameter in the Gaussian heat source energy source term, it is the Gaussian heat source energy source term and not the powder feeding equation that influences the shape and dimensions of the deposition. Consequently, the systematic error caused by the deviation of the powder feeding equation from the experimental powder flow concentration distribution no longer exists, and the calculated height and breadth of the deposition are no longer entirely greater than the experimental values. The relative error in the height of the deposited layer was as low as 1.60% at 400 W and as high as 7.61% at 700 W laser power, while the relative error in the width was as low as 1.03% at 600 W and as high as 5.58% at 500 W laser power.

The model developed in this study is used to compute the form of the deposited layer by altering the powder feeding rate and the laser power parameters. The relative error between the simulation results and the experimental findings does not surpass 8%, proving the model’s dependability in both cases.

4.2. Temperature Field Characteristics of Single-Channel Deposition

As depicted in Figure 10, the temperature field distribution of the single-channel IN718 deposited layer at various times was determined using simulation calculations of the process with a powder feeding rate of 0.2 g/s, laser power of 500 W, and a scanning speed of 10 mm/s. Within 0.05 s of the start of the process, the shape of the deposited layer has not yet stabilized, the temperature is highest in the center region of the laser spot, the surface temperature decreases rapidly away from the center of the laser spot, and the temperature field distribution on the surface of the deposited layer is approximately axisymmetric. Comparing Figure 10c,d, it is apparent that after 0.30 s of processing, the shape of the deposited layer basically develops and stabilizes, and the “trailing” phenomena of the temperature field distribution of the deposited layer becomes increasingly apparent.

Figure 11 depicts the 3D melt pool and deposition layer morphology at the moment corresponding to Figure 10. As the process continues, the deposited layer height grows, and the melt depth and melt breadth of the melt pool expand, eventually reaching a steady state. Comparing the deposited layer morphology and melt pool shape in Figure 11b–d, it is evident that the deposited layer height and melt pool size are still increasing from Figure 11b,c, while the deposited layer height and melt pool size are basically unchanged from Figure 11c,d and have reached the steady state. In this instance, the measured time for the deposition layer height and melt pool size to achieve stability is 0.25 s, and the forming start section length before the deposition layer reaches stability is 2.50 mm. In order to precisely control the shape and size of the laser deposition layer in a given process, the processing forming start section must be at least 2.50 mm in length.

4.3. Double-Channel Overlapping Deposition

4.3.1. Calculation and Comparison of Double-Channel Overlapping Deposition Shapes

Under the parameters of a powder feeding rate of 12.0 g/min, a laser power of 500 W, and a laser scanning speed of 10 mm/s, simulations of a two-channel overlap with overlapping rates of 20%, 30%, and 40% were performed, and the morphologies of the deposited layers were produced as shown in Figure 12. Comparing Figure 12a–c, the distance between the two deposition channels decreases as the overlapping rate rises, from a clear depression in the center of the two deposition channels at an overlapping rate of 20% to a prominent bulge higher in the overlapping deposition channel at an overlapping rate of 40%. The simulation findings of the dual-overlapping deposition morphology indicate that a 30% overlapping rate is suitable for the coaxial powder feeding laser directional energy deposition of the IN718 procedure.

4.3.2. Analysis of the Temperature Field and Melt Pool Characteristics of Double-Channel Overlapping Deposition

For a single-layer, two-channel deposition process with a powder feeding rate of 0.2 g/s, laser power of 500 W, laser scanning speed of 10 mm/s, and overlapping rate of 30%, numerical calculations were undertaken. Using the parallel unidirectional overlapping deposition method, the intermediate section with stable shape of the deposited layer obtained from the overlapping experiment under the same parameters was selected, and the width and fusion depth of the deposited layer after overlap were measured by ultra-field depth microscopy and compared with the simulation results, as shown in Figure 13 and Figure 14, respectively. The measured and calculated widths W₁ and W₂ of the deposited layer are 3196.78 m and 2953.15 m, respectively, and the relative error between the simulation and measurement results is 8.24%; the measured fusion depth D₃ and calculated fusion depth D₄ are 288.55 m and 303.63 m, respectively, and the relative error between the simulation and measurement results is 5.23%.

During the overlapping process, the temperature effects of the first deposition channel and the overlapping deposition channel are mutual: the thermal accumulation of the first deposition channel has an effect on the overlapping channel melt pool and deposition temperature; simultaneously, the high temperature state of the overlapping deposition channel has an effect on the temperature and cooling rate of the first deposition channel, which may even further affect the solid-state phase change. Figure 15 depicts the temperature field distribution of the deposition at various instants, with the overlap start instant serving as the zero instant. From Figure 15a–d, it can be seen that due to the effect of heat accumulation, the temperature distribution on the surface of the overlapping deposition channel is no longer symmetrical along the central axis of the overlapping channel, and the distribution of the same temperature range on the scanning side of the first channel becomes significantly larger; Concurrently, it can be seen that the isotherm spacing on the left and right sides of the central axis of the surface of the overlapping deposition channel is distinct. The temperature gradient on the side of the first deposition channel is much less than that on the side of the overlapping deposition channel, and the cooling conditions on the two sides of each deposition are clearly distinct.

In order to describe and analyze the influence of the overlapping channel temperature on the temperature of the first deposition channel more precisely, the temperature variation along the symmetry line (along the x-axis) on the surface of the first deposition channel is depicted in Figure 16 with the moment of the start of the second overlapping channel as the zero moment. The place shown by the dashed line in the picture is the beginning point of the laser scan, which is located at 0.005 m along the x-coordinate of the scanning direction in the model’s 3D coordinate system. Depending on the x-coordinate location, the figure’s curve may be subdivided into many feature sections according to the x-coordinate position: (1) The region located to the left of the dashed line. This portion of the specimen is not scanned by the laser, so the temperature profile begins slightly above room temperature at the specimen’s edge and rises slowly and then rapidly as it approaches the scan’s beginning point, indicating that the temperature gradient on the specimen near the spot is significantly greater than that further away. (2) The far right portion of the graph, corresponding to x-coordinate 0.010 m. The majority of the curves are arranged in time order from top to bottom, with the exception of the final two. This suggests that the end of the first channel remains in a cooling condition for the majority of the time after the spot leaves the first channel and enters the overlapping channel, and that rewarming does not begin until 0.31 s after the spot enters the overlapping channel. (3) On the dashed line. This place represents the beginning of the two scans. Once the spot reaches the second channel (0.01 s), the first channel has been cooled for a considerable amount of time, and the temperature is relatively low. Following this, the temperature of the first channel begins to increase from 0.01 s to 0.16 s as a result of the second channel’s energy input. As a consequence of the second scan spot’s movement away from this place, the temperature at this location from 0.21 s onwards begins to be lower than the temperature at 0.16 s and continues to fall. (4) The right side of the dotted line. For analysis, the location with x-coordinate 0.008 m is utilized as an example. At the 0.01 s mark of the overlapping channel scan, the laser beam just reaches the overlapping deposition channel, at which moment the first scan influences the location and the temperature rises to 1597.73 K. The laser point location on the overlapping channel was distant from this position at 0.06 s, 0.11 s, and 0.16 s since the overlap had just begun, this position was still in the cooling condition, and the temperature had been falling to 1351.62 K with the passage of time. As the laser point approaches this area, the temperature increases to 1436.13 K at 0.21 s and begins to warm up. At 0.31 s, the temperature reached a high of 1535.88 K. At this moment, the temperature recovery was 184.26 K. Other places in this area also had comparable findings.

According to Figure 16, the rewarming phenomenon caused by the energy input of the overlapping channel on the temperature of the first channel has been present since the position of x-coordinate 0.005 m (the starting position of the first channel), causing the temperature of the first deposition channel as a whole to increase, decrease, increase, and decrease again. The affected temperature of the first pass deposition re-rises in the range of 1000–1600 K and the amplitude is 100–300 K. During one-way parallel overlapping deposition, the rewarming of the first deposition channel modifies its residence duration, cooling rate, and temperature gradient in this temperature interval. Since the solid-state phase transition of IN718 alloy occurs mostly between 800 K and 1500 K [16], the rewarming phenomenon may influence the creation of solid-state tissue in the initial deposition channel. In order to prevent large changes in the cooling environment between the temperature zones of a deposition channel’s solid state phase shift, it is important to accomplish delayed overlap by modifying the scanning route during the overlap forming processes.

4.4. Analysis of Simulation Results for Single-Layer Multi-Channel Deposition

Simulation calculations of single-layer multi-channel laser deposition with one-way parallel scanning were performed using double-channel overlapping process parameters, i.e., a powder feeding rate of 12.0 g/min, laser power of 500 W, scanning speed of 10 mm/s, and overlapping rate of 30%. Figure 17 depicts the structure of the deposition as a function of time, revealing the formation of an overlapping deposition with favorable surface morphology as the processing continued. Figure 18 depicts the fluctuation of surface temperature field distribution with time. Comparing the four plots of (a), (b), (c), and (d), we can see that the distance between isotherms in the left area of the current overlapping deposition channel, i.e., near the side of the previous overlapping deposition channel, is significantly greater than that on the other side, whereas the temperature gradient is smaller.

To better analyze the temperature characteristics of the single-layer multi-channel and the interaction between the overlapping deposition channels, an observation point is chosen at a distance of 3 mm from the commencement of the scan along the scan path of the first deposition channel on the surface of the substrate., as depicted in Figure 19, and the temperature variation of the grid at this location with time was recorded, as depicted in Figure 20.

Figure 20 demonstrates that (1) Throughout the first deposition channel scan from 0 s to 0.6 s, the laser head is exactly above the observation point at 0.3 s, when the observation point’s temperature reaches its peak, until the completion of the first deposition channel scan at 0.6 s. (2) At the start of the second deposition channel scan, the temperature of the observation point is still falling. However, as the spot approaches, the temperature of the observation point begins to climb, and the amplitude of the temperature recovery is exactly between 200 K and 300 K. (3) In the second scan, there is a slight lag in the moment of temperature extremes at the observation point relative to the moment when the spot position is side-by-side with the observation point, and this feature appears again in the third scan, but the lag is more pronounced than in the second scan because the spot position is further away from the observation point position. (4) During the third scan, the temperature change at the observation point continued to follow a drop-rise-drop pattern, but the temperature return was significantly smaller than it was in the second scan, indicating that the temperature effect on the first deposition layer was significantly smaller in the third scan than in the second. (5) During the last 1.8 s–2.4 s, i.e., the fourth scan, the temperature at the location of the scan point has stopped rising and has been in a cooling state, but has slowed down its cooling. (6) The rewarming process in the first deposition channel maintains the temperature above about 1000 K for a longer length of time, influencing the phase composition of IN718 alloy material after solidification.

5. Conclusions

Combining the powder feeding equation with the VOF volume function model to calculate the deposition layer morphology results in the establishment of a mathematical model of the three-dimensional coaxial powder feeding laser-directed energy deposition process and the simulation calculation of the single-channel and lap-forming processes. The deposition layer’s height and breadth grew by 51.12% and 11.18%, respectively, when the powder feeding rate was raised from 9.6 g/min to 12.0 g/min. The deposition layer height and breadth grew by 30.67% and 25.31%, respectively, when the laser power was increased from 400 W to 700 W, or by 75%. The estimated height and breadth of the deposition layer are in excellent accord with experimental findings. Due to the thermal buildup of the first deposition channel, which absorbed more latent heat of melting, the melt pool expanded by 4.19 percent during lap processing in one-way parallel scanning as compared to single pass processing. During lap processing, the maximum surface temperature of 2038 K was somewhat lower than that of 2068 K during single-channel processing. During the scanning operation, the first deposition channel is likewise affected by the high-temperature condition of the lap deposition channel. There is a different degree of re-temperature at different locations, with the influence range from 1000 K to 1600 K and the re-temperature range from 100 K to 300 K. For the IN718 alloy, this affects the solid-state phase change after the solidification of the first deposition channel. On this basis, the deposition layer and temperature field are simulated for single-layer multi-channel overlap laser deposition. It is shown that the model may be used to forecast the deposition and temperature field for complicated processing procedures. The preceding findings help in the comprehension of the mechanism behind the deposition manufacturing process and the development of laser deposition manufacturing with high dimensional precision and intrinsic quality.