Geometric Method: A Novel, Fast and Accurate Solution for the Inverse Problem in Risley Prisms
Abstract
:1. Introduction
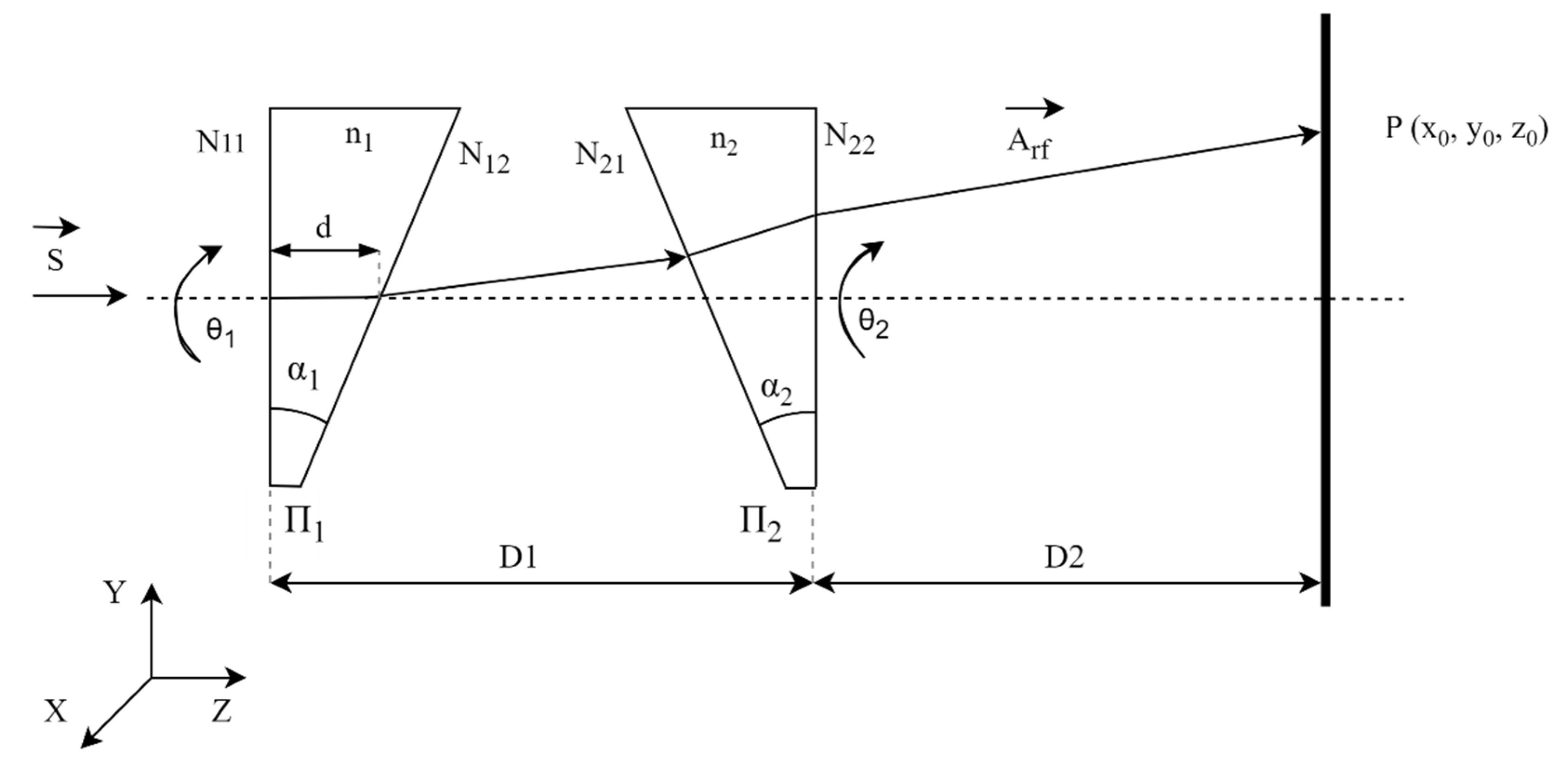
2. Proposed Inverse Solution for Risley Prisms
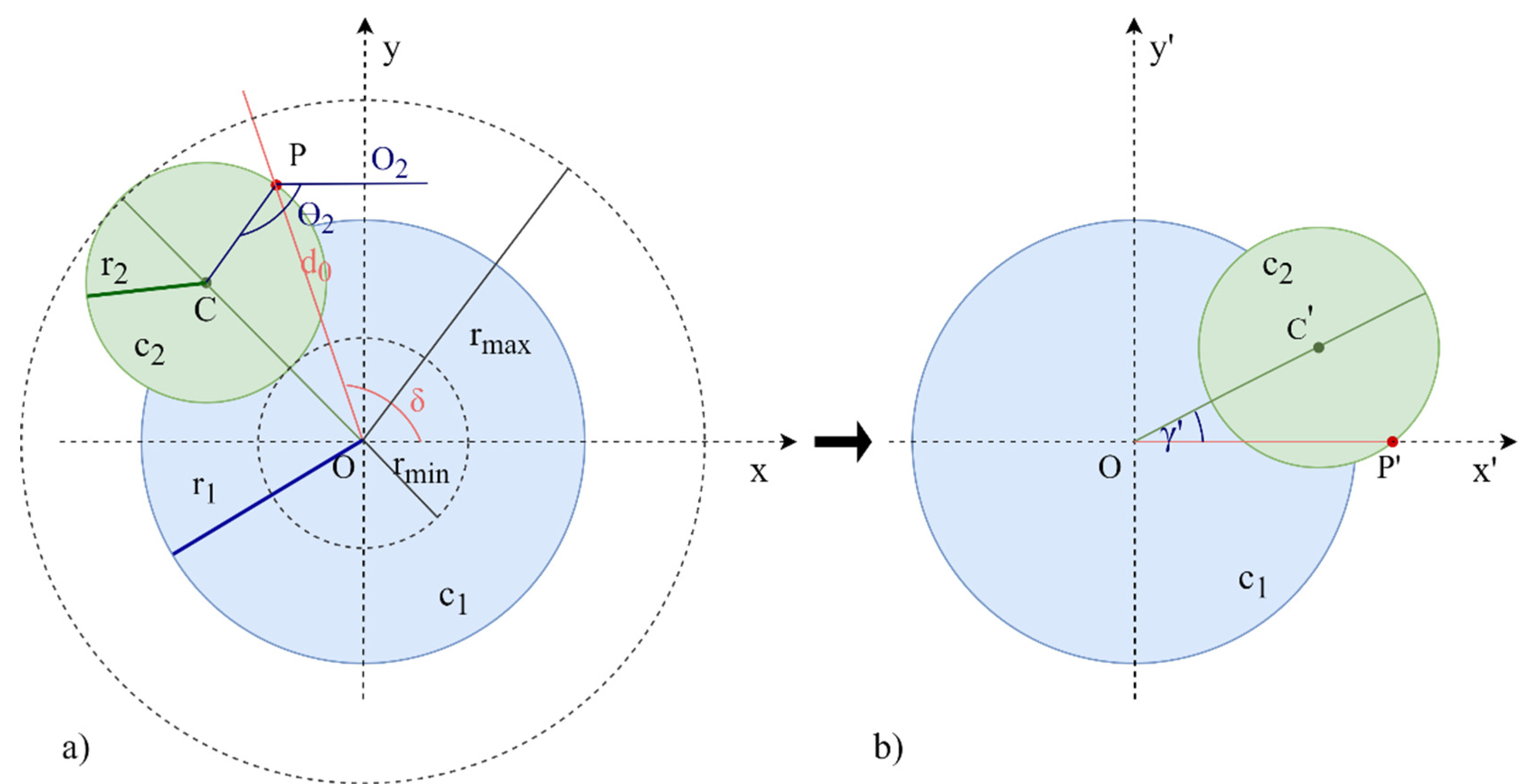
2.1. Geometric Method, Circumference Approximation
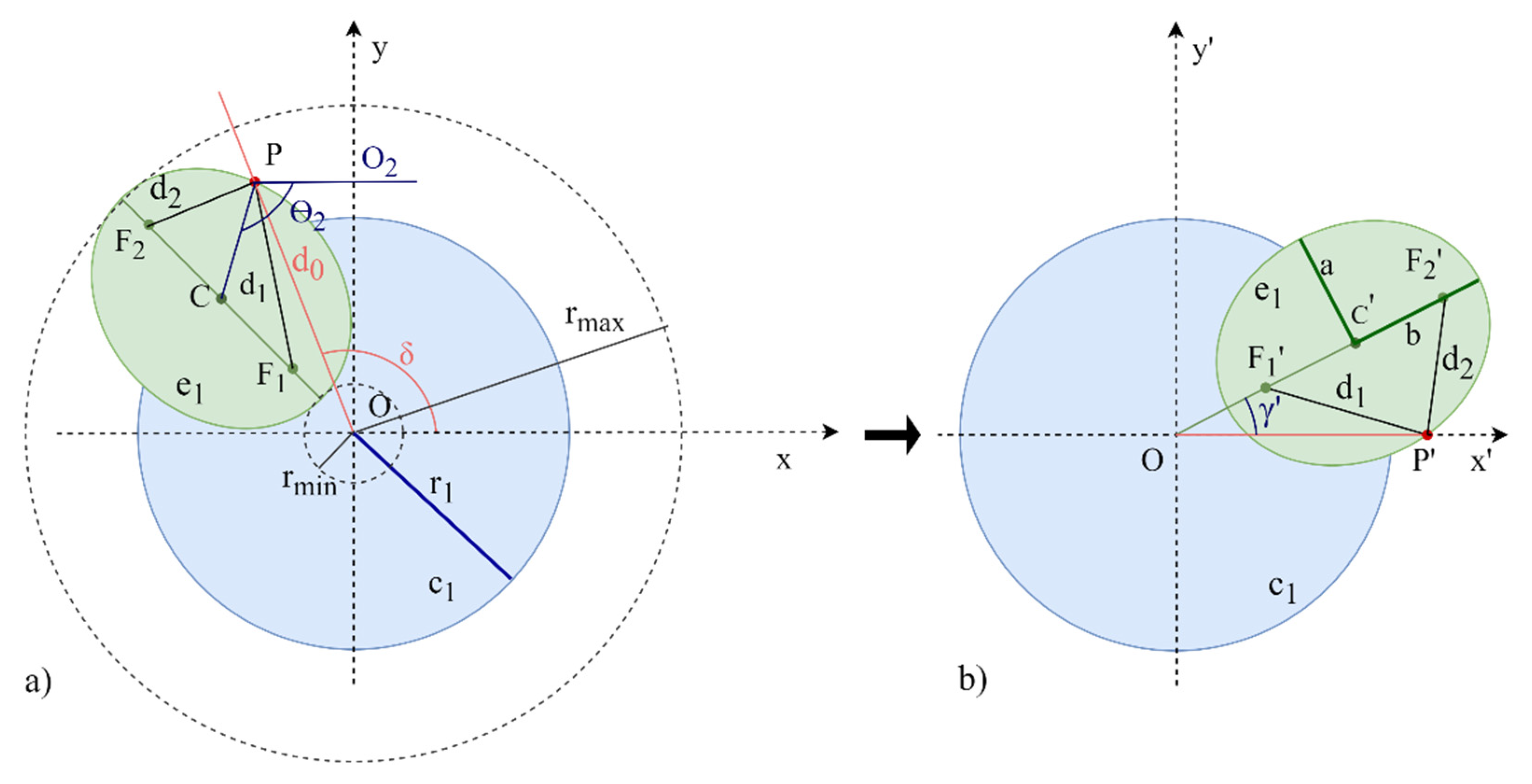
2.2. Geometric Method, Ellipse Approximation
2.2.1. Calculation of the Semi-Axis a
2.2.2. Calculation of the Rotation Angles of the Prisms
2.3. Iterative Process with Geometric Method
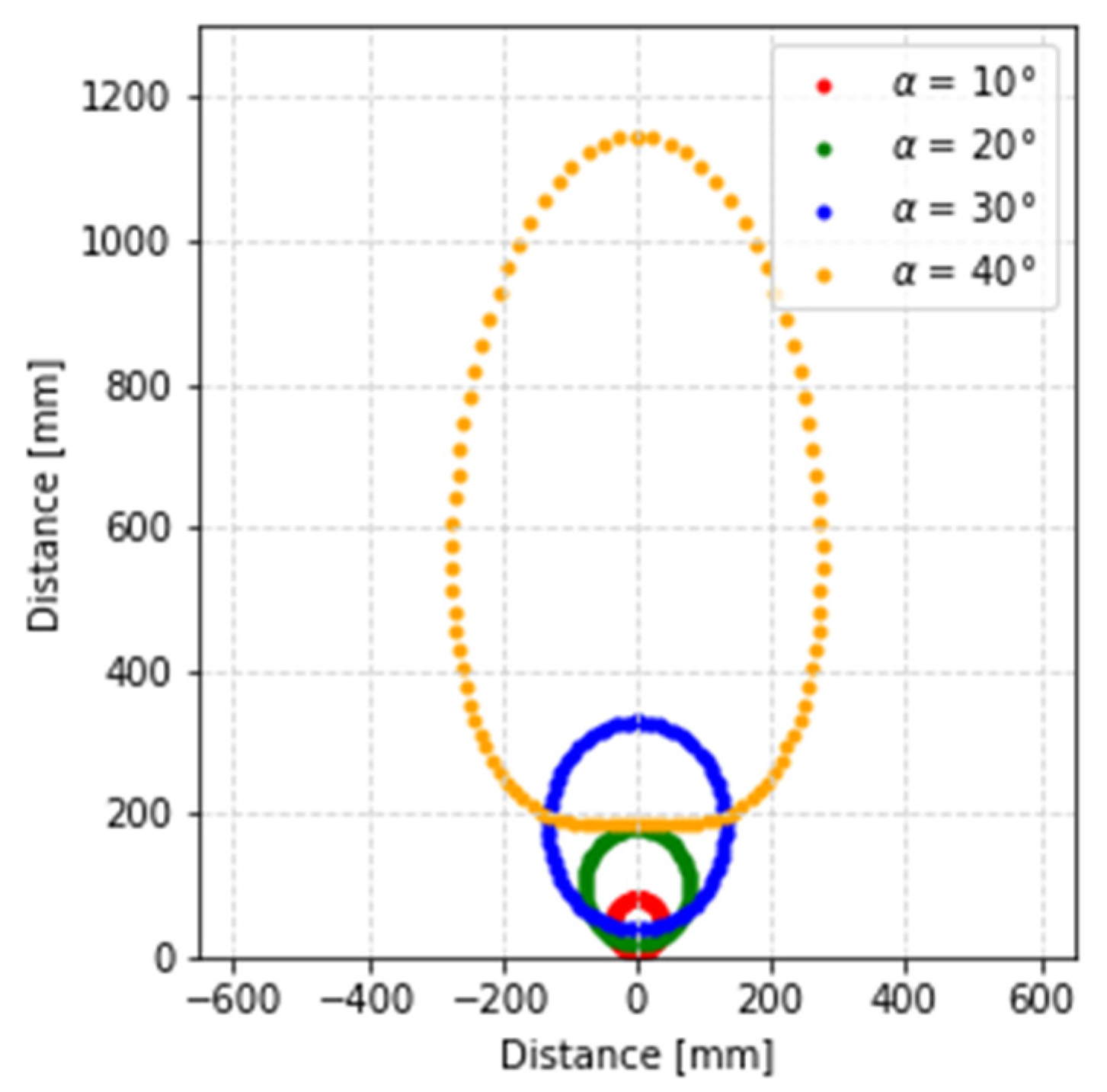
3. Results of the Geometric Method
3.1. Comparison of the Errors Obtained with the Geometric Method and the Two-Step Method
3.2. Comparative Results of the Error with the Iterative Process
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jianfeng, S.; Liren, L.; Maojin, Y.; Lingyu, W.; Mingli, Z. The effect of the rotating double-prism wide-angle laser beam scanner on the beam shape. Optik 2005, 116, 553–556. [Google Scholar] [CrossRef]
- Church, P.; Matheson, J.; Cao, X.; Roy, G. Evaluation of a steerable 3D laser scanner using a double Risley prism pair. Degrad. Environ. Sens. Process. Disp. 2017, 10197, 101970O. [Google Scholar] [CrossRef]
- Li, A.; Liu, X.; Sun, J.; Lu, Z. Risley-prism-based multi-beam scanning LiDAR for high-resolution three-dimensional imaging. Opt. Lasers Eng. 2022, 150, 106836. [Google Scholar] [CrossRef]
- Amirault, C.T.; DiMarzio, C.A. Precision pointing using a dual-wedge scanner. Appl. Opt. 1985, 24, 1302–1308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Souvestre, F.; Hafez, M.; Régnier, S. DMD-based multi-target laser tracking for motion capturing. Emerg. Digit. Micromirror Device Based Syst. Appl. II 2010, 7596, 75960B. [Google Scholar] [CrossRef]
- Yang, Y. Analytic Solution of Free Space Optical Beam Steering Using Risley Prisms. J. Light. Technol. 2008, 26, 3576–3583. [Google Scholar] [CrossRef]
- Li, A.; Gao, X.; Sun, W.; Yi, W.; Bian, Y.; Liu, H.; Liu, L. Inverse solutions for a Risley prism scanner with iterative refinement by a forward solution. Appl. Opt. 2015, 54, 9981–9989. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. Third-order theory of the Risley-prism-based beam steering system. Appl. Opt. 2011, 50, 679–686. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. Closed form analytical inverse solutions for Risley-prism-based beam steering systems in different configurations. Appl. Opt. 2011, 50, 4302–4309. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Zhou, Y.; Hei, M.; Fan, D. Theoretical and experimental determination of steering mechanism for Risley prism systems. Appl. Opt. 2013, 52, 1389–1398. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Lu, Y.; Hei, M.; Liu, G.; Fan, D. Motion control of the wedge prisms in Risley-prism-based beam steering system for precise target tracking. Appl. Opt. 2013, 52, 2849–2857. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Sun, W.; Gao, X. Nonlinear inverse solution by the look-up table method for Risley-prism-based scanner. Opt. Appl. 2016, XLVI, 4. [Google Scholar] [CrossRef]
- Alajlouni, S. Solution to the Control Problem of Laser Path Tracking Using Risley Prisms. IEEE/ASME Trans. Mechatron. 2016, 21, 1892–1899. [Google Scholar] [CrossRef]
- Bravo-Medina, B.; Strojnik, M.; Garcia-Torales, G.; Torres-Ortega, H.; Estrada-Marmolejo, R.; Beltrán-González, A.; Flores, J.L. Error compensation in a pointing system based on Risley prisms. Appl. Opt. 2017, 56, 2209–2216. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308. [Google Scholar] [CrossRef]
- Singer, S.; Singer, S. Efficient Implementation of the Nelder-Mead Search Algorithm. Appl. Numer. Anal. Comput. Math. 2004, 1, 524–534. [Google Scholar] [CrossRef]
- Powell, M. On trust region methods for unconstrained minimization without derivatives. Math. Program. 2003, 97, 605–623. [Google Scholar] [CrossRef]


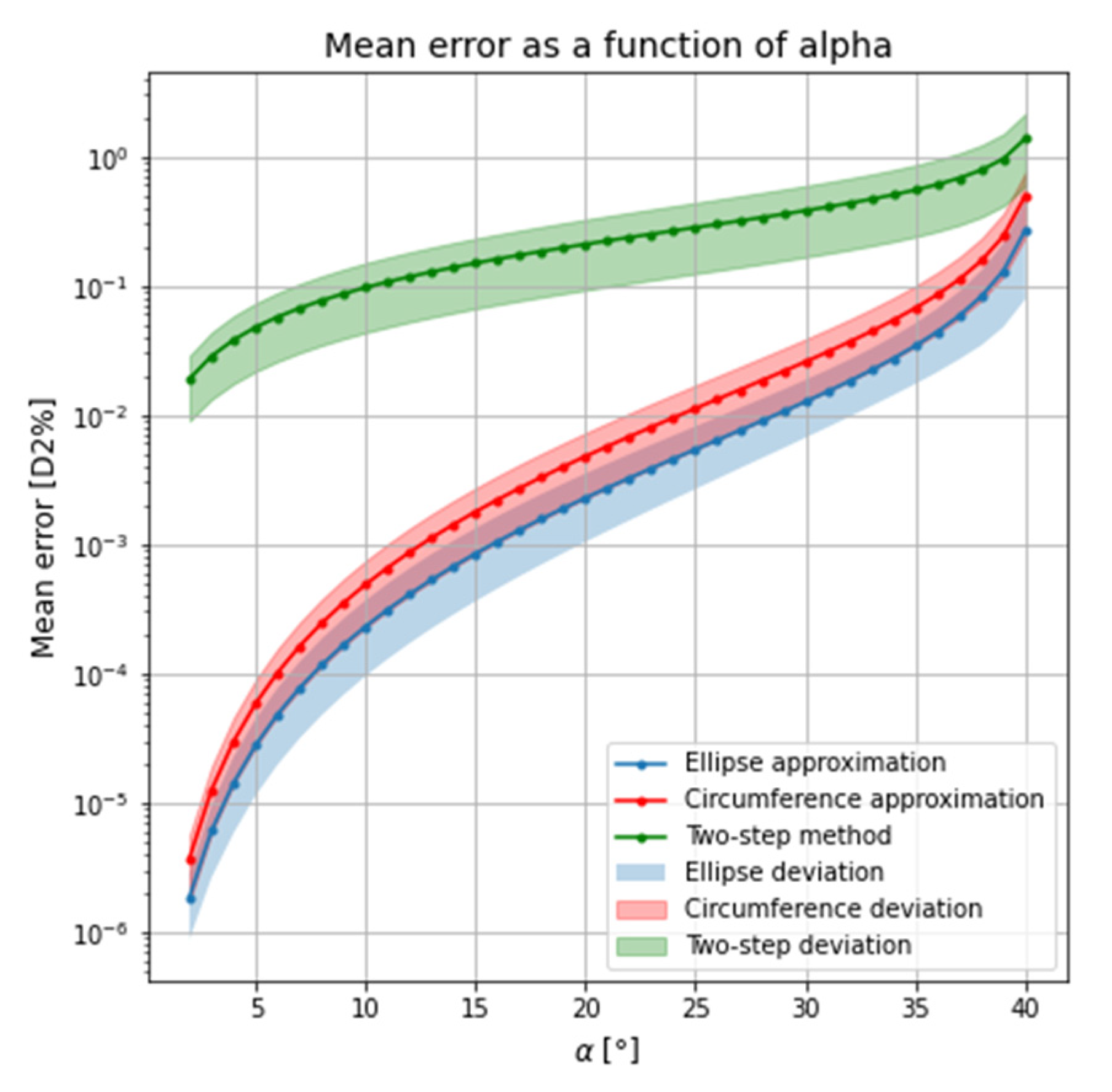
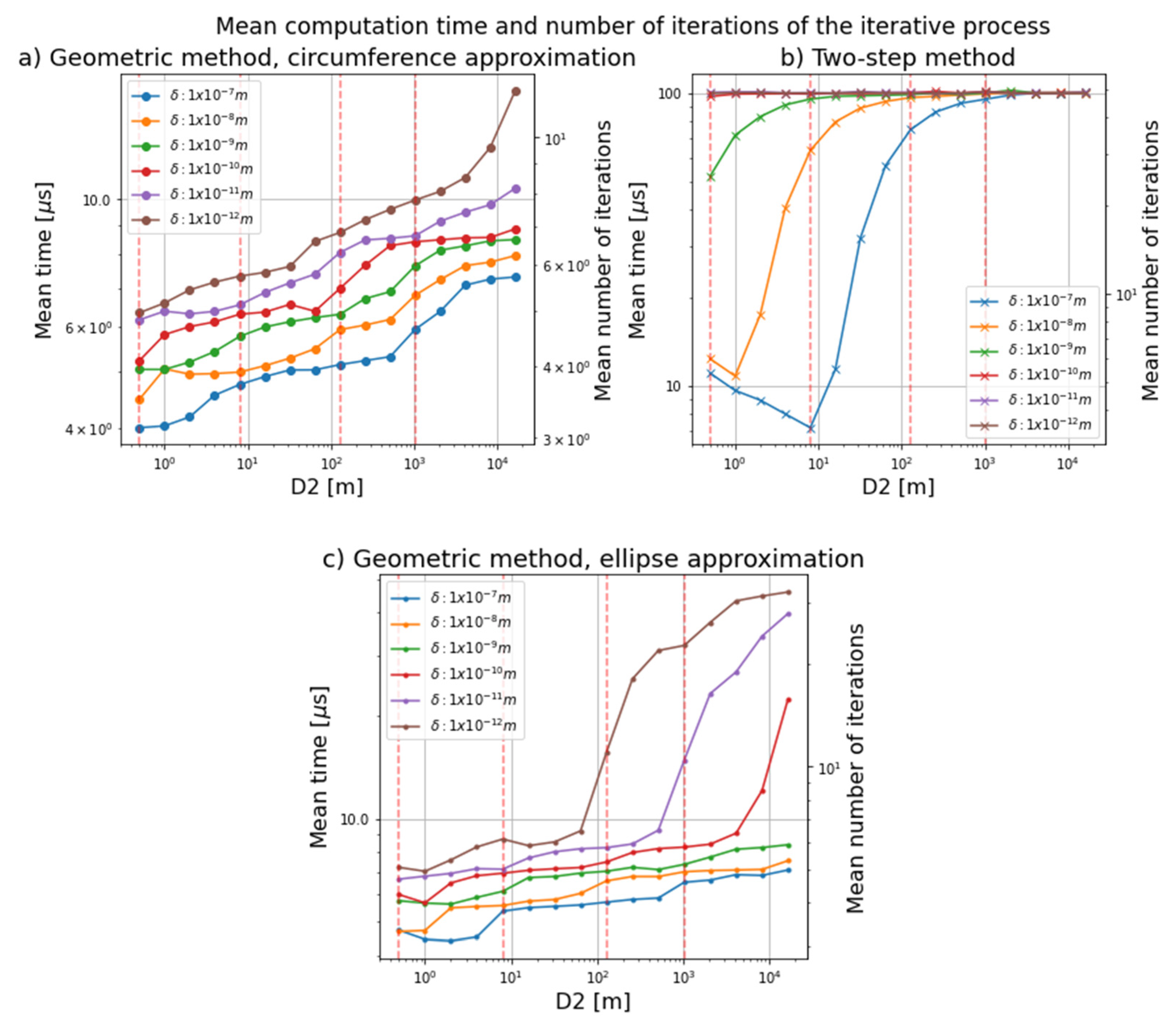
| Geometric Method | Two-Step Method | ||
|---|---|---|---|
| Circumference Approximation | Ellipse Approximation | ||
| 2.7257 | 4.3378 | 9.6737 | |
| 0.4754 | 0.5015 | 7.3917 | |
| D2 (m) | Δ (m) | Geometric Method | Two-Step Method | |
|---|---|---|---|---|
| Circumference Approximation | Ellipse Approximation | |||
| 0.5 | 3.00 | 3.21 | 5.12 | |
| 8 | 3.76 | 3.78 | 3.30 | |
| 128 | 4.06 | 4.04 | 38.10 | |
| 1024 | 4.72 | 4.64 | 48.56 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandoval, J.D.; Delgado, K.; Fariña, D.; Puente, F.d.l.; Esper-Chaín, R.; Martín, M. Geometric Method: A Novel, Fast and Accurate Solution for the Inverse Problem in Risley Prisms. Appl. Sci. 2022, 12, 11087. https://doi.org/10.3390/app122111087
Sandoval JD, Delgado K, Fariña D, Puente Fdl, Esper-Chaín R, Martín M. Geometric Method: A Novel, Fast and Accurate Solution for the Inverse Problem in Risley Prisms. Applied Sciences. 2022; 12(21):11087. https://doi.org/10.3390/app122111087
Chicago/Turabian StyleSandoval, Juan Domingo, Keyla Delgado, David Fariña, Fernando de la Puente, Roberto Esper-Chaín, and Marrero Martín. 2022. "Geometric Method: A Novel, Fast and Accurate Solution for the Inverse Problem in Risley Prisms" Applied Sciences 12, no. 21: 11087. https://doi.org/10.3390/app122111087
APA StyleSandoval, J. D., Delgado, K., Fariña, D., Puente, F. d. l., Esper-Chaín, R., & Martín, M. (2022). Geometric Method: A Novel, Fast and Accurate Solution for the Inverse Problem in Risley Prisms. Applied Sciences, 12(21), 11087. https://doi.org/10.3390/app122111087









