Model Predictive Control of Running Biped Robot
Abstract
:1. Introduction
- (1)
- D-LIPM is proposed to be used instead of a nonlinear dynamic model of a biped robot.
- (2)
- To overcome terrain uncertainties and generate the online running motion of a biped robot, hierarchical motion control with linear MPC and QP-based momentum control is proposed.
- (3)
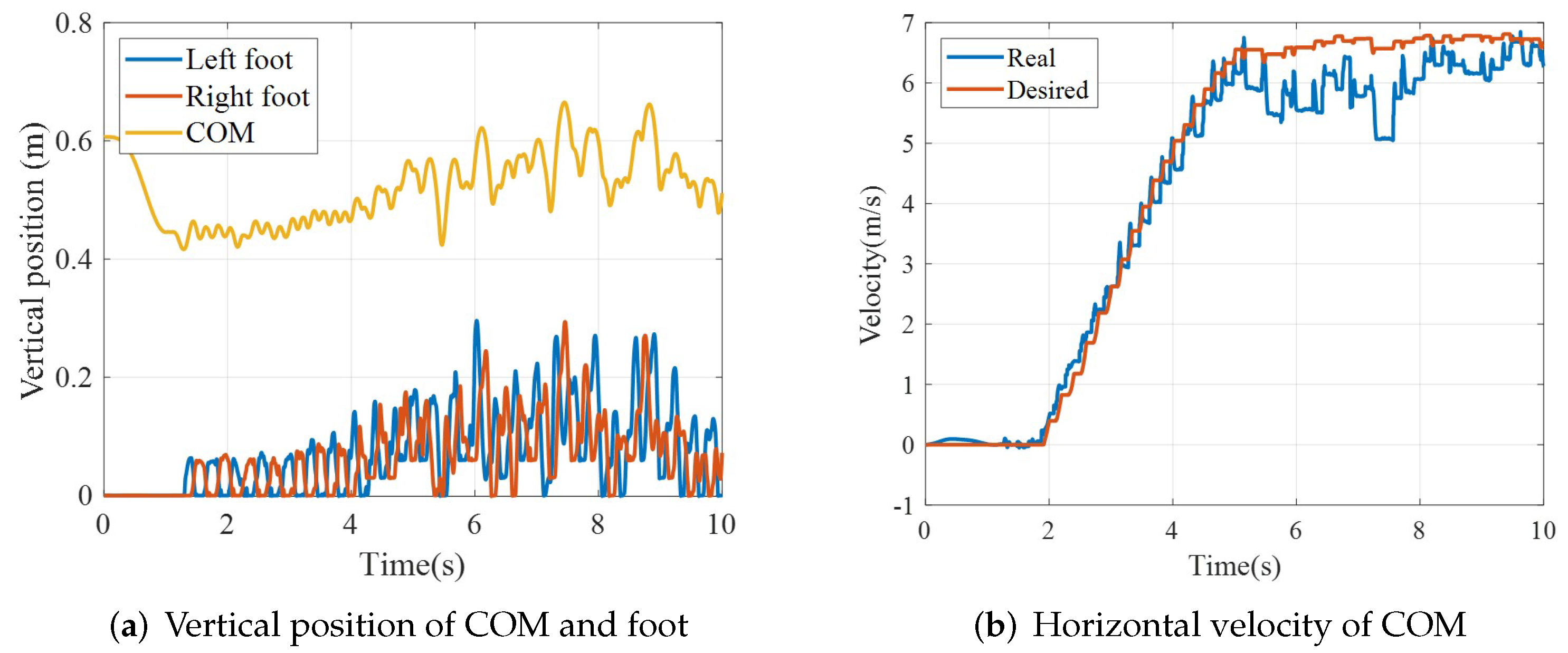
- Simulations showed that a biped robot could run at 6.5 m/s even with unobserved obstacles whose height was approximately 10 % of the length of its legs.
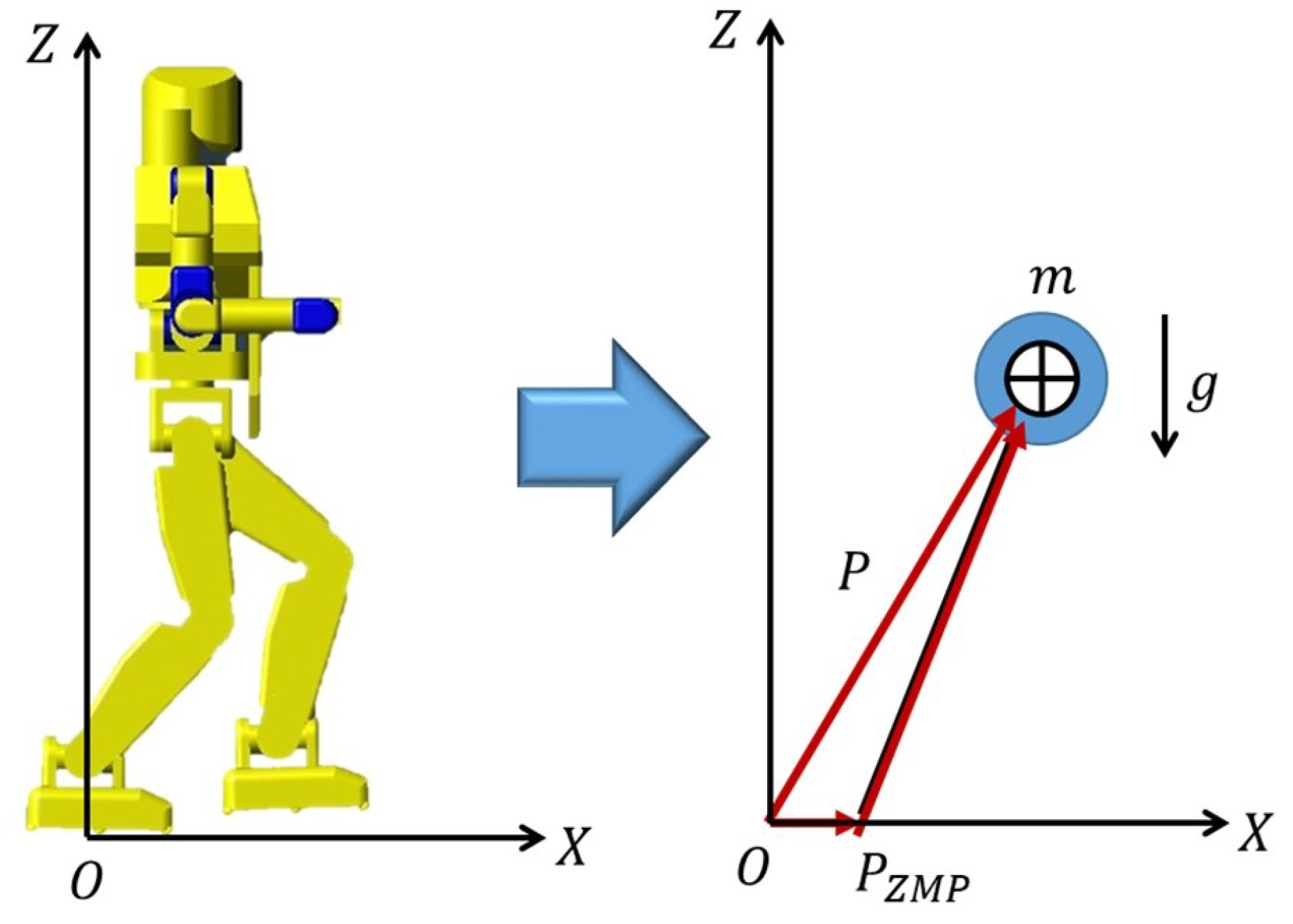
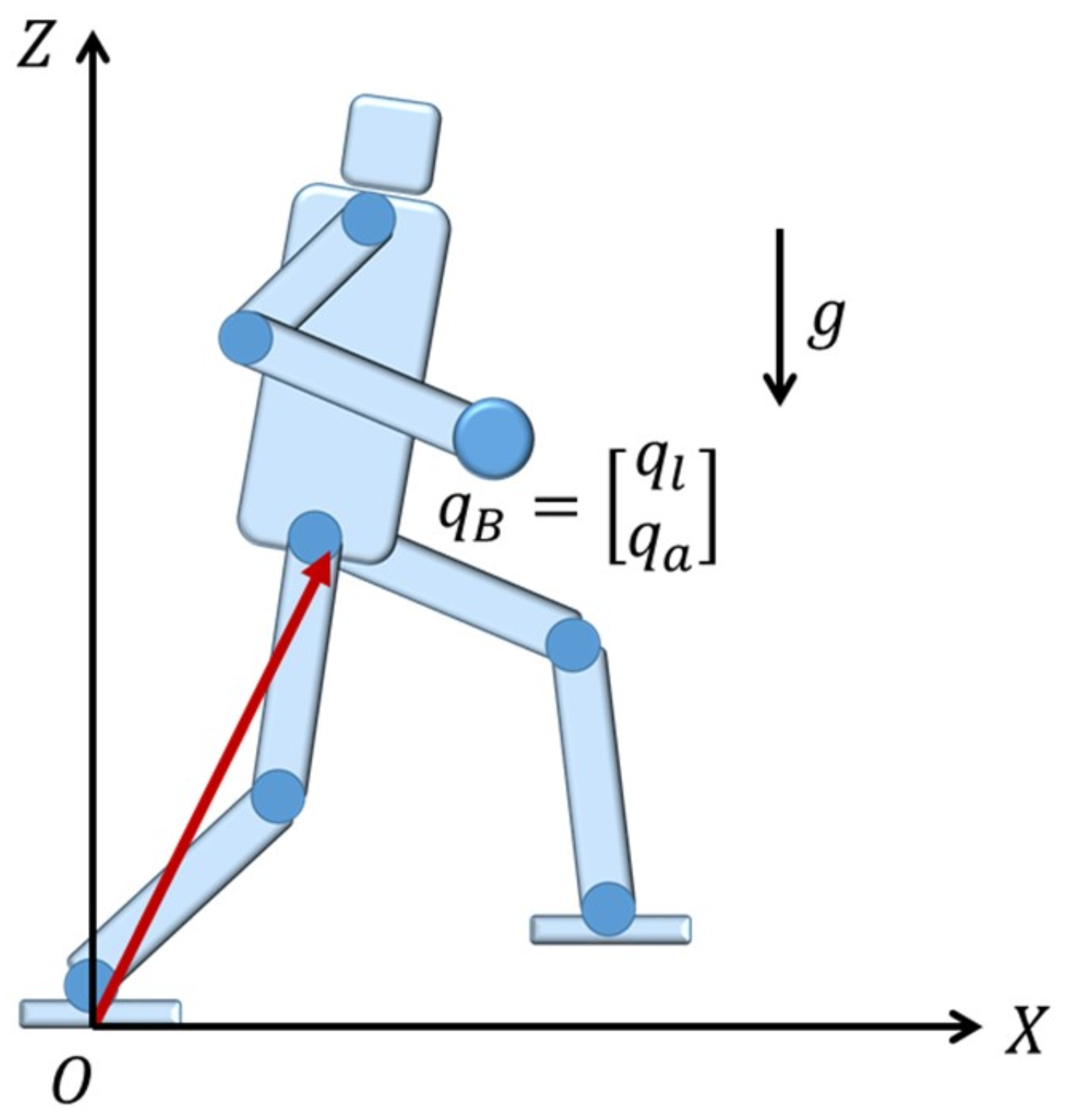
2. Model of Biped Robot
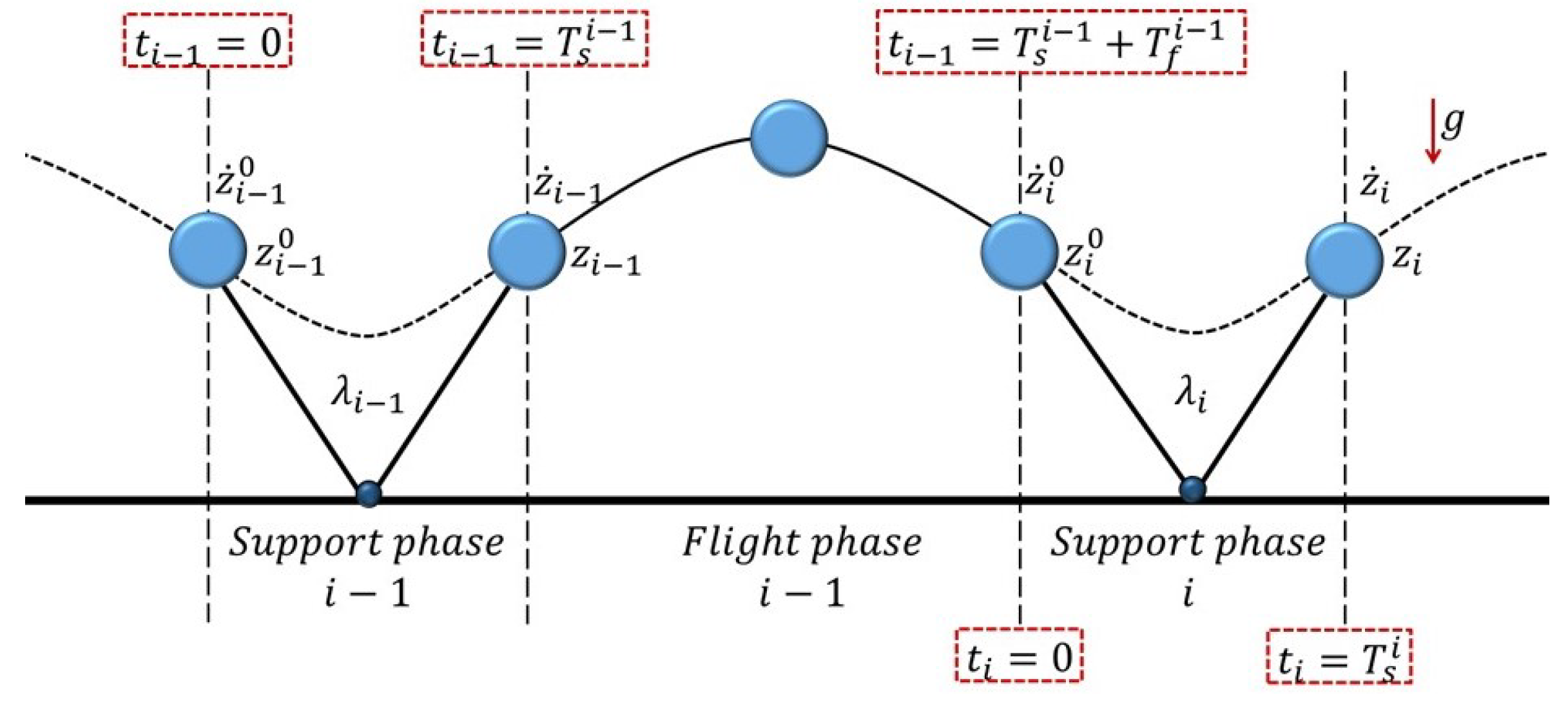
3. Placement of Landing Foot
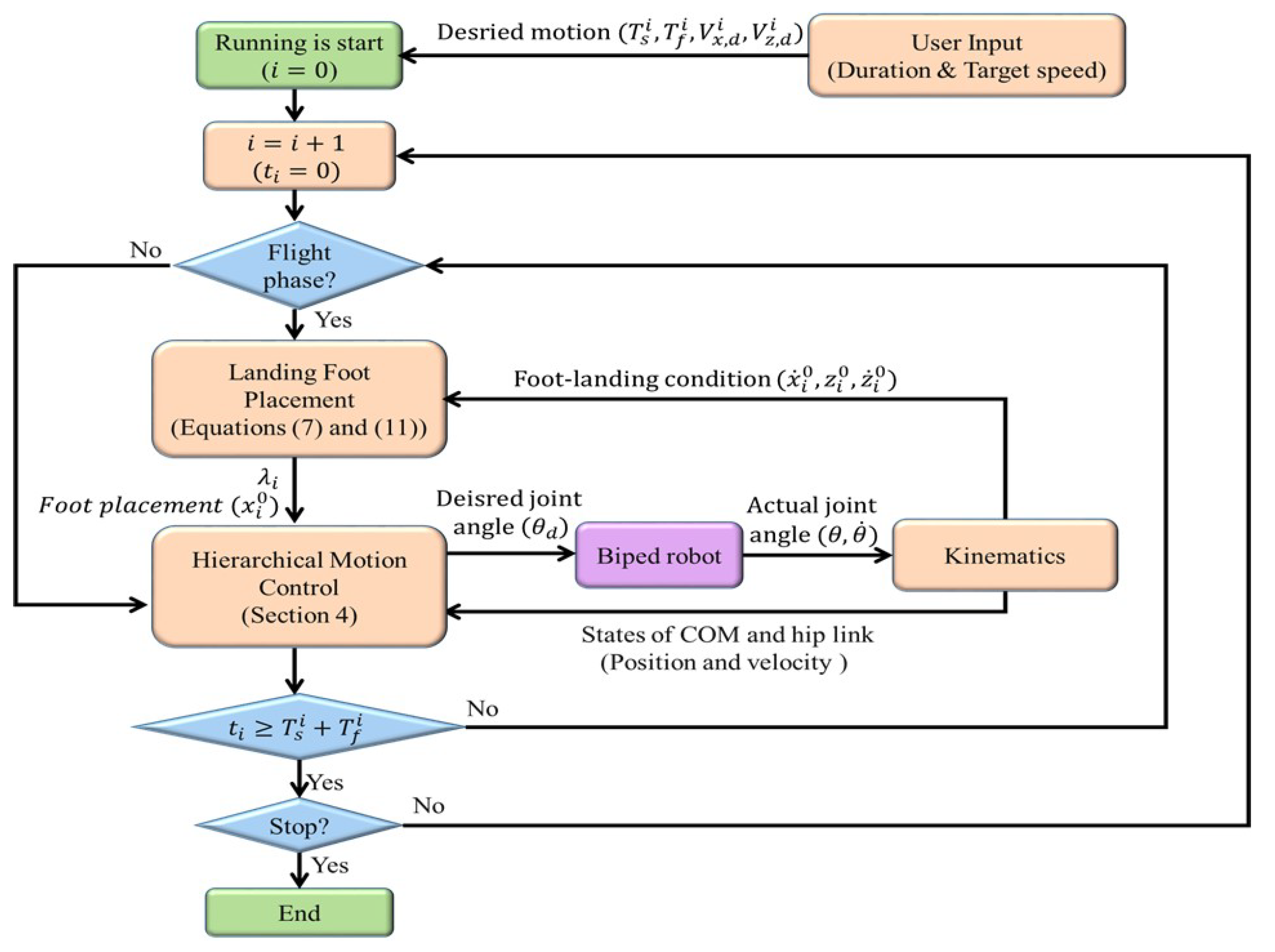
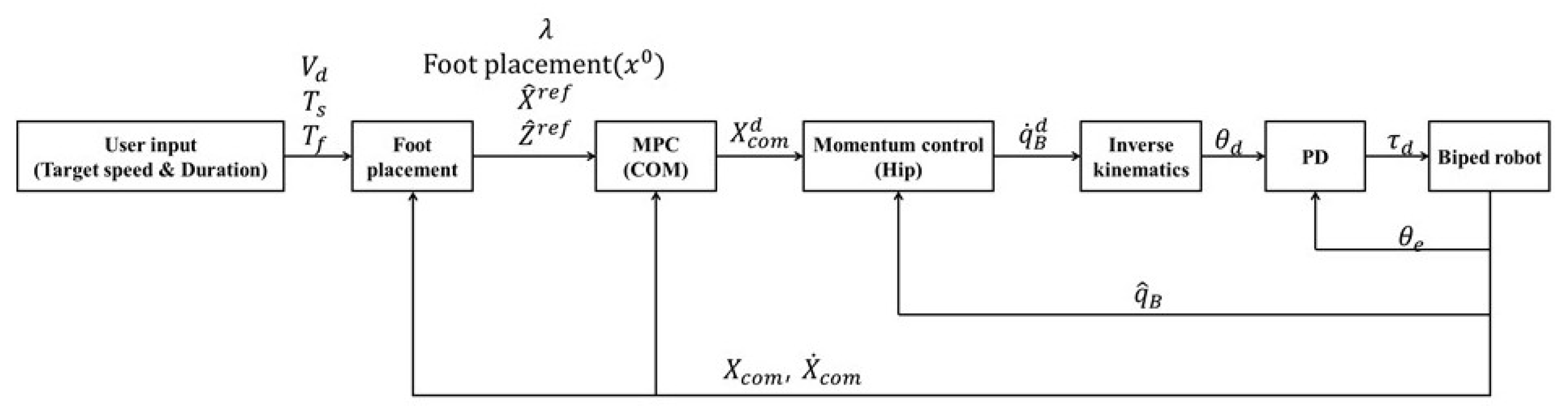
4. Hierarchical Motion Control
4.1. COM Trajectory Generation Based on MPC
4.2. Momentum Control Based on Optimization
5. Performance Validation
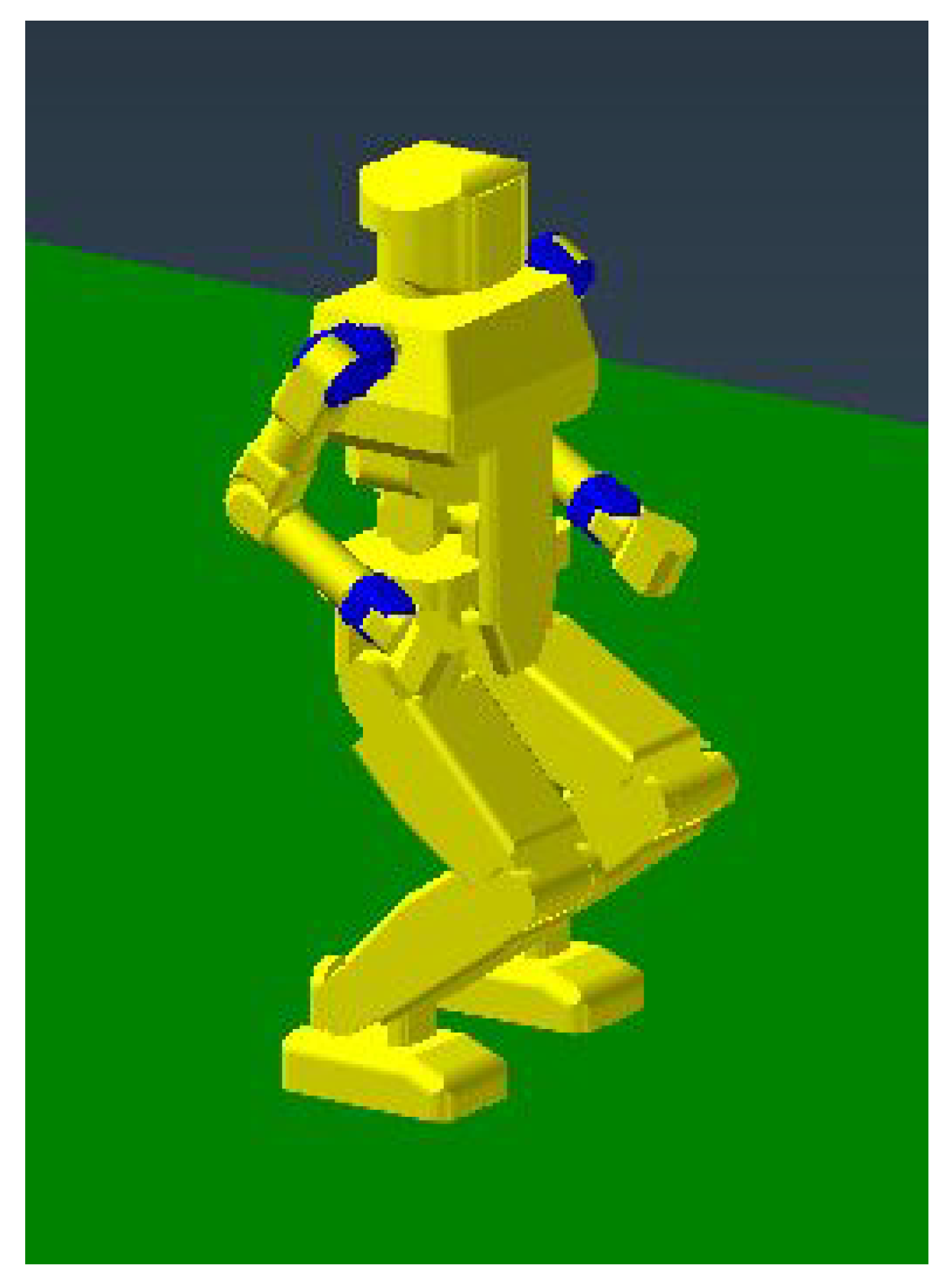
5.1. Simulation Environment
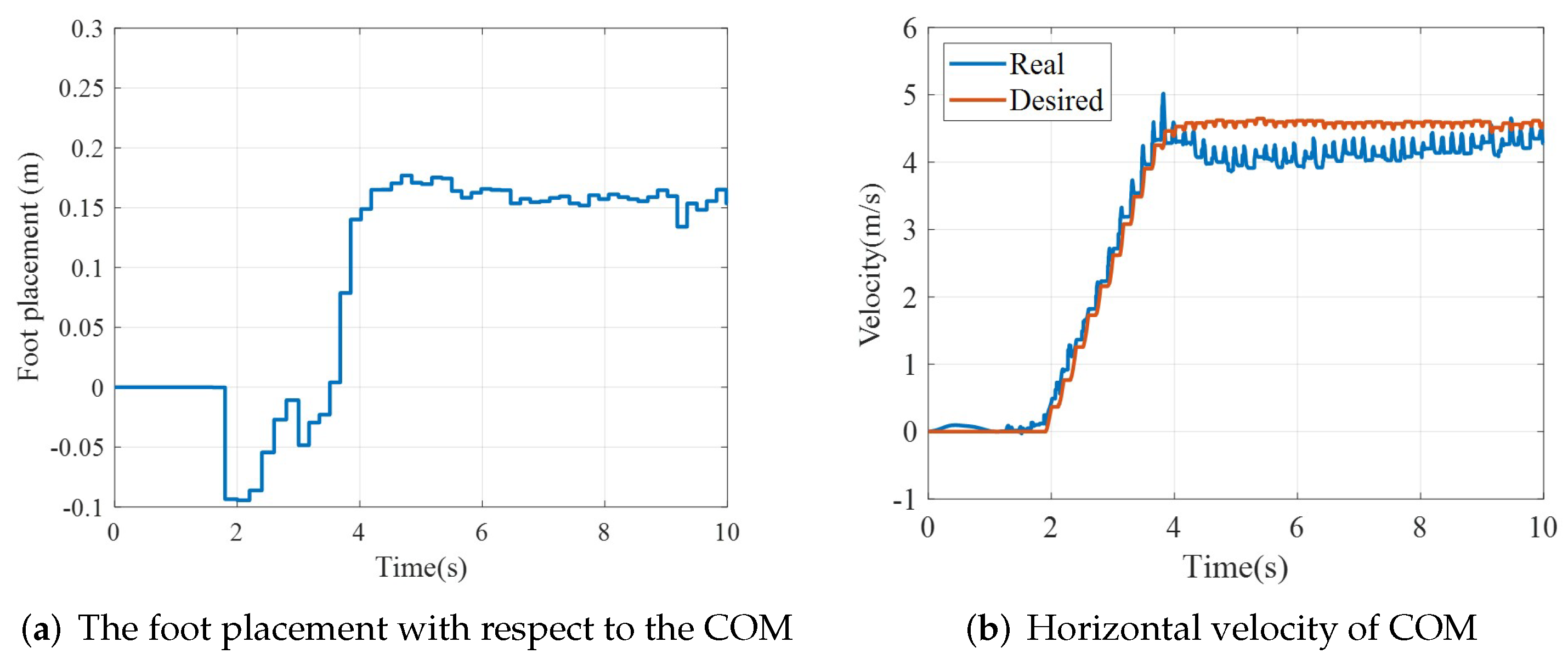
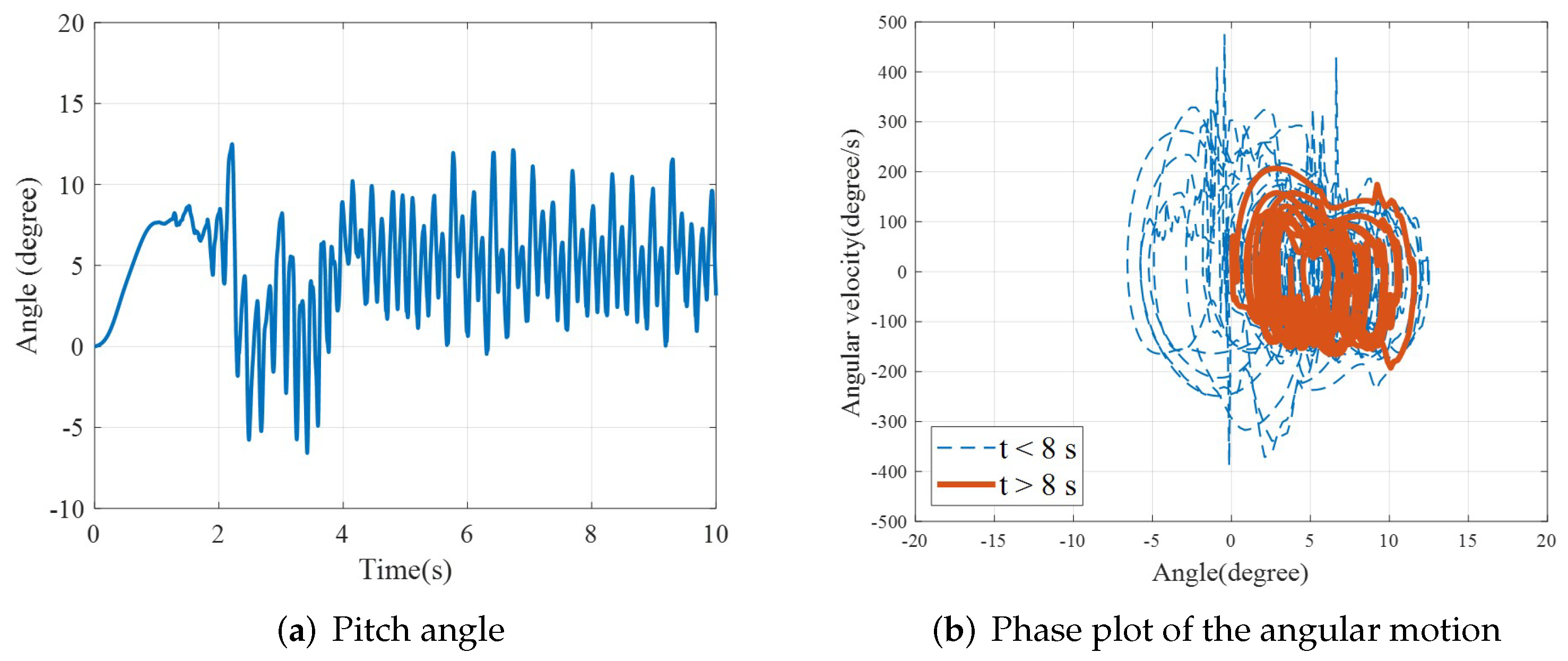
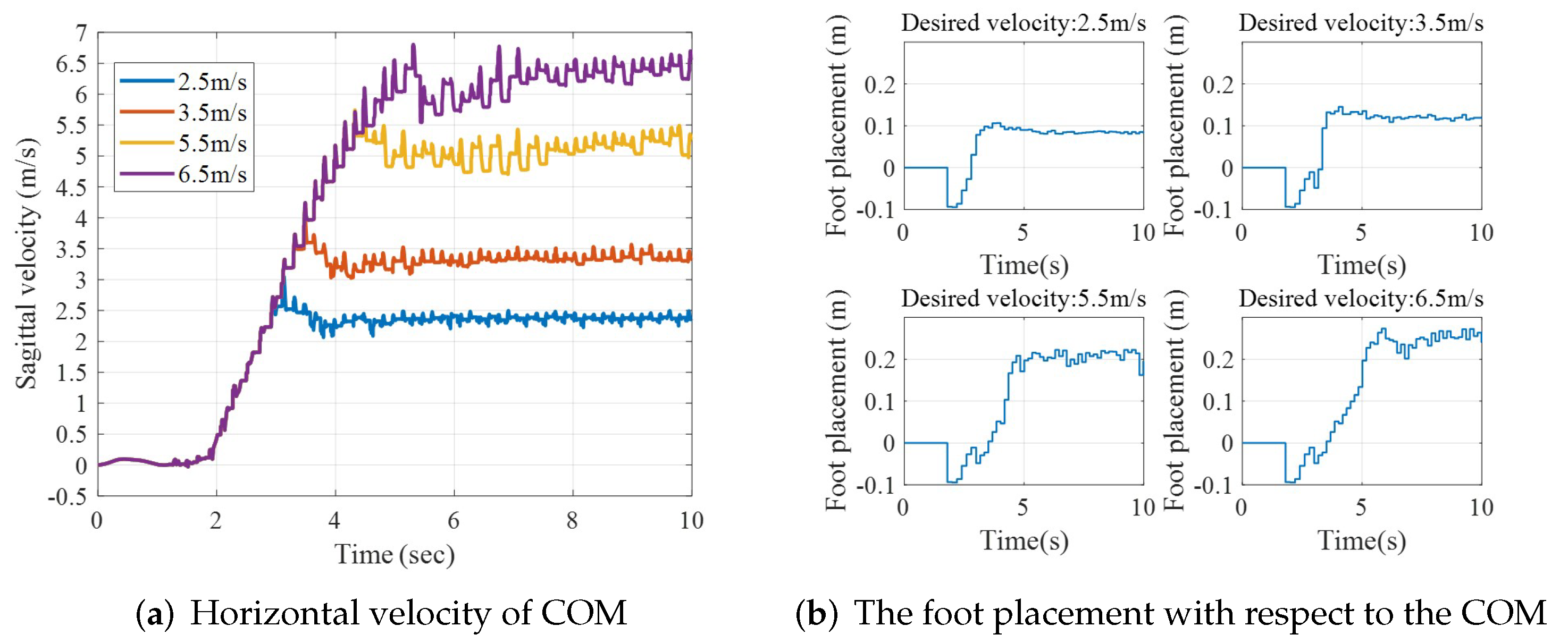
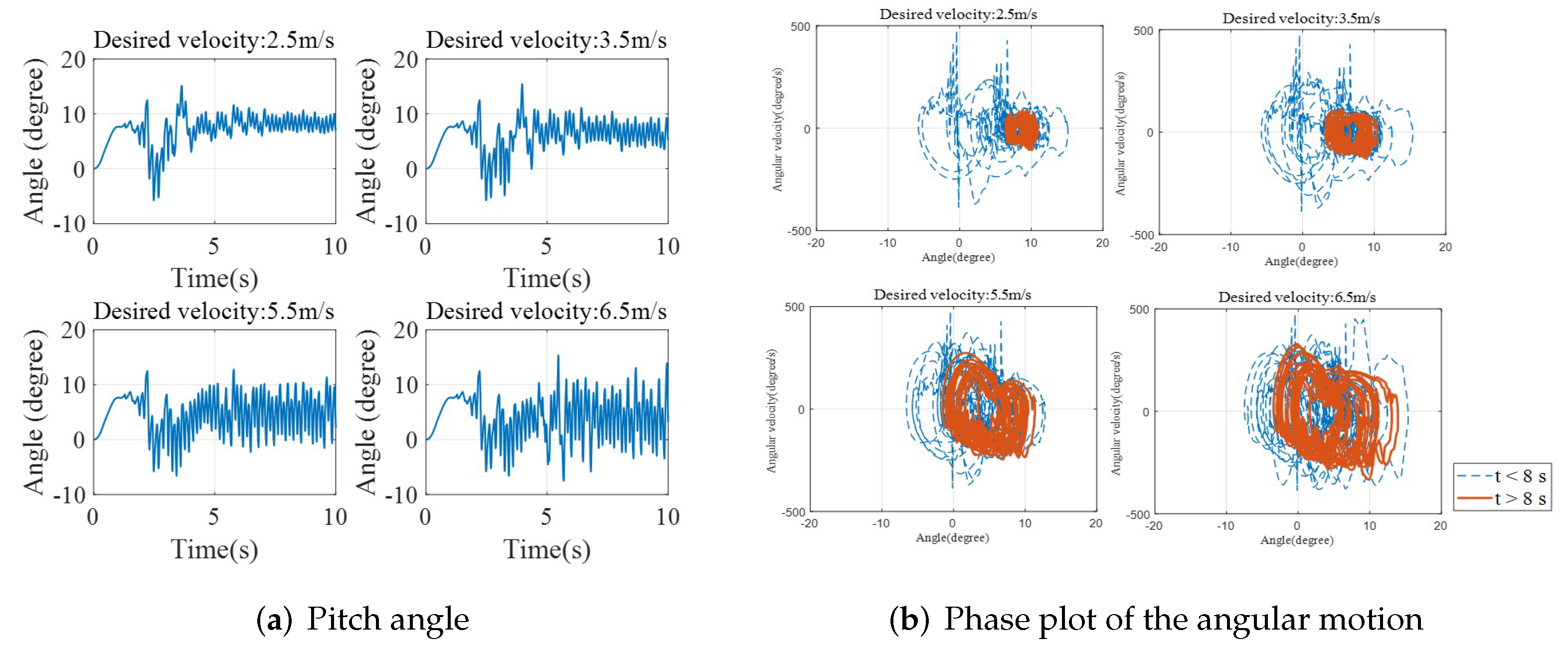
5.2. Running on Flat Terrain
5.3. Running on Uneven Terrain: Case 1
5.4. Running on Uneven Terrain: Case 2
5.5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kajita, S.; Tani, K. Study of dynamic biped locomotion on rugged terrain-theory and basic experiment. In Proceedings of the Fifth International Conference on Advanced Robotics’ Robots in Unstructured Environments, Pisa, Italy, 19–22 June 1991. [Google Scholar]
- Lee, J.H.; Park, J.H. Optimization of Postural Transition Scheme for Quadruped Robots Trotting on Various Surfaces. IEEE Access 2019, 7, 168126–168140. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Wang, S.; Wang, J.; Ma, L. Flexible gait transition for six wheel-legged robot with unstructured terrains. Robot. Auton. Syst. 2022, 150, 103989. [Google Scholar] [CrossRef]
- Waldron, K.J. Mobility and controllability characteristics of mobile robotic platforms. In Proceedings of the IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Yokoi, K.; Hirukawa, H. The 3rd linear inverted pendulum mode: A simple modeling for biped walking pattern generation. In Proceedings of the International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001. [Google Scholar]
- Park, J.H.; Kim, K.D. Biped robot walking using gravity-compensated inverted pendulum mode and computed torque control. In Proceedings of the International Conference on Advanced Robotics, Leuven, Belgium, 20–20 May 1998. [Google Scholar]
- Morimoto, J.; Endo, G.; Nakanishi, J.; Cheng, G. A Biologically Inspired Biped Locomotion Strategy for Humanoid Robots: Modulation of Sinusoidal Patterns by a Coupled Oscillator Model. IEEE Trans. Robot. 2008, 24, 1. [Google Scholar] [CrossRef] [Green Version]
- Shimmyo, S.; Sato, T.; Ohnishi, K. Biped Walking Pattern Generation by Using Preview Control Based on Three-Mass Model. IEEE Trans. Ind. Electron. 2013, 60, 11. [Google Scholar] [CrossRef]
- Flayols, T.; Prete, O.D.A.D.; Khadiv, M.; Mansard, N.; Righetti, L. Reactive Balance Control for Legged Robots under Visco-Elastic Contacts. Appl. Sci. 2021, 11, 353. [Google Scholar] [CrossRef]
- Lu, Y.; Gao, J.; Shi, X.; Tian, D.; Liu, Y. Sliding Balance Control of a Point-Foot Biped Robot Based on a Dual-Objective Convergent Equation. Appl. Sci. 2021, 11, 4016. [Google Scholar] [CrossRef]
- Kamioka, T.; Sugihara, T. Survey on model-based biped motion control for humanoid robots. Adv. Robot. 2020, 34, 21–22. [Google Scholar]
- Reibert, M.H.; Tello, T.R. Legged robots that balance. IEEE Expert 1986, 1, 4. [Google Scholar] [CrossRef]
- Hodgins, J.K.; Raibert, M.H. Adjusting Step Length for Rough Terrain Locomotion. IEEE Trans. Robot. Autom. 1991, 7, 3. [Google Scholar] [CrossRef]
- Saranli, U.; Schwind, W.J.; Koditschek, D.E. Toward the Control of a Multi-Jointed, Monoped Runner. In Proceedings of the International Conference on Advanced Robotics, Leuven, Belgium, 20–20 May 1998. [Google Scholar]
- Kwon, O.; Park, J.H. Asymmetric trajectory generation and impedance control for running of biped robots. Auton. Robot. 2009, 26, 47–78. [Google Scholar] [CrossRef]
- Thanh, D.N.; Hayashi, T.; Yamakita, M. High speed running of flat foot Biped robot with Inerter using SLIP. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics, Busan, Korea, 7–11 July 2015. [Google Scholar]
- Kajita, S.; Nagasaki, T.; Kaneko, K.; Yokoi, K.; Tanie, K. A Running Controller of Humanoid Biped HRP-2LR. In Proceedings of the International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005. [Google Scholar]
- Kajita, S.; Nagasaki, T.; Kaneko, K.; Hirukawa, H. ZMP-Based Biped Running Control. IEEE Robot. Autom. Mag. 2007, 14, 63–72. [Google Scholar] [CrossRef]
- Tajima, R.; Honda, D.; Suga, K. Fast running experiments involving a humanoid robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 18 August 2009. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Biped walking pattern generation by using preview control of zero-moment point. In Proceedings of the International Conference on Advanced Robotics, Taipei, Taiwan, 14–19 September 2003. [Google Scholar]
- Wu, A.; Geyer, H. Highly robust running of articulated bipeds in unobserved terrain. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Nir, O.; Degani, A. Reactive Control for Bipedal Running Over Random Discrete Terrain Under Uncertainty. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021. [Google Scholar]
- Wensing, P.M.; Orin, D.E. High-Speed Humanoid Running Through Control with a 3D-SLIPM Model. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robot and Systems, Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Boroujeni, M.G.; Daneshman, E.; Righetti, L.; Khadiv, M. A unified framework for walking and running of bipedal robots. In Proceedings of the International Conference on Advanced Robotics, Ljubljana, Slovenia, 6–10 December 2021. [Google Scholar]
- Kuindersma, S.; Permenter, F.; Tedrake, R. An Efficiently Solvable Quadratic Program for Stabilizing Dynamic Locomotion. In Proceedings of the International Conference on Robotics and Automation, Hong Kong, China, 31 May–5 June 2014. [Google Scholar]
- Dai, H.; Valenzuela, A.; Tedrake, R. Whole-body Motion Planning with Centroidal Dynamics and Full Kinematics. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014. [Google Scholar]
- Rathod, N.; Bratta, A.; Focchi, M.; Zanon, M.; Villarreal, O.; Semini, C.; Bemporad, A. Model Predictive Control with Environment Adaptation for Legged Locomotion. IEEE Access 2021, 9, 145710–145727. [Google Scholar] [CrossRef]
- Xi, Y.-G.; Li, D.-W.; Lin, S. Model Predictive Control—Status and Challenges. Acta Autom. Sin. 2013, 39, 222–236. [Google Scholar] [CrossRef]
- Rossiter, J.A. Model-Based Predictive Control; CRC Press: Boca Raton, FL, USA, 2017; pp. 1–318. [Google Scholar]
- Parisio, A.; Rikos, E.; Glielmo, L. A Model Predictive Control Approach to Microgrid Operation Optimization. IEEE Trans. Control. Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Wieber, P.-B. Trajectory Free Linear Model Predictive Control for Stable Walking in the Presence of Strong Perturbations. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006. [Google Scholar]
- Scianca, N.; Simone, D.D.; Lanari, L.; Oriolo, G. MPC for Humanoid Gait Generation: Stability and Feasibility. IEEE Trans. Robot. 2020, 36, 1171–1188. [Google Scholar] [CrossRef] [Green Version]
- Rutschmann, M.; Satzinger, B.; Byl, M.; Byl, K. Nonlinear model predictive control for rough-terrain robot hopping. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012. [Google Scholar]
- Carlo, J.D.; Wensing, P.M.; Katz, B.; Bledt, G.; Kim, S. Dynamic Locomotion in the MIT Cheetah 3 Through Convex Model-Predictive Control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Hopkins, M.A.; Hong, D.W.; Leonessa, A. Humanoid locomotion on uneven terrain using the time-varying divergent component of motion. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014. [Google Scholar]
- Griffin, R.J.; Leonessa, A. Model predictive control for dynamic footstep adjustment using the divergent component of motion. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016. [Google Scholar]
- Joe, H.-M.; Oh, J.-H. Balance recovery through model predictive control based on capture point dynamics for biped walking robot. Robot. Auton. Syst. 2018, 105, 1–10. [Google Scholar] [CrossRef]
- Hirukawa, H.; Hattori, S.; Harada, K.; Kajita, S.; Kaneko, K.; Kanehiro, F.; Fujiwara, K.; Morisawa, M. A Universal Stability Criterion of the Foot Contact of Legged Robots-Adios ZMP. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Resolved Momentum Control: Humanoid Motion Planning based on the Linear and Angular Momentum. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar]
- Hunt, K.H.; Crossley, F.R.E. Coefficient of Restitution Interpreted as Damping in Vibroimpact. J. Appl. Mech. 1975, 42, 440–445. [Google Scholar] [CrossRef]
- FunctionBay. Recurdyn, Solver Theoretical Manual. Available online: https://functionbay.com/documentation/onlinehelp/default.htm (accessed on 1 October 2022).
- Cha, H.-Y.; Choi, J.; Ryu, H.S.; Choi, J.H. Stick-slip algorithm in a tangential contact force model for multi-body system dynamics. J. Mech. Sci. Technol. 2011, 25, 1687–1694. [Google Scholar] [CrossRef]
- Donelan, J.M.; Kram, R. Exploring dynamic similarity in human running using simulated reduced gravity. J. Exp. Biol. 2000, 203, 2405–2415. [Google Scholar] [CrossRef]
- Vaughan, C.L.; O’Malley, M.J. Froude and the contribution of naval architecture to our understanding of bipedal locomotion. Int. J. Adv. Robot. Syst. 2005, 21, 350–362. [Google Scholar] [CrossRef]
- Omer, A.; Hashimoto, K.; Lim, H.-O.; Takanishi, A. Study of Bipedal Robot Walking Motion in Low Gravity: Investigation and Analysis. Int. J. Adv. Robot. Syst. 2014, 11, 139. [Google Scholar] [CrossRef]



| Parts | Mass (kg) | Height/Length (m) |
|---|---|---|
| Hip | 18.01 | |
| Thigh (2EA) | 2.93 | 0.265 |
| Shank (2EA) | 2.75 | 0.265 |
| Foot (2EA) | 1.93 | 0.1 |
| Total | 33.32 | 0.625 |
| Symbols | Values | Unit | Symbols | Values | Unit |
|---|---|---|---|---|---|
| k | 2000 | kN/m | 0.8 | - | |
| c | 1.0 | kNs/m | 1.0 | - | |
| 1.3 | - | 0.15 | m/s | ||
| 1.0 | - | 0.1 | m/s | ||
| 2.0 | - |
| Simulation Time | ||
|---|---|---|
| 0.100 s | 1.10 s∼3.00 s | 6.69 |
| 0.070 s | 3.00 s∼4.02 s | 7.35 |
| 0.065 s | 4.02 s∼5.34 s | 7.51 |
| 0.060 s | 5.34 s∼10.00 s | 7.69 |
| Symbols | Description | Value |
|---|---|---|
| Weight of MPC for control input in the horizontal direction | 1.0 | |
| Weight of MPC for speed in the horizontal direction | ||
| Weight of MPC for ZMP | ||
| Weight of MPC for control input in the vertical direction | 1.0 | |
| Weight of MPC for speed in the vertical direction | ||
| Weight of MPC for | ||
| Friction coefficient for friction cone of MPC | ||
| Weight of momentum control for control input | ||
| Weight of momentum control for position of linear motion | ||
| Weight of momentum control for linear momentum | ||
| Weight of momentum control for angle of angular motion | ||
| Weight of momentum control for angular momentum | ||
| Scale factor of variable weight for linear momentum | ||
| Scale factor of variable weight for angular momentum |
| Target Velocity | Foot Placement | Velocity | |
|---|---|---|---|
| 2.5 m/s | 0.085 m | 2.49 m/s | 1.0162 |
| 3.5 m/s | 0.119 m | 3.55 m/s | 2.0659 |
| 5.5 m/s | 0.214 m | 5.49 m/s | 4.9195 |
| 6.5 m/s | 0.263 m | 6.70 m/s | 7.3185 |
| Symbols | Height (mm) | Symbols | Height (mm) | Symbols | Height (mm) |
|---|---|---|---|---|---|
| A | 30 | F | 180 | K | 150 |
| B | 60 | G | 210 | L | 120 |
| C | 90 | H | 240 | M | 90 |
| D | 120 | I | 210 | N | 60 |
| E | 150 | J | 180 | O | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J.; Park, J.H. Model Predictive Control of Running Biped Robot. Appl. Sci. 2022, 12, 11183. https://doi.org/10.3390/app122111183
Cho J, Park JH. Model Predictive Control of Running Biped Robot. Applied Sciences. 2022; 12(21):11183. https://doi.org/10.3390/app122111183
Chicago/Turabian StyleCho, Jaeuk, and Jong Hyeon Park. 2022. "Model Predictive Control of Running Biped Robot" Applied Sciences 12, no. 21: 11183. https://doi.org/10.3390/app122111183
APA StyleCho, J., & Park, J. H. (2022). Model Predictive Control of Running Biped Robot. Applied Sciences, 12(21), 11183. https://doi.org/10.3390/app122111183






