Experimental Study on Shear Behavior of Interface between Different Soil Materials and Concrete under Variable Normal Stress
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Concrete Samples
2.2. Preparation of Cement Soil Sample
2.3. Preparation of Sand Sample
2.4. Preparation of Clay Samples
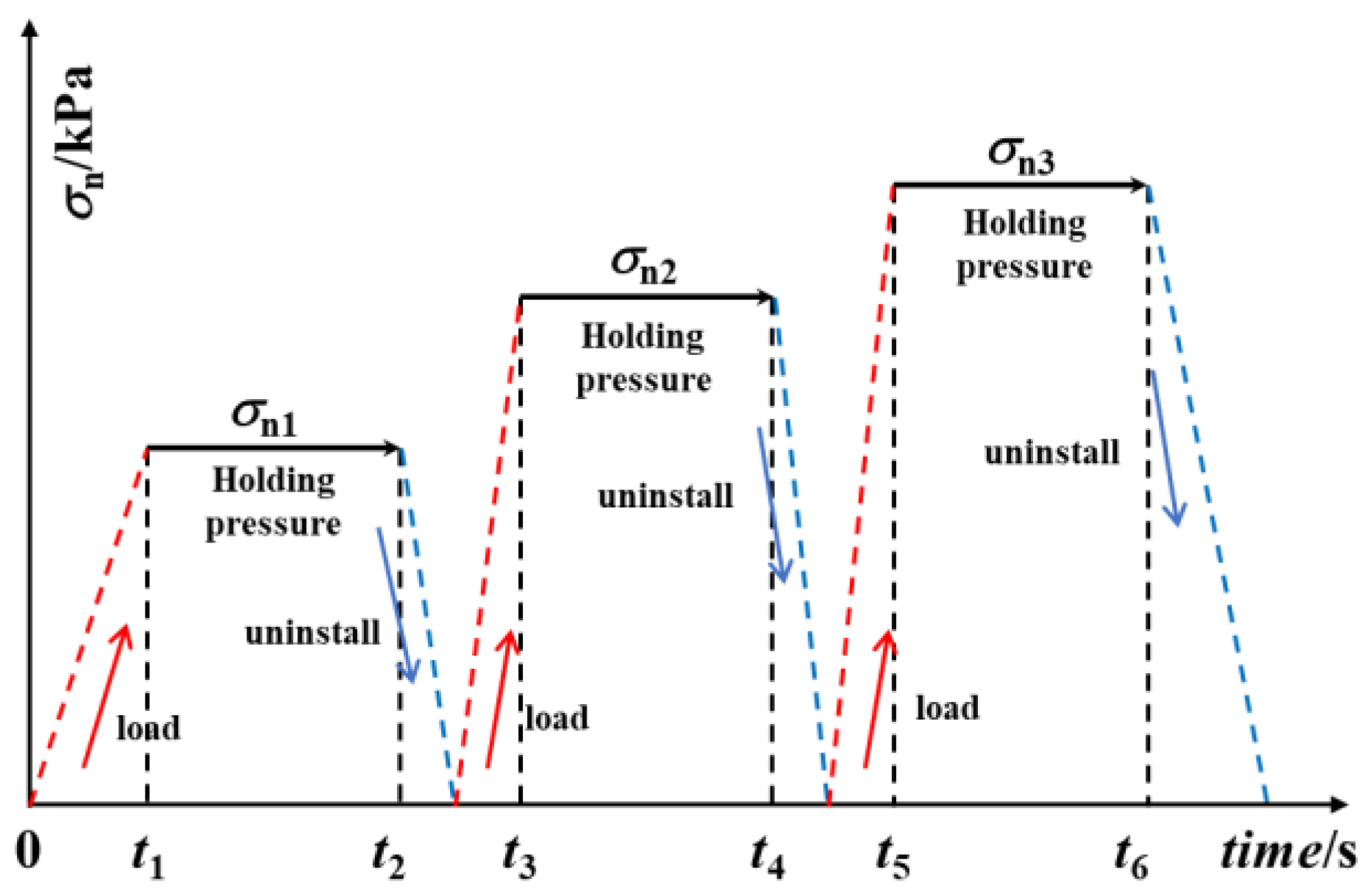
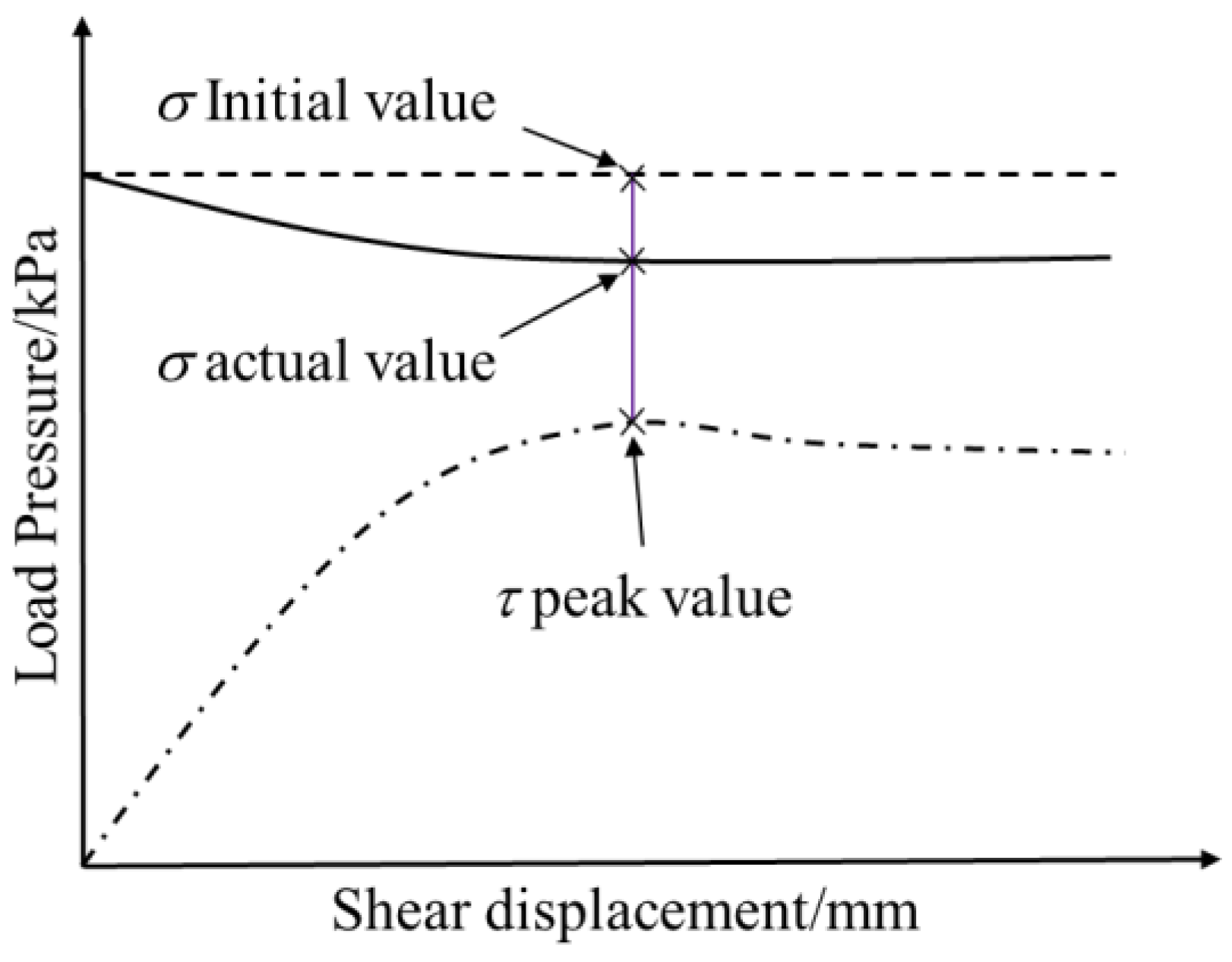
2.5. Test Procedure
3. Results
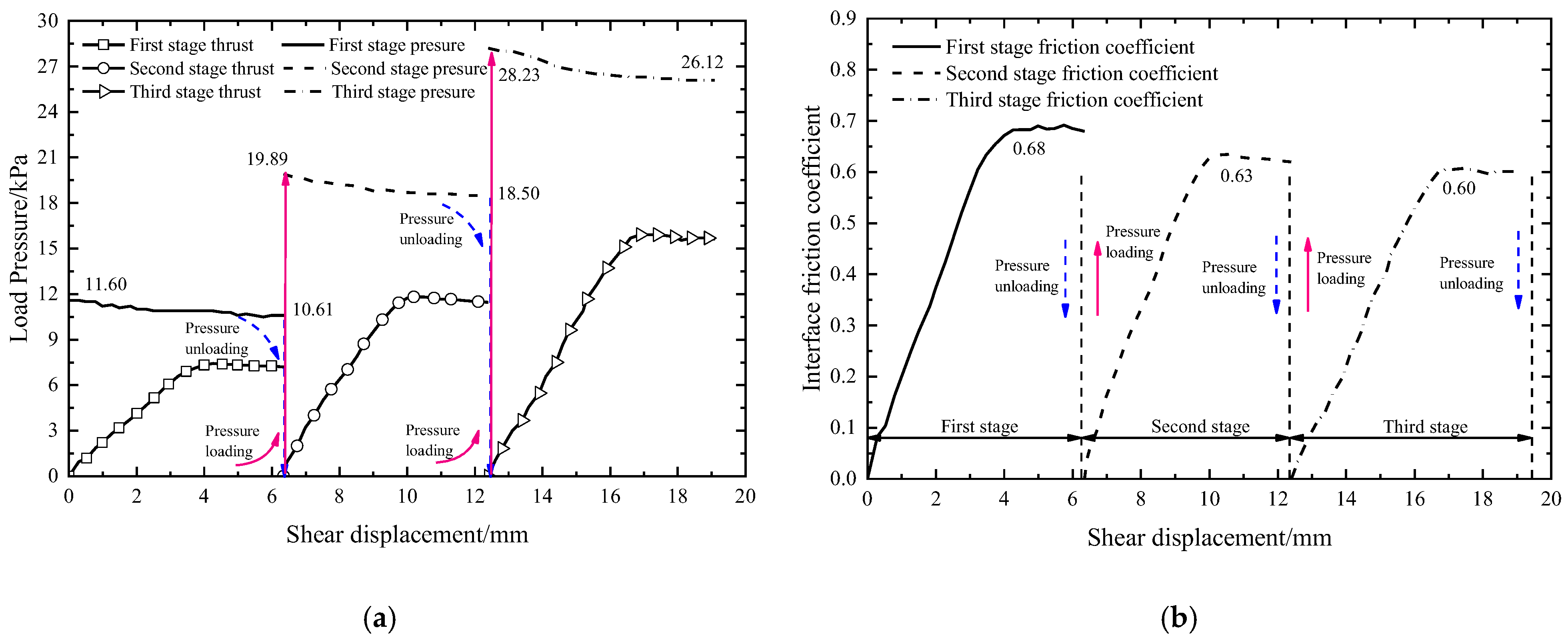
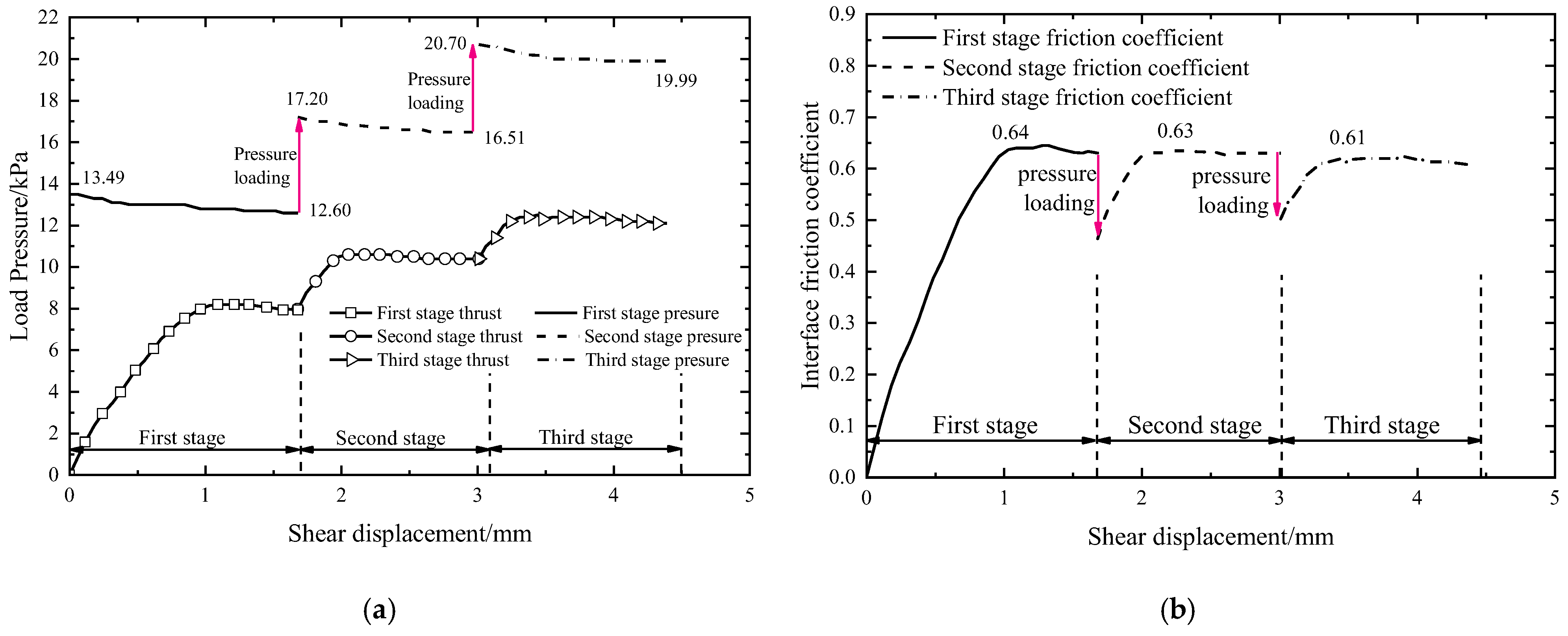
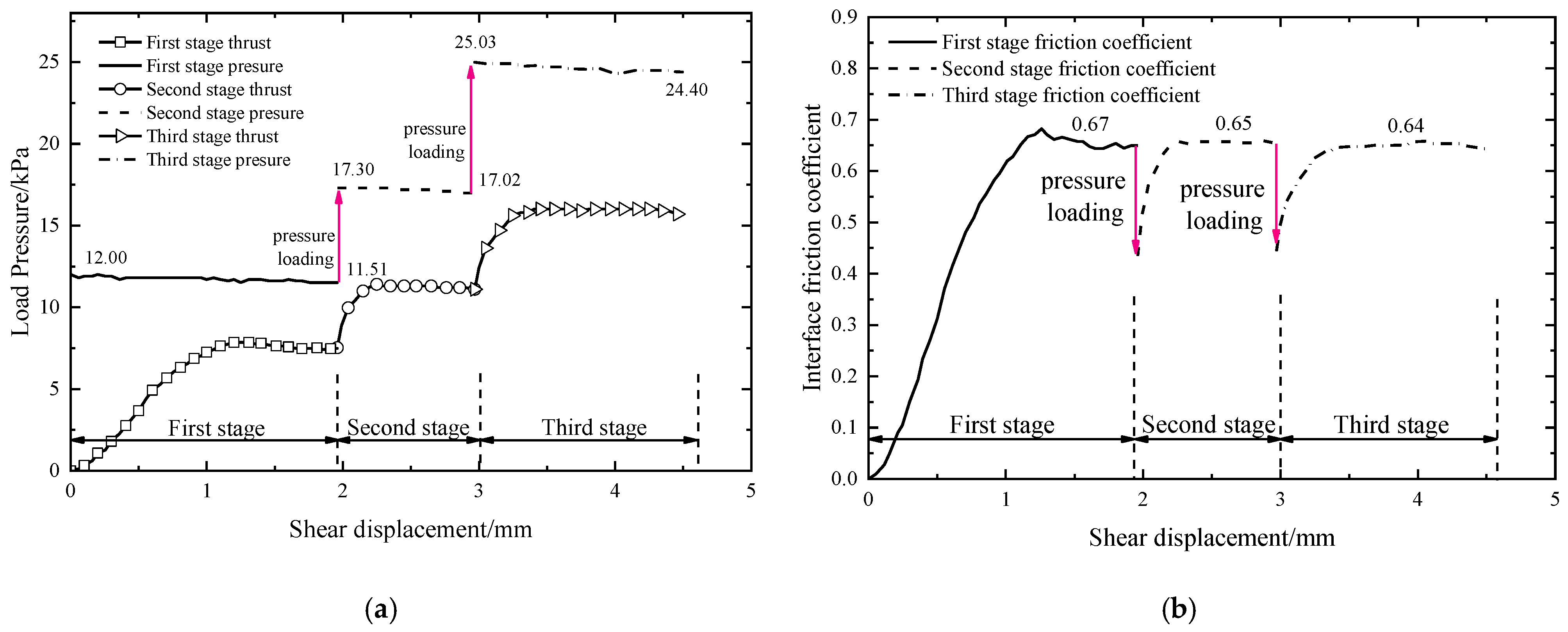
3.1. Interface Shear Test under Repeated Loading
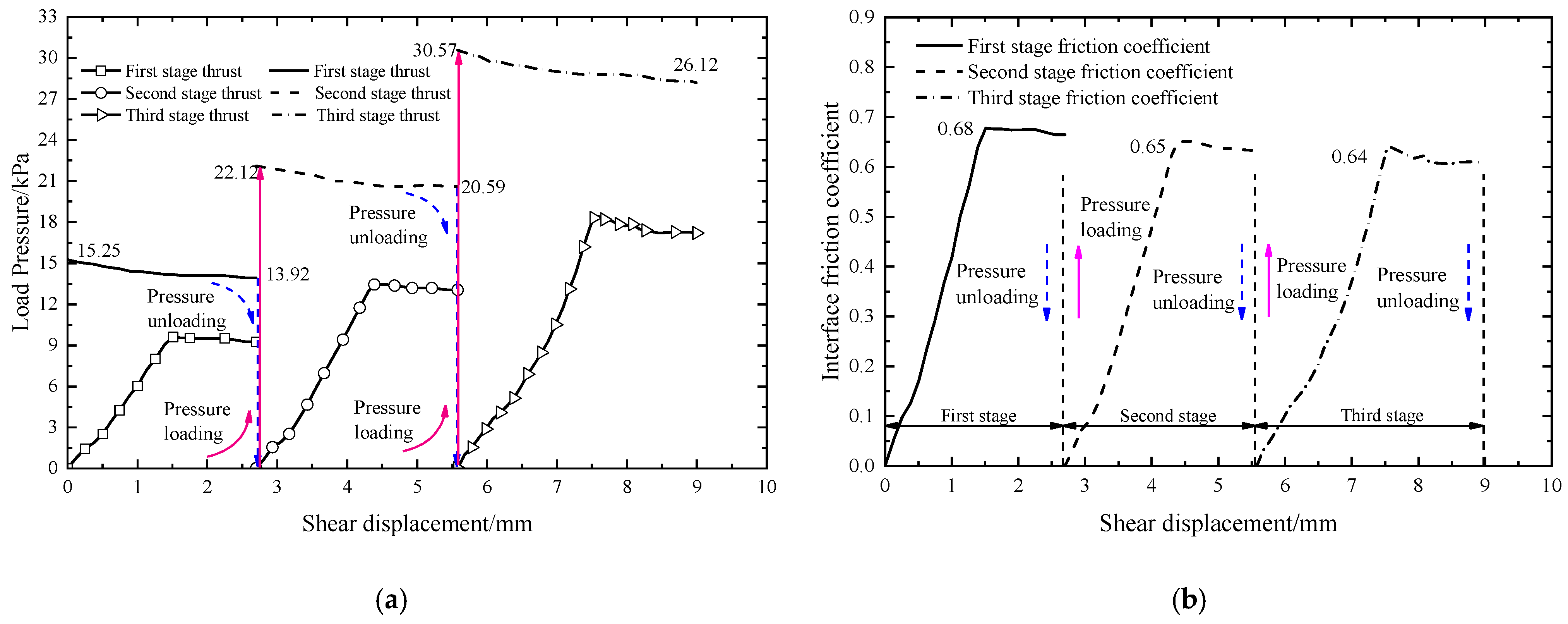
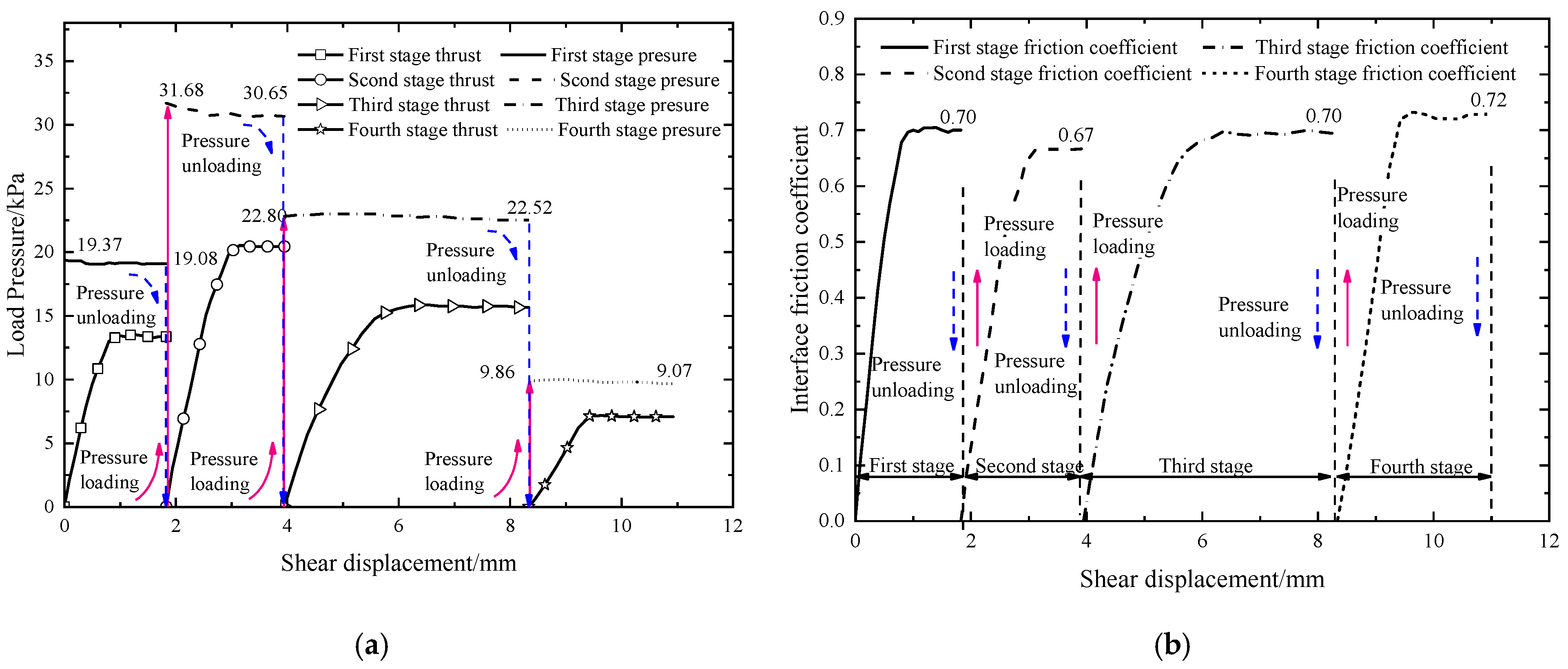
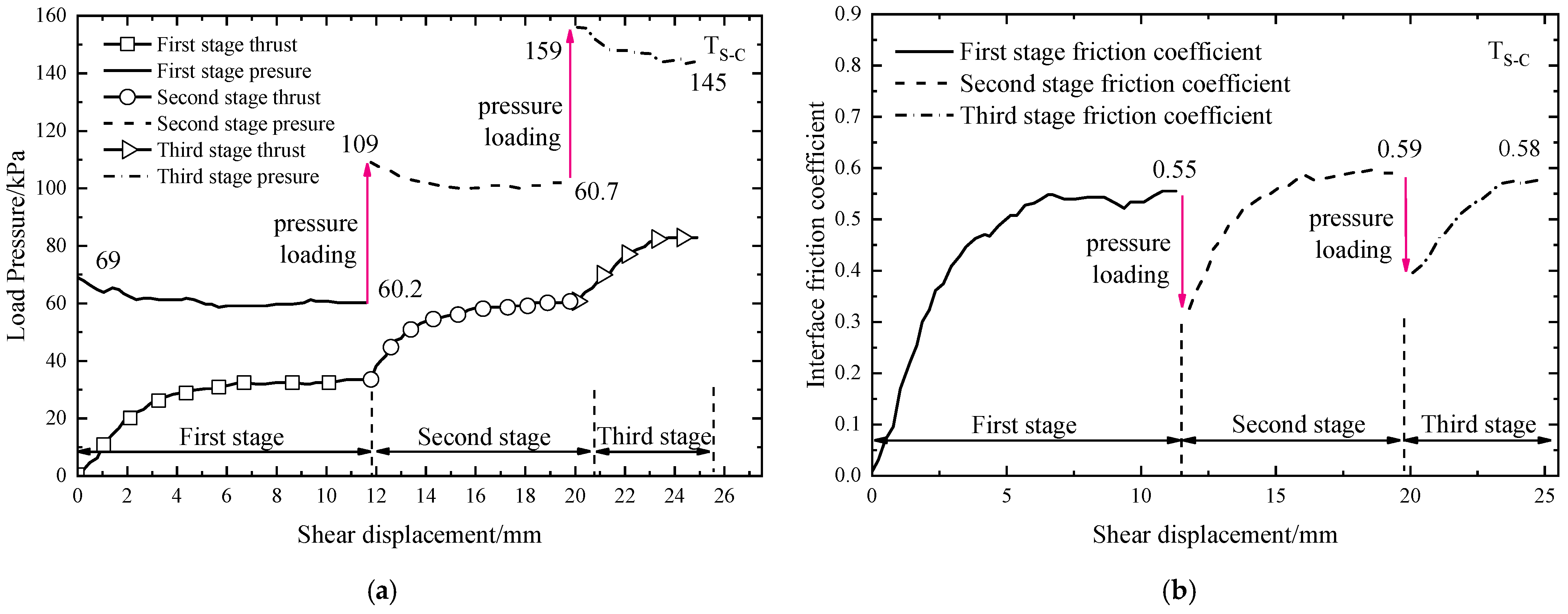
3.2. Continuous Loading Interface Shear Test
4. Discussion
4.1. Minimum Friction Coefficient of Interface
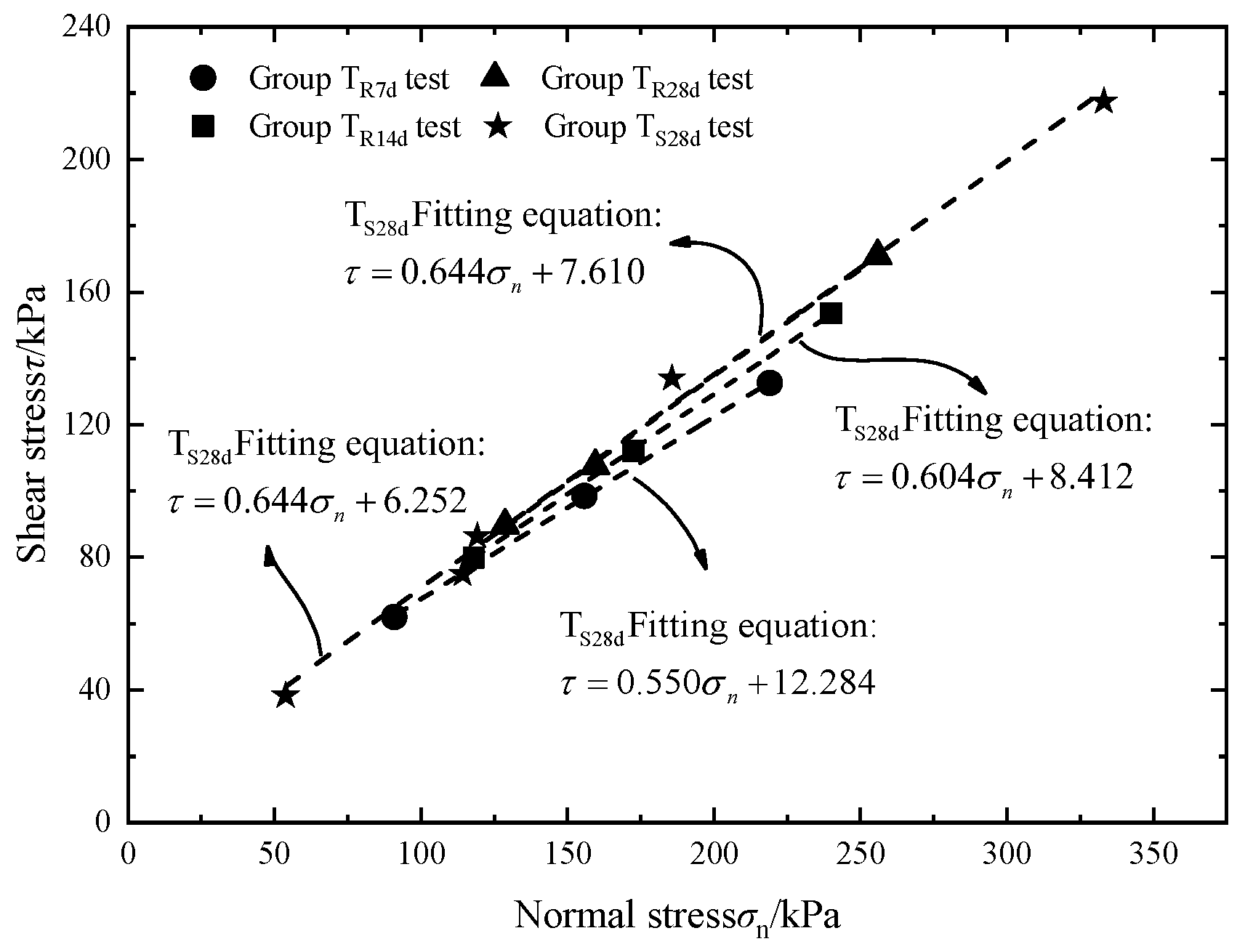
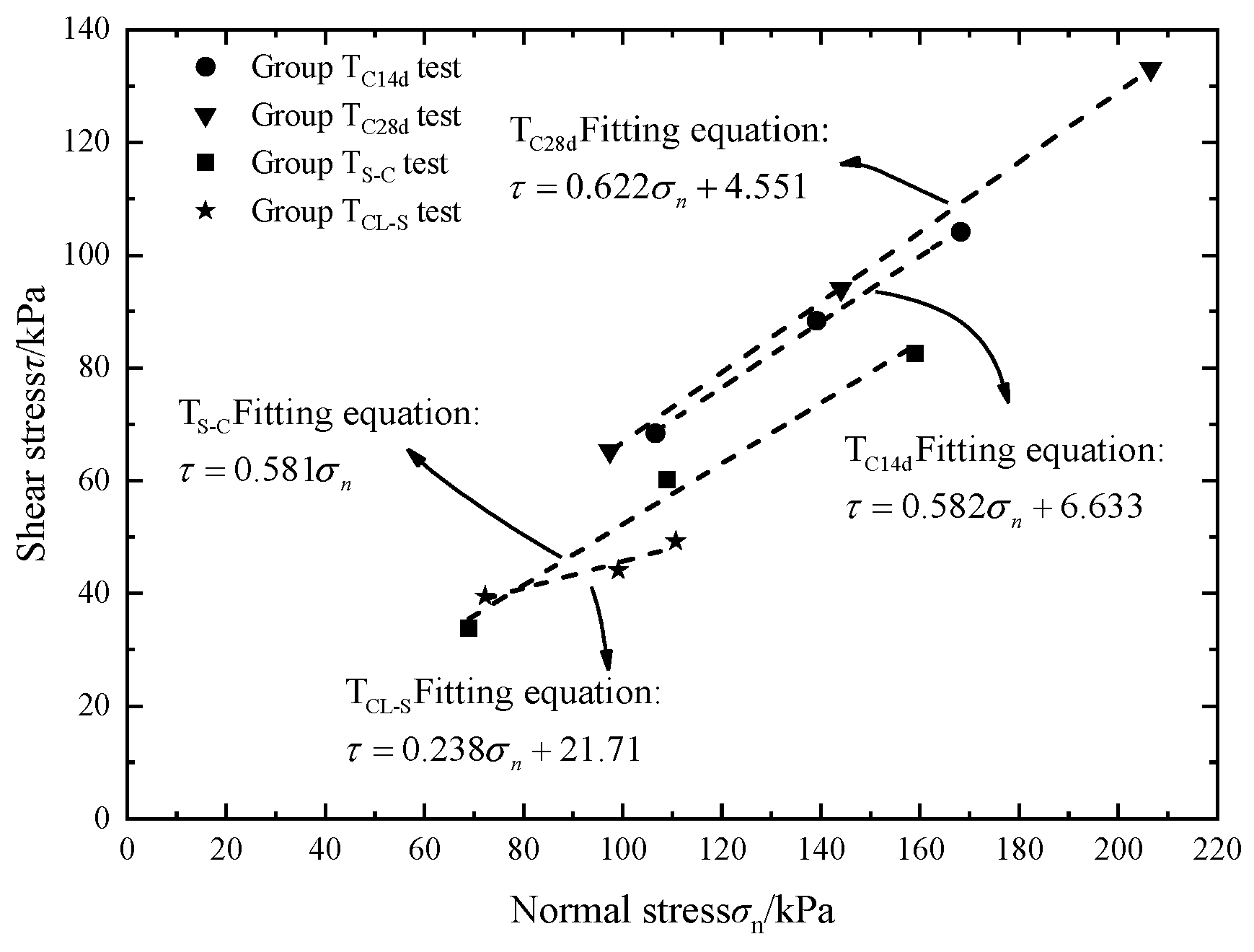
4.2. Data Fitting
4.3. Analysis of Fitting Data for Repeated Loading and Unloading of Variable Normal Stress
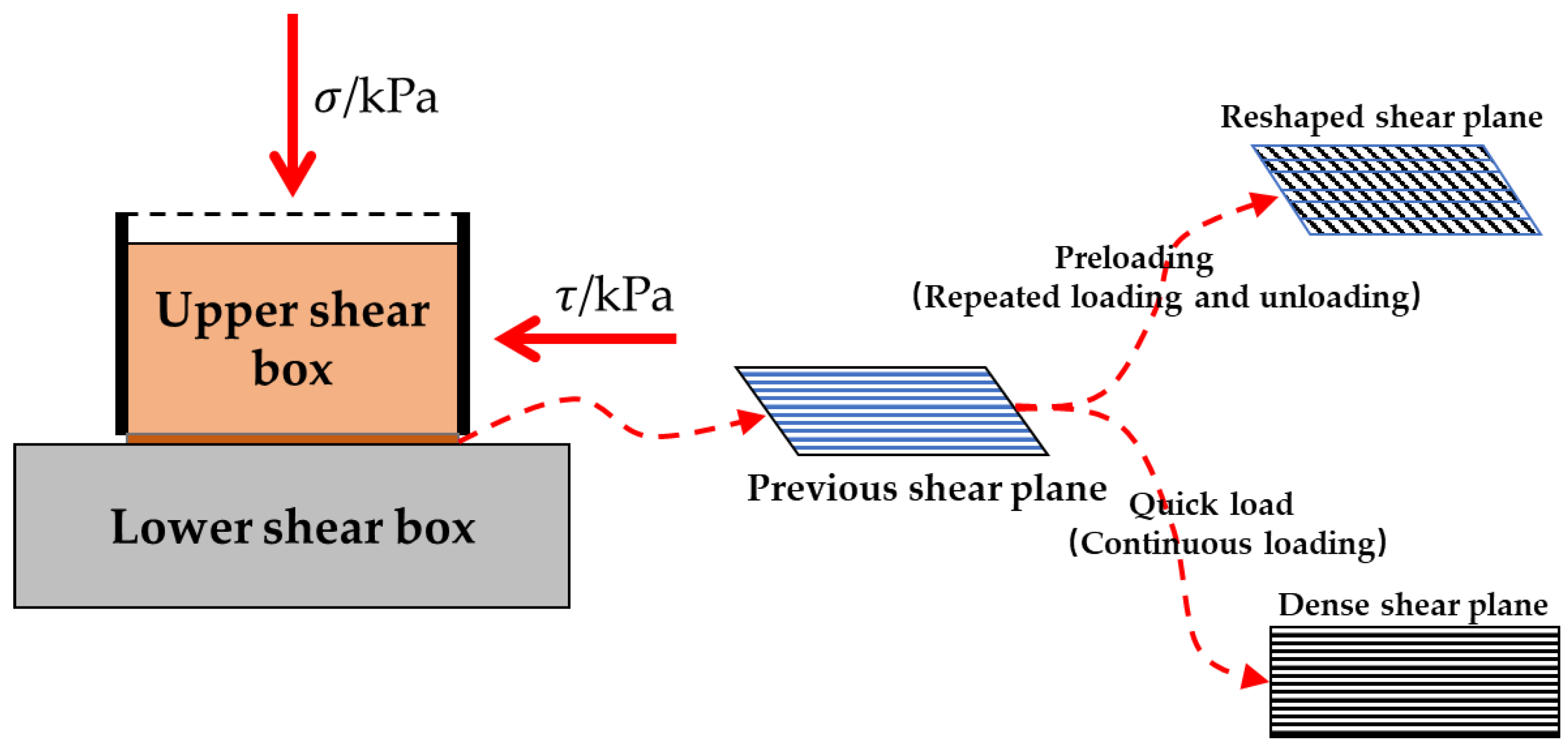
4.4. Interface Reshaping and Compaction Mechanism Analysis
4.5. Analysis of Cohesive Force on Interface Friction Coefficient
4.6. Mechanism Analysis of Critical Displacement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.Z.; Xiang-Jun, L.I.; Zhu, H.K. Test Study of Mechanical Mechanism of Shear Studs in Cable-to-Pylon Anchorage Zone of Cable-Stayed Bridge. World Bridges 2011, 3, 49–52. [Google Scholar]
- Huang, N.Q.; Ya-Ping, L.I.; Cheng, L.P. Stability calculation and numerical analysis on anchorage of suspension bridge with gravity concrete. J. Henan Univ. Urban Constr. 2014, 119, 1439–1448. [Google Scholar]
- Abdellatif, B.; Gong, W.; Dai, G.; Zhu, M. Failure envelope of a caisson foundation under combined vertical, horizontal and moment loadings. J. Southeast Univ. 2020, 36, 188–197. [Google Scholar]
- You, X.M.; Huang, H.W. Test study on mechanism of shear-slip of anchorage in suspension bridge. Rock Soil Mech. 2007, 28, 336–342. [Google Scholar]
- Liu, H.J.; Sun, P.P.; Geng, H.R.; Hao, R. Horizontal Bearing Capacity of Offshore Wind Power Pile Foundation Under Different Sea Conditions and Geological Conditions. Period. Ocean. Univ. China 2019, 8, 51–58. [Google Scholar]
- Zhang, X.L.; Liu, J.X.; Han, Y.; Du, X.L. A framework for evaluating the bearing capacity of offshore wind power foundation under complex loadings. Appl. Ocean. Res. 2018, 80, 66–78. [Google Scholar] [CrossRef]
- Guo, W.T.; Wu, Y.C. Numerical Analysis of Horizontal Bearing Capacity of Composite Pile Foundation for Offshore Wind Turbine. IOP Conf. Ser. Earth Environ. Sci. 2020, 474, 022029. [Google Scholar]
- Miura, N.; Horpibulsuk, S.; Nagaraj, T.S. Engineering behavior of cement stabilized clay at high water content. Soils Found. 2001, 41, 33–45. [Google Scholar] [CrossRef] [Green Version]
- Horpibulsuk, S.; Miura, N.; Nagaraj, T.S. Clay-water/cement ratio identity of cement admixed soft clays. J. Geotech. Geoenviron. Eng. 2005, 131, 187–192. [Google Scholar] [CrossRef]
- Horpibulsuk, S.; Miura, N.; Nagaraj, T.S. Assessment of strength development in cement-admixed high water content clays with Abrams’ law as a basis. Geotechnique 2003, 53, 439–444. [Google Scholar] [CrossRef]
- He, K.S. Present construction quality problem of deep mixing cement-soil piles and solving measures. Rock Soil Mech. 2002, 23, 778–781. [Google Scholar]
- Liu, G.S.; Li, L.; Yang, X.C. Numerical analysis of stress distribution in backfilled stopes considering interfaces between the backfill and rock walls. Int. J. Geomech. 2017, 17, 06016014. [Google Scholar] [CrossRef]
- Fang, K.; Fall, M. Effects of curing temperature on shear behaviour of cemented paste backfill-rock interface. Int. J. Rock Mech. Min. Sci. 2018, 112, 184–192. [Google Scholar] [CrossRef]
- Fang, K.; Fall, M. Chemically induced changes in the shear behaviour of interface between rock and tailings backfill undergoing cementation. Rock Mech. Rock Eng. 2019, 52, 3047–3062. [Google Scholar] [CrossRef]
- Fang, K.; Fall, M. Shear behavior of the interface between rock and cemented backfill: Effect of curing stress, drainage condition and backflling rate. Rock Mech. Rock Eng. 2020, 53, 325–336. [Google Scholar] [CrossRef]
- Basudhar, P.K. Modeling of soil–woven geotextile interface behavior from direct shear test results. Geotext. Geomembr. 2010, 28, 403–408. [Google Scholar]
- Ouagni, M.S.T.; Ngapgue, F.; Kenmogne, F.; Kammogne, A.S.T.; Koumi, S.N. Mathematical Modeling of Shear Stress and Direct Shear Test for Compressible Soil: Case of Soil Bordering the Wouri River. World Eng. Technol. 2021, 9, 22. [Google Scholar] [CrossRef]
- Shaojun, L.I.; Meng, F.; Chen, J. Development of shear test device with interface visualization for soil-structure interaction and its application. Chin. J. Rock Mech. Eng. 2012, 31, 180–188. [Google Scholar]
- Gómez, J.E.; Filz, G.M.; Ebeling, R.M.; Dove, J.E. Sand-to-Concrete Interface Response to Complex Load Paths in a Large Displacement Shear Box. Geotech. Test. J. 2008, 31, 358–369. [Google Scholar]
- Weiping, C.; Qingyuan, L.; Peng, L. Experimental study on shear mechanical properties on dense sand-concrete interface under constant and varying normal stress. Build. Struct. 2015, 44, 82–86. [Google Scholar]
- Peng, L.; Cao, W.; Lu, Q. Experimental research on shear properties of loose sand-concrete interface under constant/varying normal stress. Build. Struct. 2014, 44, 61–65. [Google Scholar]
- Shahin, M.M. Shear Behaviour of Misurata Wet Sand. Civ. Environ. Res. 2013, 11, 27–30. [Google Scholar]
- Ohara, S.; Matsuda, H. Study on the settlement of saturated clay layer induced by cyclic shear. Soils Found. 1988, 28, 103–113. [Google Scholar] [CrossRef]
- Knodel, P.C.; Talesnick, M.; Frydman, S. Simple Shear of an Undisturbed Soft Marine Clay in NGI and Torsional Shear Equipment. Geotech. Test. J. 1991, 14, 15. [Google Scholar] [CrossRef]
- Balmer, G.G. Shear strength and elastic properties of soil-cement mixtures under triaxial loading. PCA Res. Dev. Lab. 2004, 08, 20–32. [Google Scholar]
- Desplanques, Y. Amontons-Coulomb Friction Laws, A Review of the Original Manuscript. SAE Int. J. Mater. Manuf. 2015, 8, 98–103. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Dudchenko, A.V.; Kuznetso, S.V. The modified Cam-Clay (MCC) model: Cyclic kinematic deviatoric loading. Arch. Appl. Mech. 2016, 86, 2021–2031. [Google Scholar] [CrossRef]








| Number | Material Science | Loading Method | Load Classification | Curing Time of Cement Soil |
|---|---|---|---|---|
| TR7d | Cement soil-concrete | Repeated loading and unloading | 3 | 7 d |
| TR14d | Cement soil-concrete | Repeated loading and unloading | 3 | 14 d |
| TR28d | Cement soil-concrete | Repeated loading and unloading | 4 | 28 d |
| TS28d | Cement soil-concrete | Load separately | 1 | 28 d |
| TC14d | Cement soil-concrete | Continuous graded loading | 3 | 14 d |
| TC28d | Cement soil-concrete | Continuous graded loading | 3 | 28 d |
| TS-C | Sand-concrete | Continuous graded loading | 3 | |
| TCL-S | Clay-concrete | Continuous graded loading | 3 |
| Friction Coefficient | Test Group | |||
|---|---|---|---|---|
| TR7d | TR14d | TR28d | TS28d | |
| This paper μmin | 0.550 | 0.604 | 0.644 | 0.644 |
| Traditional μ | 0.510 | 0.576 | 0.616 | 0.613 |
| Change range | −7.27% | −4.64% | −4.34% | −4.81% |
| Number | TC28d | TS-C | TCL-C |
|---|---|---|---|
| Peak friction coefficient of each stage | 0.67, 0.65, 0.64 | 0.55, 0.59, 0.58 | 0.65, 0.59, 0.48 |
| Peak average | 0.653 | 0.573 | 0.573 |
| μmin | 0.622 | 0.581 | 0.238 |
| Number | TC28d | TS-C | TCL-C |
|---|---|---|---|
| First stage displacement/mm | 1.3 | 6 | 5 |
| Second stage displacement/mm | 0.2 | 2 | 0.5 |
| decline/% | −84.61% | −66.67% | −90.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhu, M.; Li, X.; Dai, G.; Yin, Q.; Liu, J.; Ling, C. Experimental Study on Shear Behavior of Interface between Different Soil Materials and Concrete under Variable Normal Stress. Appl. Sci. 2022, 12, 11213. https://doi.org/10.3390/app122111213
Liu H, Zhu M, Li X, Dai G, Yin Q, Liu J, Ling C. Experimental Study on Shear Behavior of Interface between Different Soil Materials and Concrete under Variable Normal Stress. Applied Sciences. 2022; 12(21):11213. https://doi.org/10.3390/app122111213
Chicago/Turabian StyleLiu, Hongyuan, Mingxing Zhu, Xiaojuan Li, Guoliang Dai, Qian Yin, Jing Liu, and Chen Ling. 2022. "Experimental Study on Shear Behavior of Interface between Different Soil Materials and Concrete under Variable Normal Stress" Applied Sciences 12, no. 21: 11213. https://doi.org/10.3390/app122111213
APA StyleLiu, H., Zhu, M., Li, X., Dai, G., Yin, Q., Liu, J., & Ling, C. (2022). Experimental Study on Shear Behavior of Interface between Different Soil Materials and Concrete under Variable Normal Stress. Applied Sciences, 12(21), 11213. https://doi.org/10.3390/app122111213






