A Novel Deep Reinforcement Learning Approach for Task Offloading in MEC Systems

Abstract

With the internet developing rapidly, mobile edge computing (MEC) has been proposed to offer computational capabilities to tackle the high latency caused by innumerable data and applications. Due to limited computing resources, the innovation of computation offloading technology for an MEC system remains challenging, and can lead to transmission delays and energy consumption. This paper focuses on a task-offloading scheme for an MEC-based system where each mobile device is an independent agent and responsible for making a schedule based on delay-sensitive tasks. Nevertheless, the time-varying network dynamics and the heterogeneous features of real-time data tasks make it difficult to find an optimal solution for task offloading. Existing centralized-based or distributed-based algorithms require huge computational resources for complex problems. To address the above problem, we design a novel deep reinforcement learning (DRL)-based approach by using a parameterized indexed value function for value estimation. Additionally, the task-offloading problem is simulated as a Markov decision process (MDP) and our aim is to reduce the total delay of data processing. Experimental results have shown that our algorithm significantly promotes the users’ offloading performance over traditional methods.

1. Introduction

Over recent years, the increasing number of smart mobile devices (MDs) has brought an unprecedented growth of computationally sensitive tasks, such as voice recognition, virtual/augmented reality (VR/AR), smart wearables, etc. [1]. However, these mobile tasks have heavy requirements of resourced-constrained MDs for data processing along with wideband spectrum and transmission delays.

Mobile cloud computing (MCC) is an advanced computation offloading technology for MDs [2]. In the system, mobile devices can take advantage of remote cloud servers’ resources to carry out their tasks. These servers have strong power, sufficient bandwidth, and sufficient storage space. Nevertheless, the long distance between mobile devices and the cloud server leads to inconceivable communication costs in respect of latency and energy.

Thus, mobile edge computing technology has been developed to solve these issues in a distributed manner [3]. That is to say, MEC systems are implemented by a series of computational servers or by enhancing deployed edge facilities, such as base stations (BSs) with computational and storage functions. The edge servers allow nearby users to offload intensive computation tasks to them for processing. In summary, these sensitive tasks can be transmitted and processed at once with the assistance of MEC systems, which not only ensure low latency, but also improve user experience quality (QoE). The benefits mentioned above all depend on the task-offloading technology by assigning tasks to users and BSs. Moreover, a reasonable task-offloading process is decided by many factors, such as user performances, channel conditions, and the capabilities of mobile edge devices. Hence, it is critical to formulate an optimal task-offloading decision method for MEC systems. During the decision process, we need to confirm whether tasks should be executed locally or offloaded to BSs for further execution. When large tasks are offloaded to BSs, many costs are generated in terms of communication resources, energy cost, and transmission delays.

At present, significant research has been conducted on task-offloading technology [4], which is associated with resource allocation [5]. Traditional approaches for task offloading are usually based on game theory [6], linear regression [7], and dynamic programming [8]. These approaches play important roles in some specific scenarios, while they also have disadvantages for dynamic task-offloading decisions. With the aid of deep reinforcement learning, many researchers have extended their reach to more complex scenarios, where dynamic optimization problems can be handled. Among deep Q-networks (DQNs), the study of the exploration and exploitation dilemma is an important issue for generating optimal policies. Generally speaking, $ϵ$-greedy and Boltzmann exploration are conventional solutions by randomly selecting actions in action space. However, these two mechanisms do not take uncertainty into consideration, so they take a huge amount of data to learn an optimal policy. Furthermore, it is practical to devise a multiuser offloading mechanism that can let users make decisions with the time-varying channel and queue dynamics. Hence, it is necessary to find an alternative way for efficient exploration.

In this paper, we present a task-offloading strategy for the time-varying MEC environment with the aim of minimizing the total sum of all kinds of delays, which includes computing delay, transmission delay, and queuing delay. To address the optimization problem, we formulate the problem as an MDP model, and then as an improved DQN algorithm, which provides a novel exploration method. The contributions of this paper are as follows:

• We investigate an MEC scenario with multiple MDs and multiple edge devices (EDs) where users have delay-sensitive tasks to process locally or offload to the edge sever. The tasks in our study can wait and be handled during several slots, while many other studies limit the tasks to being processed only at one slot [9].
• Due to the environmental dynamic, we elaborate the decision-making task as an MDP problem. Then, we improve the DQN algorithm by applying a parameterized indexed function. With the parameterized indexed function, the user agents can fully explore and exploit their action space and choose the optimal action for task offloading.
• Lastly, we compare it with traditional DQN algorithm and research the impact of system parameters. The experimental results validate that the task-offloading scheme that we propose greatly improves the MEC system utility.

The rest of this paper is organized as follows. In Section 2, we present the related works. In Section 3, we introduce the system model and the MDP model. In Section 4, the improved DQN algorithm is proposed to solve the MDP problem. In Section 5, the performances of the proposed algorithm are evaluated by several simulations. The conclusions are drawn in Section 6.

2. Related Work

Since MEC has made great contributions to mobile communication, several previous efforts have paid attention to the task-offloading problem of MECs. In the related work section, we classify two different categories of research directions, one is for traditional schemes and the other is for those based on DRL.

First of all, we introduce the relevant traditional methods. For instance, in [6], the authors focused on multi-data-source tasks and constructed a non-cooperative game-theoretic offloading framework for each edge node to find the optimal decision. In [7], the authors conducted an MEC system with a core cloud, where one task could be divided into several subtasks and could predict the total offloading duration using linear regression. In [8], the authors studied the MEC system with edge clouds and remote clouds to minimize the total energy consumption of multiple MDs, and then proposed an approximation algorithm based on dynamic programming to solve the mentioned problem. In [10], the authors studied a bi-level optimization approach for minimizing the total energy consumption, which is jointly investigated the task-offloading strategies and resource allocation. In [11], the authors proposed a novel computation offloading architecture and developed a heuristic algorithm to solve a mixed-integer linear problem considering the latency and operating cost. In [12], the authors proposed a blockchain-based MEC system framework and discussed two different separate approaches for optimizing user association, data rate allocation, and resource allocation. In [13], the authors designed a new MEC mechanism for the mining task-offloading issue and proposed an efficient task-offloading algorithm based on the Stackelberg game in order to maximize the utilities of mobile devices. In [14], the authors formulated an optimization model as a multiuser decision-making problem and transformed the problem into an unconstrained Lagrangian optimization (ULO) to maximize the expected offloading rate of multiple users. In [15], the authors studied an MEC system considering the proper load on task processing efficiency with the aim of minimizing the processing delay. They presented a two-stage computing offloading scheme by using an aggregative game with a load billing mechanism. In [16], the authors focused on the statistical quality of service (QoS) guarantee for task offloading to save more energy. They formulated the problem as a mixed-integer nonlinear programming problem and used convex optimization theory to ensure the QoS during the offloading process. In [17], the authors jointly optimized offloading decisions and resource allocation with the aim of maximizing the system utility in a NOMA-aided MEC. They used Lyapunov technique to decouple the optimization problem and presented an online algorithm by introducing a series of auxiliary variables. In [18], the authors researched the task scheduling problem in a cloud computing system. They proposed an adaptive load-balanced task approach (ALTS) for maximizing resource utilization. However, these above algorithms demand prior knowledge of the interaction environment and statistics of tasks and channel conditions, which may not always meet the expected requirements in actual use.

With the rise of artificial intelligence, reinforcement learning (RL)-based algorithms are able to learn computation offloading policies with no prior knowledge of MEC systems. In [19], the authors modeled a cloud computing environment where they studied the balance between local and global research which played an important role in swarm-intelligence-based meta-heuristics algorithms. They contributed an adaptive particle swarm optimization (PSO) to reduce the task execution time. In [20], the authors presented a space–air–ground-integratednetwork considering the computation offloading problem as an MDP, and then proposed a DRL approach for a UAV user to gain a lower total cost. In [21], the authors presented the framework for offloading computation tasks from an MD to an edge server with high CPU availability so that processing time may be reduced in both the MD and the server. However, these solutions, in nature, are concentrated on the decision-making problem of a single user and do not take more complex cases into account. In [22], the authors considered the task scheduling in an edge computing system and proposed an online learning iterative algorithm to jointly minimize the total cost of the execution delay and energy consumption. In [23], the authors studied a novel vehicular edge computing (VEC) task-offloading system where the roadside units (RSUs) can switch their states between sleep and work and then proposed a greedy algorithm based on DQN approach for minimizing the total delay of tasks. In [24], the authors explored the scenario of centralized user clustering with different priority tasks and proposed a DQN-based algorithm to minimize the system cost. In [25], the authors proposed a temporal attentional deterministic policy gradient (TADPG) which is based on the deep deterministic policy gradient (DDPG), and was formulated to solve the computation offloading and resource allocation problem in a single-server multi-MD MEC system. Furthermore, it is worth noting that we extend this model to a multiple-server multi-MD scenario. In [26], the authors discussed a novel task dependence model with server clusters and proposed a novel offloading approach Com-DDPG to optimize the energy consumption and latency of the system. In [27], the authors considered the multichannel access and task-offloading problem in a multiagent system and proposed a novel multiagent deep reinforcement learning (MADRL) to reduce the computation delay and increase the channel access success rate. In [28], the authors studied a multiuser offloading model and presented a decentralized epoch based offloading (DEBO) to optimize the total rewards. Furthermore, they proved that DEBO had good performances on various common scenarios. In [29], the authors paid attention to VEC considering offloading decisions in congestion situation. They modeled a system where tasks can be divided into subtasks and proposed an offloading algorithm based on a double deep Q-network.

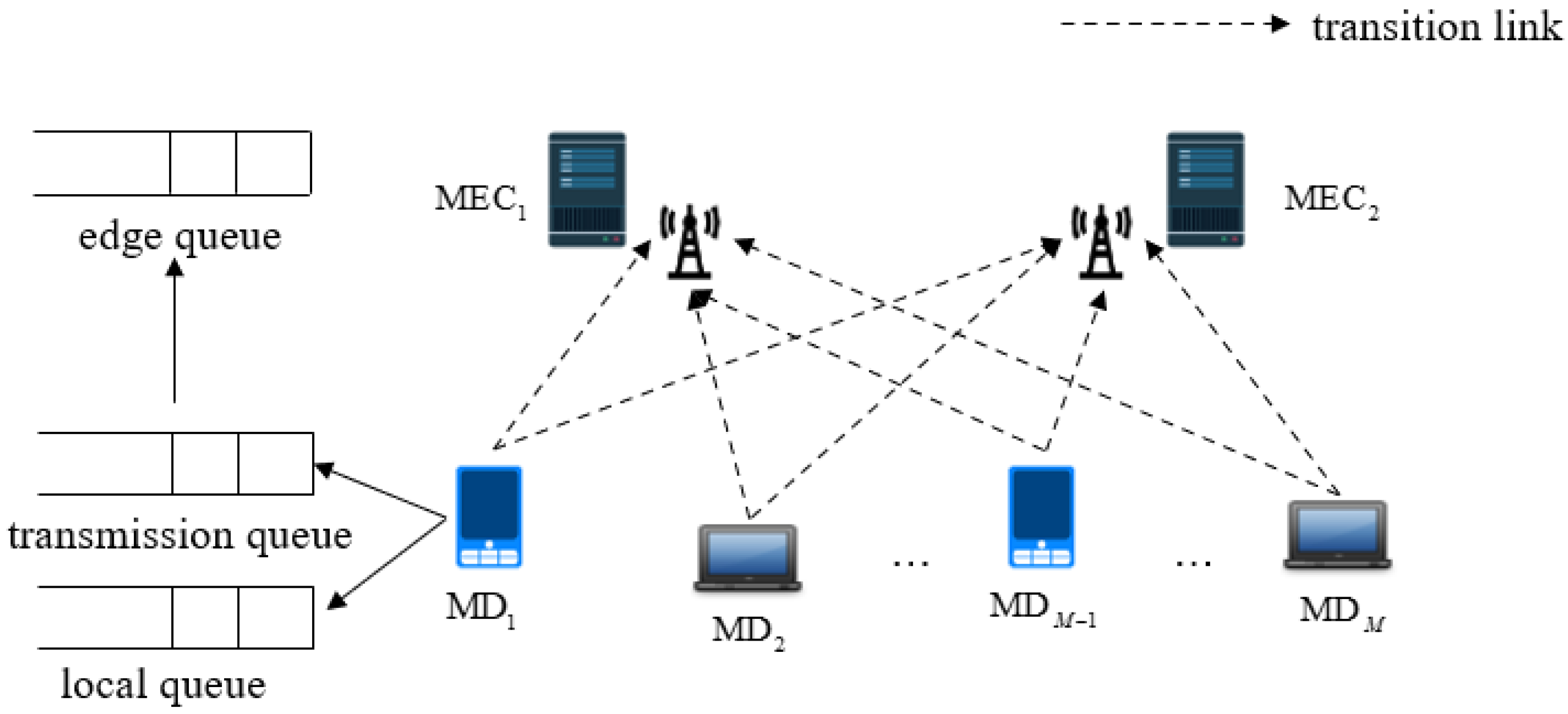
3. System Model

We consider an MEC system with a set of MDs $\mathcal{M}=\{1,2,\dots ,M\}$ and a set of EDs $\mathcal{N}=\{1,2,\dots ,N\}$, as shown in Figure 1. Each MD is equipped with an antenna, and it communicates with the BS via wireless channels. Furthermore, the connection between the BS and the MEC server is through optic fibers or copper wires [25]. In the following, we will illustrate the system model and formulate the problem.

3.1. Task Queue Model

The task queue model is based on one episode composed of a list of time slots $\mathcal{T}=\{1,2,\dots ,T\}$, where every slot has $\mu$ seconds. We use $u_m\left(t\right)$ to denote the arriving task at the MD $m\in \mathcal{M}$. At the beginning of each time slot, there are $u_m\left(t\right)\in \{1,2,\dots \}$ tasks held and waiting for allocation. Furthermore, we choose ${\lambda }_m\left(t\right)$ to present the user m’s task size arrived at slot t, which is supposed to be independent and identically distributed (i.i.d) over all slots. The queues in our system operate in a first-in first-out (FIFO) manner. Every task for executing has a deadline, ${\pi }_m$ (in time slot). If the task has not been completely executed at the time slot, $t+{\pi }_m-1$, it will be dropped by the queue.

Let $d_{m,n}^{edge}\left(t\right)$ denote the length of the queue of the MD, m, at the ED, n, in time slot t. At the edge servers, given that these queuing states always keep changing at EDs since some EDs have tasks to process while others can be free, we use $K_n\left(t\right)$ to indicate the amount of active queues of the ED, n; it will evolve as follows:

$$K_n\left(t\right)=\left\{m\right|{\lambda }_{m,n}^{edge}\left(t\right)>0or{d}_{m,n}^{edge}\left(t\right)>0,m\in M\}$$

(1)

3.2. Computing Models

(1) 

Local computing

For the user, m, if the agent decides to process the task, $u_m\left(t\right)$, at MD, m, at slot t, then the task will be placed in the user’s queuing buffer and be processed at upcoming slots. We use ${\phi }_m^{loc}\left(t\right)$ to define the amount of time slots that $u_m\left(t\right)$ has to wait before being executed and $L_m^{loc}\left(t\right)$ to present when the task is totally executed or dropped if it has not been completed at the deadline. For task $u_m\left(t\right)$, ${\phi }_m^{loc}\left(t\right)$ is computed as follows:  

$${\phi }_m^{loc}\left(t\right)=\underset{t^{{}^{\prime }}\in \{0,1,\dots ,t-1\}}{max}{L}_m^{loc}(t^{{}^{\prime }})-t+1$$

(2)

Obviously, ${\phi }_m^{loc}\left(t\right)$ depends on the tasks before task, $u_m\left(t\right)$, and, when all of them have been completed or dropped, $u_m\left(t\right)$ will be processed at $t+{\phi }_m^{loc}\left(t\right)$. In addition, $L_m^{loc}\left(t\right)$ also represents the total computation delay from arriving at the MD, m, to being completed or dropped; it is calculated as:

$$L_m^{loc}\left(t\right)=min\{t+{\phi }_m^{loc}\left(t\right)+\frac{{\lambda }_m\left(t\right)}{f_m\mu /{\xi }_m}-1,t+{\pi }_m-1\},$$

(3)

where $f_m$ denotes the CPU processing capacity of MD, m, and ${\xi }_m$ denotes the CPU cycles MD, m, required for processing a unit data [30].

(2) 

Edge Computing

When the task $u_m\left(t\right)$ is offloaded to ED n for processing, we define $L_{m,n}^{edge}\left(t\right)$ to present when the task is executed or dropped by the service. Since the queue dynamic of ED n, the MD, m, is unclear of the figure of $L_{m,n}^{edge}\left(t\right)$ until the task processing is finished. Let ${\widehat{L}}_{m,n}^{edge}\left(t\right)$ represent when the task begins to be processed:

$${\widehat{L}}_{m,n}^{edge}\left(t\right)=max\{t,\underset{t^{{}^{\prime }}\in \{0,1,\dots ,t-1\}}{max}{L}_{m,n}^{edge}(t^{{}^{\prime }})+1\}$$

(4)

The MEC servers are assumed to have adequate computing resources. Thereby, the servers are able to handle various tasks transmitted from various MDs. That is to say, once the tasks arrive at the MEC servers, they will be executed right away, and thus there is no queuing delay.

(3) 

Communication model

In this paper, we assume a wireless network that mobile devices communicate on orthogonal channels. Denote $h_{m,n}$ as the uplink channel gain between the user m and the ED n. Let P denote the user’s transmission power. The uplink transmission rate (bits per second) in the system to offload $u_m\left(t\right)$ is calculated as follows:

$$r_{m,n}^{trans}=Wlo{g}_2(1+\frac{h_{m,n}^{2}P}{{\sigma }^2}),$$

(5)

where W is the channel bandwidth and ${\sigma }^2$ is the noise power at the edge server.

Once the task, $u_m\left(t\right)$, is placed in the transmission queue at time slot t, we denote ${\phi }_m^{trans}\left(t\right)$ to define the number of time slots that $u_m\left(t\right)$ will wait for being transmitted; $L_m^{trans}\left(t\right)$ represents when the task is totally transmitted or dropped if it has not been transmitted at the deadline. For task $u_m\left(t\right)$, ${\phi }_m^{trans}\left(t\right)$ is computed as follows:

$${\phi }_m^{trans}\left(t\right)=\underset{t{}^{\prime }\in \{0,1,\dots ,t-1\}}{max}{L}_m^{trans}\left(t{}^{\prime }\right)-t+1$$

(6)

Furthermore, the time $L_m^{trans}\left(t\right)$ is computed as follows:

$$L_m^{trans}\left(t\right)=min\{t+{\phi }_m^{trans}\left(t\right)+\frac{{\lambda }_m\left(t\right)}{r_{m,n}^{trans}}-1,t+{\pi }_m-1\}$$

(7)

The offloading process includes task data transfer and its computation result between MDs and EDs. Since the wirelines between the BS and the MEC servers ensure much faster transmission speed than wireless channels, we ignore the transmission delay between them.

3.3. Problem Formulation

As a classic formulation of sequential decision making, MDP is suitable for formulating this problem. The objective of our scheme is not only to minimize the total delay of all the tasks, but also to guarantee the long-term dynamic of task queuing. The total delay of our system is defined as:

$$D_m\left(a_m\left(t\right)\right)=\alpha (L_m^{loc}\left(t\right)-t+1)+(1-\alpha )(L_{m,n}^{edge}(t^{{}^{\prime }})-t+1),$$

(8)

where $\alpha$ can be 0 or 1; if it is equal to 0, then the task, $u_m\left(t\right)$, will be offloaded to the edge service; if it is 1, then the task, $u_m\left(t\right)$, will be computed at the mobile device.

Then we use $C_m\left(t\right)$ to define the overall cost associated with the delays:

$$C_m\left(t\right)=\beta D_m\left(a_m\left(t\right)\right)+(1-\beta )C,$$

(9)

where $\beta$ can be 0 or 1; if it equals to 0, then the task, $u_m\left(t\right)$, has been dropped at the deadline, otherwise it has been completed before the deadline. C is a constant penalty for being dropped.

The optimization problem $\mathbf{P}$ is formulated as follows:

$$\begin{array}{cc}\hfill \mathbf{P}:& \underset{L_m^{loc}\left(t\right),L_{m,n}^{edge}\left(t\right)}{min}{C}_m\left(t\right),\forall m\in \{1,2,\dots ,M\}\hfill \\ \hfill & \begin{array}{cc}\hfill & \hfill s.t.D_m\left(a_m\left(t\right)\right)\le {\pi }_m.\end{array}\hfill \end{array}$$

(10)

4. Tasking Offloading Algorithm Based on DRL

Since calculating the task size and queuing information in MEC environment in advance is impossible, we raise a novel DRL-based approach to solve the mentioned MDP problem. In the section, we first consider the choice of decision model elements, then present the novel approach for task offloading.

4.1. The MDP Framework

(1) 

State Space

The state space variables usually depend on the environmental settings and thus influence the rewards gained by the chosen actions [31]. We define the state space at the current decision epoch $t\in \mathcal{T}$ as a union of the task size, ${\lambda }_m\left(t\right)$; the waiting time of computation queue, ${\phi }_m^{loc}\left(t\right)$; the waiting time of the transmission queue, ${\phi }_{m,n}^{tran}\left(t\right)$; the queue length, $d_{m,n}^{edge}\left(t\right)$; and the load level history of the edge queue, $H\left(t\right)$, which is denoted as $s\left(t\right)=\{{\lambda }_m\left(t\right),{\phi }_m^{loc}\left(t\right)$, ${\phi }_{m,n}^{tran}\left(t\right),d_{m,n}^{edge}\left(t\right),H\left(t\right)\}$. When MD, m, has a task processing request, the five-tuple state variables, $s\left(t\right)$, will be passed to the improved DQN input layer and the network will output the best action to be taken.

(2) 

Action Space

At the beginning of time slot t, firstly, the agent has to decide whether to process the task, $u_m\left(t\right)$, locally or offload it to the edge server; we denote $p_m\left(t\right)=1$ (or 0) when the task, $u_m\left(t\right)$, is executed locally (or is offloaded to the edge server), and if there is no task at time slot t, $p_m\left(t\right)=-1$. Furthermore, if the task is offloaded to the edge server, we denote $q_{m,n}\left(t\right)\in \{0,\dots ,N-1\}$ to indicate the ED that the agent chose, i.e., if the task is offloaded to the ED 4, then $q_m\left(t\right)=3$. Thus, the action can be represented by $a_m\left(t\right)=(p_m\left(t\right),q_m\left(t\right))$.

(3) 

Reward Function

The reward function has been proved to be beneficial for finding an optimal action strategy. Thus, the reward must be set appropriately to match the efficient learning process [32]. Note that there exists a situation where tasks are not completed and dropped at the deadline ${\pi }_m$, so we use a negative reward to this situation, and when tasks have been completed before ${\pi }_m$, we use a relatively positive reward to present it. Then, the reward function is denoted as:

$$r_t=\left\{\begin{array}{cc}-{\pi }_m,\hfill & \mathrm{if}{u}_m\left(t\right)\mathrm{been}\mathrm{dropped}\hfill \\ R-C_m\left(t\right),\hfill & \mathrm{if}{u}_m\left(t\right)\mathrm{been}\mathrm{processed},\hfill \end{array}\right.$$

(11)

where R is a constant. Moreover, we define a long-term accumulative reward as: $R_t=\begin{array}{c}{\sum }_{t=0}^T{\zeta }^t{r}^t\end{array}$. Here, there is a discount factor, $\zeta \in [0,1]$. Furthermore, the agent is determined to maximize the accumulative reward for minimizing the total delay through a long period, T.

4.2. DRL-Based Task Offloading

In the task-offloading decision, the agent interacts with the environment to estimate the value function through the resulting sample and learn an optimal strategy ${\pi }^{\ast }$. Both the state and action space of the system in our paper have high dimensionality and are dynamic and discrete; they have to be optimized while generating sequences. Based on the above factors, we choose the DQN-based method to optimize our decision-making algorithm.

Generally speaking, DRL uses the $ϵ$-greedy strategy to balance exploration and exploitation, where $ϵ$ refers to the probability for exploring randomly and exploiting with a chance of 1 −$ϵ$. This stochastic policy can ensure the tradeoff between exploration and exploitation, but it has to explore for a long-term extension and causes low resource utilization. In this paper, we use a novel DQN-based approach by taking advantage of a parameterized indexed function for efficient exploration.

In the proposed framework, we parameterize the state–action value function as:

$$Q(s,a)=v(s,a)+m(s,a)Z,$$

(12)

where $Z\sim N(0,1)$. Note that there are two parts for Q value function, so we utilize a dual-network consisting of a mean network for learning, $v(s,a)$, and an uncertainty network for learning, $m(s,a)$. Let $\theta =(\psi ,\omega )$ be the parameters of the trainable networks, where $\psi$,$\omega$ are the parameters of the mean and the uncertainty network. Let $\tilde{\theta }=(\tilde{\psi },\tilde{\omega })$ be the target networks’ parameters.

The overall training progress and task-offloading strategy are shown in Figure 2 and Algorithm 1. A prior mechanism is also incorporated, where each trainable network is paired with an additive prior network, and it is suited to sequential decision problems. The prior networks share the same architecture as the trainable networks, let $\overline{\theta }=(\overline{\psi },\overline{\omega })$ be its parameters and $\beta$ is the prior scale of the network. Thus, the mean network parameters are updated through the target mean network and prior network, as follows:

$$\begin{array}{cc}\hfill & {\nabla }_{\psi }{L}_v(\psi ,\tilde{\psi },\overline{\psi },D)=\hfill \\ \hfill & \frac{1}{\left|D\right|}\sum _{(s_i,a_i,r_i,s_i^{{}^{\prime }},done)\in D}{\nabla }_{\psi }{((v_{\psi }+{\beta }_1{\overline{v}}_{\overline{\psi }})(s_i,a_i)-{\tilde{Q}}_{\psi ,\tilde{\psi },\overline{\psi }})}^2,\hfill \end{array}$$

(13)

where ${\tilde{Q}}_{\psi ,\tilde{\psi },\overline{\psi }}$ is $r_i+(1-done)\gamma (v_{\tilde{\psi }}+{\beta }_1{\overline{v}}_{\overline{\psi }})(s_i^{{}^{\prime }},{\overline{a}}_i)$.

Algorithm 1 DRL-based solution for task-offloading decision in MEC system

Input: System model parameters, ${\lambda }_m\left(t\right)$, ${\phi }_m^{loc}\left(t\right)$, ${\phi }_{m,n}^{tran}\left(t\right)$, $d_{m,n}^{edge}\left(t\right)$, $H\left(t\right)$ Initialization: trainable networks—$\theta$; target networks—$\tilde{\theta }$; replay memory capacity—$R_B$; batch size—B. for each episode k = $\{1,2,\dots ,k_{max}\}$ do$\phantom{(}$       Reset task-offloading environment       Generate an initial state $s_0$       for each user m $\in \{1,2,\dots ,M\}$do           Select an action $a_t$ with the function:          $argmax\{v_{\tilde{\psi }(s^{{}^{\prime }},a^{{}^{\prime }})}+m_{\tilde{w}}(s^{{}^{\prime }},a^{{}^{\prime }})Z+{\beta }_1{v}_{\overline{\psi }(s^{{}^{\prime }},a^{{}^{\prime }})}+{\beta }_2{m}_{\overline{w}}(s^{{}^{\prime }},a^{{}^{\prime }})Z\}$           Execute action $a_t$ and calculate the reward $r_t$           Save sample data $(s_t,a_t,r_t,s_{t+1},done)$ in the experience replay buffer           Train the eval networks and periodically update the target networks with (13)–(14)     end $\phantom{(}$ end$\phantom{(}$ Output: Optimal policy ${\pi }^{\ast }$

Furthermore, the uncertainty network parameters are updated as follows:

$$\begin{array}{cc}\hfill & {\nabla }_{\omega }{L}_m(\omega ,\tilde{\omega },\overline{\omega },D)=\hfill \\ \hfill & \frac{1}{\left|D\right|}\sum _{(s_i,a_i,r_i,s_i^{{}^{\prime }},done)\in D}{\nabla }_{\omega }{((m_{\omega }+{\beta }_1{\overline{m}}_{\overline{\omega }})(s_i,a_i)-{\tilde{Q}}_{\omega ,\tilde{\omega },\overline{\omega }})}^2,\hfill \end{array}$$

(14)

where ${\tilde{Q}}_{\omega ,\tilde{\omega },\overline{\omega }}$ is $\sigma +(1-done)\gamma (m_{\tilde{\omega }}+{\beta }_1{\overline{m}}_{\overline{\omega }})(s_i^{{}^{\prime }},{\overline{a}}_i)$.

5. Simulation Results and Analysis

In this section, the simulation results are presented to prove the advantage of the proposed DRL-based task-offloading approach. Unless otherwise specified, the settings of the MEC system are as follows: the number of MDs is 20, the number of EDs is 5, the CPU frequency $f_m$ is 5 GHz, and the deadline ${\pi }_m$ is 10 slots. The DNN network where layers are fully connected [33,34] is composed of four layers that contains one input layer, two hidden layers, and one output layer. The batch size is 64 and the learning rate is 0.0001.

We also compare our algorithm with three benchmark algorithms: (1) DQN: In this algorithm, the agent makes decisions about executing a task locally or offloading it to the ED for minimizing the immediate system total delay. (2) Local computing: In this algorithm, we suppose that all MDs have a sufficient computation capability, thus all tasks are executed totally locally by their MDs. (3) Edge computing: In this algorithm, we suppose that all MDs are incapable of undertaking their computations, therefore all tasks are offloaded to the EDs for executing.

To prove the proposed theory in this paper, we conduct simulation experiments under various settings.

(1) Experiment 1—Convergency performance: In Figure 3, we compare the mean average rewards of the four algorithms; it can be seen that, with the episodes gradually increasing, due to the efficient exploration based on the indexed function, the proposed scheme achieves better convergency performance. The local scheme achieves the lowest efficiency in convergency performance. As shown in Figure 4, with the prior $\beta$ = 2.0, the proposed scheme achieves better convergency performance and obtains the highest rewards compared with the prior schemes $\beta$ = 0.5, 1.0, and 1.5.

(2) Experiment 2—Performance on average delay: In this experiment, we take the average delay of the system as the illustration to describe the advantage of the proposed algorithm. As shown in Figure 5, we consider the impact of the number of mobile devices on the average delay. With the number increasing from 10 to 30, the total delay is also increasing. The more mobile devices there are, the more tasks will be generated and executed. However, the proposed algorithm has the lowest delay compared with the other three algorithms. In Figure 6, we also consider the impact of the deadline ${\pi }_m$ for the MEC system. Once we extend the time limit, those arrival tasks will have more time for queuing and being processed. The proposed algorithm achieves slightly a lower average delay than DQN algorithm because, with extensive training, the agent has learned the optimal offloading strategy and accurately allocated the task to the relevant mobile devices. The offloading and local schemes produce relatively higher delays under the same deadlines

6. Conclusions

To satisfy the needs of MECs for modern development and to further improve the quality of service, this paper proposes a novel DRL-based task-offloading strategy for rapid processing. We investigate a multiuser, multiserver MEC system and discuss the queue dynamic of tasks as a key point. Furthermore, the target is to reduce the total delay for each user in the MEC system. By using the parameterized value function for value estimating, this algorithm can address the formed problem and determine the offloading policy efficiently without any prior knowledge. Experimental data indicate that the proposed algorithm performs better on the users’ delay than other algorithms.

Limitations: In this paper, we study a DQN-based algorithm which has discrete action space and is not suitable for scenarios which demand continuous action space. Fortunately, we can extend the proposed algorithm for partial offloading problems in a new MEC system where tasks can be partially offloaded to both users and servers. We will realize the assumption in future experiments.