Functionality Analysis of Derailment Containment Provisions through Full-Scale Testing—I: Collision Load and Change in the Center of Gravity
Abstract
:1. Introduction
2. Experimental Conditions and Methods
2.1. Real-Scale Test Site
2.2. Test Car and Acceleration Method
2.3. Derailer System
2.4. Data Acquisition System
3. Experimental Results
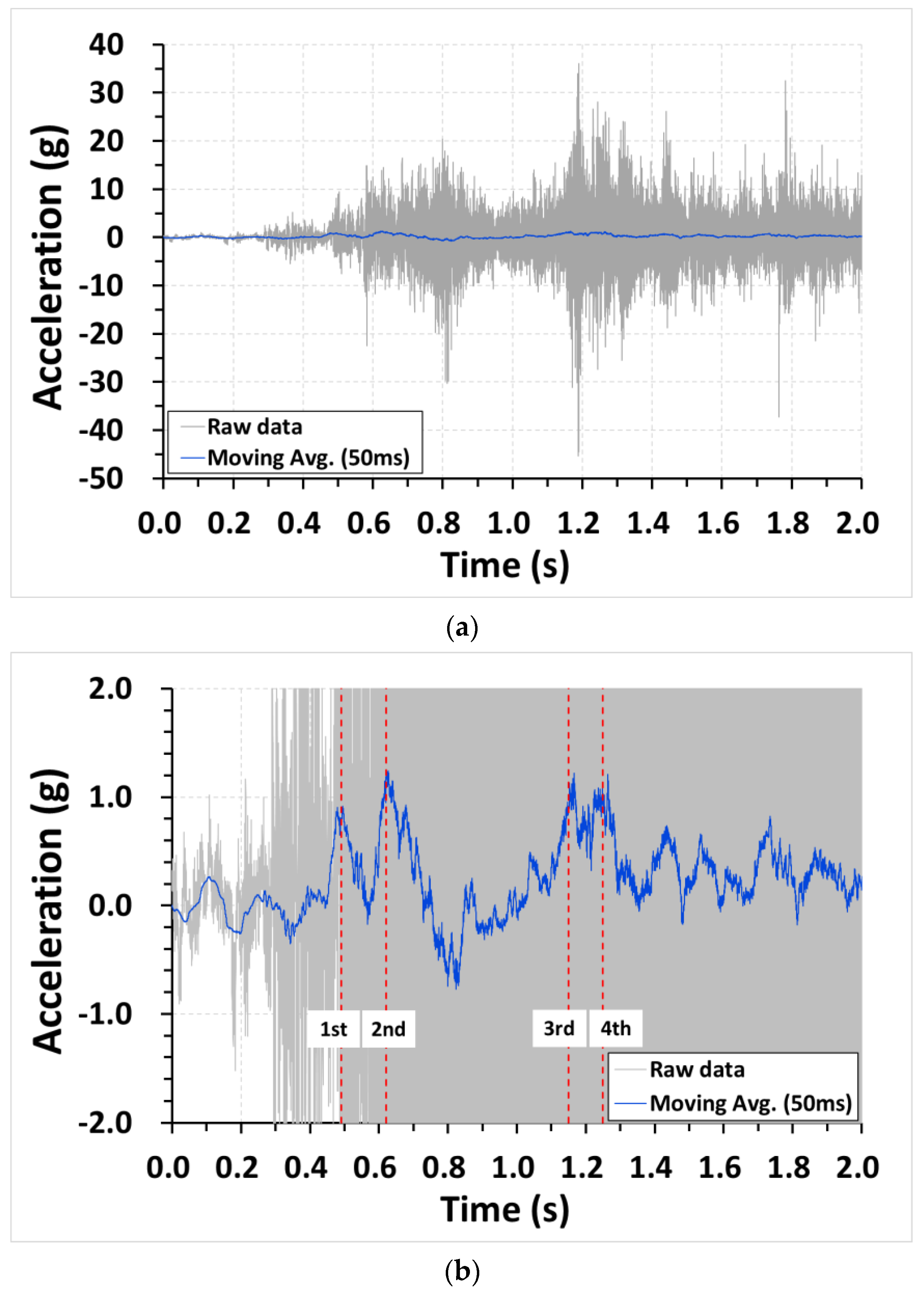
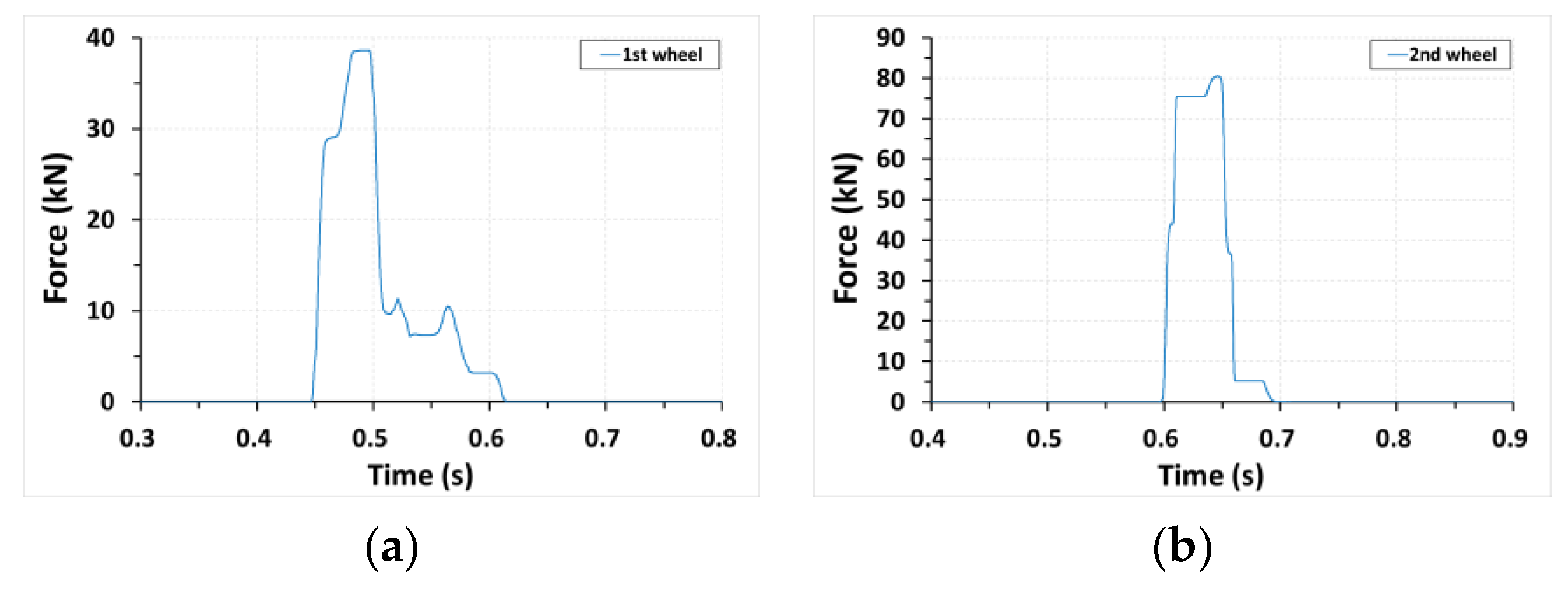
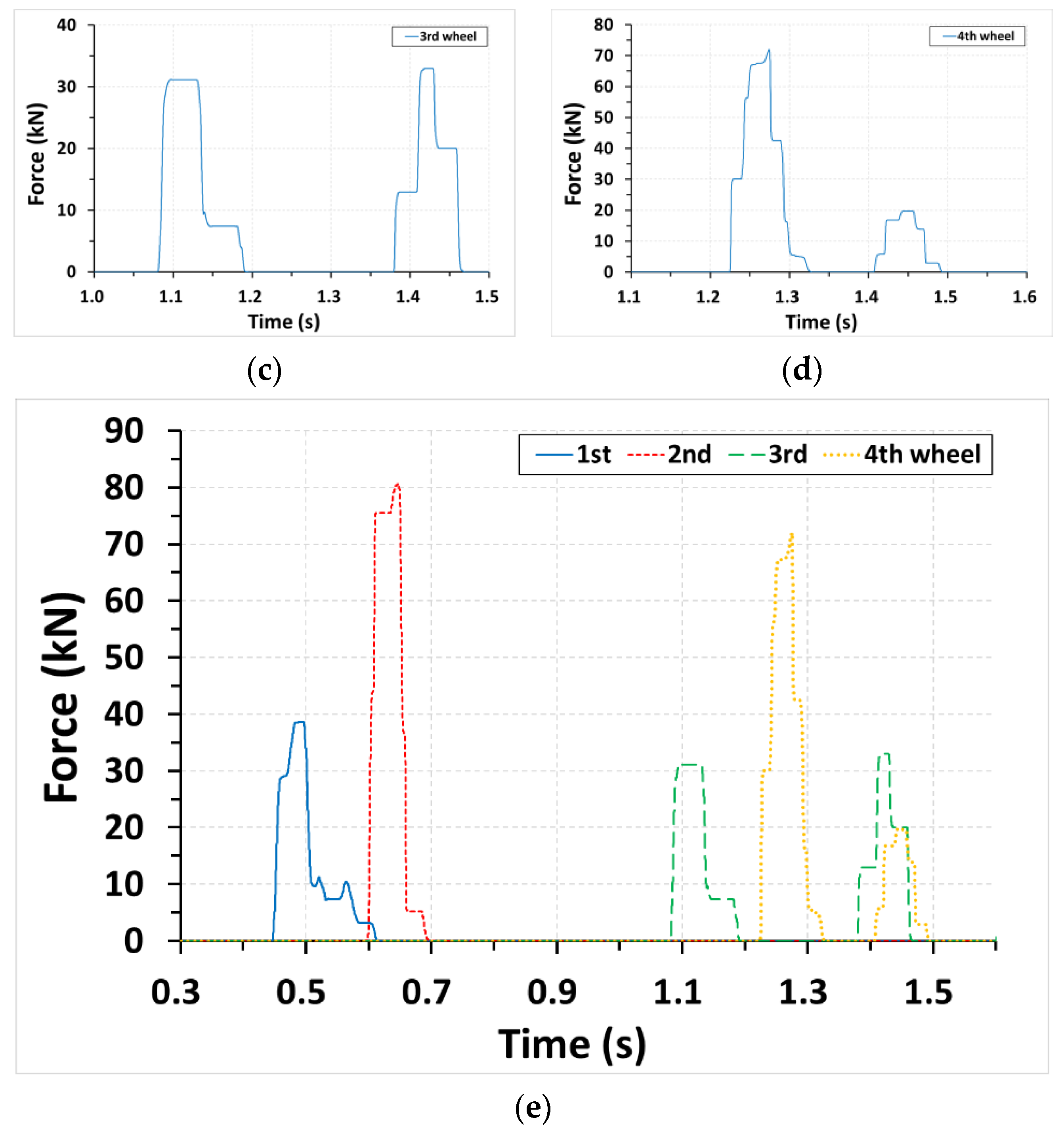
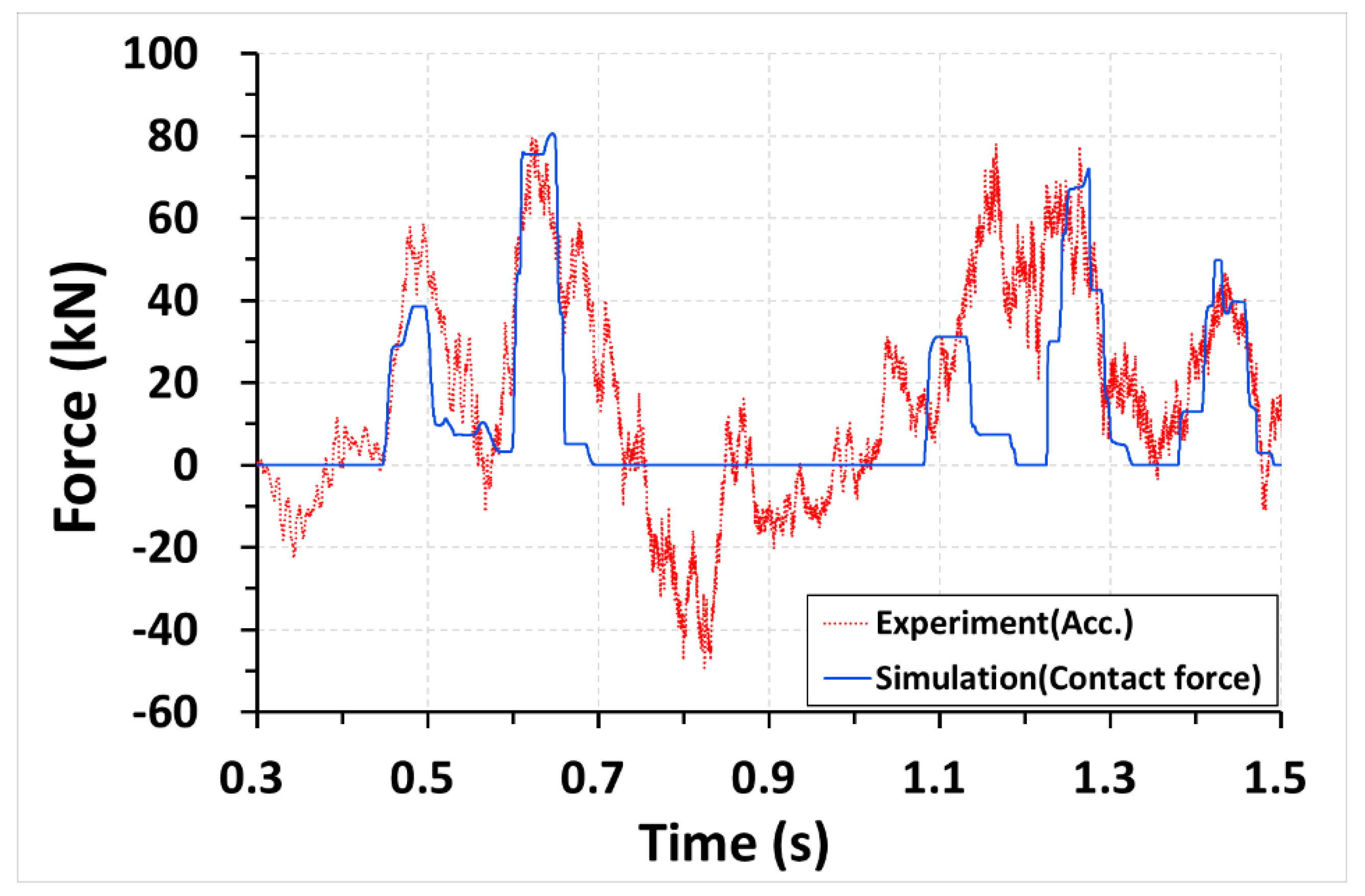
3.1. Collision Load
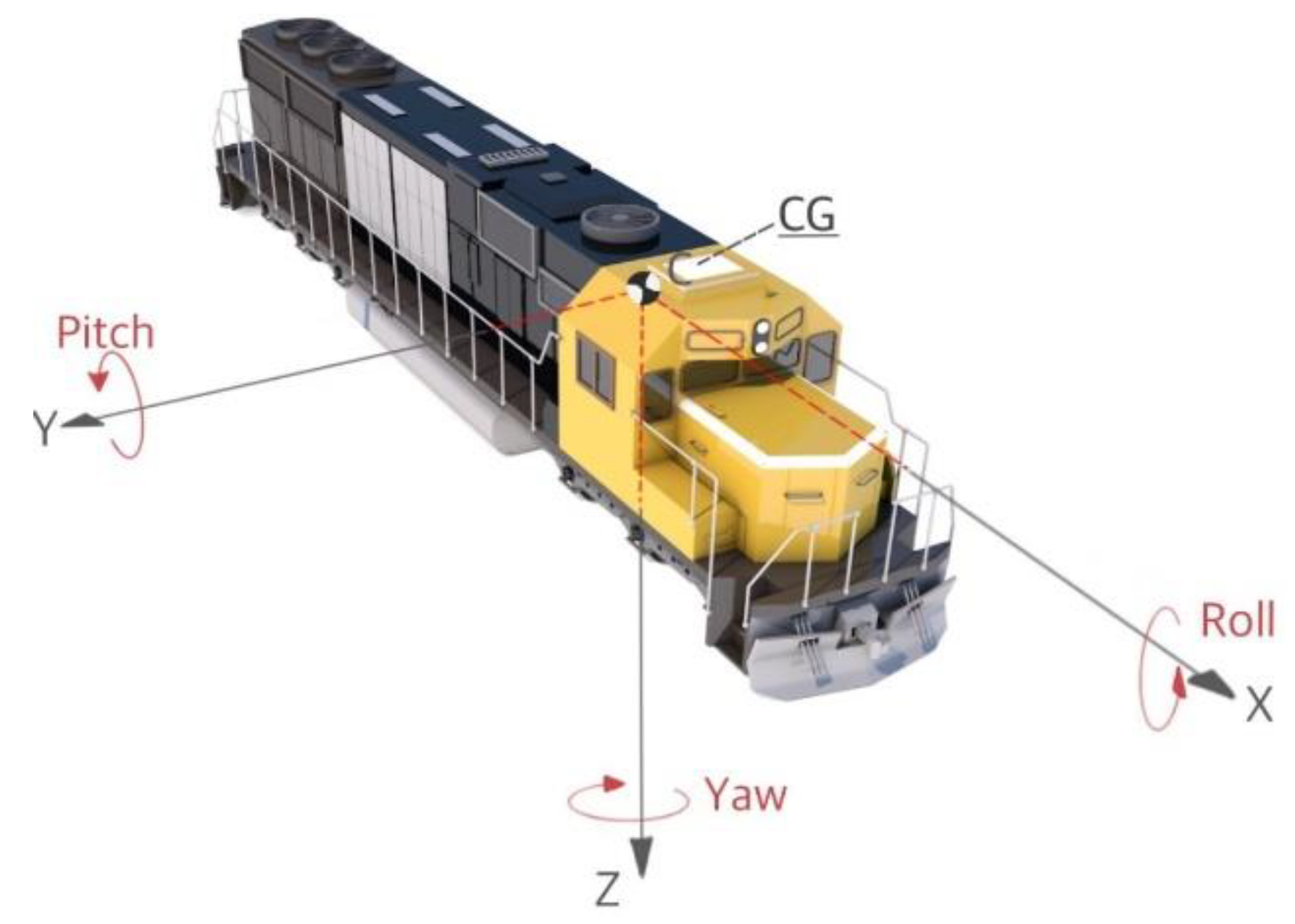
3.2. Change in Center of Gravity
4. Conclusions
- The derailment/collision tests showed that both the flat and container wagon continued to run along the track after derailing. That is, even if the sprung mass increases and the center of gravity position rises, the DCP type I can effectively restrain the derailed vehicle into the intended area;
- In the case of a long vehicle such as a trailer (railway car), the collision load when the first bogie collided with the DCP was calculated from Newton’s second law applying 50% of the total car mass and lateral car acceleration data;
- The dynamic motion of the derailed vehicle was analyzed by integrating the angular velocity data obtained from the gyro sensors on the mass center of the vehicle. As the sprung mass increased (such as the difference between container wagon and flat wagon), the vehicle body behavior (roll, pitch, and yaw) after derailment was different. This was due to the change in mass and center of gravity;
- Through the analysis of rolling behavior, it was possible to check whether the overturning phenomenon of the test car was caused by collision with DCP. Similar to a container wagon, if the total mass increases and the position of the center of gravity rises, the risk of overturning due to collision with the DCP type I may be increased compared to a flat wagon. The rolling behavior of a container wagon generated a larger rolling angle value and a larger wavelength than that of a flat wagon, but stabilized over time after collision with DCP. As a result of comparative analysis of the rolling behavior, it was judged that the DCP’s function to restrain the derailed train even if the center of gravity position rises was sufficiently exhibited without any risk of overturning (rollover accident);
- The stabilization state of the test car’s vertical behavior was confirmed through the pitching behavior analysis. The overall pitching angle trend between the two wagons was similar, but it can be seen that the relatively light flat wagon’s behavior in the vertical direction was unstable due to collisions with track components such as the fastener, sleeper hump, etc.;
- Through yawing behavior analysis, it was possible to check the test car’s derailment angle and to determine whether the driving direction of the derailed vehicle deviated from the intended area. Since the two wagons had the same length and width, the maximum yaw angle (derailment angle) was evaluated to be almost identical. Then the yawing angles of both wagons quickly approached zero. That is, it can be seen that the derailed vehicle gradually moved along the track due to the restraint effect of the DCP type I.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bae, H.U.; Yun, K.M.; Lim, N.H. Containment capacity and crashworthiness estimation of derailment containment wall on high-speed train. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 680–696. [Google Scholar] [CrossRef]
- Bae, H.U.; Yun, K.M.; Moon, J.; Lim, N.H. Impact force evaluation of the derailment containment wall for high-speed train through a collision simulation. Adv. Civ. Eng. 2018, 2018, 2626905. [Google Scholar] [CrossRef] [Green Version]
- Booz Allen Hamilton. Report on the Findings of: Current Practice and Effectiveness of Derailment Containment Provisions on High Speed Lines; HSL-Zuid Organisation: Zoetermeer, The Netherlands, 2004. [Google Scholar]
- Korea Rail Network Authority. Railway Design Guideline and Handbook—Subsidiary and Safety Facilities for Main Lined; KR C-02060; Korea Rail Network Authority: Daejeon, Korea, 2017. [Google Scholar]
- Nadal, M.J. Theorie de la stabilite des locomotives—Part II. Movement de Lacet. Ann. Mines 1896, 10, 232–255. [Google Scholar]
- Wu, X.; Chi, M.; Gao, H. The study of post-derailment dynamic behavior of railway vehicle based on running tests. Eng. Fail. Anal. 2014, 44, 382–399. [Google Scholar] [CrossRef]
- Brabie, D.; Andersson, E. Dynamic simulation of derailments and its consequences. Veh. Syst. Dyn. 2006, 44, 652–662. [Google Scholar] [CrossRef]
- Brabie, D. Wheel-sleeper impact model in rail vehicles analysis. J. Syst. Des. Dyn. 2007, 1, 468–480. [Google Scholar] [CrossRef]
- Brabie, D.; Andersson, E. Post-derailment dynamic simulation of rail vehicles—Methodology and applications. Veh. Syst. Dyn. 2008, 46, 289–300. [Google Scholar] [CrossRef]
- Brabie, D.; Andersson, E. High-speed train derailments—Minimizing consequences through Innovative design. In Proceedings of the 8th World Congress of Railway Research (WCRR 2008), Seoul, Korea, 19–21 May 2008; Union Internationale Des Chemins De Fer (UIC): Paris, France, 2008. [Google Scholar]
- Wu, X.; Chi, M.; Gao, H. Post-derailment dynamic behavior of a high-speed train under earthquake excitations. Eng. Fail. Anal. 2016, 64, 97–110. [Google Scholar] [CrossRef]
- Wu, X.; Chi, M.; Gao, H.; Ke, X.; Zeng, J.; Wu, P.; Zhu, M. Post-derailment dynamic behavior of railway vehicles travelling on a railway bridge during earthquake. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 418–439. [Google Scholar] [CrossRef]
- Ling, L.; Dhanasekar, M.; Wang, K.; Zhaia, W.; Weston, B. Collision derailments on bridges containing ballastless slab tracks. Eng. Fail. Anal. 2019, 105, 869–882. [Google Scholar] [CrossRef]
- Guo, L.; Wang, K.; Lin, J. Study of the post-derailment safety measures on low-speed derailment tests. Veh. Syst. Dyn. 2016, 54, 943–962. [Google Scholar] [CrossRef]
- Diana, G.; Sabbioni, E.; Somaschini, C.; Tarsitano, D.; Cavicchi, P.; Di Mario, M.; Labbadia, L. Full-scale derailment tests on freight wagons. Veh. Syst. Dyn. 2022, 60, 1849–1866. [Google Scholar] [CrossRef]
- Kajitani, Y.; Kato, H.; Asano, K. Development of an L-shaped guide to prevent deviation from rails. JR-EAST Tech. Rev. 2010, 15, 53–56. [Google Scholar]
- Sunami, H.; Morimura, T.; Ishikawa, S.; Adachi, M.; Sakanoue, K.; Minami, Y.; Watanabe, Y.; Soda, Y. Experiment on test track for preventing the derailed vehicle from veering off the track. Trans. Jpn. Soc. Mech. Eng. 2010, 76, 2462–2463. [Google Scholar] [CrossRef] [Green Version]
- Sunami, H.; Morimura, T.; Terumichi, Y.; Adachi, M. Model for analysis of bogie frame motion under derailment conditions based on full-scale running tests. Multibody Syst. Dyn. 2012, 27, 321–349. [Google Scholar] [CrossRef]
- Wu, X.; Chi, M.; Gao, H.; Zhang, D.; Zeng, J.; Wu, P.; Zhu, M. The study of post-derailment measures to limit the extent of a derailment. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 64–76. [Google Scholar] [CrossRef]
- Bae, H.U.; Moon, J.; Lim, S.J.; Park, J.C.; Lim, N.H. Full-Scale Train Derailment Testing and Analysis of Post-Derailment Behavior of Casting Bogie. Appl. Sci. 2020, 10, 59. [Google Scholar] [CrossRef] [Green Version]
- Song, I.H.; Kim, J.W.; Koo, J.S.; Lim, N.H. Modeling and Simulation of Collision-Causing Derailment to Design the Derailment Containment Provision Using a Simplified Vehicle Model. Appl. Sci. 2020, 10, 118. [Google Scholar] [CrossRef]
- Beason, W.L.; Hirsch, T.J.; Campise, W.L. Measurement of Heavy Vehicle Impact Forces and Inertia Properties; Final Report, FHWA/RD-89/120; Texas Transportation Institute: College Station, TX, USA, 1989. [Google Scholar]
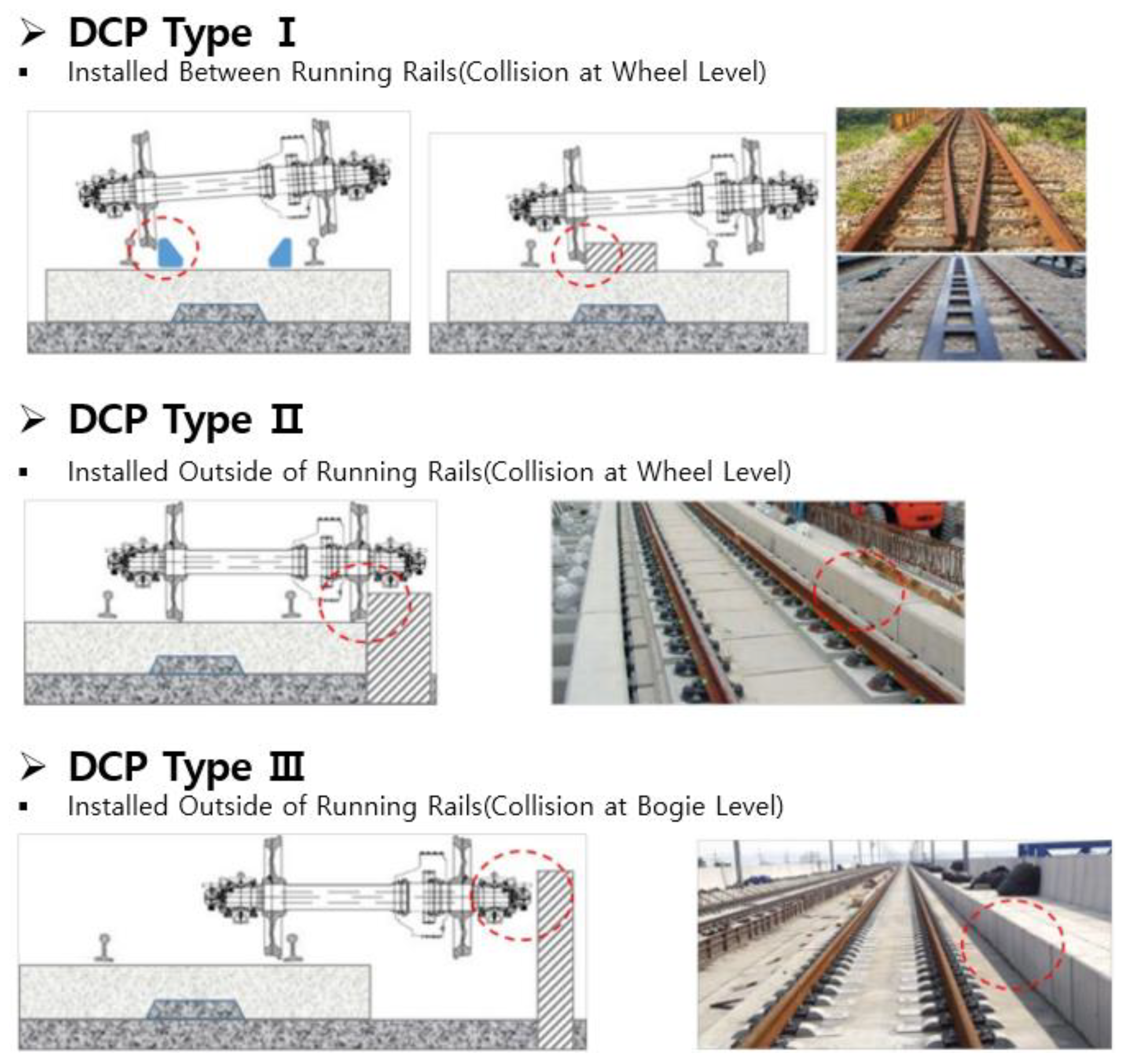

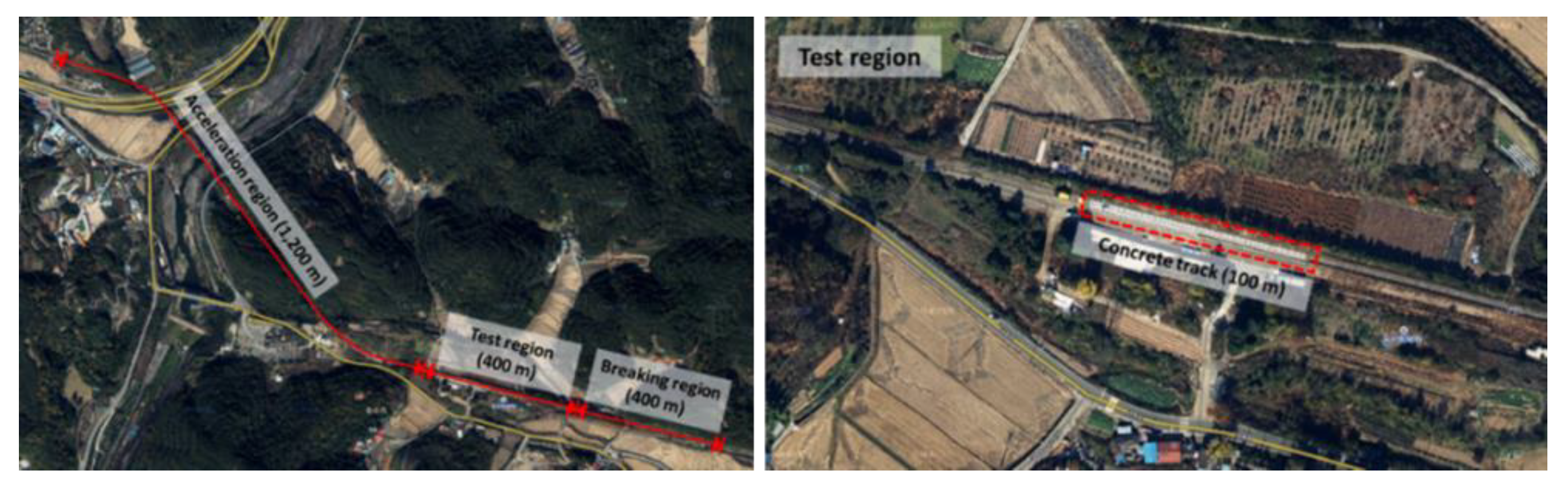
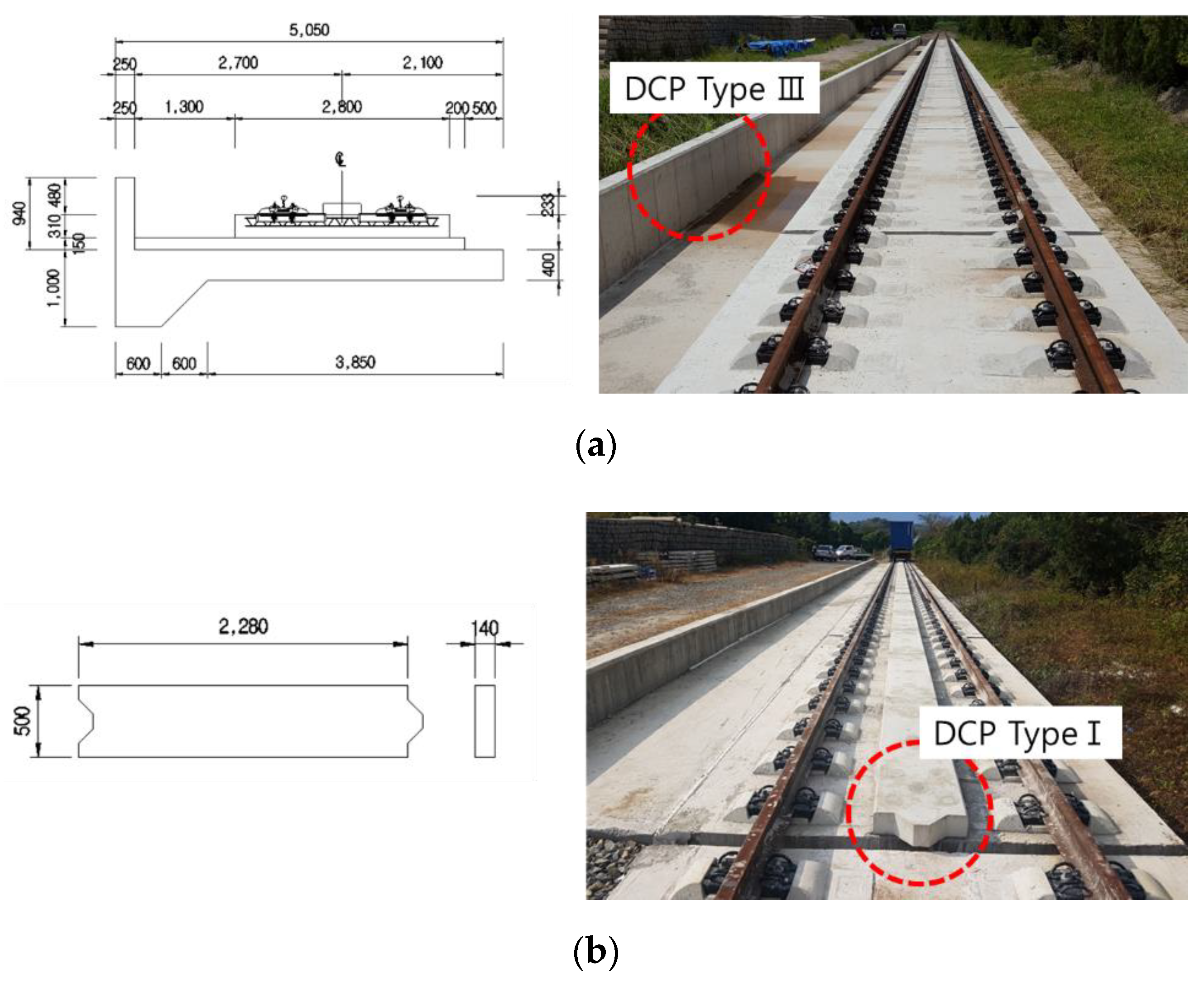

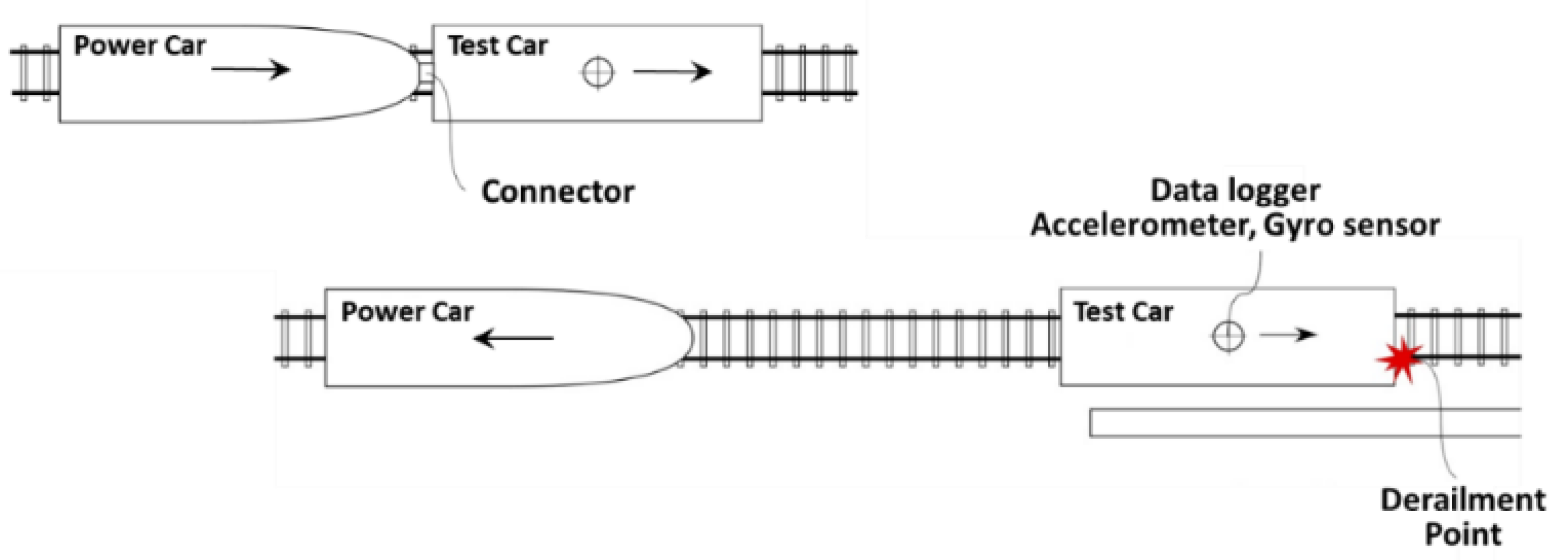








| Track Concrete Layer | DCP Panel | |
|---|---|---|
| Segment length | 6000 mm | 2280 mm |
| Width | 2800 mm | 500 mm |
| Height | 310 mm | 140 mm |
| Installation length | ≈100 m (17 EA) | ≈50 m (22 EA) |
| Flat Wagon | Container Wagon | |
|---|---|---|
| Mass Weight | 13,030 kg 127.82 kN | 17,320 kg 169.91 kN |
| Length | 12,590 mm | 12,590 mm |
| Width | 2330 mm | 2330 mm |
| Height | 906 mm | 3542 mm |
| Center of gravity (vertical) | 598 mm | 1005 mm |
| Total Mass | Lateral Acceleration | Collision Load Using 100% Mass | Collision Load Using 50% Mass | Contact Force by Simulation |
|---|---|---|---|---|
| 13,030 kg | 1.242 g | 158.79 kN | 79.40 kN | 80.57 kN |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, H.-U.; Kim, K.-J.; Park, S.-Y.; Han, J.-J.; Park, J.-C.; Lim, N.-H. Functionality Analysis of Derailment Containment Provisions through Full-Scale Testing—I: Collision Load and Change in the Center of Gravity. Appl. Sci. 2022, 12, 11297. https://doi.org/10.3390/app122111297
Bae H-U, Kim K-J, Park S-Y, Han J-J, Park J-C, Lim N-H. Functionality Analysis of Derailment Containment Provisions through Full-Scale Testing—I: Collision Load and Change in the Center of Gravity. Applied Sciences. 2022; 12(21):11297. https://doi.org/10.3390/app122111297
Chicago/Turabian StyleBae, Hyun-Ung, Kyoung-Ju Kim, Sang-Yun Park, Jeong-Jin Han, Jong-Chan Park, and Nam-Hyoung Lim. 2022. "Functionality Analysis of Derailment Containment Provisions through Full-Scale Testing—I: Collision Load and Change in the Center of Gravity" Applied Sciences 12, no. 21: 11297. https://doi.org/10.3390/app122111297







