Hyperspectral Image Classification Using 3D Capsule-Net Based Architecture
Abstract
1. Introduction
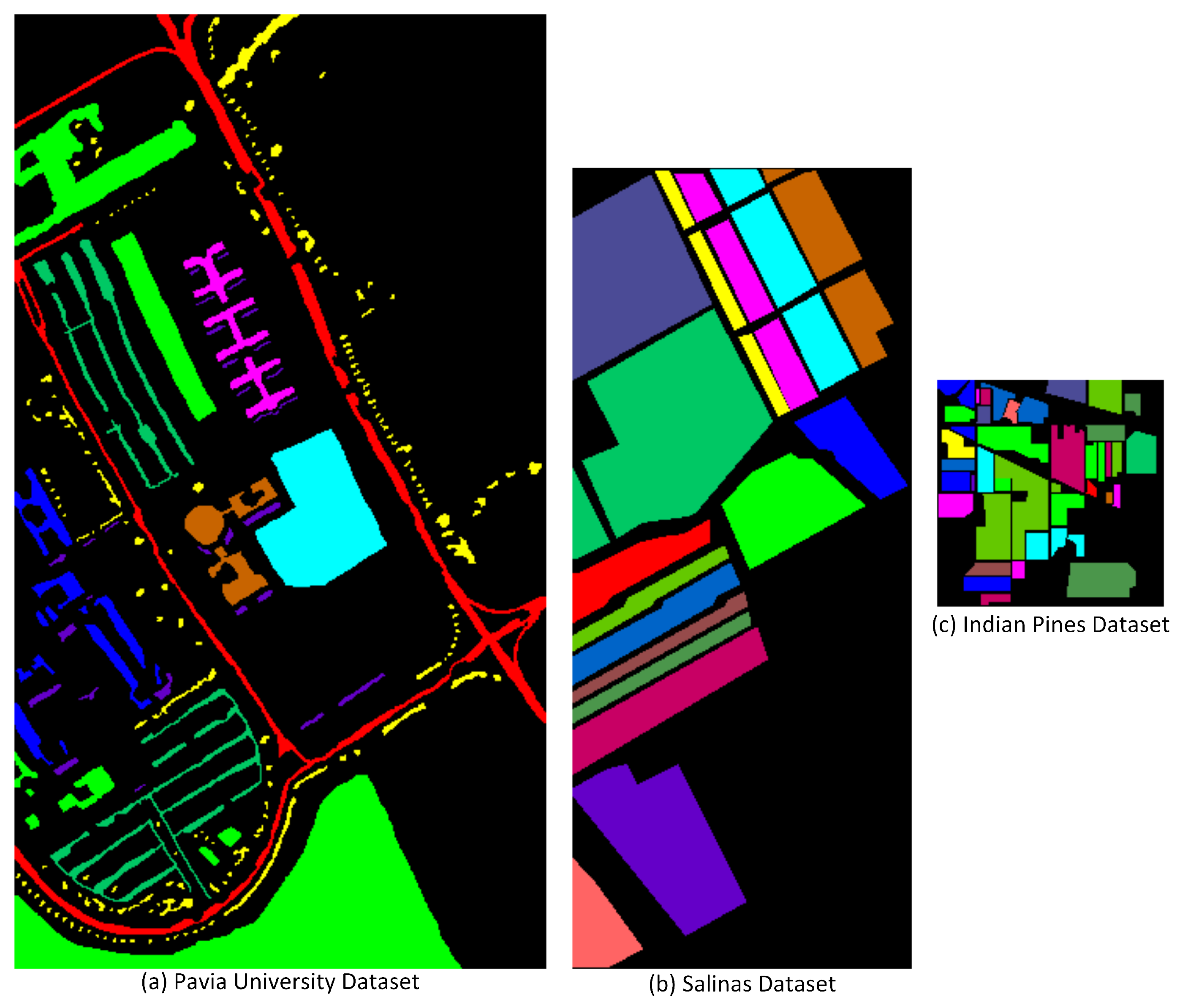
2. Dataset
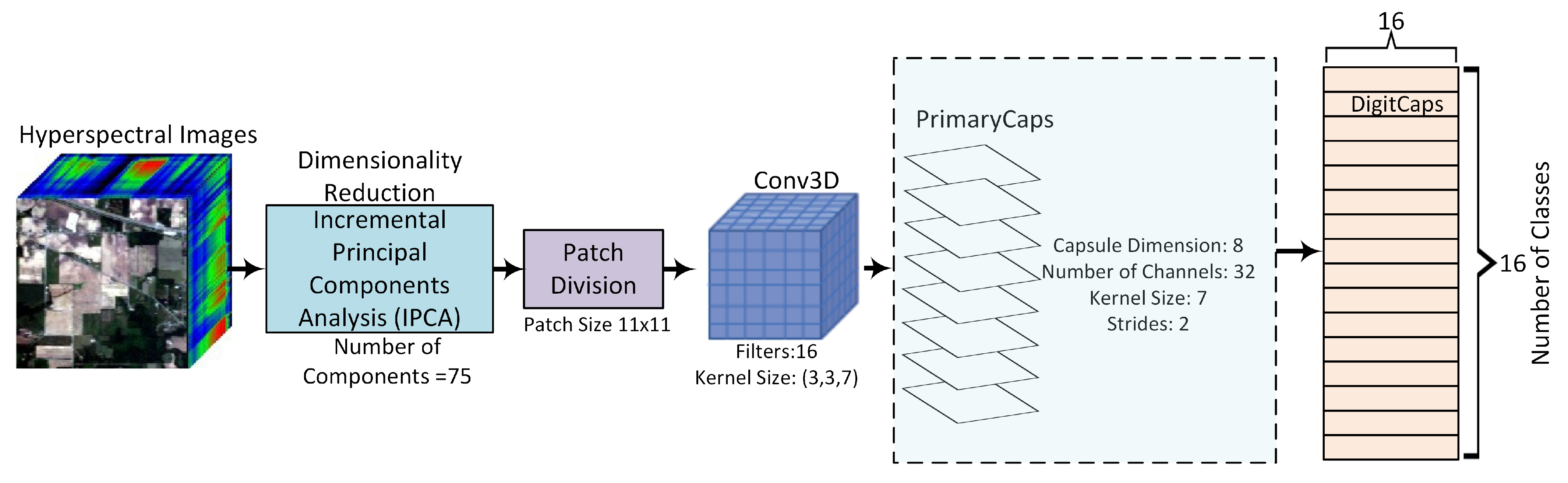
3. Proposed Methodology
3.1. IPCA
3.2. Capsule-Net
3.3. Implementation Details
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of spectral–temporal response surfaces by combining multispectral satellite and hyperspectral UAV imagery for precision agriculture applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Noor, S.S.M.; Michael, K.; Marshall, S.; Ren, J.; Tschannerl, J.; Kao, F. The properties of the cornea based on hyperspectral imaging: Optical biomedical engineering perspective. In Proceedings of the 2016 International Conference on Systems, Signals and Image Processing (IWSSIP), Sofia, Bulgaria, 1–3 June 2016; pp. 1–4. [Google Scholar]
- Wang, J.; Zhang, L.; Tong, Q.; Sun, X. The Spectral Crust project—Research on new mineral exploration technology. In Proceedings of the 2012 4th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Shanghai, China, 11 August 2012; pp. 1–4. [Google Scholar]
- Fong, A.; Shu, G.; McDonogh, B. Farm to Table: Applications for New Hyperspectral Imaging Technologies in Precision Agriculture, Food Quality and Safety. In Proceedings of the CLEO: Applications and Technology, Optical Society of America, Washington, DC, USA, 10–15 May 2020; p. AW3K-2. [Google Scholar]
- Ardouin, J.P.; Lévesque, J.; Rea, T.A. A demonstration of hyperspectral image exploitation for military applications. In Proceedings of the 2007 10th International Conference on Information Fusion, Quebec, QC, Canada, 9–12 July 2007; pp. 1–8. [Google Scholar]
- Sun, L.; He, C.; Zheng, Y.; Tang, S. SLRL4D: Joint Restoration of S ubspace L ow-R ank L earning and Non-Local 4-D Transform Filtering for Hyperspectral Image. Remote Sens. 2020, 12, 2979. [Google Scholar] [CrossRef]
- He, C.; Sun, L.; Huang, W.; Zhang, J.; Zheng, Y.; Jeon, B. TSLRLN: Tensor subspace low-rank learning with non-local prior for hyperspectral image mixed denoising. Signal Process. 2021, 184, 108060. [Google Scholar] [CrossRef]
- Yang, S.; Shi, Z. Hyperspectral image target detection improvement based on total variation. IEEE Trans. Image Process. 2016, 25, 2249–2258. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Wu, Z.; Liu, J.; Xiao, L.; Wei, Z. Supervised spectral–spatial hyperspectral image classification with weighted Markov random fields. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1490–1503. [Google Scholar] [CrossRef]
- Sun, L.; Ma, C.; Chen, Y.; Zheng, Y.; Shim, H.J.; Wu, Z.; Jeon, B. Low rank component induced spatial-spectral kernel method for hyperspectral image classification. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 3829–3842. [Google Scholar] [CrossRef]
- Sun, L.; Ma, C.; Chen, Y.; Shim, H.J.; Wu, Z.; Jeon, B. Adjacent superpixel-based multiscale spatial-spectral kernel for hyperspectral classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1905–1919. [Google Scholar] [CrossRef]
- Zhang, M.L.; Zhou, Z.H. ML-KNN: A lazy learning approach to multi-label learning. Pattern Recognit. 2007, 40, 2038–2048. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, L.; Mou, X.; Bovik, A.C. Gradient magnitude similarity deviation: A highly efficient perceptual image quality index. IEEE Trans. Image Process. 2013, 23, 684–695. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Wang, Z.; Du, B.; Guo, Y. Domain adaptation with neural embedding matching. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2387–2397. [Google Scholar] [CrossRef] [PubMed]
- Rehman, M.U.; Akhtar, S.; Zakwan, M.; Mahmood, M.H. Novel architecture with selected feature vector for effective classification of mitotic and non-mitotic cells in breast cancer histology images. Biomed. Signal Process. Control 2022, 71, 103212. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Babu Naik, G.; Ameta, P.; Baba Shayeer, N.; Rakesh, B.; Kavya Dravida, S. Convolutional Neural Network Based on Self-Driving Autonomous Vehicle (CNN). In Innovative Data Communication Technologies and Application; Springer: Berlin/Heidelberg, Germany, 2022; pp. 929–943. [Google Scholar]
- Rehman, M.U.; Cho, S.; Kim, J.; Chong, K.T. Brainseg-net: Brain tumor mr image segmentation via enhanced encoder–decoder network. Diagnostics 2021, 11, 169. [Google Scholar] [CrossRef]
- Rehman, M.U.; Cho, S.; Kim, J.H.; Chong, K.T. Bu-net: Brain tumor segmentation using modified u-net architecture. Electronics 2020, 9, 2203. [Google Scholar] [CrossRef]
- Rehman, M.U.; Tayara, H.; Chong, K.T. DL-m6A: Identification of N6-methyladenosine Sites in Mammals using deep learning based on different encoding schemes. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022. [Google Scholar] [CrossRef]
- Bensalah, N.; Ayad, H.; Adib, A.; Ibn El Farouk, A. CRAN: An hybrid CNN-RNN attention-based model for Arabic machine translation. In Networking, Intelligent Systems and Security; Springer: Berlin/Heidelberg, Germany, 2022; pp. 87–102. [Google Scholar]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- Cheng, G.; Li, Z.; Han, J.; Yao, X.; Guo, L. Exploring hierarchical convolutional features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6712–6722. [Google Scholar] [CrossRef]
- Mughees, A.; Tao, L. Multiple deep-belief-network-based spectral-spatial classification of hyperspectral images. Tsinghua Sci. Technol. 2018, 24, 183–194. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Sellami, A.; Abbes, A.B.; Barra, V.; Farah, I.R. Fused 3-D spectral-spatial deep neural networks and spectral clustering for hyperspectral image classification. Pattern Recognit. Lett. 2020, 138, 594–600. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–spatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep pyramidal residual networks for spectral–spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 740–754. [Google Scholar] [CrossRef]
- Wang, W.; Dou, S.; Jiang, Z.; Sun, L. A fast dense spectral–spatial convolution network framework for hyperspectral images classification. Remote Sens. 2018, 10, 1068. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, Z.; Du, Q.; Xu, Y.; Wei, Z. Multiscale alternately updated clique network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, Y. Study on artificial intelligence: The state of the art and future prospects. J. Ind. Inf. Integr. 2021, 23, 100224. [Google Scholar] [CrossRef]
- Kakani, V.; Nguyen, V.H.; Kumar, B.P.; Kim, H.; Pasupuleti, V.R. A critical review on computer vision and artificial intelligence in food industry. J. Agric. Food Res. 2020, 2, 100033. [Google Scholar] [CrossRef]
- Patrick, M.K.; Adekoya, A.F.; Mighty, A.A.; Edward, B.Y. Capsule networks–a survey. J. King Saud-Univ.-Comput. Inf. Sci. 2022, 34, 1295–1310. [Google Scholar]
- Sun, W.; Zhao, H.; Jin, Z. A facial expression recognition method based on ensemble of 3D convolutional neural networks. Neural Comput. Appl. 2019, 31, 2795–2812. [Google Scholar] [CrossRef]
- Lou, G.; Shi, H. Face image recognition based on convolutional neural network. China Commun. 2020, 17, 117–124. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Xiang, C.; Zhang, L.; Tang, Y.; Zou, W.; Xu, C. MS-CapsNet: A novel multi-scale capsule network. IEEE Signal Process. Lett. 2018, 25, 1850–1854. [Google Scholar] [CrossRef]
- Rehman, M.U.; Tayara, H.; Zou, Q.; Chong, K.T. i6mA-Caps: A CapsuleNet-based framework for identifying DNA N6-methyladenine sites. Bioinformatics 2022, 38, 3885–3891. [Google Scholar] [CrossRef]
| Class | Models | |||||
|---|---|---|---|---|---|---|
| DSVM | DCNN | CNN | R-VCA | 3DCNN | Proposed | |
| C1 | 88.22 | 94.21 | 93.41 | 95.02 | 94.46 | 84.2 |
| C2 | 92.31 | 95.41 | 96.80 | 94.91 | 92.19 | 98.6 |
| C3 | 95.12 | 96.98 | 95.26 | 97.36 | 98.05 | 100 |
| C4 | 95.96 | 97.56 | 93.82 | 96.99 | 97.09 | 98.9 |
| C5 | 97.03 | 95.11 | 96.22 | 94.78 | 92.16 | 100 |
| C6 | 83.03 | 96.51 | 94.02 | 98.89 | 95.10 | 100 |
| C7 | 89.64 | 95.63 | 95.04 | 96.14 | 94.06 | 100 |
| C8 | 92.03 | 97.10 | 98.01 | 95.31 | 98.91 | 100 |
| C9 | 96.12 | 94.12 | 97.02 | 93.36 | 97.03 | 87.5 |
| C10 | 91.22 | 91.85 | 98.04 | 94.21 | 94.02 | 99.2 |
| C11 | 85.13 | 93.45 | 95.32 | 94.21 | 95.21 | 99.6 |
| C12 | 91.12 | 89.48 | 86.14 | 92.14 | 95.03 | 100 |
| C13 | 86.12 | 94.25 | 94.06 | 93.84 | 96.21 | 100 |
| C14 | 95.01 | 93.85 | 97.13 | 94.96 | 96.12 | 99.4 |
| C15 | 95.02 | 94.61 | 95.23 | 95.95 | 94.18 | 99.4 |
| C16 | 92.38 | 96.85 | 96.10 | 95.91 | 95.19 | 100 |
| Parameter | Indian Pine Dataset (IPD) | |||||
|---|---|---|---|---|---|---|
| DSVM | DCNN | CNN | R-VCA | 3DCNN | Proposed | |
| OA | 92.24 | 94.86 | 94.99 | 94.26 | 96.54 | 99.41 |
| AA | 92.13 | 96.72 | 94.81 | 94.08 | 96.47 | 97.93 |
| 92.25 | 94.78 | 94.85 | 94.18 | 96.40 | 99.33 | |
| Parameter | Salinas Dataset (SD) | |||||
| DSVM | DCNN | CNN | R-VCA | 3DCNN | Proposed | |
| OA | 95.12 | 96.56 | 97.12 | 96.74 | 96.36 | 98.91 |
| AA | 95.02 | 96.31 | 97.03 | 96.61 | 96.22 | 99.44 |
| 95.07 | 96.30 | 97.15 | 96.47 | 96.28 | 98.785 | |
| Parameter | Pavia University Dataset (PUD) | |||||
| DSVM | DCNN | CNN | R-VCA | 3DCNN | Proposed | |
| OA | 92.24 | 94.86 | 94.99 | 94.26 | 96.54 | 99.74 |
| AA | 92.13 | 96.72 | 94.81 | 94.08 | 96.47 | 99.51 |
| 92.25 | 94.78 | 94.85 | 94.18 | 96.40 | 99.66 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryu, J.; Jang, Y. Hyperspectral Image Classification Using 3D Capsule-Net Based Architecture. Appl. Sci. 2022, 12, 11299. https://doi.org/10.3390/app122111299
Ryu J, Jang Y. Hyperspectral Image Classification Using 3D Capsule-Net Based Architecture. Applied Sciences. 2022; 12(21):11299. https://doi.org/10.3390/app122111299
Chicago/Turabian StyleRyu, Jihyoung, and Yeongmin Jang. 2022. "Hyperspectral Image Classification Using 3D Capsule-Net Based Architecture" Applied Sciences 12, no. 21: 11299. https://doi.org/10.3390/app122111299
APA StyleRyu, J., & Jang, Y. (2022). Hyperspectral Image Classification Using 3D Capsule-Net Based Architecture. Applied Sciences, 12(21), 11299. https://doi.org/10.3390/app122111299





