Performance and Optimization of a Dual-Stage Vibration Isolation System Using Bio-Inspired Vibration Isolators

Abstract

This paper thoroughly investigates the performance and multi-parameter optimization of a dual-stage vibration isolation system with bio-inspired isolators (BI-DSVI) under different base excitations. The dynamic equations of the BI-DSVI are derived. Then, the optimization problem is defined, where three types of base excitation (translation and rotations around the two horizontal axes) are studied. The optimization results show that the vibration transmissibility can be greatly reduced (more than 30 dB) by multi-parameter optimization, and an optimal configuration of structural parameters exists for the bio-inspired isolators. The effective vibration isolation bandwidth is significantly widened. Finally, the paper thoroughly discusses the influence of the structural parameters of the bio-inspired isolators and the base excitation types on the vibration isolation performance. The parameter studies provide useful guidelines for the application of the bio-inspired isolator in dual-stage vibration isolation.

1. Introduction

Vibration isolation is an essential part of most engineering designs. Harmful vibration will affect the mechanical properties of materials and cause fatigue and wear, leading to the destruction of structures [1,2]. The traditional linear vibration isolation system requires a lower natural frequency to achieve higher efficiency of vibration attenuation, which may degrade the isolation system’s capability of supporting the payload [3,4,5]. Thus, there is a conflict between the wider effective frequency band and larger loading capacity.

In nature, many animals have evolved simple limb trunk structures to isolate low-frequency vibrations, which can not only carry their large weight but still maintain good stability in high-speed motion. In recent years, the design of bio-inspired vibration isolators based on animal limb structures has been widely studied [6,7,8,9,10,11,12,13,14,15,16,17,18]. Jing and his coworkers presented a series of bio-inspired isolators composed of X-shaped structures and studied the dynamic characteristics of various vibration isolation systems [6,7,8,9,10,11,12,13,14]. For instance, inspired by the kangaroo’s limbs, Dai et al. [6] proposed a bio-inspired quadrilateral shape (BIQS) structure to suppress the vibration from the acquisition target to the satellite platform. They used the harmonic balance method to analyze the dynamic response of the vibration isolation system and studied the influence of BIQS’ structural parameters on the vibration isolation performance. The results show that the vibration isolator has better performance than the ordinary spring-mass-damper vibration isolator. Considering leg posture adjustment, Yan et al. [15] designed a bio-inspired polygon skeleton structure, in which the load capacity and working bandwidth can be adjusted by the initial parameters of the structure. The proposed structure can effectively suppress the vibration under various excitation conditions.

According to the above studies, bio-inspired isolators composed of X-shaped structures present excellent vibration isolation performance. However, the studies of bio-inspired isolators are currently limited to simple single-stage vibration isolation systems and the corresponding structural parameters’ analysis. In power units (gas turbines, gear pumps, etc.) or precision instruments (optical interferometers, space telescopes, etc.) with complex vibration isolation systems [19,20,21,22,23,24,25], a single-stage vibration isolation system often leads to resonant peaks and standing wave effects at high frequencies [26,27,28,29], which cannot meet the vibration isolation requirements. A dual-stage vibration isolation system draws great interest owing to its better high-frequency effect and higher stability [30,31,32,33,34,35,36].

In the dual-stage vibration isolation system, two layers of vibration isolators are installed between the control object and the base, and an intermediate mass is inserted between the two layers of vibration isolators. The inertia of the intermediate mass is used to offset part of the base excitation, to attenuate the vibration transmission rate from the base to the control object [30]. Linear isolators are usually used in the ordinary dual-stage vibration isolation system. Due to the large intermediate mass required in the dual-stage isolation system, the linear isolators will undergo excessive static deformation, resulting in instability. The bio-inspired isolators may solve this problem and further improve the effect of dual-stage vibration isolation. However, limited studies have been conducted on dual-stage vibration isolation systems using bio-inspired isolators. The influence mechanism of bio-inspired isolators on the dual-stage vibration isolation performance is still unclear. Moreover, in the real application environment of dual-stage vibration isolation systems, there are various complex excitation types, including translation and rotations. Under different excitation types, the structural parameters and placement positions of the bio-inspired isolators will exert a significant impact on the dual-stage vibration isolation performance. Thus, it is necessary to appropriately design the structural parameters and carefully determine the positions of the isolators to realize better vibration isolation performance under different excitation types.

This paper will investigate the performance of bio-inspired isolators in the dual-stage vibration isolation system. The multi-parameter optimization study of the vibration isolator’s structural parameters and placement positions will be carried out to obtain the optimal parameter configuration for the best vibration isolation performance under different excitation types.

The rest of the paper is organized as follows: Section 2 presents the dynamic model of the dual-stage vibration isolation system with bio-inspired isolators. Section 3 proposes the optimization problem and analyzes the optimization results. Section 4 performs the parameter study. The influences on the vibration isolation performance of the structural parameters of the bio-inspired isolator and the base excitations are discussed in detail. All the findings are summarized in Section 5.

2. Dynamic Model

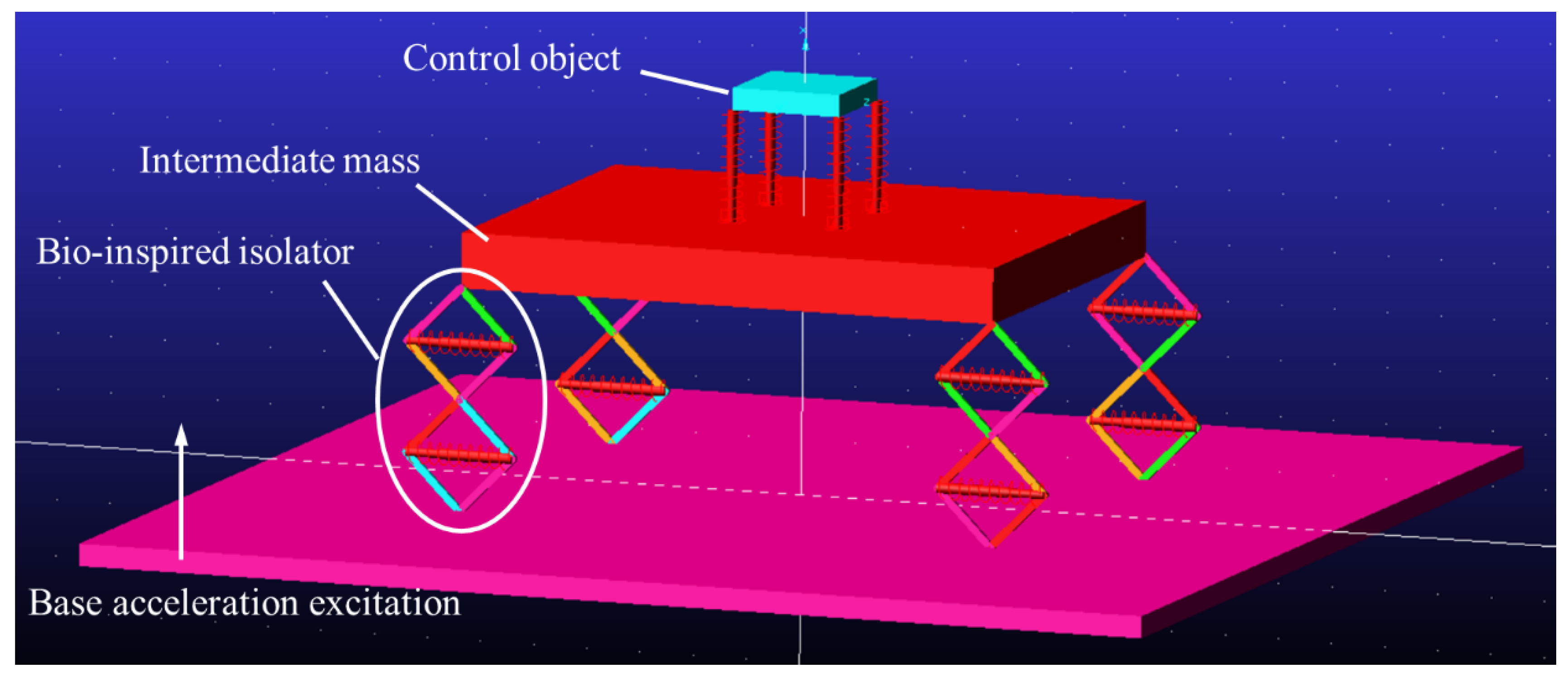
2.1. Model Description

The dual-stage vibration isolation system with the bio-inspired vibration isolator (BI-DSVI) is illustrated in Figure 1. The control object $m_u$ (which needs vibration isolation from the base excitation $z_{01}, z_{02}, z_{03}, z_{04}$) is connected to the intermediate mass $m_d$ with four linear isolators (each with linear spring $k_u$ and linear damping $c_u$). The intermediate mass is supported on the base by four bio-inspired vibration isolators, each containing a linear damping $c_d$ and a bio-inspired structure [6,7], as shown in Figure 1a. $l_d$ is the length of the connecting rods, $k_d$ is the stiffness of the transverse spring between the connecting joints, and the initial assembly angle is ${\phi }_{d0}$. The absolute displacements of the control object and the intermediate mass are $z_u$ and $z_d$, respectively. The rotation angles of the control object around its horizontal inertia principal axes paralleling the $x,y$ axes are $\alpha$ and $\beta$, and the rotation angles of the intermediate mass around its horizontal inertia principal axes paralleling the $x,y$ axes are $\psi$ and $\theta$. To simplify the problem, only the translational motion along the height direction of the isolator (i.e., the direction of the coordinate axis $z$) and the rotational motion around the horizontal coordinate axes are considered. Thus, there are six generalized coordinates in the dynamic model: $z_u,\psi ,\theta ,z_d,\alpha ,\beta$.

2.2. Governing Equations

The dynamic equations of the BI-DSVI can be described as

$$\begin{gathered} m_d{\ddot{z}}_d+c_d\left[4{\dot{z}}_d+\left(4a-L_y\right)\dot{\psi }+\left(4b-L_x\right)\dot{\theta }-{\dot{z}}_{01}-{\dot{z}}_{02}-{\dot{z}}_{03}-{\dot{z}}_{04}\right]+4c_u\left({\dot{z}}_d-{\dot{z}}_u\right) \\ +2k_d\left[B_1\left(z_d,\psi ,\theta \right)+B_2\left(z_d,\psi ,\theta \right)+B_3\left(z_d,\psi ,\theta \right)+B_4\left(z_d,\psi ,\theta \right)\right]+4k_u\left(z_d-z_u\right)=0 \end{gathered}$$

(1)

$$\begin{array}{cc}{J}_{dx}\ddot{\psi }+c_d[(4a-\hfill & 2L_y){\dot{z}}_d+\left(4a^2-L_{y}a+2L_y^2-2L_{y}a\right)\dot{\psi }+\left(4ab-L_{x}a+L_y{L}_x-2L_{y}b\right)\dot{\theta }-\left(a-L_y\right){\dot{z}}_{01}\hfill \\ & -a{\dot{z}}_{02}-a{\dot{z}}_{03}-\left(a-L_y\right){\dot{z}}_{04}]+c_u{L}_u^2\left(\dot{\psi }-\dot{\alpha }\right)\hfill \\ & +2k_d\left[\left(a-L_y\right)B_1\left(z_d,\psi ,\theta \right)+a{B}_2\left(z_d,\psi ,\theta \right)+a{B}_3\left(z_d,\psi ,\theta \right)+\left(a-L_y\right)B_4\left(z_d,\psi ,\theta \right)\right]\hfill \\ & +k_u{L}_u^2\left(\psi -\alpha \right)=0\hfill \end{array}$$

(2)

$$\begin{array}{cc}{J}_{dy}\ddot{\theta }+c_d\left[\right(4b-\hfill & 2L_x){\dot{z}}_d+\left(4ab-L_{y}b+L_x{L}_y-2L_{x}a\right)\dot{\psi }+\left(4b^2-L_{x}b+2L_x^2-2L_{x}b\right)\dot{\theta }-\left(b-L_x\right){\dot{z}}_{01}\hfill \\ & -\left(b-L_x\right){\dot{z}}_{02}-b{\dot{z}}_{03}-b{\dot{z}}_{04}]+c_u{B}_u^2\left(\dot{\theta }-\dot{\beta }\right)\hfill \\ & +2k_d\left[\left(b-L_x\right)B_1\left(z_d,\psi ,\theta \right)+\left(b-L_x\right)B_2\left(z_d,\psi ,\theta \right)+b{B}_3\left(z_d,\psi ,\theta \right)+b{B}_4\left(z_d,\psi ,\theta \right)\right]\hfill \\ & +k_u{B}_u^2\left(\theta -\beta \right)=0\hfill \end{array}$$

(3)

$$m_u{\ddot{z}}_u+4c_u\left({\dot{z}}_d-{\dot{z}}_u\right)+4k_u\left(z_d-z_u\right)=0$$

(4)

$$J_{ux}\ddot{\alpha }+c_u{L}_u^2\left(\dot{\alpha }-\dot{\psi }\right)+k_u{L}_u^2\left(\alpha -\psi \right)=0$$

(5)

$$J_{uy}\ddot{\beta }+c_u{B}_u^2\left(\dot{\beta }-\dot{\theta }\right)+k_u{B}_u^2\left(\beta -\theta \right)=0$$

(6)

$B_1\left(z_d,\psi ,\theta \right), B_2\left(z_d,\psi ,\theta \right), B_3\left(z_d,\psi ,\theta \right), B_4\left(z_d,\psi ,\theta \right)$ are functions of the three generalized coordinates $z_d,\psi ,\theta$:

$$B_1\left(z_d,\psi ,\theta \right)=\frac{l_{d}cos{\phi }_{d0}}{\sqrt{l_d^2-h_1^2}}-h_1$$

(7)

$$B_2\left(z_d,\psi ,\theta \right)=\frac{l_{d}cos{\phi }_{d0}}{\sqrt{l_d^2-h_2^2}}-h_2$$

(8)

$$B_3\left(z_d,\psi ,\theta \right)=\frac{l_{d}cos{\phi }_{d0}}{\sqrt{l_d^2-h_3^2}}-h_3$$

(9)

$$B_4\left(z_d,\psi ,\theta \right)=\frac{l_{d}cos{\phi }_{d0}}{\sqrt{l_d^2-h_4^2}}-h_4$$

(10)

where

$$\{\begin{array}{l}{h}_1=\left[z_d-\psi \left(L_y-a\right)-\theta \left(L_x-b\right)-z_{01}\right]∕4,\\ h_2=\left[z_d+\psi a-\theta \left(L_x-b\right)-z_{02}\right]/4, \\ h_3=\left(z_d+\psi a+\theta b-z_{03}\right)/4, \\ h_4=\left[z_d-\psi \left(L_y-a\right)+\theta b-z_{04}\right]/4. \end{array}$$

(11)

We assume that the base excitation is ${\ddot{z}}_{0i}=Acos(2\pi ft+{\varphi }_{0i}),i=1,2,3,4$, where $A$ is the excitation amplitude, $f$ is the excitation frequency, and ${\varphi }_{0i}$ is the initial phase. We define the vibration transmissibility as

$$T=\frac{\left|{\ddot{z}}_u\right|}{A}$$

(12)

where $| |$ represents the amplitude. In other words, the smaller the vibration transmissibility $T$, the better the vibration isolation performance. By changing the initial phase values at the four base positions, different types of base excitation can be achieved. For instance, ${\varphi }_{01}={\varphi }_{02}=0, {\varphi }_{03}={\varphi }_{04}=\pi$ means the rotation excitation of the base around the $y$ axis, and ${\varphi }_{01}={\varphi }_{04}=0, {\varphi }_{02}={\varphi }_{03}=\pi$ means the rotation excitation of the base around the $x$ axis.

In the following study of this paper, a sweep signal with amplitude $A=1 \mathrm{m}/{\mathrm{s}}^2$ will be used as the base excitation, in which excitation frequency $f$ is linearly increased with the rate 0.01 Hz/s from 2 Hz to 12 Hz. The dynamic Equations (1)–(6) will be numerically solved by the 4th-order Runge–Kutta method with a 0.01 s time step and the initial conditions are $\left[0 0 0 0 0 0\right]$. The numerical solution is verified by Adams in the Appendix A.

3. Performance Optimization Using Genetic Algorithm

In practical applications, the base excitation is often a complex motion composed of translational and rotational motions. Thus, it is necessary to optimize the bio-inspired isolator parameters and placement positions under different base excitation values. This section will discuss the optimization problem of isolator parameters and placement positions considering three different base excitation types: translation along the $z$ axis, rotation about the $x$ axis, and rotation about the $y$ axis.

3.1. Definition of the Optimization Problem

In vibration isolation, minimizing the total vibrational energy of the control object in a working frequency band is the optimization goal. By selecting optimal design parameters, the total vibrational energy will reach the minimum, and the optimal distribution of the vibration transmissibility $T$ in a given frequency band can be realized. In this paper, the motion of the control object $m_u$ is described by three generalized coordinates $z_u,\alpha ,\beta$. Thus, the total vibration energy from frequency $f_s$ to $f_e$ can be defined as

$$G={{\displaystyle \int }}_{f_s}^{f_e}\left({\left|{\ddot{z}}_u\right|}^2+{\left|\ddot{\alpha }\right|}^2+{\left|\ddot{\beta }\right|}^2\right)df$$

(13)

where $f_s=2 \mathrm{Hz}$ is the sweep start frequency and $f_e=12 \mathrm{Hz}$ is the stop frequency; the envelopes are used as the amplitude of the vibration acceleration ${\ddot{z}}_u,\ddot{\alpha },\ddot{\beta }$. A lower $G$ indicates better isolation performance. To simulate the actual complex base excitation, three typical basic excitation types are selected for the optimization research:

Excitation 1: ${\varphi }_{01}={\varphi }_{02}={\varphi }_{03}={\varphi }_{04}=0$ (translation excitation along the $z$ axis);

Excitation 2: ${\varphi }_{01}={\varphi }_{02}=0, {\varphi }_{03}={\varphi }_{04}=\pi$ (rotation excitation around the $y$ axis);

Excitation 3: ${\varphi }_{01}={\varphi }_{04}=0, {\varphi }_{02}={\varphi }_{03}=\pi$ (rotation excitation around the $x$ axis).

The design parameters contain three structural parameters of the bio-inspired isolator: the connecting rod length $l_d$, the transverse spring stiffness $k_d$, the initial assembly angle ${\phi }_{d0}$, and two placement position parameters $a,b$. Other structural parameters are shown in

Table 1. Parameters for BI-DSVI.

Parameters	Description	Values
$m_u$	Control object mass	$2 \mathrm{kg}$
$J_{ux}$	$\mathrm{Moment} \mathrm{of} \mathrm{inertia} \mathrm{about} \mathrm{axis} x$$\mathrm{of} m_u$	$1 \mathrm{kg}·{\mathrm{m}}^2$
$J_{uy}$	$\mathrm{Moment} \mathrm{of} \mathrm{inertia} \mathrm{about} \mathrm{axis} y$$\mathrm{of} m_u$	$1 \mathrm{kg}·{\mathrm{m}}^2$
$L_u$	$\mathrm{Length} \mathrm{of} m_u$	$0.1$
$B_u$	$\mathrm{Width} \mathrm{of} m_u$	$0.1 \mathrm{m}$
$k_u$	Stiffness of the linear isolator	$1000 \mathrm{N}/\mathrm{m}$
$c_u$	Damping of the linear isolator	$1 \mathrm{N}·\mathrm{s}/\mathrm{m}$
$m_d$	Intermediate mass	$10 \mathrm{kg}$
$J_{dx}$	$\mathrm{Moment} \mathrm{of} \mathrm{inertia} \mathrm{about} \mathrm{axis} x$$\mathrm{of} m_d$	$10 \mathrm{kg}·{\mathrm{m}}^2$
$J_{dy}$	$\mathrm{Moment} \mathrm{of} \mathrm{inertia} \mathrm{about} \mathrm{axis} y$$\mathrm{of} m_d$	$8 \mathrm{kg}·{\mathrm{m}}^2$
$L_x$	$\mathrm{Distance} \mathrm{between} \mathrm{bio}-\mathrm{inspired} \mathrm{isolators} \mathrm{along} \mathrm{axis} y$	$0.5 \mathrm{m}$
$L_y$	$\mathrm{Distance} \mathrm{between} \mathrm{bio}-\mathrm{inspired} \mathrm{isolators} \mathrm{along} \mathrm{axis} x$	$0.4 \mathrm{m}$
$c_d$	Damping of the bio-inspired isolator	$5 \mathrm{N}·\mathrm{s}/\mathrm{m}$

.

Based on the above description, consider the fitness function $F\left(\mathit{p}\right)=1/G\left(\mathit{p}\right)$, which represents the inverse of the total vibration energy generated by given parameter vector $\mathit{p}$. The vector $\mathit{p}$ contains all the design parameters, i.e., $\mathit{p}=\left[\begin{array}{ccccc}{l}_d& k_d& {\phi }_{d0}& a& b\end{array}\right]$. Thus, an objective function is defined as

$$\max F\left(\mathit{p}\right) \mathrm{when} {\mathit{p}}_{\mathit{l}}<\mathit{p}<{\mathit{p}}_{\mathit{u}}$$

(14)

where ${\mathit{p}}_{\mathit{l}}$ and ${\mathit{p}}_{\mathit{u}}$ are the upper and lower limits of the design parameter vector. The optimization goal is to find the maximum $F$ subjected to ${\mathit{p}}_{\mathit{l}}<\mathit{p}<{\mathit{p}}_{\mathit{u}}$ under the above three base excitations, respectively.

3.2. Optimization Procedure

In this paper, the genetic algorithm (GA) will be used to optimize the solution. Figure 2 presents the flowchart of the optimization algorithm, and the detailed steps are presented as follows:

Begin

Step1: Initialize GA parameters; the population size is set to 20, the cross probability is 0.8, the mutation probability is 0.2, the max iteration is 200, and the elitist preservation proportion is 0.1.

Step2: Define the optimization fitness function $F=1/G$ and the range of the design parameters:

$$l_d\in \left[0.2, 0.4\right] \mathrm{m},k_d\in \left[5000, 10,000\right] \mathrm{N}/\mathrm{m},{\phi }_{d0}\in \left[\frac{\pi }{6},\frac{\pi }{3}\right],a\in \left[0.1, 0.4\right] \mathrm{m},b\in \left[0.1, 0.3\right] \mathrm{m}$$

Step3: Generate a random initial population and calculate the initial fitness of all individuals.

Step4: Initialize the count number $gen=1$.

Step5: Perform selection, crossover, and mutation operations.

Step6: Update the count number $gen=gen+1$.

Step7: Go back to step 4 until $gen=200$. When $gen=200$, go to Step 8.

Step8: Output the optimal fitness value $1/G$ and the corresponding design parameters $\left[\begin{array}{ccccc}{l}_d& k_d& {\phi }_{d0}& a& b\end{array}\right]$.

End

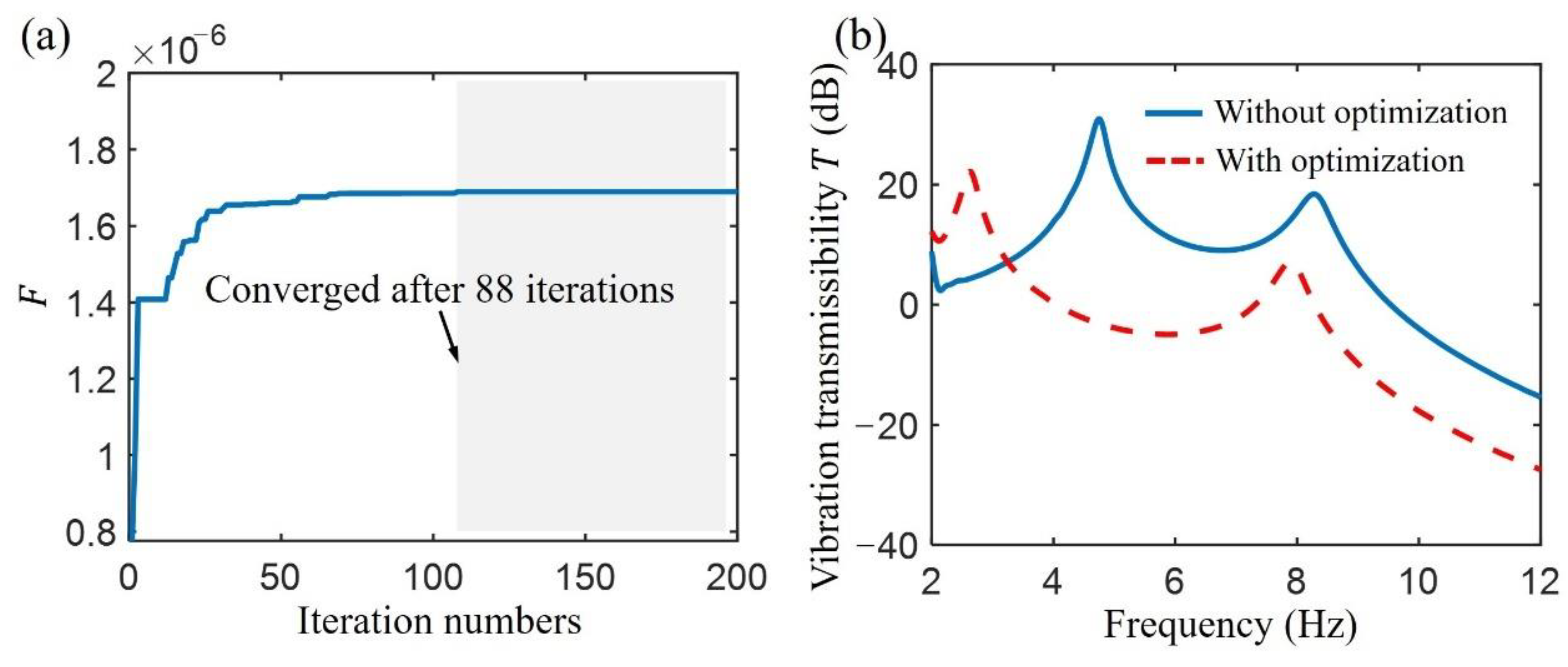
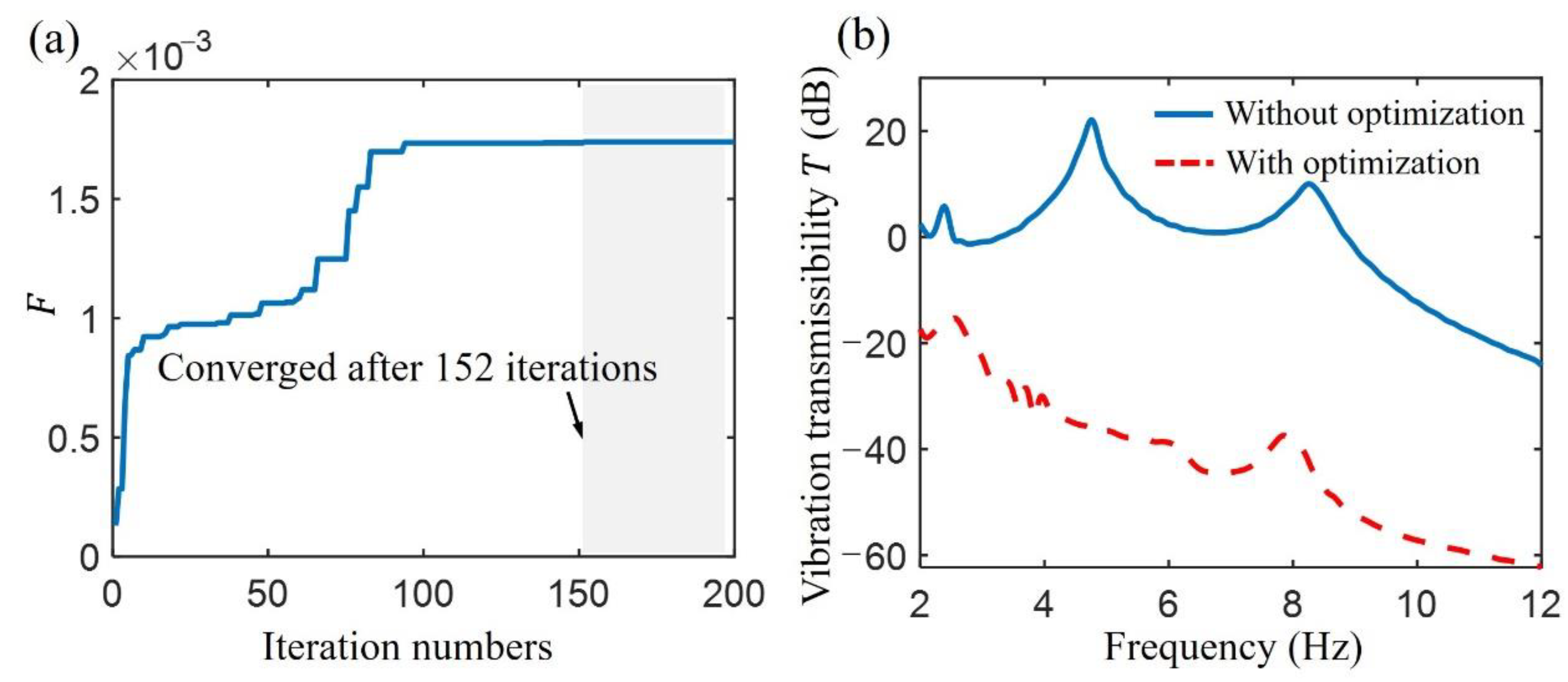
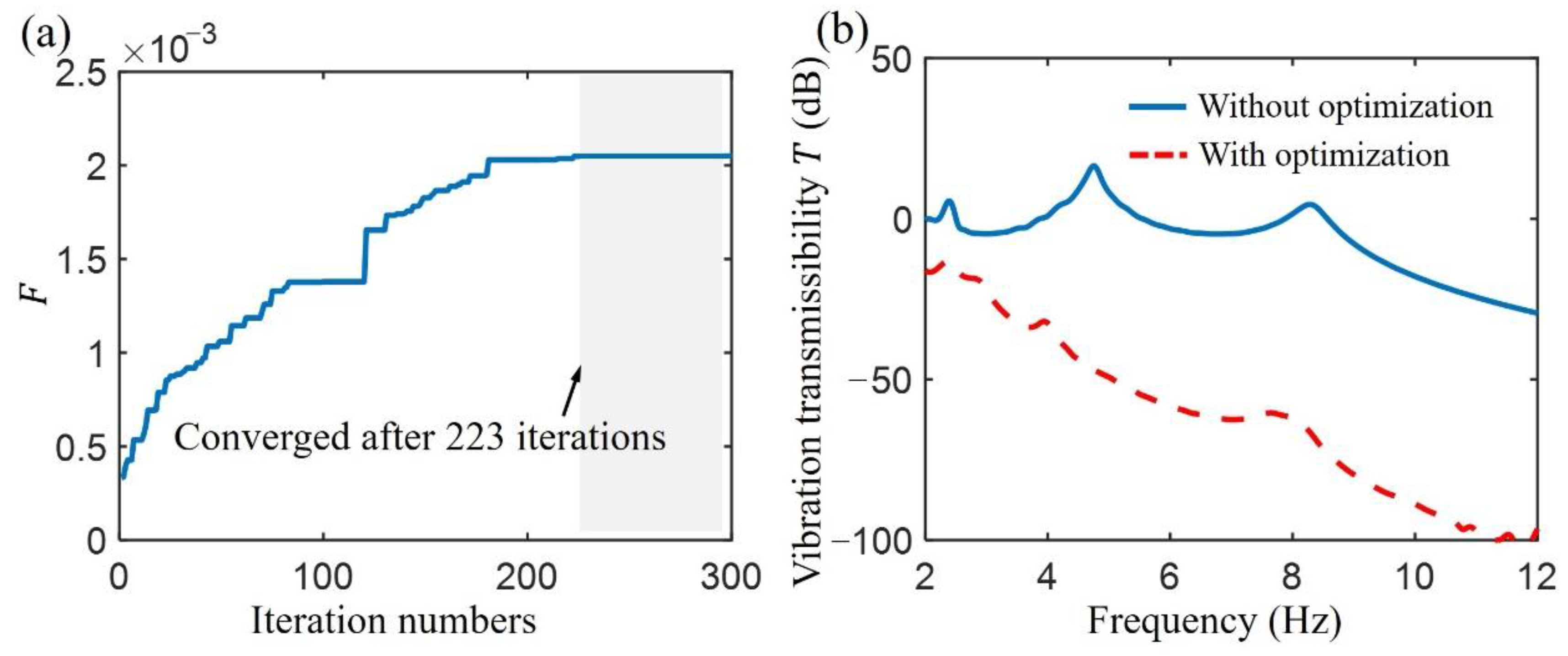
3.3. Performance Comparison

This section describes a comparison between the optimal solutions under the above three different base excitations, which would prove the effectiveness of the performance optimization of the BI-DSVI. The iteration curves and the vibration transmissibility comparison before and after optimization for the three optimization cases are presented in Figure 3, Figure 4 and Figure 5. The design parameters before optimization are taken as $l_d=0.2 \mathrm{m}, k_d=6000 \mathrm{N}/\mathrm{m}, {\phi }_{d0}=\pi /4,a=0.25 \mathrm{m},b=0.2 \mathrm{m}$.

As shown in Figure 3b, the BI-DSVI system exhibits two resonance peaks in the frequency range of 2–12 Hz. Through the optimized design, the resonance peaks are significantly reduced and the resonance frequencies are shifted to the left, which greatly broadens the vibration isolation bandwidth. The other two cases show consistent patterns. However, Figure 4b and Figure 5b present another resonance peak between 2 and 4 Hz without optimization, which is probably due to the rotational motion of the base. Through parameter optimization, the extra resonance peak is suppressed below 0 dB, which means that complete vibration isolation is realized. In the three cases, the maximum transmissibility $T$ without optimization is 30.97 dB, 22.10 dB, and 16.50 dB. At the same frequency locations, the transmissibility with optimization is −3.16 dB, −36.16 dB, and −46.96 dB. In other words, the vibrations are attenuated by 34.13 dB, 58.26 dB, 63.46 dB, respectively. Thus, the vibration isolation performance of the BI-DSVI can be greatly improved by multi-parameter optimization.

Table 2. The optimal design parameters of the three different base excitations.

Initial Phase of the Base Excitation	${\mathit{l}}_{\mathit{d}}$	${\mathit{k}}_{\mathit{d}}$	${\mathit{\phi }}_{\mathit{d}0}$	$\mathit{a}$	$\mathit{b}$
${\varphi }_{01}={\varphi }_{02}={\varphi }_{03}={\varphi }_{04}=0$	0.4	5000	$\pi /6$	0.10	0.10
${\varphi }_{01}={\varphi }_{02}=0, {\varphi }_{03}={\varphi }_{04}=\pi$	0.4	5000	$\pi /6$	0.20	0.10
${\varphi }_{01}={\varphi }_{04}=0, {\varphi }_{02}={\varphi }_{03}=\pi$	0.4	5000	$\pi /6$	0.21	0.21

presents the optimal design parameter values of the three different base excitations. For the three cases, the optimal structural parameters of the bio-inspired isolators are the same, and only the placement position parameters are different. Hence, there are optimal structural parameters of the bio-inspired isolator in a reasonable range (for instance, the stiffness $k_d$ has a lower bound to ensure the basic loading capacity), which achieves the best vibration isolation performance. In other words, for different base excitations, it is only necessary to optimize the placement positions of the isolators to obtain the optimal vibration transmissibility distribution in a frequency band.

4. Parameter Study

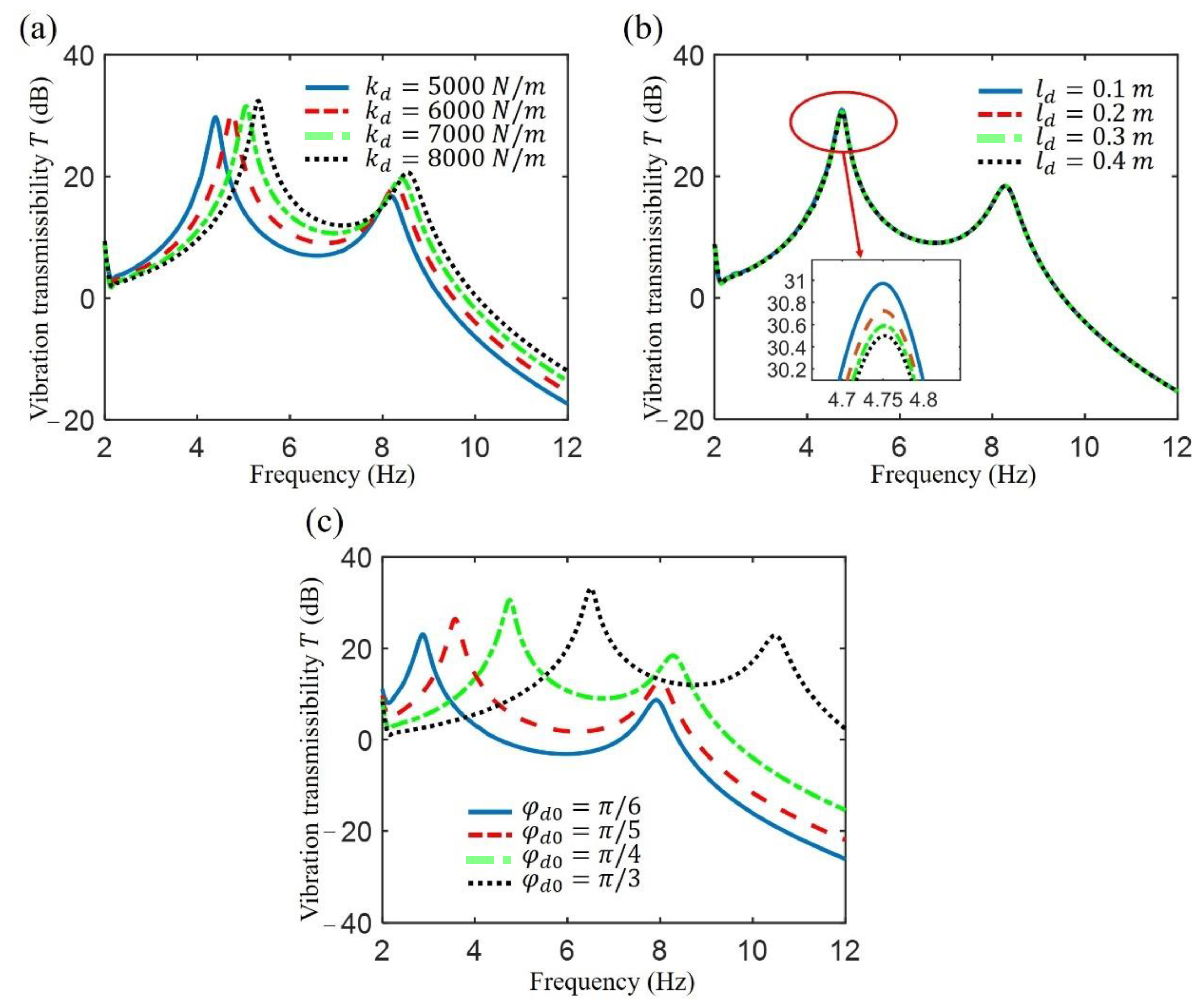
4.1. Influence of the Isolator Parameters $k_d,l_d,{\phi }_{d0}$ on Vibration Isolation Performance

To further reveal the influence of the design parameters on the vibration isolation performance, the effects of the structural parameters $k_d,l_d,{\phi }_{d0}$ on the vibration transmissibility $T$ of the BI-DSVI are investigated in this section. In the following analysis, the value of $a$ is set to 0.25 m, and $b$ is 0.2 m. The other parameter values are taken from Table 1 and the initial phase of the base excitation is ${\varphi }_{01}={\varphi }_{02}={\varphi }_{03}={\varphi }_{04}=0$.

Figure 6a shows the vibration transmissibility curves of the BI-DSVI with different transverse spring stiffness $k_d$. The values of $l_d$ and ${\phi }_{d0}$ are set to 0.4 m and $\pi /4$, respectively. It is obvious that with the increase in $k_d$, both the first and second peaks of the vibration transmissibility curves increase. In the given frequency band (2–12 Hz), as $k_d$ increases, the overall vibration transmissibility curve shifts to the right, which indicates that the effective vibration isolation bandwidth becomes narrower.

Figure 6b shows the vibration transmissibility curves of the BI-DSVI with different connecting rod lengths $l_d$. The values of $k_d$ and ${\phi }_{d0}$ are set to 6000 N/m and $\pi /4$, respectively. Near the first resonant frequency, the vibration transmissibility slightly decreases with the increase in $l_d$, which is suitable for vibration isolation. However, in the other frequency regions, $l_d$ has no effect on the vibration transmissibility.

Figure 6c shows the vibration transmissibility curves of the BI-DSVI with different initial assembly angles ${\phi }_{d0}$. The values of $l_d$ and $k_d$ are set to 0.4 m and 6000 N/m, respectively. With the angle ${\phi }_{d0}$ varying from $\pi /6$ to $\pi /3$, both the first and the second resonant frequencies increase significantly. Moreover, the peak values of the first and second resonant frequencies also increase significantly. The results indicate that a small initial assembly angle ${\phi }_{d0}$ may lead to better vibration isolation performance, including a wider effective vibration isolation bandwidth and lower resonance peak.

Through the above parameter analysis, it can be seen that the vibration isolation performance is significantly influenced by the following structural parameters: the transverse spring stiffness $k_d$ and the initial assembly angle ${\phi }_{d0}$. The connecting rod length $l_d$ also has a slight effect on the vibration isolation performance. The vibration isolation performance is better when using a smaller $k_d,{\phi }_{d0}$ and longer $l_d$. This conclusion validates the optimization results in Section 3.

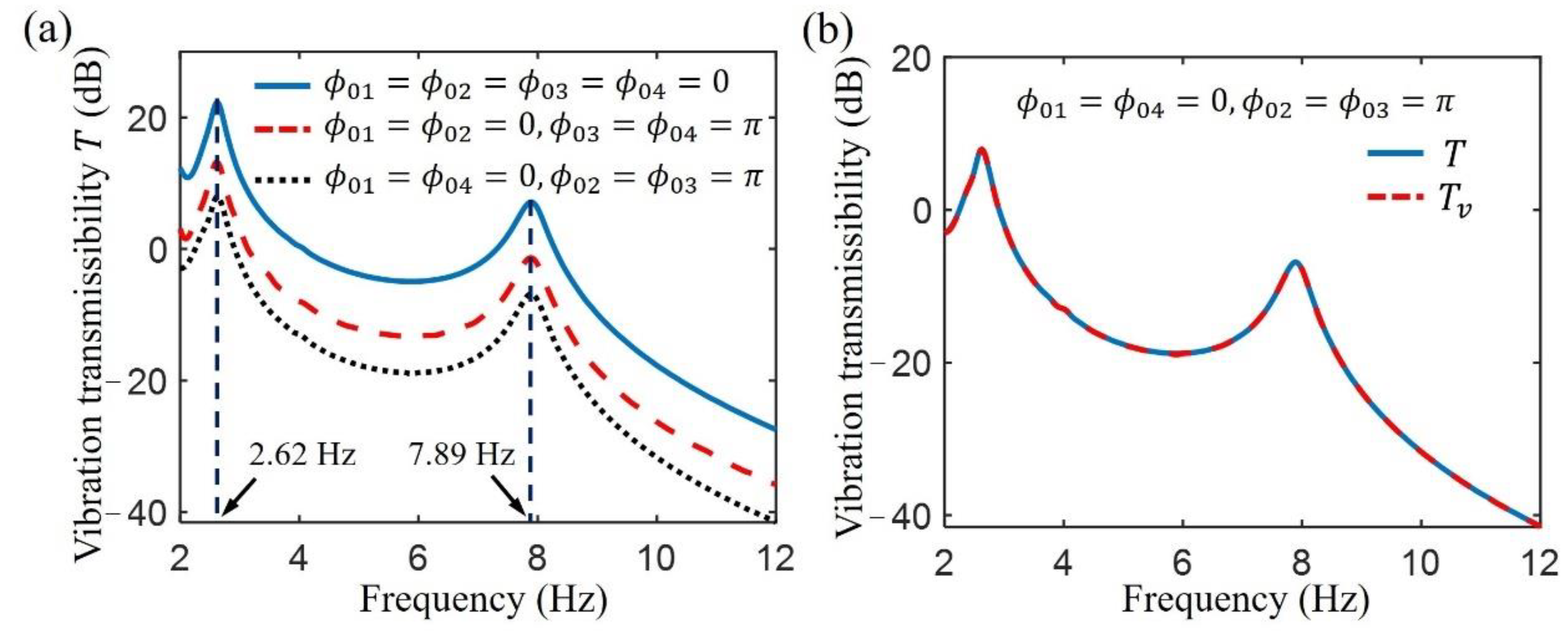
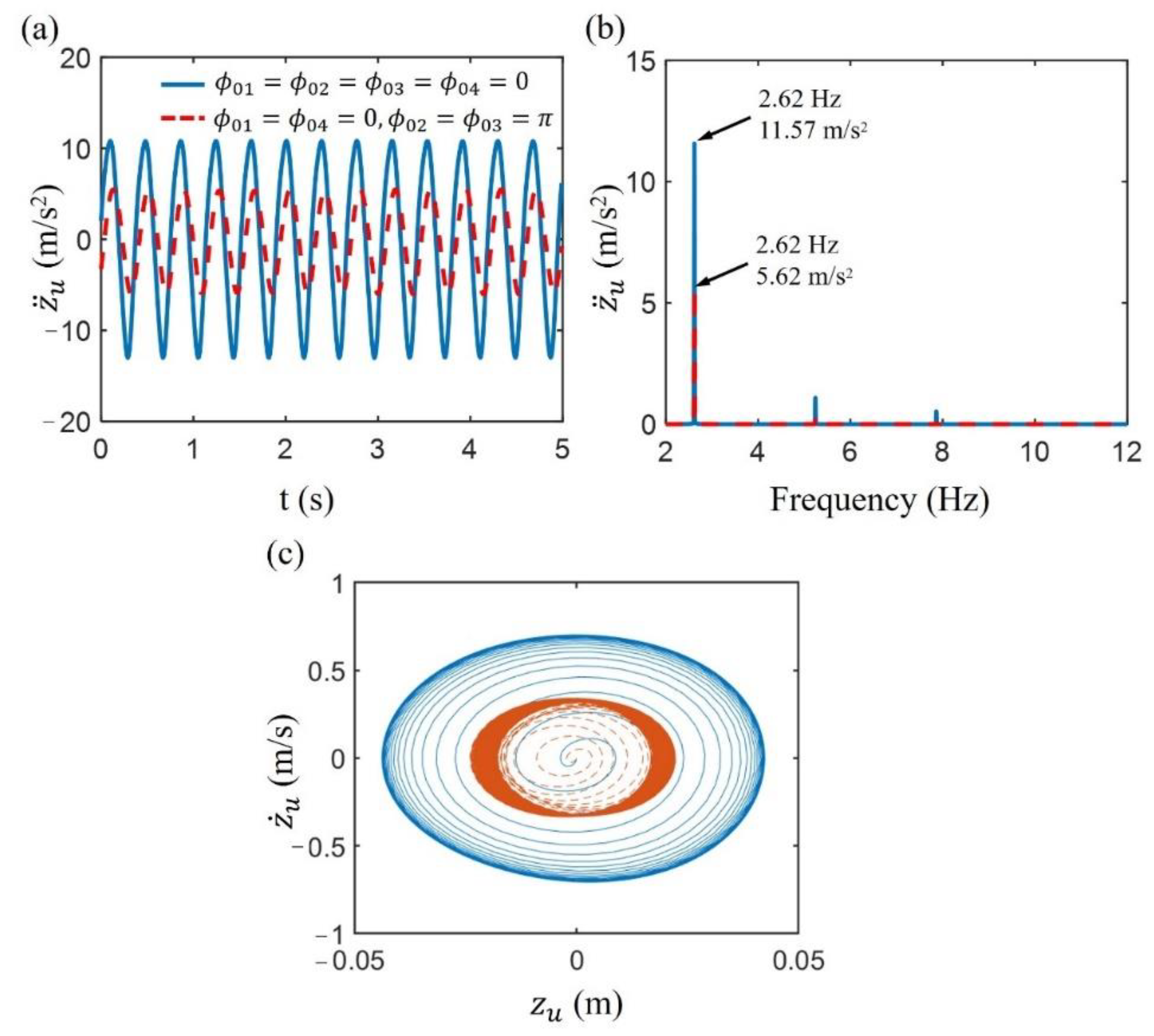
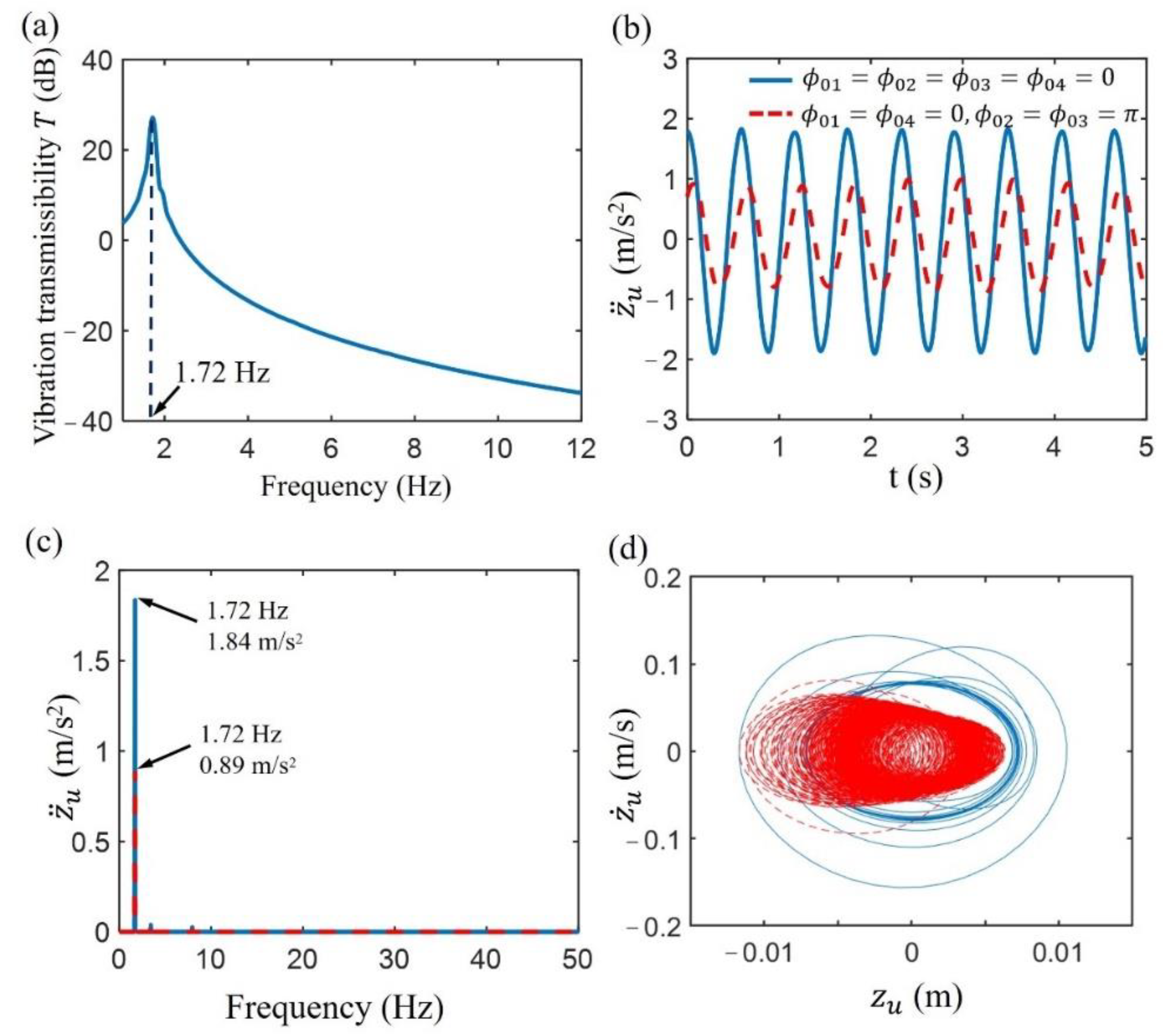
4.2. Influence of the Base Excitation on System Response

Considering the effect of the base rotation excitation on the control object $m_u$, we define the vibration transmissibility $T_v$ as

$$T_v=\frac{\left|{\ddot{z}}_v\right|}{A}$$

(15)

where ${\ddot{z}}_v={\ddot{z}}_u-\frac{L_u}{2}\alpha -\frac{B_u}{2}\beta$ represents the acceleration along the $z$ axis of a vertex of the control object $m_u$. Figure 7a shows the vibration transmissibility $T$ under the three different base excitations investigated in Section 3. The structural parameters of the bio-inspired isolators are taken from the optimal values obtained in Table 2 and the other parameters are the same as in Table 1. When the base excitation phase is 0, the whole system displays upward base acceleration, and the vibration transmissibility $T$ is relatively large. When inverse-phase base excitation is applied, the vibration transmissibility $T$ is greatly reduced. To clearly describe the influence of the base rotation excitation on the control object, the comparison curves of $T$ and $T_v$ are shown in Figure 7b. It can be seen that $T$ and $T_v$ coincide completely, which means that the motion of the vertex of the control object in the $z$ direction is consistent with $z_u$. This indicates that the bio-inspired isolator used in the BI-DSVI can well isolate the disturbance due to the base rotational motion.

To develop insight into the dynamic behaviors of the BI-DSVI in vibration isolation under different base excitations, the responses at frequency 2.62 Hz (the first resonance frequency of the BI-DSVI system) are investigated. As shown in Figure 8a,b, under the excitation of the base rolling motion, the vibration acceleration amplitude of the control object along the $z$ direction is reduced significantly, which results in the lower vibration transmissibility $T$ at frequency 2.62 Hz shown in Figure 7a. Figure 8c plots the phase trajectory of the BI-DSVI under two different base excitations. After reaching the steady state, the first excitation condition (${\varphi }_{01}={\varphi }_{02}={\varphi }_{03}={\varphi }_{04}=0$) exhibits periodic motion, while the second excitation condition (${\varphi }_{01}={\varphi }_{04}=0, {\varphi }_{02}={\varphi }_{03}=\pi$) exhibits periodic motion in which the vibration amplitude varies in a small range. It can be obtained from the above results that the base rotational motion has little influence on the translational motion along the $z$ direction of the control object. In other words, the bio-inspired isolator can effectively isolate the vibration caused by the base rotation excitation.

The dual-stage vibration isolation system is usually sensitive to base excitation with the natural frequency of the bottom vibration isolators. On this account, a simulation for a single bio-inspired isolator with an oscillator mass is conducted to find the natural frequency of the bio-inspired isolators. In the above studies, the intermediate mass and the control object mass are 12 kg in total—that is, the oscillator mass should be 3 kg. According to the optimal structural parameters and the oscillator mass, the vibration transmissibility of the single bio-inspired isolation system is calculated and is shown in Figure 9a. It can be seen that the natural frequency of the bio-inspired isolator is 1.72 Hz. Figure 9b–d show the time history results, FFT results, and phase plots of the BI-DSVI under two different base excitations ${\varphi }_{01}={\varphi }_{02}={\varphi }_{03}={\varphi }_{04}=0$ and ${\varphi }_{01}={\varphi }_{04}=0, {\varphi }_{02}={\varphi }_{03}=\pi$ at frequency 1.72 Hz. The results present similar dynamic behaviors to the base excitations with 2.62 Hz. Moreover, the amplitude of ${\ddot{z}}_u$ is much smaller than the case of 2.62 Hz, which means that the BI-DSVI is insensitive to the resonance of the bio-inspired isolators. However, as shown in Figure 9d, under the base rotation excitation, the control object exhibits asymmetric periodic motion, probably affected by the resonance of the bio-inspired isolators. In a nutshell, the isolation performance of the BI-DSVI is not much affected by the base excitation with the natural frequency of the base bio-inspired isolators.

5. Conclusions

This paper investigates the performance and multi-parameter optimization of a dual-stage vibration isolation system with bio-inspired isolators (BI-DSVI) under three different base excitations: translation along the $z$ axis, rotation about the $x$ axis, and rotation about the $y$ axis. The dynamic equations of the BI-DSVI are derived first. The optimization problem consists of five design parameters, including three structural parameters of the bio-inspired isolator and two placement position parameters. Results under three different base excitations show that there is an optimal configuration of vibration isolator parameters in a reasonable range, and the vibration transmissibility is the lowest. The vibration transmissibility can be reduced by more than 30 dB by multi-parameter optimization, and the effective vibration isolation bandwidth is significantly widened. Finally, the influence of the isolator parameters and base excitation types on the vibration isolation performance is investigated. A smaller transverse spring stiffness and initial assembly angle and longer connecting rod length lead to lower vibration transmissibility. Compared to the translation excitation along the $z$ axis, the bio-inspired isolator exhibits better vibration isolation performance under the base rotation excitation. Moreover, the BI-DSVI is insensitive to base excitation with the natural frequency of the base bio-inspired isolators.