1D Modeling Considering Noise and Vibration of Vehicle Window Brushed DC Motor
Abstract
1. Introduction
2. Modeling a Brushed DC Motor
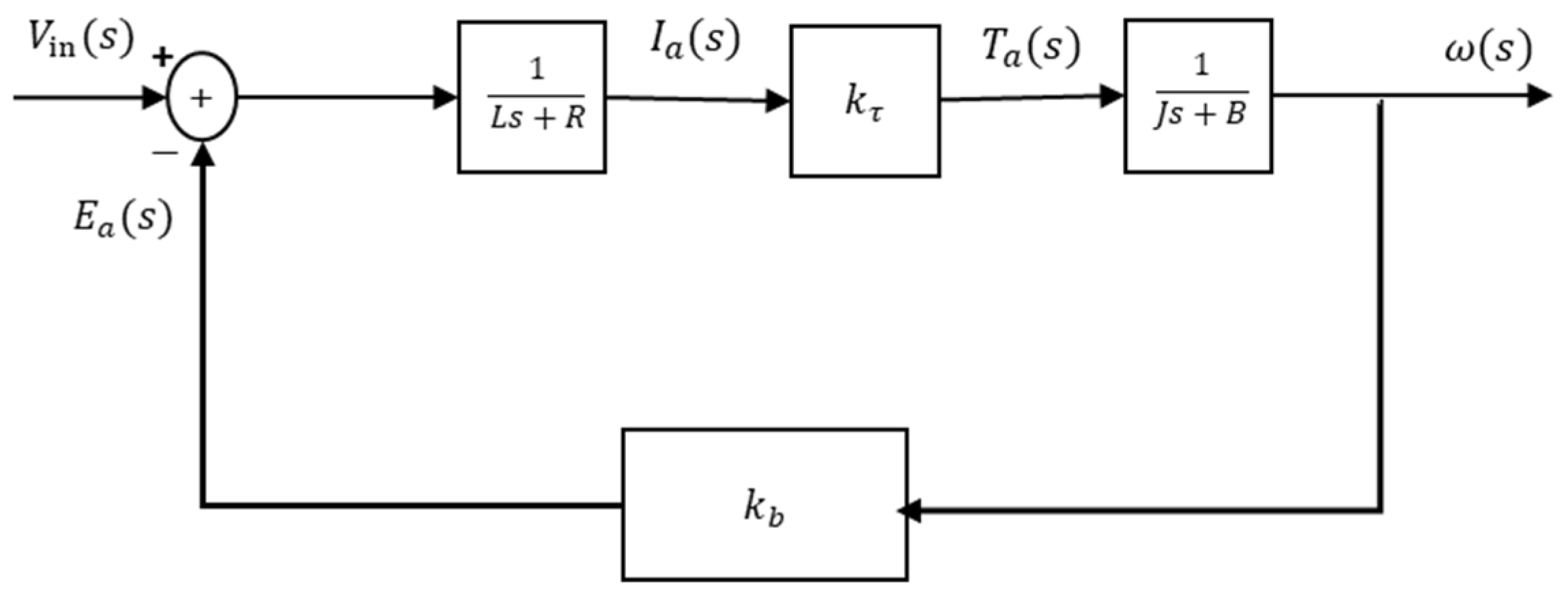
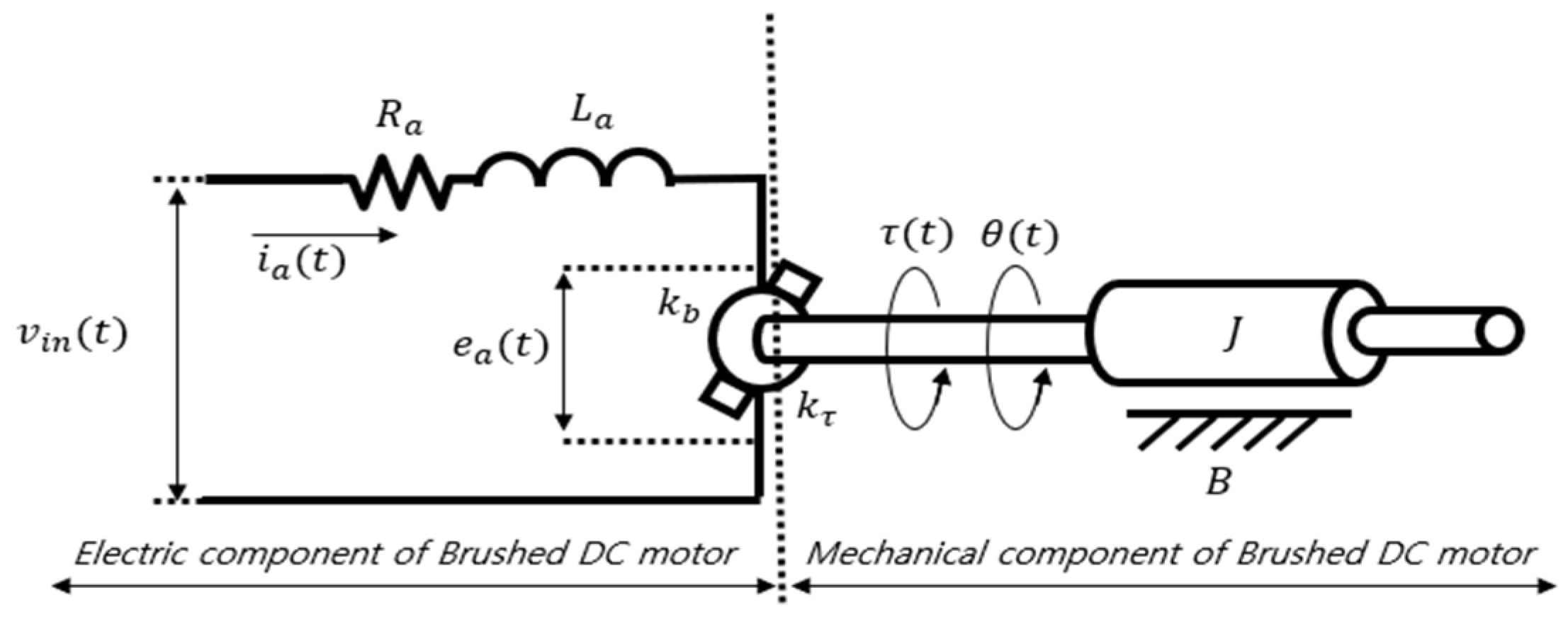
2.1. Classic Brushed DC Motor Modeling
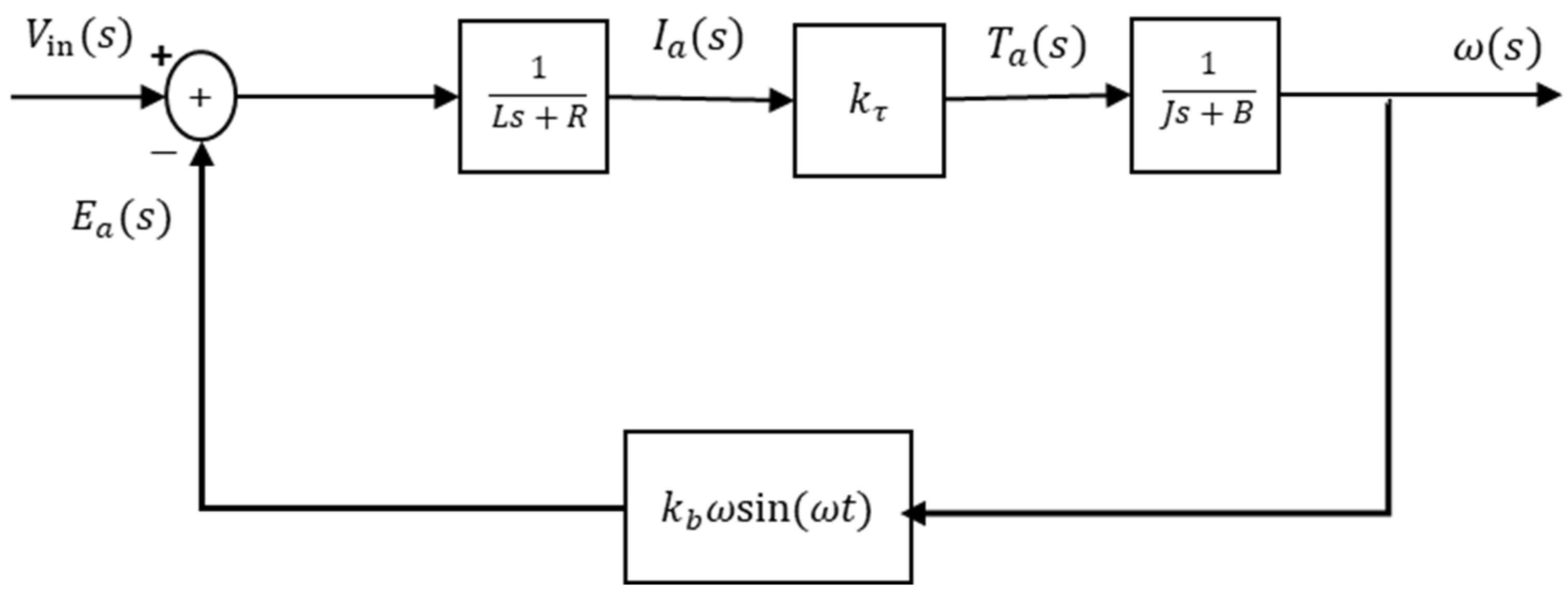
2.2. Brushed DC Motor Modeling Considering Back EMF Vibration
3. Experimental Setup
3.1. Considerations for Experimentation
3.2. Noise and Vibration Measurement of Motor with Housing
3.3. Back EMF and Noise and Vibration Measurement of Motor without Housing
4. Experiment Results and Discussion
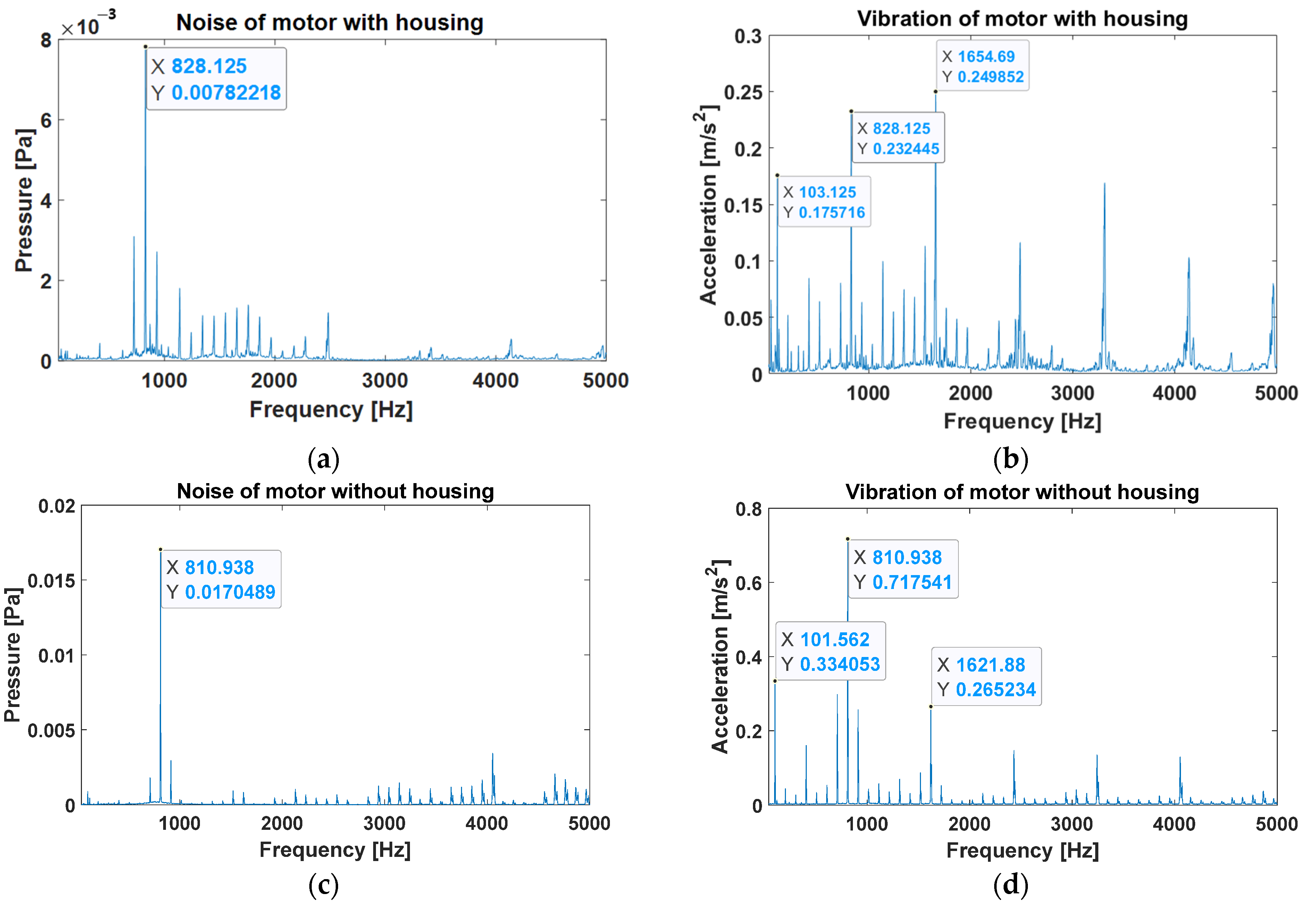
4.1. Noise and Vibration Experiment
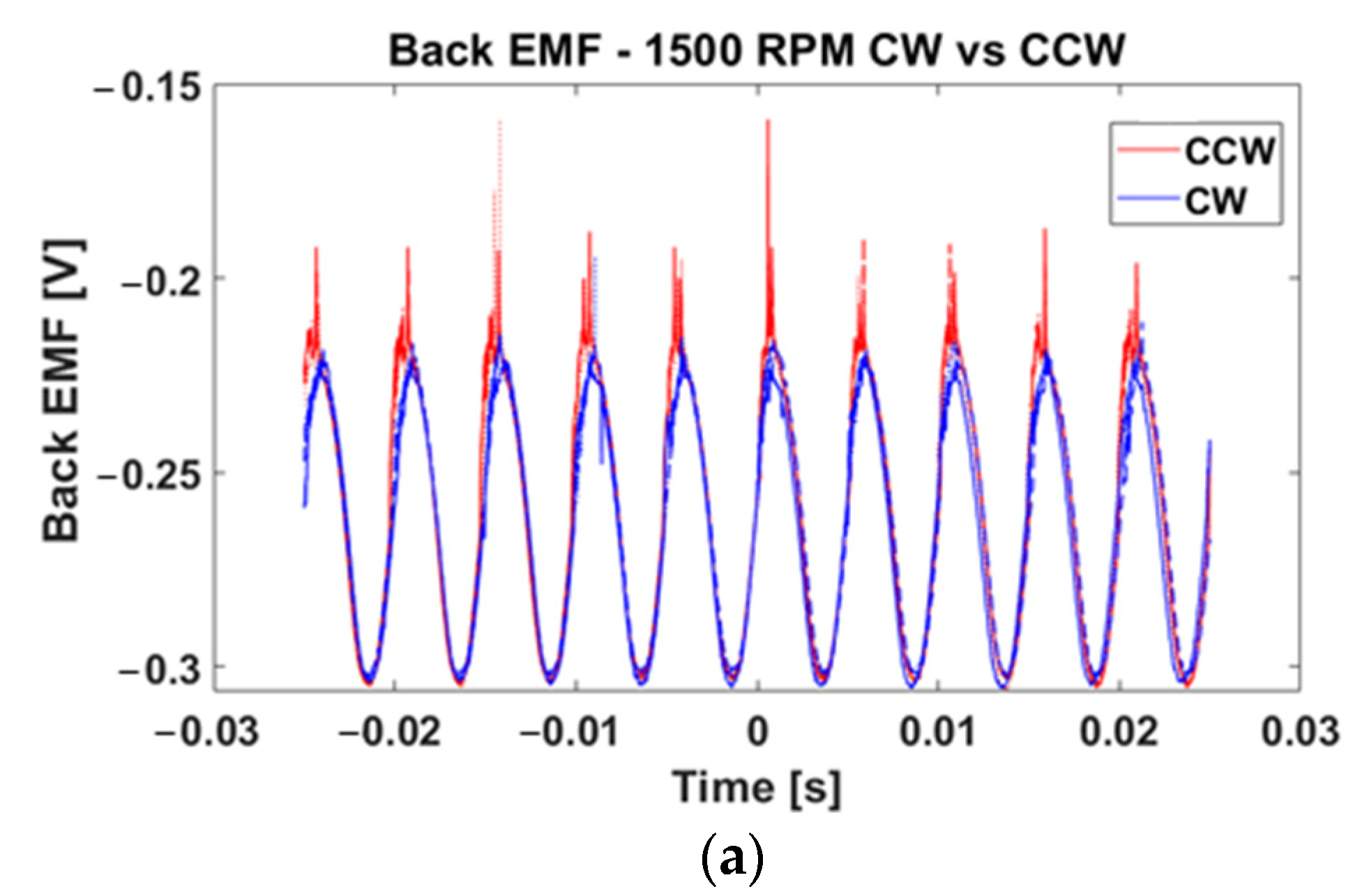
4.2. Back EMF Measurement Experiment
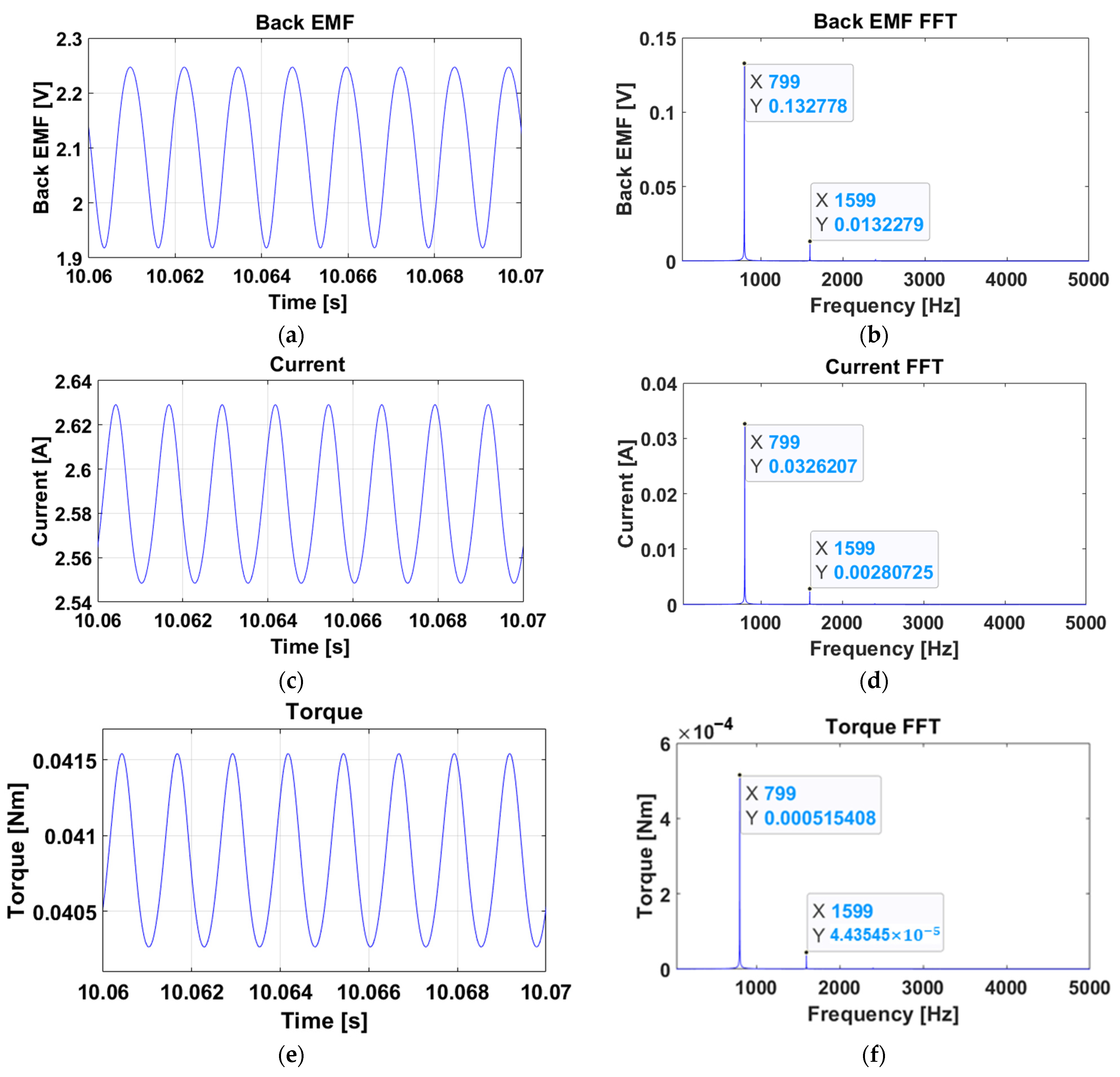
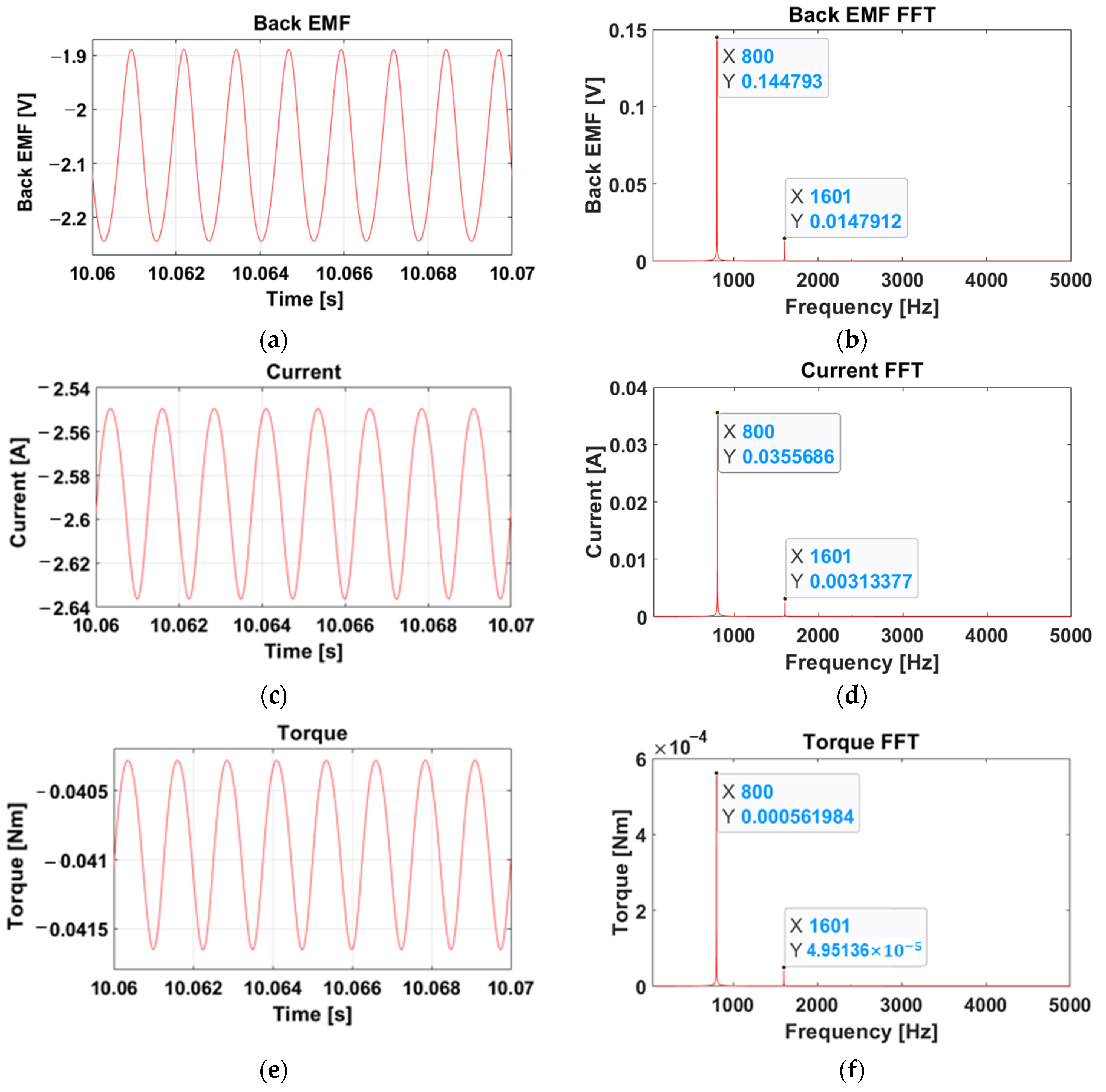
4.3. Model and Simulation Results with Vibration Components
5. Conclusions
- To create a model expressing noise and vibration from the traditional motor equation, it was confirmed that the back EMF is composed of the sum of harmonic and DC components rather than constants and is expressed as a block diagram based on the equation.
- The back EMF value was measured using an actual motor, and experiment results confirmed that the vibration components of the motor and back EMF tended to be identical. However, it was confirmed that CW and CCW, which should theoretically be the same, are different in actual motors. This was attributed to the difference between the DC component and the eighth-order component of the back EMF. However, further research on the harmonic components observed in the noise component of the CCW should be conducted.
- The entire model was constructed based on the block diagram, and it was modeled using MATLAB Simulink based on the electric circuit and transfer function. To verify the reliability of the model, the measured back EMF value was applied to the model, and it was confirmed that the predicted vibration component was consistent with the actual vibration component. This will be of great help in predicting the main vibration component in a brushed DC motor. Given that it does not include all vibration components, it can be expressed in a simpler form than the actual measurement result; however, it is still successful as it predicts the largest vibration component.
- The brushed DC motor model created in this study to predict the vibration component of the motor can be applied in various fields. For example, if R, L, and C are attached to the tip of the motor resistor and inductor and used as a filter, they can be applied to reduce noise and vibration. Alternatively, the vibration component generated by the motor can be predicted when a specific load is applied.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Pindoriya, R.M.; Mishra, A.K.; Rajpurohit, B.S.; Kumar, R. An Analysis of Vibration and Acoustic Noise of BLDC Motor Drive. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Porland, OR, USA, 5–10 August 2018. [Google Scholar]
- Kang, G.H.; Son, Y.D.; Kim, G.T. The Noise and Vibration Analysis of BLDC Motor Due to Asymmetrical Permanent-Magnet Overhang Effects. IEEE Trans. Ind. Appl. 2008, 44, 1569–1577. [Google Scholar] [CrossRef]
- Hur, J.; Reu, J.W.; Kim, B.W.; Kang, G.H. Vibration Reduction of IPM-Type BLDC Motor Using Negative Third Harmonic Elimination Method of Air-Gap Flux Density. IEEE Trans. Ind. Appl. 2011, 47, 1300–1309. [Google Scholar]
- Jafarboland, M.; Farahabadi, H.B. Optimum Design of the Stator Parameters for Noise and Vibration Reduction in BLDC Motor. IET Electr. Power Appl. 2018, 12, 1297–1305. [Google Scholar] [CrossRef]
- Shifat, T.A.; Hur, J.W. An Effective Stator Fault Diagnosis Framework of BLDC Motor Based on Vibration and Current Signals. IEEE Access 2020, 8, 106968–106981. [Google Scholar] [CrossRef]
- Cho, Y.T. Characterizing Sources of Small DC Motor Noise and Vibration. Micromachines 2018, 9, 84. [Google Scholar] [CrossRef]
- Kang, H. The Study of DC Motor Noise and Vibration. SAE Trans. 1995, 104, 2461–2467. [Google Scholar]
- Iorgulescu, M.; Beloiu, R. Study of DC Motor Diagnosis Based on the Vibration Spectrum and Current Analysis. In Proceedings of the 2012 International Conference on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 25–27 October 2012. [Google Scholar]
- Cho, Y.T. Noise Source Visualization for Small DC Motors Using Current Reference without a Reference Microphone. Micromachines 2018, 9, 290. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Sun, Y.; Cao, H. Analysis and Reduction of Electromagnetic Vibration of PM Brush DC Motors. IEEE Trans. Ind. Appl. 2019, 55, 4605–4612. [Google Scholar] [CrossRef]
- Michaelides, A.; Pollock, C. Reduction of Noise and Vibration in Switched Reluctance Motors: New Aspects. In Proceedings of the Conference Record of the 1996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting (IAS ’96), San Diego, CA, USA, 6–10 October 1996; Volume 2, pp. 771–778. [Google Scholar]
- Verma, S.P.; Balan, A. Experimental Investigations on the Stators of Electrical Machines in Relation to Vibration and Noise Problems. IEE Proc. Electr. Power Appl. 1998, 145, 455–461. [Google Scholar] [CrossRef]
- Lee, C.I.; Jang, G.H. Noninvasive Detection of Unevenly Magnetized Permanent Magnet of a Brushless Dc Motor by Characterizing Back Electromotive Force. J. Appl. Phys. 2009, 105, 105–108. [Google Scholar] [CrossRef]
- Finley, W.R.; Hodowanec, M.M.; Holter, W.G. An Analytical Approach to Solving Motor Vibration Problems. In Proceedings of the Industry Applications Society 46th Annual Petroleum and Chemical Technical Conference (Cat. No. 99CH37000), San Diego, CA, USA, 13–15 September 1999. [Google Scholar]
- Zuo, S.; Lin, F.; Wu, X. Noise Analysis, Calculation, and Reduction of External Rotor Permanent-Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2015, 62, 6204–6212. [Google Scholar] [CrossRef]
- Jung, I.; Yang, H.; Park, T.; Kim, J. A Study on Noise Reduction of a DC Motor. KSNVE 2004, 5, 764–769. [Google Scholar] [CrossRef]
- Lee, S.H.; Hong, J.P.; Hwang, S.M.; Lee, W.T.; Lee, J.Y.; Kim, Y.K. Optimal Design for Noise Reduction in Interior Permanent-Magnet Motor. IEEE Trans. Ind. Appl. 2009, 45, 1954–1960. [Google Scholar]
- Nakata, K.; Hiramoto, K.; Sanada, M.; Morimoto, S.; Takeda, Y.; Yamai, H. Noise Reduction for Switched Reluctance Motor with a Hole. In Proceedings of the Proceedings of the Power Conversion Conference-Osaka 2002 (Cat. No. 02TH8579), Osaka, Japan, 2–5 April 2002. [Google Scholar]
- Wang, S.; Yang, Z.; Liu, C. Vibration Reduction Characteristics of Permanent Magnet DC Motors with Sawtooth Edge Poles. IEEE Trans. Energy Convers. 2021, 36, 737–745. [Google Scholar] [CrossRef]
- Hong, J.; Wang, S.; Sun, Y.; Cao, H. An Effective Method with Copper Ring for Vibration Reduction in Permanent Magnet Brush DC Motors. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Aung, W.P. Analysis on Modeling and Simulink of DC Motor and Its Driving System Used for Wheeled Mobile Robot. World Acad. Sci. Eng. Technol. 2007, 32, 299–306. [Google Scholar]
- Mahfouz, A.A.; Mohammed, M.K.; Salem, F.A. Modeling, Simulation and Dynamics Analysis Issues of Electric Motor, for Mechatronics Applications, Using Different Approaches and Verification by MATLAB/Simulink. Int. J. Intell. Syst. Appl. 2013, 5, 39–57. [Google Scholar] [CrossRef]
- Aung, C.H.; Lwin, K.T.; Myint, Y.M. Modeling Motion Control System for Motorized Robot Arm Using MATLAB. Eng. Technol. 2008, 42, 372–375. [Google Scholar]
- Hwu, K.I. Applying POWERSYS and SIMULINK to Modeling Switched Reluctance Motor. Tamkang J. Sci. Eng. 2009, 12, 429–438. [Google Scholar]
- Chotai, J.; Narwekar, K. Modelling and Position Control of Brushed DC Motor. In Proceedings of the 2017 International Conference on Advances in Computing, Communication and Control (ICAC3), Mumbai, India, 1–2 December 2017. [Google Scholar]
- Barkas, D.A.; Ioannidis, G.C.; Psomopoulos, C.S.; Kaminaris, S.D.; Vokas, G.A. Brushed Dc Motor Drives for Industrial and Automobile Applications with Emphasis on Control Techniques: A Comprehensive Review. Electctronics. 2020, 9, 887. [Google Scholar] [CrossRef]
- Kwon, S.; Sim, W.; Yun, S.; Choi, J.; Park, K.; Lee, S.; Chung, J. Reduction in Operating Noise in Front-Door Window of a Vehicle. Trans. Korean Soc. Noise Vib. Eng. 2020, 30, 366–372. [Google Scholar] [CrossRef]





| Element Name | Symbol | Unit |
|---|---|---|
| Input voltage | [V] | |
| Armature resistance | ||
| Armature inductance | [H] | |
| Armature current | [A] | |
| Back EMF | [V] | |
| Motor armature inertia | J | ] |
| Viscous damping, friction coefficient | ] | |
| Motor torque | ] | |
| Motor angular position | [rad] | |
| Motor angular velocity | [rad/s] | |
| Motor torque constant | ] | |
| Motor back EMF constant | ] |
| Element Name | Symbol | Value |
|---|---|---|
| Armature resistance | ||
| Armature inductance | [H] | |
| Motor torque constant | ] | |
| Motor armature inertia | ] | |
| Viscous damping, friction coefficient | ] |
| Measured Motor Vibrations | Simulation Result of Back EMF | |||
|---|---|---|---|---|
| 8th-Order Magnitude | 8th-Order Frequency | 8th-Order Magnitude | 8th-Order Frequency | |
| CW | 0.577 | 810.94 [Hz] | 0.133 | 799 [Hz] |
| CCW | 0.830 | 825 [Hz] | 0.145 | 800 [Hz] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Kim, J.; Han, K.; Won, D. 1D Modeling Considering Noise and Vibration of Vehicle Window Brushed DC Motor. Appl. Sci. 2022, 12, 11405. https://doi.org/10.3390/app122211405
Kim H, Kim J, Han K, Won D. 1D Modeling Considering Noise and Vibration of Vehicle Window Brushed DC Motor. Applied Sciences. 2022; 12(22):11405. https://doi.org/10.3390/app122211405
Chicago/Turabian StyleKim, Hyunsu, Jiman Kim, Kwangkyu Han, and Dongkyu Won. 2022. "1D Modeling Considering Noise and Vibration of Vehicle Window Brushed DC Motor" Applied Sciences 12, no. 22: 11405. https://doi.org/10.3390/app122211405
APA StyleKim, H., Kim, J., Han, K., & Won, D. (2022). 1D Modeling Considering Noise and Vibration of Vehicle Window Brushed DC Motor. Applied Sciences, 12(22), 11405. https://doi.org/10.3390/app122211405






