A New Approach for Failure Modes, Effects, and Criticality Analysis Using ExJ-PSI Model—A Case Study on Boiler System
Abstract
1. Introduction
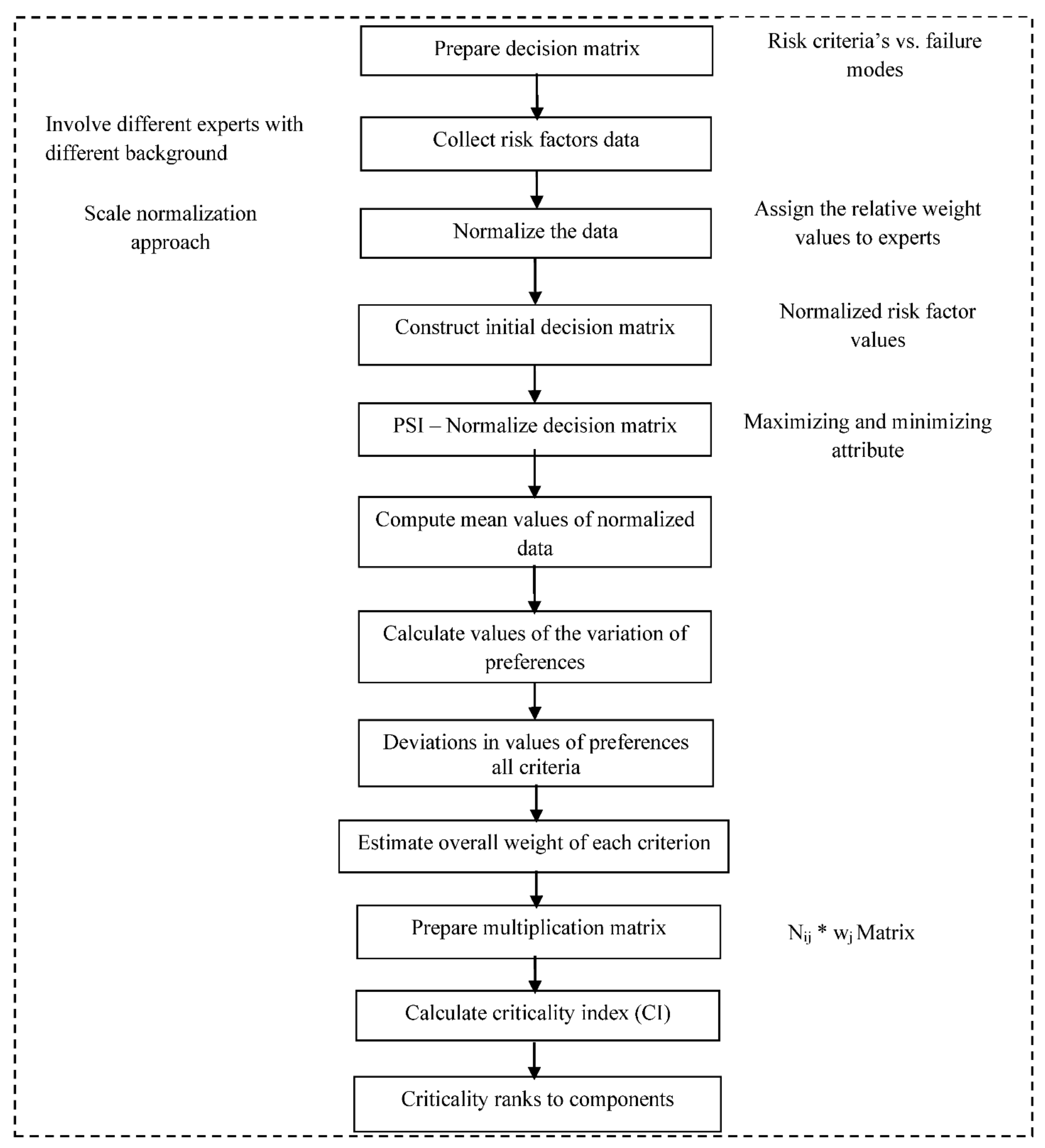
2. Framework of the Proposed ExJ-PSI Model
- Step 1: Select and arrange a set of risk factors and failure modes in the decision matrix.
- Step 2: Collect the risk factors rank data from the various experts of several industries.
- Step 3: Normalize the data collected by assigning overall weights to experts.
- Step 4: Construct initial decision matrix ‘A’ with criteria ranks,where aij is the index value. i = 1, 2, …, m along the row represents the failure modes and j = 1, 2, …, n represents the risk criteria’s along the column.
- Step 5: Normalize decision matrix ‘A’
- Step 6: Calculate the mean value of the normalized data [30].
- Step 7: Calculate the values of the variation of preferences between the values of every attribute [30].
- Step 8: Calculate the deviations in the preference value for all criteria [30].
- Step 9: Calculate the overall criteria weights for each criteria [30].
- Step 10: Prepare a matrix by multiplying .
- Step 11: Calculate the Criticality Index for all failure modes and all components.
- Step 12: Criticality rankings are given by increasing order according to the value of CIPSI, i.e., the higher value of CIPSI has a higher priority.
3. Case Study of Boiler System Used in Textile Process Industries
- Step 1: Select and arrange a set of risk factors and failure modes in the form of a decision matrix.
- Step 2: Collection of the risk factors data
- Steps 3 and 4: Normalize the collected data and construct initial decision matrix ‘A’
- Step 5: Results obtained after Normalize decision matrix ‘A’
- Step 6: Compute the mean value of the normalized data.
- Step 7: Calculate the values of the variation of preferences.
- Step 8: Calculate the deviations in the value of preference for all criteria.
- Step 9: Calculate the overall criteria weights for all criteria.
- Step 10: Results obtained after preparing a matrix by multiplying .
- Step 11: Calculate the criticality index for all components, and finally, ranks are given.
4. Results and Discussion
5. Conclusions
- It is required to consider various additional risk criteria, such as operational and maintenance time, human safety, and operational loss, to improve the effectiveness of the analysis.
- Normalizing the rankings given by a large group of experts minimizes its uncertainty due to varying work experience and skills.
- The preference section index (PSI) method uses the concept of statistics instead of weight attribute allocations in another multi-criteria decision-making (MCDM) approach and thus is observed to be more effective while deciding the relative importance when a conflict situation occurs.
- The effectiveness of the model is validated over the conventional FMECA for the case of complex systems such as boilers, and it is found very useful in prioritizing failure modes to minimize the overall losses effectively due to sudden breakdown.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Boiler Components | Failure Mode | Failure Cause | Failure Effect |
|---|---|---|---|
| Furnace | Short term overheating | Starvation of steam or water flow | Axial fish-mouth rupture |
| Furnace plate bulged | Due to internal steam pressure | System failure | |
| Layer of hardness scale over the tubes | Poor quality water supply | Slipping of hardness to boiler | |
| Shell | Shell plate bulging due to scale formation | The feed water hardness was not monitored properly | Boiler shell failure can result in catastrophe |
| Shell burst | Lamellar tear in raw material | Boiler shell failure can result in catastrophe | |
| Shell burst | By cyclic stresses | ||
| Shell burst | Due to Improper weld | ||
| Header | Deposition | Inadequate blow-down control | System failure |
| Poor pH control | Poor chemical feed control | System failure | |
| Downtime corrosion | System failure | ||
| Poor boiler feed water quality | System failure | ||
| Header corrosion due to Oxygen Pitting | Poor mechanical derator performance | System failure | |
| Downtime corrosion | System failure | ||
| Oxygen in-leakage | System failure | ||
| Scavenger underfeed | System failure | ||
| Intake vent/Air vent | Air vent fails to open and close | Corrosion due to gases in the air | Reduces steam pressure, |
| Reduces heat transfer rates andproductivity | |||
| Trap malfunctioning | Presence of air in steam lines | Affects on process timing and quality of steam | |
| Combustion Chamber | Incorrect burner sequence | Faulty flame detector | Production stopping |
| Too much fuel being fired | Irregularities in flame patterns | Production stopping | |
| Too much excess air trapped | Blockages in air or fuel flow | Lower production | |
| Uneven combustion | Clogged fuel nozzles | High temp. on combustor wall can spall the chamber | |
| High emissions | High temperature in the primary zone high NOx | Incomplete combustion leading to increasing temp and system failure | |
| Water Tubes | Short term Overheating | Starvation of steam or water flow | Axial fish-mouth rupture |
| Blockages from debris | Axial fish-mouth rupture | ||
| Thin lip failure of tube | Due to rapid heating | Rupture | |
| Tube joints failure | Dissimilar metal welds | System failure | |
| Crack and holes | Calcium and magnesium layer increases | Boiler should closed | |
| Tube surface corrosion | Due to presence of moisture content | Tube failure | |
| Deposits formed at the top of drum | Due to refractory brick deterioration | Partially blocking the blow down channel ports | |
| Boiler tube blisters/bulges | Due to presence of internal scale | Tube failure | |
| Supply Water Temperature Sensor | Incorrect signal from sensor element | Reduced signal level | Potential processing error |
| Impedance mismatch | |||
| A/D conversion error | |||
| Loss of signal from sensor element | Chip failure | Loss of signal to processor | |
| Corroded sensor | |||
| Power supply loss of voltage | power supply malfunction | Loss of signal to processor | |
| Calibration error | Software error | Potential system malfunction | |
| Error in algorithm | |||
| Back flow preventer valve | Jam and closed | Dirt andcorrosion | No water supply |
| Fails to open | Corrosion and power loss | False trip andcomponent failure | |
| Coil open | Electrical andsurge | False trip | |
| Coil Short | Corrosion and wire | False trip | |
| Temperature regulator | Short | Electrical failure | No cooling |
| Open continuous | Electrical andsurge | false trip | |
| Fail to operate | Electrical failure | System effect | |
| Unstable response | Electrical failure/aging | Equipment failure | |
| Feed water Pump- Motor | Bearing worn out | Poor lubrication | Noisy |
| Overloading | Heat build-up | ||
| Contamination | Stator seized | ||
| High temperature | |||
| Insulation stator/rotor fails | |||
| Electrical windings open or short | Excessive high temperature | Motor will not run | |
| Sparking at brushes | |||
| Armature cracked | Fatigue | Armature seized or rubbing stator | |
| Misalignment | |||
| Bearing failure | |||
| Feed Water Pump | The strainer failure | The strainer is clogged | Pump Fails |
| Rust of tank | A lot of sediment in the water | Failure of mechanical seal and cause a leak | |
| condensate is too hot for the pump | steam traps fail | Failure of pump impeller | |
| Mechanical seal failure | Pump leakage | Pump failure | |
| Electrical failure of pump | The voltage supplied to the pump is not correct | Failure of circuit breaker and winding burns | |
| Impeller failure | Impeller is clogged | Mechanical failure of pump | |
| Shaft failure | Overload work, misalignment, corrosion | Pump vibration, pump works but does not provide flow | |
| Deterioration of the bearings | Lubrication failure | Insufficient flow | |
| Improper mountings | Pump vibrates or is noisy | ||
| Abnormal load on motor | Pump failure | ||
| Contamination present | Pump failure | ||
| Pump housing volute damaged/Volute Erosion | Cavitation, corrosion andvibration | Leak in the pump body | |
| Pump low efficiency | Electric motor failed | Low flow warming | |
| Low discharge pressure | |||
| Reduction in pump pressure | Pump cavitation | Pump noise and vibration | |
| Strainer | Strainer clogging | Due to dust anddirt and improper cleaning | Water flow problem |
| Channeling | High differential pressures flow | Circulation of unfiltered | |
| Fatigue cracks | Cyclic flow | Fluid | |
| Media migration | Vibration or cyclic flow | Release of filter media | |
| Feed Water tank | Oxygen pitting | Poor mechanical derator performance | Equipment failure |
| Downtime corrosion | |||
| Poor boiler feed water quality | |||
| Deposition | Inadequate blowdown control | Equipment failure | |
| Improper water supply | Workers unawareness | Boiler system failure | |
| Rust/corrosion | Dust or impurities enters | Tank failure | |
| Leak | Corrosion | Lost water and quality of water | |
| Water level controller | Fails to operate | Due to corrosion | Boiler failure and hazardous to operator |
| Fails to provide signal | Electrical failure | ||
| Feed water hose | Hose Block | Impurities present in water | Insufficient water supply to boiler |
| Hose leakage | The shell of the fitting was crimped too much or too little during assembly | Many parts get corroded | |
| The fitting has blown off the hose | The hose was not inserted deeply enough | Hazardous to operators | |
| Hose is hard and brittle | The hose was exposed to heat exceeding the maximum recommended temperature | Chance of hose failure | |
| Water Softner | Fail to operate | Water contamination | Scaling anddamage of boiler tubes |
| No softening | Excess scaling | Reduction in boiler efficiency andproduction | |
| Too much softening | Premature boiler failure | ||
| Deaerator | Deaerator spray zone corrosion on SS shell | Due to high chlorides | Boiler system failure |
| Deaerator inlet header spray pipe failure | Due to high pressure and temp | ||
| Excessive derator venting | Deaerator steam supply PRV stuck open | Steam pressure low/wastage of steam | |
| Deaerator spray valve spring failure | Due to excess pressure | Derator failure | |
| ReturnWater Temperature Sensor | Incorrect signal from sensor element | Reduced signal level | Potential processing error |
| Impedance mismatch | |||
| A/D conversion error | |||
| Loss of signal from sensor element | Chip failure | Loss of signal to processor | |
| Corroded sensor | |||
| Power supply loss of voltage | power supply malfunction | Loss of signal to processor | |
| Calibration error | Software error | Potential system malfunction | |
| Error in Algorithm | |||
| Drain pump | Drain hose leakage | Due to corrosion, dust and dirt | System failure |
| Drain hose blockage | Dirt andcorrosion | Inefficient drainage | |
| Pump gear wear | Material defect | Pump failure | |
| Strainer is clogged | Improper cleaning | Pump failure | |
| Condensate filter | Internal leakage | Due to aging | Equipment failure |
| Clogging | Due to impurities and operators unawareness | System failure | |
| Induced Draft (ID) Fan | Motor or contactor failure | Dust anddirt particles | Loss of control of parameters- temp. |
| Fan failure/fails to start | Electrical or mechanical failure | System level effect | |
| Failure due to jamming of blades | Due to foreign material and dust | Equipment Failure | |
| De-function or pressure drop | Due to aging | Affects system performance | |
| Forced Draft (FD) Fan | Fan operate with high vibration level | Bearing fails | Equipment damage/failure |
| Housing wear | |||
| Unbalanced fan blade | |||
| Corrosion | Aging | Equipment failure | |
| Physical damage | Crash | ||
| Foreign material build up | Lack of cleaning | ||
| Noise in motor | Motor bearing failure | Low production due to fatigue to operator | |
| Mechanical dust collector (MDC) | Leakage | Due to corrosion | Equipment failure |
| Blockage | Due to lack of cleaning | Equipment failure | |
| Burner | Oil gas burner failure | Dust and dirt particles enters in to burner | Boiler stops functioning |
| Faulty flame sensor | Manufacturing defect | Chances of furnace explosion if unburnt coal moisture entered in furnace | |
| High furnace pressure | Failure of PRV | Steam pressure and temperature increases | |
| Low combustion air | Variation in drum level | Required pressure and temp not obtain | |
| Feed Motor | Open or shorted winding | Excessively high temperature | Motor will not run |
| Worn bearing | Poor lubrication | Noisy | |
| Contamination | Seized | ||
| Overloading or high temperature | Heat build up | ||
| Cracked housing | Fatigue, external shock and vibration | Leakage, shorted or seized | |
| Sheared armature shaft | Fatigue | Seized | |
| Misalignment | Armature rubbing stator | ||
| Bearing failure | Motor failure |
References
- Patil, S.S.; Bewoor, A.K. Reliability analysis of a steam boiler system by expert judgment method and best-fit failure model method: A new approach. Int. J. Qual. Reliab. Manag. 2020, 38, 389–409. [Google Scholar] [CrossRef]
- Patil, S.S.; Bewoor, A.K.; Patil, R.B. Availability analysis of a steam boiler in textile process industries using failure and repair data: A case study. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2021, 7, 021002. [Google Scholar] [CrossRef]
- Hajiagha, S.H.R.; Hashemi, S.S.; Mohammadi, Y.; Zavadskas, K. Fuzzy belief structure based VIKOR method: An application for ranking delay causes of Tehran metro system by FMEA criteria. Transport 2016, 31, 108–118. [Google Scholar] [CrossRef]
- Chang, C.L.; Wei, C.C.; Lee, Y.H. Failure mode and effects analysis using fuzzy method and grey theory. Kybernetes 1999, 28, 1072–1080. [Google Scholar] [CrossRef]
- Braglia, M. MAFMA: Multi-attribute failure mode analysis. Int. J. Qual. Reliab. Manag. 2000, 17, 1017–1033. [Google Scholar] [CrossRef]
- Braglia, M.; Frosolini, M.; Montanari, R. Fuzzy TOPSIS approach for failure mode, effects and criticality analysis. Qual. Reliab. Eng. Int. 2003, 19, 425–443. [Google Scholar] [CrossRef]
- Seyed-Hosseini, S.M.; Safaei, N.; Asgharpour, M.J. Reprioritization of failures in a system failure mode and effects analysis by decision making trial and evaluation laboratory technique. Reliab. Eng. Syst. Saf. 2006, 91, 872–881. [Google Scholar] [CrossRef]
- Chatzimouratidis, A.I.; Pilavachi, P.A. Sensitivity analysis of technological, economic and sustainability evaluation of power plants using the analytic hierarchy process. Energy Policy 2009, 37, 778–798. [Google Scholar] [CrossRef]
- Suebsomran, A. Critical maintenance of thermal power plant using the combination of failure mode effect analysis and AHP approches. Asian Int. J. Sci. Technol. Prod. Manuf. Eng. 2010, 3, 1–6. [Google Scholar]
- Zammori, F.; Gabbrielli, R. ANP/RPN: A multi criteria evaluation of the risk priority number. Qual. Reliab. Eng. Int. 2012, 28, 85–104. [Google Scholar] [CrossRef]
- Silvestri, A.; De Felice, F.; Petrillo, A. Multi-criteria risk analysis to improve safety in manufacturing systems. Int. J. Prod. Res. 2012, 50, 4806–4821. [Google Scholar] [CrossRef]
- Kutlu, A.C.; Ekmekçioglu, M. Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP. Expert Syst. Appl. 2012, 39, 61–67. [Google Scholar] [CrossRef]
- Singh, R.K.; Kulkarni, M.S. Criticality analysis of power-plant equipments using the Analytic Hierarchy Process. Int. J. Ind. Eng. Technol. 2013, 3, 1–14. [Google Scholar]
- Liu, H.C.; Fan, X.J.; Li, P.; Chen, Y.Z. Evaluating the risk of failure modes with extended MULTIMOORA method under fuzzy environment. Eng. Appl. Artif. Intell. 2014, 34, 168–177. [Google Scholar] [CrossRef]
- Adhikary, D.; Bose, K.; Bose, G.; Mitra, S. Multi criteria FMECA for coal-fired thermal power plants using COPRAS-G. Int. J. Qual. Reliab. Manag. 2014, 31, 601–614. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Ding, X.F.; Su, Q. Improving risk evaluation in FMEA with a hybrid multiple criteria decision making method. Int. J. Qual. Reliab. Manag. 2015, 32, 763–782. [Google Scholar] [CrossRef]
- Vahdani, B.; Salimi, M.; Charkhchian, M. A new FMEA method by integrating fuzzy belief structure and TOPSIS to improve risk evaluation process. Int. J. Adv. Manuf. Technol. 2015, 77, 357–368. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Shan, M.M.; Shao, L.N. Failure mode and effects analysis using intuitionistic fuzzy hybrid TOPSIS approach. Soft Comput. 2015, 19, 1085–1098. [Google Scholar] [CrossRef]
- Zhou, Q.; Thai, V.V. Fuzzy and grey theories in failure mode and effect analysis for tanker equipment failure prediction. Saf. Sci. 2016, 83, 74–79. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.-X.; Li, P.; Su, Q. Failure mode and effect analysis under uncertainty: An integrated multiple criteria decision making approach. IEEE Trans. Reliab. 2016, 65, 1380–1392. [Google Scholar] [CrossRef]
- Jagtap, H.P.; Bewoor, A.K. Use of analytic hierarchy process methodology for criticality analysis of thermal power plant equipments. Mater. Today Proc. 2017, 4, 1927–1936. [Google Scholar] [CrossRef]
- Certa, A.; Hopps, F.; Inghilleri, R.; La Fata, C.M. A Dempster-Shafer Theory-based approach to the Failure Mode, Effects and Criticality Analysis (FMECA) under epistemic uncertainty: Application to the propulsion system of a fishing vessel. Reliab. Eng. Syst. Saf. 2017, 159, 69–79. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Liu, H.C. New approach for failure mode and effect analysis using linguistic distribution assessments and TODIM method. Reliab. Eng. Syst. Saf. 2017, 167, 302–309. [Google Scholar] [CrossRef]
- Zhao, H.; You, J.X.; Liu, H.C. Failure mode and effect analysis using MULTIMOORA method with continuous weighted entropy under interval-valued intuitionistic fuzzy environment. Soft Comput. 2017, 21, 5355–5367. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, C.; Wei, B.; Tang, Y. Failure mode and effects analysis based on Z-numbers. Intell. Autom. Soft Comput. 2017, 2017, 1–8. [Google Scholar] [CrossRef]
- Carpitella, S.; Certa, A.; Izquierdo, J.; La Fata, C.M. A combined multi-criteria approach to support FMECA analyses: A real-world case. Reliab. Eng. Syst. Saf. 2018, 169, 394–402. [Google Scholar] [CrossRef]
- Tian, Z.; Wang, J.; Zhang, H. An integrated approach for failure mode and effects analysis based on fuzzy best-worst, relative entropy, and VIKOR methods. Appl. Soft Comput. 2018, 72, 636–646. [Google Scholar] [CrossRef]
- Fattahi, R.; Khalilzadeh, M. Risk evaluation using a novel hybrid method based on FMEA, extended MULTIMOORA, and AHP methods under fuzzy environment. Saf. Sci. 2018, 102, 290–300. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, J.M.; Wang, R.X.; Chen, K.; Gao, Z.Y.; Zheng, W. Failure mode and effects analysis by using the house of reliability-based rough VIKOR approach. IEEE Trans. Reliab. 2018, 67, 230–248. [Google Scholar] [CrossRef]
- Pancholi, N.; Bhatt, M. FMECA based maintenance planning through COPRAS-G and PSI. J. Qual. Maint. Eng. 2018, 24, 224–243. [Google Scholar] [CrossRef]
- Gugaliya, A.; Boral, S.; Naikan, V.N.A. A hybrid decision making framework for modified failure mode effects and criticality analysis: A case study on process plant induction motors. Int. J. Qual. Reliab. Manag. 2019, 36, 1266–1283. [Google Scholar] [CrossRef]
- Javadi, M.A.; Khodabakhshi, S.; Ghasemiasl, R.; Jaberi, R. Sensivity analysis of a multi-generation system based on a gas/hydrogen-fueled gas turbine for producing hydrogen, electricity and freshwater. Energy Convers. Manag. 2022, 252, 115085. [Google Scholar] [CrossRef]
- Javadi, M.A.; Najafi, N.J.; Abhari, M.K.; Jaberi, R.; Pourtaba, H. 4E analysis of three different configurations of a combined cycle power plant integrated with a solar power tower system. Sustain. Energy Technol. Assess. 2021, 48, 101599. [Google Scholar] [CrossRef]
- Chin, K.S.; Wang, Y.M.; Gary, K.K.P.; Yang, J.B. Failure mode and effects analysis using a group-based evidential reasoning approach. Comput. Oper. Res. 2009, 36, 1768–1779. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Lin, Q.L. Fuzzy failure mode and effects analysis using fuzzy evidential reasoning and belief rule-based methodology. IEEE Trans. Reliab. 2013, 62, 23–36. [Google Scholar] [CrossRef]
- Patil, S.S.; Bewoor, A.K.; Kumar, R.; Ahmadi, M.H.; Sharifpur, M.; Praveen Kumar, S. Development of Optimized Maintenance Program for a Steam Boiler System Using Reliability-Centered Maintenance Approach. Sustainability 2022, 14, 10073. [Google Scholar] [CrossRef]
- Patil, S.S.; Bewoor, A.K. Optimization of maintenance strategies for steam boiler system using reliability-centered maintenance (RCM) model–A case study from Indian textile industries. Int. J. Qual. Reliab. Manag. 2022, 39, 1745–1765. [Google Scholar] [CrossRef]
- Patil, S.S.; Bewoor, A.K.; Patil, R.B.; Mellal, M.A. Trends Based Reliability Availability and Maintainability (RAM) Assessment of a Steam Boiler. In Predictive Analytics—Modeling and Optimization; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2020; pp. 261–272. [Google Scholar]
- Patil, S.S.; Bewoor, A.K.; Kumar, R.; Iliev, I.K. Development of Reliability Block Diagram (RBD) Model for Reliability Analysis of a Steam Boiler System. In Predictive Analytics in System Reliability; Springer Series in Reliability Engineering; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Green, R.A. The Delphi technique in educational research. SAGE Open 2014, 4, 2. [Google Scholar] [CrossRef]
- Shaker, F.; Shahin, A.; Jahanyan, S. Developing a two-phase QFD for improving FMEA: An integrative approach. Int. J. Qual. Reliab. Manag. 2019, 36, 1454–1474. [Google Scholar] [CrossRef]
- Guerrero, H.H.; Bradley, J.R. Failure modes and effects analysis: An evaluation of group versus individual performance. Prod. Oper. Manag. 2013, 22, 1524–1539. [Google Scholar] [CrossRef]
| Sr. No | Failure Effect Severity Category | Severity Category Description | Rank |
|---|---|---|---|
| 1 | Very High | The failure of the boiler system may cause risk to the operator’s life with or without warning. | 10 |
| 2 | Failure causes complete system failure or system inoperable. | 9 | |
| 3 | The system requires major maintenance, is time-consuming, and incurs very high maintenance costs. | 8 | |
| 4 | High | Loss of primary function. | 7 |
| 5 | System performance is degraded. | 6 | |
| 6 | Moderate | Moderate effect on system performance. | 5 |
| 7 | The subsystem/component requires major repair, moderate cost of repair. | 4 | |
| 8 | Low | Subsystem/component requires minor repair and low maintenance costs. | 3 |
| 9 | Minor effect on system performance. | 2 | |
| 10 | Very Minor | Very minor effects or no effect on system performance. | 1 |
| Sr. No | Occurrence Criterion | Ranking Meaning | Possible Failure Rate | Rank |
|---|---|---|---|---|
| 1 | Very Frequent | Occurrence is almost certain | Every Month | 10 |
| Between 1 month to 3 months | 9 | |||
| 2 | Frequent | Failure occurs repeatedly | Between 3 months to 6 months | 8 |
| Between 6 months to 1 Year | 7 | |||
| 3 | Occasional | Failure occurs occasionally | Between 1 Year to 4 Years | 6 |
| Between 4 Years to 8 Years | 5 | |||
| 4 | Remote | Few failures expected | Between 8 Years to 10 Years | 4 |
| Between 10 Years to 12 Years | 3 | |||
| 5 | Extremely unlikely | Occurrence is quite unlikely | Between 12 Years to 15 Years | 2 |
| More than 15 Years | 1 |
| Sr. No | Detectability | Criteria Meaning | Rank |
|---|---|---|---|
| 1 | Impossible | The present system is not able to detect failure mode or cause, or there is no control over failure. | 10 |
| 2 | Absolute Uncertain | 9 | |
| 3 | Highly Difficult | Very low probability the current monitoring system detects the failure | 8 |
| 4 | Moderately Difficult | 7 | |
| 5 | Difficult | 6 | |
| 6 | Less Difficult | Possibly detecting the failure. | 5 |
| 7 | Very less Difficult | 4 | |
| 8 | Easy to Detect | High probability the current method can detect the failure | 3 |
| 9 | Very easy to detect | 2 | |
| 10 | Almost certain | Present method almost certainly detect the failure | 1 |
| Sr. No | Maintenance Criterion | Ranking Meaning for Maintenance | Rank |
|---|---|---|---|
| 1 | Extensive Damage | Component replacement is required, and the maintenance time required is more than 60 h | 9–10 |
| 2 | Major Damage | Very difficult to repair, and the maintenance time required is between 40 to 60 h | 7–8 |
| 3 | Localized Damage | Difficult to repair, and the maintenance time required is between 20–40 h | 5–6 |
| 4 | Minor Damage | Easy to repair, and the maintenance time required is between 2 to 20 h | 3–4 |
| 5 | Slight Damage | Very easy to repair, and the maintenance time required is less than 2 h | 1–2 |
| Sr. No | Criterion for Safety | Ranking Meaning | Rank |
|---|---|---|---|
| 1 | Very High Dangerous | Multiple/Single fatalities | 9–10 |
| 2 | Highly Dangerous | Permanent injury to the operator | 7–8 |
| 3 | Moderate Dangerous | Major physical injury to the operator | 5–6 |
| 4 | Minor Dangerous | No permanent or minor injury to the operator | 3–4 |
| 5 | Very less Dangerous | Failure doesn’t affect to human life | 1–2 |
| Sr. No | Criterion | Ranking Meaning for Production/Quality Loss | Rank |
|---|---|---|---|
| 1 | Extensive Loss | The loss is not recoverable. More than 5 days of production loss. | 9–10 |
| 2 | Major Loss | The loss is 50% recoverable. Up to 3 to 5 days of production loss. | 7–8 |
| 3 | Moderate loss | The loss is not wholly recoverable through normal production. Up to 1 to 3 days of production loss. | 5–6 |
| 4 | Minor Loss | Loss is recoverable through normal production. Up to 2 to 24 h of production loss. | 3–4 |
| 5 | Little to no effect | Loss can be easily recovered. Less than 2 h of production loss. | 1–2 |
| Sr. No | Experience in Years | Number of Boilers Handling | Number of Employees under Supervision | Proficiency in the Field | Scale |
|---|---|---|---|---|---|
| 1 | >20 | 16–20+ | 10+ | Specific Boiler Inspection course and certification | 5 |
| 2 | 16–20 Y | 11–15 | 8–10 | Highly qualified | 4 |
| 3 | 11–15 Y | 7–10 | 5–7 | Qualified and Boiler Attendant Course | 3 |
| 4 | 5–10 Y | 3–6 | 2–4 | Less qualified with Boiler Attendant Course | 2 |
| 5 | <5 | <3 | <2 | Less Educated | 1 |
| Expert No | Experience in Years | No of Boilers Handling | No of Employees under Supervision | Proficiency in the Field | Experts Overall Weightage | ||||
|---|---|---|---|---|---|---|---|---|---|
| Weightage | Relative Weight | Weightage | Relative Weight | Weightage | Relative Weight | Weightage | Relative Weight | ||
| Ex1 | 2 | 0.087 | 2 | 0.1 | 5 | 0.1852 | 5 | 0.2381 | 0.6103 |
| Ex2 | 3 | 0.1304 | 5 | 0.25 | 5 | 0.1852 | 3 | 0.1429 | 0.7085 |
| Ex3 | 5 | 0.2174 | 3 | 0.15 | 3 | 0.1111 | 2 | 0.0952 | 0.5737 |
| Ex4 | 5 | 0.2174 | 3 | 0.15 | 2 | 0.0741 | 1 | 0.0476 | 0.4891 |
| Ex5 | 2 | 0.087 | 1 | 0.05 | 3 | 0.1111 | 3 | 0.1429 | 0.391 |
| Ex6 | 4 | 0.1739 | 4 | 0.2 | 5 | 0.1852 | 4 | 0.1905 | 0.7496 |
| Component | Failure Mode | Failure Cause | Failure Effect | SV | O | D | M | S | L |
|---|---|---|---|---|---|---|---|---|---|
| Severity | Occurrence | Detection | Maintenance | Safety | Loss | ||||
| Water Tubes | Short term overheating | Starvation of steam or water flow | Axial fish-mouth rupture | 4.25 | 3.22 | 2.63 | 3.29 | 2.56 | 3.07 |
| Blockages from debris | Axial fish-mouth rupture | 4.48 | 3.99 | 2.67 | 3.39 | 2.37 | 3.24 | ||
| Thin lip failure of the tube | Due to rapid heating | Rupture | 4.47 | 3.67 | 2.86 | 2.80 | 2.02 | 3.34 | |
| Tube joints failure | Dissimilar metal welds | System failure | 4.78 | 3.38 | 2.63 | 3.29 | 2.16 | 3.20 | |
| Crack and holes | Calcium and magnesium layer increases | The boiler should be closed | 5.03 | 3.45 | 2.38 | 3.15 | 1.93 | 3.45 | |
| Tube surface corrosion | Due to the presence of moisture content | Tube failure | 3.81 | 2.60 | 2.51 | 2.60 | 1.61 | 2.65 | |
| Deposits formed in the top of the drum | due to refractory brick deterioration | partially blocking the blowdown channel ports | 4.29 | 3.09 | 2.30 | 2.99 | 2.09 | 2.78 | |
| Boiler tube blisters/bulges | Due to presence of internal scale | Tube failure | 4.94 | 2.95 | 2.92 | 2.66 | 1.97 | 3.05 | |
| Feed Water Pump | The strainer failure | The strainer is clogged | Pump Fails | 2.67 | 3.73 | 1.93 | 2.38 | 1.58 | 2.31 |
| Rust of tank | A lot of sediment in the water | Failure of mechanical seal and cause a leak | 3.11 | 3.35 | 1.96 | 2.96 | 1.87 | 2.13 | |
| condensate is too hot for the pump | steam traps fail | Failure of pump’s impeller | 2.47 | 3.84 | 1.90 | 2.38 | 1.75 | 2.15 | |
| mechanical seal failure | Pump leakage | Pump failure | 2.70 | 3.28 | 2.31 | 3.21 | 1.84 | 2.41 | |
| Electrical failure of the pump | The voltage supplied to the pump is not correct. | Failure of circuit breaker and winding burns | 2.89 | 3.49 | 2.04 | 3.21 | 1.69 | 1.98 | |
| Impeller Failure | Impeller is clogged | Mechanical failure of pump | 2.67 | 3.13 | 2.20 | 3.37 | 1.45 | 2.39 | |
| Shaft failure | Overload work, Misalignment, Corrosion | Pump vibration, Pump works but does not provide flow | 3.57 | 3.06 | 2.16 | 3.38 | 1.16 | 2.44 | |
| Deterioration of the bearings | Lubrication failure | Insufficient flow | 2.71 | 3.16 | 2.44 | 3.44 | 1.42 | 2.32 | |
| Improper mountings | Pump vibrates or is noisy. | 2.71 | 3.48 | 2.32 | 3.10 | 1.34 | 2.24 | ||
| Abnormal load on motor | Pump failure | 3.37 | 3.24 | 2.50 | 3.25 | 1.28 | 2.54 | ||
| Contamination present | Pump failure | 2.25 | 3.52 | 2.29 | 3.33 | 1.40 | 2.21 | ||
| Pump housing volute damaged/Volute erosion | Cavitation, corrosion and Vibration | Leak in the pump body | 2.80 | 2.92 | 1.97 | 3.28 | 1.56 | 2.46 | |
| Pump low efficiency | Electric motor failed | Low flow warming | 2.63 | 2.89 | 2.10 | 3.18 | 1.38 | 2.75 | |
| Low discharge pressure | 2.39 | 2.81 | 2.22 | 2.87 | 1.50 | 2.15 | |||
| Reduction in pump pressure | Pump cavitation | Pump noise and vibration | 3.02 | 2.88 | 2.31 | 3.31 | 1.77 | 2.04 |
| Component | Failure Mode | Failure Cause | Failure Effect | SV | O | D | M | S | L |
|---|---|---|---|---|---|---|---|---|---|
| Water Tubes | Short term overheating | Starvation of steam or water flow | Axial fish-mouth rupture | 0.5294 | 0.8079 | 0.7238 | 0.7245 | 0.4534 | 0.6446 |
| Blockages from debris | Axial fish-mouth rupture | 0.5026 | 0.6511 | 0.7107 | 0.7028 | 0.4898 | 0.6111 | ||
| Thin lip failure of the tube | Due to rapid heating | Rupture | 0.5034 | 0.7091 | 0.6636 | 0.8500 | 0.5743 | 0.5937 | |
| Tube joints failure | Dissimilar metal welds | System failure | 0.4709 | 0.7696 | 0.7220 | 0.7238 | 0.5375 | 0.6188 | |
| Crack and holes | Calcium and magnesium layer increases | The boiler should be closed | 0.4472 | 0.7533 | 0.7994 | 0.7548 | 0.6005 | 0.5742 | |
| Tube surface corrosion | Due to the presence of moisture content | Tube failure | 0.5900 | 1.0000 | 0.7560 | 0.9148 | 0.7198 | 0.7462 | |
| Deposits formed at the top of the drum | Due to refractory brick deterioration | Partially blocking the blowdown channel ports | 0.5249 | 0.8423 | 0.8279 | 0.7969 | 0.5546 | 0.7127 | |
| Boiler tube blisters/bulges | Due to the presence of an internal scale | Tube failure | 0.4552 | 0.8829 | 0.6499 | 0.8942 | 0.5883 | 0.6502 | |
| Feed Water Pump | The strainer failure | The strainer is clogged | Pump fails | 0.8432 | 0.6967 | 0.9862 | 1.0007 | 0.7326 | 0.8559 |
| Rust of tank | A lot of sediment in the water | Failure of mechanical seal and cause a leak | 0.7227 | 0.7757 | 0.9677 | 0.8031 | 0.6203 | 0.9296 | |
| condensate is too hot for the pump | steam traps fail | Failure of the pump’s impeller | 0.9122 | 0.6777 | 1.0018 | 0.9993 | 0.6648 | 0.9224 | |
| mechanical seal failure | Pump leakage | Pump failure | 0.8323 | 0.7919 | 0.8231 | 0.7422 | 0.6310 | 0.8216 | |
| Electrical failure of the pump | The voltage supplied to the pump is notcorrect. | Failure of circuit breaker and winding burns | 0.7776 | 0.7457 | 0.9337 | 0.7414 | 0.6864 | 1.0008 | |
| Impeller Failure | Impeller is clogged | Mechanical failure of the pump | 0.8416 | 0.8316 | 0.8643 | 0.7062 | 0.8009 | 0.8296 | |
| Shaft failure | Overload work, misalignment, corrosion | Pump vibration, pump works but does not provide flow | 0.6300 | 0.8492 | 0.8783 | 0.7041 | 1.0029 | 0.8131 | |
| Deterioration of the bearings | Lubrication failure | Insufficient flow | 0.8292 | 0.8224 | 0.7782 | 0.6915 | 0.8159 | 0.8547 | |
| Improper mountings | Pump vibrates or is noisy. | 0.8308 | 0.7471 | 0.8178 | 0.7673 | 0.8657 | 0.8833 | ||
| Abnormal load on the motor | Pump failure | 0.6683 | 0.8033 | 0.7615 | 0.7327 | 0.9098 | 0.7811 | ||
| Contamination present | Pump failure | 1.0022 | 0.7383 | 0.8303 | 0.7147 | 0.8286 | 0.8959 | ||
| Pump housing volute damaged/Volute erosion | Cavitation, corrosion andvibration | Leak in the pump body | 0.8041 | 0.8899 | 0.9628 | 0.7252 | 0.7436 | 0.8038 | |
| Pump low efficiency | Electric motor failed | Low flow warming | 0.8550 | 0.8997 | 0.9055 | 0.7476 | 0.8426 | 0.7204 | |
| Low discharge pressure | 0.9421 | 0.9242 | 0.8552 | 0.8283 | 0.7759 | 0.9231 | |||
| Reduction in pump pressure | Pump cavitation | Pump noise and vibration | 0.7446 | 0.9017 | 0.8243 | 0.7198 | 0.6560 | 0.9690 |
| Component | Failure Mode | Failure Cause | Failure Effect | SV | O | D | M | S | L |
|---|---|---|---|---|---|---|---|---|---|
| Nij × wj | Nij × wj | Nij × wj | Nij × wj | Nij × wj | Nij × wj | ||||
| Water Tubes | Short term overheating | Starvation of steam or water flow | Axial fish-mouth rupture | 0.0870 | 0.1356 | 0.1212 | 0.1216 | 0.0752 | 0.1073 |
| Blockages from debris | Axial fish-mouth rupture | 0.0826 | 0.1093 | 0.1190 | 0.1179 | 0.0813 | 0.1017 | ||
| Thin lip failure of the tube | Due to rapid heating | Rupture | 0.0827 | 0.1191 | 0.1112 | 0.1426 | 0.0953 | 0.0989 | |
| Tube joints failure | Dissimilar metal welds | System failure | 0.0774 | 0.1292 | 0.1209 | 0.1215 | 0.0892 | 0.1030 | |
| Crack and holes | Calcium and magnesium layer increases | The boiler should be closed | 0.0735 | 0.1265 | 0.1339 | 0.1267 | 0.0996 | 0.0956 | |
| Tube surface corrosion | Due to the presence of moisture content | Tube failure | 0.0969 | 0.1679 | 0.1266 | 0.1535 | 0.1194 | 0.1242 | |
| Deposits formed at the top of the drum | Due to refractory brick deterioration | Partially blocking the blowdown channel ports | 0.0862 | 0.1414 | 0.1387 | 0.1337 | 0.0920 | 0.1187 | |
| Boiler tube blisters/bulges | Due to the presence of an internal scale | Tube failure | 0.0748 | 0.1482 | 0.1089 | 0.1500 | 0.0976 | 0.1083 | |
| Feed Water Pump | The strainer failure | The strainer is clogged | Pump fails | 0.1385 | 0.1170 | 0.1652 | 0.1679 | 0.1215 | 0.1425 |
| Rust of tank | A lot of sediment in the water | Failure of mechanical seal and cause a leak | 0.1187 | 0.1302 | 0.1621 | 0.1348 | 0.1029 | 0.1548 | |
| Condensate is too hot for the pump | Steam traps fail | Failure of the pump impeller | 0.1499 | 0.1138 | 0.1678 | 0.1677 | 0.1103 | 0.1536 | |
| Mechanical seal failure | Pump leakage | Pump failure | 0.1367 | 0.1330 | 0.1379 | 0.1245 | 0.1047 | 0.1368 | |
| Electrical failure of the pump | The voltage supplied to the pump is not correct | Failure of circuit breaker and winding burns | 0.1278 | 0.1252 | 0.1564 | 0.1244 | 0.1139 | 0.1666 | |
| Impeller failure | Impeller is clogged | Mechanical failure of the pump | 0.1383 | 0.1396 | 0.1448 | 0.1185 | 0.1329 | 0.1381 | |
| Shaft failure | Overload work, misalignment, corrosion | Pump vibration, pump works but does not provide flow | 0.1035 | 0.1426 | 0.1471 | 0.1181 | 0.1664 | 0.1354 | |
| Deterioration of the bearings | Lubrication failure | Insufficient flow | 0.1362 | 0.1381 | 0.1303 | 0.1160 | 0.1354 | 0.1423 | |
| Improper mountings | Pump vibrates or is noisy | 0.1365 | 0.1254 | 0.1370 | 0.1288 | 0.1436 | 0.1471 | ||
| Abnormal load on the motor | Pump failure | 0.1098 | 0.1349 | 0.1276 | 0.1229 | 0.1509 | 0.1301 | ||
| Contamination present | Pump failure | 0.1647 | 0.1240 | 0.1391 | 0.1199 | 0.1375 | 0.1492 | ||
| Pump housing volute damaged/Erosion | Cavitation, corrosion andvibration | Leak in the pump body | 0.1321 | 0.1494 | 0.1613 | 0.1217 | 0.1234 | 0.1338 | |
| Pump low efficiency | Electric motor failed | Low flow warming | 0.1405 | 0.1511 | 0.1517 | 0.1254 | 0.1398 | 0.1199 | |
| Low discharge pressure | 0.1548 | 0.1552 | 0.1432 | 0.1390 | 0.1287 | 0.1537 | |||
| Reduction in pump pressure | Pump cavitation | Pump noise and vibration | 0.1223 | 0.1514 | 0.1381 | 0.1208 | 0.1088 | 0.1613 |
| Sub-Systems | Component | Overall CI of Component | Criticality Rank | Overall CI of Sub-System | Criticality Rank |
|---|---|---|---|---|---|
| Combustion and Ignition System | Furnace | 1.5559 | 22 | 13.7475 | 2 |
| Shell | 2.1224 | 19 | |||
| Header | 5.1139 | 6 | |||
| Intake vent/Air vent | 1.8910 | 21 | |||
| Combustion chamber | 3.0643 | 10 | |||
| Feed Water Supply System | Water tubes | 5.3936 | 3 | 49.953 | 1 |
| Supply water temperature sensor | 5.2401 | 4 | |||
| Backflow preventer valve | 2.7529 | 12 | |||
| Temperature regulator | 2.7632 | 11 | |||
| Feed water pump motor | 6.5052 | 2 | |||
| Feed water pump | 12.2870 | 1 | |||
| Strainer | 2.7128 | 13 | |||
| Feed water tank | 4.4311 | 9 | |||
| Water level controller | 1.0964 | 25 | |||
| Feed water hose | 2.2889 | 18 | |||
| Water softner | 2.0131 | 20 | |||
| Deaerator | 2.4687 | 15 | |||
| Blow-down System | Return water temperature sensor | 5.2306 | 5 | 9.0564 | 3 |
| Drain pump | 2.5268 | 14 | |||
| Condensate filter | 1.2990 | 24 | |||
| Emission Control System | Induced Draft (ID) fan | 2.3364 | 17 | 8.1287 | 4 |
| Forced Draft (FD) fan | 4.4738 | 8 | |||
| Mechanical dust collector (MDC) | 1.3185 | 23 | |||
| Fuel Supply System | Burner | 2.3683 | 16 | 7.3796 | 5 |
| Feed motor | 5.0113 | 7 |
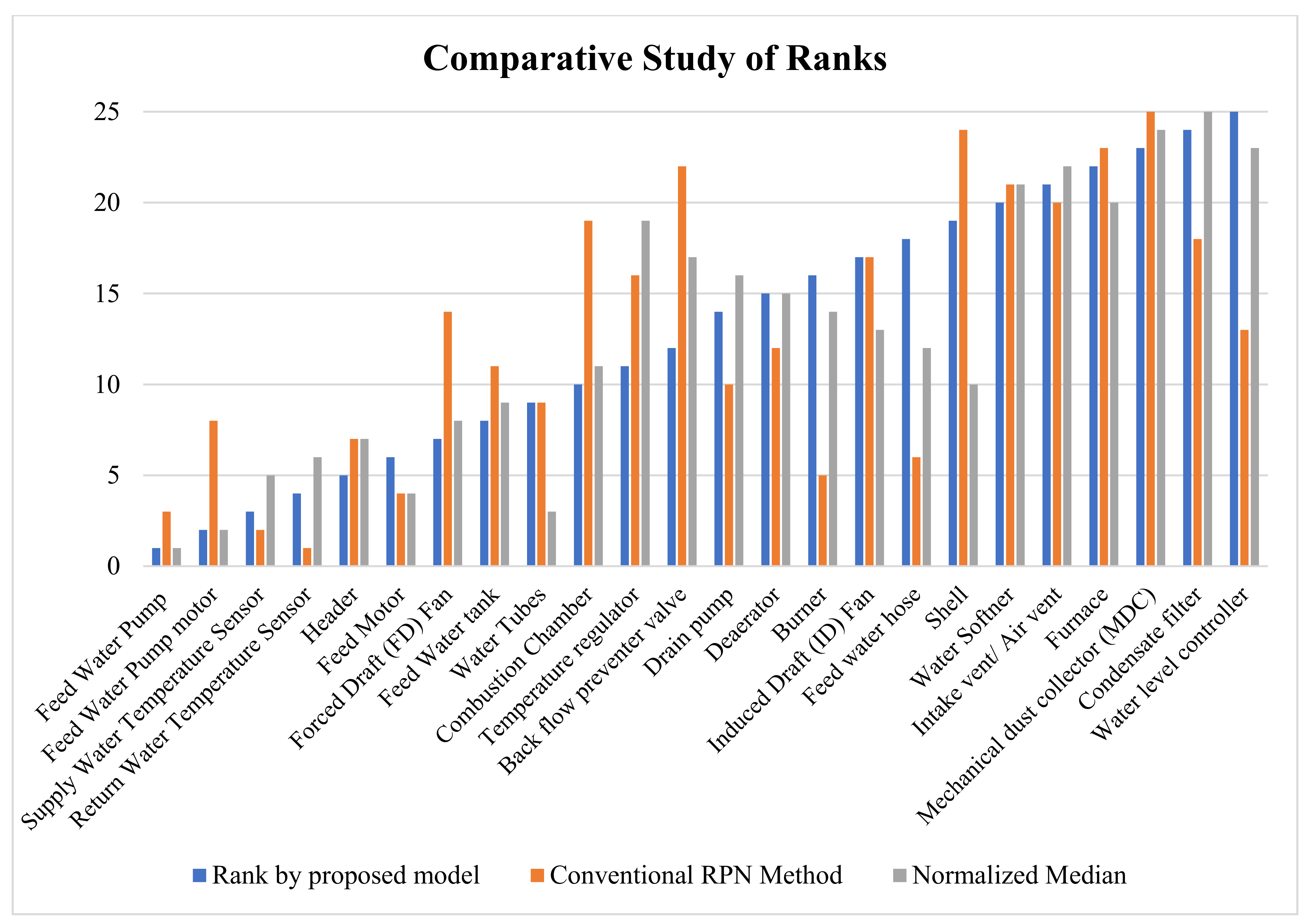
| Component | Rank by Proposed Model | Conventional RPN Method | Normalized Median | Component | Rank by Proposed Model | Conventional RPN Method | Normalized Median |
|---|---|---|---|---|---|---|---|
| Feed Water Pump | 01 | 03 | 01 | Drain pump | 14 | 10 | 16 |
| Feed Water Pump motor | 02 | 08 | 02 | Deaerator | 15 | 12 | 15 |
| Supply Water Temperature Sensor | 03 | 02 | 05 | Burner | 16 | 05 | 14 |
| Return Water Temperature Sensor | 04 | 01 | 06 | Induced Draft (ID) Fan | 17 | 17 | 13 |
| Header | 05 | 07 | 07 | Feed water hose | 18 | 06 | 12 |
| Feed Motor | 06 | 04 | 04 | Shell | 19 | 24 | 10 |
| Forced Draft (FD) Fan | 07 | 14 | 08 | Water Softner | 20 | 21 | 21 |
| Feed Water tank | 08 | 11 | 09 | Intake vent/Air vent | 21 | 20 | 22 |
| Water Tubes | 09 | 09 | 03 | Furnace | 22 | 23 | 20 |
| Combustion Chamber | 10 | 19 | 11 | Mechanical dust collector (MDC) | 23 | 25 | 24 |
| Temperature regulator | 11 | 16 | 19 | Condensate filter | 24 | 18 | 25 |
| Back flow preventer valve | 12 | 22 | 17 | Water level controller | 25 | 13 | 23 |
| Strainer | 13 | 15 | 18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patil, S.S.; Bewoor, A.K.; Patil, R.B.; Kumar, R.; Ongar, B.; Sarsenbayev, Y.; PraveenKumar, S.; Ibrahim, A.M.M.; Alsoufi, M.S.; Elsheikh, A. A New Approach for Failure Modes, Effects, and Criticality Analysis Using ExJ-PSI Model—A Case Study on Boiler System. Appl. Sci. 2022, 12, 11419. https://doi.org/10.3390/app122211419
Patil SS, Bewoor AK, Patil RB, Kumar R, Ongar B, Sarsenbayev Y, PraveenKumar S, Ibrahim AMM, Alsoufi MS, Elsheikh A. A New Approach for Failure Modes, Effects, and Criticality Analysis Using ExJ-PSI Model—A Case Study on Boiler System. Applied Sciences. 2022; 12(22):11419. https://doi.org/10.3390/app122211419
Chicago/Turabian StylePatil, Suyog S., Anand K. Bewoor, Rajkumar B. Patil, Ravinder Kumar, Bulbul Ongar, Yerlan Sarsenbayev, Seepana PraveenKumar, Ahmed Mohamed Mahmoud Ibrahim, Mohammad S. Alsoufi, and Ammar Elsheikh. 2022. "A New Approach for Failure Modes, Effects, and Criticality Analysis Using ExJ-PSI Model—A Case Study on Boiler System" Applied Sciences 12, no. 22: 11419. https://doi.org/10.3390/app122211419
APA StylePatil, S. S., Bewoor, A. K., Patil, R. B., Kumar, R., Ongar, B., Sarsenbayev, Y., PraveenKumar, S., Ibrahim, A. M. M., Alsoufi, M. S., & Elsheikh, A. (2022). A New Approach for Failure Modes, Effects, and Criticality Analysis Using ExJ-PSI Model—A Case Study on Boiler System. Applied Sciences, 12(22), 11419. https://doi.org/10.3390/app122211419












