Self-Organized Fuzzy Neural Network Nonlinear System Modeling Method Based on Clustering Algorithm
Abstract
:1. Introduction
2. Preliminary Knowledge
2.1. K-Means Clustering Algorithm
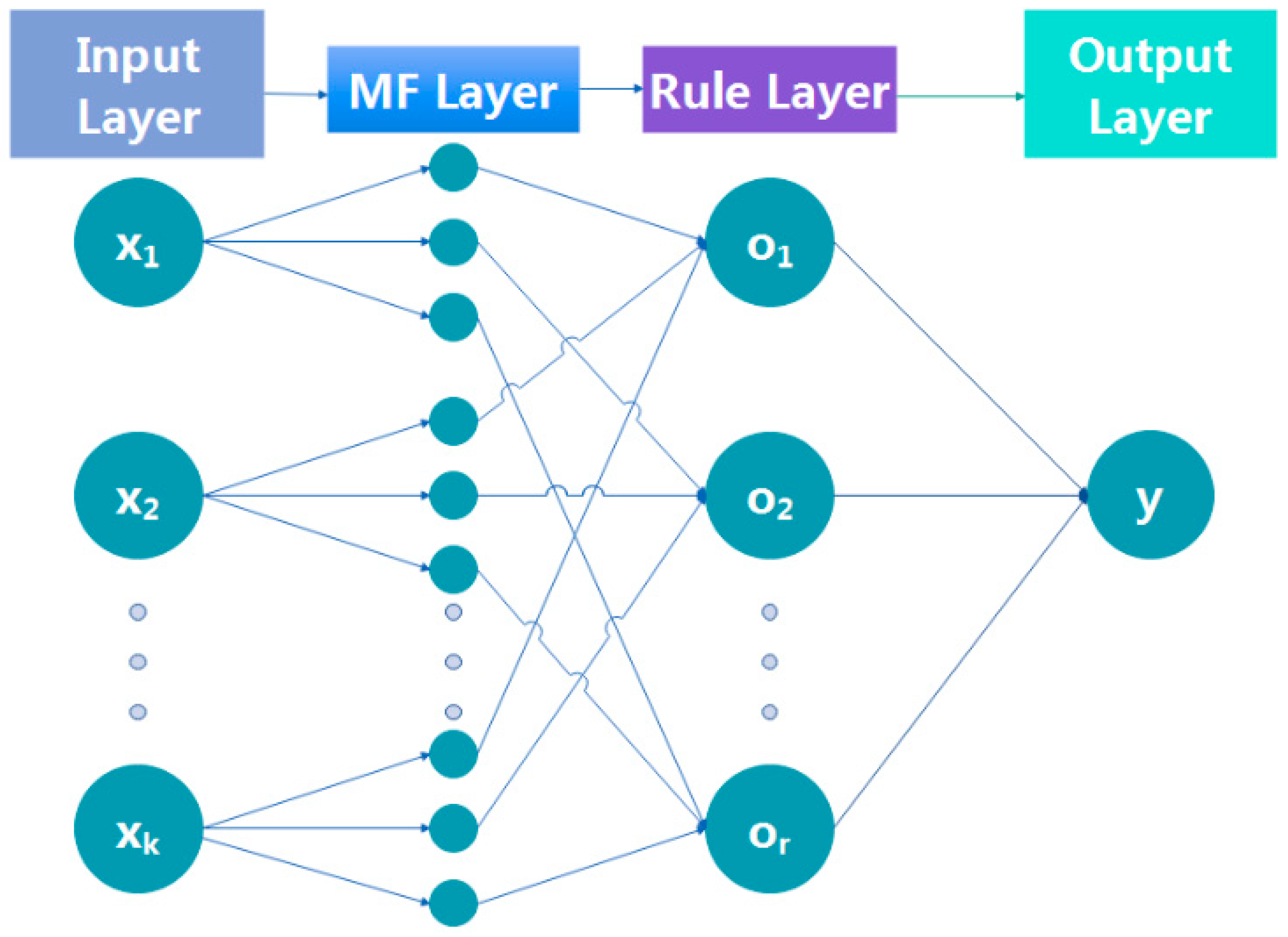
2.2. Fuzzy Neural Network
3. Implementation of Modeling Methods
3.1. Self-Organizing Mechanism
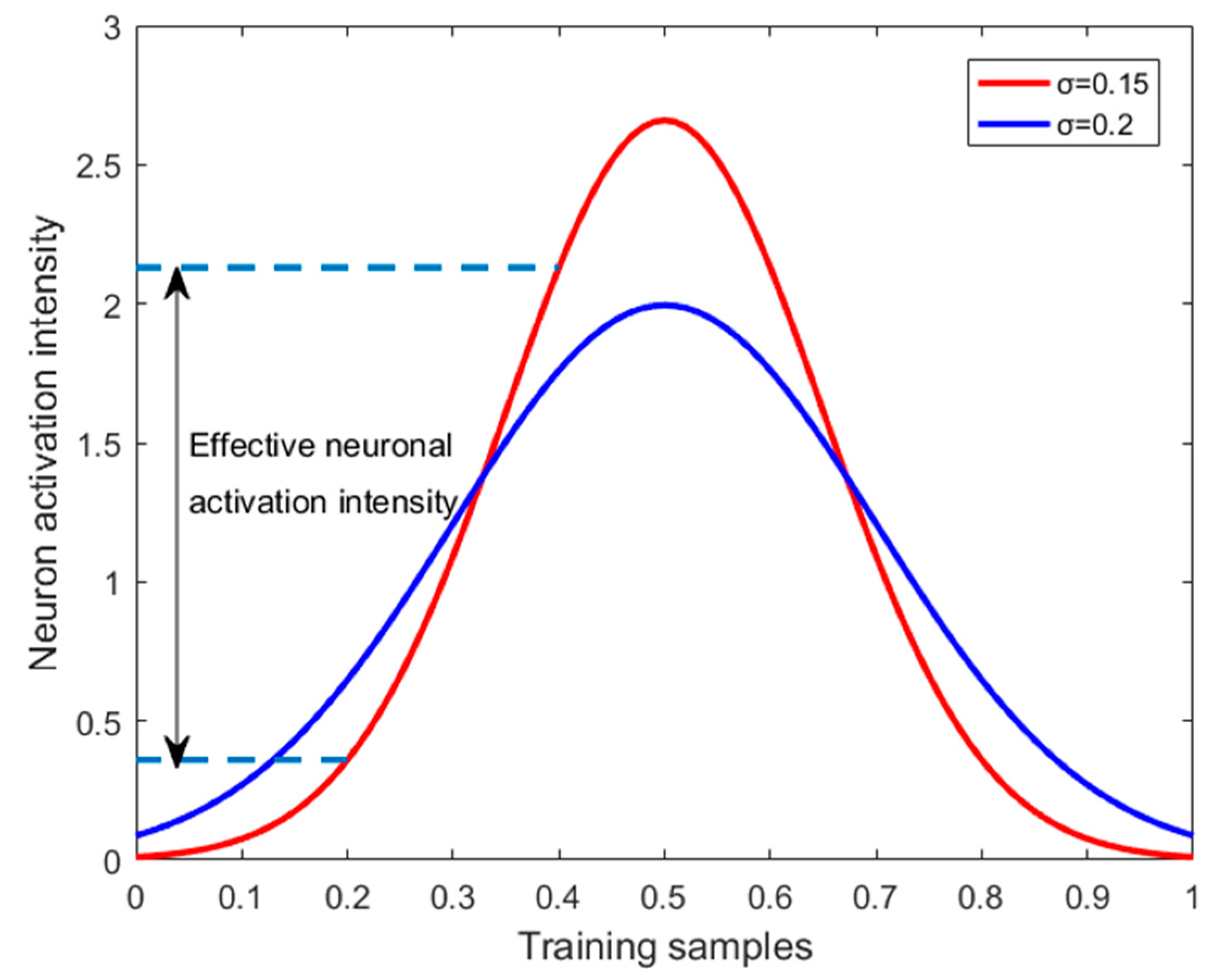
3.1.1. Neuronal Growth
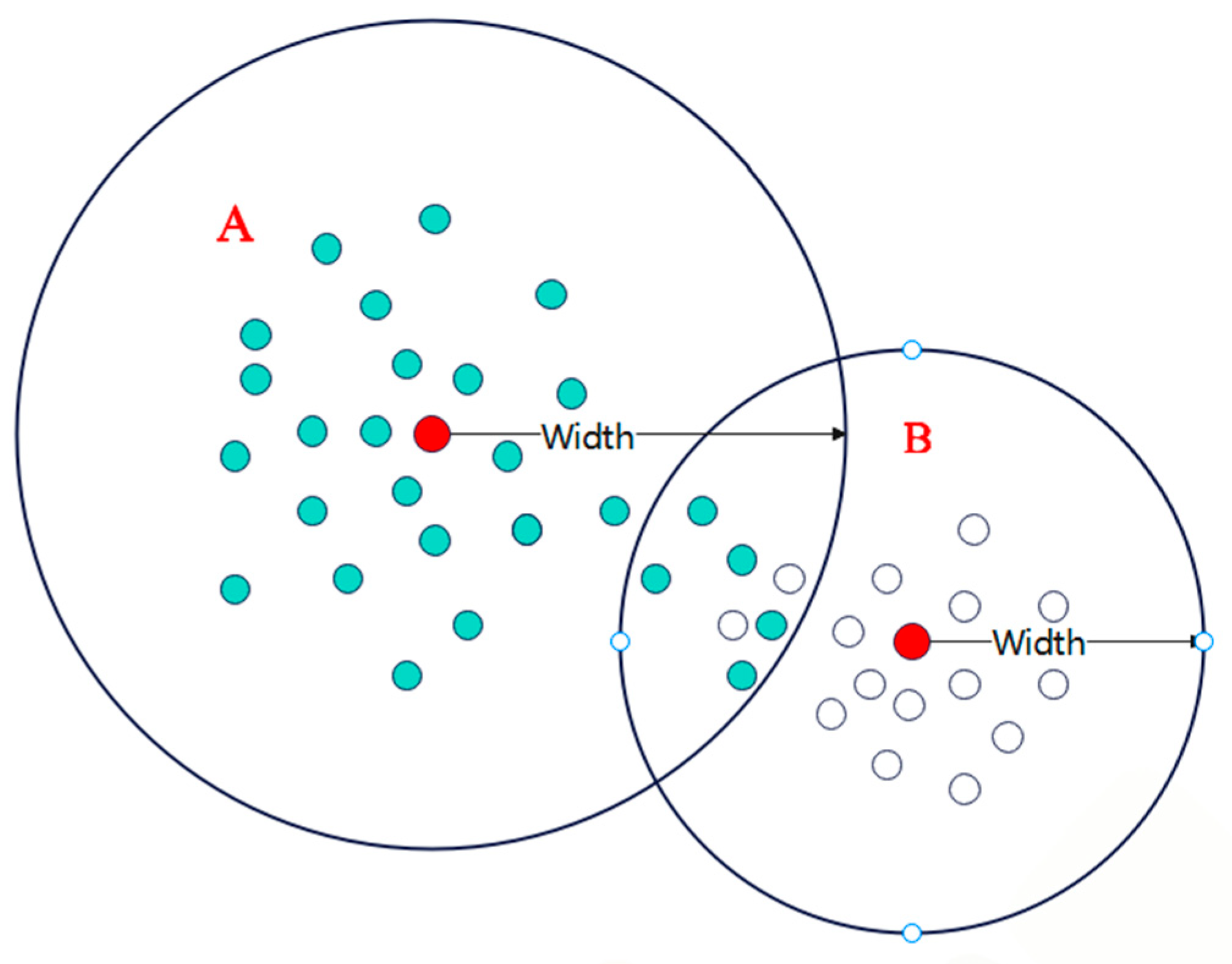
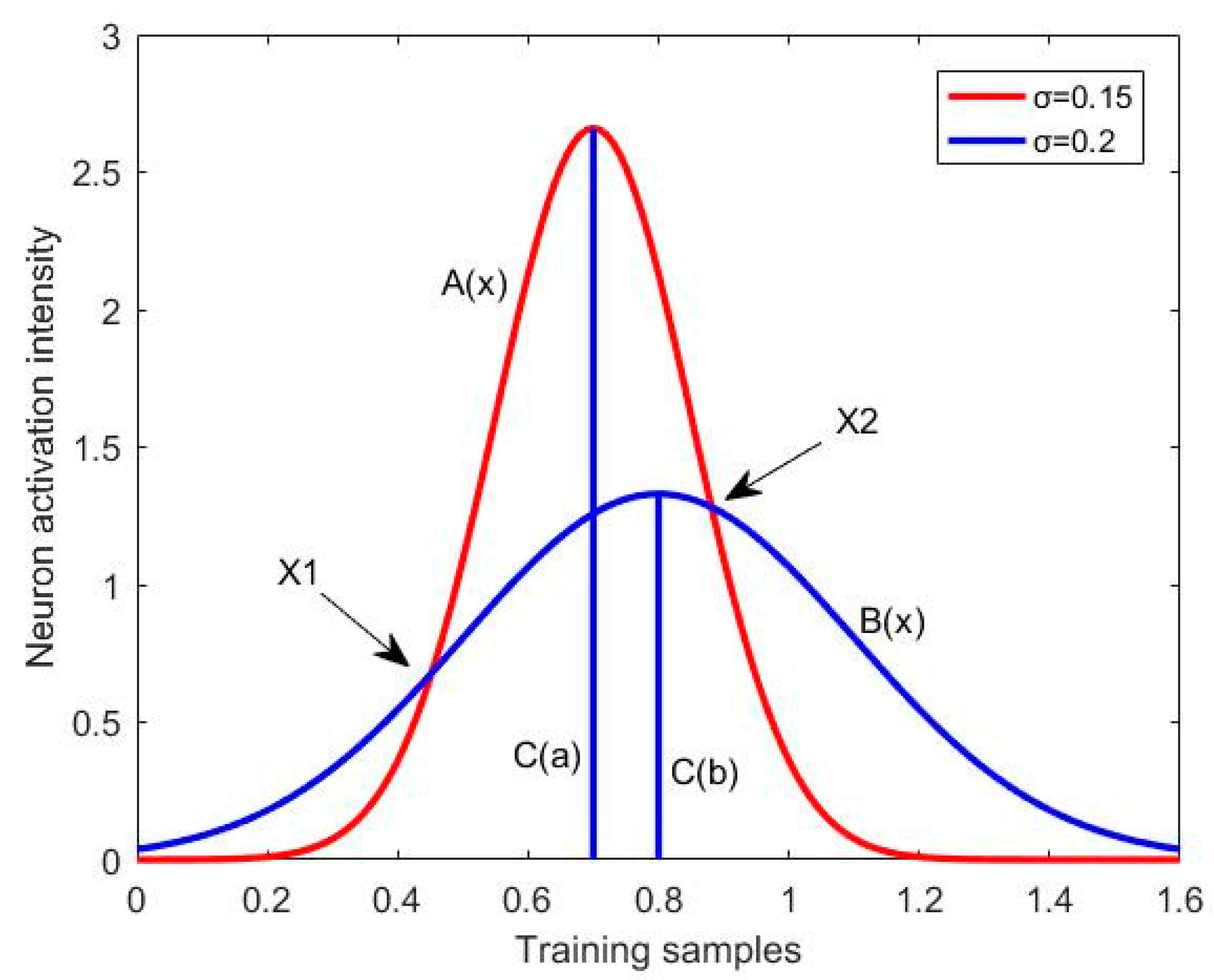
3.1.2. Adjustment of Neuron Width
3.1.3. Neuron Deletion
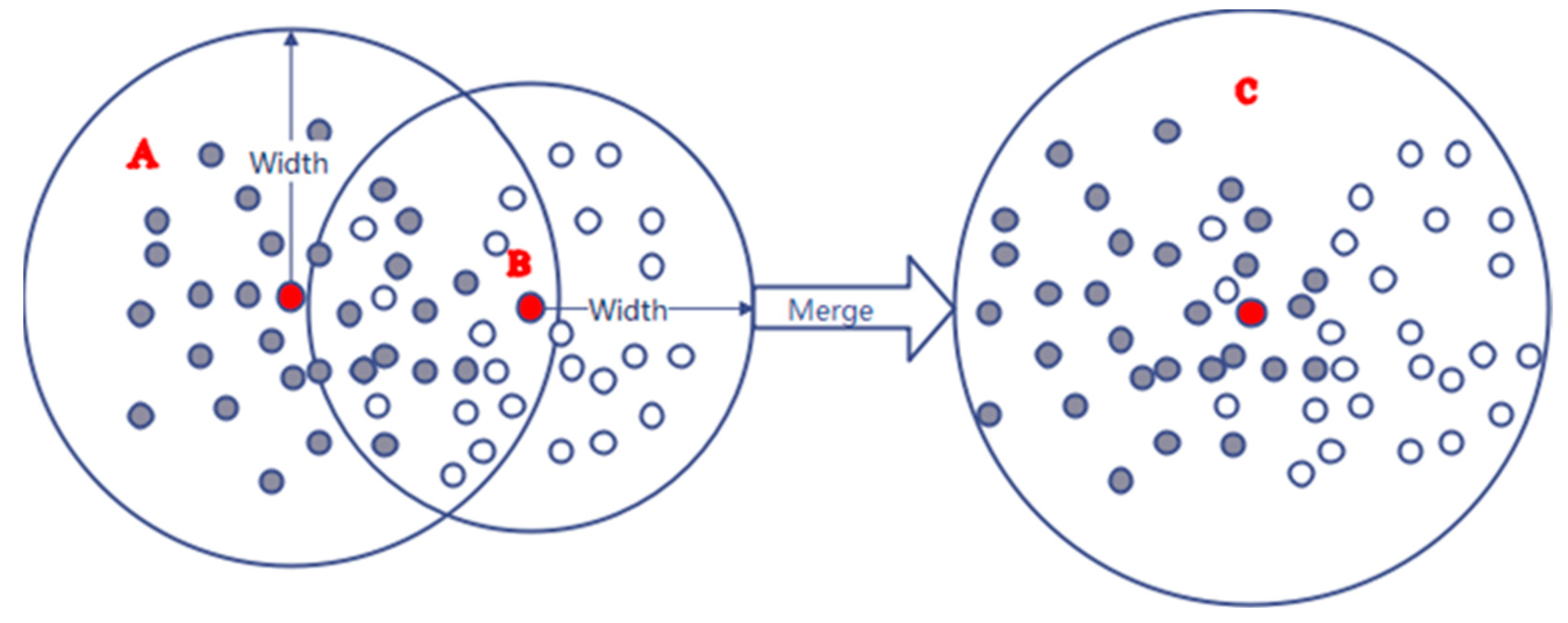
3.1.4. Merging of Network-Rule Neurons
3.2. Adaptive Second-Order Learning Algorithm
| Algorithm 1: Pseudocodes for constructing SOFNN-CA network |
| Input: The input data in the training set are generally four inputs. Output: Single output datum in training set. |
|
3.3. Convergence Analysis
3.3.1. Under a Fixed Structure
3.3.2. Structural Dynamic Adjustment Phase
4. Simulation Analysis
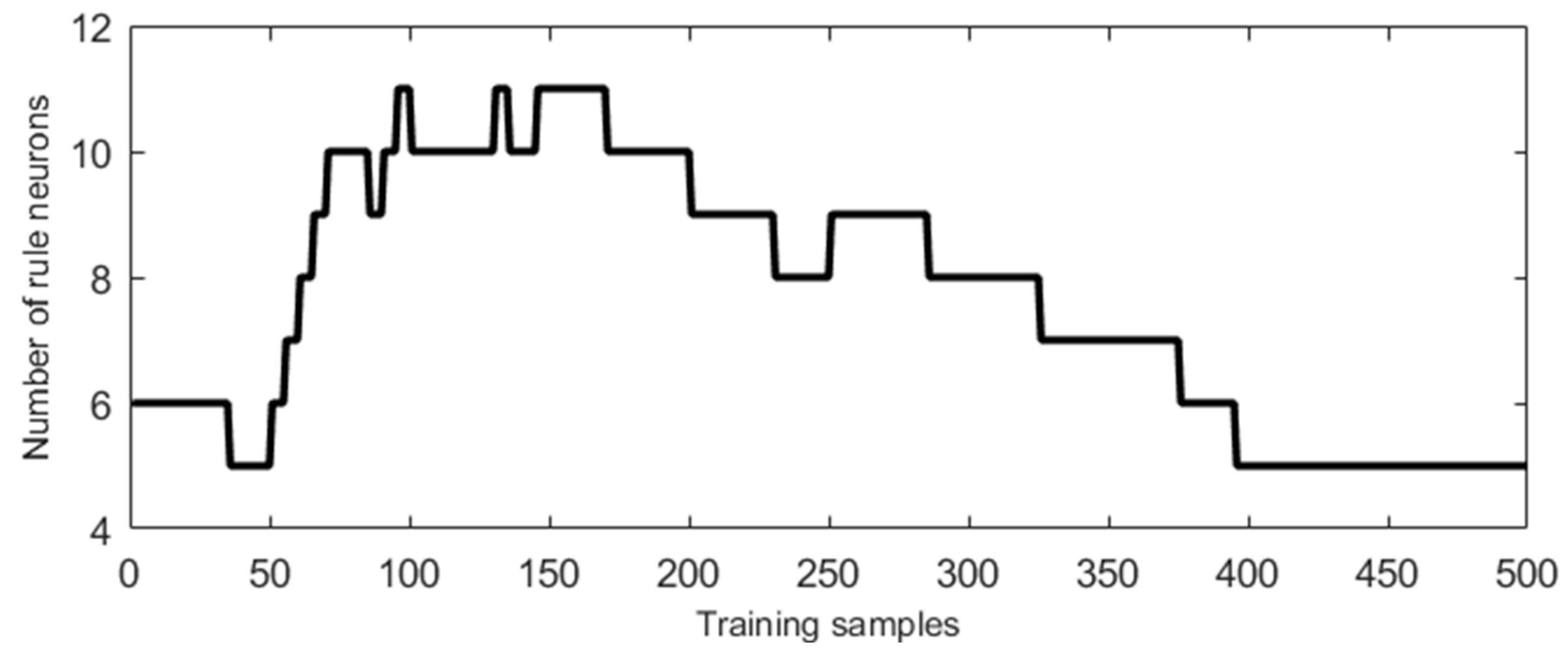
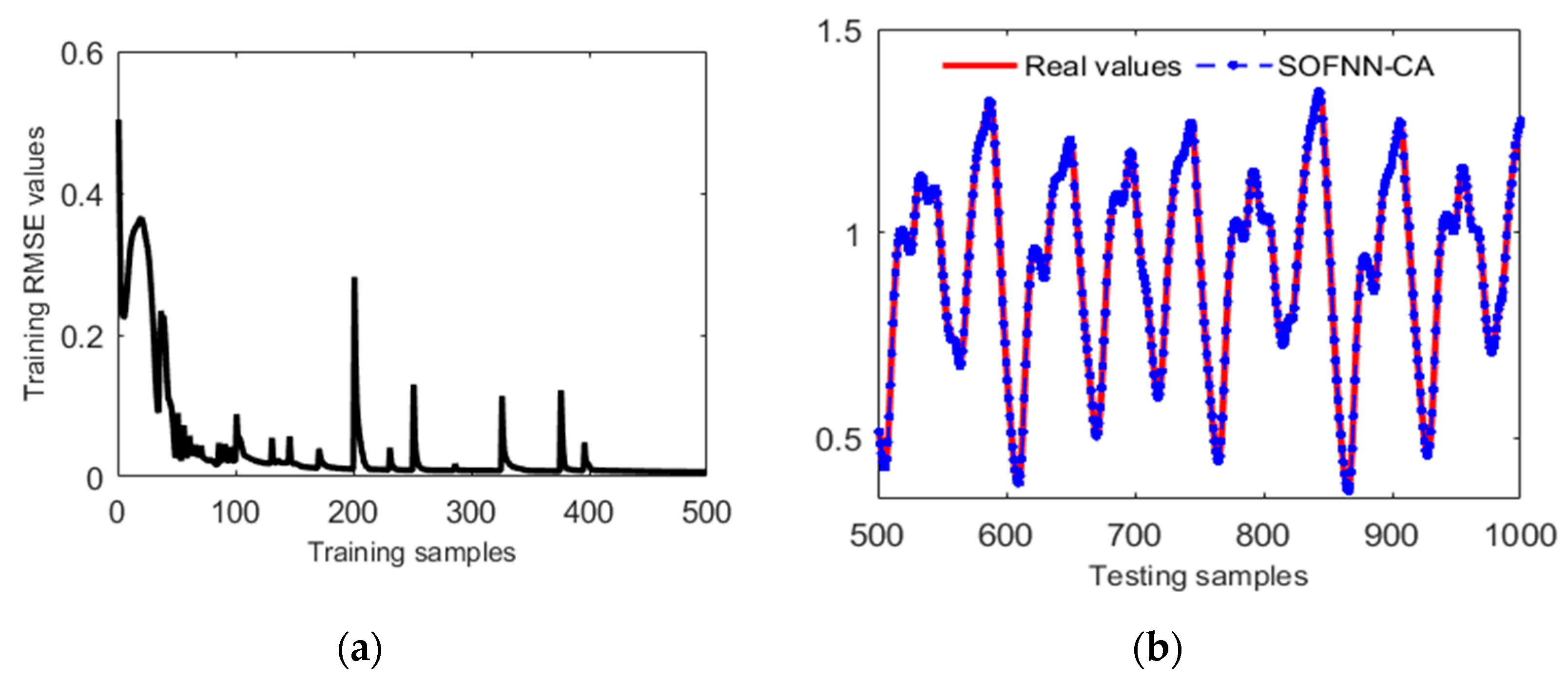
4.1. Mackey–Glass Time-Series Forecasting
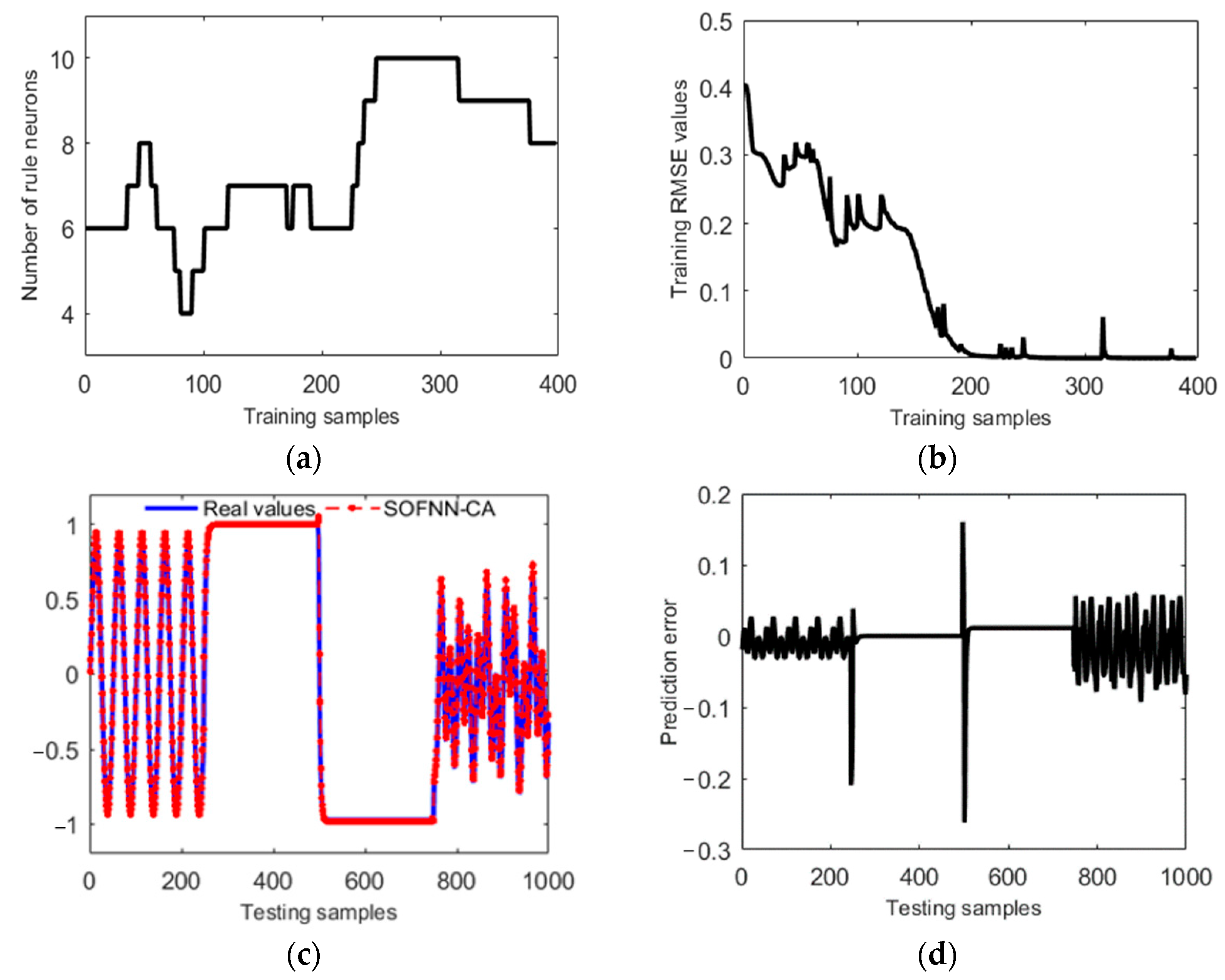
4.2. Identification of Nonlinear Systems
4.3. Combined Cycle Power-Plant Power-Output Forecast
4.4. Prediction of Benzene Levels in Air
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, P.; Sun, F.; Liu, Y.; Wang, Y.; Li, G.; Che, Y. Mapping future droughts under global warming across China: A combined multi-timescale meteorological drought index and SOM-Kmeans approach. Weather. Clim. Extrem. 2021, 31, 100304. [Google Scholar] [CrossRef]
- Iyer, H. Model Discrimination for Nonlinear Regression Models. Technometrics 1990, 32, 448–450. [Google Scholar] [CrossRef]
- Aldeen, M.; Crusca, F. Modular Modelling of Nonlinear Complex Systems. In Proceedings of the 2003 4th International Conference on Control and Automation Proceedings, Montreal, QC, Canada, 12 June 2003; pp. 698–702. [Google Scholar]
- Sachtleben, R.; Peleska, J. Effective grey-box testing with partial FSM models. Softw. Test. Verif. Rel. 2022, 32, e1806. [Google Scholar] [CrossRef]
- Cecati, C.; Kolbusz, J.; Rozycki, P.; Siano, P.; Wilamowski, B.M. A Novel RBF Training Algorithm for Short-Term Electric Load Forecasting and Comparative Studies. IEEE Trans. Ind. Electron. 2015, 62, 6519–6529. [Google Scholar] [CrossRef]
- Akhtar, I.; Kirmani, S.; Ahmad, M.; Ahmad, S. Average Monthly Wind Power Forecasting Using Fuzzy Approach. IEEE Access 2021, 9, 30426–30440. [Google Scholar] [CrossRef]
- Czarnowski, I.; Jedrzejowicz, J.; Jedrzejowicz, P. Designing RBFNs Structure Using Similarity-Based and Kernel-Based Fuzzy C-Means Clustering Algorithms. IEEE Access 2020, 9, 4411–4422. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Y.; Duan, W.; Zhao, H. Nonlinear systems modelling based on self-organizing fuzzy neural network with hierarchical pruning scheme. Appl. Soft Comput. 2020, 95, 106516. [Google Scholar] [CrossRef]
- Gholami, V.; Khaleghi, M.R.; Sahour, H.; Amri, M.A.H. Prediction of soil splash erosion using fuzzy network-CANFIS. Arab. J. Geosci. 2022, 15, 1604. [Google Scholar] [CrossRef]
- Han, H.-G.; Lin, Z.-L.; Qiao, J.-F. Modeling of nonlinear systems using the self-organizing fuzzy neural network with adaptive gradient algorithm. Neurocomputing 2017, 266, 566–578. [Google Scholar] [CrossRef]
- Wu, S.; Er, M.J.; Ni, M.; Leithead, W.E. A fast approach for automatic generation of fuzzy rules by generalized dynamic fuzzy neural networks. In Proceedings of the 2000 American Control Conference (ACC), Chicago, IL, USA, 28–30 June 2000; Volume 4, pp. 2453–2457. [Google Scholar]
- Wu, S.; Er, M.J. Dynamic fuzzy neural networks-a novel approach to function approximation. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2000, 30, 358–364. [Google Scholar] [CrossRef]
- Han, H.; Zhang, L.; Wu, X.; Qiao, J. An Efficient Second-Order Algorithm for Self-Organizing Fuzzy Neural Networks. IEEE Trans. Cybern. 2017, 49, 14–26. [Google Scholar] [CrossRef]
- Han, H.; Wu, X.-L.; Qiao, J.-F. Nonlinear Systems Modeling Based on Self-Organizing Fuzzy-Neural-Network With Adaptive Computation Algorithm. IEEE Trans. Cybern. 2013, 44, 554–564. [Google Scholar] [CrossRef]
- Wang, G.; Qiao, J. An Efficient Self-Organizing Deep Fuzzy Neural Network for Nonlinear System Modeling. IEEE Trans. Fuzzy Syst. 2021, 30, 1. [Google Scholar] [CrossRef]
- Lughofer, E. Evolving fuzzy systems: Fundamentals, reliability, interpretability, useability and applications. In Proceedings of the 2015 7th International Joint Conference on Computational Intelligence (IJCCI), Lisbon, Portugal, 12–14 November 2015; p. 11. [Google Scholar]
- Škrjanc, I.; Iglesias, J.A.; Sanchis, A.; Leite, D.F.; Lughofer, E.D.; Gomide, F. Evolving fuzzy and neuro-fuzzy approaches in clustering, regression, identification, and classification: A Survey. Inf. Sci. 2019, 490, 344–368. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Lee, S.-J.; Ouyang, C.-S.; Wu, C.-H. Air quality prediction by neuro-fuzzy modeling approach. Appl. Soft Comput. 2019, 86, 105898. [Google Scholar] [CrossRef]
- Leng, G.; McGinnity, T.M.; Prasad, G. Design for Self-Organizing Fuzzy Neural Networks Based on Genetic Algorithms. IEEE Trans. Fuzzy Syst. 2006, 14, 755–766. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, H.; Zhang, Y. Nonlinear system modeling using self-organizing fuzzy neural networks for industrial applications. Appl. Intell. 2020, 50, 1657–1672. [Google Scholar] [CrossRef]
- Lughofer, E. Improving the robustness of recursive consequent parameters learning in evolving neuro-fuzzy systems. Inf. Sci. 2020, 545, 555–574. [Google Scholar] [CrossRef]
- Yu, H.; Wilamowski, B.M. Neural Network Training with Second Order Algorithms. In Human—Computer Systems Interaction: Backgrounds and Applications 2; Hippe, Z.S., Kulikowski, J.L., Mroczek, T., Eds.; Springer: Berlin, Heidelberg, 2012; Volume 99, pp. 463–476. [Google Scholar]
- Qiao, J.; Meng, X.; Li, W. An incremental neuronal-activity-based RBF neural network for nonlinear system modeling. Neurocomputing 2018, 302, 1–11. [Google Scholar] [CrossRef]
- Caron, M.; Misra, I.; Mairal, J.; Goyal, P.; Bojanowski, P.; Joulin, A. Unsupervised Learning of Visual Features by Contrasting Cluster Assignments. arXiv 2021, arXiv:2006.09882. [Google Scholar]
- Fei, J.; Wang, T. Adaptive fuzzy-neural-network based on RBFNN control for active power filter. Int. J. Mach. Learn. Cybern. 2018, 10, 1139–1150. [Google Scholar] [CrossRef]
- Milstein, J.N.; Koch, C. Dynamic Moment Analysis of the Extracellular Electric Field of a Biologically Realistic Spiking Neuron. Neural Comput. 2008, 20, 2070–2084. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lughofer, E.; Cernuda, C.; Kindermann, S.; Pratama, M. Generalized smart evolving fuzzy systems. Evol. Syst. 2015, 6, 269–292. [Google Scholar] [CrossRef]
- Ghorbani, H. Mahalanobis distance and its application for detecting multivariate outliers. Facta Univ. Ser. Math. Inform. 2019, 34, 583–595. [Google Scholar] [CrossRef]
- Xie, S.; Xie, Y.; Huang, T.; Gui, W.; Yang, C. Generalized Predictive Control for Industrial Processes Based on Neuron Adaptive Splitting and Merging RBF Neural Network. IEEE Trans. Ind. Electron. 2018, 66, 1192–1202. [Google Scholar] [CrossRef]
- Lughofer, E.; Bouchot, J.-L.; Shaker, A. On-line elimination of local redundancies in evolving fuzzy systems. Evol. Syst. 2011, 2, 165–187. [Google Scholar] [CrossRef]
- Li, W.; Qiao, J.; Zeng, X.-J. Online and Self-Learning Approach to the Identification of Fuzzy Neural Networks. IEEE Trans. Fuzzy Syst. 2020, 30, 649–662. [Google Scholar] [CrossRef]
- Li, W.; Qiao, J.; Zeng, X.-J. Accurate similarity analysis and computing of Gaussian membership functions for FNN simplification. In Proceedings of the 2015 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, 15–17August 2015; pp. 402–409. [Google Scholar]
- Wilamowski, B.M. Modified EBP algorithm with instant training of the hidden layer. In Proceedings of the IECON’97 23rd International Conference on Industrial Electronics, Control, and Instrumentation (Cat. No.97CH36066), New Orleans, LA, USA, 14 November 1997; Volume 3, pp. 1097–1101. [Google Scholar]
- Yu, H.; Wilamowski, B.M. Levenberg–Marquardt Training. In Intelligent Systems; Wilamowski, B.M., Irwin, J.D., Eds.; CRC Press: Boca Raton, FL, USA, 2018; pp. 12–16. [Google Scholar]
- Kreinovich, V.; Nguyen, H.T.; Ouncharoen, R. How to Estimate Forecasting Quality: A System-Motivated Derivation of Symmetric Mean Absolute Percentage Error (SMAPE) and Other Similar Characteristics. 2014. Available online: https://scholarworks.utep.edu/cs_techrep/865/ (accessed on 6 August 2022).
- Glass, L.; Mackey, M. Mackey-Glass equation. Scholarpedia 2010, 5, 6908. [Google Scholar] [CrossRef]
- Malek, H.; Ebadzadeh, M.M.; Rahmati, M. Three new fuzzy neural networks learning algorithms based on clustering, training error and genetic algorithm. Appl. Intell. 2012, 37, 280–289. [Google Scholar] [CrossRef]
- Juang, C.-F.; Lin, Y.-Y.; Tu, C.-C. A recurrent self-evolving fuzzy neural network with local feedbacks and its application to dynamic system processing. Fuzzy Sets Syst. 2010, 161, 2552–2568. [Google Scholar] [CrossRef]
- Abiyev, R.H.; Kaynak, O. Fuzzy Wavelet Neural Networks for Identification and Control of Dynamic Plants—A Novel Structure and a Comparative Study. IEEE Trans. Ind. Electron. 2008, 55, 3133–3140. [Google Scholar] [CrossRef]
- Tüfekci, P. Prediction of full load electrical power output of a base load operated combined cycle power plant using machine learning methods. Int. J. Electr. Power Energy Syst. 2014, 60, 126–140. [Google Scholar] [CrossRef]
- Wang, N. A Generalized Ellipsoidal Basis Function Based Online Self-constructing Fuzzy Neural Network. Neural Process. Lett. 2011, 34, 13–37. [Google Scholar] [CrossRef]
- De Vito, S.; Massera, E.; Piga, M.; Martinotto, L.; Di Francia, G. On field calibration of an electronic nose for benzene estimation in an urban pollution monitoring scenario. Sens. Actuators B 2008, 129, 750–757. [Google Scholar] [CrossRef]
- De Vito, S.; Piga, M.; Martinotto, L.; Di Francia, G. CO, NO2 and NOx urban pollution monitoring with on-field calibrated electronic nose by automatic bayesian regularization. Sens. Actuators B 2009, 143, 182–191. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, Y.; Qiao, J. An adaptive task-oriented RBF network for key water quality parameters prediction in wastewater treatment process. Neural Comput. Appl. 2021, 33, 11401–11414. [Google Scholar] [CrossRef]

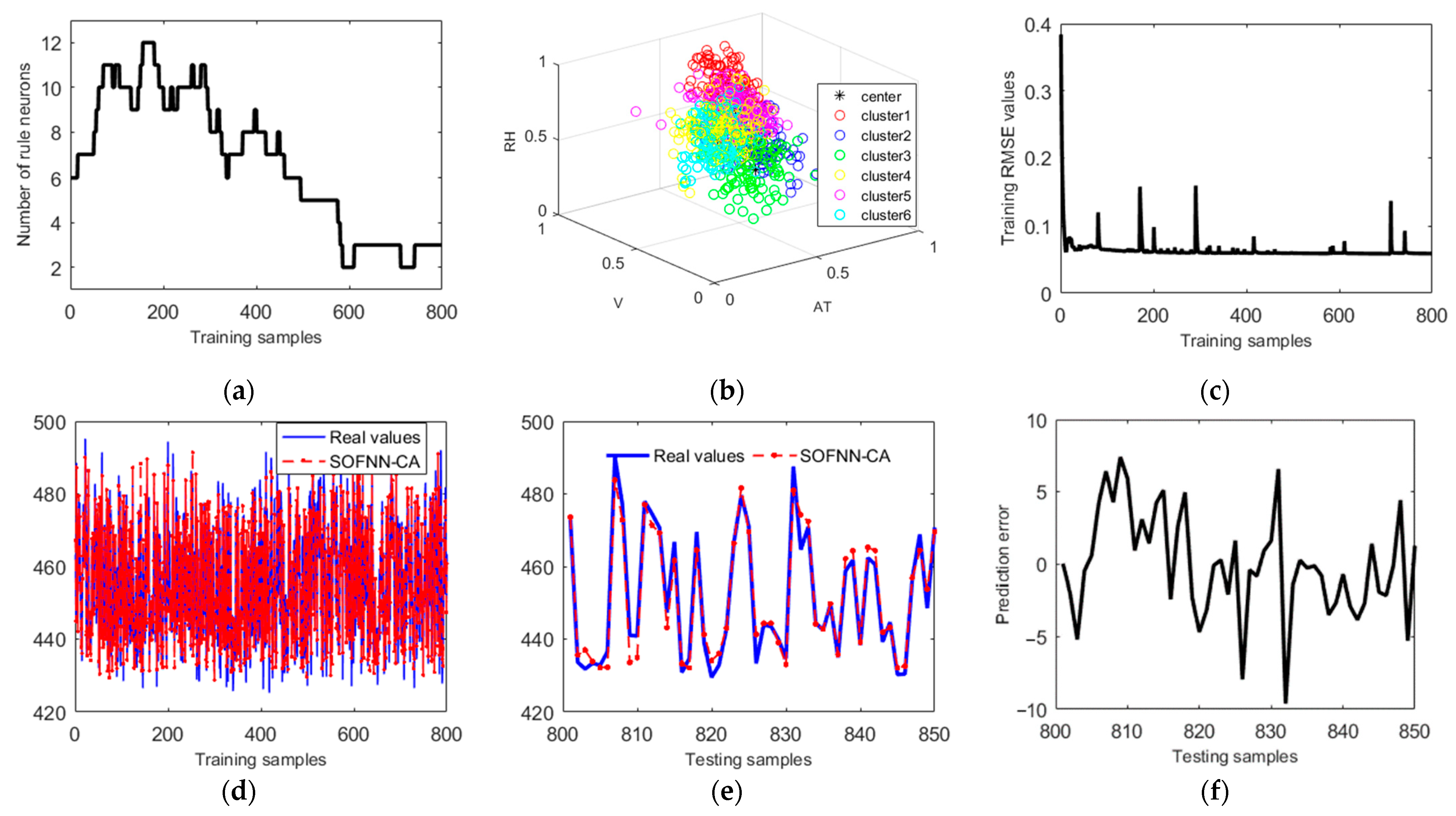
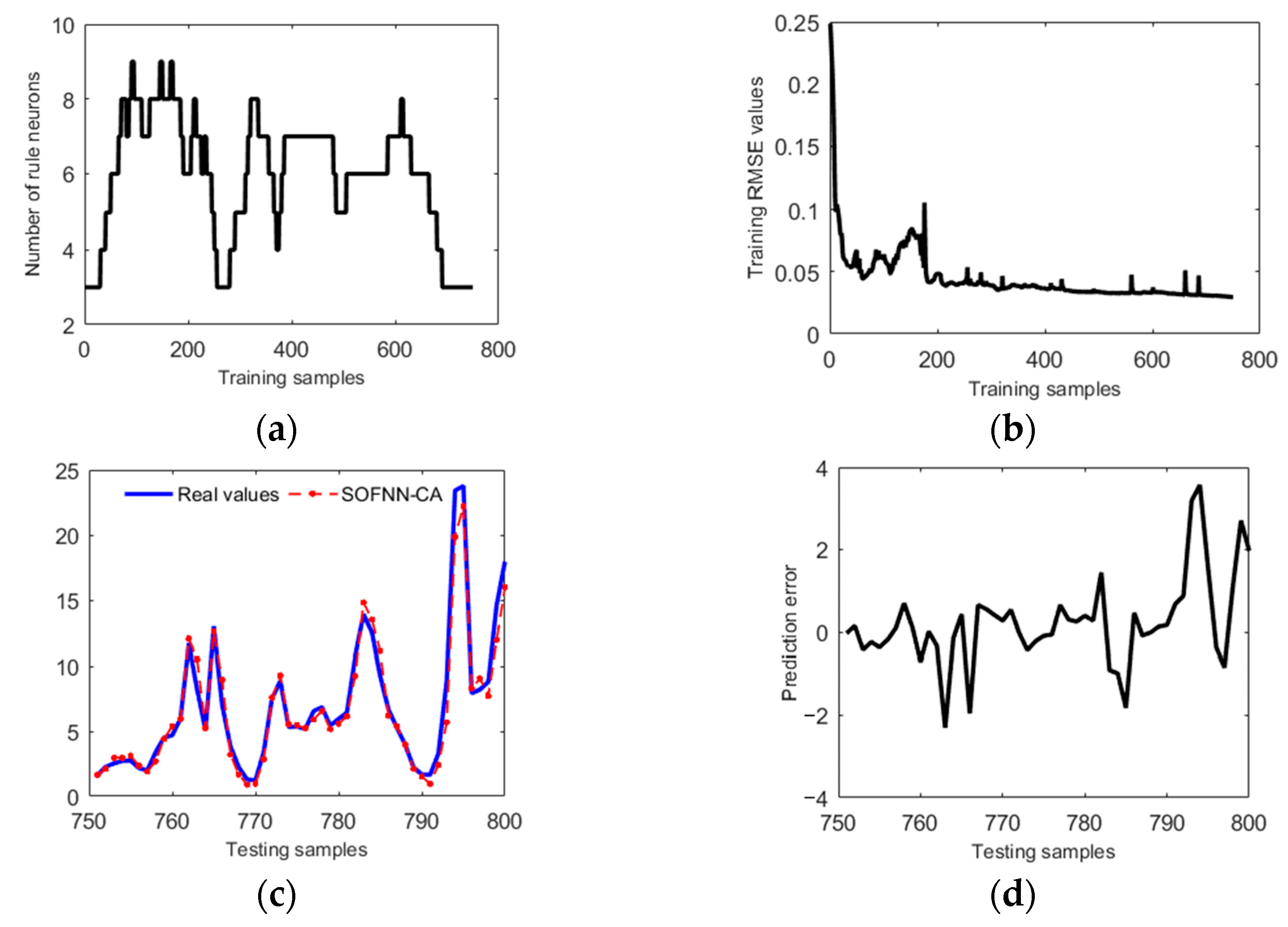
| Method | Rule Neurons | Testing RMSE | Testing APE | CPU Times (s) |
|---|---|---|---|---|
| SOFNN-CA | 5 | 0.0058 | 0.0055 | 6.62 |
| SOFNN-ALA [20] | 6 | 0.0066 | 0.0058 | 7.24 |
| SOFNN-AGA [10] | 6 | 0.0119 | 0.0076 | 21.20 |
| SOFNN-ACA [14] | 7 | 0.0201 | 0.0076 | 27.33 |
| SOFNN-GA [19] | 7 | 0.0132 | 0.0094 | 168.35 |
| FNN-EBP [37] | 8 | 0.0142 | 0.0131 | 37.05 |
| Method | Rule Neurons | Testing RMSE | Testing APE | CPU Times (s) |
|---|---|---|---|---|
| SOFNN-CA | 8 | 0.0171 | 0.0490 | 5.11 |
| SOFNN-ALA [20] | 6 | 0.0297 | 0.0954 | 3.73 |
| SOFNN-AGA [10] | 6 | 0.0090 | 0.0464 | 13.10 |
| RSEFNN-LF [38] | 4 1 | 0.0280 1 | 0.0652 1 | 35.31 1 |
| FWNN [39] | 5 1 | 0.0201 1 | 0.0904 1 | 37.72 1 |
| Method | Rule Neurons | Training RMSE | Testing RMSE | CPU Times (s) |
|---|---|---|---|---|
| SOFNN-CA | 3 | 4.1616 | 3.6034 | 11.26 |
| SOFNN-HPS [8] | 7 | 4.0718 | 3.7469 | - |
| GEBF-OSFNN [41] | 9 1 | 4.2483 1 | 3.8327 1 | - |
| GD-FNN [11] | 15 1 | 3.8945 1 | 4.8510 1 | - |
| D-FNN [12] | 19 1 | 3.7485 1 | 4.2545 1 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Wang, Z. Self-Organized Fuzzy Neural Network Nonlinear System Modeling Method Based on Clustering Algorithm. Appl. Sci. 2022, 12, 11435. https://doi.org/10.3390/app122211435
Zhang T, Wang Z. Self-Organized Fuzzy Neural Network Nonlinear System Modeling Method Based on Clustering Algorithm. Applied Sciences. 2022; 12(22):11435. https://doi.org/10.3390/app122211435
Chicago/Turabian StyleZhang, Tong, and Zhendong Wang. 2022. "Self-Organized Fuzzy Neural Network Nonlinear System Modeling Method Based on Clustering Algorithm" Applied Sciences 12, no. 22: 11435. https://doi.org/10.3390/app122211435
APA StyleZhang, T., & Wang, Z. (2022). Self-Organized Fuzzy Neural Network Nonlinear System Modeling Method Based on Clustering Algorithm. Applied Sciences, 12(22), 11435. https://doi.org/10.3390/app122211435









