Predicting the Wafer Material Removal Rate for Semiconductor Chemical Mechanical Polishing Using a Fusion Network
Abstract
1. Introduction
- The proposed method is a deep learning model that can incorporate domain knowledge into the model by encoding the knowledge as shallow features. Additionally, the remaining features can go through a deep neural network to learn discriminative feature embeddings.
- The experiments are performed on the dataset from the 2016 PHM Data Challenge. To the best of our knowledge, the performance based on the proposed model outperforms all other methods in the existing literature.
- Finally, the prediction accuracy of the proposed method is demonstrated through extensive experiments.
2. Related Work
3. Proposed Method
3.1. Dataset
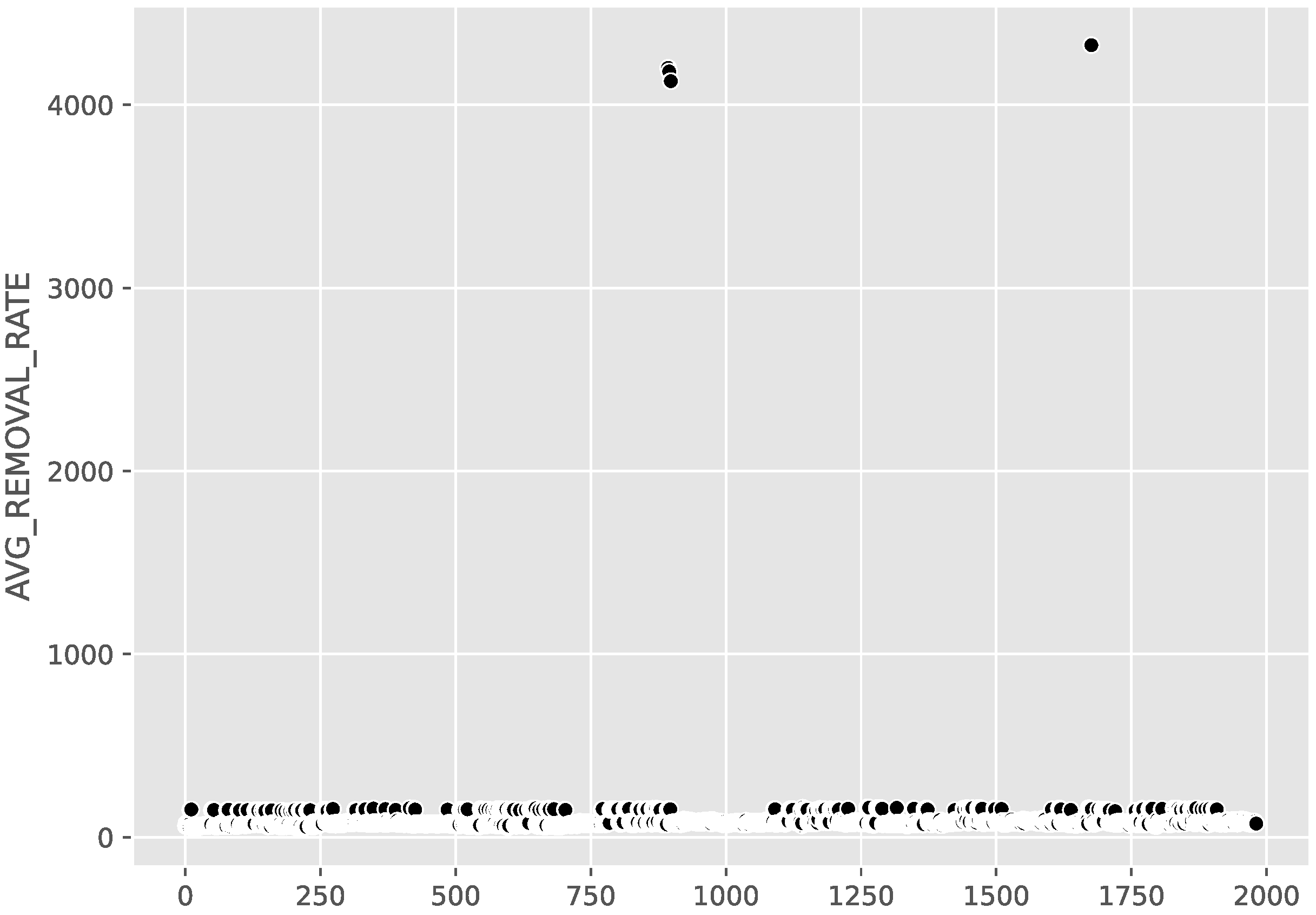
3.2. Outlier Detection
3.3. Feature Engineering
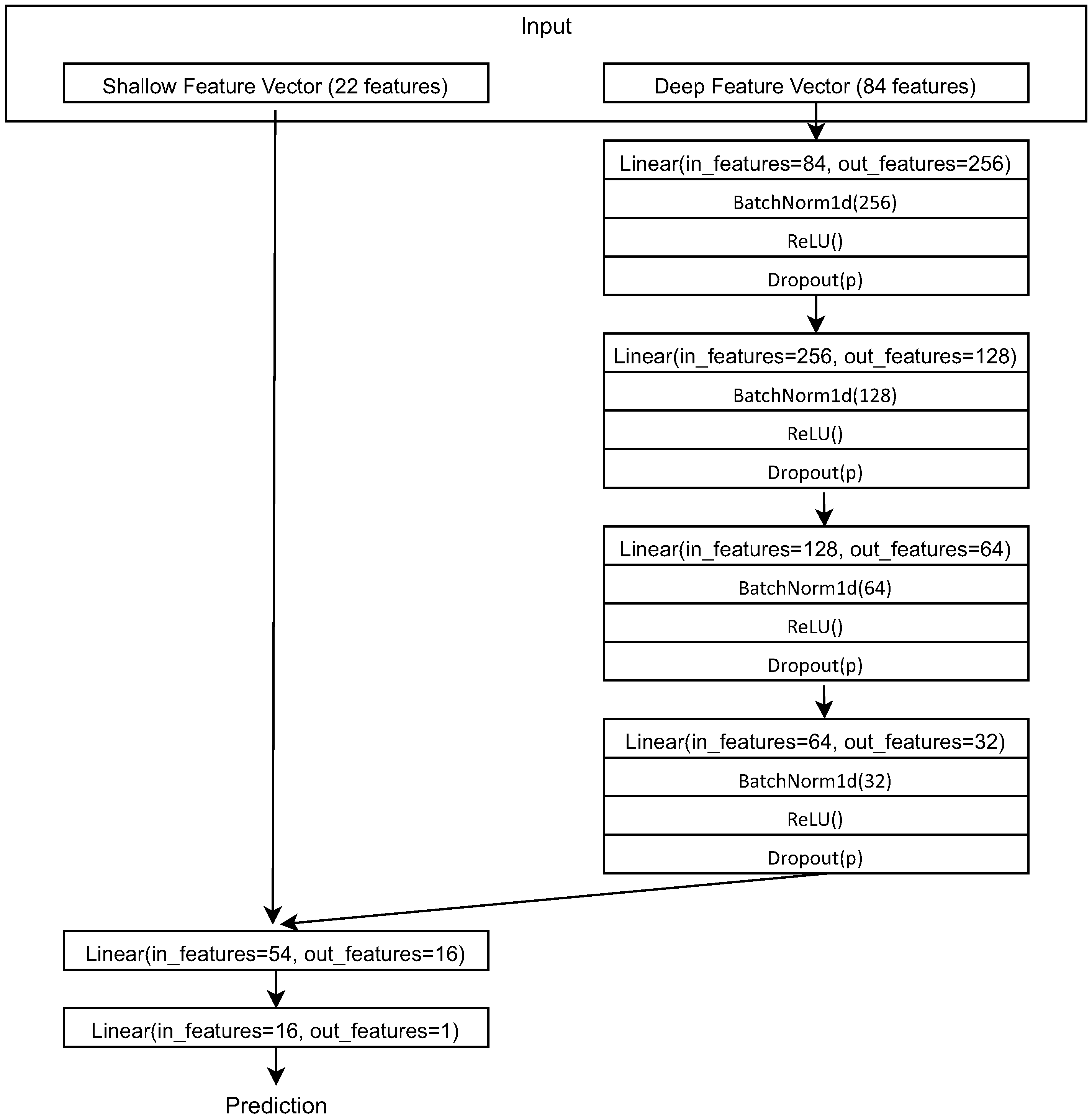
3.4. Fusion Network
4. Results and Discussions
4.1. Comparison Methods
4.2. Evaluation Metric
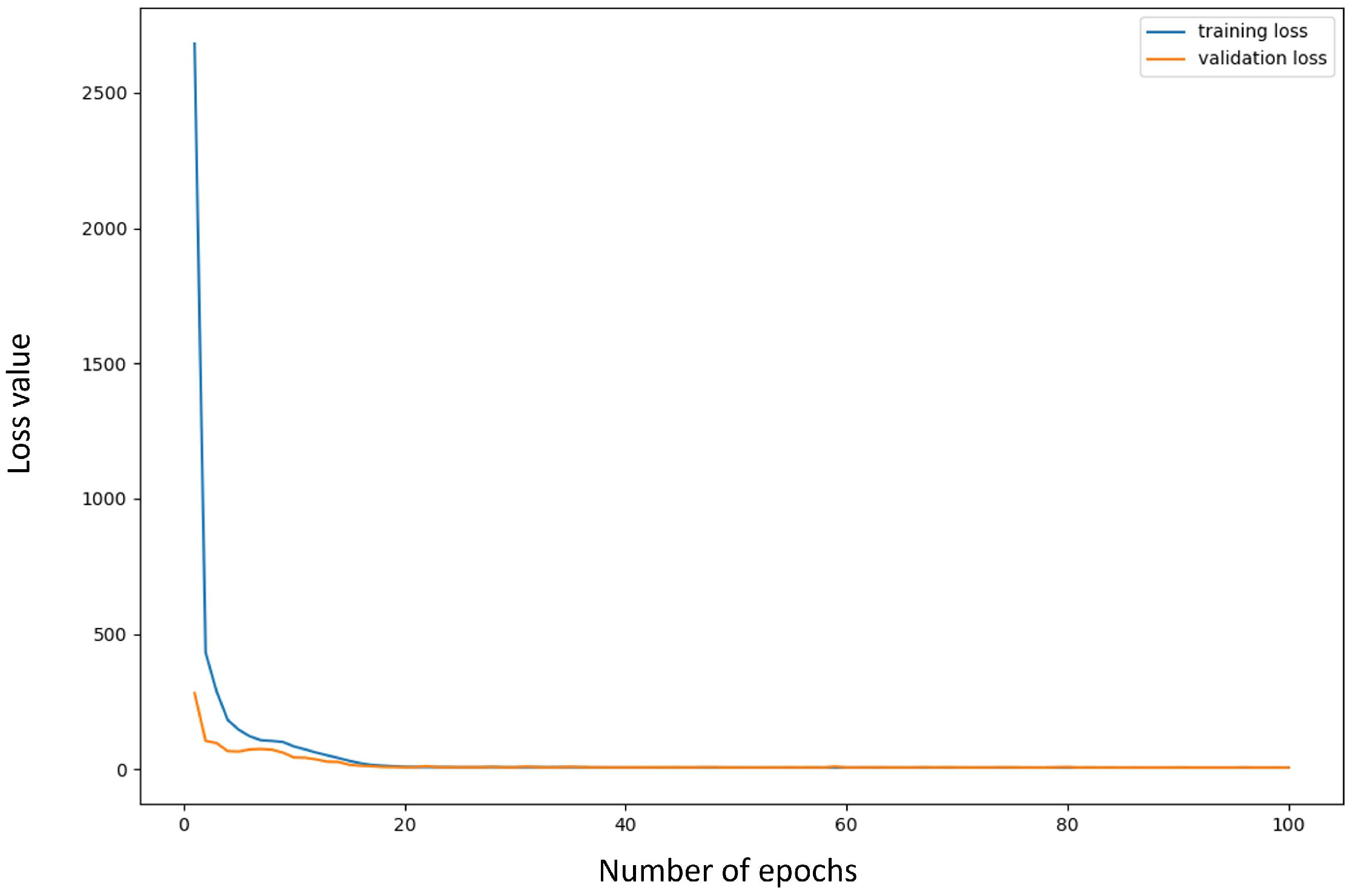
4.3. Experimental Results
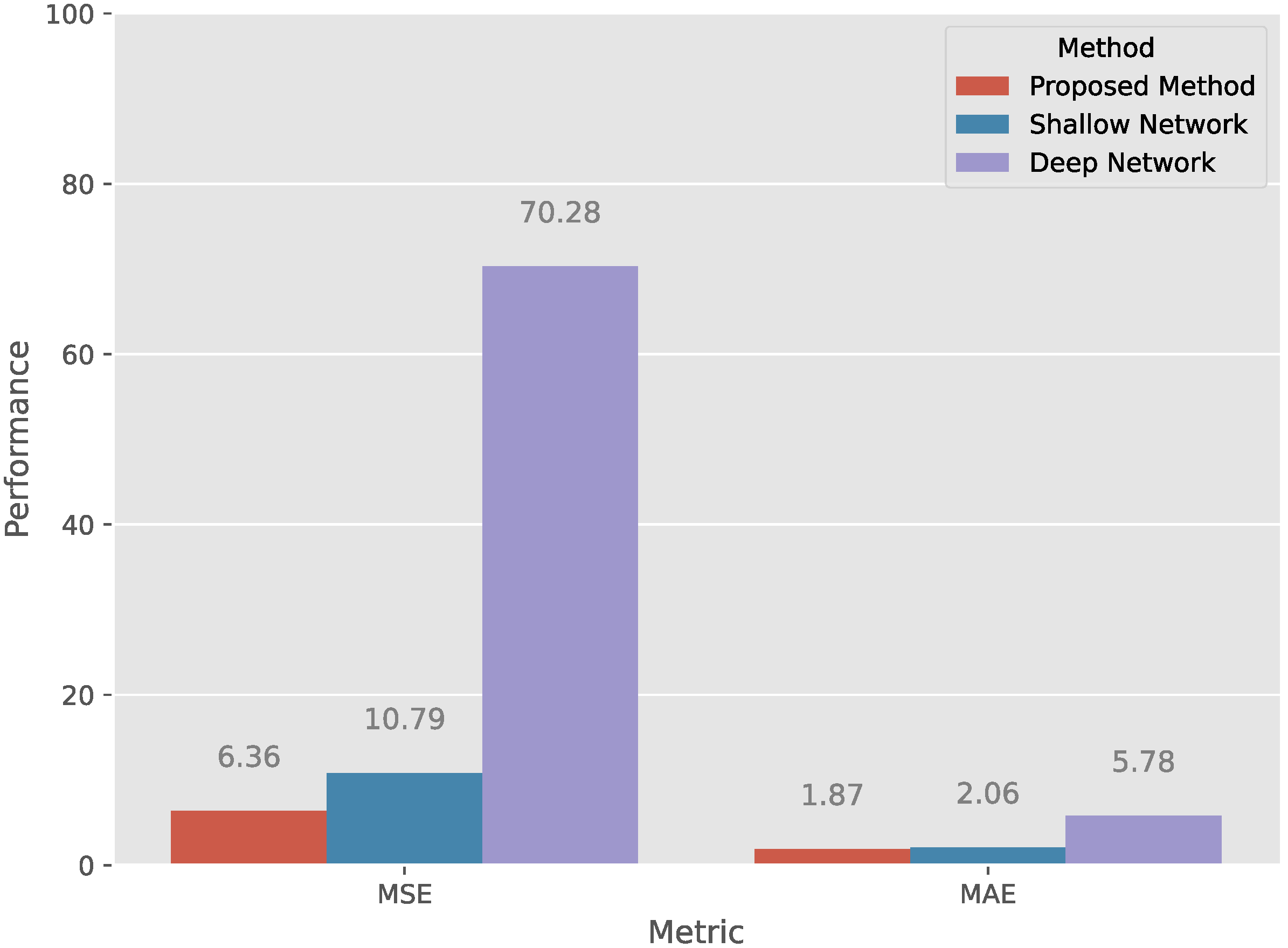
4.4. Fusion Network vs. Shallow Network vs. Deep Network
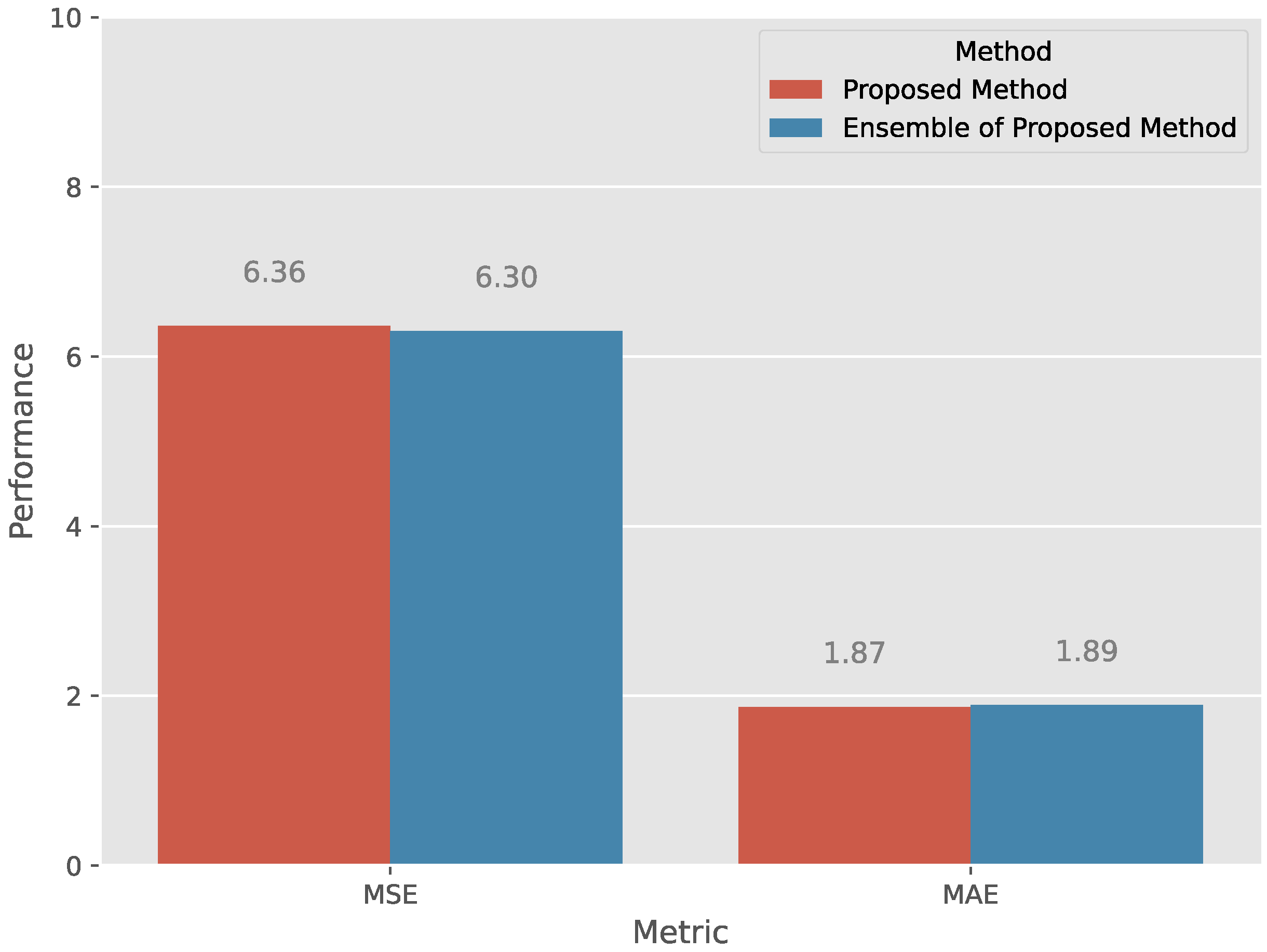
4.5. Ensemble Learning
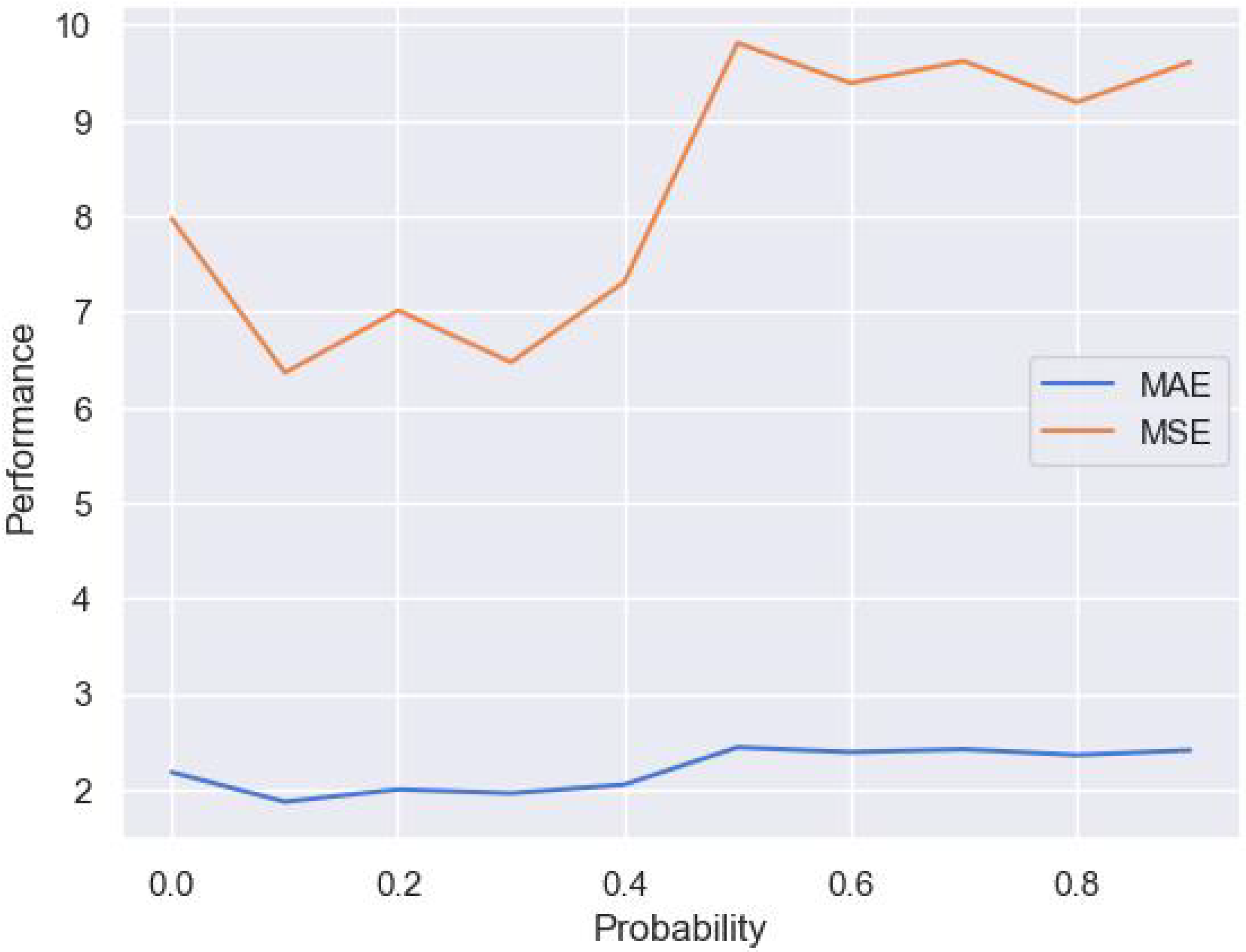
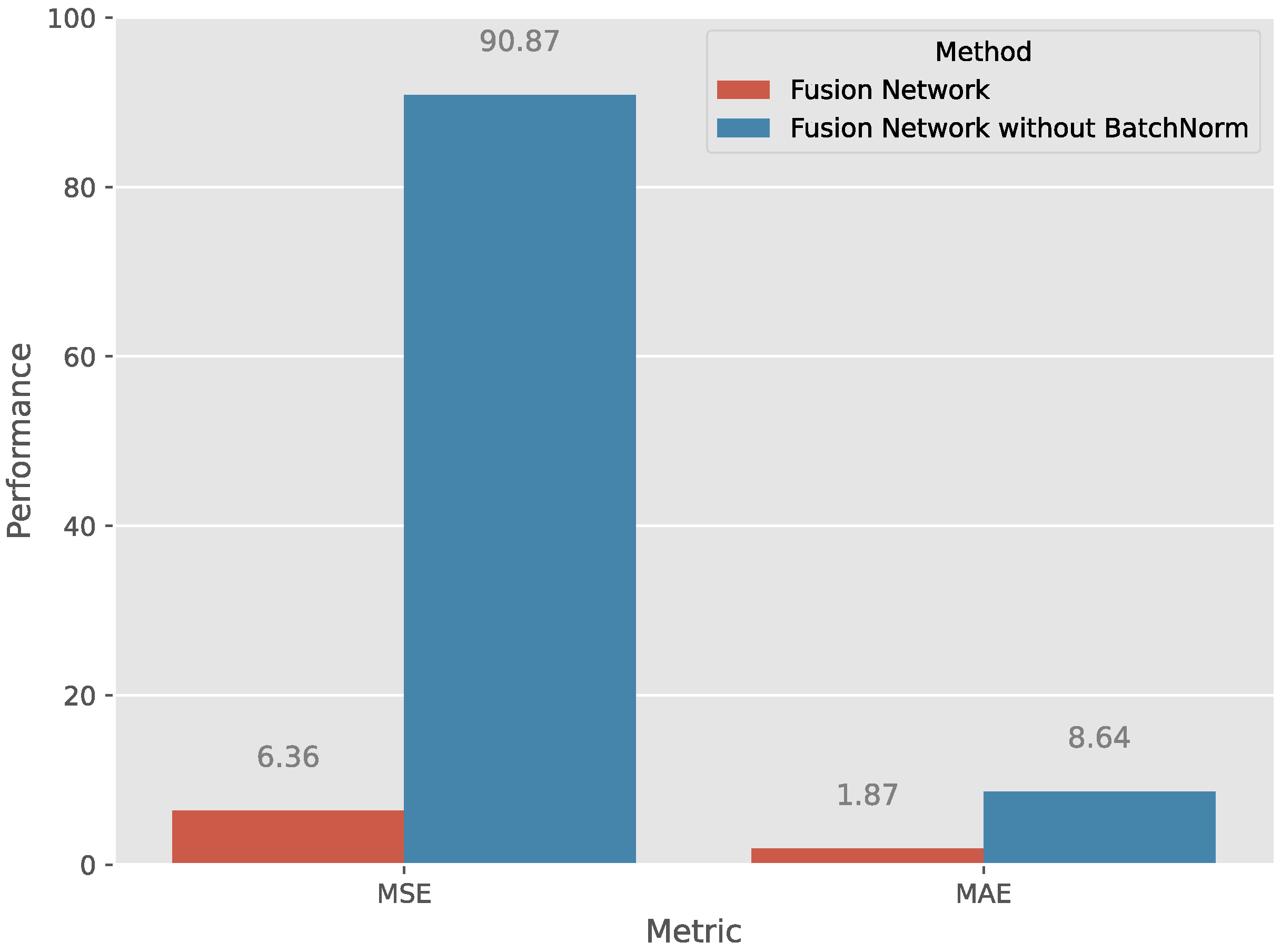
4.6. The Impact of Dropout Probability and Batch Normalization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, W.T.; Blue, J.; Roussy, A.; Pinaton, J.; Reis, M.S. A Structure Data-Driven Framework for Virtual Metrology Modeling. IEEE Trans. Autom. Sci. Eng. 2019, 17, 1297–1306. [Google Scholar] [CrossRef]
- Cho, Y.; Liu, P.; Jeon, S.; Lee, J.; Bae, S.; Hong, S.; Kim, Y.H.; Kim, T. Simulation and Experimental Investigation of the Radial Groove Effect on Slurry Flow in Oxide Chemical Mechanical Polishing. Appl. Sci. 2022, 12, 4339. [Google Scholar] [CrossRef]
- Duan, Y.; Liu, M.; Dong, M.; Wu, C. A two-stage clustered multi-task learning method for operational optimization in chemical mechanical polishing. J. Process Control 2015, 35, 169–177. [Google Scholar] [CrossRef]
- Zhao, Y.; Chang, L.; Kim, S. A mathematical model for chemical–mechanical polishing based on formation and removal of weakly bonded molecular species. Wear 2003, 254, 332–339. [Google Scholar] [CrossRef]
- Jeong, S.; Jeong, K.; Choi, J.; Jeong, H. Analysis of correlation between pad temperature and asperity angle in chemical mechanical planarization. Appl. Sci. 2021, 11, 1507. [Google Scholar] [CrossRef]
- Evans, C.J.; Paul, E.; Dornfeld, D.; Lucca, D.A.; Byrne, G.; Tricard, M.; Klocke, F.; Dambon, O.; Mullany, B.A. Material removal mechanisms in lapping and polishing. CIRP Ann. 2003, 52, 611–633. [Google Scholar] [CrossRef]
- Qin, C.; Hu, Z.; Tang, A.; Yang, Z.; Luo, S. An efficient material removal rate prediction model for cemented carbide inserts chemical mechanical polishing. Wear 2020, 452, 203293. [Google Scholar] [CrossRef]
- Park, S.; Lee, H. Electrolytically Ionized Abrasive-Free CMP (EAF-CMP) for Copper. Appl. Sci. 2021, 11, 7232. [Google Scholar] [CrossRef]
- Son, J.; Lee, H. Contact-area-changeable CMP conditioning for enhancing pad lifetime. Appl. Sci. 2021, 11, 3521. [Google Scholar] [CrossRef]
- Liu, H.; Wang, F.; Guo, D.; Liu, X.; Zhang, X.; Sun, F. Active Object Discovery and Localization Using Sound-Induced Attention. IEEE Trans. Ind. Inform. 2020, 17, 2021–2029. [Google Scholar] [CrossRef]
- Wang, Y.G.; Zhang, L.C.; Biddut, A. Chemical effect on the material removal rate in the CMP of silicon wafers. Wear 2011, 270, 312–316. [Google Scholar] [CrossRef]
- Jeng, Y.R.; Huang, P.Y. Impact of Abrasive Particles on the Material Removal Rate in CMP A Microcontact Perspective. Electrochem. Solid State Lett. 2004, 7, 40–43. [Google Scholar] [CrossRef]
- Oliver, M.R.; Schmidt, R.E.; Robinson, M. CMP pad surface roughness and CMP removal rate. In Proceedings of the 198th Meeting of the Electrochemical Society, 4th International Symposium on CMP, Phoenix, AZ, USA, 23–25 October 2000; Volume 26, pp. 77–83. [Google Scholar]
- Park, K.H.; Kim, H.J.; Chang, O.M.; Jeong, H.D. Effects of pad properties on material removal in chemical mechanical polishing. J. Mater. Process. Technol. 2007, 187, 73–76. [Google Scholar] [CrossRef]
- Ng, W.X.; Chan, H.K.; Teo, W.K.; Chen, I.M. Programming a robot for conformance grinding of complex shapes by capturing the tacit knowledge of a skilled operator. IEEE Trans. Autom. Sci. Eng. 2015, 14, 1020–1030. [Google Scholar] [CrossRef]
- Dambon, O.; Demmer, A.; Peters, J. Surface interactions in steel polishing for the precision tool making. CIRP Ann. 2006, 55, 609–612. [Google Scholar] [CrossRef]
- Oh, S.; Seok, J. An integrated material removal model for silicon dioxide layers in chemical mechanical polishing processes. Wear 2009, 266, 839–849. [Google Scholar] [CrossRef]
- Carvalho, T.P.; Soares, F.A.; Vita, R.; Francisco, R.d.P.; Basto, J.P.; Alcalá, S.G. A systematic literature review of machine learning methods applied to predictive maintenance. Comput. Ind. Eng. 2019, 137, 106024. [Google Scholar] [CrossRef]
- Dinh, T.Q.; Marco, J.; Greenwood, D.; Ahn, K.K.; Yoon, J.I. Data-based predictive hybrid driven control for a class of imperfect networked systems. IEEE Trans. Ind. Inform. 2018, 14, 5187–5199. [Google Scholar] [CrossRef]
- Wan, J.; Tang, S.; Li, D.; Wang, S.; Liu, C.; Abbas, H.; Vasilakos, A.V. A Manufacturing Big Data Solution for Active Preventive Maintenance. IEEE Trans. Ind. Inform. 2017, 13, 2039–2047. [Google Scholar] [CrossRef]
- Ibrahim, A.; Eltawil, A.; Na, Y.; El-Tawil, S. A machine learning approach for structural health monitoring using noisy data sets. IEEE Trans. Autom. Sci. Eng. 2019, 17, 900–908. [Google Scholar] [CrossRef]
- Purwins, H.; Barak, B.; Nagi, A.; Engel, R.; Höckele, U.; Kyek, A.; Cherla, S.; Lenz, B.; Pfeifer, G.; Weinzierl, K. Regression methods for virtual metrology of layer thickness in chemical vapor deposition. IEEE/ASME Trans. Mechatron. 2013, 19, 1–8. [Google Scholar] [CrossRef]
- Kourti, T. Application of latent variable methods to process control and multivariate statistical process control in industry. Int. J. Adapt. Control Signal Process. 2005, 19, 213–246. [Google Scholar] [CrossRef]
- Park, C.; Kim, Y.; Park, Y.; Kim, S.B. Multitask learning for virtual metrology in semiconductor manufacturing systems. Comput. Ind. Eng. 2018, 123, 209–219. [Google Scholar] [CrossRef]
- Choi, J.E.; Hong, S.J. Machine learning-based virtual metrology on film thickness in amorphous carbon layer deposition process. Meas. Sensors 2021, 16, 100046. [Google Scholar] [CrossRef]
- Hirai, T.; Kano, M. Adaptive Virtual Metrology Design for Semiconductor Dry Etching Process Through Locally Weighted Partial Least Squares. IEEE Trans. Semicond. Manuf. 2015, 28, 137–144. [Google Scholar] [CrossRef]
- Tsai, J.; Chou, P.; Chou, J. Color Filter Polishing Optimization Using ANFIS With Sliding-Level Particle Swarm Optimizer. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 50, 1193–1207. [Google Scholar] [CrossRef]
- Di, Y.; Jia, X.; Lee, J. Enhanced virtual metrology on chemical mechanical planarization process using an integrated model and data-driven approach. Int. J. Progn. Health Manag. 2017, 8, 31. [Google Scholar] [CrossRef]
- Wang, P.; Gao, R.X.; Yan, R. A deep learning-based approach to material removal rate prediction in polishing. CIRP Ann. 2017, 66, 429–432. [Google Scholar] [CrossRef]
- Yu, T.; Li, Z.; Wu, D. Predictive modeling of material removal rate in chemical mechanical planarization with physics-informed machine learning. Wear 2019, 426, 1430–1438. [Google Scholar] [CrossRef]
- Yang, B.; Liu, R.; Zio, E. Remaining useful life prediction based on a double-convolutional neural network architecture. IEEE Trans. Ind. Electron. 2019, 66, 9521–9530. [Google Scholar] [CrossRef]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the COMPSTAT’2010, Paris, France, 22–27 August 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar]
- Ge, R.; Huang, F.; Jin, C.; Yuan, Y. Escaping from saddle points—Online stochastic gradient for tensor decomposition. In Proceedings of the Conference on Learning Theory, PMLR, Paris, France, 3–6 July 2015; pp. 797–842. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; Omnipress: Madison, WI, USA, 2010; pp. 807–814. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Jia, X.; Di, Y.; Feng, J.; Yang, Q.; Dai, H.; Lee, J. Adaptive virtual metrology for semiconductor chemical mechanical planarization process using GMDH-type polynomial neural networks. J. Process Control 2018, 62, 44–54. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, Y.; Luo, H.; Yin, S. Prediction of material removal rate in chemical mechanical polishing via residual convolutional neural network. Control Eng. Pract. 2021, 107, 104673. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Ba, J.; Caruana, R. Do deep nets really need to be deep? In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]


| Group | Chamber ID | Stage ID | MRR Range | Sample Size | |
|---|---|---|---|---|---|
| Training | Testing | ||||
| High-speed | 1, 2, 3 | A | 138–163 | 431 | 73 |
| Low-speed (A) | 4, 5, 6 | A | 53–89 | 983 | 165 |
| Low-speed (B) | 4, 5, 6 | B | 53–102 | 987 | 186 |
| Parameter | Description |
|---|---|
| Dropout probability | 0.1 |
| Optimizer | Adam |
| Initial learning rate | 0.01 |
| Batch size | 16 |
| Number of epochs | 100 |
| Activation function | ReLU |
| Loss function | Loss |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.-L.; Tseng, C.-J.; Hsaio, W.-H.; Wu, S.-H.; Lu, S.-R. Predicting the Wafer Material Removal Rate for Semiconductor Chemical Mechanical Polishing Using a Fusion Network. Appl. Sci. 2022, 12, 11478. https://doi.org/10.3390/app122211478
Liu C-L, Tseng C-J, Hsaio W-H, Wu S-H, Lu S-R. Predicting the Wafer Material Removal Rate for Semiconductor Chemical Mechanical Polishing Using a Fusion Network. Applied Sciences. 2022; 12(22):11478. https://doi.org/10.3390/app122211478
Chicago/Turabian StyleLiu, Chien-Liang, Chun-Jan Tseng, Wen-Hoar Hsaio, Sheng-Hao Wu, and Shu-Rong Lu. 2022. "Predicting the Wafer Material Removal Rate for Semiconductor Chemical Mechanical Polishing Using a Fusion Network" Applied Sciences 12, no. 22: 11478. https://doi.org/10.3390/app122211478
APA StyleLiu, C.-L., Tseng, C.-J., Hsaio, W.-H., Wu, S.-H., & Lu, S.-R. (2022). Predicting the Wafer Material Removal Rate for Semiconductor Chemical Mechanical Polishing Using a Fusion Network. Applied Sciences, 12(22), 11478. https://doi.org/10.3390/app122211478






