A Pragmatic Approach to Modeling Combinations of Plant Operational States in Multi-Unit Nuclear Power Plant Probabilistic Safety Assessment
Abstract
:1. Introduction
1.1. Modeling POS Combinations as an Issue in MUPSA
1.2. Limitation of Existing Studies
- Special attribute (OS-A01-S2): “For multi-unit PSAs, a representative set of combinations of POSs for each unit is selected to account for the most likely combinations. The selected combinations include at least one with all reactors in operation at full power and one for each reactor unit in an LPSD POS.”
- Special attribute (OS-B01-S1): “Further grouping of POSs for each reactor unit in a multi-unit PSA may be required to keep the combination of POSs modeled to a manageable level. Such further grouping is done so as not to mask the potential for initiating events that impact multiple reactor units concurrently.”
1.3. Objective and Scope of This Study
2. Proposed Approach to Modeling POS Combinations in MUPSA
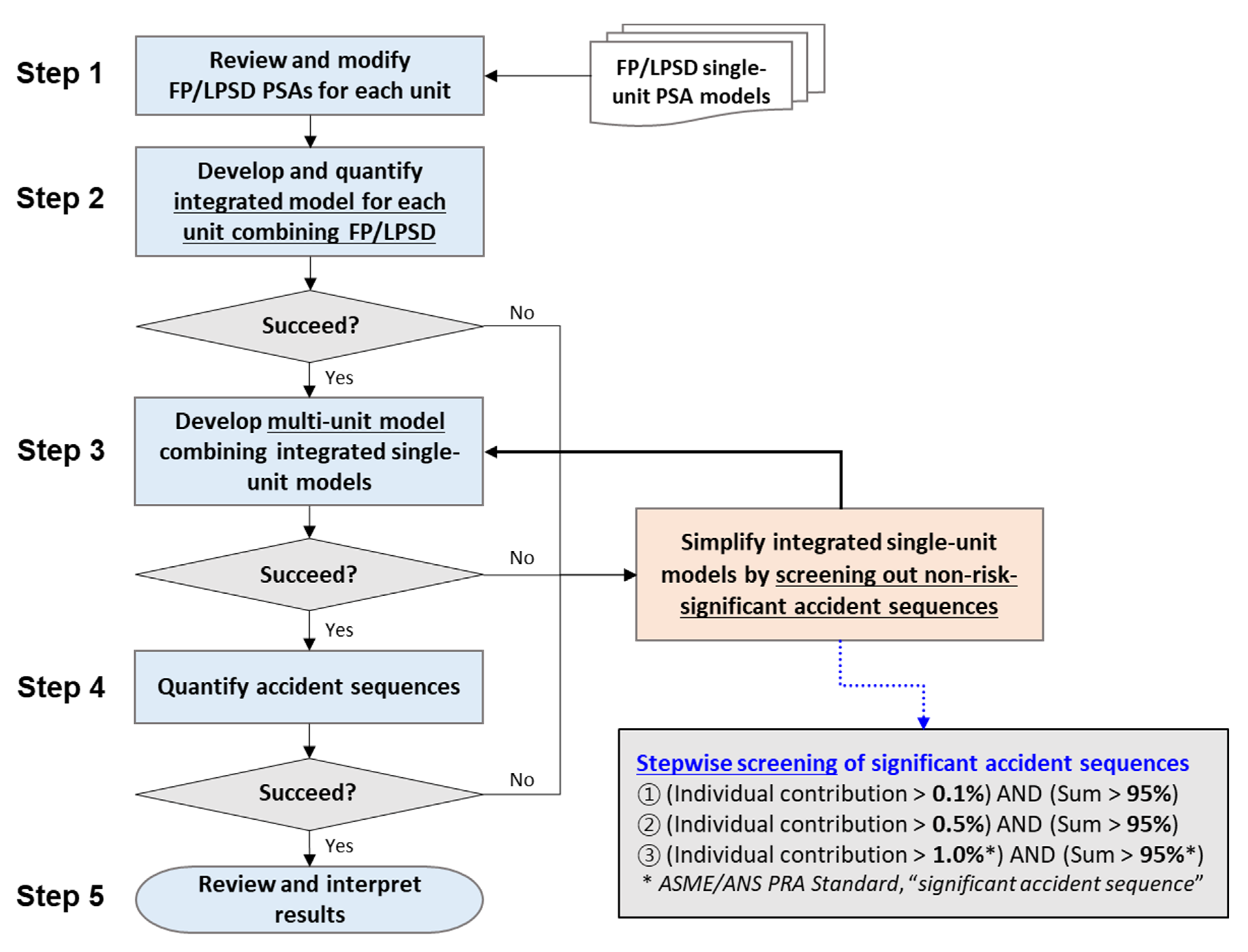
2.1. Step 1: Review and Modification of PSA Models for Each Unit
- Considering the scope of the MUPSA and the risk metrics, the FP and LPSD SUPSA models for each unit are reviewed to check whether they contain all the information necessary to develop a MUPSA model, and if necessary, the SUPSA models are revised.
- The SUPSA models for different units are thoroughly reviewed to check for lack of consistency in terms of key factors, such as hazards or IE grouping, event tree/fault tree models, data used, and major assumptions. If it is judged that the effects that the lack of consistency between the units may have on the MUPSA results are not negligible, the SUPSA models are revised to ensure inter-unit consistency.
- For both FP and LPSD models for each unit, event tree and fault tree logics unrelated to the IE being analyzed (e.g., multi-unit loss of offsite power) are removed or set to FALSE, leaving only the logics related to the IE. This can reduce the size of the models for each unit.
- “Unit identifiers” (e.g., “U1-XXX”) are added to the names of all gates and basic events in order to distinguish between units. An identifier involving the corresponding units (e.g., “U12-XXX”) is attached for those related to a system or component shared between two or more units. For those treated as completely dependent between units (e.g., multi-unit IE), the same gate or basic event is applied equally to all corresponding unit models with no unit identifiers.
2.2. Step 2: Development and Quantification of an Integrated Model for Each Unit
- Depending on the POS, gates with the same name may have different logic, and basic events with the same name may have different probabilities. Therefore, in order to distinguish such gates and basic events between POSs, “POS identifiers” are added to the names of all gates and basic events (e.g., “XXX-P2”).
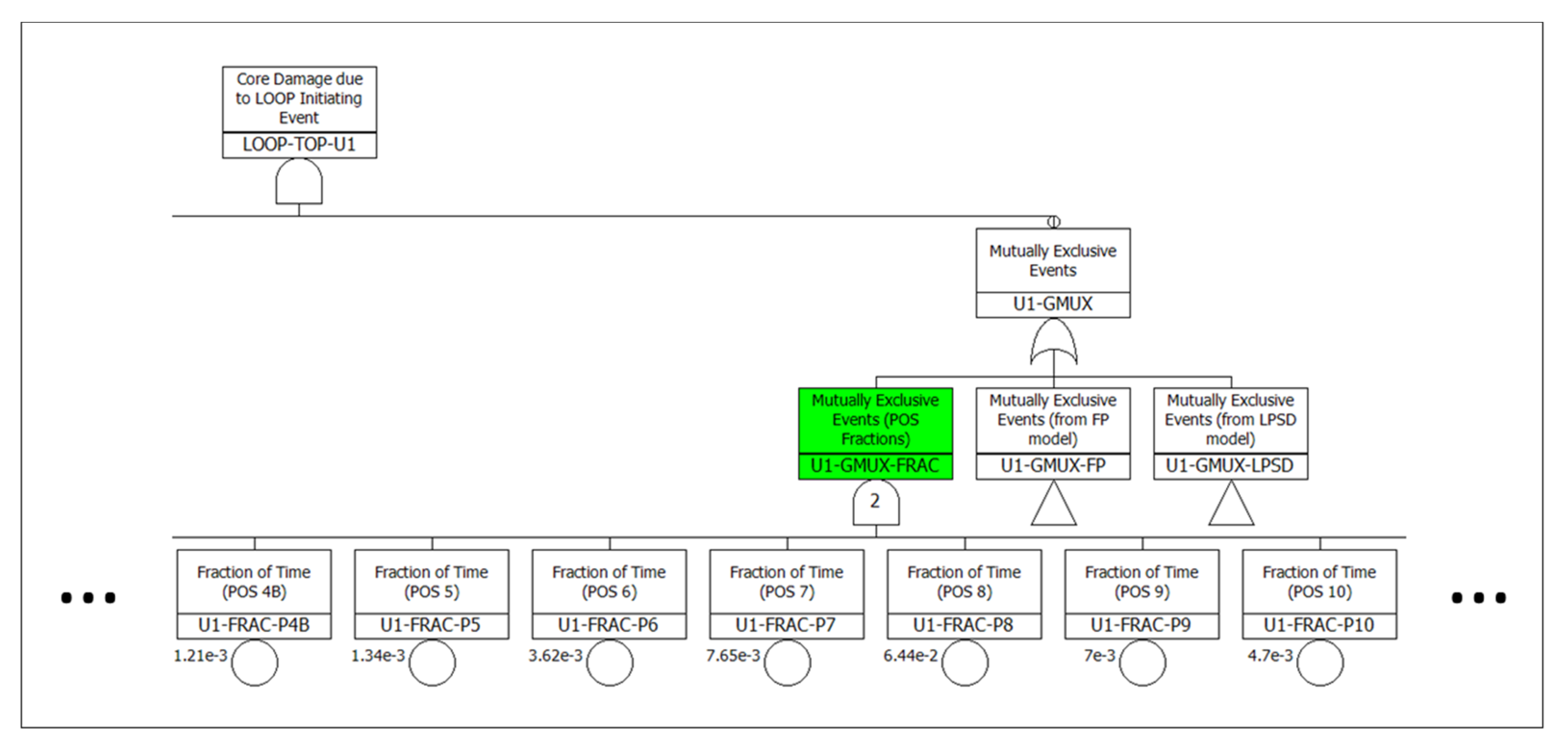
- “POS basic events” that represent the fraction of time spent in each POS are added (e.g., U1-FRAC-PO, U1-FRAC-P2, and U1-FRAC-P3 colored in yellow in Figure 3) and combined with the logic for the corresponding POS under AND gates. The fraction of time for each event can usually be calculated from the FP and LPSD SUPSA results, and the sum of these fractions should be 1.
- Since each unit can only be in one POS at a time, the POS basic events are modeled as mutually exclusive events, as shown in Figure 4. This modeling may not be necessary depending on the logic of the MUPSA model.
- (1)
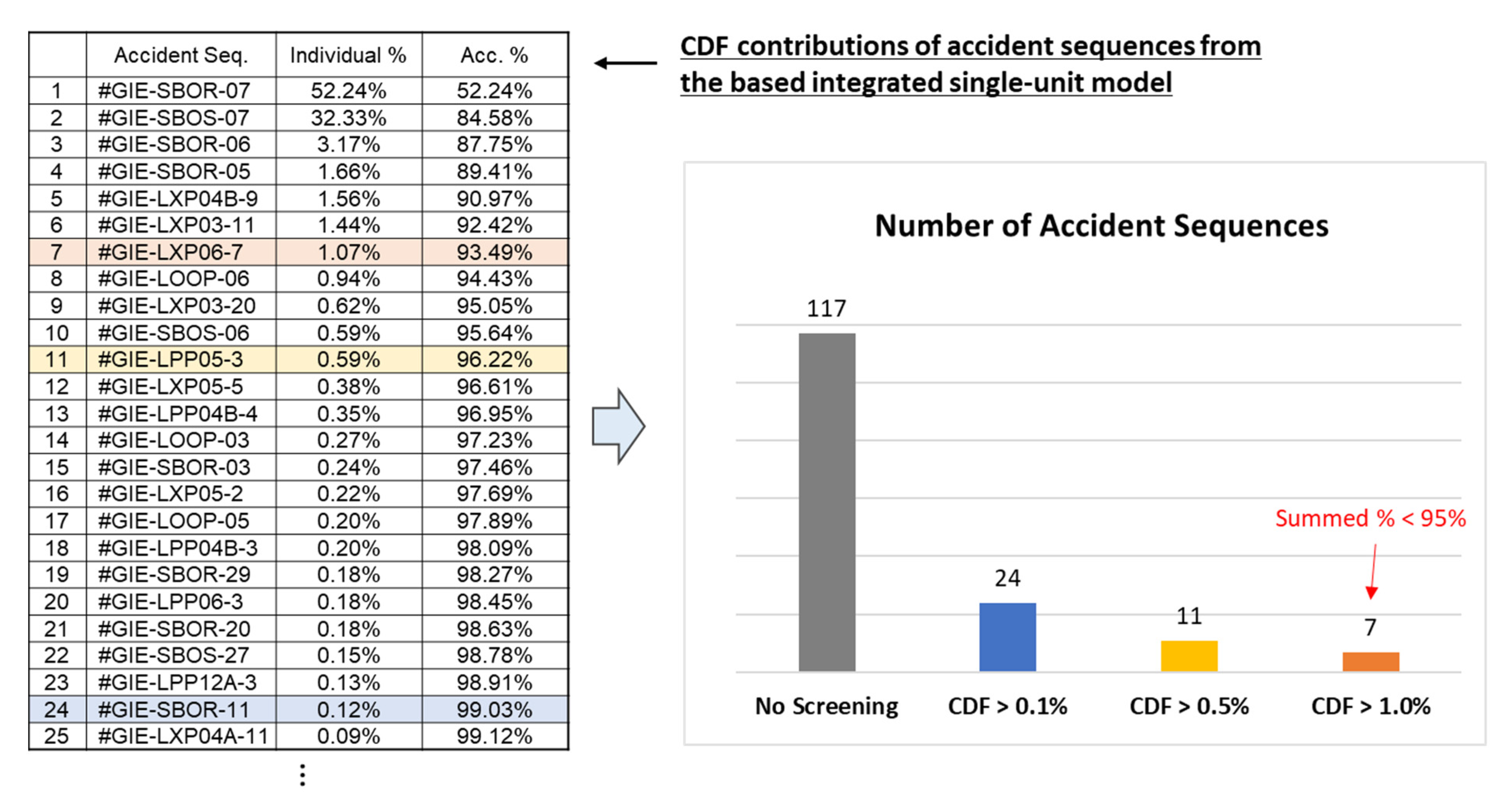
- Individual accident sequences with a contribution greater than 0.1% to the given risk metric are selected as long as the sum of the contributions from the selected sequences is greater than 95%. (If the quantification fails again after applying this criterion, the second-level criterion is applied.)
- (2)
- Individual accident sequences with a contribution greater than 0.5% to the given risk metric are selected as long as the sum of the contributions from the selected sequences is greater than 95%. (If the quantification fails again after applying this criterion, the third-level criterion is applied.)
- (3)
- Individual accident sequences with a contribution greater than 1% to the given risk metric are selected as long as the sum of the contributions from the selected sequences is greater than 95%.
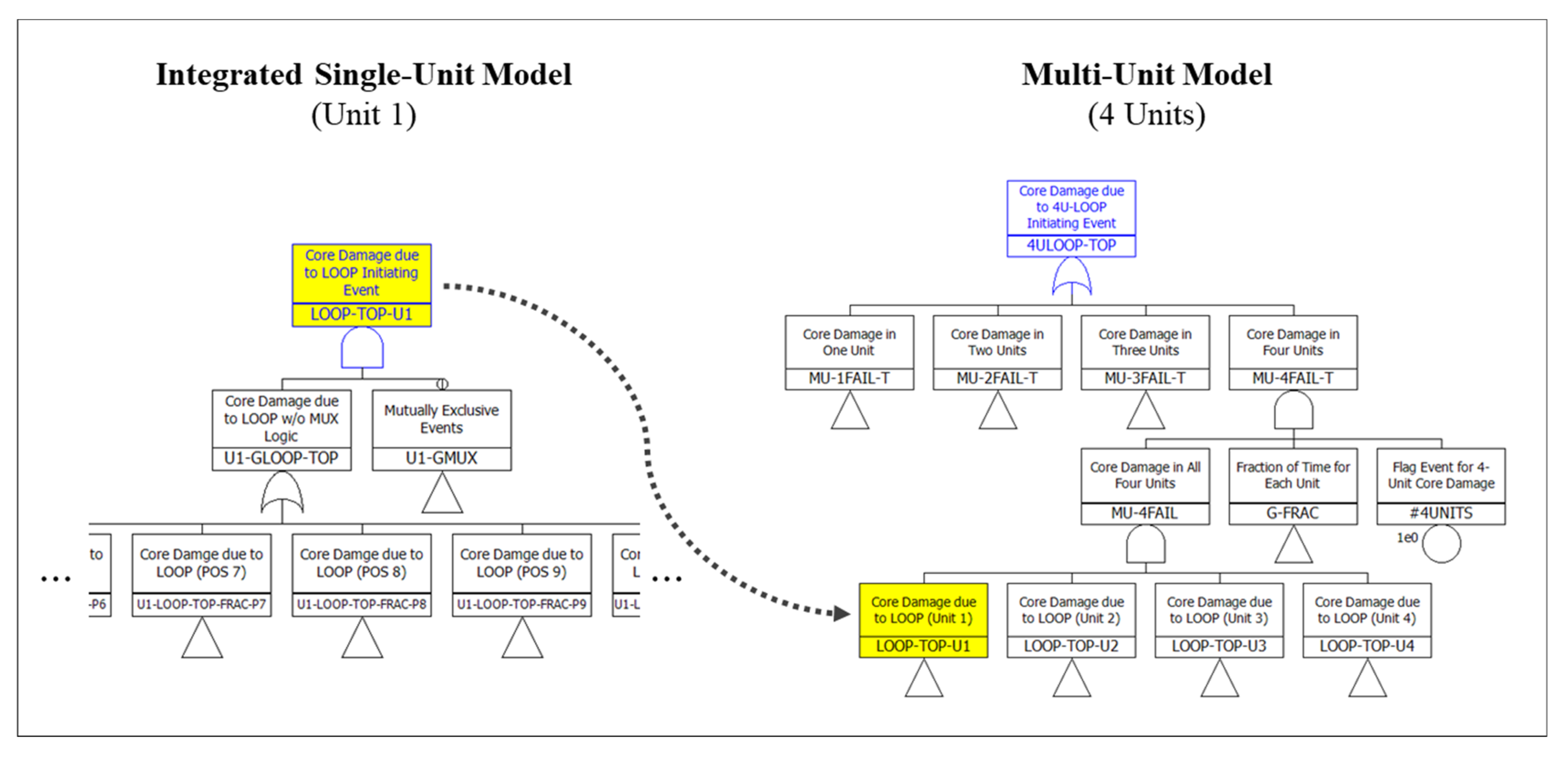
2.3. Step 3: Development of a Multi-Unit Model Combining Integrated Single-Unit Models
2.4. Step 4: Quantification of Accident Sequences for the Multi-Unit Model
2.5. Step 5: Review and Interpretation of Results
3. Case Study
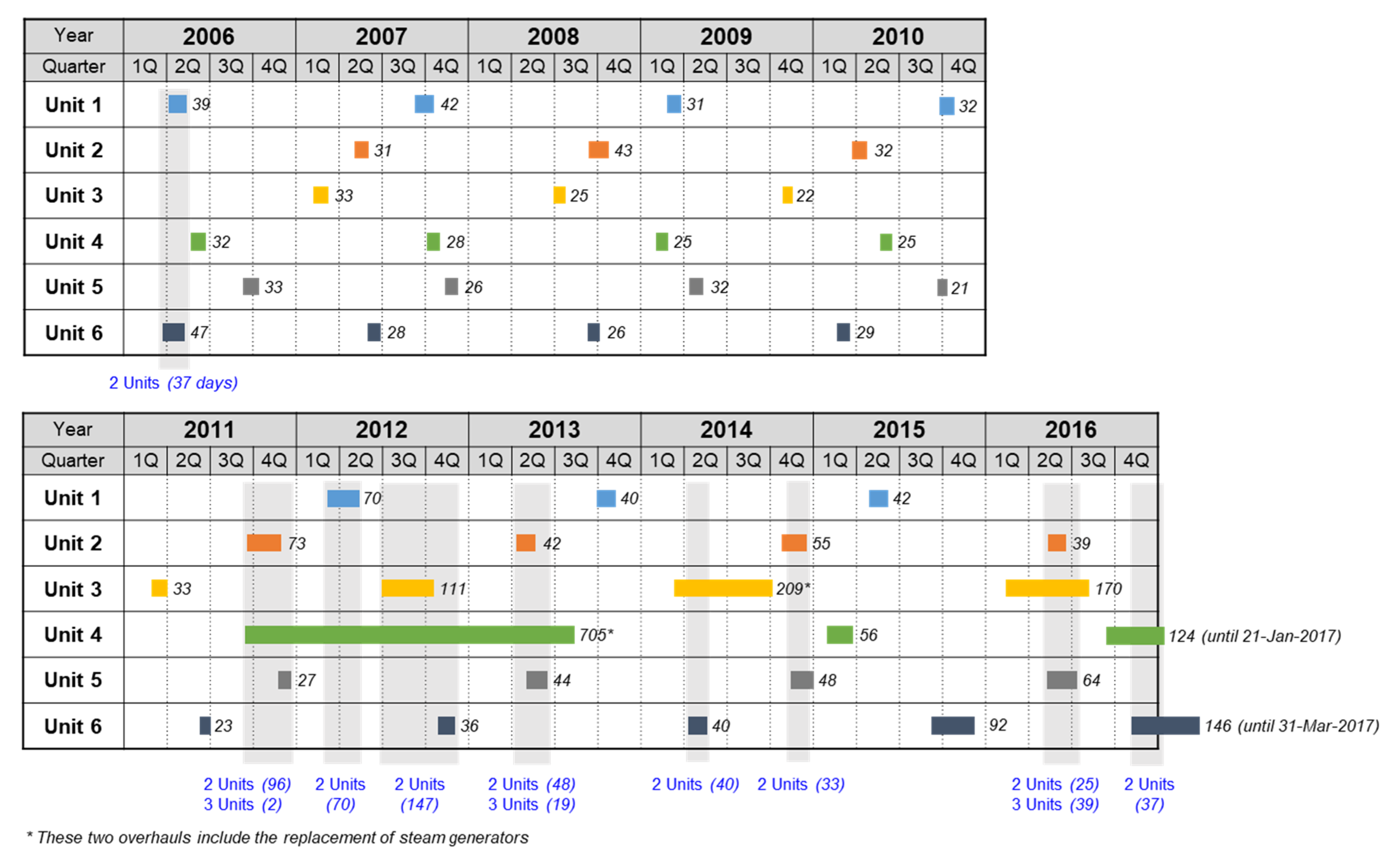
3.1. Data Collection and Estimation of the Fraction of Time for Each POS
3.2. Example MUPSA Cases with Different Numbers of Units
3.2.1. Scope and Method
- In each of the four cases, the reference site consists of one to five pairs of twin units.
- All units at the site are identical OPR1000 units. All structures, systems, and components except diesel generators (DGs) are identical across the units.
- Emergency DGs (EDGs) are identical for each pair of twin units (e.g., Units 1 and 2) but not between units in different pairs (e.g., Units 1 and 3).
- Each pair of twin units shares an alternative AC DG (AAC DG) of the same type as the EDGs. For each shared AAC DG, priority follows the unit number (e.g., Unit 1 → Unit 2).
- The MU-LOOP IE is a weather-related LOOP caused by severe weather conditions such as a typhoon, so it affects all units at the site simultaneously.
- Offsite power recovery actions are completely dependent across all units, while the other HFEs are independent between units because each unit has its own operating crew working in a physically separate control room or building.
- The adverse effects of core damage or radioactive release from one unit on operator actions in other adjacent units at the site [19] are negligible.
- Portable equipment that has already been or is planned to be installed as part of the Multi-barrier Accident Coping Strategy (MACST) for Korean NPPs is not credited.
3.2.2. Results
- As the number of units involved increased, the model size, site CDF, and multi-unit CDF increased almost linearly while the run time and the number of MCSs increased exponentially.
- The quantification for the SU-LOOP model with about 58,000 events succeeded to produce results in less than a minute, eliminating the need to screen out non-risk-significant accident sequences in Step 2.
- For each number of units, the development of the MUPSA model in the form of a single-top fault tree was successful, so there was no need to go to the screening step in Step 3 either.
- In the 2-unit, 4-unit, and 6-unit cases, the quantification of the MUPSA model successfully yielded results within a reasonable time without performing the screening step. However, in the 10-unit case, the quantification failed without screening.
4. Discussion and Conclusions
- Even though the base integrated single-unit model used in this study was very large, i.e., containing about 37,000 gates and 21,000 basic events, compared to a FP or LPSD SUPSA model for NPPs, the quantification of the MUPSA models combining the single-unit models succeeded within a reasonable time without screening any accident sequences for the 2-, 4-, and 6-unit cases.
- In the 10-unit case, the quantification failed without screening, but it succeeded after reducing the model size by about 43% by excluding the accident sequences in each integrated single-unit model with a CDF contribution of less than 0.1%.
- The MCSs obtained in each case covered a very large number of POS combinations, for example, about 50,000 combinations in the 6-unit case without screening.
- It was found that the MCSs involving very unlikely combinations, such as four or more units being in shutdown POSs, were mostly truncated by the cutoff value of 1E-14/yr, while the MCSs involving very likely combinations, such as all units being at-power, accounted for the majority.
- A comparison of the quantification results for the 6-unit case according to the three levels of screening criteria showed that as the level increases, the model size and computation time were significantly reduced by eliminating more accident sequences, while the reductions in the number of MCSs and CDF values were relatively small, especially for the multi-unit CDF with little change.
- This approach can be applied to site-level or multi-unit PSAs for actual NPP sites with a large number of reactor units. The case study was conducted for up to 10 units, but the approach applies to MUPSA involving more than 10 units depending on the size and logic complexity of each unit model.
- With this approach, there is no need to select a representative set of POS combinations. Therefore, it is possible to reduce the conservatism caused by selecting a small number of POS combinations.
- This approach can effectively reduce computational burden without losing much accuracy or realism by screening out non-risk-significant accident sequences in a stepwise manner according to the quantification results.
- While the case study assumed all identical units for simplicity, many multi-unit NPP sites have different types of reactor units. For example, the Kori site in the Republic of Korea has four different types of operating units: WH600, WH900, OPR1000, and APR1400 [6,11]. Although the proposed approach has no limitations in application to MUPSAs involving non-identical units, application of this approach to various other cases, for example, MUPSAs involving non-identical units and other multi-unit IEs such as seismic events, will provide a better understanding of its strengths and limitations.
- Future work should also be directed toward further investigation of the three screening criteria levels. Quantification may still fail even if the model size is reduced by applying the screening criteria depending on the model to be analyzed, the software used for model development and quantification, and the environment in which the computer system operates. In such cases, rather than mechanically applying the screening criteria, it is necessary to consider more relaxed criteria, such as excluding the condition for the summed contribution to be greater than 95%, to obtain quantification results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AAC DG | Alternative AC Diesel Generator |
| APR1400 | Advanced Power Reactor 1400 MWe |
| CCDP | Conditional Core Damage Probability |
| CCF | Common Cause Failure |
| CDF | Core Damage Frequency |
| DG | Diesel Generator |
| EDG | Emergency Diesel Generator |
| FP | Full Power |
| HFE | Human Failure Event |
| IE | Initiating Event |
| KHNP | Korea Hydro & Nuclear Power, Co., Ltd. |
| LOOP | Loss of Offsite Power |
| LPSD | Low Power and Shutdown |
| MCS | Minimal Cut Set |
| MUPSA | Multi-Unit Probabilistic Safety Assessment |
| NPP | Nuclear Power Plant |
| O/H | Overhaul |
| OPR1000 | Optimized Power Reactor 1000 MWe |
| POS | Plant Operational State |
| PSA | Probabilistic Safety Assessment |
| SOS | Site Operating State |
| SUPSA | Single-Unit Probabilistic Safety Assessment |
| WH | Westinghouse |
References
- Zhou, T.; Modarres, M.; Droguett, E.L. Multi-unit nuclear power plant probabilistic risk assessment: A comprehensive survey. Reliab. Eng. Syst. Saf. 2021, 213, 107782. [Google Scholar] [CrossRef]
- Canadian Nuclear Safety Commission. Proceedings of the Summary Report of the International Workshop on Multi-Unit Probabilistic Safety Assessment, Ottawa, ON, Canada, 17–20 November, 2014.
- International Atomic Energy Agency. Multi-Unit Probabilistic Safety Assessment. In Safety Reports Series No. 110, Final Draft; IAEA: Vienna, Austria, 2021. [Google Scholar]
- International Atomic Energy Agency. Attributes of Full Scope Level 1 Probabilistic Safety Assessment (PSA) for Applications in Nuclear Power Plants. In IAEA-TECDOC-1804; IAEA: Vienna, Austria, 2016. [Google Scholar]
- Kim, D.-S.; Han, S.H.; Park, J.H.; Lim, H.G.; Kim, J.H. Multiunit Level 1 probabilistic safety assessment: Approaches and their application to a six-unit NPP site. Nucl. Eng. Technol. 2018, 50, 1217–1233. [Google Scholar] [CrossRef]
- Jang, S.; Kim, Y.; Jae, M. A site risk assessment for internal events: A case study. Reliab. Eng. Syst. Saf. 2021, 215, 107876. [Google Scholar] [CrossRef]
- Ferrante, F.; Maioli, A.; Kiper, K.; Trull, C.; Sivori, A.A. Practical insights for assessing multi-unit risk to support risk-informed decision-making. In Proceedings of the ANS PSA 2021 International Topical Meeting on Probabilistic Safety Assessment and Analysis, Columbus, OH, USA, 7–12 November 2021. [Google Scholar]
- Kiper, K.; Maioli, A. A Framework for addressing site integrated risk. In Proceedings of the ANS PSA 2015 International Topical Meeting on Probabilistic Safety Assessment and Analysis, Sun Valley, ID, USA, 26–30 April 2015. [Google Scholar]
- Sivori, A.; Kiper, K.; Maioli, A.; Teolis, D. Further development of a framework for addressing site integrated risk. In Proceedings of the ANS PSA 2017 International Topical Meeting on Probabilistic Safety Assessment and Analysis, Pittsburgh, PA, USA, 24–28 September 2017. [Google Scholar]
- Mandelli, D.; Parisi, C.; Alfonsi, A.; Maljovec, D.; Boring, R.; Ewing, S.; St Germain, S.; Smith, C.; Rabiti, C.; Rasmussen, M. Multi-unit dynamic PRA. Reliab. Eng. Syst. Saf. 2019, 185, 303–317. [Google Scholar] [CrossRef]
- Jeon, H.; Oh, K.; Park, J. Approach to developing Level 1 multi-unit PSA models and insights from the models. In Proceedings of the Asian Symposium on Risk Assessment and Management (ASRAM) 2019, Gyeongju, Korea, 30 September–2 October 2019. [Google Scholar]
- Bareith, A. An initiative towards site-level risk assessment for Paks NPP. In Proceedings of the International Workshop on Status of Site Level PSA (including Multi-Unit PSA) Developments, Munich, Germany, 18–20 July 2018. [Google Scholar]
- Yoo, H.; Jin, K.; Heo, G. Study of combinations of site operating states for multi-unit PSA. Nucl. Eng. Technol. 2021, 53, 3247–3255. [Google Scholar] [CrossRef]
- KAERI. Development of Site Risk Assessment and Management Technology Including Extreme External Events. In KAERI/RR-4225/2016; Korea Atomic Energy Research Institute: Daejeon, Korea, 2017. [Google Scholar]
- ASME/ANS. Addenda to ASME/ANS RA-S-2008, Standard for Level 1/Large Early Release Frequency Probabilistic Risk Assessment for Nuclear Power Plant Applications. In ASME/ANS RA-Sb-2013; The American Society of Mechanical Engineers & American Nuclear Society: New York, NY, USA, 2013. [Google Scholar]
- Han, S.H.; Oh, K.; Lim, H.G.; Yang, J.E. AIMS-MUPSA software package for multi-unit PSA. Nucl. Eng. Technol. 2018, 50, 1255–1265. [Google Scholar] [CrossRef]
- Jung, W.S.; Han, S.H.; Ha, J. A fast BDD algorithm for large coherent fault trees analysis. Reliab. Eng. Syst. Saf. 2004, 83, 369–374. [Google Scholar] [CrossRef]
- Korea Hydro & Nuclear Power Co., Ltd. LPSD Internal Events Level 1 PSA Report for Hanul Units 3 and 4; KHNP: Kyeongju, Korea, 2015. [Google Scholar]
- Yoon, J.Y.; Kim, D.-S. Estimating the adverse effects of inter-unit radioactive release on operator actions at a multi-unit site. Reliab. Eng. Syst. Saf. 2022, 228, 108764. [Google Scholar] [CrossRef]
- Han, S.H.; Lim, H.G.; Jang, S.C.; Yang, J.E. AIMS-PSA: A software for integrated PSA. In Proceedings of the 13th International Conference on Probabilistic Safety Assessment and Management (PSAM 13), Seoul, Korea, 2–7 October 2016. [Google Scholar]
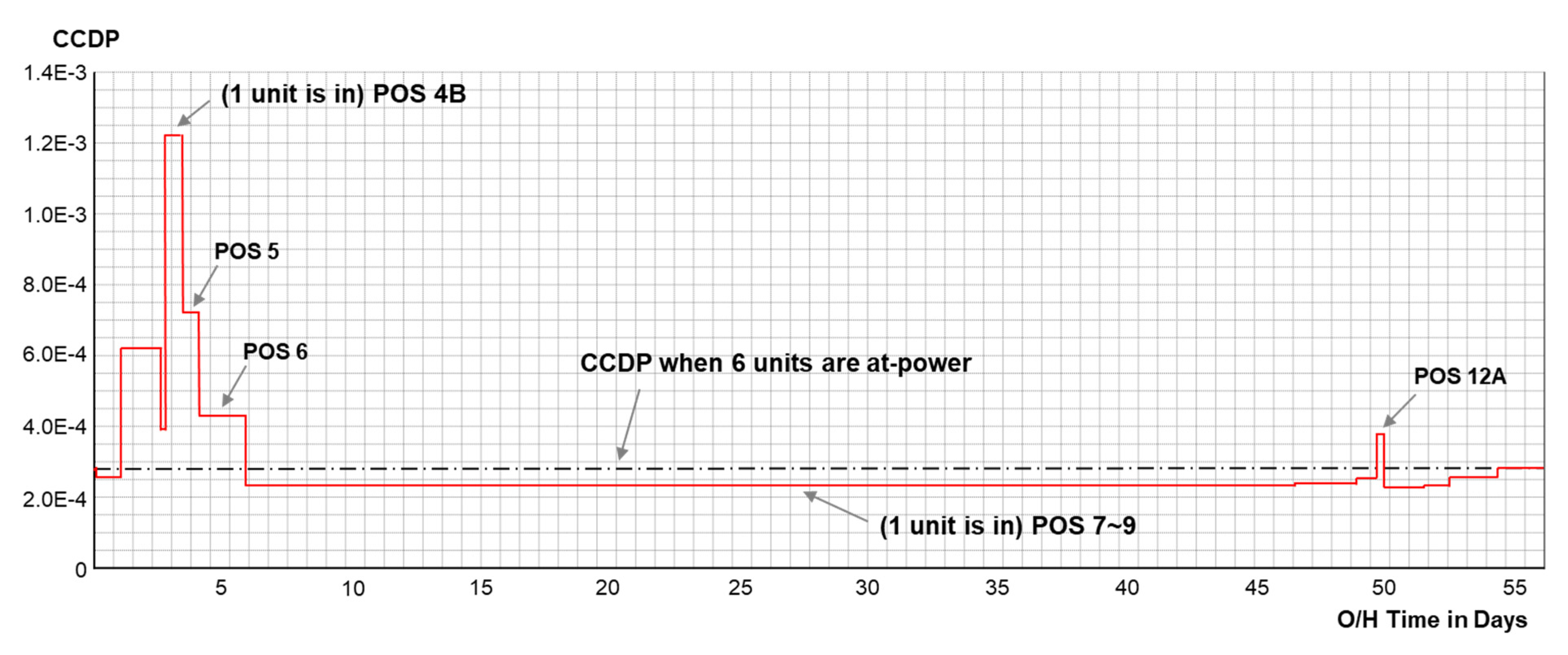


| References | Organization | Number of Reactor Units | Description of Modeling POS Combinations |
|---|---|---|---|
| IAEA [3] | International Atomic Energy Agency | 4 | Assuming all units were in FP operation, only one combination of all units at FP was modeled. |
| Kim, et al. [5] | Korea Atomic Energy Research Institute | 6 | |
| Jang, et al. [6] | Hanyang University | 7 | |
| Ferrante, et al. [7] | Electric Power Research Institute | 2 | Three site operating states (SOSs) were defined according to the operating mode (at-power or shutdown) for each unit, but only one combination of both units at FP was analyzed in pilot plant studies. |
| Kiper and Maioli [8] Sivori, et al. [9] | Westinghouse Electric Company | 2 | A number of logical multi-unit configurations were analyzed, and three SOSs were defined, but only one combination of both units at FP was applied in the case study. |
| Mandelli, et al. [10] | Idaho National Laboratory | 3 | To illustrate a dynamic MUPSA approach, only one combination was selected and modeled, where two units were at FP, and one was in mid-loop. |
| Jeon, et al. [11] | Korea Hydro & Nuclear Power | 9 | Five SOSs were defined. All but two selected units were assumed to be at FP, and for each of the two units, only one POS with the highest CCDP was modeled. |
| Bareith [12] | NUBIKI Nuclear Safety Research Institute | 4 | A total of 115 viable combinations for four reactors and four spent fuel pools were defined through a detailed evaluation, but only one combination of two units at FP was considered in the small-scale pilot study. |
| Yoo, et al. [13] | Kyung Hee University | 7 | To demonstrate a simulation model for estimating the fraction of time for each combination, 15 LPSD POSs for each unit were classified into three groups. |
| Number of Units in O/H | Number of Days | Fraction of Time (%) |
|---|---|---|
| 0 | 1875 | 46.7 |
| 1 | 1484 | 36.9 |
| 2 | 599 | 14.9 |
| 3 | 60 | 1.5 |
| 4 to 6 | 0 | 0.0 |
| Sum | 4018 | 100.0 |
| POS | Description | Unit 1 | Unit 2 | Unit 3 | Unit 4 | Unit 5 | Unit 6 |
|---|---|---|---|---|---|---|---|
| At-Power | At-power operation (including full-power and low-power) | 89.4% | 92.5% | 85.3% | 75.6% | 93.0% | 92.4% |
| POS 2 | Cooldown with SGs | 0.2% | 0.2% | 0.2% | 0.2% | 0.2% | 0.2% |
| POS 3 | Cooldown with SCS | 0.3% | 0.3% | 0.3% | 0.3% | 0.3% | 0.3% |
| POS 4A | RCS draindown (pressurizer manway closed) | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| POS 4B | RCS draindown (pressurizer manway open) | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% |
| POS 5 | 1st mid-loop operation | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% |
| POS 6 | Fill for refueling | 0.4% | 0.3% | 0.3% | 0.3% | 0.4% | 0.4% |
| POS 7 | Offload | 0.8% | 0.7% | 0.7% | 0.7% | 0.8% | 0.8% |
| POS 8 | Maintenance while defueled | 6.4% | 3.9% | 11.0% | 20.8% | 2.8% | 3.4% |
| POS 9 | Onload | 0.7% | 0.6% | 0.6% | 0.6% | 0.7% | 0.7% |
| POS 10 | RCS draindown after refueling | 0.5% | 0.4% | 0.4% | 0.4% | 0.5% | 0.5% |
| POS 11 | 2nd mid-loop operation | 0.2% | 0.1% | 0.1% | 0.1% | 0.2% | 0.2% |
| POS 12A | RCS refill (pressurizer manway open) | 0.1% | 0.0% | 0.0% | 0.0% | 0.1% | 0.1% |
| POS 12B | RCS refill (pressurizer manway closed) | 0.3% | 0.3% | 0.3% | 0.3% | 0.3% | 0.3% |
| POS 13 | RCS heatup with SCS isolation | 0.2% | 0.2% | 0.2% | 0.2% | 0.2% | 0.2% |
| POS 14 | RCS heatup with SGs | 0.4% | 0.3% | 0.3% | 0.3% | 0.4% | 0.4% |
| Total | - | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| Model | SU-LOOP | 2U-LOOP | 4U-LOOP | 6U-LOOP | 10U-LOOP |
|---|---|---|---|---|---|
| Model size (sum) Number of gates Number of basic events | 58,084 37,112 20,972 - | 114,308 71,826 42,482 - | 228,304 143,652 84,652 - | 342,299 215,477 126,822 - | 570,494 359,127 211,367 - |
| Run time (sec.) | 56 | 155 | 639 | 2,001 | N/A |
| Number of MCS | 221,374 | 771,915 | 2,902,484 | 6,618,173 | N/A |
| Site CDF | 1.36 × 10−6 | 2.24 × 10−6 | 4.21 × 10−6 | 6.35 × 10−6 | N/A |
| Multi-unit CDF | N/A | 9.68 × 10−8 | 1.72 × 10−7 | 2.70 × 10−7 | N/A |
| Screening Criteria | No Screening | >0.1% | >0.5% | >1.0% |
|---|---|---|---|---|
| Model size (sum) | 342,299 | 196,583 | 145,967 | 121,067 |
| Number of gates | 215,477 | 125,975 | 93,395 | 77,285 |
| Number of basic | 126,822 | 70,608 | 52,572 | 43,782 |
| events | - | - | - | - |
| Run time (sec.) | 2001 | 551 | 257 | 181 |
| Number of MCS | 7,116,674 | 6,618,173 | 5,604,299 | 5,010,444 |
| Site CDF | 6.41 × 10−6 (-) | 6.35 × 10−6 (98.9%) | 6.13 × 10−6 (95.6%) | 5.93 × 10−6 (92.5%) |
| Multi-unit CDF | 2.71 × 10−7 (-) | 2.70 × 10−7 (99.7%) | 2.69 × 10−7 (99.4%) | 2.69 × 10−7 (99.3%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-S.; Park, J.H. A Pragmatic Approach to Modeling Combinations of Plant Operational States in Multi-Unit Nuclear Power Plant Probabilistic Safety Assessment. Appl. Sci. 2022, 12, 11486. https://doi.org/10.3390/app122211486
Kim D-S, Park JH. A Pragmatic Approach to Modeling Combinations of Plant Operational States in Multi-Unit Nuclear Power Plant Probabilistic Safety Assessment. Applied Sciences. 2022; 12(22):11486. https://doi.org/10.3390/app122211486
Chicago/Turabian StyleKim, Dong-San, and Jin Hee Park. 2022. "A Pragmatic Approach to Modeling Combinations of Plant Operational States in Multi-Unit Nuclear Power Plant Probabilistic Safety Assessment" Applied Sciences 12, no. 22: 11486. https://doi.org/10.3390/app122211486
APA StyleKim, D.-S., & Park, J. H. (2022). A Pragmatic Approach to Modeling Combinations of Plant Operational States in Multi-Unit Nuclear Power Plant Probabilistic Safety Assessment. Applied Sciences, 12(22), 11486. https://doi.org/10.3390/app122211486






