Research on the Robustness of Active Headrest with Virtual Microphones to Human Head Rotation

Abstract

The movement and rotation of the human head can significantly degrade the control performance of active headrests with virtual microphones. This paper investigates the performance robustness of an active headrest with virtual microphones against the head rotation in a pure tone diffracted diffuse sound field. A physical model of a headrest system with a diffractive sphere is firstly developed, based on which the influence of acoustic transfer responses on the performance robustness against head rotation is analyzed. Then, the multi-objective optimization with constraints is developed to improve the performance robustness of the system, by designing optimized plant responses. Simulation results show that the method is effective in improving the robustness of single and dual channel systems. For a dual-channel headrest system with the proposed arrangements of secondary sources and microphones, the promotion of the minimum noise reduction is more than 7 dB after optimization when the head rotates from −90 degrees to 90 degrees at 125 Hz, 250 Hz and 500 Hz. In addition, the influence of different parameters on the optimization method is discussed for this dual-channel system. Finally, experiments carried out in an ordinary room validate the effectiveness of the proposed method.

1. Introduction

The active headrest is a local active control system that creates a quiet zone around the human ear through secondary sources and error microphones near the human head [1]. The “electronic sound absorber” proposed by Olson and May can be regarded as a prototype for an active headrest, which uses analogue circuits to adjust the output of a loudspeaker to reduce the noise at a microphone or absorb acoustic energy [1]. Since the 1980s, active headrests have been widely studied due to their potential applications in vehicles, factories, residential houses, etc. [2,3,4].

One of the main criteria for evaluating the performance of an active headrest is the size of the quiet zone it generates, which has proven to be very limited. For example, the 10 dB zone of quiet created in a free diffuse sound field when using a remote secondary source seems to be a sphere with a diameter of about one-tenth of a wavelength [5]. When the cancellation point is in the near field of a piston secondary source, the 10 dB zone of quiet forms a spherical shell with a diameter of no more than one-tenth of a wavelength around the secondary source at low frequencies, and becomes a sphere with a diameter of about one-tenth of a wavelength at high frequencies [6,7]. To obtain higher noise reduction, error microphones should be placed as close as possible to human ears, which will interfere with the movement of the human head. Therefore, a virtual sensing technique has been applied to the active headrest to predict and control the sound pressure at human ears by placing physical microphones away from the human head, which is equivalent to placing a virtual microphone at the human ear and projecting the active quiet zone around it [8]. There are various techniques to predict acoustic signals at the human ear, such as the virtual microphone arrangement (VMA) [8], the remote microphone technique (RMT) [9,10], the difference prediction approach [11] and the Kalman filter approach [12].

In practice, the primary sound field and plant responses change as the head moves, leading to the degradation of the performance for the active headrest using virtual sensing techniques [9]. At present, there are two main methods to solve this problem, a moving virtual microphone technique that creates moving quiet zones [9,13] and a robustness optimization method [14]. For the former method, plant models and observation filters for different head positions are measured and stored in advance, where the observation filters are derived from the transfer functions of remote physical microphones and the virtual microphone in the primary sound field. A head tracking system then monitors the head position and updates the control filters using prestored models and filters corresponding to the head position, achieving a quiet zone that follows the movement of the head [9]. Head tracking technologies based on visual localization and infrared localization have been applied to active headrests [9,15], and it has been shown that such methods can achieve good noise reduction performance as the human head moves to different positions. However, these methods suffer from high complexity and cost, due to an additional head tracking system and the considerable storage space.

By optimizing the plant models, the latter method can improve the noise reduction performance of the system when the head deviates from the original position. Lei et al. used this method to optimize the active headrest system, extending the 10 dB quiet zone at 250 Hz by 4–6 cm in the direction of lateral head movement [14]. However, other kinds of human head movement have not been considered. The performance improvement of this method is less than the former, but the system is less complex and easier to implement.

Most previous research has considered head translation [9,13,14], while few have addressed head rotation [15]. To reduce the degradation of noise control performance when the head rotates, Han et al. suggested accessing a fixed optimal wiener filter for the controller by minimizing an improved cost function, which is defined as the sum of the mean squared error of human ears at different positions [15]. Experimental results show that the proposed active headrest system, combining with the infrared head tracking technique, effectively controls broadband noise when the head is translated or rotated. The system is non-adaptive, does not require any virtual error microphones, and therefore has difficulty tracking time-varying sound fields and acoustic transfer paths.

Head rotation is of the same importance as translation. For example, when one rests on a car headrest, the head lateral movement may be naturally confined to a small range due to the limited width of the headrest. In addition, usually only a little back and forth movement takes place. Instead, the head is often rotated in order to find a more comfortable sitting position and stays at a certain rotation angle. Furthermore, some wrap-around headrests further limit the translation of the human head when head rotation becomes an issue. Therefore, discussions on the robustness to head rotation is meaningful and will be the major task of this paper.

Most research is based on the measured acoustic transfer responses to optimize the system, lacking a systematic analysis of the variation and optimization of the acoustic transfer responses in practical situations. In this paper, a physical model of an active noise-reducing headrest with a diffractive rigid sphere in the diffuse sound field was developed to analyze the variation of acoustic transfer responses. Then the noise reduction performance of the active headrest system using a virtual sensing technique was analyzed. The system robustness against head rotation was then improved by the design of an optimized plant transfer responses. While most previous studies have been based on single channel systems, there is some research using dual-channel systems to improve system performance [16,17,18,19]. The performance of single channel and dual-channel systems are compared in this paper and the influence of a physical system arrangement is discussed. Moreover, the effects of several parameters on optimization performance are analyzed based on a horizontally arranged dual-channel system. Finally, the simulation results are verified by experiments in an ordinary room.

2. Theory

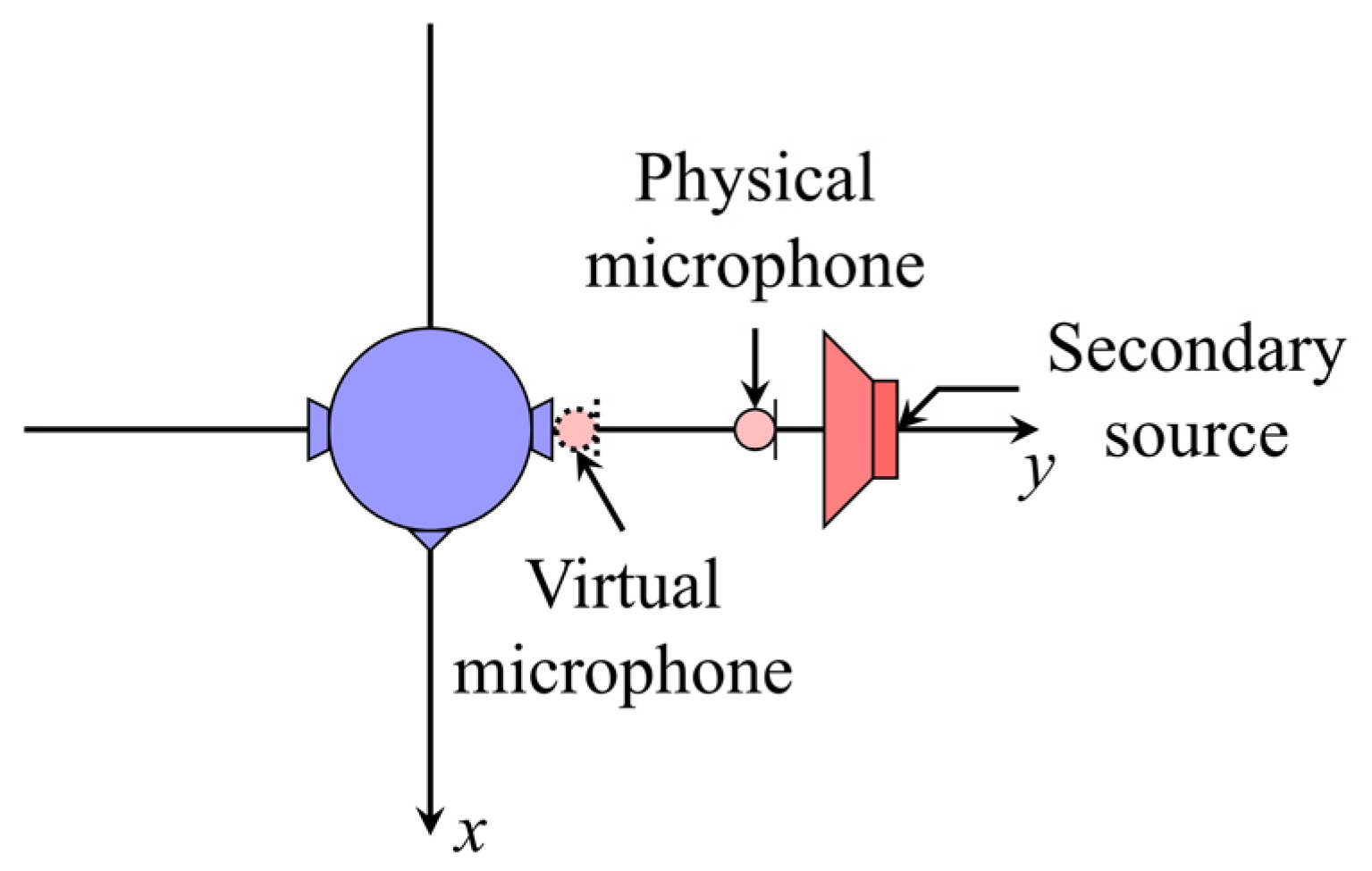
2.1. Primary Sound Field

The sound fields are assumed to be harmonic and the optimal control is derived through numerical calculations in frequency domains. Figure 1 demonstrates the spherical coordinates used in this paper where the head is modelled as a rigid sphere of radius a with the center of the sphere located at the origin. The primary sound field is assumed to be a diffracted diffuse field, and each of its samples is simulated by the superposition of plane waves with random phases and amplitudes from different directions. With the introduction of a rigid sphere, the sample of diffuse field pressure at r = (r,θ,ϕ) can be expressed as [20]

$$\begin{array}{l}{p}_p\left(r\right)=\frac{1}{\sqrt{N_p}}{\displaystyle \sum _{i=1}^{N_p}{P}_{pi}\left(r\right)},\\ \end{array}$$

(1)

$$\begin{array}{ll}{P}_{pi}\left(r\right)=& P_{\mathrm{A}i}{e}^{-jk{\phi }_{0i}}{\displaystyle \sum _{l=0}^{\infty }{(-j)}^l\left(2l+1\right)[j_l(kr)-\frac{j_l^{’}(ka)}{h_l^{’}(ka)}{h}_l(kr)]}\\ & \times \left\{P_l\left(\cos {\theta }_i\right)P_l(\cos \theta )+{\displaystyle \sum _{m=1}^{l}2\frac{\left(l-m\right)!}{\left(l+m\right)!}{P}_l^m\left(\cos {\theta }_i\right)P_l^m\left(\cos \theta \right)\cos \left[m\left(\varphi -{\varphi }_i\right)\right]}\right\},\end{array}$$

(2)

where k is the wave number, N_p is the number of plane waves, P_Ai and φ_0i are the amplitude and phase of the ith plane wave which are taken from uniform distributions of [0, 1] and [−π, π], respectively. The incidence direction of the ith plane wave is expressed as n_i = (1,θ_i,ϕ_i), where the elevation angle θ_i is uniformly distributed in [0, π] for a total of N_s, and, on the circumference of the circle where the elevation angle θ_i is located, the azimuth angle takes uniform values in [−π, π], for a total of 2N_ssinθ_i. The factor sinθ_i ensures that, on average, the incident waves are uniform at all angles. j_l(x) is the spherical Bessel function of order l, h_l(x) is the spherical Hankel function of order l, and P_l^m(x) denotes the mth associated Legendre function of order l, which becomes the Legendre polynomial for the case m = 0. When N_p is large enough, Equation (1) is an appropriate estimation of a sample of the primary diffuse field. In this paper, N_s is set to 30 when N_p = 1116, and the average of mean square sound pressure from 30 primary sound field samples is used for simulations.

2.2. Secondary Sound Field

Secondary sources can be approximated as monopoles in low frequency range. Due to the close distances between secondary sources and the error microphones of the active headrest, only the direct sound from the secondary sources is considered. With the diffracting rigid sphere shown in Figure 1, the sound pressure at the receiving point r = (r,θ,ϕ) generated by a secondary source at r_s = (r_s,θ_s,ϕ_s) can be expressed as [20]

$$p_s(r)=Z_s(r)q_s,$$

(3)

$$\begin{array}{ll}{Z}_s(r)=& \frac{k\omega \rho }{4\pi }{\displaystyle \sum _{l=0}^{\infty }(2l+1)[j_l(k{r}_{<})-\frac{j_l^{’}(ka)}{h_l^{’}(ka)}{h}_l(k{r}_{<})]h_l(k{r}_{>})}\\ & \times \left\{P_l\left(\cos {\theta }_s\right)P_l(\cos \theta )+{\displaystyle \sum _{m=1}^{l}2\frac{\left(l-m\right)!}{\left(l+m\right)!}{P}_l^m\left(\cos {\theta }_s\right)P_l^m\left(\cos \theta \right)\cos \left[m\left(\varphi -{\varphi }_s\right)\right]}\right\},\end{array}$$

(4)

where ω is the angular frequency, ρ is the air density, q_s is the source strength of the point source, Z_s is the acoustic transfer impedance from the secondary source to the receiving point, r_> = max(r_s,r) and r_< = min(r_s,r). Equation (4) can be used in the calculation of plant responses, including the physical plant response between the secondary source and the physical microphone, as well as the virtual plant response between the secondary source and the virtual microphone.

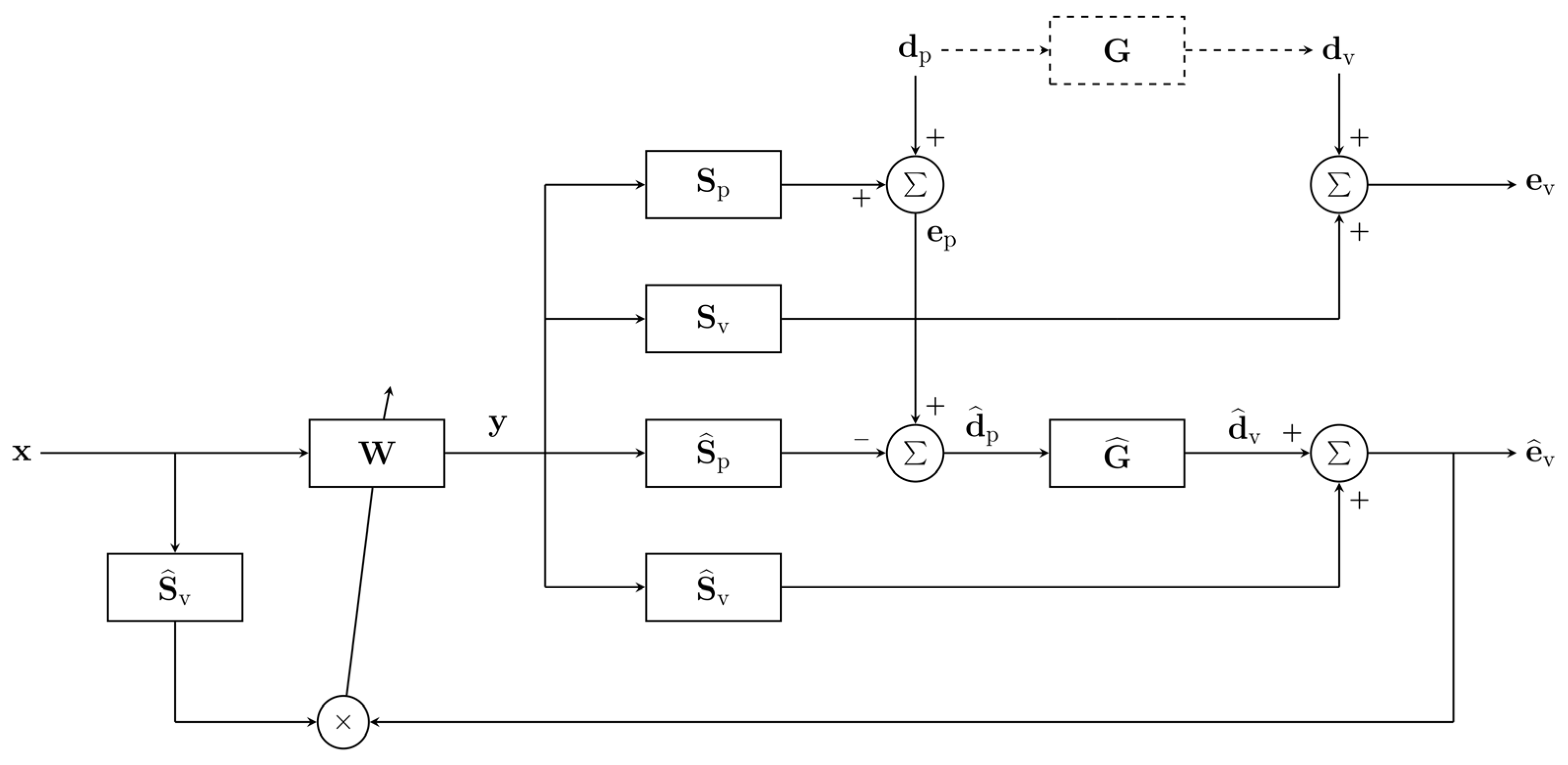
2.3. Active Control System with Remote Microphone Technique

The active headrest studied in this paper combines the remote microphone technique with the filtered-x least mean square (FxLMS) algorithm for adaptive feedforward control. In this section, the residual noise at any location in the active headrest system is formulated and the robustness optimization method for improving the noise reduction performance against the human head rotation is presented. All signals are formulated in the frequency domain in the following, as their dependence on frequency is excluded for notational convenience.

Figure 2 shows the block diagram of the FxLMS algorithm with the remote microphone technique. Assuming there are n virtual microphones, m physical microphones and l secondary sources, the error signals, e_v, at the virtual microphones can be expressed as

$$e_{\mathrm{v}}=d_{\mathrm{v}}+S_{\mathrm{v}}y=P_{\mathrm{v}}x+S_{\mathrm{v}}Wx,$$

(5)

where e_v = [e_v1, e_v2, …, e_vn]^T, d_v = [d_v1, d_v2, …, d_vn]^T is the vector of primary noise signals at the virtual microphones at a given frequency, S_v is the matrix of virtual plant responses, y = [y₁, y₂, …, y_l]^T is the vector of control signals, x is the vector of reference signals, P_v is the matrix of the primary transfer responses between x and d_v, W is the matrix of control filters. d_p = [d_p1, d_p2, …, d_pm]^T is the vector of primary noise signals at the physical microphones, G is the transfer response between d_v and d_p, then d_v can be written as

$$d_{\mathrm{v}}=G{d}_{\mathrm{p}},$$

(6)

where d_p = P_px, d_v = P_vx, and P_p is the matrix of the primary transfer responses between x and d_p. The optimized solution of G can be estimated by minimizing the cost function shown below

$$J_G=\mathrm{trace}\text{{}E[(d_{\mathrm{v}}-\widehat{G}{d}_{\mathrm{p}}){(d_{\mathrm{v}}-\widehat{G}{d}_{\mathrm{p}})}^{\mathrm{H}}+\mathsf{\lambda }\widehat{G}{\widehat{G}}^{\mathrm{H}}]\text{}},$$

(7)

where the superscript H is the Hermitian operator, E[] is the expectation operator, and λ is the regularization factor. Then $\widehat{G}$_opt can be calculated by [9]

$${\widehat{G}}_{\mathrm{opt}}=P_{\mathrm{v}}Q{P}_{\mathrm{p}}^{\mathrm{H}}{\left(P_{\mathrm{p}}Q{P}_{\mathrm{p}}^{\mathrm{H}}+\mathsf{\lambda }I\right)}^{-1},$$

(8)

where Q = E[xx^H] is the power spectral density matrix for x and I is the identity matrix.

Without actual microphones to pick up error signals at the virtual microphone positions, the estimated virtual error signals ${\widehat{e}}_{\mathrm{v}}$ can be expressed as

$${\widehat{e}}_{\mathrm{v}}={\widehat{G}}_{\mathrm{opt}}{\widehat{d}}_{\mathrm{p}}+{\widehat{S}}_{\mathrm{v}}y,$$

(9)

where ${\widehat{S}}_{\mathrm{v}}$ is the corresponding estimated model of the transfer response S_v, and ${\widehat{d}}_{\mathrm{p}}$ can be expressed as

$${\widehat{d}}_{\mathrm{p}}=e_{\mathrm{p}}-{\widehat{S}}_{\mathrm{p}}y,$$

(10)

$$e_{\mathrm{p}}=d_{\mathrm{p}}+S_{\mathrm{p}}y,$$

(11)

where e_p = [e_p1, e_p2, …, e_pm]^T is the vector of error signals at the physical microphones, S_p is the matrix of physical plant responses, ${\widehat{S}}_{\mathrm{p}}$ is the corresponding estimated model. The estimated models of the transfer responses are usually pre-modelled at the nominal head position, which might differ from the real responses with head movement. Substituting Equations (10) and (11) into Equation (9) yields

$${\widehat{e}}_{\mathrm{v}}={\widehat{G}}_{\mathrm{opt}}{d}_{\mathrm{p}}+\left[{\widehat{S}}_{\mathrm{v}}+{\widehat{G}}_{\mathrm{opt}}\left(S_{\mathrm{p}}-{\widehat{S}}_{\mathrm{p}}\right)\right]y={\widehat{G}}_{\mathrm{opt}}{d}_{\mathrm{p}}+Sy,$$

(12)

where S is the matrix of effective plant responses between y and ${\widehat{e}}_{\mathrm{v}}$, which is defined as

$$S={\widehat{G}}_{\mathrm{opt}}\left(S_{\mathrm{p}}-{\widehat{S}}_{\mathrm{p}}\right)+{\widehat{S}}_{\mathrm{v}}.$$

(13)

The cost function of the active control system with remote microphone technique shown in Figure 2 is defined as

$$J_{\mathrm{y}}=\mathrm{trace}\text{{}E[{\widehat{e}}_{\mathrm{v}}{\widehat{e}}_{\mathrm{v}}^{\mathrm{H}}]\text{}}=\mathrm{trace}\text{{}E[\left({\widehat{G}}_{\mathrm{opt}}{d}_{\mathrm{p}}+Sy\right){\left({\widehat{G}}_{\mathrm{opt}}{d}_{\mathrm{p}}+Sy\right)}^{\mathrm{H}}]\text{}}.$$

(14)

By minimizing the cost function, the optimal control signals can be derived as [9]

$$y_{\mathrm{opt}}=-{\left(S^{\mathrm{H}}S\right)}^{-1}{S}^{\mathrm{H}}{\widehat{G}}_{\mathrm{opt}}{d}_{\mathrm{p}}.$$

(15)

The performance of the system is evaluated by the noise reduction at an evaluation point close to the human ear. The virtual microphone of a single-channel system may be located at the evaluation point, while the virtual microphone positions of a dual-channel system may not coincide with the evaluation point. The residual noise signal measured at the evaluation point by a measurement microphone, e_m, can then be expressed as

$$e_{\mathrm{m}}=d_{\mathrm{m}}+S_{\mathrm{m}}y,$$

(16)

where d_m is the primary noise signal at the measurement microphone, and S_m is the vector of secondary transfer responses from control sources to the measurement microphone. The residual noise factor β_r is defined as the ratio of e_m to d_m when the control output is optimized and can be expressed as

$${\beta }_{\mathrm{r}}=\frac{e_{\mathrm{m}}}{d_{\mathrm{m}}}=1+\frac{S_{\mathrm{m}}{y}_{\mathrm{opt}}}{d_{\mathrm{m}}}=1-\frac{S_{\mathrm{m}}{\left(S^{\mathrm{H}}S\right)}^{-1}{S}^{\mathrm{H}}{\widehat{G}}_{\mathrm{opt}}{d}_{\mathrm{p}}}{d_{\mathrm{m}}},$$

(17)

where the smaller the factor β_r, the greater the noise reduction.

2.4. Robustness Optimization Method

The use of active headrests involves a transfer path identification stage and a control stage. The various estimates of the transfer response in Equation (15), ${\widehat{S}}_{\mathrm{v}}$, ${\widehat{S}}_{\mathrm{p}}$ and ${\widehat{G}}_{\mathrm{opt}}$, are derived at the identification stage with the head at the nominal position. As the head is rotated or moved, the system still uses these estimated transfer responses with the head at the nominal position, which deviate from the real responses at the new position, leading to reduced control performance.

When the human head is rotated by θ, the residual noise factor at the measurement microphone is

$${\beta }_{\mathrm{r}}\left(\theta \right)=1-\frac{S_{\mathrm{m}}\left(\theta \right){\left(S^{\mathrm{H}}\left(\theta \right)S\left(\theta \right)\right)}^{-1}{S}^{\mathrm{H}}\left(\theta \right){\widehat{G}}_{\mathrm{opt}}{d}_{\mathrm{p}}\left(\theta \right)}{d_{\mathrm{m}}\left(\theta \right)},$$

(18)

$$S\left(\theta \right)={\widehat{G}}_{\mathrm{opt}}\left(S_{\mathrm{p}}\left(\theta \right)-{\widehat{S}}_{\mathrm{p}}\right)+{\widehat{S}}_{\mathrm{v}},$$

(19)

where S_m(θ), S_p(θ), d_p(θ) and d_m(θ) are the corresponding transfer response matrices and the primary noise vectors as the head rotated by θ. Correspondingly, the noise reduction can be written as

$$NR\left(\theta \right)=-{20\log }_{10}\left(\left|{\beta }_{\mathrm{r}}\left(\theta \right)\right|\right).$$

(20)

The aim of the study is to maintain good noise reduction at the human ear when the head rotates. The human head can be approximated as a sphere, with the different ear positions lying on a horizontal plane as it rotates, so the problem is equivalent to having better results at all points on the horizontal circle of the human ear when the head is in its nominal position. A straightforward approach is to deploy multiple virtual microphones on the “ear circle” and minimizing the virtual error signals from them simultaneously to acquire the optimal control signals. However, this approach includes multiple error signals, which significantly increases the computational effort of the adaptive algorithm. An alternative approach does not add virtual error signals and directly optimizes the transfer response models to average or limit the noise reduction of the human ear at each position to obtain similar performance. The cost function is defined as the maximum residual noise factor, expressed respectively as

$$J={\Vert {\beta }_{\mathrm{r}}\left(\theta \right)\Vert }_{\infty },$$

(21)

For the cost function of Equation (14), the update equation of the vector of control signals when using the adaptive algorithm can be obtained by using the stochastic gradient descent method, expressed as [9]

$$y(n+1)=y(n)-\alpha {\widehat{S}}_{\mathrm{v}}^{\mathrm{H}}{\widehat{e}}_{\mathrm{v}}\left(n\right),$$

(22)

where α is the iteration step size. Substituting Equation (12) into Equation (22) yields

$$y(n+1)=y(n)-\alpha {\widehat{S}}_{\mathrm{v}}^{\mathrm{H}}({\widehat{G}}_{\mathrm{opt}}{d}_{\mathrm{p}}\left(n\right)+Sy(n)).$$

(23)

When the convergence is achieved, y(n + 1) = y(n), and therefore the expression in the parentheses in Equation (23) is zero. Then the vector of control signals is derived as

$$y_{\infty }=-{\left({\widehat{S}}_{\mathrm{v}}^{\mathrm{H}}S\right)}^{-1}{\widehat{S}}_{\mathrm{v}}^{\mathrm{H}}{\widehat{G}}_{\mathrm{opt}}{d}_{\mathrm{p}}\left(n\right).$$

(24)

By subtracting Equation (24) from both sides of Equation (23), the update equation can be written as

$$y(n+1)-y_{\infty }=\left(I-\alpha {\widehat{S}}_{\mathrm{v}}^{\mathrm{H}}S\right)\left(y(n)-y_{\infty }\right).$$

(25)

Then, the condition that ensure the stability of the adaptive algorithm can be obtained as [9]

$$\mathrm{Re}\left(\mathrm{eig}\left({\widehat{S}}_{\mathrm{v}}^{\mathrm{H}}S\right)\right)>0.$$

(26)

It is worth mentioning that the real parts of the eigenvalues of ${\widehat{S}}_{\mathrm{v}}^{\mathrm{H}}S$ are always positive when S_p = ${\widehat{S}}_{\mathrm{p}}$, at which point the stability constraint is automatically satisfied.

As the head is generally in the nominal position for a relatively long time, a lower limit threshold for noise reduction can be set. Therefore, the optimization problem with constraints to be solved can be expressed as

$$\underset{{\widehat{S}}_{\mathrm{v}}or\widehat{G}}{\min }J={\Vert {\beta }_{\mathrm{r}}\left(\theta \right)\Vert }_{\infty },$$

(27)

$$s.t.\mathrm{Re}\left(\mathrm{eig}\left({\widehat{S}}_{\mathrm{v}}^{\mathrm{H}}S\left(\theta \right)\right)\right)>0,\mathrm{for}\mathrm{all}\theta ,$$

(28)

$$s.t.NR\left(\theta \right)>N{R}_0,\theta =0,$$

(29)

where θ = 0 denotes the head in the nominal position. Equation (27) indicates that the robustness optimization method achieves the optimization objective of minimizing the maximum value of the residual noise factor for different rotation angles by optimizing the vector of virtual plant models ${\widehat{S}}_{\mathrm{v}}$ or $\widehat{G}$, while Equations (28) and (29) are constraints on the system stability and on the noise reduction of the head at the nominal position, respectively. Although there are many ways to solve this multi-objective optimization problem with constrains, such as the sequential quadratic programming (SQP) method [21], the genetic algorithm (GA) [22] and the particle swarm optimization (PSO) [23], the genetic algorithm [22] was used for this paper due to its generality, robustness, and because it is not biased towards the locally optimal solution.

3. Simulations

Based on the physical model and optimization methods described above, the robustness of the active headrest system to human head rotation is investigated in this section. The angle of human head rotation ranges from −90° to 90°, where the positive sign denotes the clockwise rotation and the negative sign denotes the counterclockwise rotation from the top view. An active headrest system with two secondary sources is shown in Figure 3, with the y coordinates of the secondary sources and the physical microphones at ±30 cm and ±25 cm respectively, while the virtual microphones are on the y-axis, 2 cm away from the surface of the rigid sphere with a radius of 8.5 cm, which are also the evaluation points for measuring the noise reduction performance. Assuming weak coupling effects between the transmission channels of the secondary sources, a single channel system on only the left side of the head can be discussed, so this is hereafter referred to as a single channel active headrest system.

As for an active headrest system with four secondary sources, two different layouts are discussed as shown in Figure 4. Again, due to the weak coupling effects of the transmission channels of the secondary sources on either side of the human head, only the dual-channel system on the left side of the head is considered. The physical system of layout A is symmetrical about the y-axis in the xy-plane, with two secondary sources on each side of the head and corresponding physical microphones near each secondary source. The y coordinates of secondary sources and physical microphones are ±30 cm and ±18 cm respectively, while each secondary source, its corresponding physical microphone and the origin are aligned on the same line, which has an angle α of 30° with the y-axis. The evaluation points are located at the midpoint of the two virtual microphones spaced 2 cm apart, as in the single channel control system, which are on the y-axis and 2 cm from the surface of the rigid sphere. For layout B, the virtual microphone positions remain the same, and the relative positions of the secondary sources and physical microphones to the rigid sphere are the same as in layout A, except that they are arranged in the yz-plane.

Since active headrest systems are generally used at low frequencies, simulations are carried out in a tonal sound field in this paper, with the tonal frequencies of 125, 250 and 500 Hz. Simulation results for these frequencies show similar patterns, with only results for 250 Hz provided in detail due to the length of the article.

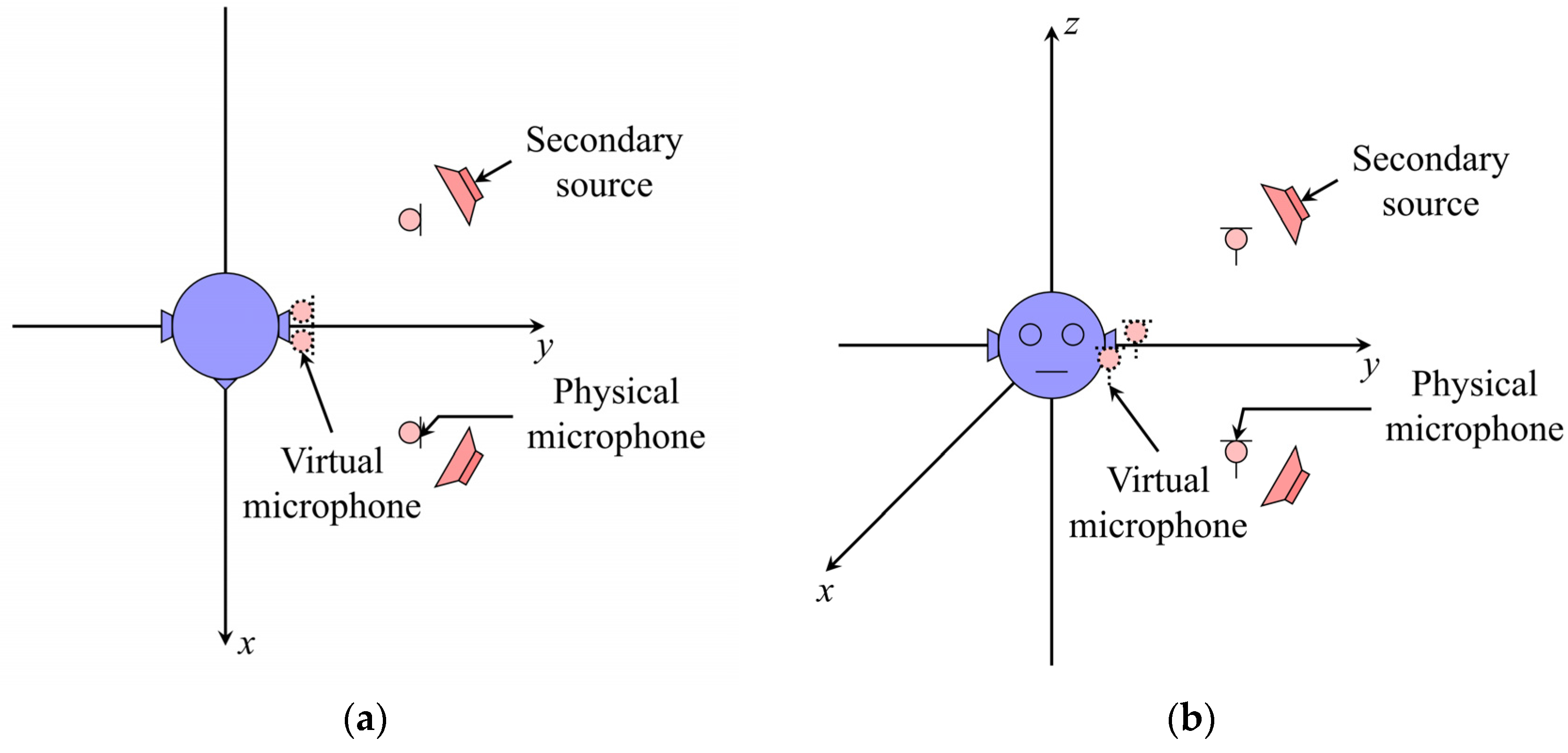
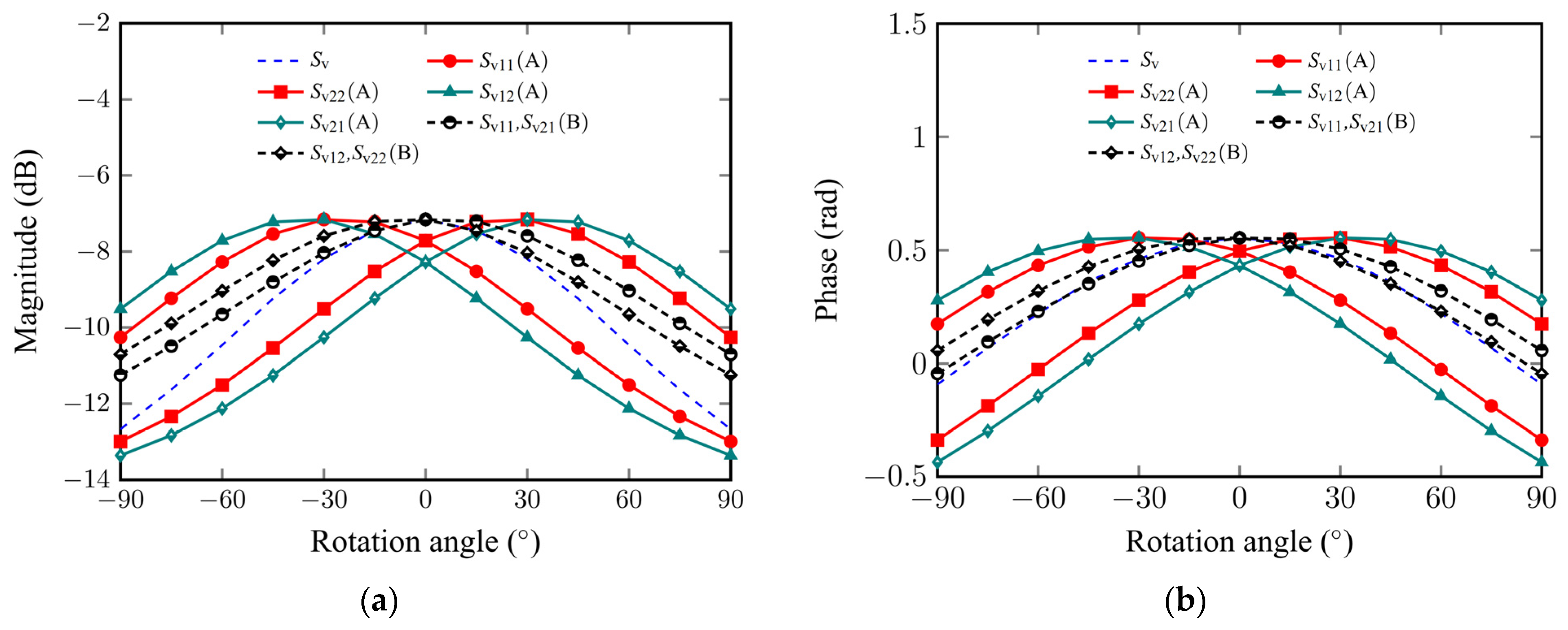
3.1. Transfer Response Analysis

The main cause for the deterioration in noise reduction performance when the head rotates is the variation of the transfer responses, including the transfer responses S_p for physical plants, the transfer responses S_v for virtual plants and the transfer responses G between the virtual microphone locations and the physical microphone locations in the primary field. However, the transfer responses S_p almost remain unchanged during head rotation, so only the variation curves of the other two transfer responses of a single channel system are shown in Figure 5. Since the primary diffuse field contains multiple sound field samples, the variation curves of the transfer response G are given in Figure 5c,d for each of the five sound field samples, which are chosen from 30 primary sound field samples. In Figure 5c, Sample 1 displays the maximum variation of magnitude among 30 primary field samples while Sample 2 displays the minimum variation of magnitude. In Figure 5d, Sample 3 displays the minimum variation of phase among 30 primary field samples while Sample 4 displays the maximum variation of phase. It can be concluded that the transfer response S_v varies more with the head rotation than the transfer response G, thus only these kind of transfer responses are analyzed and optimized later. Figure 6 demonstrates the variation curves of transfer responses S_v for single channel system and dual-channel system with two layouts when head rotates, where the subscript i and j (i, j = 1, 2) of S_vij indicate that the transfer response is between the ith secondary source and the jth virtual microphone. The dual-channel system with layout A has the maximum variation of both magnitude and phase, with a maximum variation of 6.2 dB in amplitude and 1.0 rad in phase. As for the dual-channel system with layout B, similar to the single channel system, the variation curves are also symmetrical about the rotation angle of 0. Its maximum difference in amplitude is 4.1 dB, less than the 5.5 dB of the single channel system, while the phase variation curve is very similar to that of the single channel system and varies very little, with a maximum difference of only 0.6 rad.

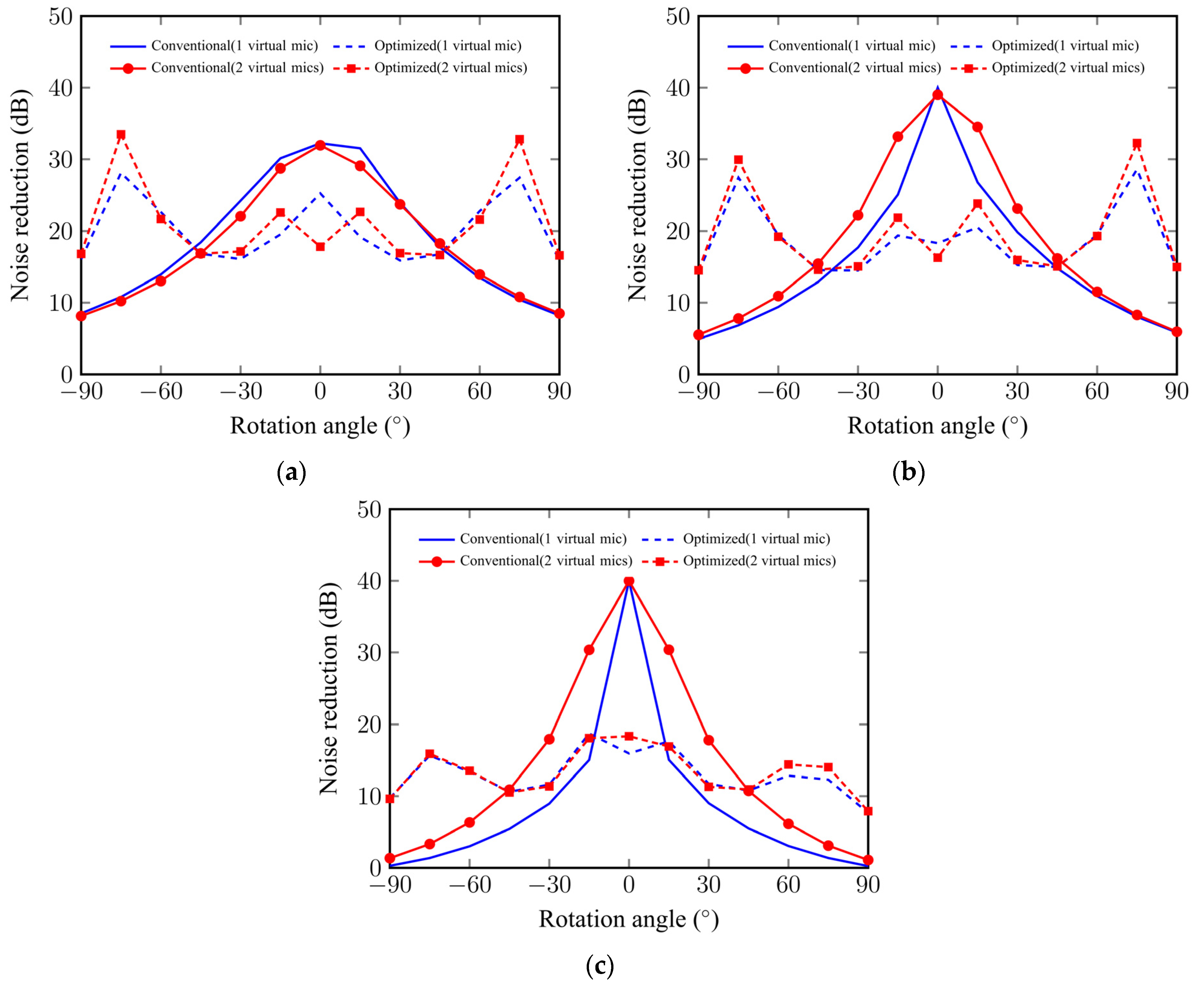
3.2. System Performance

The noise reduction performance of a single channel system, whose layout is shown in Figure 3 is discussed firstly. The range of the optimization angle is set as [−90°, 90°], including the maximum rotation angle in practical scenarios, such as a passenger sleeping in a couchette train. However, in practical applications the range should be set for specific requirements. If designed for all head rotation angles simultaneously, error microphones of the multiple virtual error microphone method need to be evenly distributed over half the “ear circle”, which is too large in range and results in poor noise reduction performance at each virtual error point. Similarly, the optimal virtual plant model of the transfer response model optimization method is difficult to satisfy for all rotation angles. Then the system performance is optimized against the head rotation in the positive and negative directions separately. The multiple virtual microphone method optimizes two filters for the virtual microphone locations of a quarter of the “ear circle” in the positive and negative directions, while the transfer response model optimization designs two virtual plant models corresponding to the two directions. For the latter method, the transfer response model for the nominal position was chosen to be the one with the larger noise reduction of the optimization results in the two directions.

For the multiple virtual microphone method, 13 virtual error points are evenly distributed on the “ear circle” and the measurement microphone coincides with these virtual error points when the head rotates 15° × i (i = 0…6) clockwise and counterclockwise. For transfer response model optimization, the virtual error microphone is placed near the ear as shown in Figure 3 and moves accordingly to the head rotation. It was concluded in the previous section that S_v changes the most with the head rotation, so only the model of S_v was optimized, while the models of S_p and G were obtained with the head at the nominal position.

Figure 7 presents the noise attenuation NR with respect to the head rotation angle before and after optimization with two optimization methods, where the rotation angles are set as 15° × i (i = 0…6) clockwise and counterclockwise. In the following, if not specified, NR₀ in Equation (29), i.e., the threshold of the noise reduction at the nominal position, is set to 10 dB. It has been shown that for conventional systems without optimization, the noise attenuation can exceed 40 dB at the nominal position and decrease as the head rotation angle increases, with the noise attenuation less than 10 dB at rotation angles over 45° and a minimum NR is 3.0 dB at the maximum rotation angle. When using multiple virtual microphones, noise reduction performance is improved for rotation angles over 30°, and the range of rotation angles with a noise attenuation of over 10 dB is increased to 60°, and the minimum noise attenuation improves to 5.7 dB. Although the noise reduction decreases when the rotation angle is small, the difference in noise reduction when the rotation angle changes is significantly reduced compared to the original system, which can lead to a better subjective listening experience. However, multiple virtual signals significantly increase the computational effort of the adaptive algorithm, and the performance robustness to changes in the acoustic transfer paths may be reduced due to the addition of several times more acoustic transfer paths.

It has been shown that for the transfer response model optimization method, noise reduction is only 1.7–6.2 dB at rotation angles of ±30° and ±45° than with multiple virtual microphones, while the optimization performance at most rotation angles is very close to each other, with a difference of less than 1.5 dB. As noise reduction performance is already good at angles of ±30° and ±45°, this difference does not affect the subjective listening experience when the human head is rotated. Therefore, the transfer response model optimization method can be used to improve the robustness against human head rotation.

Figure 7 shows that the noise reduction of the optimized single channel system is still less than 10 dB as the head rotates over 60°, and the minimum noise reduction is only 5.5 dB. Increasing the number of secondary sources can improve the noise reduction performance, so a dual-channel system can be adopted [16,17,18]. The control performances of the dual-channel system before and after optimization of the transfer response model with the two physical system arrangements in Figure 4 are compared in Figure 8, while the control performances of the single channel system are also given. It is shown that the performance of the dual-channel system before optimization with layout A is improved in comparison with the original single channel system, with noise attenuation over 10 dB at rotation angles less than 60°, but the improvement decreases as the rotation angle increases, with a minimum reduction of 5.5 dB. After optimization, the noise reduction exceeds 14.5 dB at every head rotation angle, with less of a difference in noise reduction at most angles, except for ±75° where noise reduction is significantly higher. It performs better than the optimized single channel system because the noise reduction is only slightly less at ±30° and ±45°, but the improvement in noise reduction exceeds 6.0 dB at all other angles. However, for the dual-channel system with layout B, the performance improvement is insignificant compared with the single channel system. The difference in noise reduction at each rotation angle before optimization is less than 2.4 dB, while after optimization the corresponding performance curves for both systems are shown to have similar trends and values, with the difference in noise reduction between the two being less than 4.2 dB at each rotation angle. It can be explained that the transfer responses for virtual plants of both systems remain relatively close to each other as the human head rotates, as shown in Figure 6, suggesting that the second source of the dual-channel system with layout B does not offer more degrees of freedom.

Results at other frequencies, namely 125 Hz and 500 Hz, are then presented. Figure 9 depicts the control performance of the original system at three frequencies with head rotation. It is shown that as the head rotates, the noise attenuation decreases faster at higher frequencies because of the shrunken quiet zone. The minimum noise reduction is only 1.1 dB at the maximum rotation angle at 500 Hz.

Figure 10 presents the noise control performance before and after optimization at 125 Hz and 500 Hz, showing the similar significant improvement in noise control performance for larger rotation angles. Compared with the noise attenuation before optimization, the minimum value increases from 7.8 dB to 16.6 dB at 125 Hz and from 1.1 dB to 7.9 dB at 500 Hz. In summary, the method improves the robustness to the human head rotation for the frequencies of interest and makes the difference between the noise reduction for different rotation angles smaller.

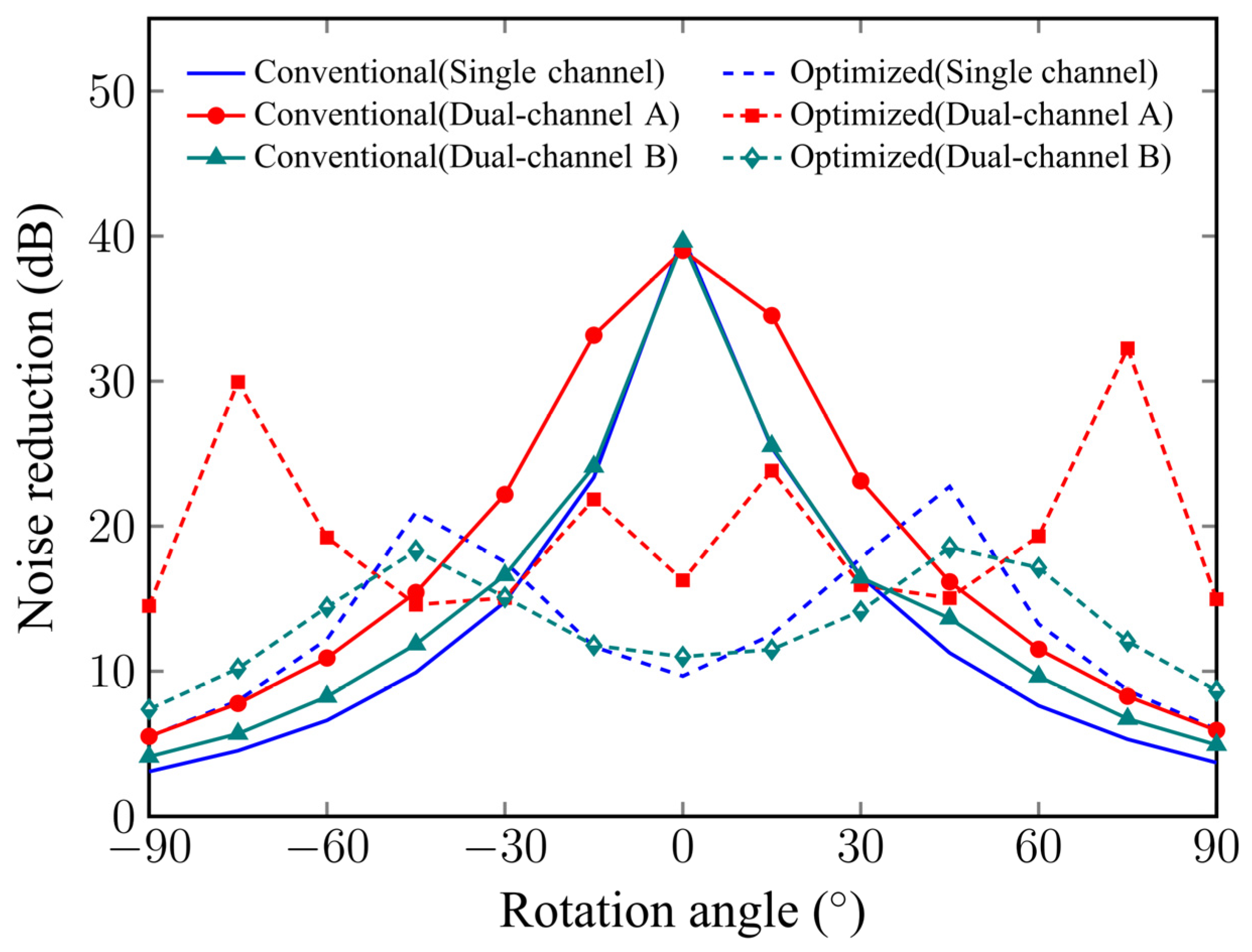
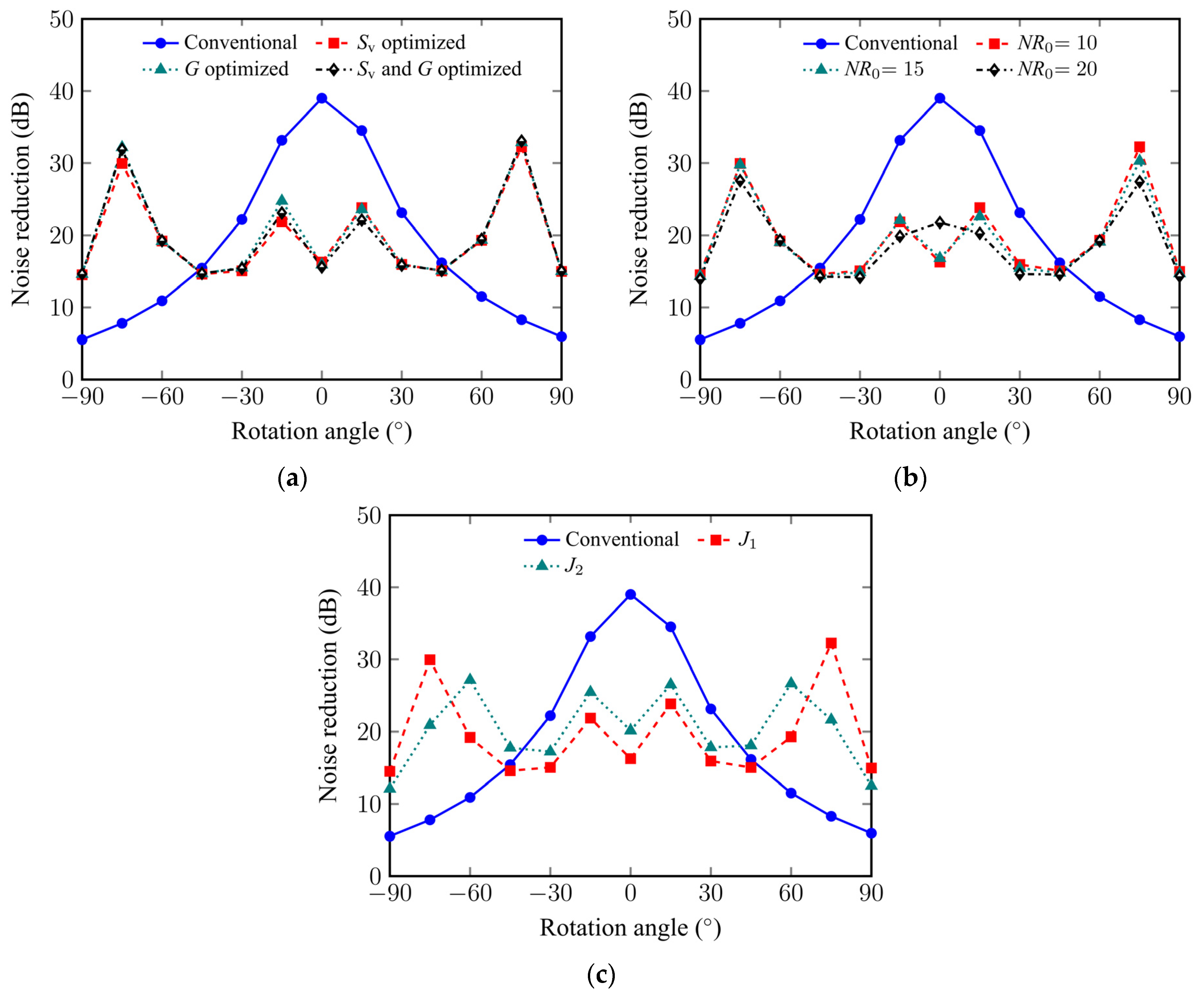
3.3. Influence of Different Parameters

There are a few parameters that have an impact on the results of the transfer response model optimization method. Firstly, three types of transfer response model, whose variation with head rotation has been analyzed in Section 3.1, may influence the noise reduction performance, and the model of S_v has been chosen for optimization. The optimization results with the model of S_v optimized, the model of G optimized and the models of S_v and G optimized simultaneously are presented in Figure 11a and it can be concluded that there is almost no difference between the three results. This can be explained by Equation (17), where the cost function is determined by ${\widehat{S}}_{\mathrm{v}}^{-1}{\widehat{G}}_{\mathrm{opt}}$ when the transfer response S_p remains almost constant with head rotation (which is usually the case). Since ${\widehat{S}}_{\mathrm{v}}^{-1}{\widehat{G}}_{\mathrm{opt}}$ can be regarded as an adjustable parameter, optimizing either model of S_v or G is equivalent to adjusting the entire ${\widehat{S}}_{\mathrm{v}}^{-1}{\widehat{G}}_{\mathrm{opt}}$ to minimize the cost function.

The lower threshold of noise reduction at the nominal position can be another factor influencing the optimization result. The noise attenuation with respect to the head rotation angle after optimization for different NR₀ constraints is shown in Figure 11b. It is shown that the higher the NR₀, the better the control performance at the nominal position, but will slightly reduce the noise attenuation at other rotation angles, especially those where the noise reduction is fairly high, such as ±15° and ±75°.

The previous analyses are based on cost function of the maximum residual noise factor. However, there are also some other general cost functions which can be taken into account, such as the sum of squared residual noise factor at each position, denoted as J₂, and the corresponding noise attenuation curve after optimization is shown as the dotted line in Figure 11c. Comparing with the red dashed line depicting the optimization result based on J₁, i.e., the maximum residual noise factor, the optimized system performance is better when the head rotates from −60° to 60°, but at larger rotation angles the performance is worse with the minimum noise attenuation still at −90°, which is 2.4 dB lower than that based on J₁. It can be concluded that, if the minimum reduction at all rotation angles is important, J₁ is better, but when only considering the control performance of rotation angles less than 60°, J₂ is more suitable. Moreover, when considering the subjective listening experience, it is necessary to take into account more factors than the amount of noise reduction in the cost function, such as the uniformity of the noise reduction. This issue is subject to further research.

As can be seen from Layout B, using two virtual microphones did not provide more degrees of freedom to significantly improve performance, therefore it is necessary to discuss the case where only one virtual microphone is used in the system with Layout A. A virtual microphone is placed right at the measurement microphone position, the midpoint of the line connecting the two virtual microphones in Figure 4a. Figure 12 shows the noise reduction performances of the system with single virtual microphone before and after optimization at 125 Hz, 250 Hz and 500 Hz and compares them with the results of the system using two virtual microphones. It can be seen that the noise reduction performance using two virtual microphones is better before optimization, except at 125 Hz where the performance is closer, and the advantage is greater at higher frequencies. This is because simultaneous control of the sound pressure at the two virtual error microphones corresponds to simultaneous control of both the sound pressure at a single point and the sound pressure gradient on the line connecting the two virtual sensors, resulting in a wider zone of quiet in the direction of the line. After optimization, the performance of the system with two virtual microphones is better than that of the system with single virtual microphone at most rotation angles, but the advantages are very limited.

4. Experiments

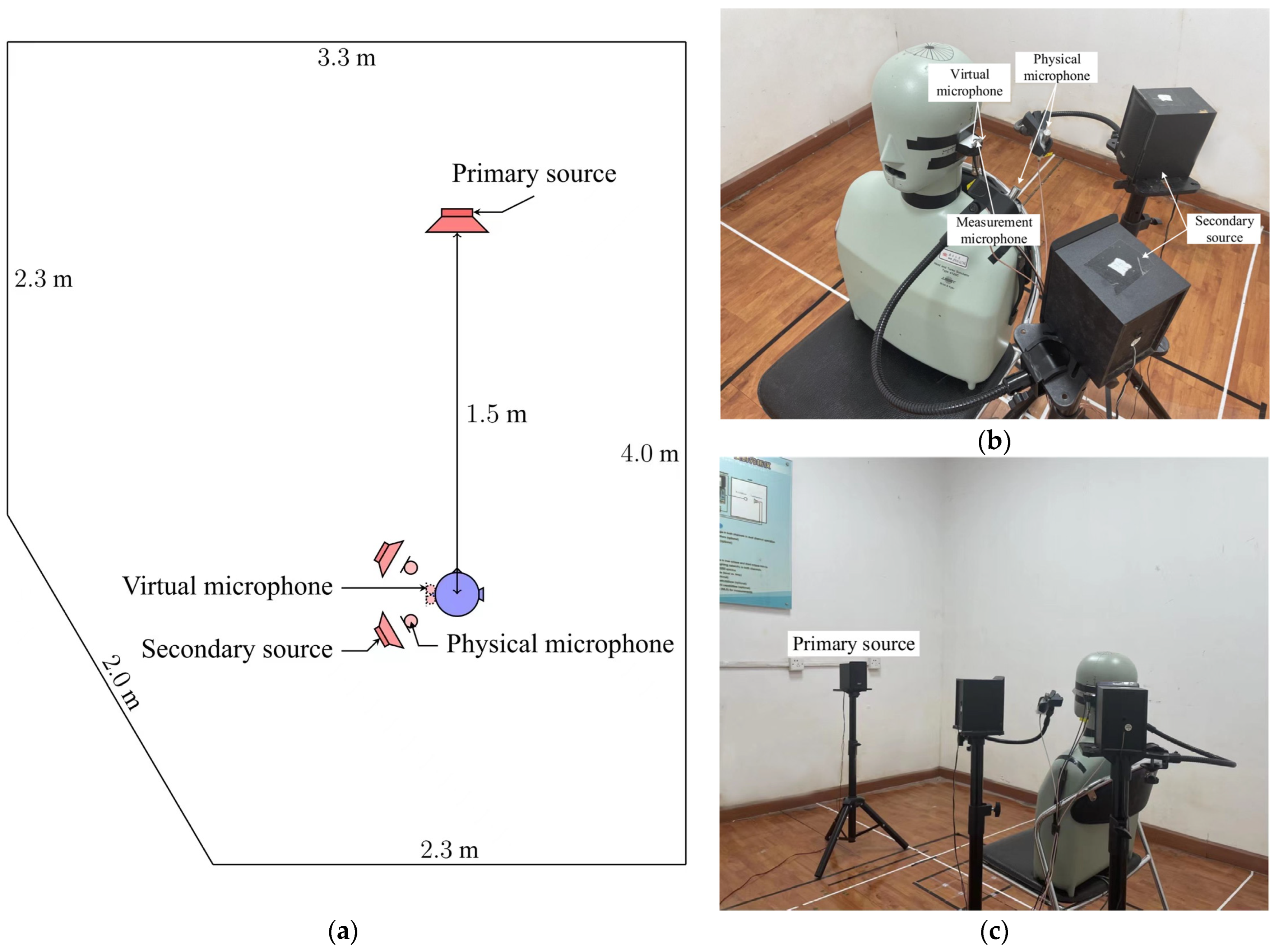
4.1. Setup

Off-line experiments were conducted in an approximately rectangular room with dimensions of 4.0 m × 3.3 m × 3.0 m with reverberation time T60 = 1.5~2.0 s at 100~1000 Hz, i.e., the sound fields and transfer functions were measured in advance and used to calculate the performance of the system. With the reflections of all the surfaces of the room, the sound field in the room is close to the supposed primary sound field mentioned above. A dummy head (B&K, Type 4128C) on a seat was placed in the middle of the room with the primary source in front of it, 1.5 m from the center of the head, as shown in Figure 13a. The primary source was a 5” loudspeaker with a height of 1 m, the same height as the human ear. The coordinate system was established with the origin at the center of the dummy head, the positive direction of the x-axis pointing to the primary source, the positive direction of y-axis points to the left ear, and the z-axis was perpendicular to the x-y plane. A dual-channel system was located near the left ear of the dummy head, and the arrangement of secondary sources, physical microphones and virtual microphones was consistent with the model depicted in Figure 4 for simulations. It should be noted that the measurement microphone and the virtual microphones are connected and fixed to the head using a structure, so that the measurement microphone was 2 cm from the human ear canal and the two virtual microphones were located in front of and behind it at a distance of 1 cm. Their relative position was fixed when the dummy head rotated. The control source and the microphones in front of the ear were denoted as control source 1 and microphone 1, while those behind the ear were denoted as control source 2 and microphone 2. Figure 13b,c shows the photographs of the experimental environment.

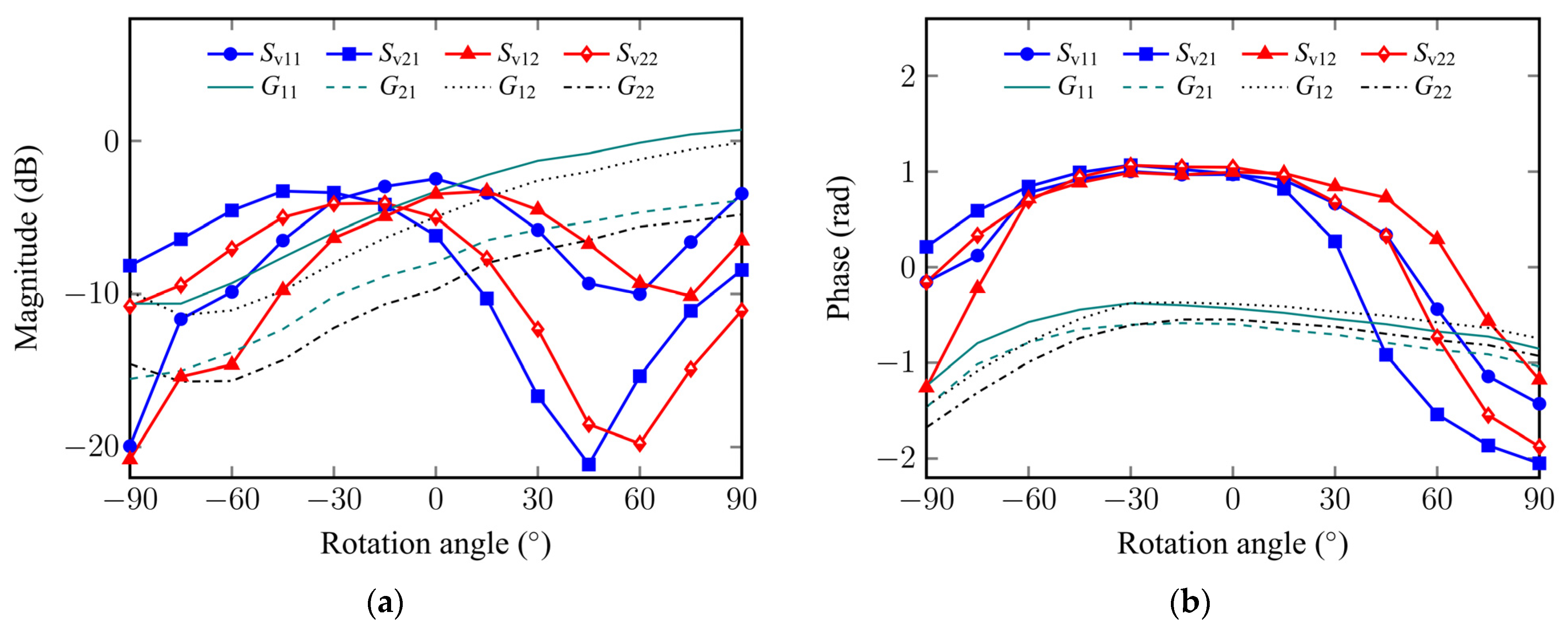
4.2. Analysis of Acoustic Transfer Responses

The variation of acoustic transfer responses of the system was analyzed first. Transfer responses S_vij for virtual plants and transfer responses G_ij between the virtual microphone locations and the physical microphone locations in the primary field with respect to the angle of human head rotation at 250 Hz are shown in Figure 14, where i, j = 1, 2. It can be seen from the four curves with marker in blue and red that the maximum variation of the transfer responses S_vij is about 17.9 dB in magnitude and 3.1 rad in phase, greater than the 6.2 dB and 1.0 rad in the simulation results, a variance which is related to the reflections in the room. The variation tendency between the simulated and measured results is similar in most cases, however, due to room reflections, the amplitude of the measured transfer responses increases with human head rotation angles greater than approximately 45 degrees, which is not consistent with the simulation results.

The transfer responses G_ij are shown as the teal and black curves without marker, with a maximum variation of about 11.7 dB in magnitude and 1.1 in phase, which is less than the transfer responses S_vij. The transfer responses S_pij for physical plants are given in Figure 15, where it can be seen that the transfer responses S_pij remain almost constant as head rotates, with a variation of less than 1 dB in magnitude and 0.4 rad in phase. These results are consistent with the analyses in Section 3.1 and verify that the transfer responses of the virtual plants vary more with the head rotation than other transfer responses.

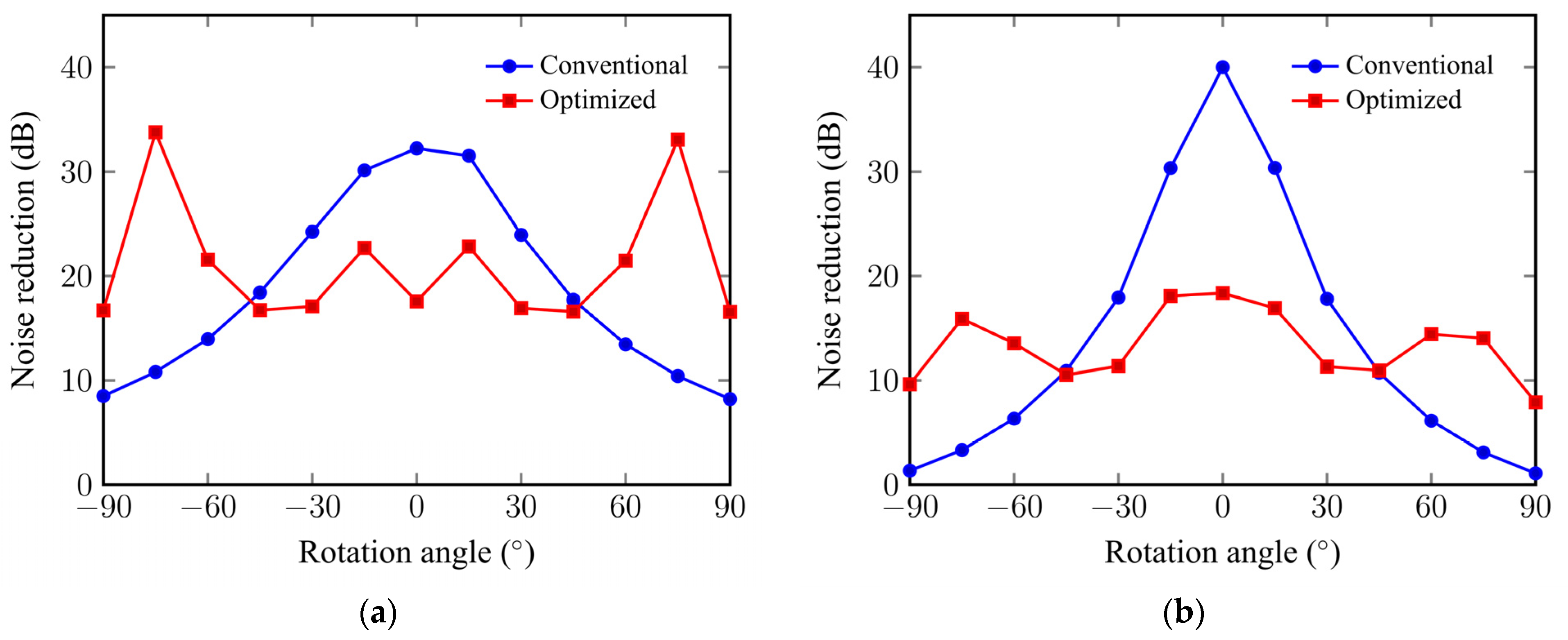
4.3. Noise Control Performance

The measured transfer responses in the previous section are used to optimize the models of the virtual plant responses and calculate the noise attenuation before and after optimization. Due to the complex sound field in the room, the calculated noise attenuation curves with the head rotation can vary considerably even for two frequencies with 1 Hz difference. For more general, the noise attenuation is evaluated in 1/3 octave bandwidth, where the sound energy for each 1/3 octave is counted from that of five uniformly distributed sampling frequencies within that bandwidth. Figure 16 presents the noise attenuation curves with head rotation for 1/3 octave with 125 Hz, 250 Hz and 500 Hz as the center frequency before and after optimization. It can be seen that, before optimization, the noise reduction achieves a maximum at the initial position and decreases as head rotates, with the larger the rotation angle, the less the noise reduction. After optimization, the noise reduction variation curve flattens out relatively, i.e., the noise reduction at larger rotation angles increases while that near the initial position decreases. In addition, the system performance with single virtual microphone is also presented as a comparison. It can be seen that the results before optimization perform the same as the simulation results, but for the results after optimization, the advantage is more pronounced when using two virtual microphones than when using single virtual microphone. This is because in the more complex primary sound field, the system with two virtual microphones provides four virtual secondary path models for optimization, more than the two path models for the system with a single virtual microphone, so the performance is better due to the increase in degrees of freedom.

After optimization, the minimum noise reduction increases from −0.1 dB to 9.0 dB at 500 Hz, which experiences a significant improvement and the performance curves for clockwise and counterclockwise rotation are largely symmetrical. For 250 Hz, the optimization results in a better performance improvement for the counterclockwise head rotation case than the clockwise one, mainly due to an unexpected trough in the amplitude response curve of the virtual plant. Thus, the minimum noise reduction increases from −1.2 dB to 6.0 dB for clockwise head rotation, with an improvement of 7.2 dB; however, for counterclockwise head rotation the improvement is from −0.9 dB to 11.4 dB with an increase of 12.3 dB. As at 250 Hz, the optimization results in better noise reduction at 125 Hz with the clockwise head rotation, increasing the minimum noise reduction from 14.3 dB to 21.7 dB, with an improvement of 7.4 dB; however, the minimum noise reduction increases by 10.7 dB when the head is turned counterclockwise. In summary, the robustness optimization method increases the minimum noise reduction by at least 7.2 dB, and the difference in noise reduction at different head rotation angles becomes smaller.

5. Conclusions

The robustness of an active headrest system with virtual sensing to the head rotation has been investigated. A theoretical model has been developed to analyze the variation of three acoustic transfer responses with the head rotation and their effect on noise reduction performance. The simulation results show that the performance deterioration with the head rotation is mainly related to the variation of the transfer responses for virtual plants and the transfer responses between the virtual microphone locations and the physical microphone locations in the primary field.

A robust optimization method has been used to minimize the maximum value of the residual noise at error points for different angles of human head rotation by designing optimal virtual plant models, which improves the robustness of the system against head rotation. This performs similarly as when using multiple virtual microphones around the human head at most rotation angles, but it requires less computation and is more practical. Using the optimization method, an optimized horizontally arranged dual-channel system provides a significant improvement in noise reduction performance at different head rotation angles in the frequency band of interest, which cannot be achieved by a single-channel system.

The parameters of the method have an impact on the performance of the optimization. Although optimization of the transfer response of G achieves similar results to optimization of the transfer response S_v, the latter is more general because S_v is not sensitive to the primary sound field. Setting a different lower threshold of noise reduction at the initial head position has little change in noise reduction performance as it only slightly affects the performance at positions where the rotation angle is very small.

Finally, off-line experiments were carried out in an ordinary room, using the actual measured sound field and acoustic transfer functions for system optimization and to calculate the performance of the system. The results validate the effectiveness of the proposed optimization method. In future work, the control performance of the proposed method for broadband noise will be investigated and real-time experiments will be carried out in practical applications, such as active control systems for road noise in vehicles.