Robust Near-Optimal Aerocapture Guidance Method Based on Saturation Function
Abstract
1. Introduction
2. Aerocapture Modeling and Maneuver Description
2.1. Three-DOF Dynamic Model
2.2. Impulsive Orbital Maneuvers
3. Guidance Law Design Based on Saturation Function
3.1. Longitudinal Guidance Law
3.2. Lateral Guidance Law
3.3. Architecture of the Numerical Predictor-Corrector Guidance
4. Simulations and Result Analysis
4.1. Algorithm Verification and Analysis
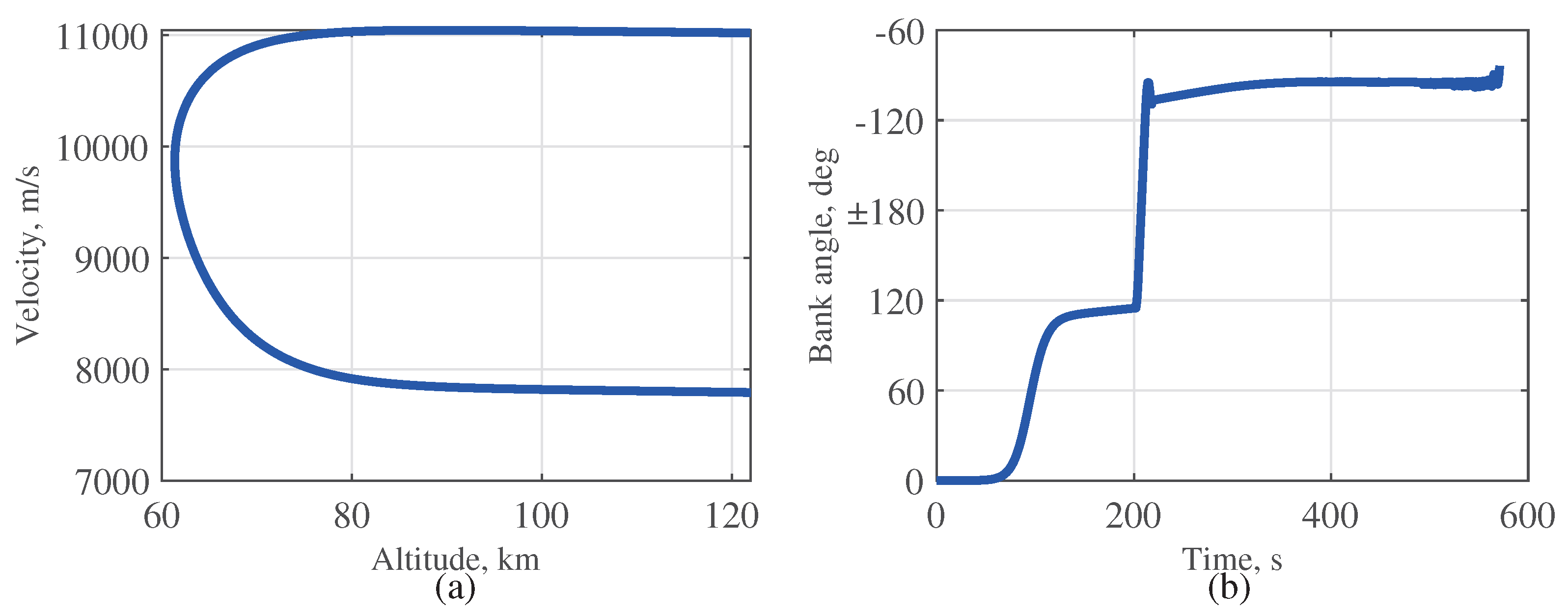
4.1.1. Preliminary Monte Carlo Simulation
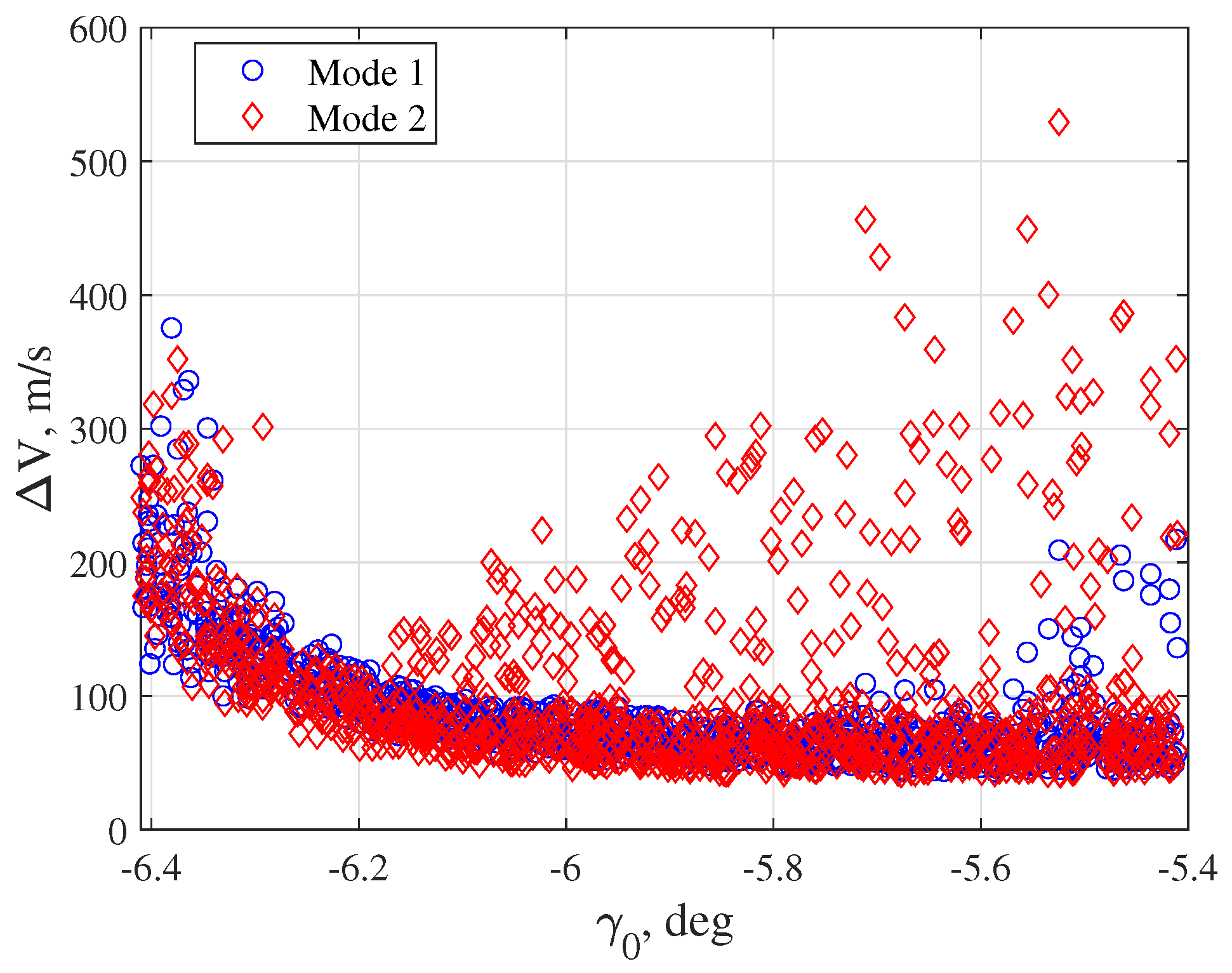
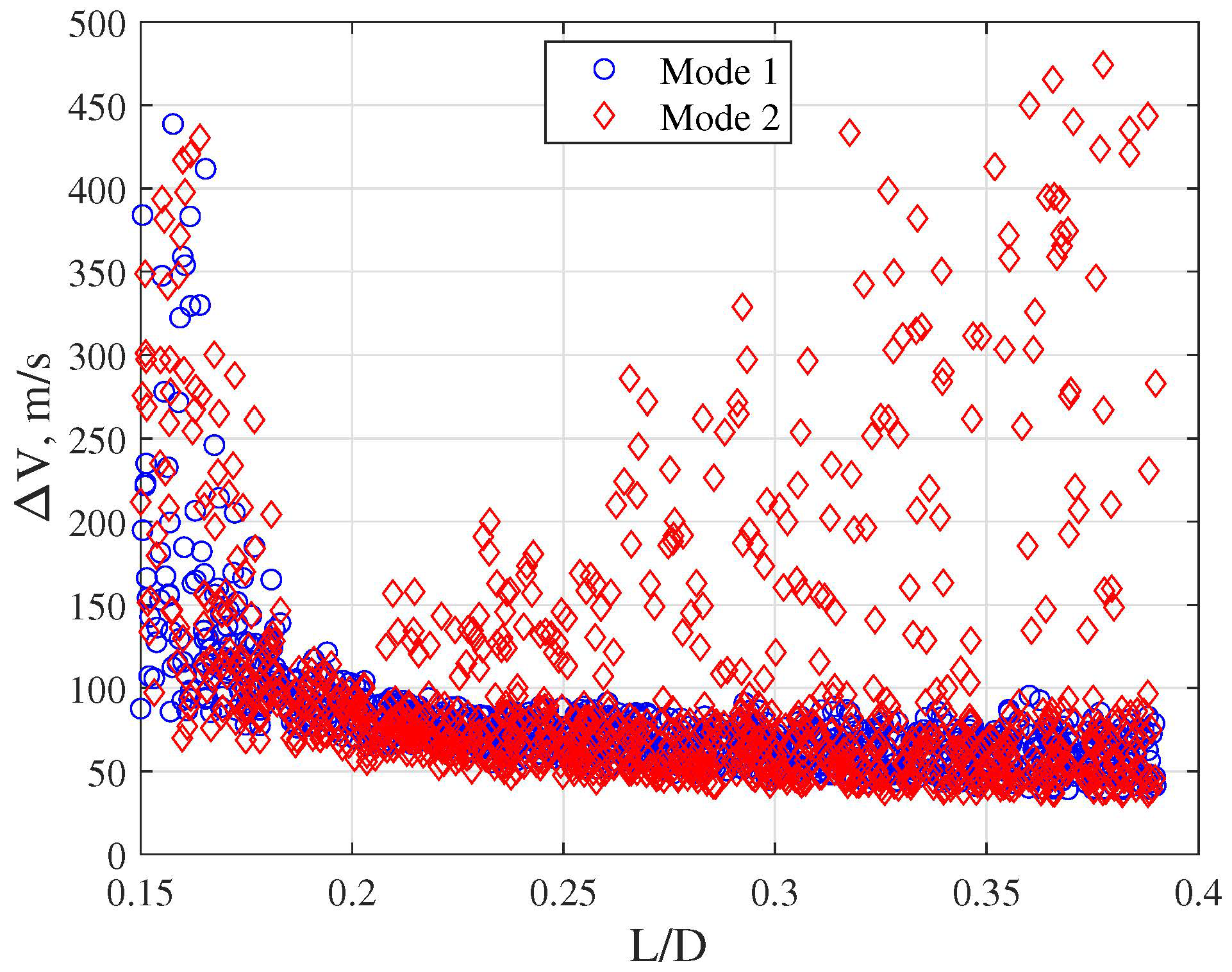
4.1.2. Parameter Impact Analysis and Comparison
4.2. Mars Aerocapture Mission
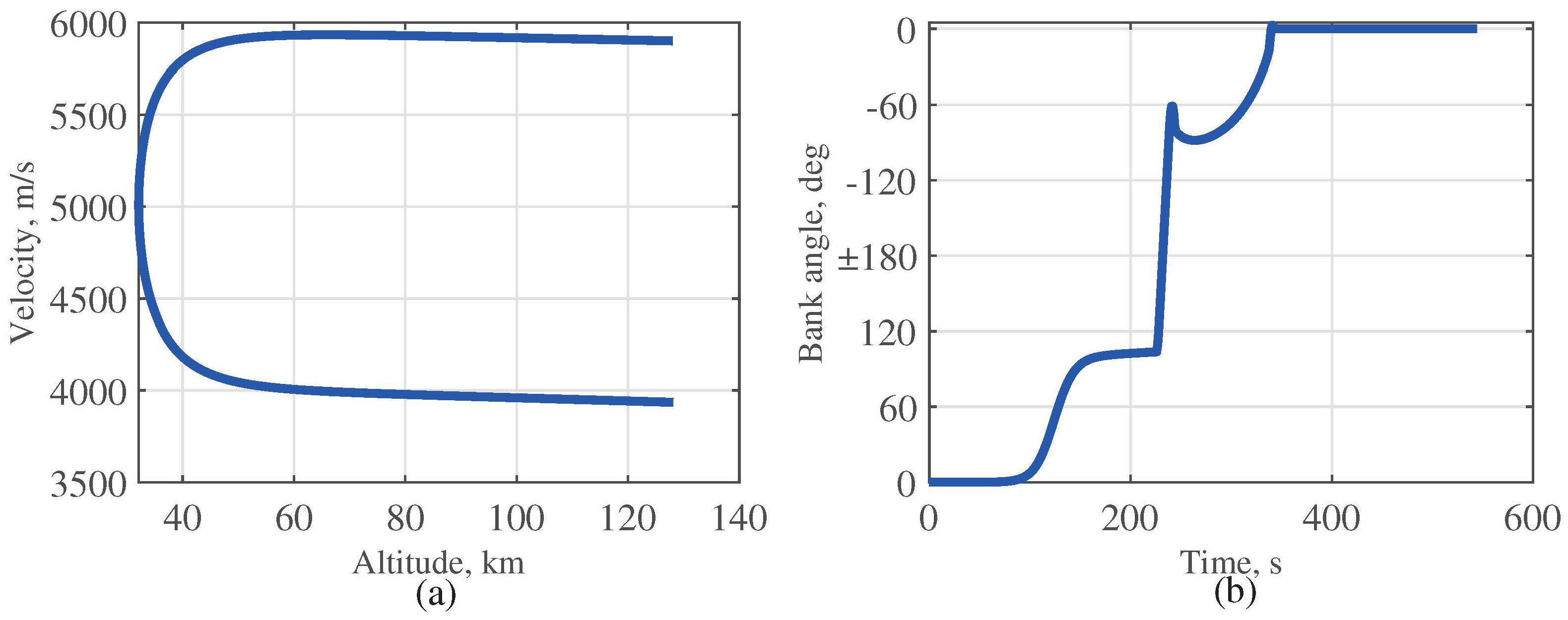
4.2.1. Preliminary Monte Carlo Simulation
4.2.2. Parameter Impact Analysis and Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoffman, S. A comparison of aerobraking and aerocapture vehicles for interplanetary missions. In Proceedings of the Astrodynamics Conference, Seattle, WA, USA, 22–25 August 1984; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1984. [Google Scholar] [CrossRef]
- Hall, J.L.; Noca, M.A.; Bailey, R.W. Cost-Benefit Analysis of the Aerocapture Mission Set. J. Spacecr. Rocket. 2005, 42, 309–320. [Google Scholar] [CrossRef]
- Lockwood, M.K. Titan Aerocapture Systems Analysis. In Proceedings of the 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Huntsville, AL, USA, 20–23 July 2003; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2003. [Google Scholar] [CrossRef]
- Way, D.; Powell, R.; Masciarelli, J.; Starr, B.; Edquist, K. Aerocapture Simulation and Performance for the Titan Explorer Mission. In Proceedings of the 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Huntsville, AL, USA, 20–23 July 2003; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2003. [Google Scholar] [CrossRef]
- Munk, M.M.; Moon, S.A. Aerocapture Technology Development Overview. In Proceedings of the 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008. [Google Scholar] [CrossRef]
- Spilker, T.R.; Adler, M.; Arora, N.; Beauchamp, P.M.; Cutts, J.A.; Munk, M.M.; Powell, R.W.; Braun, R.D.; Wercinski, P.F. Qualitative Assessment of Aerocapture and Applications to Future Missions. J. Spacecr. Rocket. 2019, 56, 536–545. [Google Scholar] [CrossRef]
- Austin, A.; Afonso, G. Enabling and Enhancing Science Exploration Across the Solar System: Aerocapture Technology for SmallSat to Flagship Missions. Bull. Am. Astron. Soc. 2021, 54, 1–8. [Google Scholar]
- Cihan, I.H.; Kluever, C.A. Analytical Earth-Aerocapture Guidance with Near-Optimal Performance. J. Guid. Control. Dyn. 2021, 44, 45–56. [Google Scholar] [CrossRef]
- Gurley, J.G. Guidance for an aerocapture maneuver. J. Guid. Control. Dyn. 1993, 16, 505–510. [Google Scholar] [CrossRef]
- Ro, T.; Queen, E. Study of martian aerocapture terminal point guidance. In Proceedings of the 23rd Atmospheric Flight Mechanics Conference, Snowmass, CO, USA, 10–12 August 1998; p. 4571. [Google Scholar]
- Rozanov, M.; Guelman, M. Aeroassisted orbital maneuvering with variable structure control. Acta Astronaut. 2008, 62, 9–17. [Google Scholar] [CrossRef]
- Kozynchenko, A.I. Development of optimal and robust predictive guidance technique for Mars aerocapture. Aerosp. Sci. Technol. 2013, 30, 150–162. [Google Scholar] [CrossRef]
- Zhang, S.J.; Açikmeşe, B.; Swei, S.S.M.; Prabhu, D. Convex programming approach to real-time trajectory optimization for Mars aerocapture. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–7. [Google Scholar]
- Han, H.; Qiao, D.; Chen, H.; Li, X. Rapid planning for aerocapture trajectory via convex optimization. Aerosp. Sci. Technol. 2019, 84, 763–775. [Google Scholar] [CrossRef]
- Yao, Q.; Han, H.; Qiao, D. Nonsingular Fixed-Time Tracking Guidance for Mars Aerocapture with Neural Compensation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3686–3696. [Google Scholar] [CrossRef]
- Masciarelli, J.; Rousseau, S.; Fraysse, H.; Perot, E. An analytic aerocapture guidance algorithm for the Mars Sample Return Orbiter. In Proceedings of the Atmospheric Flight Mechanics Conference. American Institute of Aeronautics and Astronautics, Denver, CO, USA, 14–17 August 2000. [Google Scholar] [CrossRef]
- Cerimele, C.; Gamble, J. A simplified guidance algorithm for lifting aeroassist orbital transfer vehicles. In Proceedings of the 23rd Aerospace Sciences Meeting, Reno, NV, USA, 14–17 January 1985; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1985. [Google Scholar] [CrossRef]
- Hanak, C.; Crain, T.; Masciarelli, J. Revised Algorithm for Analytic Predictor-Corrector Aerocapture Guidance: Exit Phase. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit. American Institute of Aeronautics and Astronautics, Austin, TX, USA, 11–14 August 2003. [Google Scholar] [CrossRef]
- Hamel, J.F.; de Lafontaine, J. Improvement to the Analytical Predictor-Corrector Guidance Algorithm Applied to Mars Aerocapture. J. Guid. Control. Dyn. 2006, 29, 1019–1022. [Google Scholar] [CrossRef]
- Peng, Y.; Xu, B.; Lu, X.; Fang, B.; Zhang, H. Analytical Predictive Guidance Algorithm Based on Single Ballistic Coefficient Switching for Mars Aerocapture. Int. J. Aerosp. Eng. 2019, 2019, 5765901. [Google Scholar] [CrossRef]
- DiCarlo, J.L. Aerocapture Guidance Methods for High Energy Trajectories. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Gamble, J.; Cerimele, C.; Moore, T.; Higgins, J. Atmospheric guidance concepts for an aeroassist flight experiment. J. Astronaut. Sci. 1988, 36, 45–71. [Google Scholar]
- Putnam, Z.R.; Braun, R.D. Drag-modulation flight-control system options for planetary aerocapture. J. Spacecr. Rocket. 2014, 51, 139–150. [Google Scholar] [CrossRef]
- Lu, P.; Cerimele, C.J.; Tigges, M.A.; Matz, D.A. Optimal aerocapture guidance. J. Guid. Control Dyn. 2015, 38, 553–565. [Google Scholar] [CrossRef]
- Lu, P.; Brunner, C.W.; Stachowiak, S.J.; Mendeck, G.F.; Tigges, M.A.; Cerimele, C.J. Verification of a fully numerical entry guidance algorithm. J. Guid. Control Dyn. 2017, 40, 230–247. [Google Scholar] [CrossRef]
- Matz, D.A.; Lu, P.; Mendeck, G.F.; Sostaric, R.R. Application of a fully numerical guidance to Mars aerocapture. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017; p. 1901. [Google Scholar]
- Miele, A.; Wang, T.; Lee, W.; Zhao, Z. Optimal trajectories for the aeroassisted flight experiment. Acta Astronaut. 1990, 21, 735–747. [Google Scholar] [CrossRef]
- Han, H.; Qiao, D.; Chen, H. Optimal ballistic coefficient control for Mars aerocapture. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 2175–2180. [Google Scholar]
- Zhang, G.; Wen, C.; Han, H.; Qiao, D. Aerocapture Trajectory Planning Using Hierarchical Differential Dynamic Programming. J. Spacecr. Rocket. 2022, 1–13. [Google Scholar] [CrossRef]
- Webb, K. Evaluation of an Optimal Aerocapture Guidance Algorithm for Human Mars Missions. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2016. [Google Scholar]
- Webb, K.D.; Lu, P.; Dwyer Cianciolo, A.M. Aerocapture Guidance for a Human Mars Mission. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017; p. 1900. [Google Scholar]
- Lu, P. Entry guidance: A unified method. J. Guid. Control Dyn. 2014, 37, 713–728. [Google Scholar] [CrossRef]
- Lockwood, M.K.; Queen, E.M.; Way, D.W.; Powell, R.W.; Edquist, K.; Starr, B.W.; Hollis, B.R.; Zoby, E.V.; Hrinda, G.A.; Bailey, R.W. Aerocapture Systems Analysis for a Titan Mission; Technical Report; NASA: Washington, DC, USA, 2006.
- Mazzaracchio, A. Flight-path angle guidance for aerogravity-assist maneuvers on hyperbolic trajectories. J. Guid. Control. Dyn. 2015, 38, 238–248. [Google Scholar] [CrossRef]
- Lafleur, J.M. The Conditional Equivalence of ΔV Minimization and Apoapsis Targeting in Numerical Predictor-Corrector Aerocapture Guidance; NASA: Washington, DC, USA, 2011.
- Li, X.; Qiao, D.; Macdonald, M. Energy-saving capture at Mars via backward-stable orbits. J. Guid. Control Dyn. 2019, 42, 1136–1145. [Google Scholar] [CrossRef]
- Li, X.; Qiao, D.; Circi, C. Mars High Orbit Capture Using Manifolds in the Sun-Mars System. J. Guid. Control Dyn. 2020, 43, 1383–1392. [Google Scholar] [CrossRef]
- Han, H.; Li, X.; Qiao, D. Aerogravity-assist capture into the three-body system: A preliminary design. Acta Astronaut. 2022, 198, 26–35. [Google Scholar] [CrossRef]
- Justh, H.; Justus, C.; Keller, V. Global reference atmospheric models, including thermospheres, for mars, venus and earth. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006; p. 6394. [Google Scholar]






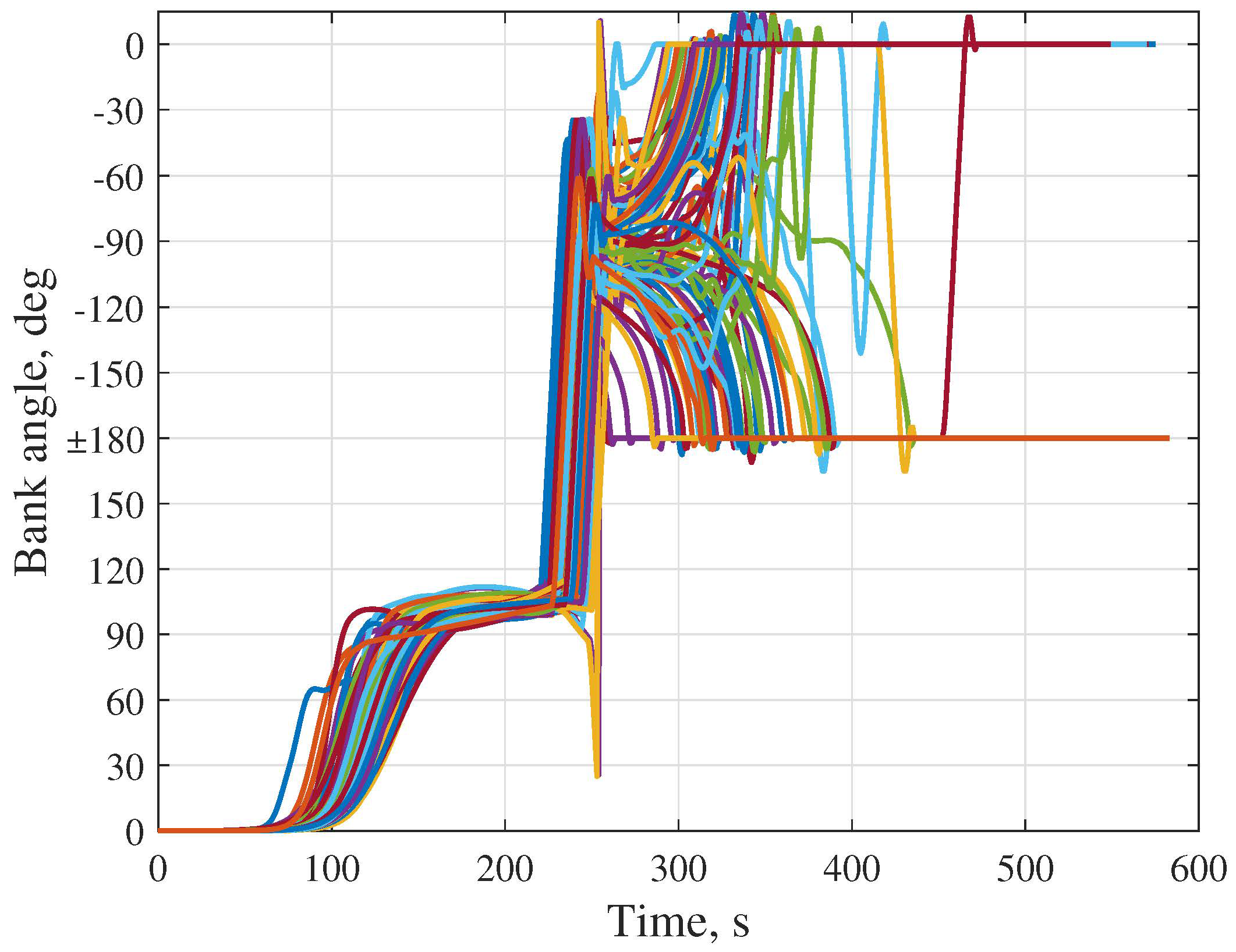
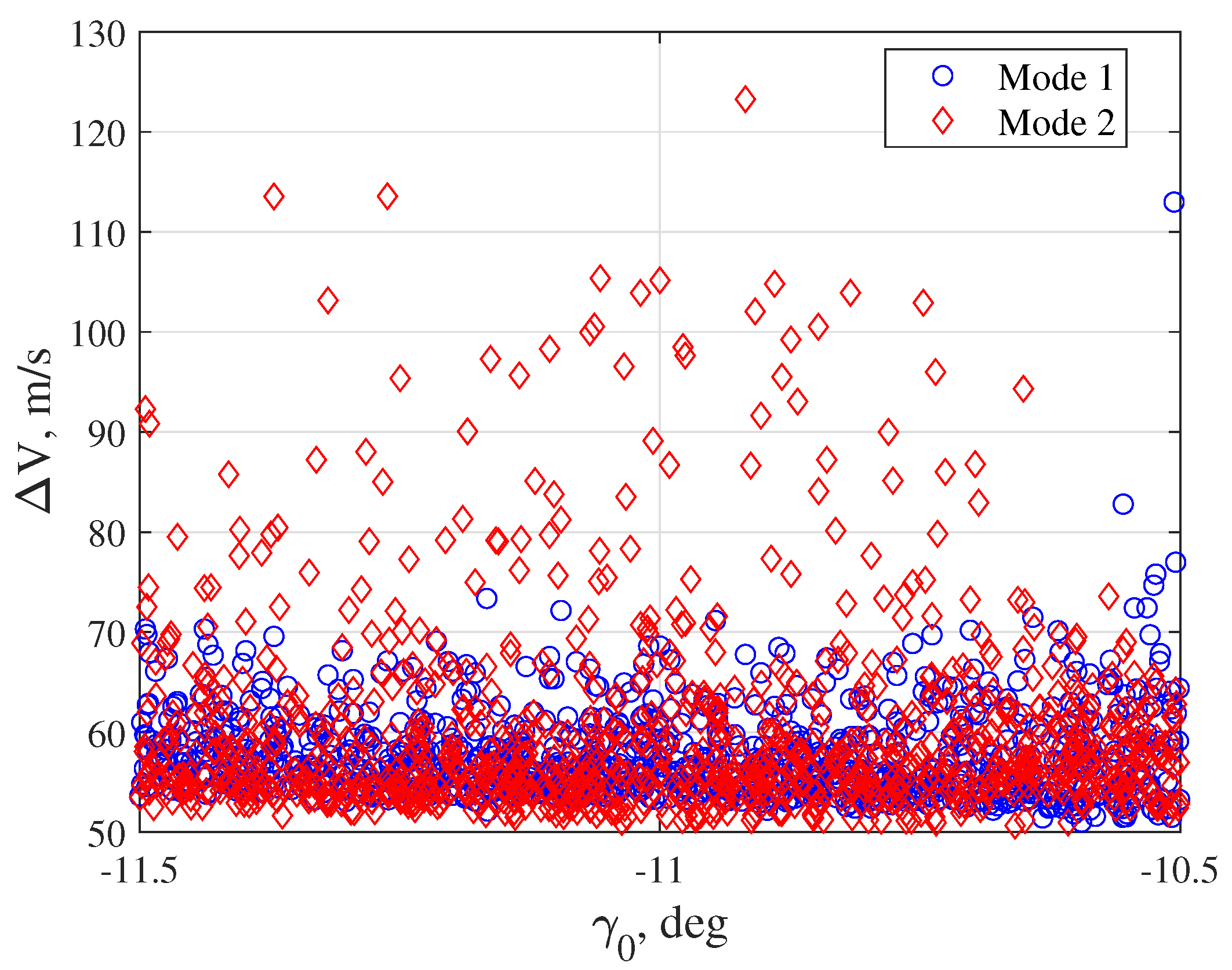
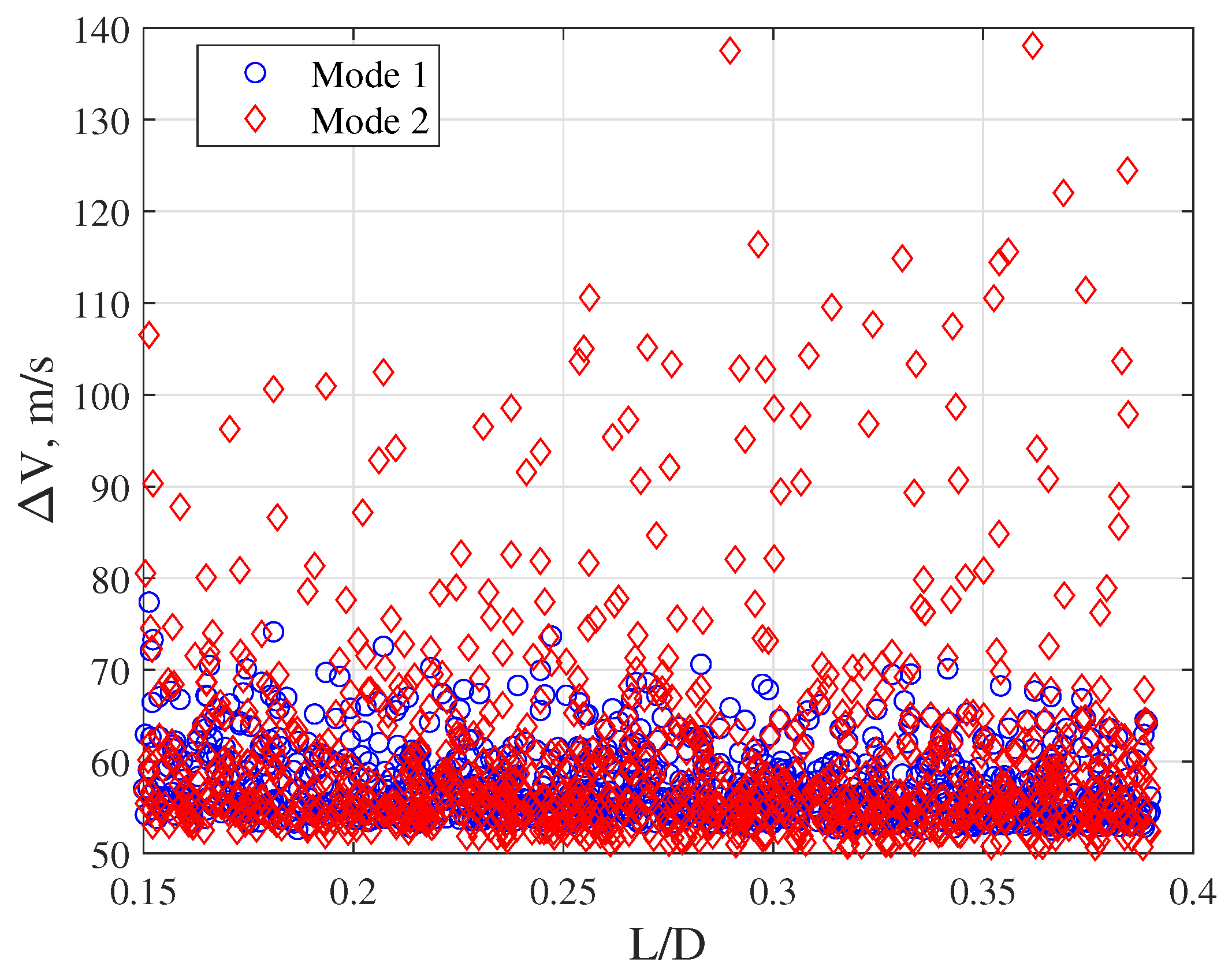
| EI State | Value (Earth Aerocapture) | Value (Mars Aerocapture) |
|---|---|---|
| Altitude | 121.92 km | 128 km |
| Longitude | −116.5 deg | −116.5 deg |
| Latitude | −46.67 deg | −46.67 deg |
| Velocity | 11.02 km/s | 5.9 km/s |
| Flight-path angle | −5.91 deg | −11 deg |
| Heading angle | 0.00 deg | 0.00 deg |
| Orbital inclination | 90 deg | 90 deg |
| State | Distribution | Dispersion |
|---|---|---|
| Longitude | Gaussian | |
| Latitude | Gaussian | |
| Velocity | Gaussian | |
| Flight-path angle | Gaussian | |
| Heading angle | Gaussian |
| Parameter | Distribution | Dispersion |
|---|---|---|
| Lift coefficient | Gaussian | |
| Drag coefficient | Gaussian | |
| Mass | Uniform |
| Parameter | Mode 1: Total , m/s | Mode 2: Total , m/s | Mode 1: Inclination Deviation, deg | Mode 2: Inclination Deviation, deg |
|---|---|---|---|---|
| Mean | 65.1257 | 113.3175 | 0.0485 | 2.3632 |
| Maximum | 85.1014 | 346.2785 | 0.4903 | 4.1306 |
| Minimum | 44.6487 | 42.1140 | −0.2110 | −0.0115 |
| Standard deviation | 9.9212 | 78.9862 | 0.1387 | 0.9319 |
| Parameter | Mode 1: Total , m/s | Mode 2: Total , m/s | Mode 1: Inclination Deviation, deg | Mode 2: Inclination Deviation, deg |
|---|---|---|---|---|
| Mean | 56.8421 | 61.7943 | 0.0151 | −0.0763 |
| Maximum | 70.3198 | 145.5577 | 0.4898 | 0.6589 |
| Minimum | 52.9646 | 51.5100 | −0.4415 | −0.4480 |
| Standard deviation | 3.7831 | 16.3686 | 0.2111 | 0.2048 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Han, H.; Teng, R.; Qin, T. Robust Near-Optimal Aerocapture Guidance Method Based on Saturation Function. Appl. Sci. 2022, 12, 11513. https://doi.org/10.3390/app122211513
Chen J, Han H, Teng R, Qin T. Robust Near-Optimal Aerocapture Guidance Method Based on Saturation Function. Applied Sciences. 2022; 12(22):11513. https://doi.org/10.3390/app122211513
Chicago/Turabian StyleChen, Jilin, Hongwei Han, Rui Teng, and Tong Qin. 2022. "Robust Near-Optimal Aerocapture Guidance Method Based on Saturation Function" Applied Sciences 12, no. 22: 11513. https://doi.org/10.3390/app122211513
APA StyleChen, J., Han, H., Teng, R., & Qin, T. (2022). Robust Near-Optimal Aerocapture Guidance Method Based on Saturation Function. Applied Sciences, 12(22), 11513. https://doi.org/10.3390/app122211513





