An Analytical Solution for the Deformation of Soft Ground Reinforced by Columnar Inclusions under Equal Stress Conditions
Abstract
:1. Introduction
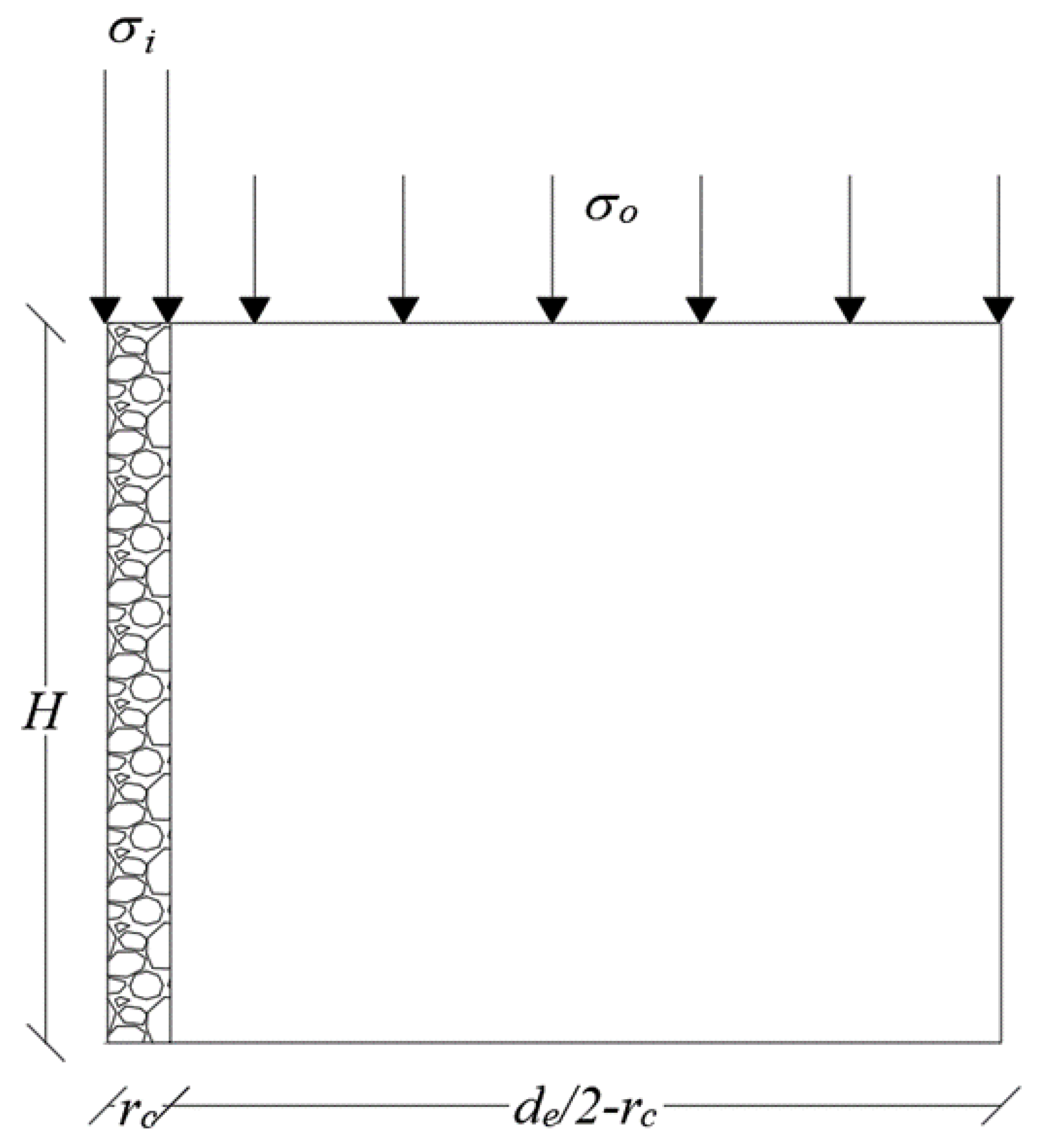
2. Model Formulation and Analysis
2.1. Existing Solution for Deformation Analysis of the Column-Reinforced Foundation
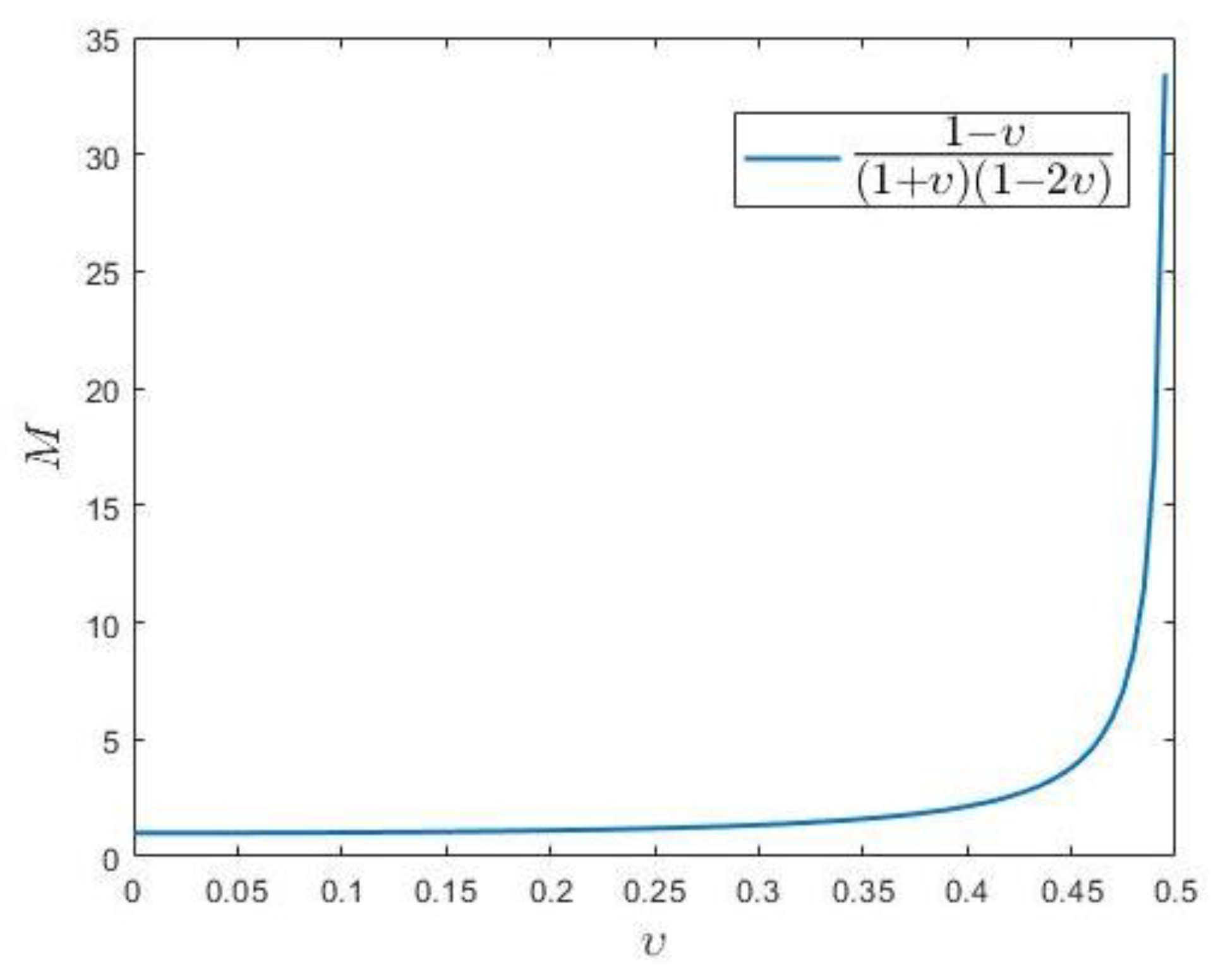
2.2. Mathematical Modeling
- (1)
- The radial displacement u is assumed to be equal to zero everywhere throughout the soil column model. Because the radial displacement is negligible compared to the vertical displacement under vertical load conditions.
- (2)
- The vertical displacement of the surrounding soil W is expressed by the vertical surface displacement w(r) and the shape function ϕ(z) as
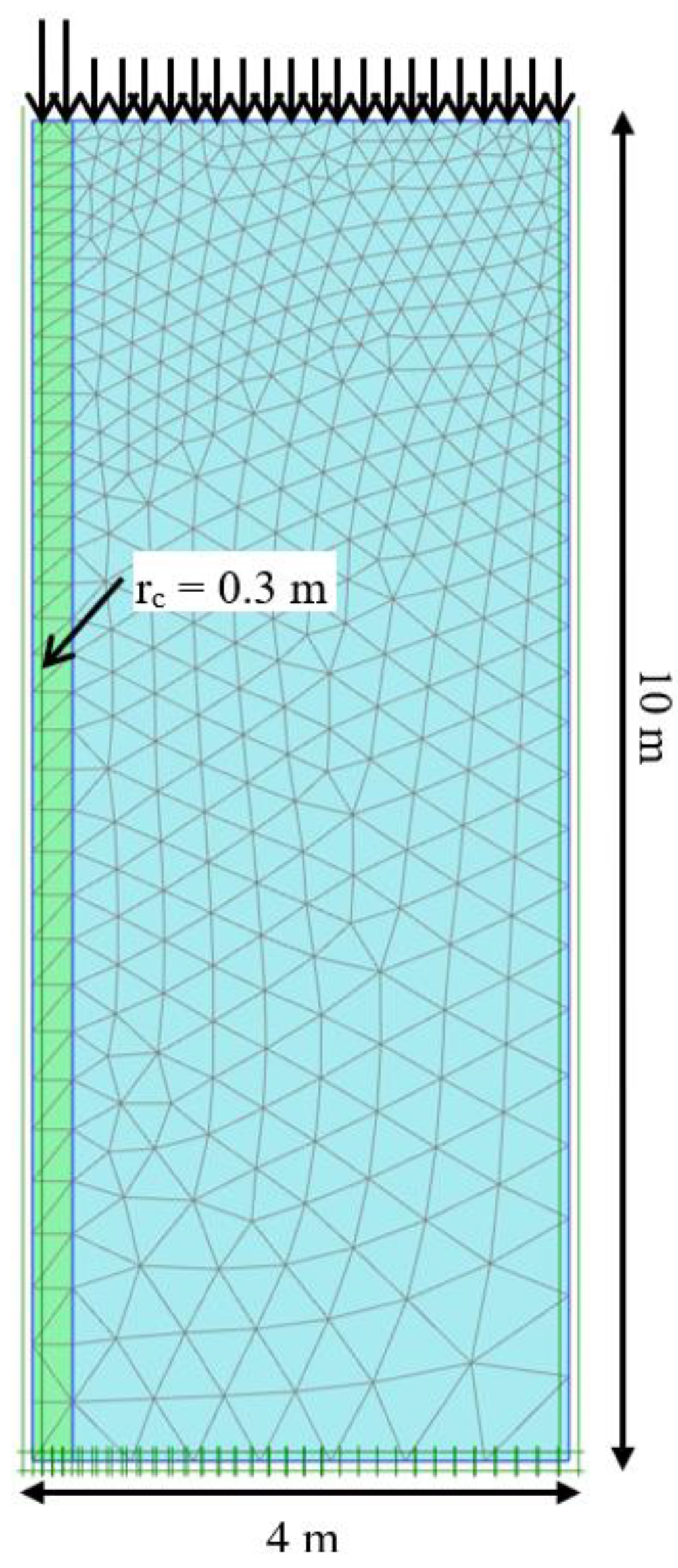
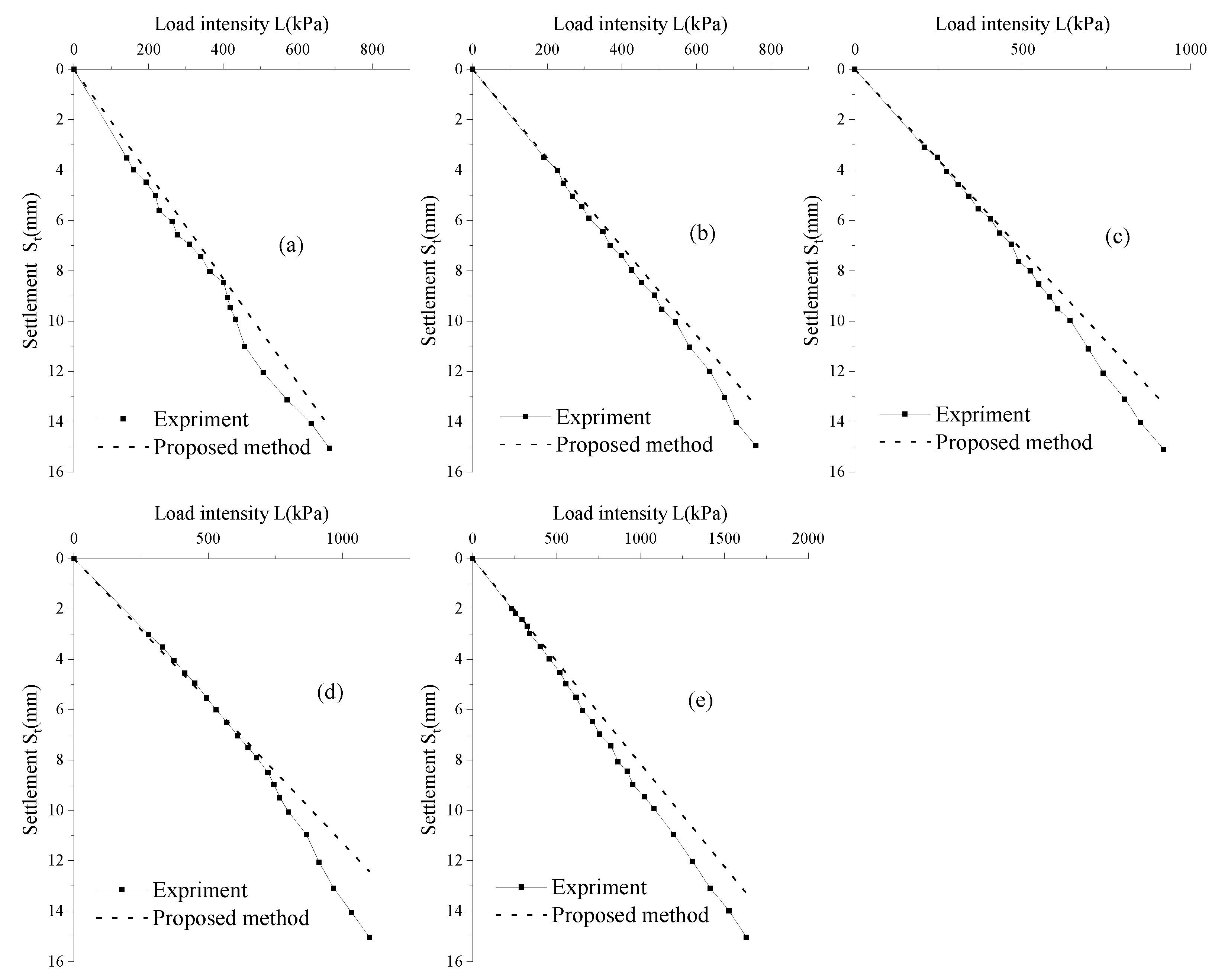
3. Comparison with the Finite Element Method
3.1. FEM Model
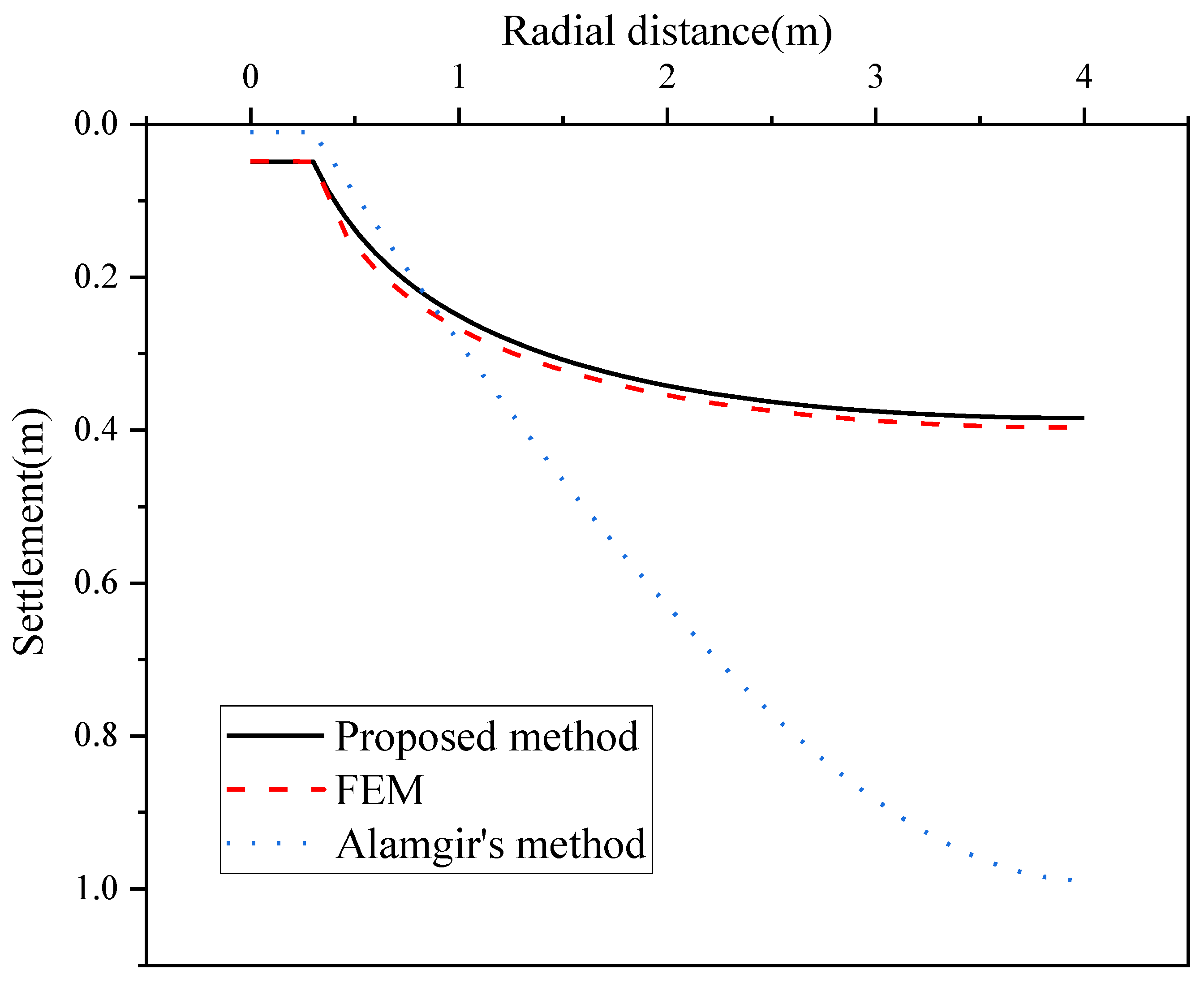
3.2. Comparison with the Proposed Method
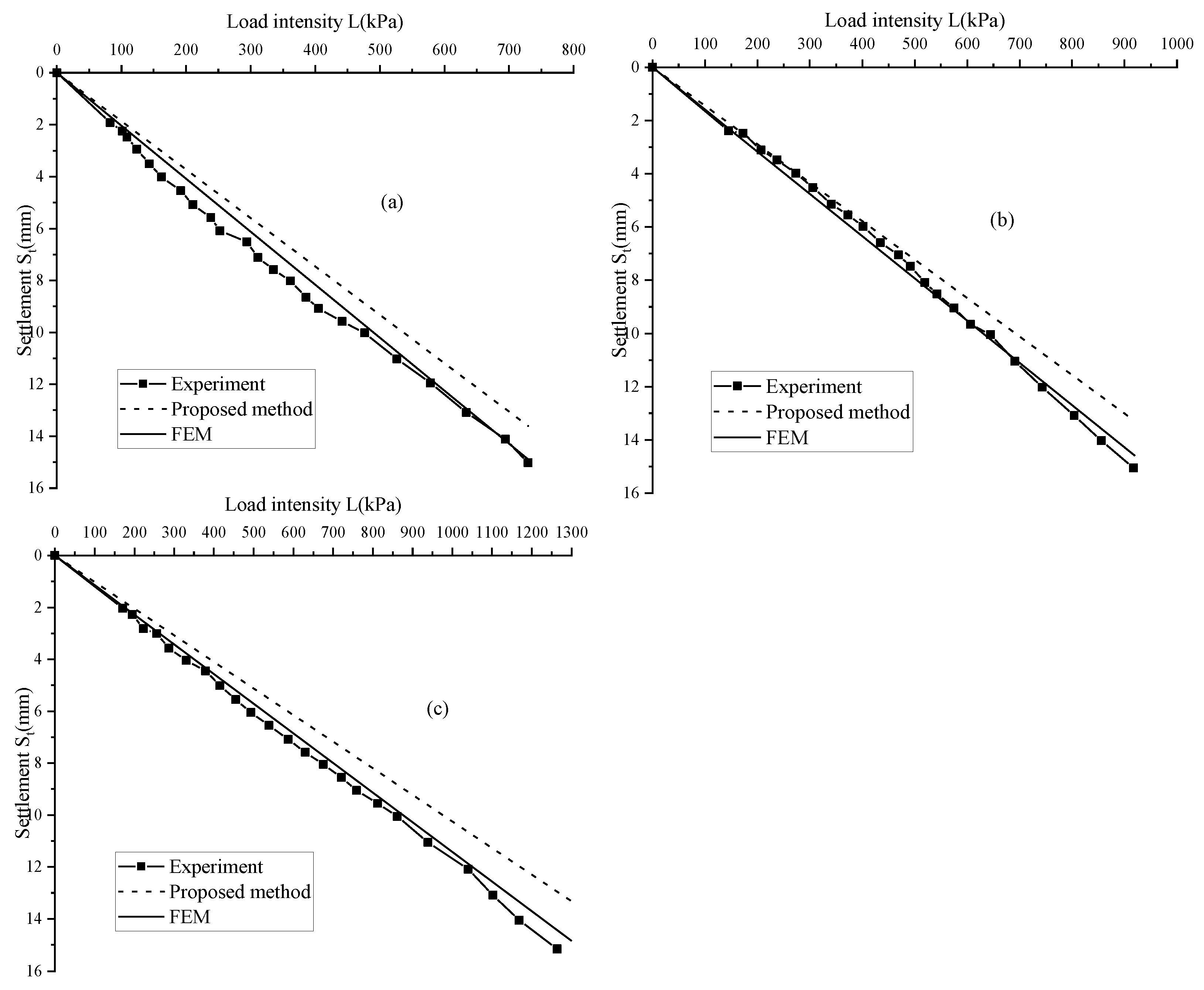
4. Case History Study
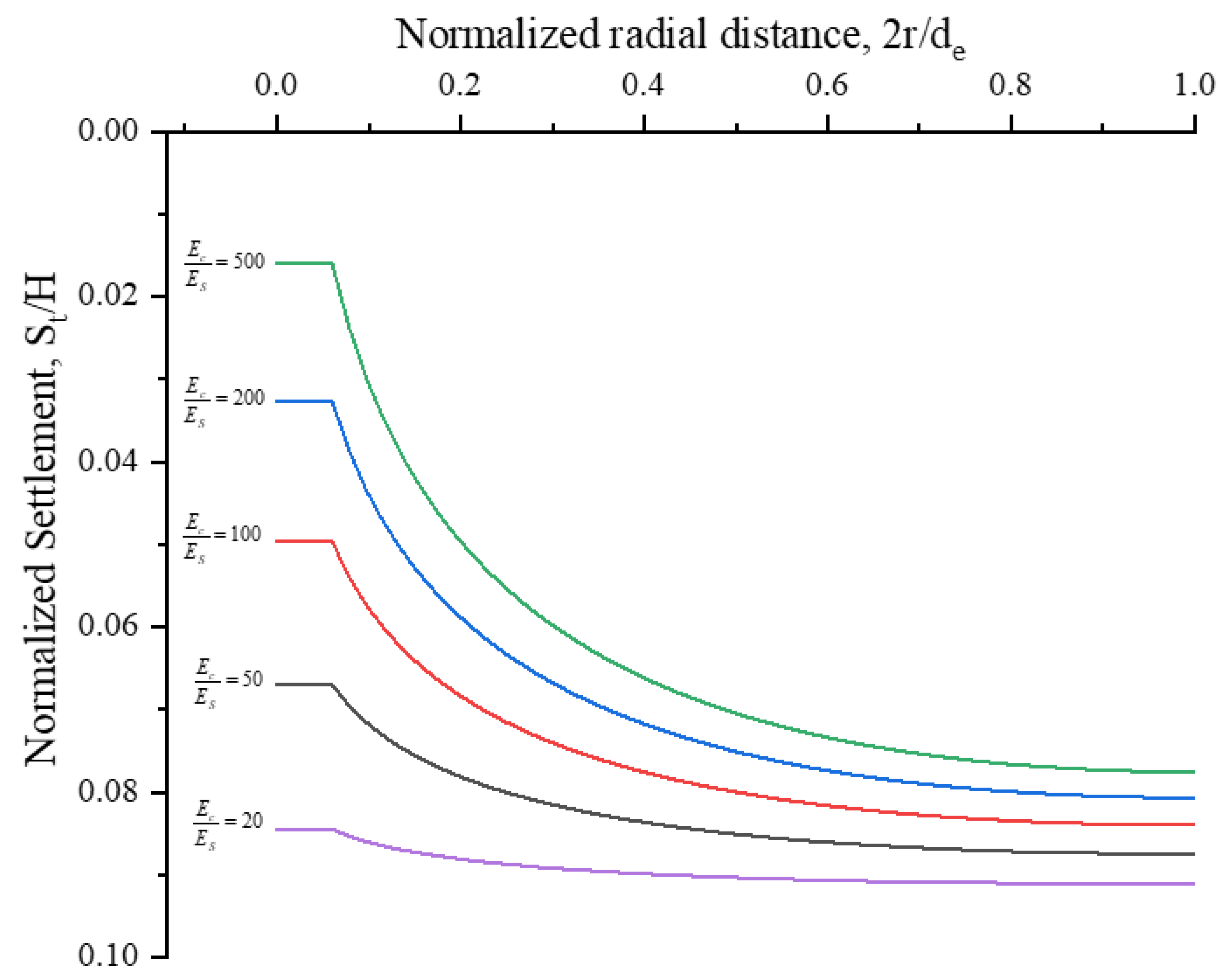
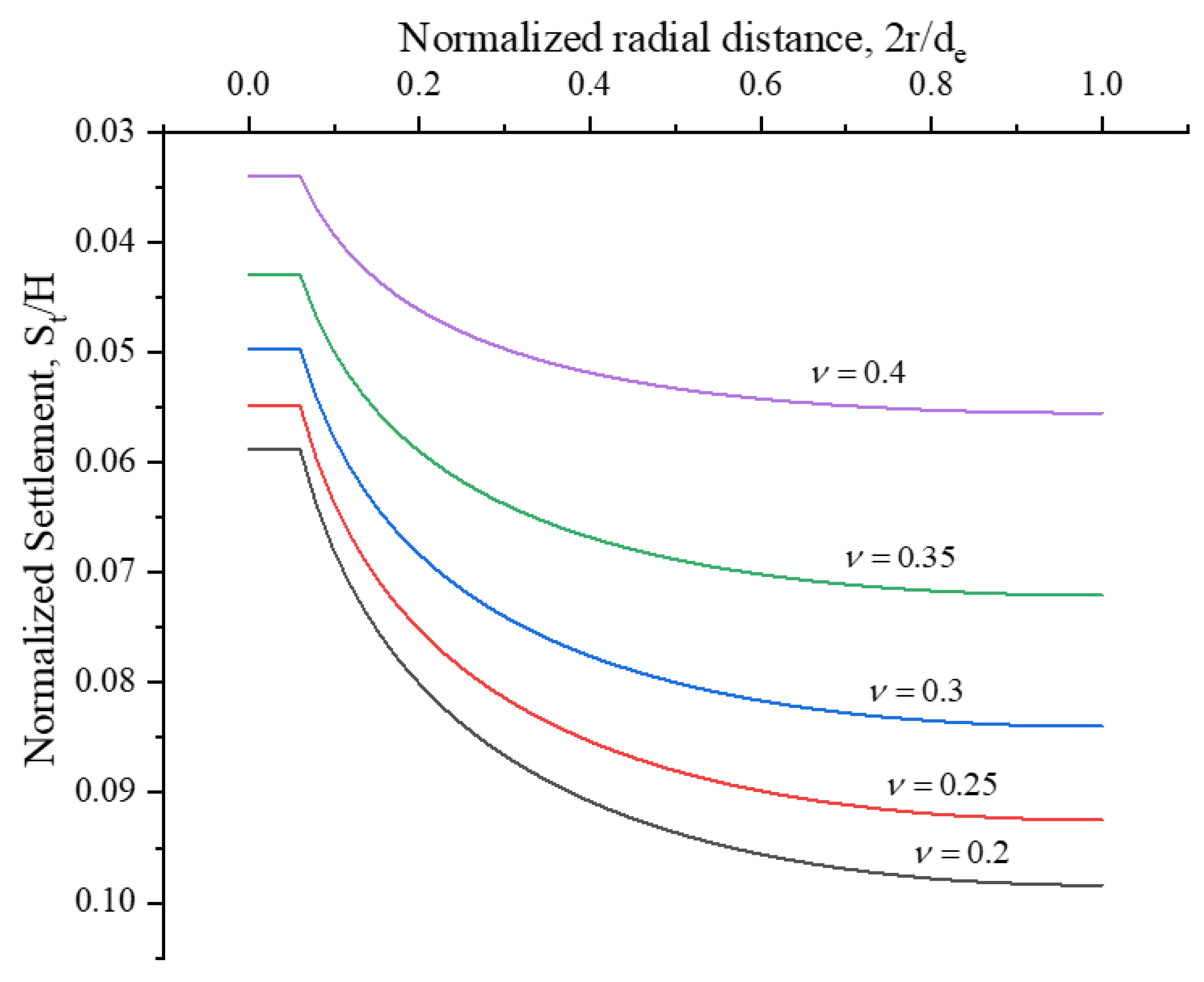
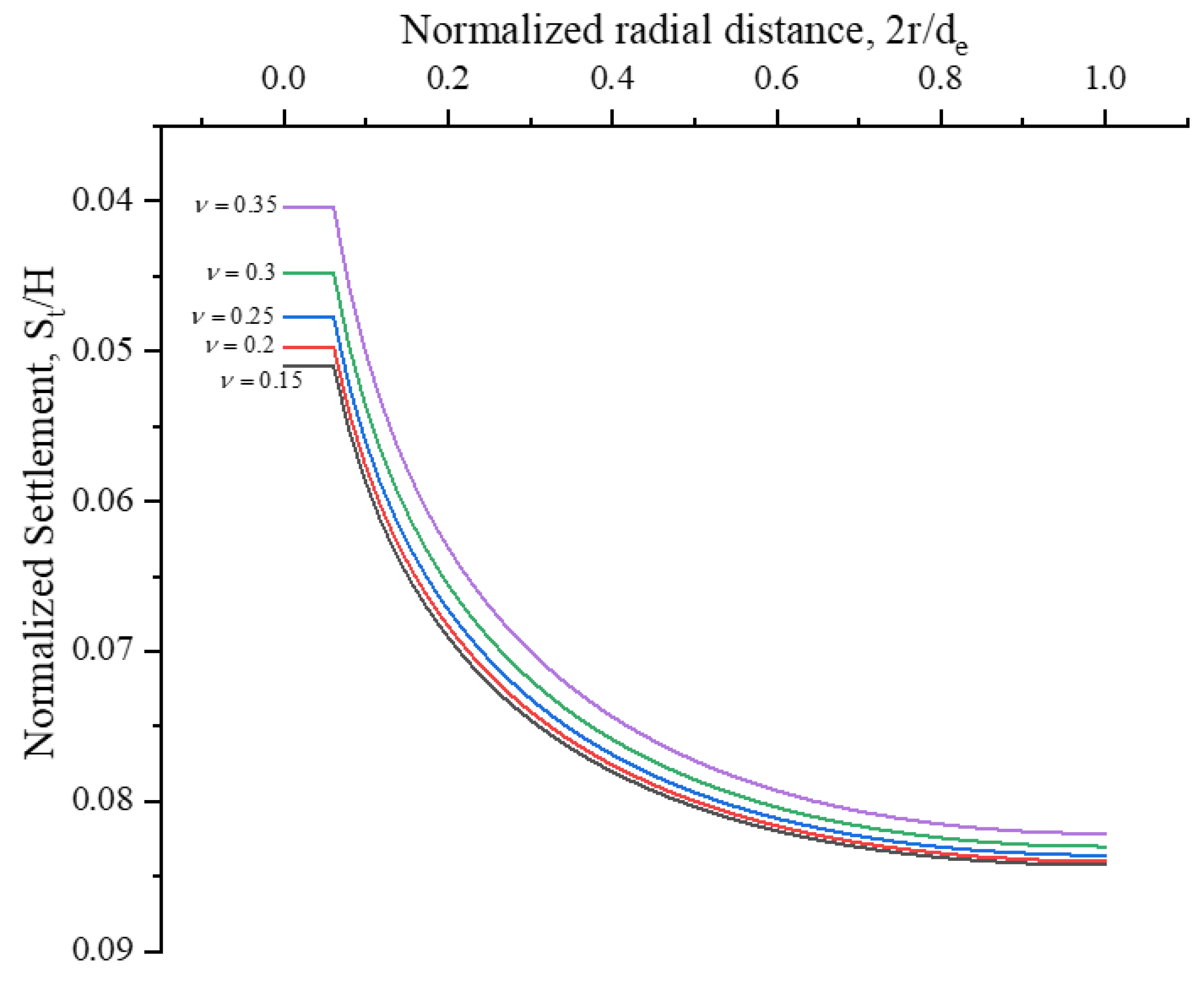
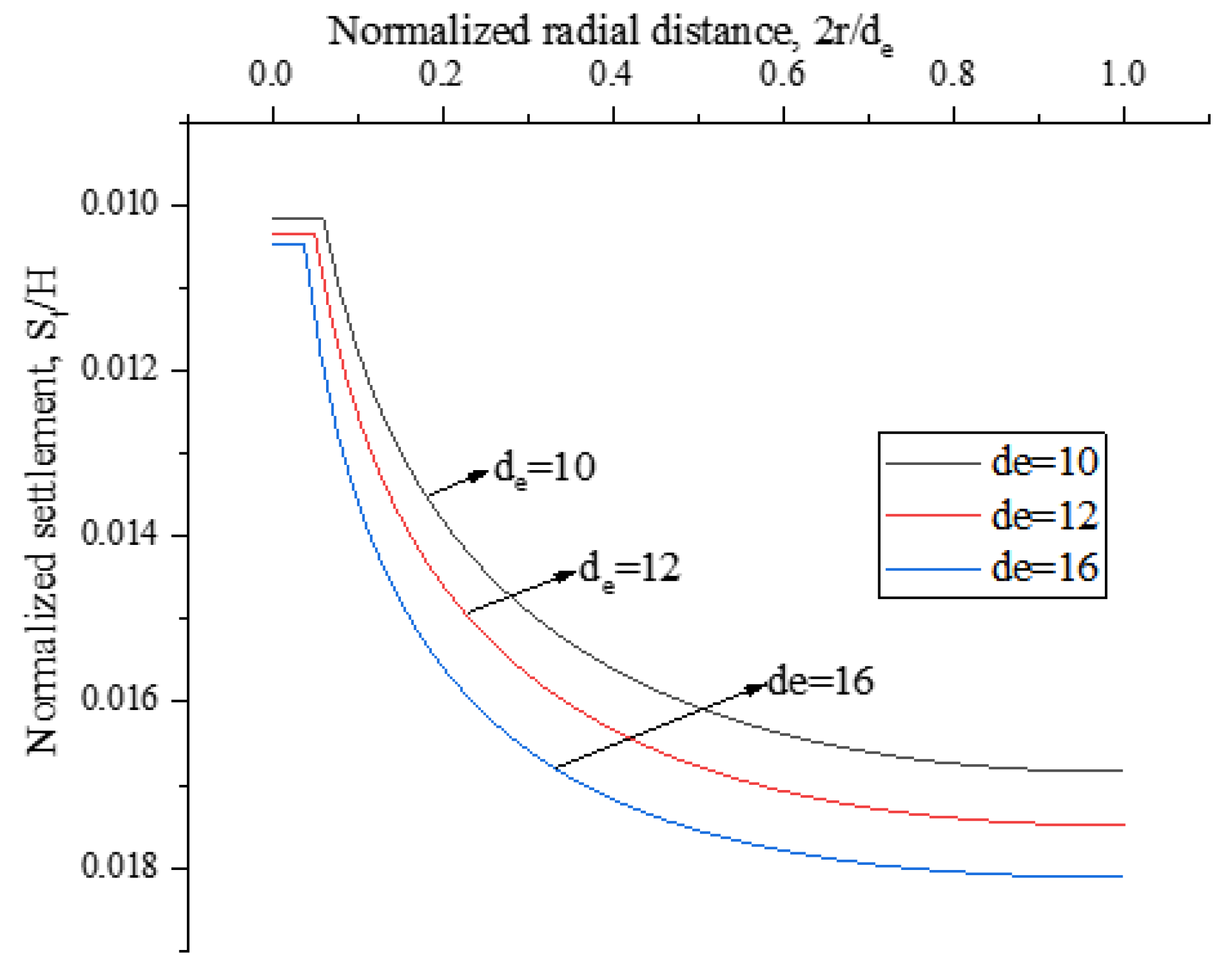
5. Parametric Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Manohar, R.; Patel, S. Ground Improvement with Stone Columns—A Review. In Advances in Civil Engineering; Springer: Singapore, 2021. [Google Scholar]
- Singh, I.; Sahu, A. A Review on Stone Columns used for Ground Improvement of Soft Soil. In Proceedings of the of the 4th World Congress on Civil, Structural, and Environmental Engineering (CSEE’19), Rome, Italy, 7–9 April 2019. [Google Scholar]
- Mohapatra, S.R.; Rajagopal, K.; Sharma, J. Direct shear tests on geosynthetic-encased granular columns. Geotext. Geomembr. 2016, 44, 396–405. [Google Scholar] [CrossRef]
- Basack, S.; Indraratna, B.; Rujikiatkamjorn, C. Modeling the Performance of Stone Column–Reinforced Soft Ground under Static and Cyclic Loads. J. Geotech. Geoenvironmental Eng. 2016, 142, 04015067. [Google Scholar] [CrossRef]
- Ghosh, B.; Fatahi, B.; Khabbaz, H.; Nguyen, H.H.; Kelly, R. Field study and numerical modelling for a road embankment built on soft soil improved with concrete injected columns and geosynthetics reinforced platform. Geotext. Geomembr. 2021, 49, 804–824. [Google Scholar] [CrossRef]
- Dar, L.A.; Shah, M.Y. Accuracy analysis of 2D numerical methods of deep-seated failure analysis in embankments on stone column reinforced ground. Innov. Infrastruct. Solut. 2021, 7, 86. [Google Scholar] [CrossRef]
- Chen, J.-F.; Li, L.-Y.; Zhang, Z.; Zhang, X.; Xu, C.; Rajesh, S.; Feng, S.-Z. Centrifuge modeling of geosynthetic-encased stone column-supported embankment over soft clay. Geotext. Geomembr. 2021, 49, 210–221. [Google Scholar] [CrossRef]
- Pereira, P.G.d.S.; Pacheco, M.P.; Lima, B.T. Numerical analysis of soft soil improved with stone column technique. REM-Int. Eng. J. 2021, 74, 319–327. [Google Scholar] [CrossRef]
- Mohapatra, D.; Kumar, J. Homogenization based kinematic limit analysis for finding the stability of an embankment over soft clay reinforced with granular columns. Comput. Geotech. 2022, 142, 104562. [Google Scholar] [CrossRef]
- You, S.-K.; Lee, J.; Gabr, M.A. Experimental evaluation of recycled aggregate porous concrete piles for soft ground improvement. Mar. Georesources Geotechnol. 2016, 34, 712–720. [Google Scholar] [CrossRef]
- Fahmi, K.S.; Kolosov, E.; Fattah, M.Y. Behavior of Different Materials for Stone Column Construction. J. Eng. Appl. Sci. 2019, 14, 1162–1168. [Google Scholar]
- Aslani, M.; Nazariafshar, J.; Ganjian, N. Experimental Study on Shear Strength of Cohesive Soils Reinforced with Stone Columns. Geotech. Geol. Eng. 2019, 37, 2165–2188. [Google Scholar] [CrossRef]
- Mehrannia, N.; Nazariafshar, J.; Kalantary, F. Experimental investigation on the bearing capacity of stone columns with granular blankets. Geotech. Geol. Eng. 2018, 36, 209–222. [Google Scholar] [CrossRef]
- Chen, J.-F.; Wang, X.-T.; Xue, J.-F.; Zeng, Y.; Feng, S.-Z. Uniaxial compression behavior of geotextile encased stone columns. Geotext. Geomembr. 2018, 46, 277–283. [Google Scholar] [CrossRef]
- Dash, S.K.; Bora, M.C. Bora, Improved performance of soft clay foundations using stone columns and geocell-sand mattress. Geotext. Geomembr. 2013, 41, 26–35. [Google Scholar] [CrossRef]
- Bong, T.; Kim, S.-R.; Kim, B.-I. Prediction of Ultimate Bearing Capacity of Aggregate Pier Reinforced Clay Using Multiple Regression Analysis and Deep Learning. Appl. Sci. 2020, 10, 4580. [Google Scholar] [CrossRef]
- Dar, L.A.; Shah, M.Y. Three Dimensional Numerical Study on Behavior of Geosynthetic Encased Stone Column Placed in Soft Soil. Geotech. Geol. Eng. 2021, 39, 1901–1922. [Google Scholar] [CrossRef]
- Piccinini, I. Ground Improvement with Stone Columns—Methods of Calculating Settlement Improvement Factor; University of Glasgow, School of Engineering: Glasgow, UK, 2015. [Google Scholar]
- Abhishek, S.V.; Rajyalakshmi, K.; Madhav, M.R. Engineering of ground with granular piles: A critical review. International J. Geotech. Eng. 2016, 10, 337–357. [Google Scholar] [CrossRef]
- Castro, J.; Cimentada, A.; da Costa, A.; Cañizal, J.; Sagaseta, C. Consolidation and deformation around stone columns: Comparison of theoretical and laboratory results. Comput. Geotech. 2013, 49, 326–337. [Google Scholar] [CrossRef]
- Çadır, C.C.; Vekli, M.; Şahinkaya, F. Numerical analysis of a finite slope improved with stone columns under the effect of earthquake force. Nat. Hazards 2021, 106, 173–211. [Google Scholar] [CrossRef]
- Tang, L.; Cong, S.; Ling, X.; Lu, J.; Elgamal, A. Numerical study on ground improvement for liquefaction mitigation using stone columns encased with geosynthetics. Geotext. Geomembr. 2015, 43, 190–195. [Google Scholar] [CrossRef]
- Castro, J. An analytical solution for the settlement of stone columns beneath rigid footings. Acta Geotech. 2016, 11, 309–324. [Google Scholar] [CrossRef] [Green Version]
- Deb, K. Modeling of granular bed-stone column-improved soft soil. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1267–1288. [Google Scholar] [CrossRef]
- Sexton, B.G.; McCabe, B.A.; Castro, J. Appraising stone column settlement prediction methods using finite element analyses. Acta Geotech. 2014, 9, 993–1011. [Google Scholar] [CrossRef] [Green Version]
- Aboshi, H.; Ichimoto, E.; Enoki, M.; Harada, K. The Compozer—A Method to Improve Characteristics of Soft Clays by Inclusion of Large Diameter sand Columns. In Proceedings of the International Conference on Soil Reinforcements: Reinforced Earth and Other Techniques, Paris, France, 20–22 March 1979; pp. 211–216. [Google Scholar]
- Chow, Y.K. Settlement Analysis of Sand Compaction Pile. Soils Found. 1996, 36, 111–113. [Google Scholar] [CrossRef] [Green Version]
- Balaam, N.P.; Booker, J.R. Analysis of rigid rafts supported by granular piles. Int. J. Numer. Anal. Methods Geomech. 1981, 5, 379–403. [Google Scholar] [CrossRef]
- Balaam, N.P.; Booker, J.R. Effect of stone column yield on settlement of rigid foundations in stabilized clay. Int. J. Numer. Anal. Methods Geomech. 1985, 9, 331–351. [Google Scholar] [CrossRef]
- Priebe, H.J. The design of vibro replacement. Ground Eng. 1995, 28, 31. [Google Scholar]
- Pulko, B.; Majes, B. Simple and Accurate Prediction of Settlements of Stone Column Reinforced soil. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering; IOS Press: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Zhang, L.; Zhao, M.; Shi, C.; Zhao, H. Settlement Calculation of Composite Foundation Reinforced with Stone Columns. Int. J. Geomech. 2013, 13, 248–256. [Google Scholar] [CrossRef]
- Zhao, L.-S.; Zhou, W.-H.; Yuen, K.-V. A simplified axisymmetric model for column supported embankment systems. Comput. Geotech. 2017, 92, 96–107. [Google Scholar] [CrossRef]
- Alamgir, M.; Miura, N.; Poorooshasb, H.; Madhav, M. Deformation analysis of soft ground reinforced by columnar inclusions. Comput. Geotech. 1996, 18, 267–290. [Google Scholar] [CrossRef]
- Deb, K.; Mohapatra, S.R. Analysis of stone column-supported geosynthetic-reinforced embankments. Appl. Math. Model. 2013, 37, 2943–2960. [Google Scholar] [CrossRef]
- Zhao, L.-S.; Zhou, W.-H.; Geng, X.; Yuen, K.-V.; Fatahi, B. A closed-form solution for column-supported embankments with geosynthetic reinforcement. Geotext. Geomembr. 2019, 47, 389–401. [Google Scholar] [CrossRef] [Green Version]
- Tanahashi, H. Pasternak Model Formulation of Elastic Displacements in the Case of a Rigid Circular Foundation. J. Asian Archit. Build. Eng. 2007, 6, 167–173. [Google Scholar] [CrossRef]
- Vallabhan, C.V.G.; Das, Y.C. Parametric Study of Beams on Elastic Foundations. J. Eng. Mech. 1988, 114, 2072–2082. [Google Scholar] [CrossRef]
- Jones, R.; Xenophontos, J. The Vlasov foundation model. Int. J. Mech. Sci. 1977, 19, 317–323. [Google Scholar] [CrossRef]
- Vlasov, V.Z. Beams, plates and shells on elastic foundation. Isr. Program Sci. Transl. 1966. Available online: https://scirp.org/reference/referencespapers.aspx?referenceid=577015 (accessed on 22 September 2022).
- Malekpoor, M.R.; Poorebrahim, G. Behavior of Compacted Lime—(Well-graded) Soil columns: Large scale tests and numerical modelling. KSCE J. Civ. Eng. 2014, 19, 893–903. [Google Scholar] [CrossRef]







| Ec (kPa) | νc | Es (kPa) | νs |
|---|---|---|---|
| 1,000,000 | 0.2 | 1000 | 0.4 |
| Material | E (kPa) | ν |
|---|---|---|
| Clay | 12,000 | 0.41 |
| Sand | 20,000 | 0.3 |
| Column | 200,000 | 0.21 |
| Material | Property | Value |
|---|---|---|
| Surrounding soil | Modulus of elasticity, Es: kPa | 4000 |
| Poisson’s ratio, νs: | 0.3 | |
| Stone column | Modulus of elasticity, Ec: kPa | 400,000 |
| Poisson’s ratio, νc: | 0.2 | |
| Length, H: m | 10 | |
| Radius of stone column, rc: m | 0.3 | |
| Radius of model, de/2: m | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Lok, T.M.-H.; Zhou, W.-H.; Zhao, L.-S. An Analytical Solution for the Deformation of Soft Ground Reinforced by Columnar Inclusions under Equal Stress Conditions. Appl. Sci. 2022, 12, 11574. https://doi.org/10.3390/app122211574
Zhou Z, Lok TM-H, Zhou W-H, Zhao L-S. An Analytical Solution for the Deformation of Soft Ground Reinforced by Columnar Inclusions under Equal Stress Conditions. Applied Sciences. 2022; 12(22):11574. https://doi.org/10.3390/app122211574
Chicago/Turabian StyleZhou, Zan, Thomas Man-Hoi Lok, Wan-Huan Zhou, and Lin-Shuang Zhao. 2022. "An Analytical Solution for the Deformation of Soft Ground Reinforced by Columnar Inclusions under Equal Stress Conditions" Applied Sciences 12, no. 22: 11574. https://doi.org/10.3390/app122211574






