Geometric Parameter Self-Calibration Based on Projection Feature Matching for X-Ray Nanotomography
Abstract
:1. Introduction
2. Materials and Methods
2.1. System Structure and Geometric Srtifacts
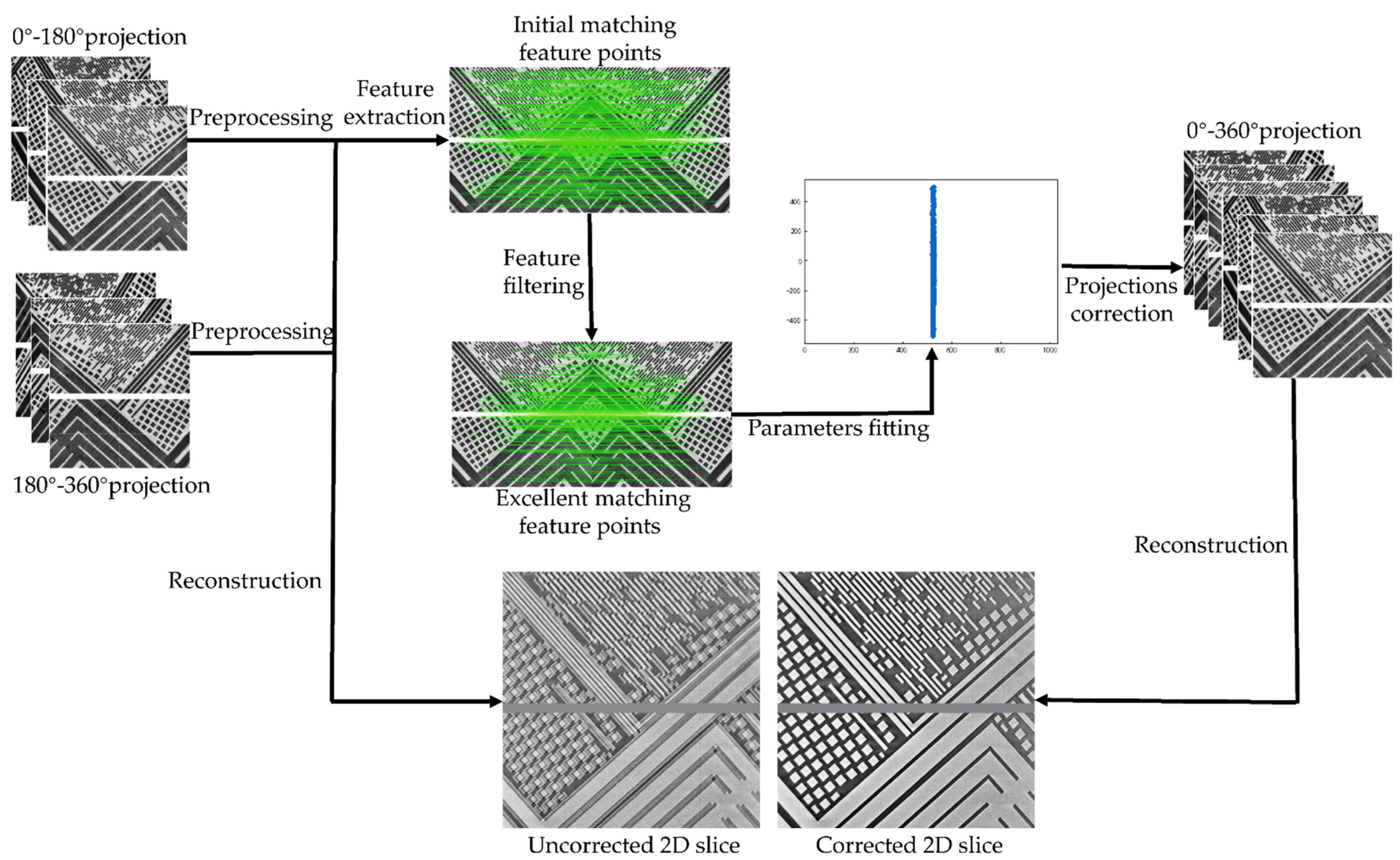
2.2. Geometric Parameter Calibration Process
2.2.1. Projection Image Preprocessing
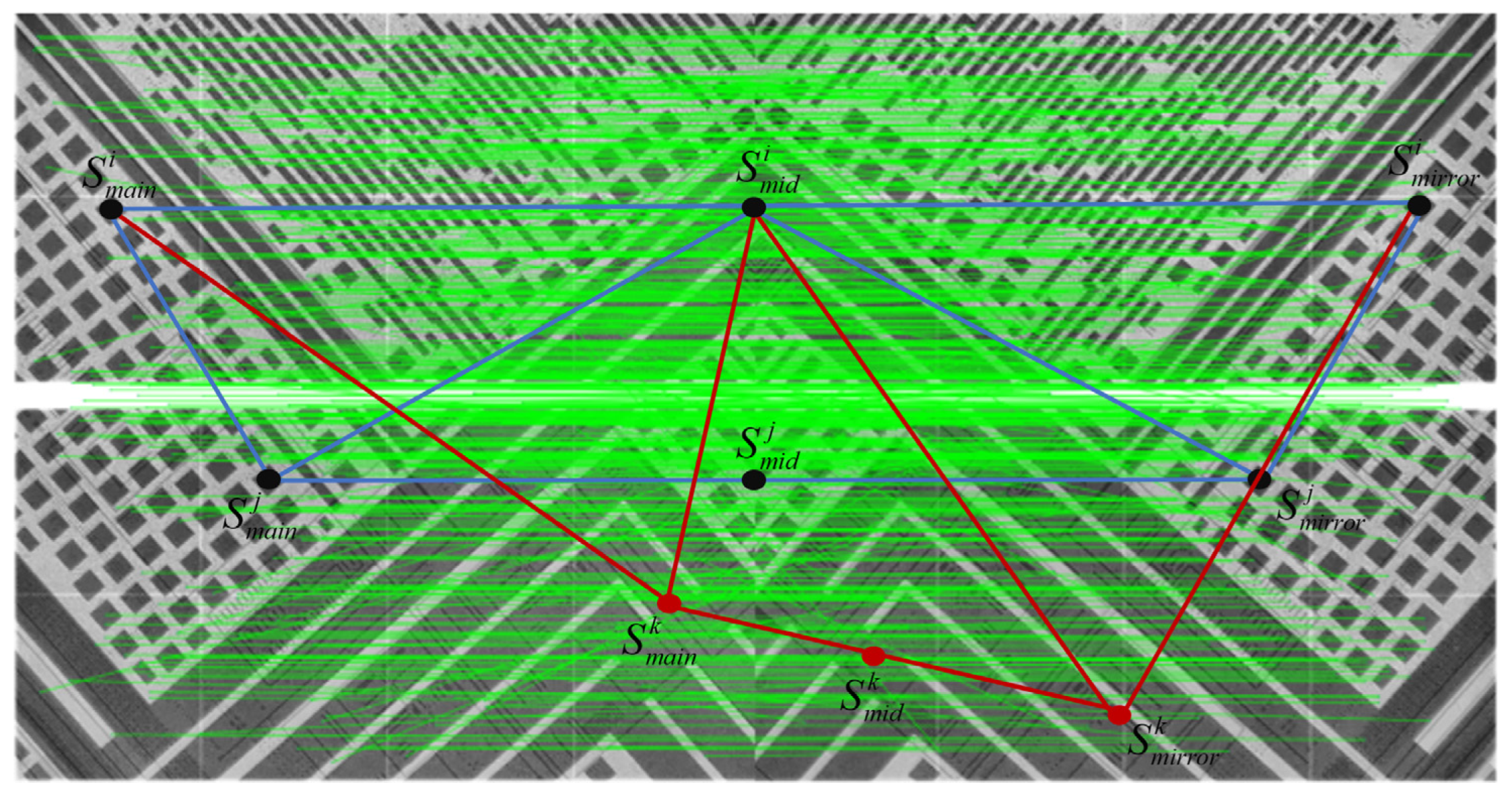
2.2.2. Projection Image Processing
2.2.3. Parameter Fitting and Projection Correction
3. Experiment
3.1. Simulation Experiments
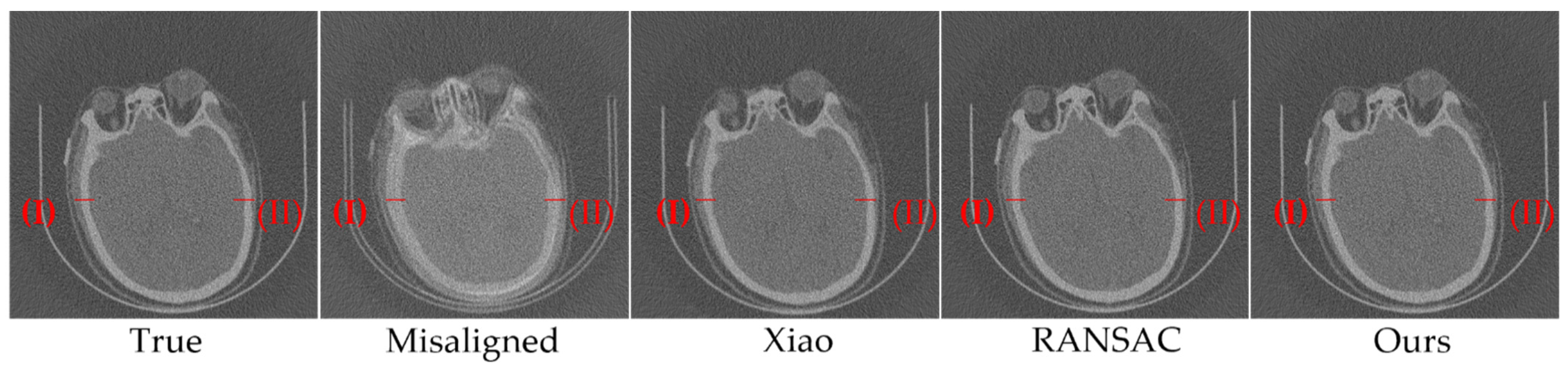
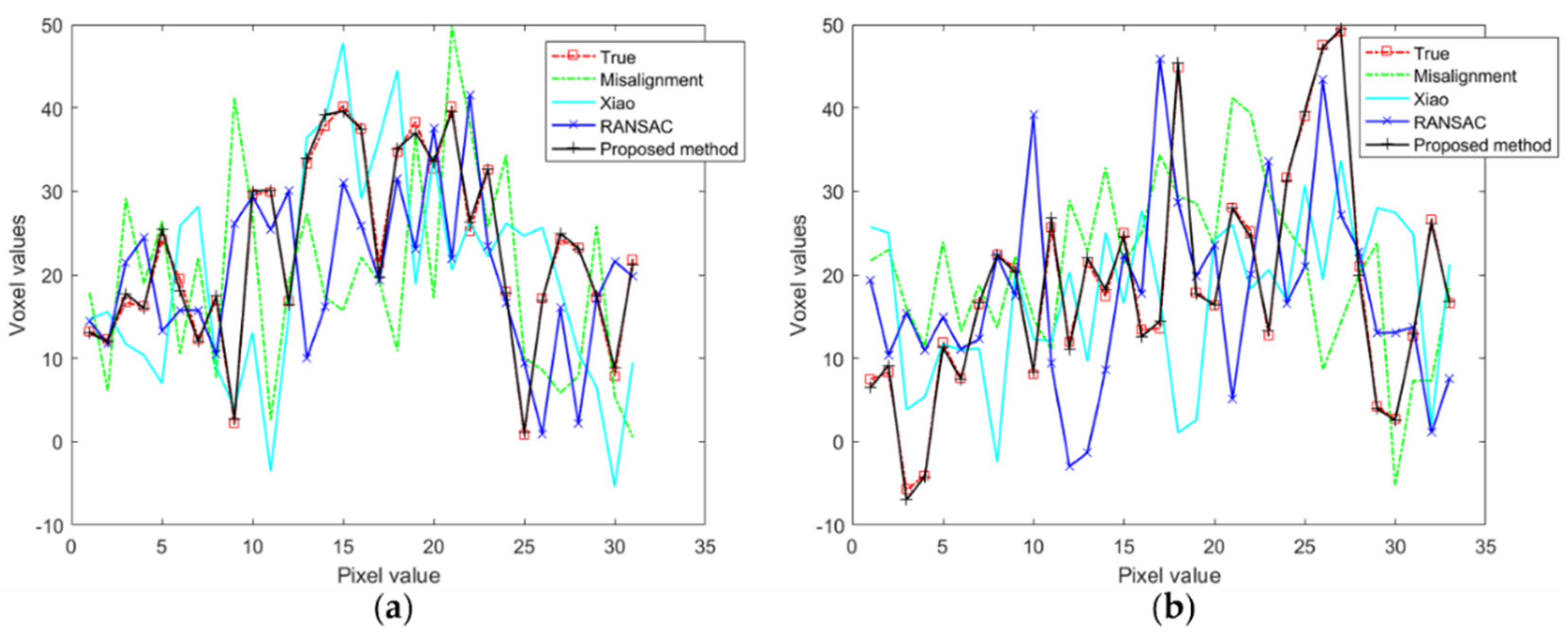
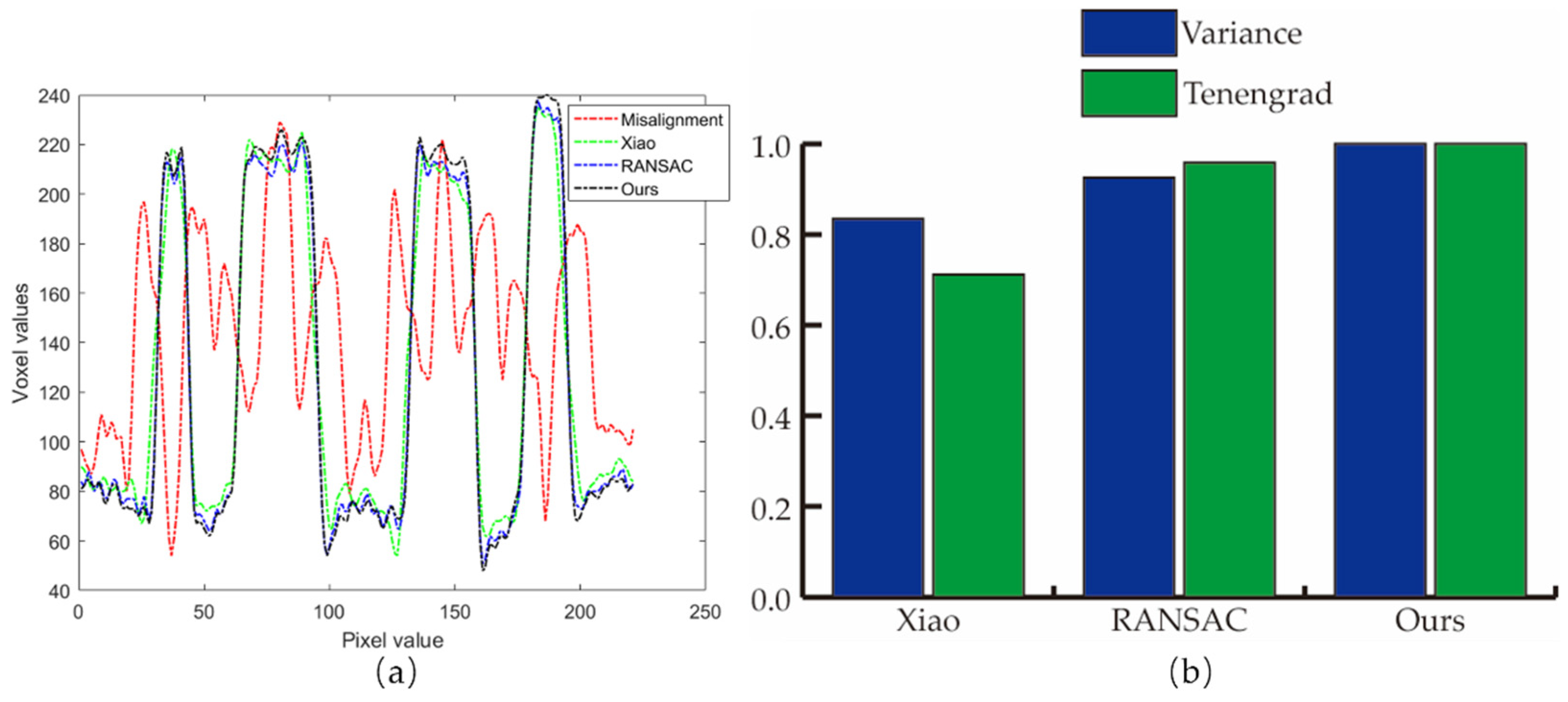
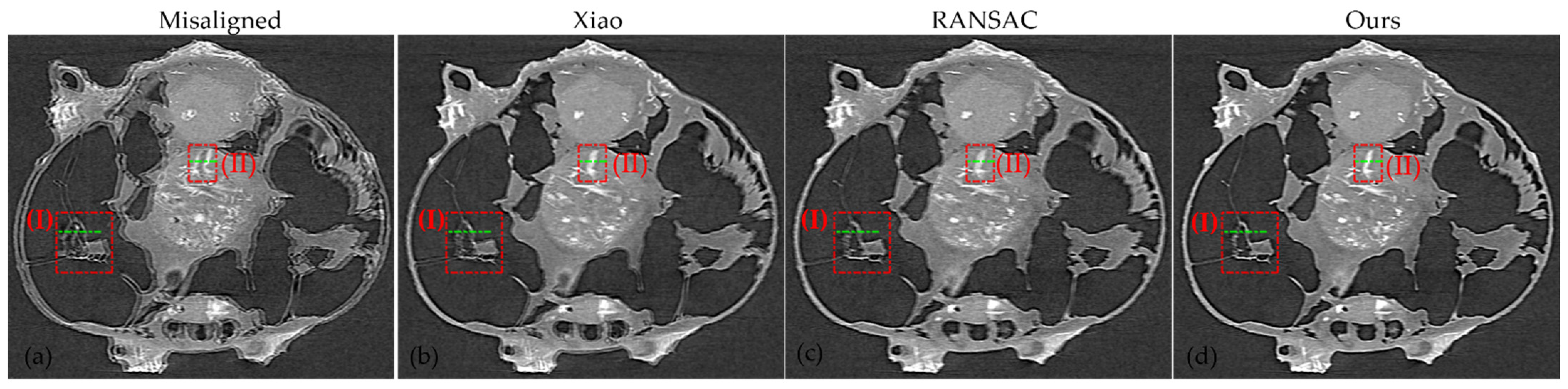
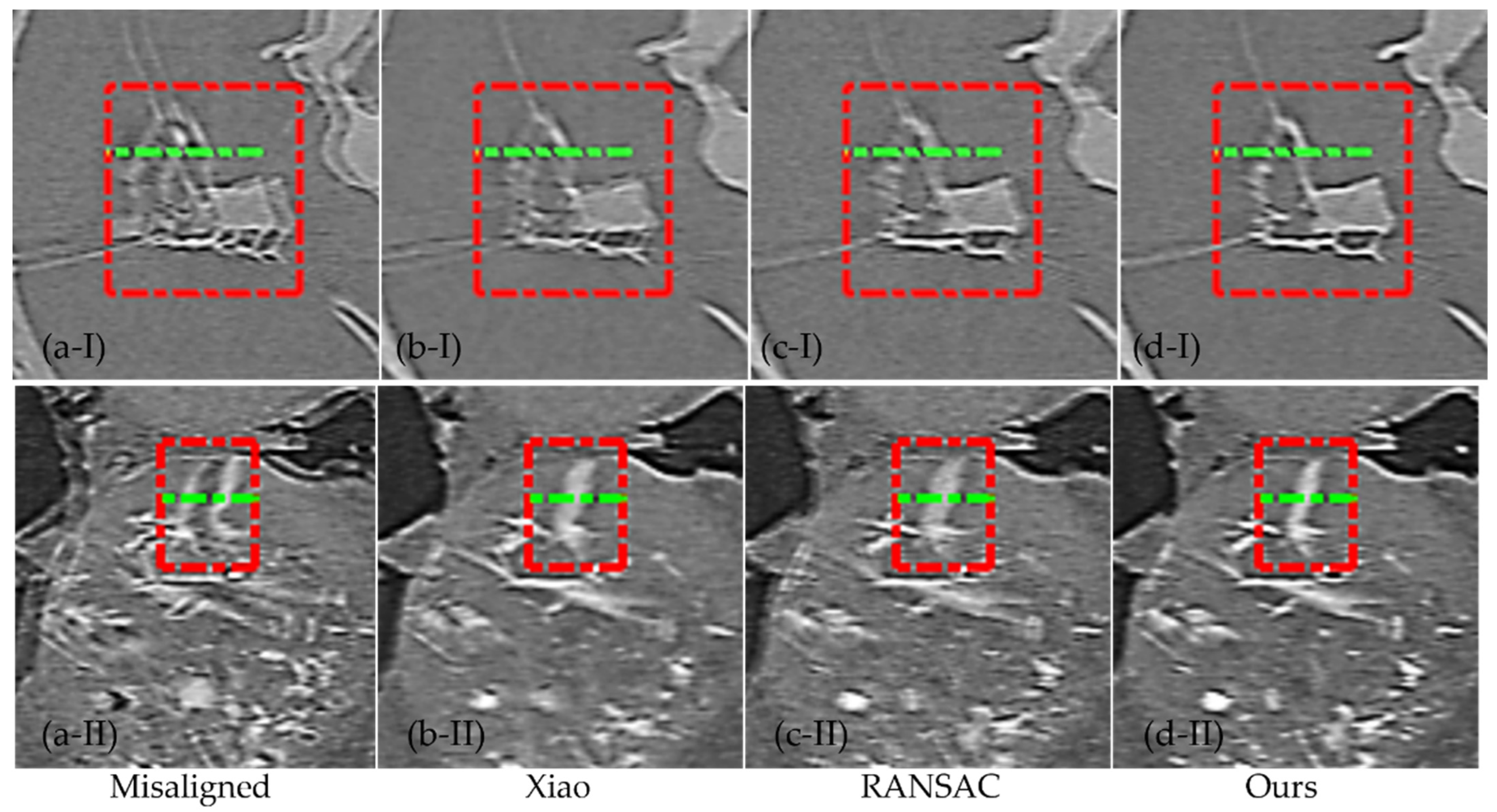
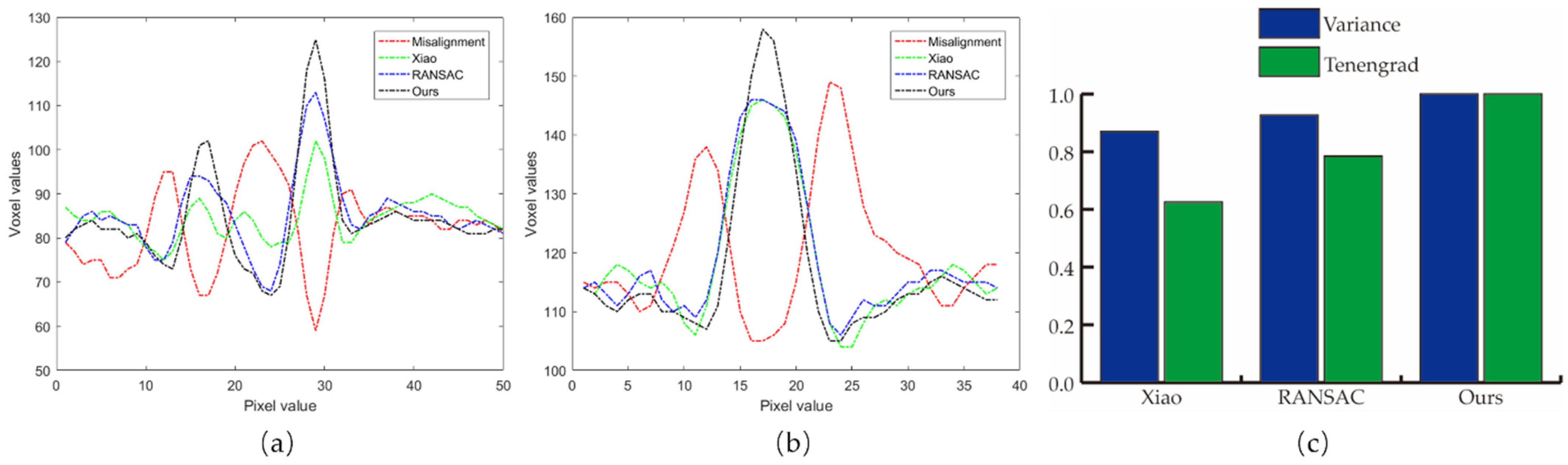
3.2. Nanotomography Experimental Section
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Graetz, J.; Müller, D.; Balles, A.; Fella, C. Lenseless X-Ray Nano-Tomography down to 150 Nm Resolution: On the Quantification of Modulation Transfer and Focal Spot of the Lab-Based NtCT System. J. Instrum. 2021, 16, P01034. [Google Scholar] [CrossRef]
- Ferrucci, M.; Leach, R.K.; Giusca, C.; Carmignato, S.; Dewulf, W. Towards Geometrical Calibration of X-Ray Computed Tomography Systems—A Review. Meas. Sci. Technol. 2015, 26, 092003. [Google Scholar] [CrossRef]
- Biguenet, M.; Chaumillon, E.; Sabatier, P.; Paris, R.; Vacher, P.; Feuillet, N. Discriminating between Tsunamis and Tropical Cyclones in the Sedimentary Record Using X-Ray Tomography. Mar. Geol. 2022, 450, 106864. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Reinicke, T. On the Use of X-Ray Computed Tomography in Assessment of 3D-Printed Components. J. Nondestruct. Eval. 2020, 39, 75. [Google Scholar] [CrossRef]
- Noo, F.; Clackdoyle, R.; Mennessier, C.; White, T.A.; Roney, T.J. Analytic Method Based on Identification of Ellipse Parameters for Scanner Calibration in Cone-Beam Tomography. Phys. Med. Biol. 2000, 45, 3489–3508. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Kwan, A.L.C.; Miller, D.F.; Boone, J.M. A Geometric Calibration Method for Cone Beam CT Systems: A Geometric Calibration Method for Cone Beam CT. Med. Phys. 2006, 33, 1695–1706. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, J.; Hu, X.; Zou, J.; Hu, X. Geometric Parameters Estimation and Calibration in Cone-Beam Micro-CT. Sensors 2015, 15, 22811–22825. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Lu, J.; Sun, Y.; Liu, J.; Cheng, K. A Geometric Calibration Approach for an Industrial Cone-Beam CT System Based on a Low-Rank Phantom. Meas. Sci. Technol. 2022, 33, 035401. [Google Scholar] [CrossRef]
- Mayo, S.; Miller, P.; Gao, D.; Sheffield-Parker, J. Software Image Alignment for X-Ray Microtomography with Submicrometre Resolution Using a SEM-Based X-Ray Microscope. J. Microsc. 2007, 228, 257–263. [Google Scholar] [CrossRef]
- Kyriakou, Y.; Lapp, R.M.; Hillebrand, L.; Ertel, D.; Kalender, W.A. Simultaneous Misalignment Correction for Approximate Circular Cone-Beam Computed Tomography. Phys. Med. Biol. 2008, 53, 6267–6289. [Google Scholar] [CrossRef]
- Kingston, A.M.; Sakellariou, A.; Sheppard, A.P.; Varslot, T.K.; Latham, S.J. An Auto-Focus Method for Generating Sharp 3D Tomographic Images. In Developments in X-Ray Tomography VII, Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 19 August 2010; Stock, S.R., Ed.; SPIE: Bellingham, WA, USA, 2010; p. 78040J. [Google Scholar]
- Tan, S.; Cong, P.; Liu, X.; Wu, Z. An Interval Subdividing Based Method for Geometric Calibration of Cone-Beam CT. NDT E Int. 2013, 58, 49–55. [Google Scholar] [CrossRef]
- Yang, X.; De Carlo, F.; Phatak, C.; Gürsoy, D. A Convolutional Neural Network Approach to Calibrating the Rotation Axis for X-Ray Computed Tomography. J. Synchrotron Radiat. 2017, 24, 469–475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, K.; Yan, B. Correction of Geometric Artifact in Cone-Beam Computed Tomography through a Deep Neural Network. Appl. Opt. 2021, 60, 1843. [Google Scholar] [CrossRef] [PubMed]
- Panetta, D.; Belcari, N.; Del Guerra, A.; Moehrs, S. An Optimization-Based Method for Geometrical Calibration in Cone-Beam CT without Dedicated Phantoms. Phys. Med. Biol. 2008, 53, 3841–3861. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patel, V.; Chityala, R.N.; Hoffmann, K.R.; Ionita, C.N.; Bednarek, D.R.; Rudin, S. Self-Calibration of a Cone-Beam Micro-CT System: Self-Calibration of a Cone-Beam Micro-CT System. Med. Phys. 2008, 36, 48–58. [Google Scholar] [CrossRef]
- Meng, Y.; Gong, H.; Yang, X. Online Geometric Calibration of Cone-Beam Computed Tomography for Arbitrary Imaging Objects. IEEE Trans. Med. Imaging 2013, 32, 278–288. [Google Scholar] [CrossRef]
- Xiao, K.; Han, Y.; Xi, X.; Yan, B.; Bu, H.; Li, L. A Parameter Division Based Method for the Geometrical Calibration of X-Ray Industrial Cone-Beam CT. IEEE Access 2018, 6, 48970–48977. [Google Scholar] [CrossRef]
- Lin, Q.; Yang, M.; Meng, F.; Sun, L.; Tang, B. Calibration Method of Center of Rotation under the Displaced Detector Scanning for Industrial CT. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2019, 922, 326–335. [Google Scholar] [CrossRef]
- Torr, P.H.S.; Zisserman, A. MLESAC: A New Robust Estimator with Application to Estimating Image Geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Tsui, B.M.W. A Graphical Method for Determining the In-Plane Rotation Angle in Geometric Calibration of Circular Cone-Beam CT Systems. IEEE Trans. Med. Imaging 2012, 31, 825–833. [Google Scholar] [CrossRef]
- Ferrucci, M.; Ametova, E.; Carmignato, S.; Dewulf, W. Evaluating the Effects of Detector Angular Misalignments on Simulated Computed Tomography Data. Precis. Eng. 2016, 45, 230–241. [Google Scholar] [CrossRef]
- Zhang, N. Computing Optimised Parallel Speeded-Up Robust Features (P-SURF) on Multi-Core Processors. Int. J. Parallel Program. 2010, 38, 138–158. [Google Scholar] [CrossRef]
- Muja, M.; Lowe, D.G. Scalable Nearest Neighbor Algorithms for High Dimensional Data. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2227–2240. [Google Scholar] [CrossRef] [PubMed]
- Aja-Fernandez, S.; Estepar RS, J.; Alberola-Lopez, C.; Westin, C.F. Image quality assessment based on local variance. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; IEEE: Pasadena, NJ, USA, 2006; pp. 4815–4818. [Google Scholar]
- Yeo TT, E.; Ong, S.H.; Sinniah, R. Autofocusing for tissue microscopy. Image Vis. Comput. 1993, 11, 629–639. [Google Scholar]




| The distance from the X-ray source to rotation axis | |
| The distance from the X-ray source to the detector | |
| The position of the axis of rotation on the detector plane | |
| The position of the mid-plane in the detector plane | |
| The rotation angle of the flat plate detector along the | |
| The rotation angle of the detector around the axis | |
| The rotation angle of the detector along the |
| (°) | ||
|---|---|---|
| Truth parameters | 255.000 | 2.000 |
| Parameters Calculated by Xiao | 255.000 | 2.137 |
| Parameters Calculate by RANSAC | 255.012 | 1.951 |
| Parameters Calculated by our method | 254.997 | 1.995 |
| 10% | 20% | |||
|---|---|---|---|---|
| (°) | (°) | |||
| Truth parameters | 255.000 | 2.000 | 255.000 | 2.000 |
| Parameters Calculated by Xiao | 256.000 | 2.349 | 256.000 | 2.589 |
| Parameters Calculate by RANSAC | 254.984 | 1.947 | 255.111 | 1.879 |
| Parameters Calculated by our method | 254.989 | 1.989 | 254.979 | 1.978 |
| (°) | ||
|---|---|---|
| Parameters Calculated by Xiao | 523.00 | −0.152 |
| Parameters Calculate by RANSAC | 523.47 | −0.059 |
| Parameters Calculated by our method | 523.93 | −0.014 |
| (°) | ||
|---|---|---|
| Parameters Calculated by Xiao | 509.00 | 0.290 |
| Parameters Calculate by RANSAC | 512.53 | 0.312 |
| Parameters Calculated by our method | 512.05 | 0.035 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Han, Y.; Li, L.; Xi, X.; Tan, S.; Zhu, L.; Liu, M.; Yan, B. Geometric Parameter Self-Calibration Based on Projection Feature Matching for X-Ray Nanotomography. Appl. Sci. 2022, 12, 11675. https://doi.org/10.3390/app122211675
Yang S, Han Y, Li L, Xi X, Tan S, Zhu L, Liu M, Yan B. Geometric Parameter Self-Calibration Based on Projection Feature Matching for X-Ray Nanotomography. Applied Sciences. 2022; 12(22):11675. https://doi.org/10.3390/app122211675
Chicago/Turabian StyleYang, Shuangzhan, Yu Han, Lei Li, Xiaoqi Xi, Siyu Tan, Linlin Zhu, Mengnan Liu, and Bin Yan. 2022. "Geometric Parameter Self-Calibration Based on Projection Feature Matching for X-Ray Nanotomography" Applied Sciences 12, no. 22: 11675. https://doi.org/10.3390/app122211675
APA StyleYang, S., Han, Y., Li, L., Xi, X., Tan, S., Zhu, L., Liu, M., & Yan, B. (2022). Geometric Parameter Self-Calibration Based on Projection Feature Matching for X-Ray Nanotomography. Applied Sciences, 12(22), 11675. https://doi.org/10.3390/app122211675






