An Efficient Boundary-Type Meshless Computational Approach for the Axial Compression on the Part Boundary of the Circular Shaft (Brazilian Test)
Abstract
:Featured Application
Abstract
1. Introduction
2. Radial Basis Function with Compact Support (RBFCS)
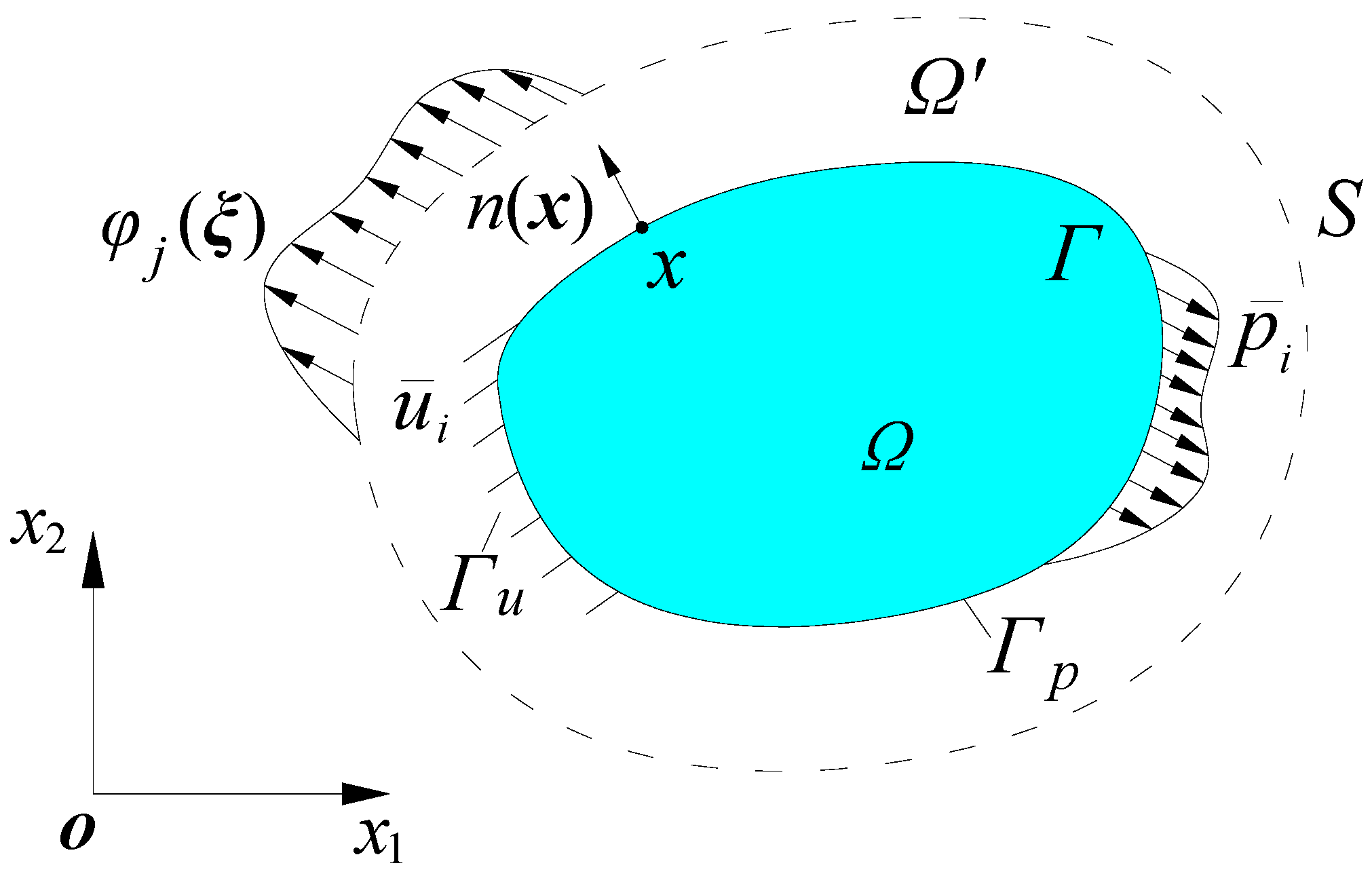
3. The Virtual Boundary Meshless Galerkin Method with the Partial Differential Equation on the Weak Term
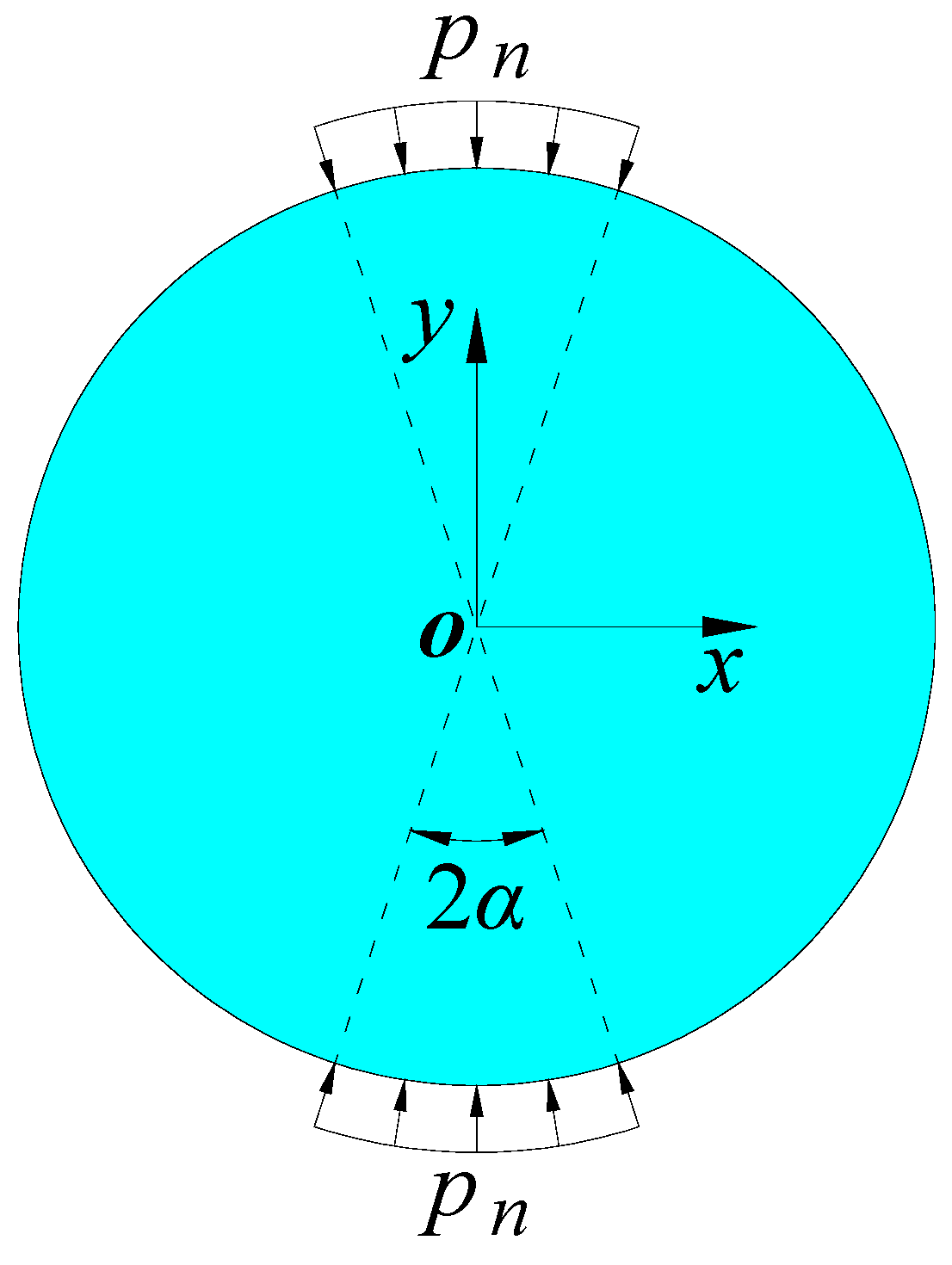
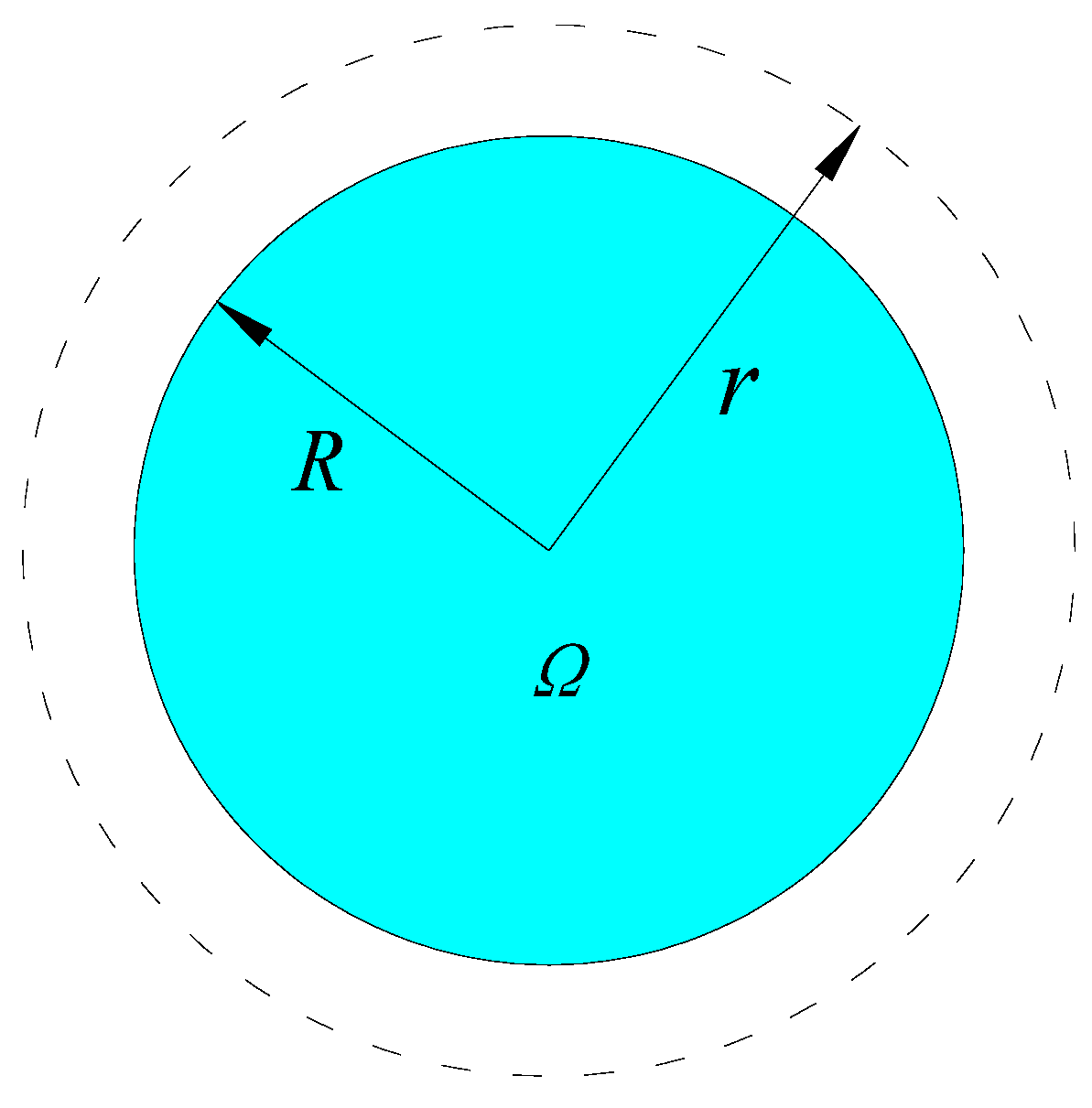
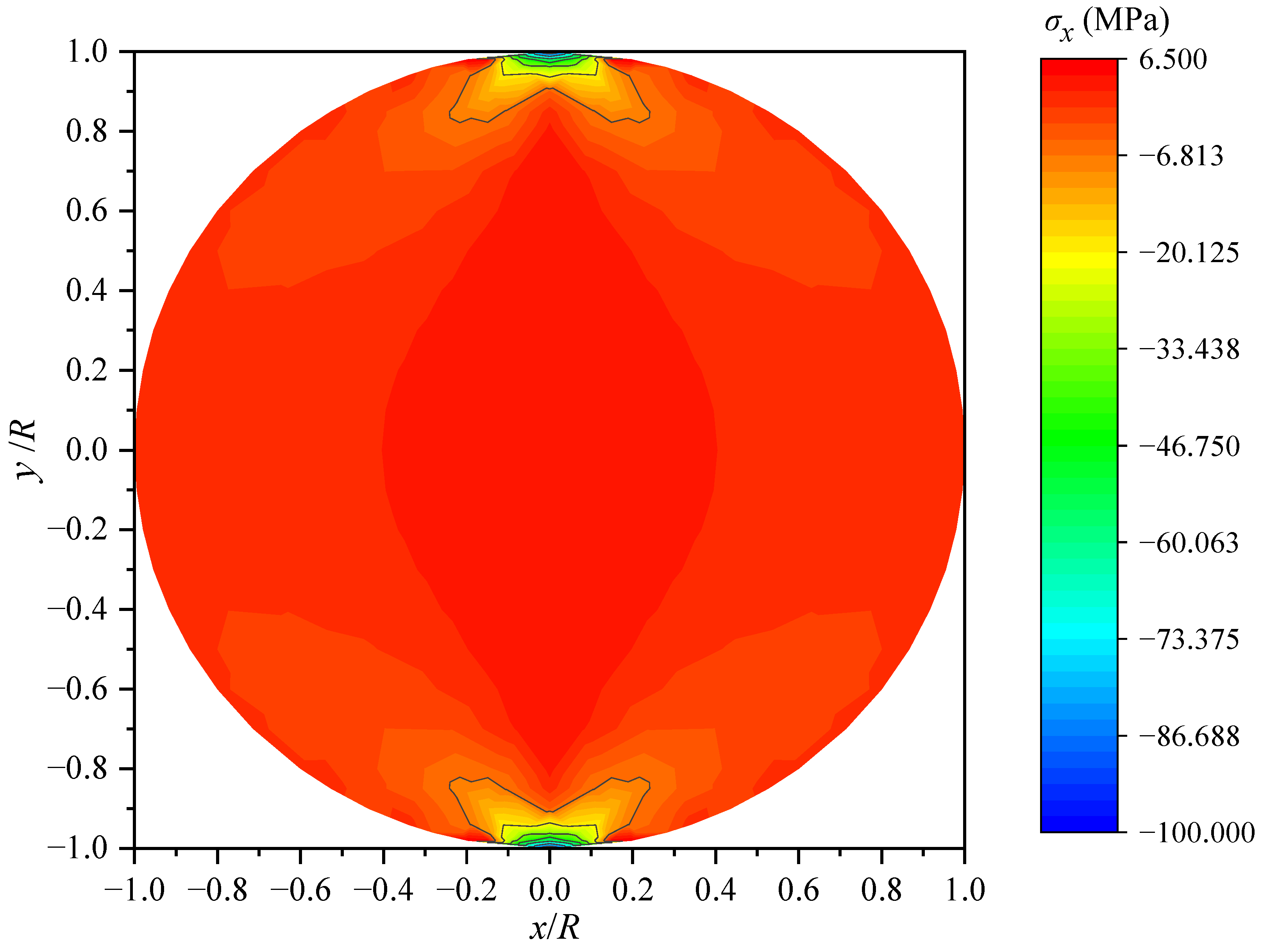
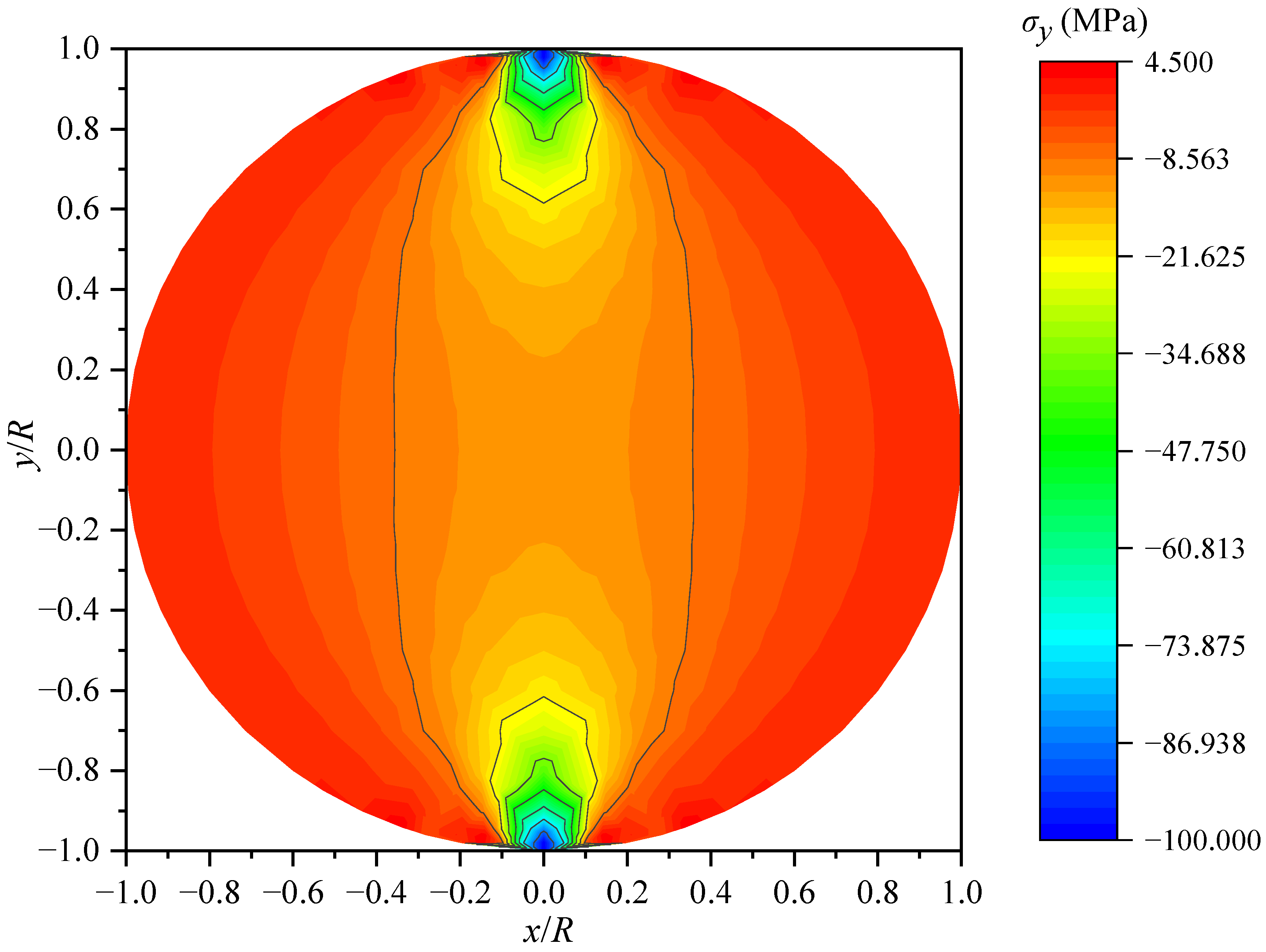
4. Numerical Example: The Axial Compression on the Part Boundary of the Circular Shaft
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Padilla, A.; Genedy, M.; Knight, E.E.; Rougier, E.; Stormont, J.; Taha, M.M.R. Monitoring Postpeak Crack Propagation in Concrete in the Brazilian Tension Test. J. Mater. Civ. Eng. 2022, 34, 04022110-1–04022110-10. [Google Scholar] [CrossRef]
- Efimov, V.P. Brazilian Tensile Strength Testing. J. Min. Sci. 2021, 57, 922–932. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.X.; Li, Y.W.; Tao, F.Y.; Yan, M.S. Experimental research and numerical simulation: Strength and rupture patterns of coal under Brazilian tensile test. Int. J. Oil Gas Coal Technol. 2021, 26, 225–244. [Google Scholar] [CrossRef]
- Torabi, A.R.; Motamedi, M.A.; Bahrami, B.; Noushak, M.; Cicero, S.; Alvarez, J.A. Determination of Translaminar Notch Fracture Toughness for Laminated Composites Using Brazilian Disk Test. Polymers 2022, 14, 3246. [Google Scholar] [CrossRef] [PubMed]
- Xiao, P.; Zhao, G.Y.; Liu, H.X. Failure Transition and Validity of Brazilian Disc Test under Different Loading Configurations: A Numerical Study. Mathematics 2022, 10, 2681. [Google Scholar] [CrossRef]
- Haeri, H.; Shahriar, K.; Marji, M.F.; Moarefvand, P. Experimental and numerical study of crack propagation and coalescence in pre-cracked rock-like disks. Int. J. Rock Mech. Min. Sci. 2014, 67, 20–28. [Google Scholar] [CrossRef]
- Lanaro, F.; Sato, T.; Stephansson, O. Microcrack modelling of Brazilian tensile tests with the boundary element method. Int. J. Rock Mech. Min. Sci. 2009, 46, 450–461. [Google Scholar] [CrossRef]
- Cheng, A.H.D.; Cheng, D.T. Heritage and early history of the boundary element method. Eng. Anal. Bound. Elem. 2005, 29, 268–302. [Google Scholar] [CrossRef]
- Sun, H.C.; Li, X.H.; Zhang, L. Virtual Boundary Element-Collocation Method for Solving Problems of Elasticity. Comput. Struct. Mech. Appl. 1991, 8, 15–23. (In Chinese) [Google Scholar]
- Sun, H.C.; Zhang, L.Z.; Xu, Q.; Zhang, Y.M. Nonsingularity Boundary Element Methods; Dalian University of Technology Press: Dalian, China, 1999. (In Chinese) [Google Scholar]
- Xu, Q.; Sun, H.C. Virtual boundary element least-square collocation method. Chin. J. Comput. Mech. 1997, 14, 166–173. (In Chinese) [Google Scholar]
- Xu, Q.; Zhang, Z.J.; Si, W. Virtual boundary meshless least square collocation method for calculation of 2D multi-domain elastic problems. Eng. Anal. Bound. Elem. 2012, 36, 696–708. [Google Scholar] [CrossRef]
- Yang, D.S.; Xu, Q. Virtual boundary meshless least square integral method with moving least squares approximation for 2D elastic problem. Eng. Anal. Bound. Elem. 2013, 37, 616–623. [Google Scholar] [CrossRef]
- Xu, Q.; Yang, D.S. Solving multi-domain 2D heat conduction problems by the least squares collocation method with RBF interpolation on virtual boundary. Eng. Anal. Bound. Elem. 2014, 42, 37–44. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. Boundary meshfree methods based on the boundary point interpolation methods. Eng. Anal. Bound. Elem. 2004, 28, 475–487. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Hoskins, E.R. Rock failure under the confined brazilian test. J. Geophys. Res. 1966, 71, 2651–2659. [Google Scholar] [CrossRef]
- Kuang, G.N.; Xiong, Z.N.; Song, Z.X. Boundary Element Method in Practical Engineering; Chinese Railway Press: Beijing, China, 1989. (In Chinese) [Google Scholar]

| Coordinates | (0, 0) | (0, 0.1) | (0, 0.2) | (0, 0.3) | (0, 0.4) | (0, 0.5) | (0, 0.6) | (0, 0.7) | (0, 0.8) | |
|---|---|---|---|---|---|---|---|---|---|---|
| σx | BEM | 3.936 | 3.934 | 3.928 | 3.917 | 3.895 | 3.853 | 3.761 | 3.519 | 2.644 |
| VSM | 3.914 | 3.913 | 3.909 | 3.901 | 3.885 | 3.851 | 3.774 | 3.562 | 2.766 | |
| DDM | 3.955 | 3.955 | 3.954 | 3.951 | 3.944 | 3.926 | 3.876 | 3.714 | 3.009 | |
| the paper | 3.979 | 3.978 | 3.973 | 3.965 | 3.948 | 3.913 | 3.836 | 3.621 | 2.791 | |
| Ass | 3.979 | 3.978 | 3.973 | 3.965 | 3.948 | 3.913 | 3.836 | 3.621 | 2.792 | |
| σy | BEM | −11.925 | −12.082 | −12.574 | −13.462 | −14.875 | −17.061 | −20.514 | −26.333 | −27.410 |
| VSM | −11.871 | −12.026 | −12.513 | −13.392 | −14.791 | −16.954 | −20.370 | −26.122 | −37.065 | |
| DDM | −12.003 | −12.162 | −12.659 | −13.558 | −14.991 | −17.214 | −20.744 | −26.740 | −38.322 | |
| the paper | −11.979 | −12.139 | −12.638 | −13.542 | −14.982 | −17.216 | −20.758 | −26.766 | −38.330 | |
| Ass | −11.979 | −12.139 | −12.638 | −13.542 | −14.982 | −17.216 | −20.758 | −26.766 | −38.332 | |
| Coordinates | (0, 0) | (0.1, 0) | (0.2, 0) | (0.3, 0) | (0.4, 0) | (0.5, 0) | (0.6, 0) | (0.7, 0) | (0.8, 0) | |
|---|---|---|---|---|---|---|---|---|---|---|
| σx | BEM | 3.936 | 3.783 | 3.359 | 2.752 | 2.074 | 1.426 | 0.877 | 0.462 | 0.186 |
| VSM | 3.914 | 3.763 | 3.343 | 2.741 | 2.069 | 1.425 | 0.879 | 0.464 | 0.187 | |
| DDM | 3.955 | 3.800 | 3.372 | 2.760 | 2.077 | 1.424 | 0.872 | 0.454 | 0.176 | |
| the paper | 3.979 | 3.824 | 3.393 | 2.778 | 2.092 | 1.438 | 0.885 | 0.469 | 0.193 | |
| Ass | 3.979 | 3.824 | 3.393 | 2.778 | 2.092 | 1.438 | 0.885 | 0.469 | 0.193 | |
| σy | BEM | −11.925 | −11.616 | −10.742 | −9.437 | −7.886 | −6.255 | −4.680 | −3.245 | −1.992 |
| VSM | −11.871 | −11.565 | −10.700 | −9.412 | −7.875 | −6.261 | −4.701 | −3.279 | −2.036 | |
| DDM | −12.003 | −11.692 | −10.814 | −9.505 | −7.949 | −6.316 | −4.741 | −3.309 | −2.060 | |
| the paper | −11.979 | −11.666 | −10.779 | −9.459 | −7.889 | −6.242 | −4.654 | −3.210 | −1.951 | |
| Ass | −11.979 | −11.686 | −10.779 | −9.459 | −7.889 | −6.242 | −4.654 | −3.210 | −1.951 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, J.; Wang, H.; Mou, H. An Efficient Boundary-Type Meshless Computational Approach for the Axial Compression on the Part Boundary of the Circular Shaft (Brazilian Test). Appl. Sci. 2022, 12, 11806. https://doi.org/10.3390/app122211806
Ling J, Wang H, Mou H. An Efficient Boundary-Type Meshless Computational Approach for the Axial Compression on the Part Boundary of the Circular Shaft (Brazilian Test). Applied Sciences. 2022; 12(22):11806. https://doi.org/10.3390/app122211806
Chicago/Turabian StyleLing, Jing, Hongying Wang, and Hongzhong Mou. 2022. "An Efficient Boundary-Type Meshless Computational Approach for the Axial Compression on the Part Boundary of the Circular Shaft (Brazilian Test)" Applied Sciences 12, no. 22: 11806. https://doi.org/10.3390/app122211806
APA StyleLing, J., Wang, H., & Mou, H. (2022). An Efficient Boundary-Type Meshless Computational Approach for the Axial Compression on the Part Boundary of the Circular Shaft (Brazilian Test). Applied Sciences, 12(22), 11806. https://doi.org/10.3390/app122211806





