Mechanical Analysis of Frozen Wall with Trapezoidal Temperature Field Distribution Based on Unified Strength Theory
Abstract
:1. Introduction
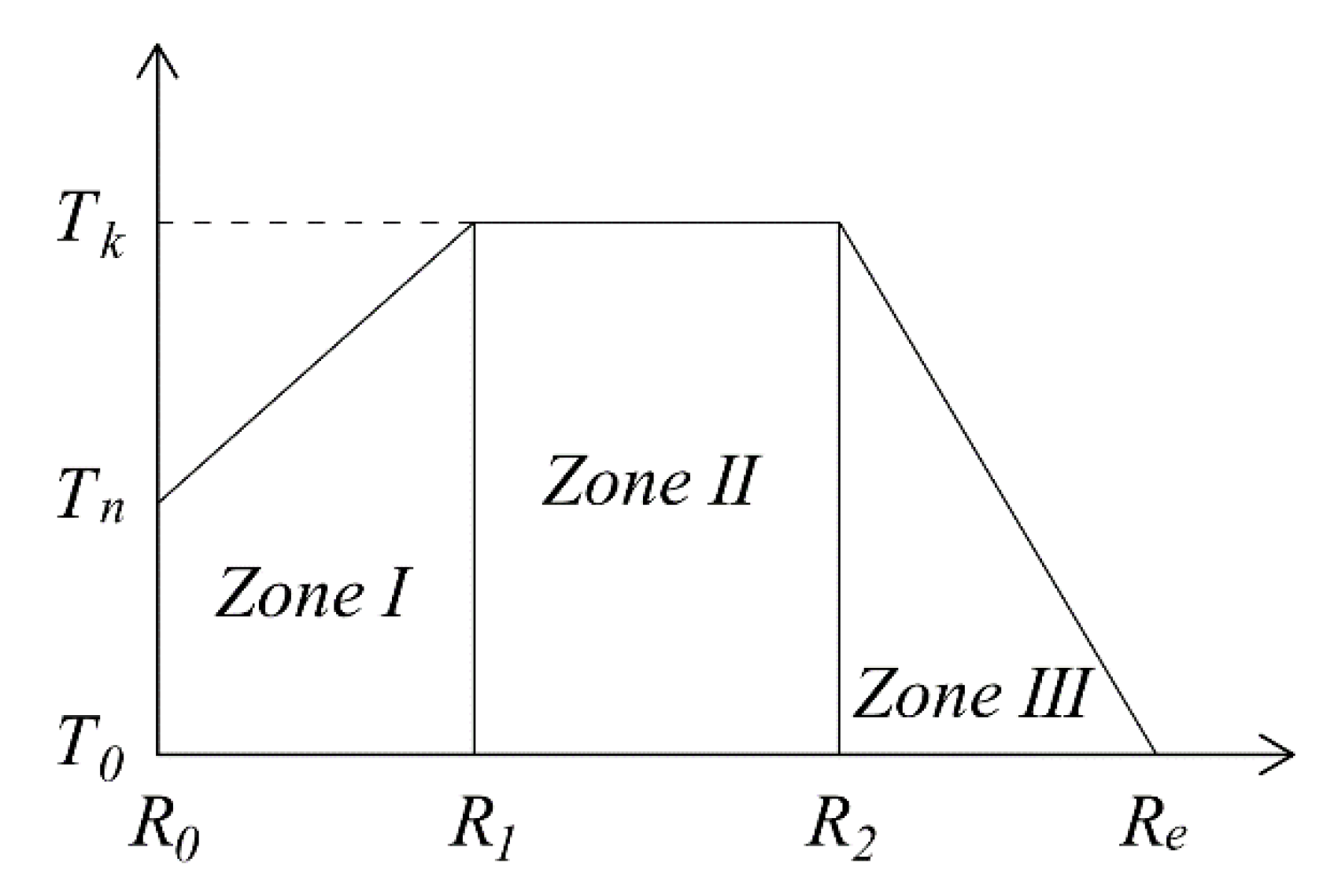
2. Equivalent Temperature Field
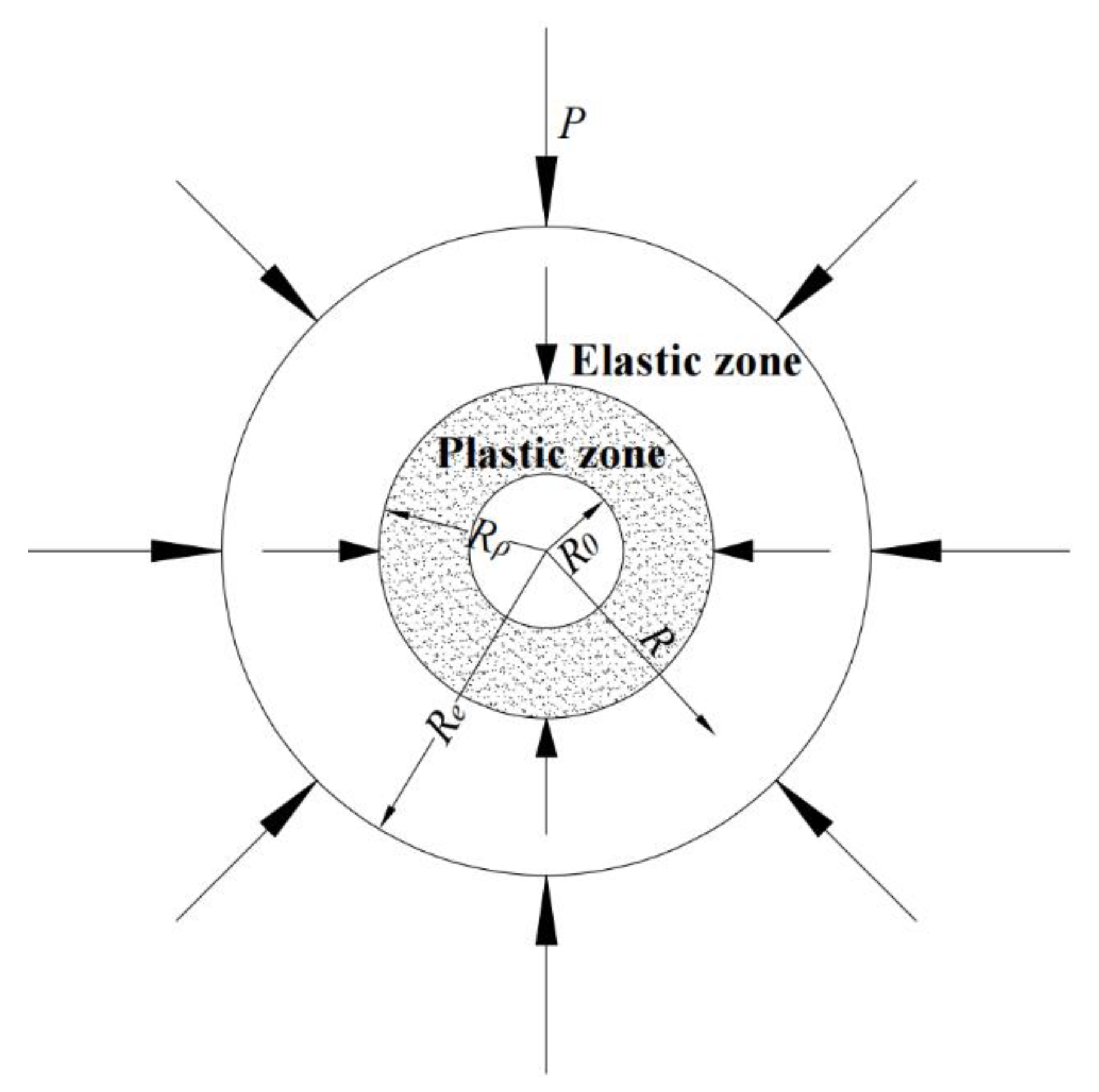
3. Mechanical Model of a Frozen Wall
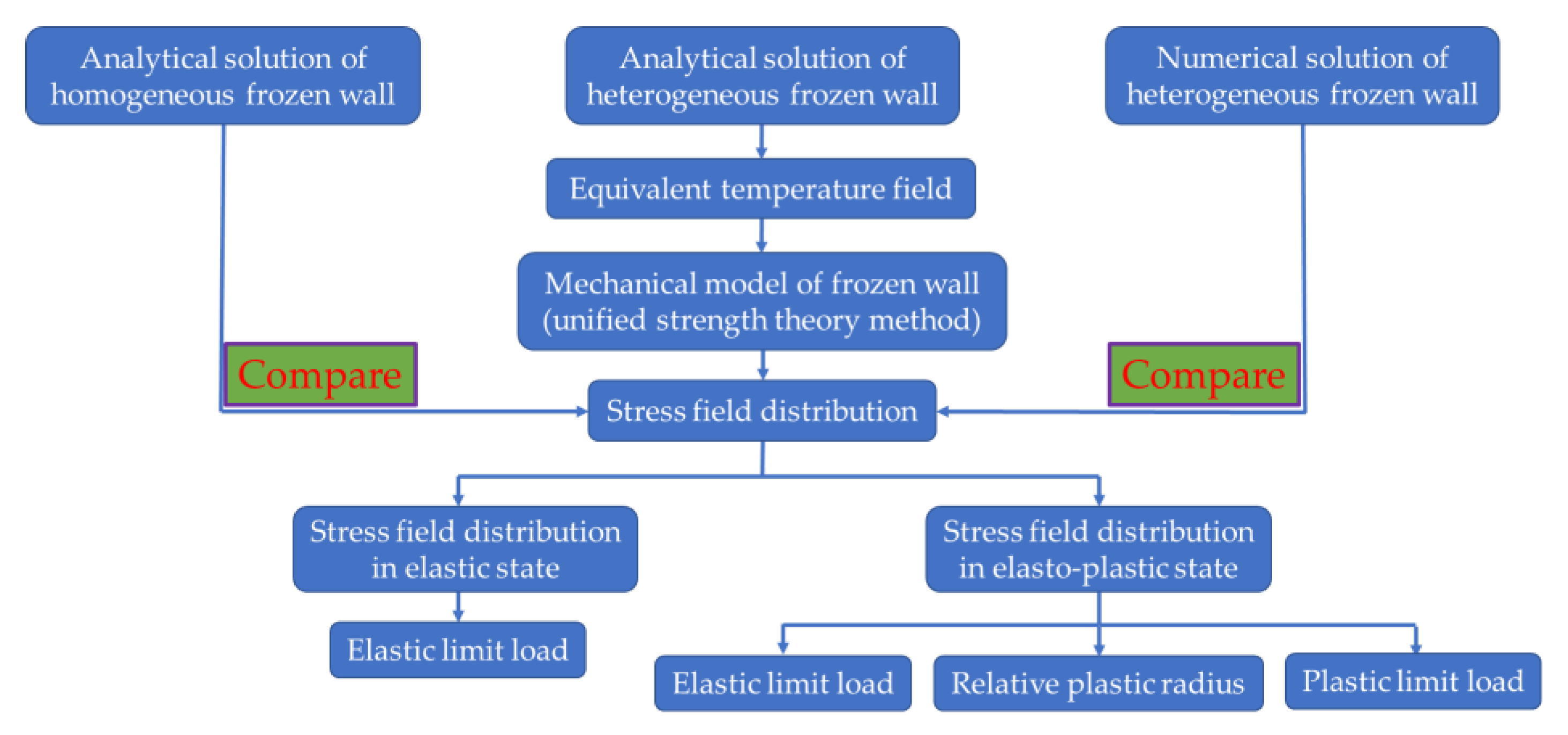
4. Model Solving
4.1. Solution of Stress Field in the Elastic State
4.2. Elastic–Plastic Analysis of Frozen Wall
4.2.1. Solution of Stress Field in the Plastic Zone
4.2.2. Solution of Stress Field in the Elastic Region
4.2.3. Solution of Relative Radius in the Plastic Zone
4.3. Elastic Limit Load
4.4. Plastic Limit Load
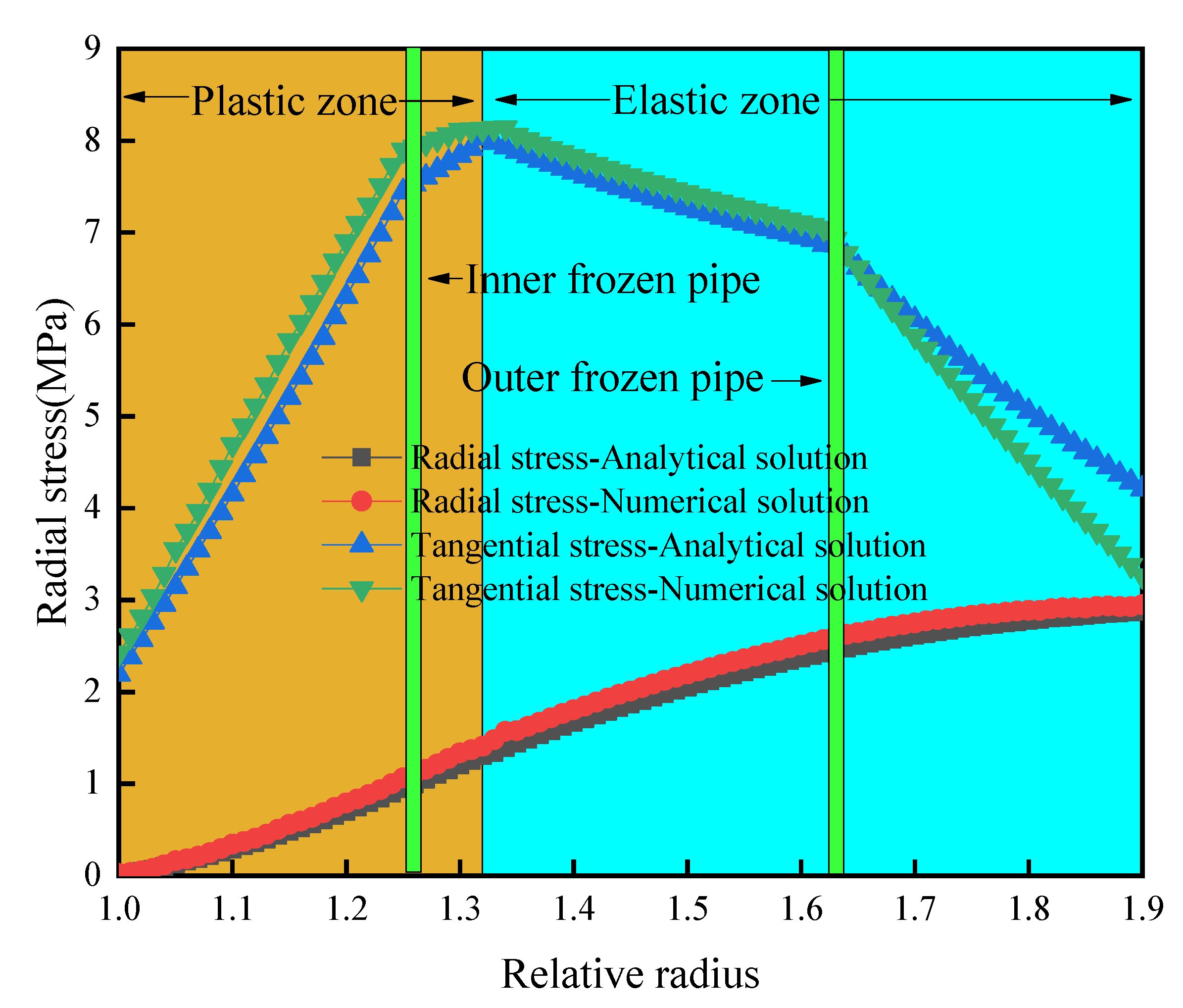
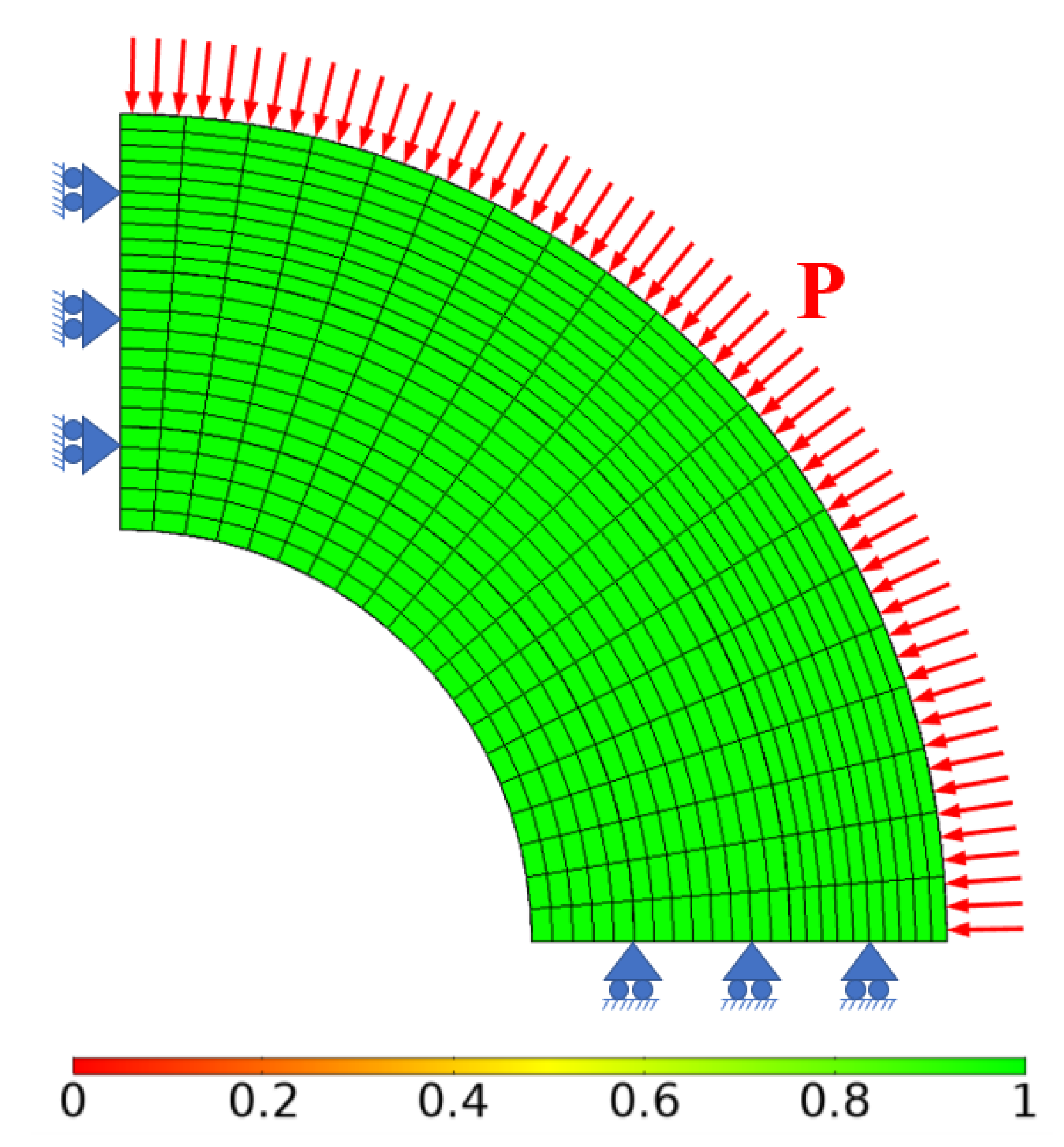
5. Stress Field Distribution of Frozen Wall and Numerical Verification: A Case Study
6. Discussion
7. Conclusions
- Considering the FGM characteristics of the frozen wall, the temperature field of the double-row-pipe frozen wall is equivalent to a trapezoidal distribution along the radial direction, and the elastic modulus E and cohesion c of the frozen wall are considered to be linearly distributed with the radius. Based on unified strength theory, the analytical solutions of the elastic–plastic stress field, the elastic ultimate bearing capacity, the plastic ultimate bearing capacity, and the relative radius of the plastic zone of the double-row-pipe frozen wall are derived; the results can provide a theoretical reference for the design of frozen wall.
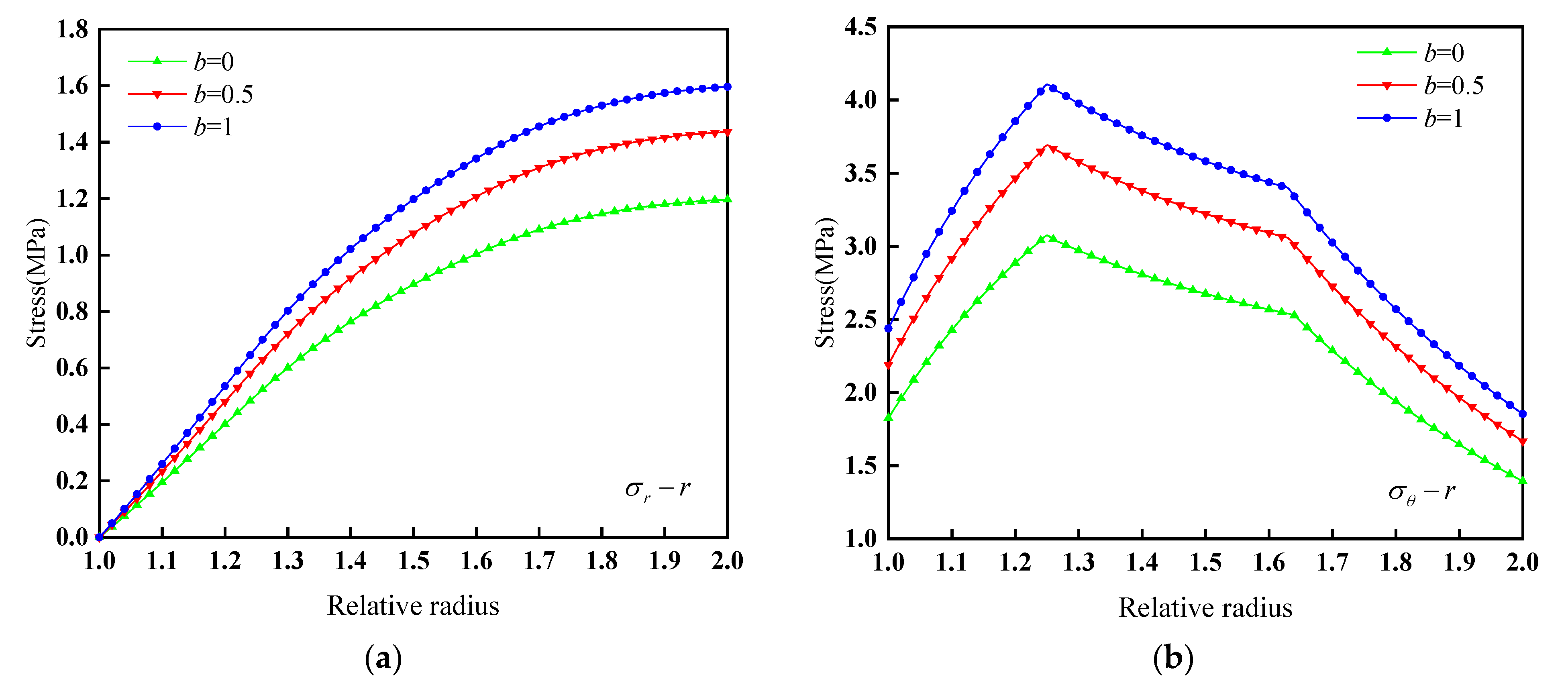
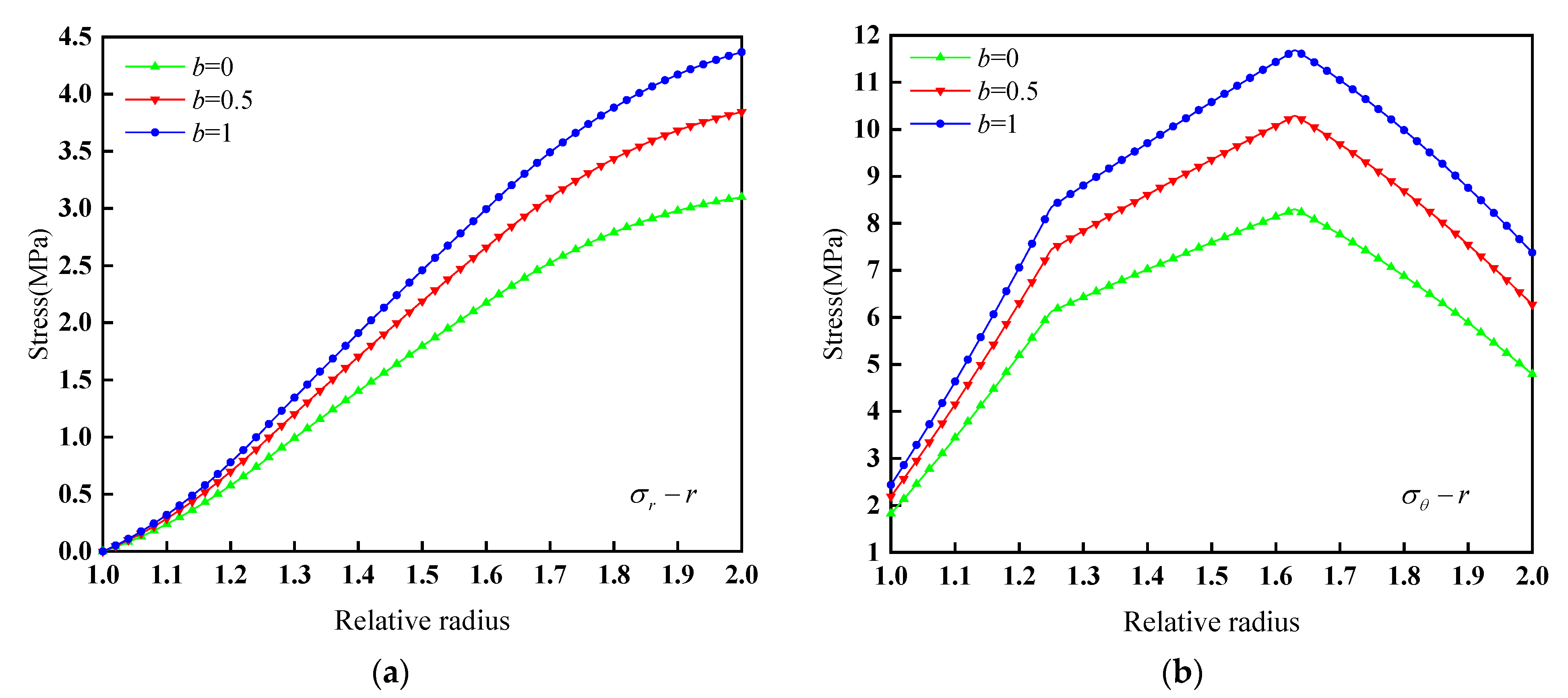
- We analyzed a frozen wall with a vertical depth of 225 m in Qingdong Mine. When b is 0.5, the elastic ultimate bearing capacity of the frozen wall is 1.44 MPa, and the plastic ultimate bearing capacity of the frozen wall is 3.55 MPa. The external load p = 2.925 MPa of the frozen wall is between the elastic ultimate bearing capacity and the plastic ultimate bearing capacity, indicating that the stress state of the frozen wall is safe. Under the action of external load, the relative radius of the plastic zone of the frozen wall is 1.32, which is located between the inner and outer frozen pipes.
- Based on the Qingdong Mine, the analytical solution was calculated and compared with the numerical solution, and it is concluded that the stress distribution of the two solutions is consistent, which mutually verifies the accuracy of the two solutions.
- The strength theory parameter b has an important influence on the stress state of heterogeneous and homogeneous frozen walls. The radial stress increases with the increase in b and the relative radius r, the tangential stress increases with the increase in b, and the tangential stress first increases and then decreases with the increase in r. The elastic ultimate bearing capacity Pe and Pp of the frozen wall increase with the increase in b. When b increases from 0 to 1, the elastic ultimate bearing capacity and plastic ultimate bearing capacity of the heterogeneous frozen wall increase by 33.3% and 40.8%, respectively, and the elastic ultimate bearing capacity and plastic ultimate bearing capacity of the homogeneous frozen wall increase by 33.3% and 41.0%, respectively. The relative radius of the plastic zone decreases with the increase in b.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Zhou, X.; Jiang, G.; Li, F.; Gao, W.; Han, Y.; Wu, T.; Ma, W. Comprehensive review of artificial ground freezing applications to urban tunnel and underground space engineering in China in the last 20 years. J. Cold Reg. Eng. 2022, 36, 04022002. [Google Scholar] [CrossRef]
- Cheng, H. Shaft Sinking Theory and Technology of Deep Alluvium Freezing Method, 1st ed.; Science Press: Beijing, China, 2016. [Google Scholar]
- Nikolaev, P.; Sedighi, M.; Rajabi, H.; Pankratenko, A. Artificial ground freezing by solid carbon dioxide-Analysis of thermal performance. Tunn. Undergr. Sp. Technol. 2022, 130, 104741. [Google Scholar] [CrossRef]
- Hu, J.; Li, K.; Wu, Y.; Zeng, D.; Wang, Z. Optimization of the Cooling Scheme of Artificial Ground Freezing Based on Finite Element Analysis: A Case Study. Appl. Sci. 2022, 12, 8618. [Google Scholar] [CrossRef]
- Zhou, J.; Guo, Z.; Wang, C.; Li, Z.; Zhou, H.; Pei, W. Analysis of freeze-thaw response and pore characteristics of artificially frozen soft soil under combined formation seepage. Appl. Sci. 2022, 12, 10687. [Google Scholar] [CrossRef]
- Wu, T.; Zhou, X.; Zhang, L.; Zhang, X.; He, X.; Xu, Y. Theory and technology of real-time temperature field monitoring of vertical shaft frozen wall under high-velocity groundwater conditions. Cold Reg. Sci. Technol. 2021, 189, 10337. [Google Scholar] [CrossRef]
- Long, W.; Rong, C.; Shi, H.; Huang, S.; Wang, Z.; Duan, Y.; Ma, H. Temperature field and stability analysis of the frozen wall based on the actual position of freezing holes. Appl. Sci. 2022, 12, 8943. [Google Scholar] [CrossRef]
- Wang, B.; Rong, C.; Cheng, H.; Yao, Z.; Cai, H. Research and application of the local differential freezing technology in deep alluvium. Adv. Civ. Eng. 2020, 2020, 9381468. [Google Scholar] [CrossRef]
- Hu, X.; Wu, Y.; Li, X. A field study on the freezing characteristics of freeze-sealing pipe roof used in ultra-shallow buried tunnel. Appl. Sci. 2019, 9, 1532. [Google Scholar] [CrossRef] [Green Version]
- Long, W.; Rong, C.; Duan, Y.; Guo, K. Numerical calculation of temperature field of freeze-sealing pipe roof of method in Gongbei tunnel. Cold Geol. Explor. 2020, 48, 160–168. [Google Scholar]
- Hu, J.; Jiang, B.; Zeng, H.; Chen, Y.; Zhu, Y. Temperature field numerical analysis of different freeze pipe spacing of vertical frozen soil wall reinforcement at shield shaft. Appl. Mech. Mater. 2014, 580–583, 738–741. [Google Scholar] [CrossRef]
- Pang, C.; Cai, H.; Hong, R.; Li, M.; Yang, Z. Evolution law of three-dimensional non-uniform temperature field of tunnel construction using local horizontal freezing technique. Appl. Sci. 2022, 12, 8093. [Google Scholar] [CrossRef]
- Dong, X.; Yu, S.; Zhang, Y.; Wang, Y. The causes and prevention measures of water inflow at cross passage located in sandy gravel layers and constructed by artificial ground freezing. Chin. J. Undergr. Sp. Eng. 2022, 18, 322–329. [Google Scholar]
- Liu, X.; Shen, Y.; Zhang, Z.; Liu, Z.; Wang, B.; Tang, T.; Liu, C. Field measurement and numerical investigation of artificial ground freezing for the construction of a subway cross passage under groundwater flow. Transp. Geotech. 2022, 37, 100869. [Google Scholar] [CrossRef]
- Yao, Z.; Cheng, H. Study on frost-heaving force in retaining structure with row-pile and frozen soil wall for deep foundation pit. Chin. J. Rock Mech. Rock Eng. 2004, 23, 1521–1524. [Google Scholar]
- Akagawa, S. Artificially frozen ground and related engineering technology in Japan. Sci. Cold Arid Reg. 2021, 13, 77–86. [Google Scholar]
- Wang, R.; Li, D.; Wang, X. Calculating frozen wall stress and displacement fields by Mohr-Coulomb strength criterion. Ind. Constr. 2005, 35, 40–42. [Google Scholar]
- Yang, W.; Yang, Z.; Han, T.; Zhang, C.; Bo, D. Elastic design theory of frozen soil wall based on interaction between frozen soil wall and surrounding rock. Chin. J. Geotech. Eng. 2012, 34, 516–519. [Google Scholar]
- Yang, W.; Yang, Z.; Bo, D. Elastic-plastic design theory of frozen soil wall based on interaction between frozen wall and surrounding rock. Chin. J. Geotech. Eng. 2013, 35, 175–180. [Google Scholar]
- Yang, W.; Du, Z.; Yang, Z.; Bo, D. Plastic design theory of frozen soil wall based on interaction between frozen soil wall and surrounding rock. Chin. J. Geotech. Eng. 2013, 35, 1857–1862. [Google Scholar]
- Zhang, C.; Zhao, J.; Wei, X. Investigation the stress field and displacement field on the frozen wall based on the unified strength theory. Chin. J. Undergr. Sp. Eng. 2008, 4, 465–469. [Google Scholar]
- Hu, X. A mechanical model of interaction of frozen soil wall and surrounding earth mass in unloaded state. J. China Coal Soc. 2001, 26, 507–511. [Google Scholar]
- Hu, X. Determination of load on frozen soil wall in unloaded state. J. Tongji Univ. 2002, 37, 6–10. [Google Scholar]
- Hu, X. Average temperature model of double-row-pipe frozen soil wall by equivalent trapezoid method. AIP Conf. Proc. 2010, 1233, 1333–1338. [Google Scholar]
- Hu, X. Average temperature calculation for straight single-row-piped frozen soil wall. J. Glaciol. Geocryol. 2010, 32, 778–785. [Google Scholar]
- Hu, X.; Zhao, F.; She, S.; Shu, C. Equivalent parabolic arch method of average temperature calculation for straight double-row-pipe frozen soil wall. J. China Coal Soc. 2012, 37, 28–32. [Google Scholar]
- Hu, X.; Ren, H. A trapezoidal-parabolic arch superimposed equivalent temperature field model and its average temperature formula for triple-row-pipe freezing. J. China Coal Soc. 2014, 39, 78–83. [Google Scholar]
- Hu, X.; Shu, C.; She, S. Elastic-plastic analytical solution for functionally graded material frozen soil wall with parabolic property under uniform load. J. China Coal Soc. 2012, 37, 379–384. [Google Scholar]
- Hu, X.; Shu, C. Stress field analysis of functionally graded material frozen soil wall in double-row-pipe shaft freezing. Eng. Mech. 2014, 31, 145–153. [Google Scholar]
- Rong, C.; Wang, B.; Peng, S.; Cheng, H. Study on mechanical characteristics of functionally graded material frozen soil wall basing on Druker-Prager strength criterion. J. Guangxi Univ. 2015, 40, 1339–1344. [Google Scholar]
- Wang, B.; Rong, C.; Cheng, H.; Wang, Z. Theoretical analysis of the double-row-pipe frozen soil wall basing on Druker-Prager strength criterion. Sci. Technol. Eng. 2016, 16, 44–62. [Google Scholar]
- Wang, B.; Rong, C.; Cheng, H. Stress analysis of heterogeneous frozen wall considering interaction with surrounding soil. J. China Coal Soc. 2017, 42, 354–361. [Google Scholar]
- Cao, X.; Zhao, J.; Zhang, C. Elastoplastic stress analysis of frozen soil wall based on unified strength theory. Rock Soil Mech. 2017, 38, 769–774. [Google Scholar]
- Xu, Z. A Concise Course of Elasticity, 3rd ed.; Higher Education Press: Beijing, China, 2002. [Google Scholar]
- Hu, X.; Yu, M. Amendment of the twin-shear criterion and its application to calculation of earth pressure. Chin. J. Geotech. Eng. 2005, 27, 283–287. [Google Scholar]
- GB 50384—2016; Code for Design of Coal Mine Shaft and Chamber. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=SCSF&dbname=SCSF&filename=SCSF00072028&uniplatform=NZKPT&v=9klx80ksI66TfUeL7OlNdUePEPWk8JciYPxgnvTytCnIYyg6TlCV8WC_QigOzLbn (accessed on 18 August 2016).


| b | P (MPa) | Heterogeneous Frozen Wall | Homogeneous Frozen Wall | ||||||
|---|---|---|---|---|---|---|---|---|---|
| rρ | Pe (MPa) | Pp (MPa) | K | rρ | Pe (MPa) | Pp (MPa) | K | ||
| 0 | 2.925 | 1.63 | 1.20 | 3.11 | 1.06 | 1.94 | 1.35 | 2.93 | 2.17 |
| 0.2 | 1.44 | 1.31 | 3.44 | 1.18 | 1.57 | 1.47 | 3.28 | 2.23 | |
| 0.4 | 1.35 | 1.40 | 3.73 | 1.28 | 1.45 | 1.57 | 3.52 | 2.24 | |
| 0.6 | 1.30 | 1.47 | 3.97 | 1.36 | 1.37 | 1.66 | 3.75 | 2.26 | |
| 0.8 | 1.26 | 1.54 | 4.19 | 1.43 | 1.32 | 1.73 | 3.95 | 2.28 | |
| 1 | 1.23 | 1.60 | 4.38 | 1.50 | 1.28 | 1.80 | 4.13 | 2.29 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Shi, H.; Long, W.; Shi, X. Mechanical Analysis of Frozen Wall with Trapezoidal Temperature Field Distribution Based on Unified Strength Theory. Appl. Sci. 2022, 12, 11879. https://doi.org/10.3390/app122311879
Wu Y, Shi H, Long W, Shi X. Mechanical Analysis of Frozen Wall with Trapezoidal Temperature Field Distribution Based on Unified Strength Theory. Applied Sciences. 2022; 12(23):11879. https://doi.org/10.3390/app122311879
Chicago/Turabian StyleWu, Yangyong, Hao Shi, Wei Long, and Xin Shi. 2022. "Mechanical Analysis of Frozen Wall with Trapezoidal Temperature Field Distribution Based on Unified Strength Theory" Applied Sciences 12, no. 23: 11879. https://doi.org/10.3390/app122311879
APA StyleWu, Y., Shi, H., Long, W., & Shi, X. (2022). Mechanical Analysis of Frozen Wall with Trapezoidal Temperature Field Distribution Based on Unified Strength Theory. Applied Sciences, 12(23), 11879. https://doi.org/10.3390/app122311879






