Modeling and HDA-CR Solution of Multi-Period Allocation Scheme of Hazardous Materials under Uncertainty
Abstract
:Featured Application
Abstract
1. Introduction
2. Research Overview
3. Problem Description and Modeling
3.1. Problem Description
3.2. Problem Assumptions
3.3. Allocation Risk Model
3.3.1. The Traffic Accident Probability
3.3.2. Population Density
3.3.3. Accident Impact Range
3.3.4. Allocation Risk Measures
3.4. Multi-Period Hazardous Materials Allocation Model
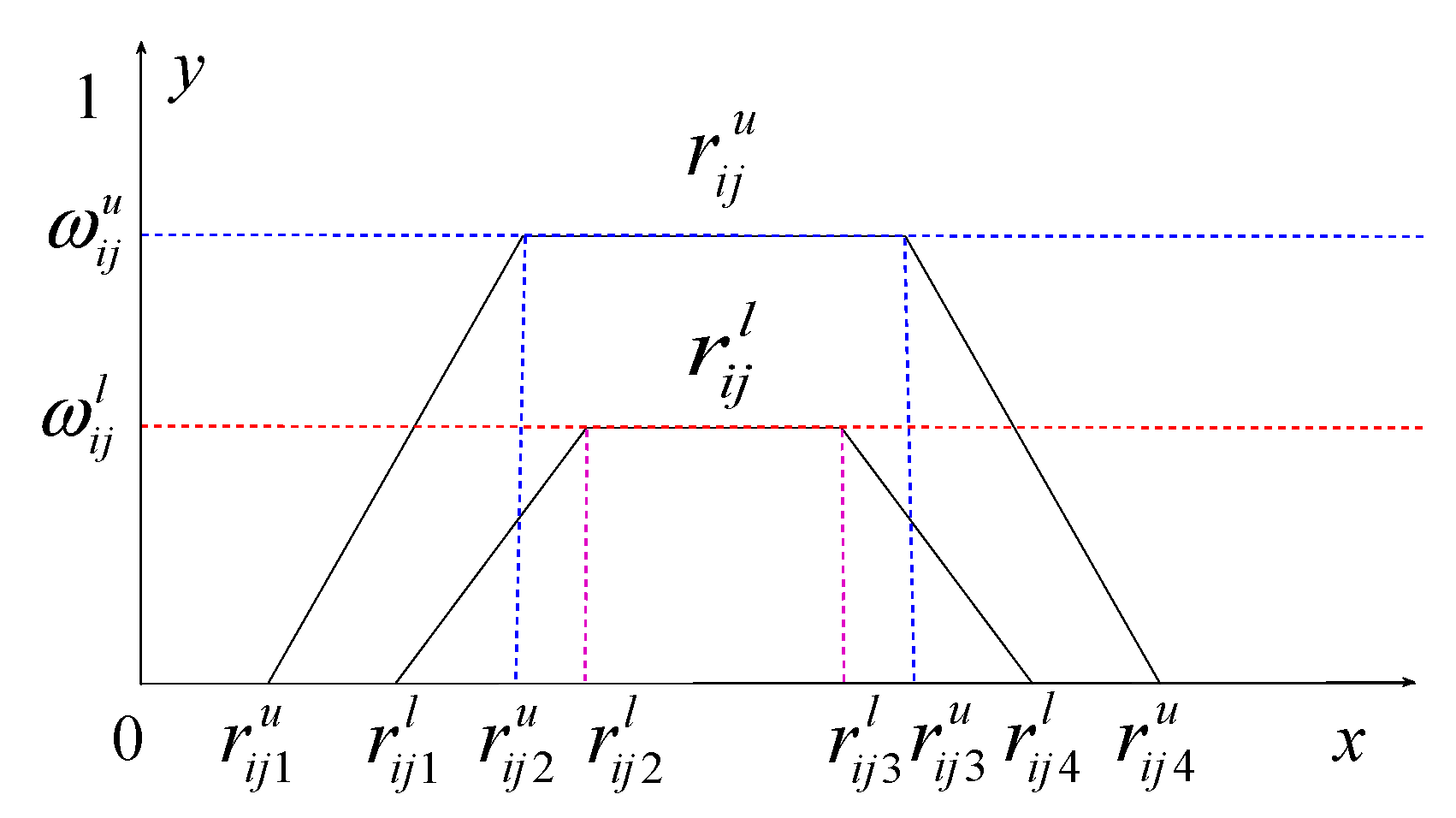
3.5. Bilevel Chance Constrained Programming Model
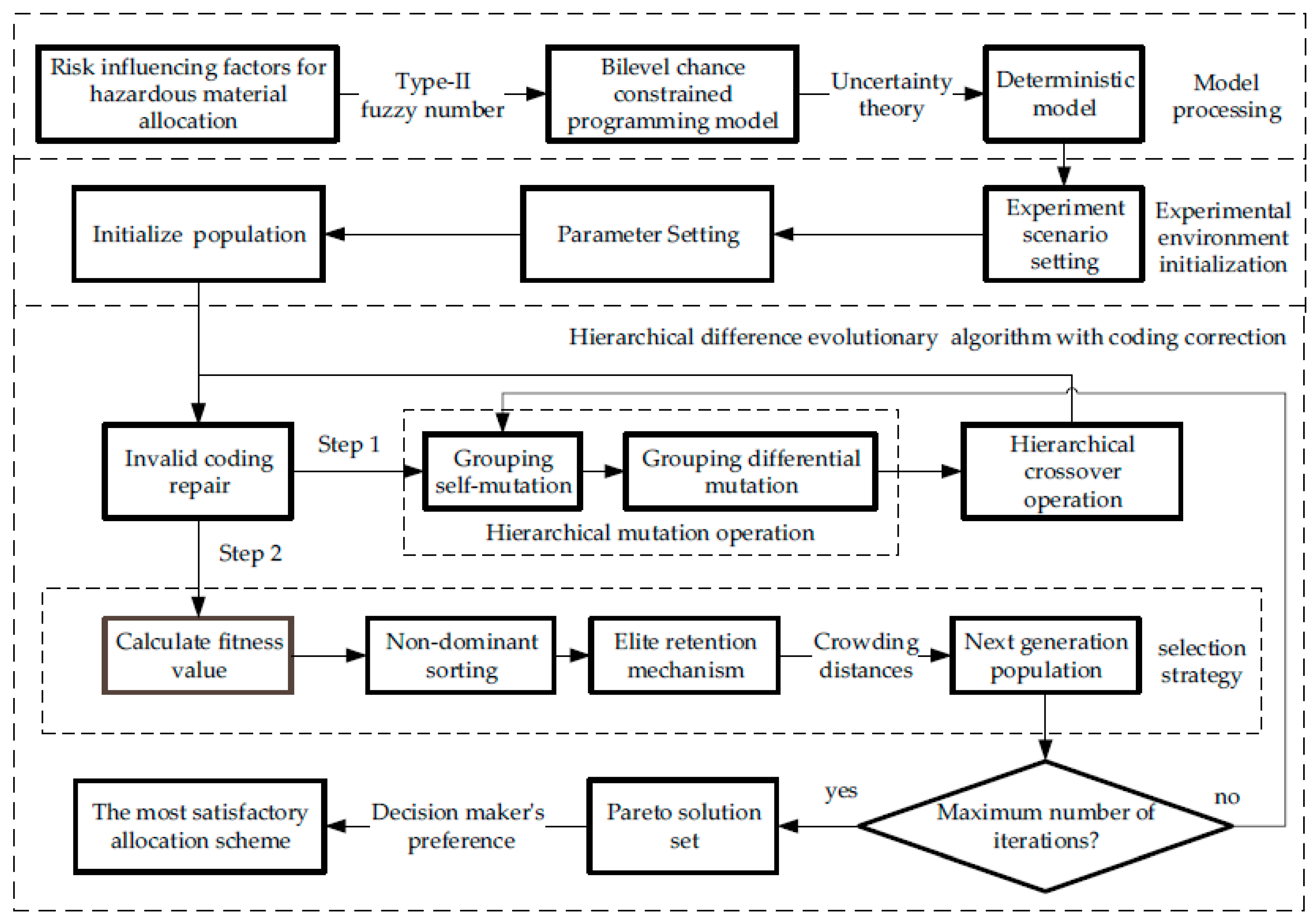
4. Solution Method
4.1. Structure of Individuals and Initialization of Populations
4.2. Coding Repair Strategy
4.3. Hierarchical Mutation Operation
4.4. Hierarchical Crossover Operation
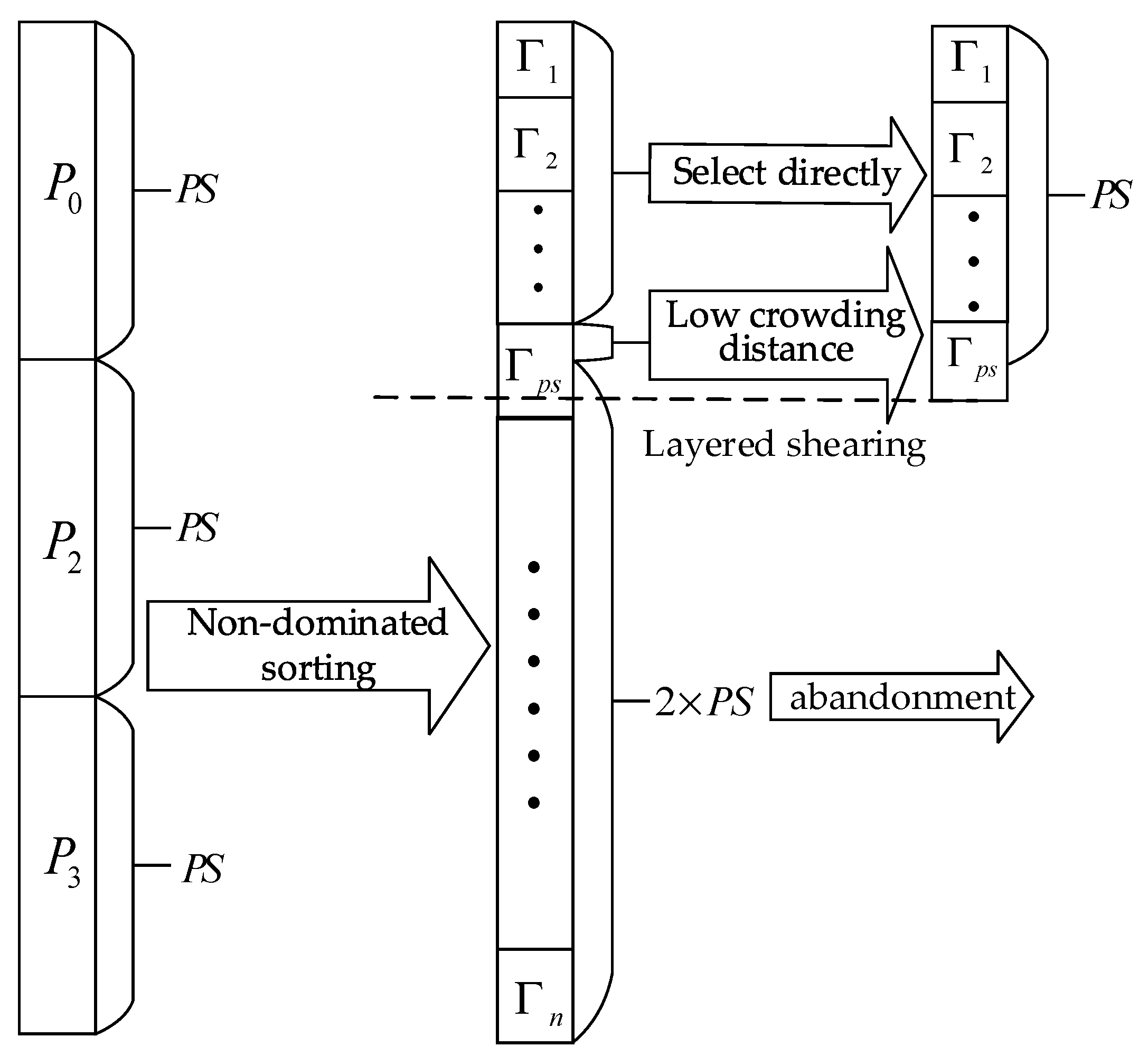
4.5. Population Selection Strategy
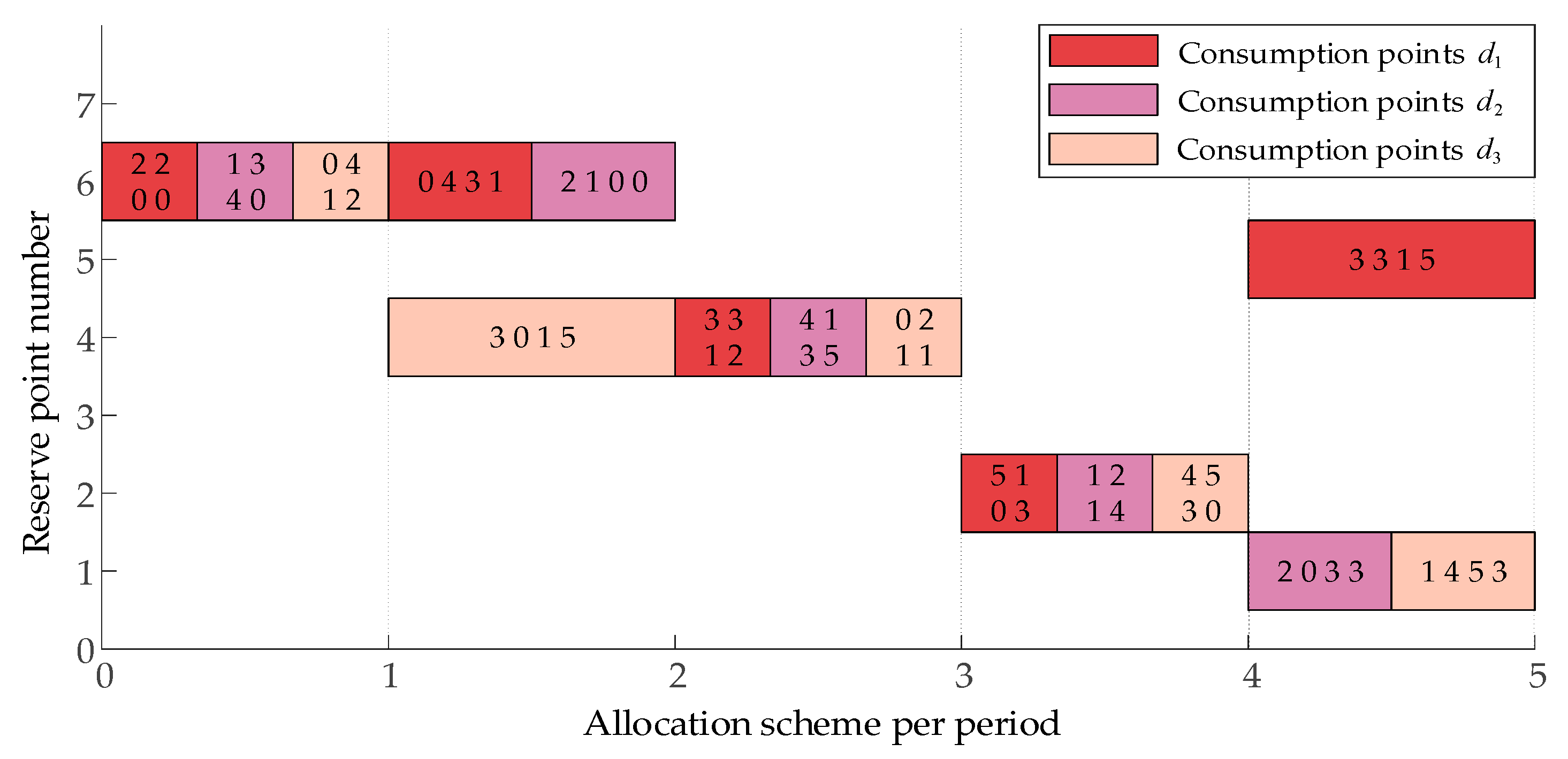
5. Examples and Results
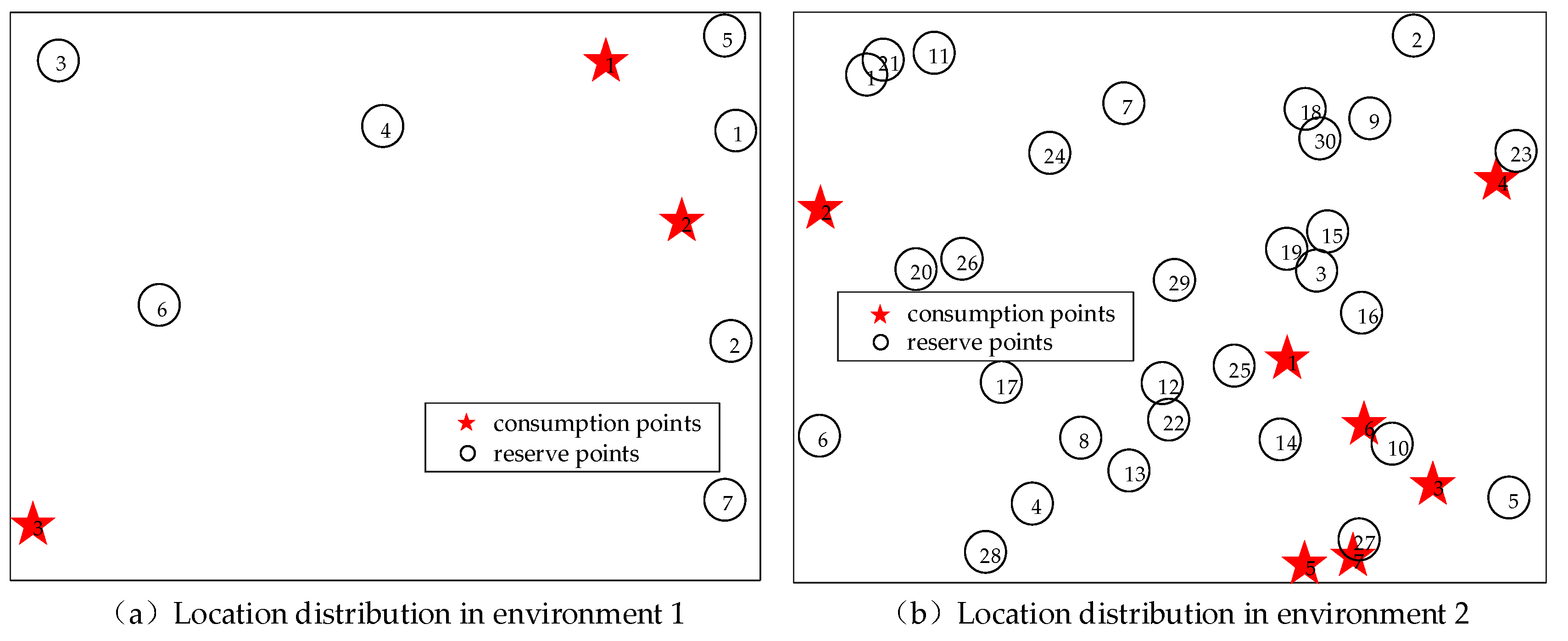
5.1. Experimental Scene Setup
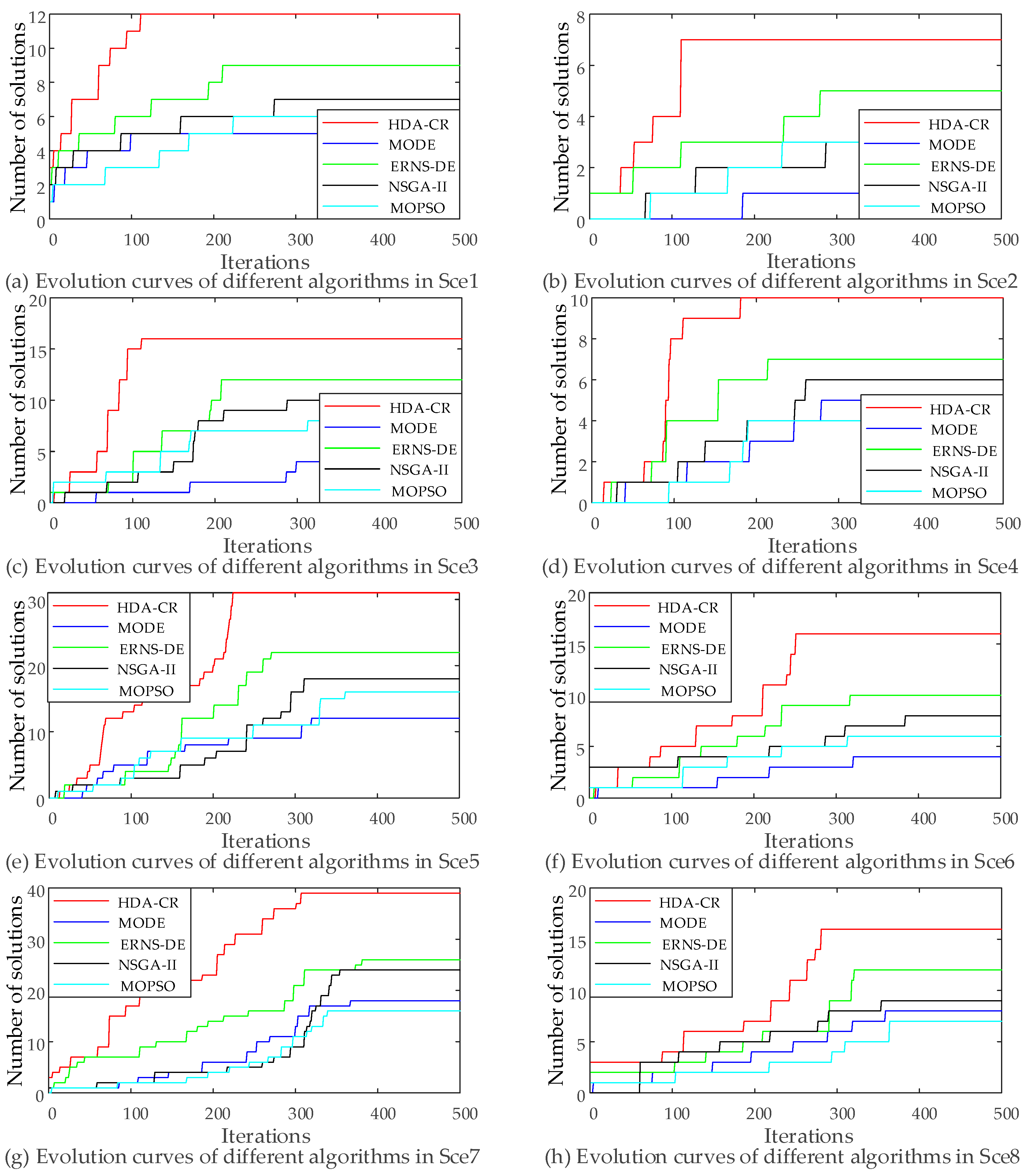
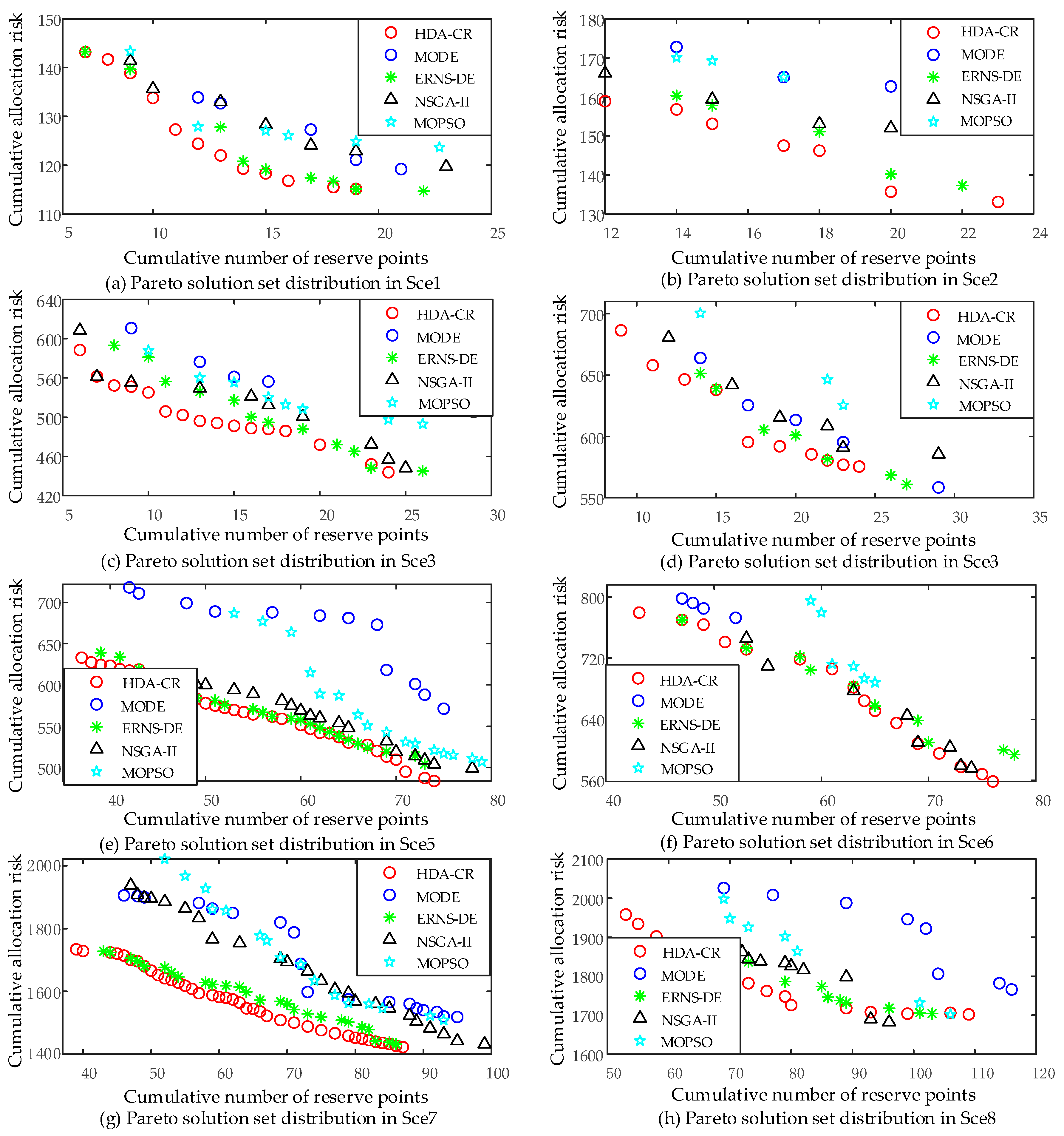
5.2. Algorithm Comparison Analysis
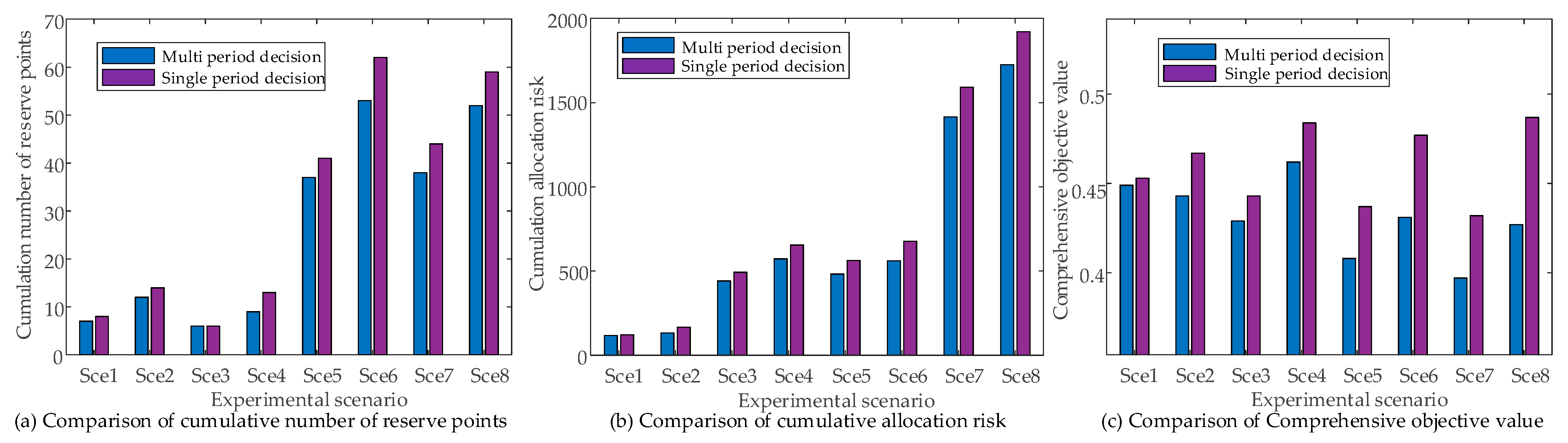
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gawlik-Kobylińska, M. Current Issues in Combating Chemical, Biological, Radiological, and Nuclear Threats to Empower Sustainability: A Systematic Review. Appl. Sci. 2022, 12, 8315. [Google Scholar] [CrossRef]
- Izdebski, M.; Jacyna-Goda, I.; Goda, P. Minimisation of the probability of serious road accidents in the transport of hazardous materials. Reliab. Eng. Syst. Saf. 2022, 217, 108093. [Google Scholar] [CrossRef]
- Zografos, K.G.; Androutsopoulos, K.N. A heuristic algorithm for solving hazardous materials distribution problems. Eur. J. Oper. Res. 2004, 152, 507–519. [Google Scholar] [CrossRef]
- Li, S.; Zu, Y.; Fang, H.; Liu, L.; Fan, T. Design Optimization of a HAZMAT Multimodal Hub-and-Spoke Network with Detour. Int. J. Environ. Res. Public Health 2021, 18, 12470. [Google Scholar] [CrossRef]
- Saat, M.R.; Barkan, C.P.L. Generalized railway tank car safety design optimization for hazardous materials transport: Addressing the trade-off between transportation efficiency and safety. J. Hazard. Mater. 2011, 189, 62–68. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wu, Q.; Li, S.; Li, Y.; Fan, T. Risk Assessment of Hazmat Road Transportation Considering Environmental Risk under Time-Varying Conditions. Int. J. Environ. Res. Public Health 2021, 18, 9780. [Google Scholar] [CrossRef]
- Korytárová, J.; Hromádka, V. Risk Assessment of Large-Scale Infrastructure Projects—Assumptions and Context. Appl. Sci. 2021, 11, 109. [Google Scholar] [CrossRef]
- Park, B.-C.; Lim, C.; Oh, S.-J.; Lee, J.-E.; Jung, M.-J.; Shin, S.-C. Development of Fire Consequence Prediction Model in Fuel Gas Supply System Room with Changes in Operating Conditions during Liquefied Natural Gas Bunkering. Appl. Sci. 2022, 12, 7996. [Google Scholar] [CrossRef]
- Krejci, L. Risk analysis of hazardous materials transportation. Int. Verk. 2019, 71, 43–45. [Google Scholar]
- Verter, V.; Kara, B.Y. A GIS-based framework for hazardous materials transport risk assessment. Risk Anal. 2001, 21, 1109–1120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Topuz, E.; Talinli, I.; Aydin, E. Integration of environmental and human health risk assessment for industries using hazardous materials: A quantitative multi criteria approach for environmental decision makers. Environ. Int. 2011, 37, 393–403. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Huang, Z.; Zhang, J.; Zhang, R.; Ma, S. Multifactor Uncertainty Analysis of Construction Risk for Deep Foundation Pits. Appl. Sci. 2022, 12, 8122. [Google Scholar] [CrossRef]
- Holeczek, N. Hazardous materials truck transportation problems: A classification and state of the art literature review. Transp. Res. Part D Transp. Environ. 2019, 69, 305–328. [Google Scholar] [CrossRef]
- Kazantzi, V.; Kazantzis, N.; Gerogiannis, V.C. Risk informed optimization of a hazardous material multi-periodic transportation model. J. Loss Prev. Process Ind. 2011, 24, 767–773. [Google Scholar] [CrossRef]
- Du, J.; Li, X.; Yu, L.; Dan, R.; Zhou, J. Multi-depot vehicle routing problem for hazardous materials transportation: A fuzzy bilevel programming. Inf. Sci. 2017, 399, 201–218. [Google Scholar] [CrossRef]
- Zero, L.; Bersani, C.; Sacile, R.; Laarabi, M.H. Bi-objective shortest path problem with one fuzzy cost function applied to hazardous materials transportation on a road network. In Proceedings of the 2016 11th System of Systems Engineering Conference (SoSE), Kongsberg, Norway, 12–16 June 2016; pp. 1–5. [Google Scholar]
- Yan, S.; Wang, S.S.; Chang, Y.H. Cash transportation vehicle routing and scheduling under stochastic travel times. Eng. Optim. 2014, 46, 289–307. [Google Scholar] [CrossRef]
- Pamučar, D.; Ljubojević, S.; Kostadinović, D.; Đorović, B. Cost and risk aggregation in multi-objective route planning for hazardous materials transportation-A neuro-fuzzy and artificial bee colony approach. Expert Syst. Appl. 2016, 65, 1–15. [Google Scholar] [CrossRef]
- Berglund, P.G.; Kwon, C. Robust facility location problem for hazardous waste transportation. Netw. Spat. Econ. 2014, 14, 91–116. [Google Scholar] [CrossRef]
- Zhou, Y.; He, J.; Nie, Q. A comparative runtime analysis of heuristic algorithms for satisfiability problems. Artif. Intell. 2009, 173, 240–257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berliński, M.; Warchulski, E.; Kozdrowski, S. Applications of Metaheuristics Inspired by Nature in a Specific Optimisation Problem of a Postal Distribution Sector. Appl. Sci. 2022, 12, 9384. [Google Scholar] [CrossRef]
- Rathore, N.; Jain, P.K.; Parida, M. A Sustainable Model for Emergency Medical Services in Developing Countries: A Novel Approach Using Partial Outsourcing and Machine Learning. Risk Manag. Healthc. Policy 2022, 15, 193–218. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Hao, W.; Pan, F.; Xiang, W. Road screening and distribution route multi-objective robust optimization for hazardous materials based on neural network and genetic algorithm. PLoS ONE 2018, 13, e0198931. [Google Scholar] [CrossRef]
- Bula, G.A.; Prodhon, C.; Gonzalez, F.A.; Afsar, H.M.; Velasco, N. Variable neighborhood search to solve the vehicle routing problem for hazardous materials transportation. J. Hazard. Mater. 2017, 324 Pt B, 472–480. [Google Scholar] [CrossRef]
- Zero, L.; Bersani, C.; Paolucci, M.; Sacile, R. Two new approaches for the bi-objective shortest path with a fuzzy objective applied to HAZMAT transportation. J. Hazard. Mater. 2019, 375, 96–106. [Google Scholar] [CrossRef]
- Kaup, M.; Łozowicka, D.; Baszak, K.; Ślączka, W.; Kalbarczyk-Jedynak, A. Risk Analysis of Seaport Construction Project Execution. Appl. Sci. 2022, 12, 8381. [Google Scholar] [CrossRef]
- Erkut, E.; Verter, V. Modeling of Transport Risk for Hazardous Materials. Oper. Res. 1998, 46, 625–642. [Google Scholar] [CrossRef] [Green Version]
- Ohn, S.W.; Namgung, H. Interval Type-II Fuzzy Inference System Based on Closest Point of Approach for Collision Avoidance between Ships. Appl. Sci. 2020, 10, 3919. [Google Scholar] [CrossRef]
- Pramanik, S.; Jana, D.K.; Mondal, S.K.; Maiti, M. A fixed-charge transportation problem in two-stage supply chain network in Gaussian type-II fuzzy environments. Inf. Sci. 2015, 325, 190–214. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Liu, Y.K. Type-II fuzzy variables and their arithmetic. Soft Comput. 2010, 14, 729–747. [Google Scholar] [CrossRef]
- Kundu, P.; Majumder, S.; Kar, S.; Maiti, M. A method to solve linear programming problem with interval type-II fuzzy parameters. Fuzzy Optim. Decis. Mak. 2019, 18, 103–130. [Google Scholar] [CrossRef]
- Eltaeib, T.; Mahmood, A. Differential Evolution: A Survey and Analysis. Appl. Sci. 2018, 8, 1945. [Google Scholar] [CrossRef]
- Sedak, M.; Rosić, B. Multi-Objective Optimization of Planetary Gearbox with Adaptive Hybrid Particle Swarm Differential Evolution Algorithm. Appl. Sci. 2021, 11, 1107. [Google Scholar] [CrossRef]
- Hou, Y.; Wu, Y.L.; Liu, Z.; Han, H.; Wang, P. Dynamic multi-objective differential evolution algorithm based on the information of evolution progress. Sci. China-Technol. Sci. 2021, 64, 1676–1689. [Google Scholar] [CrossRef]
- Basu, M. Economic environmental dispatch of hydrothermal power system. Int. J. Electr. Power Energy Syst. 2010, 32, 711–720. [Google Scholar] [CrossRef]
- Su, Z.; Zhang, G.; Liu, Y.; Yue, F.; Jiang, J. Multiple emergency resource allocation for concurrent incidents in natural disasters. Int. J. Disaster Risk Reduct. 2016, 17, 199–212. [Google Scholar] [CrossRef]
- Trivedi, V.; Ramteke, M. Using following heroes operation in multi-objective differential evolution for fast convergence. Appl. Soft Comput. 2021, 104, 107225. [Google Scholar] [CrossRef]
- Zhang, C.; Imran, M.; Liu, M.; Li, Z.; Gao, H.; Duan, H.; Zhou, S.; Liu, X. Two Point Mutations on CYP51 Combined With Induced Expression of the Target Gene Appeared to Mediate Pyrisoxazole Resistance in Botrytis cinerea. Front. Microbiol. 2020, 11, 1396. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, H.; Zhang, X.; Jin, Y. Effectiveness and efficiency of non-dominated sorting for evolutionary multi- and many-objective optimization. Complex Intell. Syst. 2017, 3, 247–263. [Google Scholar] [CrossRef]
- Su, Z.P.; Zhang, G.F.; Jiang, J.G.; Yue, F.; Zhang, T. Multi-objective approach to emergency resource allocation using none-dominated sorting based differential evolution. Acta Autom. Sin. 2017, 43, 195–214. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Beiranvand, V.; Mobasher-Kashani, M.; Abu Bakar, A. Multi-objective PSO algorithm for mining numerical association rules without a priori discretization. Expert Syst. Appl. 2014, 41, 4259–4273. [Google Scholar] [CrossRef]
- Wang, L.P.; Ren, Y.; Qiu, Q.C.; Qiu, F.Y. Survey on Performance Indicators for Multi-Objective Evolutionary Algorithms. Chin. J. Comput. 2021, 44, 1590–1619. [Google Scholar]
- Nuh, J.; Koh, T.; Baharom, S.; Osman, M.; Kew, S. Performance Evaluation Metrics for Multi-Objective Evolutionary Algorithms in Search-Based Software Engineering: Systematic Literature Review. Appl. Sci. 2021, 11, 3117. [Google Scholar] [CrossRef]


| Parameters | Parameter Significance |
|---|---|
| The th reserve point | |
| The th consumption point | |
| Initial reserve quantity of hazardous materials of type at | |
| Remaining reserve quantity of hazardous materials of type at after period | |
| Demand for hazardous materials of type at in period | |
| Generalized distance between and | |
| Decision variables, quantity of hazardous materials of type allocated from to in period | |
| Population density on the section from to | |
| Vehicle traffic accidents on the section from to | |
| Accident impact range of hazardous materials of type | |
| Risk threshold | |
| Cumulative allocation risk | |
| Cumulative quantity of reserve points performing the allocation task | |
| degree of confidence |
| Population Size | Self-Mutation Probability | Scaling Factor | Hierarchical Coefficient | Crossover Probability | Maximum Number of Iterations |
|---|---|---|---|---|---|
| 30 | (0.1 0.5 0.8) | 1 | (0.3 0.6) | 0.5 | 500 |
| Experimental Scenarios | Environment Settings | Supply and Demand Cases | Period Numbers |
|---|---|---|---|
| Sce 1 | Environment 1 | Case 1 | 5 |
| Sce 2 | Environment 1 | Case 2 | 5 |
| Sce 3 | Environment 2 | Case 1 | 5 |
| Sce 4 | Environment 2 | Case 2 | 5 |
| Sce 5 | Environment 1 | Case 1 | 24 |
| Sce 6 | Environment 1 | Case 2 | 24 |
| Sce 7 | Environment 2 | Case 1 | 24 |
| Sce 8 | Environment 2 | Case 2 | 24 |
| Experimental Scenarios | HDA-CR | MODE | ERNS-DE | NSGA-II | MOPSO | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | SC | HV | T | CS | HV | T | CS | HV | T | CS | HV | T | CS | HV | |
| Sce 1 | 6.918 | 0.111 | 0.625 | 6.508 | 0.6 | 0.122 | 6.376 | 0.583 | 0.462 | 7.216 | 0.6 | 0.371 | 7.700 | 0.6 | 0.128 |
| Sce 2 | 5.756 | 0 | 0.688 | 4.929 | 0.444 | 0.387 | 4.308 | 0.714 | 0.584 | 3.355 | 0.667 | 0.428 | 5.710 | 0.556 | 0.411 |
| Sce 3 | 10.429 | 0.083 | 0.642 | 11.281 | 0.429 | 0.483 | 9.711 | 0.562 | 0.573 | 12.327 | 0.714 | 0.477 | 13.192 | 0.571 | 0.209 |
| Sce 4 | 9.301 | 0 | 0.655 | 5.721 | 0.5 | 0.241 | 8.220 | 0.5 | 0.523 | 6.951 | 0.5 | 0.507 | 10.518 | 0.667 | 0.350 |
| Sce 5 | 18.964 | 0.091 | 0.462 | 19.291 | 0.4 | 0.084 | 18.192 | 0.612 | 0.407 | 21.300 | 0.1 | 0.410 | 22.221 | 0.6 | 0.217 |
| Sce 6 | 17.397 | 0.1 | 0.687 | 11.278 | 0.546 | 0.197 | 16.406 | 0.5 | 0.635 | 13.690 | 0.636 | 0.523 | 19.2914 | 0.723 | 0.342 |
| Sce 7 | 22.140 | 0 | 0.753 | 21.812 | 0.667 | 0.172 | 21.464 | 0.564 | 0.658 | 22.308 | 0.5 | 0.560 | 22.904 | 0.5 | 0.418 |
| Sce 8 | 21.402 | 0.083 | 0.799 | 17.315 | 0.692 | 0.452 | 20.174 | 0.562 | 0.725 | 19.157 | 0.885 | 0.504 | 18.207 | 0.615 | 0.431 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, X.; Wang, W.; Miao, Q. Modeling and HDA-CR Solution of Multi-Period Allocation Scheme of Hazardous Materials under Uncertainty. Appl. Sci. 2022, 12, 11970. https://doi.org/10.3390/app122311970
Liu X, Zhang X, Wang W, Miao Q. Modeling and HDA-CR Solution of Multi-Period Allocation Scheme of Hazardous Materials under Uncertainty. Applied Sciences. 2022; 12(23):11970. https://doi.org/10.3390/app122311970
Chicago/Turabian StyleLiu, Xianguang, Xiaofeng Zhang, Wenfei Wang, and Qinglin Miao. 2022. "Modeling and HDA-CR Solution of Multi-Period Allocation Scheme of Hazardous Materials under Uncertainty" Applied Sciences 12, no. 23: 11970. https://doi.org/10.3390/app122311970




