Next Article in Journal
Effect of a Conical Cellulose Structure on Horseradish Peroxidase Biomacromolecules
Previous Article in Journal
Improved DeepFM Recommendation Algorithm Incorporating Deep Feature Extraction
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 12
Issue 23
10.3390/app122311993
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Seventy-Five Years since the Point-Contact Transistor: Germanium Revisited

by
Efstratia N. Sgourou
1,
Aspassia Daskalopulu
2,
Lefteri H. Tsoukalas
3,
George Stamoulis
2,
Ruslan V. Vovk
4 and
Alexander Chroneos
2,5,*
1
Solid State Physics Section, University of Athens, Panepistimiopolis Zografos, 15784 Athens, Greece
2
Department of Electrical and Computer Engineering, University of Thessaly, 38333 Volos, Greece
3
School of Nuclear Engineering, Purdue University, West Lafayette, IN 47907, USA
4
Department of Physics, V. N. Karazin Kharkiv National University, 4 Svobody Sq., 61077 Kharkiv, Ukraine
5
Department of Materials, Imperial College London, London SW7 2BP, UK
*
Author to whom correspondence should be addressed.
Appl. Sci. 2022, 12(23), 11993; https://doi.org/10.3390/app122311993
Submission received: 23 October 2022 / Revised: 15 November 2022 / Accepted: 21 November 2022 / Published: 24 November 2022
(This article belongs to the Section Materials Science and Engineering)
Browse Figures
Versions Notes

Abstract

:
The advent of the point-contact transistor is one of the most significant technological achievements in human history with a profound impact on human civilization during the past 75 years. Although the first transistor was made of germanium it was soon replaced by silicon, a material with lower intrinsic carrier mobilities but with a substantially better native oxide. Interestingly, more than two decades ago, germanium was once again considered as a mainstream microelectronic material, since the introduction of high-k dielectrics allowed the consideration of channel materials irrespective of the quality of their native oxide. After about 50 years of limited studies on the defect processes in germanium, the community once again focused on its applicability for mainstream electronic applications. Nevertheless, there are some bottlenecks that need to be overcome, and it was the aim of the present review to discuss the progress in the understanding of the defect processes of Ge.

1. Introduction

December 2022 marks the 75th anniversary since the invention of the transistor, which decisively impacted the evolution of computers and communications and, consequently, on all life as we know it today.
On 16 December 1947, John Bardeen, Walter Brattain and William Shockley produced the first successful semiconductor amplifier, a fruit tendered by two years of collaboration on solid-state physics at Bell Labs. Some of Brattain’s and Shockley’s lab notes, including the ones recording the day of their presentation as well as those present at that historical moment, can be seen in [1]. A week later, on 23 December, they presented their invention to lab officials as a “magnificent Christmas present”, in Shockley’s words. John Pierce assisted the group by proposing the simple name “transistor” for their invention, which up to that point they referred to as “the point-contact solid state amplifier”, a device that could amplify and switch electrical signals and took the form of a tiny bit of germanium, plastic and gold. Bell Labs presented the transistor to the world a year later, on 30 June 1948, at a press conference held in New York. It was speculated at the time that “it may have far-reaching significance in electronics and electrical communication”, but perhaps its actual importance had not been fully envisaged at the time, since it is nowadays regarded as the most important invention of the 20th century. The magnificent three were awarded the 1956 Nobel Prize in Physics for this invention, and Bardeen went on to win the prize again in 1972 along with Leon Cooper and John Robert Schrieffer for their BCS microscopic theory of superconductivity.
Bardeen and Brattain published their findings regarding the invention of the transistor in 1948 [2]. The underlying concept of their work was electron mobility in a semiconductor. Previously, electric current flow had been controlled by fragile glass vacuum tubes, and what was sought was an alternative new device that would be smaller and consume less energy. Tubes had brought on electronic circuits during the first half of the twentieth century and had been employed in the implementation of radio, television, radar, the sound recording and reproduction of long-distance telephone networks, and analog and early digital computers. Transistors exploit the low resistivity of materials, such as silicon and germanium, conduct electric current in the solid state, and the flow can be controlled in useful ways by various means, for example by exposure to an electric field or through doping, i.e., the intentional introduction of impurities into pure semiconductor material in order to modulate its structural and electrical properties. Hence, the coming of the transistor literally revolutionised the electronics industry and effectively introduced the Information Age, where the economy relies primarily on information technology [3]. The first principles of field-effect transistors (FET), i.e., transistors that employ an electric field to control the flow of current in a semiconductor, are traced back to Julius Edgar Lilienfeld’s work in 1925 [4]. Bardeen, Brattain and Shockley’s structure faced the problem of surface state, where traps on the semiconductor surface hinder electron mobility. An accidental discovery by Frosch and Derick in 1955 that silicon dioxide prevents dopants from diffusing into silicon led, later, in 1956, Atalla and Kahng to invent the MOSFET, which shares the same principles as the original transistor and solves the surface state problem.
The MOSFET transistor has been used extensively in integrated circuits [5] and plays a critical role in today’s technological, industrial and market landscape, where the economy is increasingly digitised and “smart”. Enabling technology such as clean rooms, photolithography and planar process rendered integrated circuit manufacture fast and low cost, and since the early 1970s we have witnessed a proliferation of microprocessors. The MOSFET has been scaled down in size continuously through the years, and while once channel lengths were several micrometres, modern integrated circuits include transistors with channel lengths in the order of 10 nanometres. Moore’s law [6] about chip density, i.e., that the number of semiconductor components that can be included on a chip increases exponentially, though undisputed for a number of years in the semiconductor industry, has recently come under revision [7], and fabrication capabilities and techniques have been taken into consideration. The promise of GAAFET (Gate All Around FET) devices, where a 2 nm spacing can result in nearly 50 bn transistors in a square cm chip, opens new vistas for high-performance, lower-fabrication-costs and increased-reliability semiconductors with great application potential in AI and machine learning (AI/ML) and neuromorphic computing. It should be noted that many in the industry consider neuromorphic computing to have greater engineering significance than quantum computing given the latter’s scores of issues with stability and practical deployment. Pushing against Moore’s Law and taking into account advancements in enabling technologies, an opportune moment is offered for reviewing Germanium in the spirit of recalling its original role at the onset of the semiconductor revolution 75 years ago and its great promise for the future.
In the present review we considered (a) transistors and artificial intelligence and (b) the key Ge defect-engineering processes and their impact on devices and (c) highlighted the open issues and perspectives for the future.

2. Transistors and Artificial Intelligence

Artificial intelligence applications are mushrooming in the industrial, retail, education, health care, military, research, resource management, and consumer services sectors. Much of this growth is enabled by machine learning capabilities, that is, the processing of massive amounts of data in order to create models that can be used quickly (ideally in real time) for the accurate classification of newly encountered problems that can subsequently be solved by applying learned problem-solving approaches. This creates new challenges for semiconductor design and implementation and new opportunities for growth for the semiconductor industry [8]. The global AI market is expected to grow to USD 1811.8 billion by 2030, and demand for semiconductor chips is expected to reflect this rise. According to McKinsey, AI accelerator chips will be in demand five times more than semiconductors used in non-AI applications [9].
All AI applications rely on hardware. First, the amount of data that needs to be stored and processed requires efficient memory systems through which data can be moved fast. Second, the integration of nonvolatile memory and processing logic renders “system on a chip” processors possible in order to meet the requirements of AI algorithms. It is quite expensive to build special purpose AI chips for each potential application, and a generic AI platform that could be adapted to the specific features of an application area would be more cost efficient and provide a common ground for a whole ecosystem of applications.
The semiconductor industry itself can benefit from AI for the reduction in material loss and production time and increased quality control of the production process and the final product. Very recently a new type of adaptive transistor, which can be dynamically switched during run-time to perform different logical tasks, was announced by scientists at the technical University of Vienna who have been working on adaptive electronics. The new flexible transistor is based on pure germanium and does not require doping and therefore no new manufacturing processes [10]. The flexible transistor creates new possibilities for chip design and for both schools of artificial intelligence, namely symbolic-based approaches, which can potentially use multivalued logics and life-based approaches that employ neural networks. The functional diversification of the new transistor is achieved by exploiting the electronic structure of germanium and modulating circuit behaviour via a control electrode, for instance to change the behaviour of an NAND gate into an NOR, as the need arises. This adaptability results in smaller numbers of transistors for the performance of computations, hence leading to energy and time savings.

3. From Ge to Si and Back

Although in the first breakthrough the point-contact transistor and subsequent devices were based on Ge, it was Si that soon dominated the technology. This was mainly due to the requirement of a native oxide on top of the semiconducting material. In particular, germanium dioxide (GeO2) was inappropriate as it is unstable during the processing required (water soluble) for the formation of microelectronic devices. Conversely, silicon dioxide (SiO2), the native oxide of Si, is a material with excellent material properties and dielectric properties that was appropriate for scaling and device (metal-oxide semiconductor field-effect transistor (MOSFET) etc.) formation for decades.
During the reign of Si, the reports on the material’s properties and the defect processes of Ge were very limited (refer to [11,12] and the references therein). The community during this period was focused on Si and the effort to aggressively scale it to follow Moore’s law. This was interrupted by the advent of high-k dielectric materials that in essence removed the requirement of a native oxide layer (such as SiO2 in Si), and therefore high mobility materials, mainly Ge, that were plagued by inappropriate native oxides were once more considered [13,14,15,16,17,18,19,20,21,22]. The aim of the community is currently to be able to create Ge-based microelectronic devices and, in particular, n- and p-channel MOSFETs for higher mobility complementary metal-oxide semiconductors (CMOS). At this point of the evolution of microelectronic devices we have reached devices with characteristic dimensions of only a few nanometers and, therefore, effects at the atomic level are more important than ever. In particular, it is absolutely necessary to control the intrinsic defects in the lattice, the placement and the transport properties of dopants. For example, even the migration and out-diffusion of a few atoms in the doped region will have significant implications in its conductivity! For numerous years the defect processes in Si have been determined; however, there have been studies in the defect processes and the applicability of Ge in microelectronic devices mainly after 2000 [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75], when the possibility of Ge-based devices was once more considered.

4. Defect Processes in Ge

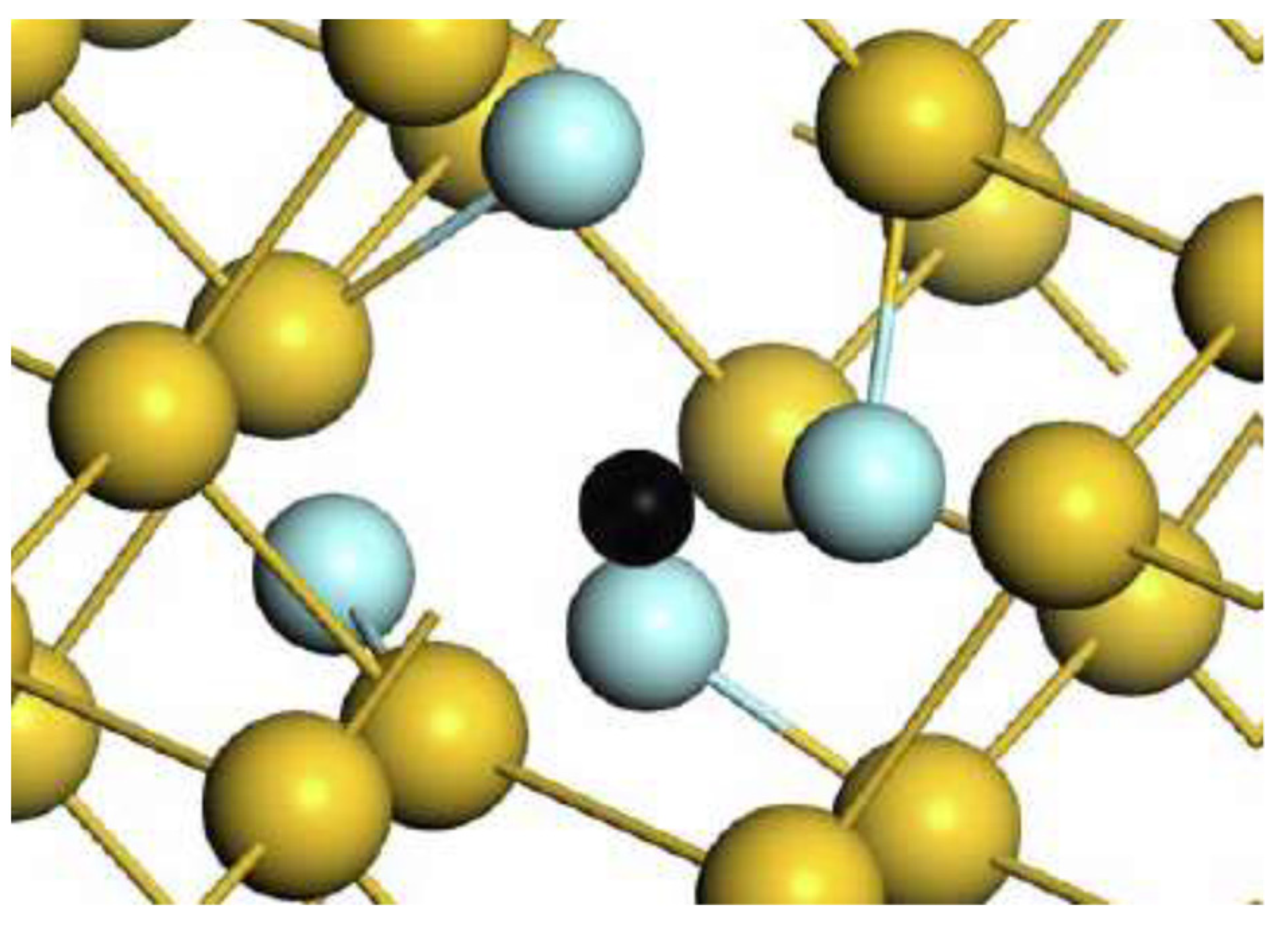
4.1. Intrinsic Point Defects

The first defects that need to be considered are the intrinsic defects, i.e., self-interstitial and vacancies. These defects always exist in semiconductors for thermodynamic reasons, and their concentration in equilibrium conditions is dependent upon their formation energy. Typically, the formation energies of self-interstitial and vacancies in semiconducting materials are high, and therefore their concentrations are not significant even at higher temperatures. Nevertheless, during growth (the Czochralski crystal growth process), dopant incorporation (ion implantation) and processing there is a significantly higher concentration of intrinsic defects that forms in the lattice. This non-equilibrium concentration of intrinsic point defects is typically orders of magnitude higher than the one expected under equilibrium conditions. The concentration and properties of these intrinsic defects is important as they are the vehicles of self- and dopant diffusion, and consequently their control is key in order to be able determine the electrical activation of dopants and the dopant profile in n- or p-type regions [11,12,27,29].
Although Ge and Si are isostructural, they have a number of key differences. As was mentioned above, the main reason for the community to revisit Ge is the higher mobility of electrons and holes (although the electron mobility in some III-V compounds such as GaAs is even higher). Considering intrinsic point defects, the vacancy in Ge is the key defect, and this is not the case in Si [11,27,42,43]. This has a profound impact on the diffusion and deactivation of donor atoms, as will become evident in the coming sub-section.
Studies on point defects and self-diffusion in Ge were performed more than 65 years ago (for example [76,77]), however, it was the seminal study by Werner et al. [11] that determined that the vacancies in Ge are the energetically favourable defect with concentrations that were more significant than in Si under equilibrium conditions. This study was thereafter confirmed by density functional theory (DFT) calculations that predicted that the formation energy of the vacancies is lower than the formation energy of the self-interstitial in Ge [11,27,42,43]. Further evidence to support the prevalence of the vacancy self-diffusion mechanism was derived from experiments concerning copper diffusion in dislocation-free germanium [78,79,80]. Concerning that the self-interstitial in Ge under equilibrium conditions is never of importance and does not practically contribute to self-diffusion (refer to [59] and the references therein), the charge state of the vacancy in Ge under n-type doping conditions was determined to be doubly negatively charged [38,44]. Figure 1 is the Arrhenius plot comparing self-diffusion with dopant diffusion in Ge.

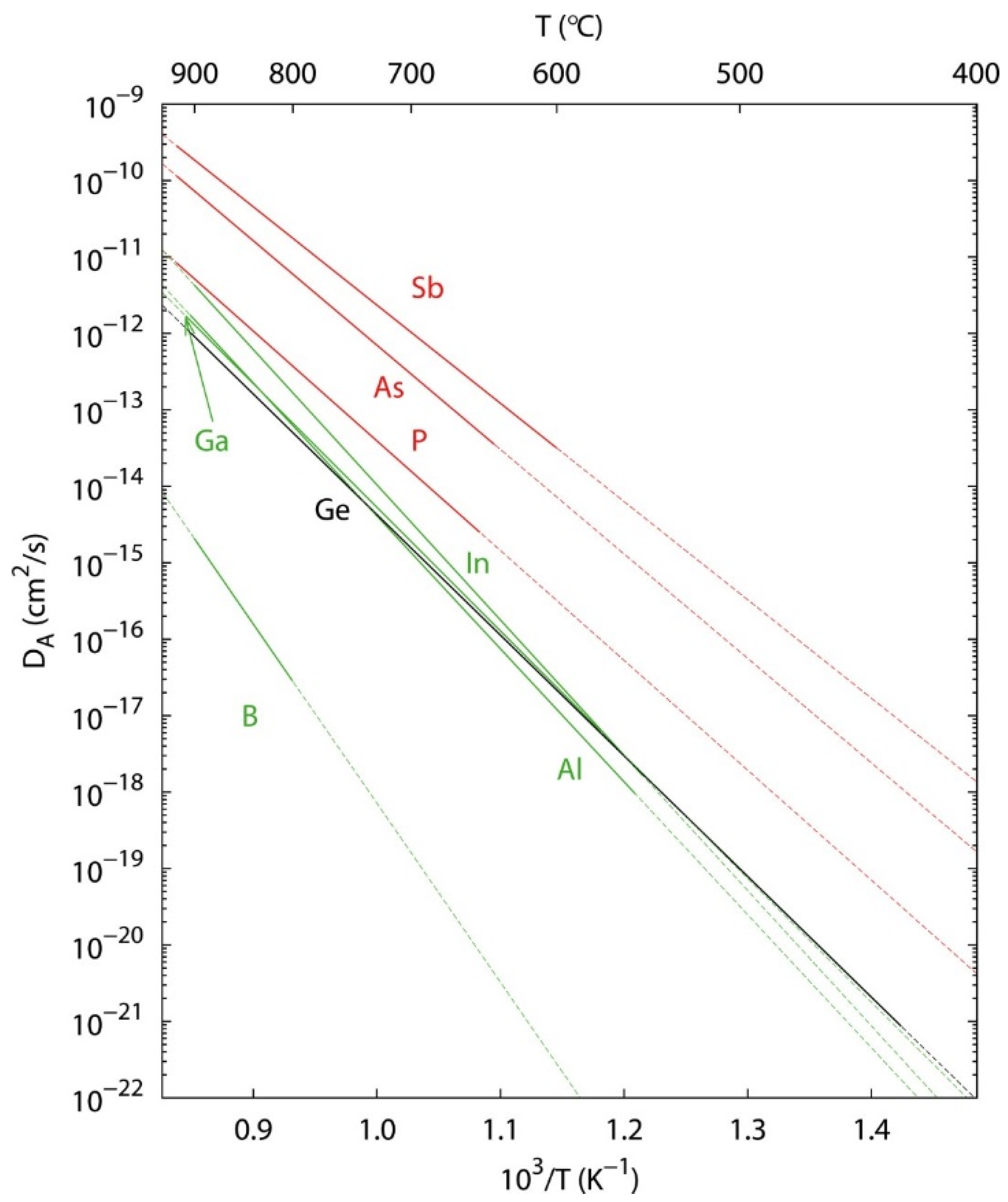
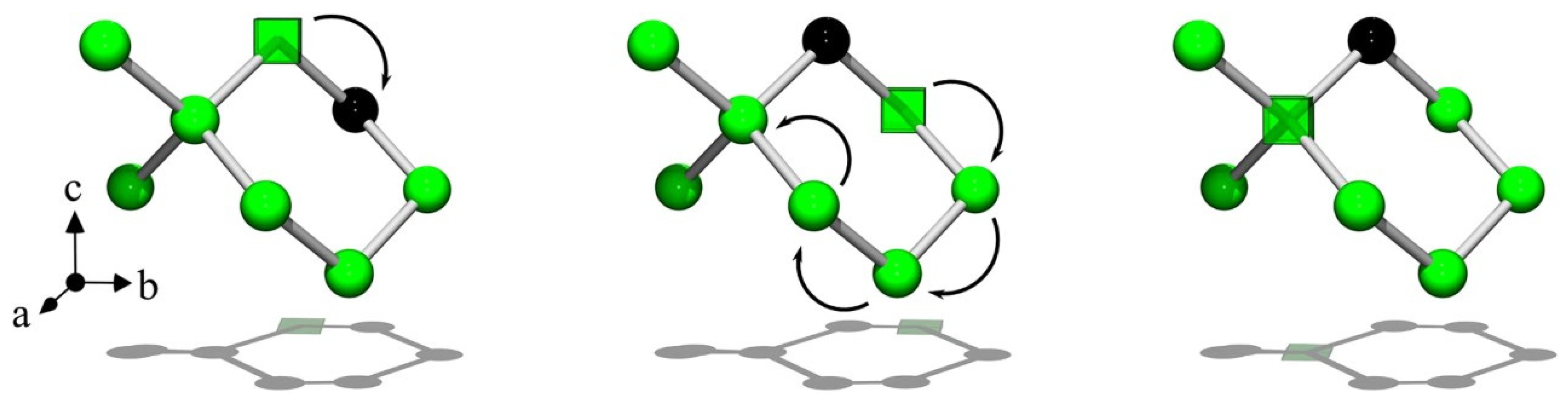
4.2. Donor Atoms

The technologically important donor atoms (D) in Ge are phosporous (P), arsenic (As) and antimony (Sb). As indicated above, the prevalent intrinsic point defect in Ge is the vacancy. These occupy substitutional positions in the Ge lattice and, as they can be easily ionised at room temperature, they readily offer an electron to Ge, thus increasing its conductivity. What is left behind is a positively charged dopant that can attract the negatively charged vacancies that diffuse in the lattice if the latter approach it at a nearest neighbour site. It has been calculated using DFT that there is strong binding between the dopant and the vacancy [43]. For the donor atom to diffuse in the lattice it is not enough to just exchange positions with this vacancy, but it has to migrate via the longer-range ring mechanism of diffusion (refer to Figure 2) [81]. This mechanism is effectively dictated by the symmetry of the diamond lattice and, in essence, the vacancy has to migrate in a ring of atoms around the donor atom for the atom to progress to the next lattice position. This ring has to be repeated for every hop of the donor atom in the lattice [43]. There is good agreement between the determined activation energies of diffusion and the ones derived by DFT using the ring mechanism of diffusion for P, As and Sb [42,43].
During the formation of the n-type regions there is a significant concentration of vacancies that considerably exceeds the concentration of vacancies under equilibrium condition. This interacts with the donor atoms forming DV pairs, which migrate in the lattice and can lead to larger clusters of the form DnVm with n typically up to 4 (refer to Figure 3) [32,35]. These larger clusters are practically immobile; however, they can lead to the deactivation of a significant portion of the donor atoms [35,56].
Codoping strategies were proposed to eliminate or reduce the influence of vacancy defects that control both the diffusion of n-type dopants and their deactivation [44,45,82,83]. Oversized dopant atoms (such as Sn, Hf and Pb) and carbon reduce the mobility of the donor atoms; however, they do not solve the problem of the formation of defect–dopant clusters that lead to deactivation [54,82]. The most effective defect-engineering strategy was proposed using DFT [83] and was thereafter determined to work using experiments [56,84,85,86,87,88]. Interestingly, this prompted Jung et al. [84] to conclude that F passivation can be used to improve the performance of Ge-based MOSFETs and p-i-n diodes.
For Si, it is established that F can be used to suppress self-interstitial and boron (B) diffusion [88,89,90,91,92]. How does fluorine solve the problem of diffusion and deactivation for donor atoms in Ge? The introduction of F atoms in the Ge lattice will result in the saturation of vacancy dangling bonds. This occurs when the migrating F atom encounters a V in the lattice, and the predicted binding energy of the resultant FV pair is −1.19 eV [83]. Each vacancy has four dangling bonds, so it can attract up to four F atoms, thus forming F4V clusters (binding energy −5.00 eV, schematic representation in Figure 4), whereas every divacancy has six dangling bonds and can form up to the F6V2 cluster (binding energy −8.56 eV) [83]. The binding energies for the formation of fluorine–vacancy pairs is significantly higher than the binding energies for the formation of donor–vacancy pairs (−0.52 eV for PV to −0.70 eV for SbV) [83]. This in turn implies that, if there is a sufficiently high F concentration, the F can attract most of the vacancies in the lattice, thus reducing the possibility of the formation of DnV (n = 1–4) defects [83]. Consequently, the donor atoms do not have vacancies to diffuse into in the lattice, nor do they have the opportunity to form larger deactivating clusters [83]. Therefore, F codoping solves both problems and is a defect-engineering way to form n-type doped regions in advances Ge based devices.

4.3. Acceptor Atoms

The main difference in acceptor atoms (B, indium (In), gallium (Ga) and aluminum (Al)) to the donor atoms considered above is that they do not migrate at a fast rate in the lattice [70,93,94,95,96,97,98,99]. This is because B repels vacancies, whereas In, Ga and Al are only weakly bound to vacancies [43]. For B, it was determined by the proton irradiation experiments conducted by Bracht et al. [94] that an interstitial mechanism is prevalent. Under equilibrium conditions, self-interstitials have a negligible concentration, but proton irradiation forms a supersaturation of self-interstitials that enhances B diffusion and suppresses vacancy-mediated diffusion [94]. These experimental results, in conjunction with the DFT study by Janke et al. [100], provide evidence for an interstitially mediated diffusion mechanism for B. On the other hand, In, Ga and Al can diffuse via the vacancy mechanism but with considerably higher activation enthalpies of diffusion as compared to the P, As, and Sb atoms considered above [43,59,101,102]. This is also evident in Figure 3, where the p-type dopants have considerably lower diffusivities as compared to the n-type dopants.
From a technological perspective, the limited diffusion of B and the acceptable activation level can lead to the formation of efficient p-type regions for devices, taking advantage of the higher hole mobility of Ge as compared to Si.

4.4. Carbon and Oxygen Impurities

During crystal growth and the processing of Ge wafers there is an introduction of defects in the Ge lattice. In particular, during the Czochralski crystal growth process there is a significant concentration of carbon and oxygen input in the Ge lattice that exceeds the equilibrium concentration of carbon and oxygen defects [33]. This is again analogous to the case for Czochralski-grown Si, with the important difference being that there is a higher content of carbon and oxygen defects that has implications on the defect processes [103,104,105,106,107]. Although there is an impact of these defects on the properties of donor and acceptor atoms in Si, there is only limited information in terms of Ge. Brotzmann et al. [44] determined that the diffusion of donor atoms is retarded in the presence of carbon atoms in Ge; however, there is no benefit for the deactivation of the donor atoms via the formation of DnVm clusters. The related subsequent DFT results supported these findings by predicting that although carbon atoms result in higher migration energies for DV pairs via the ring mechanism of diffusion (and thus retard the diffusion of donor atoms), they do not impact the formation of extended clusters containing donor atoms and vacancies [45]. At any rate, the study of Liu et al. [86] determined that there is efficient junction control using C co-implanted into P in pre-amorphised Ge.
Considering the impact of oxygen interstitial atoms on the diffusion of p-type dopants such as B, it was recently determined by Kipke et al. [70] that a high oxygen concentration is linked with increased B diffusion. In particular, the diffusion of B was significantly enhanced in parts of the sample where the oxygen concentration exceeded 1019 cm−3 (i.e., it was orders of magnitude higher than the equilibrium dopant concentration) [70]. Nevertheless, such high oxygen concentrations could be possible from the quartz ampule used in the experiment and from oxidation near the surface [70]. This study prompted the DFT study by Kuganathan et al. [72], as it was anticipated that oxygen interstitials would interact with other acceptor dopants such as Ga. This study revealed that the binding energies required to form Ga substitutional–oxygen interstitial (Oi) defects are limited [72].

5. Open Issues and Perspectives for the Future

Here, we will aim to raise a number of open issues and perspectives that will need to be considered so as to consider the defect processes in Ge as a fairly complete field.
Considering oxygen and carbon defects, what is missing from the literature at the present time is an understanding of how these defects could attract vacancies in a competitive manner to form CV pairs and VOi (A-centre), in this was reducing the available vacancies for dopant atoms. This is particularly important for donor atoms because vacancies are their vehicles for diffusion and may cause deactivation via the formation of larger clusters. The A-centre in Ge and its impact is far less understood in Ge as compared to Si although they have a similar configuration [52,108,109,110,111,112,113].
Strain induces changes to the electronic properties of microelectronic materials [40,114,115,116,117,118]. For example, a significant disadvantage for the implementation of Ge in optoelectronic applications is its indirect bandgap (0.67 eV), which can be engineered to a direct bandgap of 2.91 eV upon the application of significant compressive strain [118]. As was recently demonstrated, strained few-atomic-layer (effectively two-dimensional) Ge can exhibit blue photoluminescence at room temperature as well as quantum confinement effects [118]. With respect to nanoelectronic devices, strain can be used to enhance carrier mobilities, as was demonstrated by the paradigm of strained Si, SiGe and Ge channels for MOSFETs (refer to [119] and the references therein).
Another issue that needs to be determined is the impact of surface and interfaces on the conductivity and diffusion properties of nanoelectronic devices. It should be stressed that in nanoelectronic systems where the characteristic dimensions are a few nanometers, there is a significant percentage of the atoms at the interfaces and surface or at regions in close vicinity to these. As has been determined in previous studies (for example [120,121,122,123] and the references therein), mainly for oxide interfaces, there will be profound deviations from the bulk-like defects and electronic properties. Therefore, these need to be investigated for Ge interfaces using both advanced simulation techniques and thermodynamic methodologies such as the cBΩ model [124,125,126,127,128,129,130,131,132,133]. The absolute limit, of course, for advanced simulation work on surfaces/interfaces is germanene, the two-dimensional form of Ge that is analogous to graphene [134,135,136,137] where all the atoms are at the surface or interface, and the use of machine learning or related techniques [138,139,140,141,142]. Finally, it should be considered that Ge is an important material for quantum technologies, as it may be employed in devices aiming to encode, process and transmit quantum information [143].

6. Conclusions

Seventy-five years after the invention of the Ge point-contact transistor, there are still barriers for the acceptance of Ge as a mainstream material for electronic applications. There was a gap for nearly 50 years on the systematic study of Ge defect processes, which have once again been studied by the community over the past 20 or so years. The advent of high-k dielectrics alleviated the problematic oxide issue for Ge. However by that time, Si-based microelectronics were dominant, with their defect processes and properties being understood at a level at which we comprehend very few materials, if any. On the contrary, the early studies concerned cruder experimental work that is not relevant anymore, whereas the gap in understanding of the properties and control of dopants and defects requires further work. This is particularly important in the era of nanoelectronics, where surface/interfacial effects become very important in retaining acceptable active donor/acceptor profiles and the emergence of quantum effects (i.e., tunneling) that can impact the properties of devices.
The dominant intrinsic defect in Ge is the lattice vacancy that has a significant impact on the electronic and diffusion properties of dopants. Concerning acceptors, the situation is clearer, and p-type regions can be formed with B-doped Ge. Donor atoms in Ge require further care due to their higher diffusion and deactivation cluster formation. Codoping strategies with F seem to be appropriate. Other defects need to be investigated in detail, such as carbon, oxygen and metals. At any rate, the extreme miniaturization of devices offers opportunities for exciting research on these systems from both a technological and fundamental science perspective.

Author Contributions

The manuscript was written and edited by all authors. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Brattain, W. Bell Labs Logbook, December 1947. Available online: https://www.pbs.org/transistor/science/labpages/labpg1.html (accessed on 20 October 2022).
  2. Bardeen, J.; Brattain, W. The transistor, a semiconductor triode. Phys. Rev. 1948, 74, 230–231. [Google Scholar] [CrossRef]
  3. Riordan, M.; Hoddeson, L. Crystal Fire: The Birth of the Information Age; W. W. Norton: New York, NY, USA, 1997. [Google Scholar]
  4. Lilienfeld, J.E. Method and Apparatus for Controlling Electric Currents. U.S. Patent 1745175A, 8 October 1926. [Google Scholar]
  5. Bassett, R. To the Digital Age: Research Labs, Start-up Companies, and the Rise of MOS Technology; JHU Press: Baltimore, MD, USA, 2002; pp. 12–28. [Google Scholar]
  6. Moore, G.E. Cramming more components onto integrated circuits. Electronics 1965, 38, 114–118. [Google Scholar] [CrossRef]
  7. Burg, D.; Ausubel, J.H. Moore’s Law revisited through intel chip density. PLoS ONE 2021, 16, e0256245. [Google Scholar] [CrossRef]
  8. International Roadmap for Devices and Systems (IRDS), 2020 Edition, IEEE. Available online: https://irds.ieee.org/topics/semiconductors-and-artificial-intelligence (accessed on 20 October 2022).
  9. McKinsey and Company, Artificial Intelligence Hardware: New Opportunities for Semiconductor Companies, December 2018. Available online: https://www.mckinsey.com/~/media/McKinsey/Industries/Semiconductors/Our%20Insights/Artificial%20intelligence%20hardware%20New%20opportunities%20for%20semiconductor%20companies/Artificial-intelligence-hardware.ashx (accessed on 20 October 2022).
  10. Sistani, M.; Böckle, R.; Falkensteiner, D.; Luong, M.A.; den Hertog, M.I.; Lugstein, A.; Weber, W.M. Nanometer-scale Ge-based adaptable transistors providing programmable negative differential resistance enabling multivalued logic. ACS Nano 2021, 15, 18135–18141. [Google Scholar] [CrossRef] [PubMed]
  11. Werner, M.; Mehrer, H.; Hochheimer, H.D. Effect of hydrostatic pressure, temperature, and doping on self-diffusion in germanium. Phys. Rev. B 1985, 32, 3930–3937. [Google Scholar] [CrossRef]
  12. Stolwijk, N.A.; Bracht, H. Diffusion in Silicon, Germanium and Their Alloys; Landolt-Börnstein New Series; Subvolume A Springer: New York, NY, USA, 1998; Volume III/33. [Google Scholar]
  13. Cheng, B.H.; Cao, M.; Rao, R.; Inani, A.; Voorde, P.V.; Greene, W.M.; Stork, J.M.C.; Yu, Z.P.; Zeitzoff, P.M.; Woo, J.C.S. The impact of high-k gate dielectrics and metal gate electrodes on sub-100 nm MOSFET’s. IEEE Trans. Electron Dev. 1999, 46, 1537–1544. [Google Scholar] [CrossRef]
  14. Smith, R.C.; Ma, T.; Hoilien, N.; Tsung, L.Y.; Bevan, M.J.; Colombo, L.; Roberts, J.; Campbell, S.A.; Gladfelter, W.L. Chemical vapour deposition of the oxides of titanium, zirconium and hafnium for use as high-k materials in microelectronic devices. A carbon-free precursor for the synthesis of hafnium dioxide. Adv. Mater. Opt. Electron. 2000, 10, 105–114. [Google Scholar] [CrossRef]
  15. Ngai, T.; Qi, W.J.; Sharma, R.; Fretwell, J.; Chen, X.; Lee, J.C.; Benerjee, S. Electrical properties of ZrO2 gate dielectric on SiGe. Appl. Phys. Lett. 2000, 76, 502–504. [Google Scholar] [CrossRef]
  16. Frank, M.M.; Koester, S.J.; Copel, M.; Ott, J.A.; Paruchuri, V.K.; Shang, H.; Loesing, R. Hafnium oxide gate dielectrics on sulfur-passivated germanium. Appl. Phys. Lett. 2006, 89, 112905. [Google Scholar] [CrossRef]
  17. Saraswat, K.C.; Chui, C.O.; Krishnamohan, T.; Nayfeh, A.; McIntyre, P. Ge based high performance nanoscale MOSFETs. Microelectron. Eng. 2005, 80, 15–21. [Google Scholar] [CrossRef]
  18. Kamata, Y. High-k/Ge MOSFTETs for future nanoelectronics. Mater. Today 2008, 11, 30–38. [Google Scholar] [CrossRef]
  19. Chroneos, A.; Dimoulas, A. Defect configuration of high-k cations in germanium. J. Appl. Phys. 2012, 111, 023714. [Google Scholar] [CrossRef]
  20. Broqvist, P.; Binder, J.F.; Pasquarello, A. Formation of substoichiometric GeOx at the Ge-HfO2 interface. Appl. Phys. Lett. 2010, 97, 202908. [Google Scholar] [CrossRef]
  21. Chroneos, A.; Schwingenschlögl, U.; Dimoulas, A. Impurity diffusion, point defect engineering and surface/interface passivation in germanium. Ann. Phys. 2012, 524, 123–132. [Google Scholar] [CrossRef]
  22. Wu, M.L.; Wu, Y.H.; Chao, C.Y.; Lin, C.C.; Wu, C.Y. Crystalline ZrTiO4 gated Ge metal oxide semiconductor devices with amorphous Yb2O3 as a passivation layer. IEEE Trans. Nanotechnol. 2013, 12, 1018–1021. [Google Scholar] [CrossRef]
  23. Giese, A.; Stolwijk, N.A.; Bracht, H. Double-hump diffusion profiles of copper and nickel in germanium wafers yielding vacancy-related diffusion. Appl. Phys. Lett. 2000, 77, 642–644. [Google Scholar] [CrossRef]
  24. Da Silva, A.J.R.; Janotti, A.; Fazzio, A.; Baierle, R.J.; Mota, R. Self-interstitial defect in germanium. Phys. Rev. B 2000, 62, 9903–9906. [Google Scholar] [CrossRef]
  25. Coutinho, J.; Jones, R.; Briddon, P.R.; Öberg, S. Oxygen and dioxygen centers in Si and Ge: Density functional calculations. Phys. Rev. B 2000, 62, 10824. [Google Scholar] [CrossRef]
  26. Tsouroutas, P.; Tsoukalas, D.; Florakis, A.; Zergioti, I.; Serafetinides, A.A.; Cherkashin, N.N.; Marty, B.; Claverie, A. Laser annealing for n+/p junction formation in germanium. Mater. Sci. Semicond. Proc. 2006, 9, 644–649. [Google Scholar] [CrossRef]
  27. Bracht, H.; Brotzmann, S. Atomic transport in germanium and the mechanism of arsenic diffusion. Mater. Sci. Semicond. Proc. 2006, 9, 471–476. [Google Scholar] [CrossRef]
  28. Chroneos, A.; Skarlatos, D.; Tsamis, C.; Christofi, A.; McPhail, D.S.; Hung, R. Implantation an diffusion of phosphorous in germanium. Mater. Sci. Semicond. Proc. 2006, 9, 640–643. [Google Scholar] [CrossRef]
  29. Pinto, H.M.; Coutinho, J.; Torres, V.J.B.; Öberg, S.; Briddon, P.R. Formation energy and migration barrier of a Ge vacancy from ab initio studies. Mater. Sci. Semicond. Proc. 2006, 9, 498–502. [Google Scholar] [CrossRef]
  30. Silvestri, H.H.; Bracht, H.; Hansen, J.L.; Larsen, A.N.; Haller, E.E. Diffusion of silicon in crystalline germanium. Semicond. Sci. Technol. 2006, 21, 758–762. [Google Scholar] [CrossRef] [Green Version]
  31. Haller, E.E. Germanium: From its discovery to SiGe devices. Mater. Sci. Semicond. Proc. 2006, 9, 408–422. [Google Scholar] [CrossRef] [Green Version]
  32. Chroneos, A. Isovalent impurity-vacancy complexes in germanium. Phys. Status Solidi B 2007, 244, 3206–3210. [Google Scholar] [CrossRef]
  33. Claeys, C.; Simoen, E. Germanium-Based Technologies: From Materials to Devices; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
  34. Vanhellemont, J.; Spiewak, P.; Sueoka, K. On the solubility and diffusivity of the intrinsic point defects in germanium. J. Appl. Phys. 2007, 101, 036103. [Google Scholar] [CrossRef]
  35. Chroneos, A.; Grimes, R.W.; Uberuaga, B.P.; Brotzmann, S.; Bracht, H. Vacancy-arsenic clusters in germanium. Appl. Phys. Lett. 2007, 91, 192106. [Google Scholar] [CrossRef]
  36. Schneider, S.; Bracht, H.; Petersen, M.C.; Lundsgaard Hansen, J.; Nylandsted Larsen, A. Proton irradiation of germanium isotope multilayer structures at elevated temperatures. J. Appl. Phys. 2008, 103, 033517. [Google Scholar] [CrossRef]
  37. Chroneos, A.; Bracht, H.; Grimes, R.W.; Uberuaga, B.P. Phosphorous clustering in germanium-rich silicon germanium. Mater. Sci. Eng. B 2008, 154–155, 72–75. [Google Scholar] [CrossRef]
  38. Naganawa, M.; Shimizu, Y.; Uematsu, M.; Itoh, K.M.; Sawano, K.; Shiraki, Y.; Haller, E.E. Charge states of vacancies in germanium investigated by simultaneous observation of germanium self-diffusion and arsenic diffusion. Appl. Phys. Lett. 2008, 93, 191905. [Google Scholar] [CrossRef]
  39. Janke, C.; Jones, R.; Coutinho, J.; Öberg, S.; Briddon, P.R. Ab initio investigation of phosphorus diffusion paths in germanium. Phys. Rev. B 2008, 77, 195210. [Google Scholar] [CrossRef]
  40. Chroneos, A.; Bracht, H.; Jiang, C.; Uberuaga, B.P.; Grimes, R.W. Nonlinear stability of E centers in Si1-xGex: Electronic structure calculations. Phys. Rev. B 2008, 78, 195201. [Google Scholar] [CrossRef] [Green Version]
  41. Hüger, E.; Tietze, U.; Lott, D.; Bracht, H.; Bougeard, D.; Haller, E.E.; Schmidt, H. Self-diffusion in germanium isotope multilayers at low temperatures. Appl. Phys. Lett. 2008, 93, 162104. [Google Scholar] [CrossRef] [Green Version]
  42. Brotzmann, S.; Bracht, H. Intrinsic and extrinsic diffusion of phosphorous, arsenic, and antimony in germanium. J. Appl. Phys. 2008, 103, 033508. [Google Scholar] [CrossRef]
  43. Chroneos, A.; Bracht, H.; Grimes, R.W.; Uberuaga, B.P. Vacancy-mediated dopant diffusion activation enthalpies for germanium. Appl. Phys. Lett. 2008, 92, 172103. [Google Scholar] [CrossRef] [Green Version]
  44. Brotzmann, S.; Bracht, H.; Lundsgaard Hansen, J.; Nylandsted Larsen, A.; Simoen, E.; Haller, E.E.; Christensen, J.S.; Werner, P. Diffusion and defect reactions between donors, C, and vacancies in Ge. I Experimental results. Phys. Rev. B 2008, 77, 235207. [Google Scholar] [CrossRef] [Green Version]
  45. Chroneos, A.; Grimes, R.W.; Uberuaga, B.P.; Bracht, H. Diffusion and defect reactions between donors, C, and vacancies in Ge. II Atomistic calculations of related complexes. Phys. Rev. B 2008, 77, 235208. [Google Scholar] [CrossRef]
  46. Kube, R.; Bracht, H.; Chroneos, A.; Posselt, M.; Schmidt, B. Intrinsic and extrinsic diffusion of indium in germanium. J. Appl. Phys. 2009, 106, 063534. [Google Scholar] [CrossRef] [Green Version]
  47. Chroneos, A. Effect of germanium substrate loss and nitrogen on dopant diffusion in germanium. J. Appl. Phys. 2009, 105, 056101. [Google Scholar] [CrossRef]
  48. Decoster, S.; De Vries, B.; Wahl, U.; Correia, J.G.; Vantomme, A. Lattice location study of implanted In in Ge. J. Appl. Phys. 2009, 105, 083522. [Google Scholar] [CrossRef]
  49. Chroneos, A.; Jiang, C.; Grimes, R.W.; Schwingenschlögl, U.; Bracht, H. Defect interactions in Sn1-xGex alloys. Appl. Phys. Lett. 2009, 94, 252104. [Google Scholar] [CrossRef] [Green Version]
  50. Chroneos, A.; Jiang, C.; Grimes, R.W.; Schwingenschlögl, U.; Bracht, H. E centers in Si1-x-yGexSny alloys. Appl. Phys. Lett. 2009, 95, 112101. [Google Scholar] [CrossRef] [Green Version]
  51. Bruno, E.; Mirabella, S.; Scapellato, G.; Impellizzeri, G.; Terrasi, A.; Priolo, F.; Napolitani, E.; De Salvador, D.; Mastramatteo, M.; Carnera, A. Mechanism of B diffusion in crystalline Ge under proton irradiation. Phys. Rev. B 2009, 80, 033204. [Google Scholar] [CrossRef]
  52. Chroneos, A.; Londos, C.A.; Bracht, H. A-centers and isovalent impurities in germanium: Density functional theory calculations. Mater. Sci. Eng. B 2011, 176, 453–457. [Google Scholar] [CrossRef]
  53. Chroneos, A. Dopant-vacancy cluster formation in germanium. J. Appl. Phys. 2010, 107, 076102. [Google Scholar] [CrossRef] [Green Version]
  54. Tahini, H.; Chroneos, A.; Grimes, R.W.; Schwingenschlögl, U. Diffusion of tin in germanium: A GGA+U approach. Appl. Phys. Lett. 2011, 99, 162103. [Google Scholar] [CrossRef] [Green Version]
  55. Pulikkotil, J.J.; Chroneos, A.; Schwingenschlögl, U. Structure of Sn1−xGex random alloys as obtained from the coherent potential approximation. J. Appl. Phys. 2011, 110, 036105. [Google Scholar] [CrossRef] [Green Version]
  56. Impellizzeri, G.; Boninelli, S.; Priolo, F.; Napolitani, E.; Spinella, C.; Chroneos, A.; Bracht, H. Fluorine effect on As diffusion in Ge. J. Appl. Phys. 2011, 109, 113527. [Google Scholar] [CrossRef]
  57. Stolwijk, N.A.; Lerner, L. Vacancy properties in germanium probed by cobalt diffusion. J. Appl. Phys. 2011, 110, 033526. [Google Scholar] [CrossRef]
  58. Tahini, H.; Chroneos, A.; Grimes, R.W.; Schwingenschlögl, U.; Dimoulas, A. Strain induced changes to the electronic structure of germanium. J. Phys. Condens. Matter 2012, 24, 195802. [Google Scholar] [CrossRef] [PubMed]
  59. Chroneos, A.; Bracht, H. Diffusion of n-type dopants in germanium. Appl. Phys. Rev. 2014, 1, 011301. [Google Scholar] [CrossRef] [Green Version]
  60. Chroneos, A.; Sgourou, E.N.; Londos, C.A.; Schwingenschlögl, U. Oxygen defect processes in silicon and silicon germanium. Appl. Phys. Rev. 2015, 2, 021306. [Google Scholar] [CrossRef] [Green Version]
  61. Simoen, E.; Schaekers, M.; Liu, J.B.; Luo, J.; Zhao, C.; Barla, K.; Collaert, N. Defect engineering for shallow n-type junctions in germanium: Facts and fiction. Phys. Status Solidi A 2016, 213, 2799–2808. [Google Scholar] [CrossRef]
  62. Chroneos, A.; Grimes, R.W.; Bracht, H.; Uberuaga, B.P. Engineering the free vacancy and active donor concentrations in phosphrous and arsenic double donor-doped germanium. J. Appl. Phys. 2008, 104, 113724. [Google Scholar] [CrossRef] [Green Version]
  63. Sigillito, A.J.; Tyryshkin, A.M.; Beeman, J.W.; Haller, E.E.; Itoh, K.M.; Lyon, S.A. Large stark tuning of donor electron spin qubits in germanium. Phys. Rev. B 2016, 94, 125204. [Google Scholar] [CrossRef] [Green Version]
  64. Kujala, J.; Sudkamp, T.; Slotte, J.; Makkonen, I.; Tuomisto, F.; Bracht, H. Vacancy-donor complexes in highly n-type Ge doped with As, P and Sb. J. Phys. Condens. Matter 2016, 28, 335801. [Google Scholar] [CrossRef]
  65. Saltas, V.; Chroneos, A.; Vallianatos, F.A. Composition and temperature dependence of self-diffusion in Si1-xGex alloys. Sci. Rep. 2017, 7, 1374. [Google Scholar] [CrossRef] [Green Version]
  66. Sgourou, E.N.; Panayiotatos, Y.; Vovk, R.V.; Chroneos, A. Toward defect engineering strategies to optimize energy and electronic materials. Appl. Sci. 2017, 7, 674. [Google Scholar] [CrossRef] [Green Version]
  67. Prussing, J.K.; Hamdana, G.; Bougeard, D.; Peiner, E.; Bracht, H. Quantitative scanning spreading resistance microscopy on n-type dopant diffusion profiles in germanium and the origin of dopant deactivation. J. Appl. Phys. 2019, 125, 085105. [Google Scholar] [CrossRef]
  68. Christopoulos, S.R.G.; Kuganathan, N.; Chroneos, A. Electronegativity and doping Si1-xGex alloys. Sci. Rep. 2020, 10, 7459. [Google Scholar] [CrossRef]
  69. Prucnal, S.; Liedke, M.O.; Wang, X.S.; Butterling, M.; Posselt, M.; Knoch, J.; Windgassen, H.; Hirschmann, E.; Berencen, Y.; Rebohle, L.; et al. Dissolution of donor-vacancy clusters in heavily doped n-type germanium. New J. Phys. 2020, 22, 123036. [Google Scholar] [CrossRef]
  70. Kipke, F.; Sudkamp, T.; Prussing, J.K.; Bougeard, D.; Bracht, H. Diffusion of boron in germanium at 800–900 °C revisited. J. Appl. Phys. 2020, 127, 025703. [Google Scholar] [CrossRef]
  71. Saputro, R.H.; Matsumura, R.; Fukata, N. Dopant redistribution in high-temperature-grown Sb-doped Ge epitaxial films. Cryst. Growth Des. 2021, 21, 6523–6528. [Google Scholar] [CrossRef]
  72. Kuganathan, N.; Bracht, H.; Davazoglou, K.; Kipke, F.; Chroneos, A. Impact of oxygen on gallium doped germanium. AIP Advances 2021, 11, 065122. [Google Scholar] [CrossRef]
  73. Igumbor, E.; Olaniyan, O.; Dongho-Nguimbo, G.M.; Mapasha, R.E.; Ahmad, S. Electronic properties and defect levels induced by n/p-type defect complexes in Ge. Mater. Sci. Semicond. Proc. 2022, 150, 106906. [Google Scholar] [CrossRef]
  74. Kuganathan, N.; Grimes, R.W.; Chroneos, A. Nitrogen-vacancy defects in germanium. AIP Adv. 2022, 12, 045110. [Google Scholar] [CrossRef]
  75. Chroneos, A.; Grimes, R.W.; Tsamis, C. Atomic scale simulations of arsenic-vacancy complexes in germanium and silicon. Mater. Sci. Semicond. Proc. 2006, 9, 536–540. [Google Scholar] [CrossRef]
  76. Letaw Jr, H.; Portnoy, W.M.; Slifkin, L. Self-diffusion in germanium. Phys. Rev. 1956, 102, 636–639. [Google Scholar] [CrossRef]
  77. Valenta, M.W.; Ramasastry, C. Effect of heavy doping on the self-diffusion of germanium. Phys. Rev. 1957, 106, 73–75. [Google Scholar] [CrossRef]
  78. Stolwijk, N.A.; Frank, W.; Hölzl, J.; Pearton, S.J.; Haller, E.E. Diffusion and solubility of copper in germanium. J. Appl. Phys. 1985, 57, 5211–5219. [Google Scholar] [CrossRef]
  79. Bracht, H.; Stolwijk, N.A.; Mehrer, H. Diffusion and solubility of copper, silver, and gold in germanium. Phys. Rev. B 1991, 43, 14465–14477. [Google Scholar] [CrossRef] [PubMed]
  80. Bracht, H. Copper related diffusion phenomena in germanium and silicon. Mater. Sci. Semicond. Proc. 2004, 7, 113–124. [Google Scholar] [CrossRef]
  81. Hu, S.M. On interaction potential, correlation factor, vacancy mobility, and activation energy of impurity diffusion in diamond lattice. Phys. Stat. Sol. (B) 1973, 60, 595–604. [Google Scholar] [CrossRef]
  82. Tahini, H.A.; Chroneos, A.; Grimes, R.W.; Schwingenschlögl, U.; Bracht, H. Point defect engineering strategies to retard phosphorous diffusion in germanium. Phys. Chem. Chem. Phys. 2013, 15, 367–371. [Google Scholar] [CrossRef] [PubMed]
  83. Chroneos, A.; Grimes, R.W.; Bracht, H. Fluorine cooping in germanium to suppress donor diffusion an093d deactivation. J. Appl. Phys. 2009, 106, 063707. [Google Scholar] [CrossRef] [Green Version]
  84. Jung, W.S.; Park, J.H.; Nainani, A.; Nam, D.; Saraswat, K.C. Fluorine passivation of vacancy defects in bulk germanium for Ge metal-oxide-semiconductor field-effect transistor application. Appl. Phys. Lett. 2012, 101, 072104. [Google Scholar] [CrossRef]
  85. Impellizzeri, G.; Napolitani, E.; Boninelli, S.; Sullivan, J.P.; Roberts, J.; Buckman, S.J.; Ruffell, S.; Priolo, F.; Privitera, V. Role of F on the electrical activation of As in Ge. ECS J. Solid State Sci. Technol. 2012, 1, Q44–Q46. [Google Scholar] [CrossRef]
  86. El Mubarek, H.A.W. Reduction of phosphorus diffusion in germanium by fluorine implantation. J. Appl. Phys. 2013, 114, 223512. [Google Scholar] [CrossRef]
  87. Liu, J.B.; Luo, J.; Simoen, E.; Niu, Y.X.; Yang, F.; Wang, G.L.; Wang, W.W.; Chen, D.P.; Li, J.F.; Zhao, C.; et al. Junction control by carbon and phosphorus co-implantation in pre-amorphized germanium. ECS J. Solid State Sci. Technol. 2016, 5, P315–P319. [Google Scholar] [CrossRef]
  88. Lopez, G.M.; Fiorentini, V.; Impellizzeri, G.; Mirabella, S.; Napolitani, E. Fluorine in Si: Native-defect complexes and the suppression of impurity diffusion. Phys. Rev. B 2005, 72, 045219. [Google Scholar] [CrossRef]
  89. Lopez, G.M.; Fiorentini, V. Large fluorine-vacancy clusters in Si and their capture efficiency for self-interstitials. Appl. Phys. Lett. 2006, 89, 092113. [Google Scholar] [CrossRef]
  90. Harrison, S.A.; Edgar, T.F.; Hwang, G.S. Prediction of the anomalous fluorine-silicon interstitial pair diffusion in crystalline silicon. Phys. Rev. B 2006, 74, 121201. [Google Scholar] [CrossRef]
  91. Kiga, R.; Uematsu, M.; Itoh, K.M. Effect of fluorine on the suppression of boron diffusion in pre-amorphized silicon. J. Appl. Phys. 2020, 128, 105701. [Google Scholar] [CrossRef]
  92. Sio, H.C.; Kang, D.; Liu, R.; Stuckelberger, J.; Samundsett, C.; Macdonald, D. Fluorine passivation of defects and interfaces in crystalline silicon. ACS Appl. Mater. Interfaces 2021, 13, 32503–32509. [Google Scholar] [CrossRef]
  93. Satta, A.; Simoen, E.; Clarysse, T.; Janssens, T.; Benedetti, A.; De Jaeger, B.; Meuris, M.; Vandervorst, W. Diffusion, activation, and recrystallization of boron implanted in preamorphized and crystalline germanium. Appl. Phys. Lett. 2005, 87, 172109. [Google Scholar] [CrossRef]
  94. Impellizzeri, G.; Mirabella, S.; Irrera, A.; Grimaldi, M.G.; Napolitani, E. Ga-implantation in Ge: Electrical activation and clustering. J. Appl. Phys. 2009, 106, 013518. [Google Scholar] [CrossRef]
  95. Bracht, H.; Schneider, S.; Klug, J.N.; Liao, C.Y.; Hansen, J.L.; Haller, E.E.; Larsen, A.N.; Bougeard, D.; Posselt, M.; Wundisch, C. Interstitial-mediated diffusion in germanium under proton irradiation. Phys. Rev. Lett. 2009, 103, 255501. [Google Scholar] [CrossRef] [Green Version]
  96. Schneider, S.; Bracht, H.; Klug, J.N.; Hansen, J.L.; Larsen, A.N.; Bougeard, D.; Haller, E.E. Radiation-enhanced self- and boron diffusion in germanium. Phys. Rev. B 2013, 87, 115202. [Google Scholar] [CrossRef] [Green Version]
  97. Mirabella, S.; De Salvador, D.; Napolitani, E.; Bruno, E.; Priolo, F. Mechanisms of boron diffusion in silicon and germanium. J. Appl. Phys. 2013, 113, 031101. [Google Scholar] [CrossRef]
  98. Milazzo, R.; Linser, M. Impelizzeri, G.; Scarpa, D.; Giarola, M.; Sanson, A.; Mariotto, G.; Andrighetto, A.; Carnera, A.; Napolitani, E. P-type doping of Ge by Al ion implantation and pulsed laser melting. Appl. Surf. Sci. 2020, 509, 145230. [Google Scholar] [CrossRef]
  99. Foster, N.D.; Miller, A.J.; Hutchins-Delgado, T.A.; Smyth, C.M.; Wanke, M.C.; Lu, Z.M.; Luhman, D.R. Thermal activation of low-density Ga implanted in Ge. Appl. Phys. Lett. 2022, 120, 201902. [Google Scholar] [CrossRef]
  100. Janke, C.; Jones, R.; Öberg, S.; Briddon, P.R. Ab initio investigation of boron diffusion paths in germanium. J. Mater. Sci. Mater. Electron. 2007, 18, 775–780. [Google Scholar] [CrossRef]
  101. Chroneos, A.; Kube, R.; Bracht, H.; Grimes, R.W.; Schwingenschlogl, U. Vacancy-indium clusters in implanted germanium. Chem. Phys. Lett. 2010, 490, 38–40. [Google Scholar] [CrossRef]
  102. Wang, G.J.; Mei, H.; Meng, X.H.; Mei, D.M.; Yang, G. The electrical properties and distribution of indium in germanium crystals. Mater. Sci. Semicond. Proc. 2018, 74, 342–346. [Google Scholar] [CrossRef]
  103. Corbett, J.W.; Watkins, G.D.; Mc Doland, R.S. New oxygen infrared bands in annealed irradiated silicon. Phys. Rev. 1964, 135, A1381–A1385. [Google Scholar] [CrossRef]
  104. Goesele, U.; Laveant, P.; Scholz, R.; Engler, N.; Werner, P. Diffusion engineering by carbon in Silicon, in Si Front-End Processing- Physics and Technology of Dopant-defect Interaction II. Mater. Res. Soc. Symp. Proc. 2000, 610, B7.1.1–B7.1.12. [Google Scholar]
  105. Chroneos, A.; Londos, C.A. Interaction of A-centers with isovalent impurities in silicon. J. Appl. Phys. 2010, 107, 093518. [Google Scholar] [CrossRef] [Green Version]
  106. Sgourou, E.N.; Timerkaeva, D.; Londos, C.A.; Aliprantis, D.; Chroneos, A.; Caliste, D.; Pochet, P. Impact of isovalent doping on the trapping of vacancy and interstitial related defects in Si. J. Appl. Phys. 2013, 113, 113506. [Google Scholar] [CrossRef] [Green Version]
  107. Murin, L.I.; Tolkacheva, E.A.; Lastovskii, S.B.; Markevich, V.P.; Mullins, J.; Peaker, A.R.; Svensson, B.G. Interaction of radiation-induced self-interstitials with vacancy-oxygen related defects VnO2 (n from 1 to 3) in silicon. Phys. Stat. Solidi A 2019, 216, 1800609. [Google Scholar] [CrossRef]
  108. Chroneos, A.; Londos, C.A.; Sgourou, E.N.; Pochet, P. Point defect engineering strategies to suppress A-center formation in silicon. Appl. Phys. Lett. 2011, 99, 241901. [Google Scholar] [CrossRef] [Green Version]
  109. Wang, H.; Chroneos, A.; Londos, C.A.; Sgourou, E.N.; Schwingenschlögl, U. A-centers in silicon studied with hybrid density functional theory. Appl. Phys. Lett. 2013, 103, 052101. [Google Scholar] [CrossRef]
  110. Wang, H.; Chroneos, A.; Sgourou, E.N.; Londos, C.A.; Schwingenschlogl, U. Carbon related defects in irradiated silicon revisited. Sci. Rep. 2014, 4, 4909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  111. Qin, Y.Z.; Wang, P.; Jin, S.J.; Cui, C.; Yang, D.R.; Yu, X.G. Effects of nitrogen doping on vacancy-oxygen complexes in neutron irradiated Czochralski silicon. Mater. Sci. Semicond. Proc. 2019, 98, 65–69. [Google Scholar] [CrossRef]
  112. Kras’ko, M.M.; Kolosiuk, A.G.; Neimash, V.B.; Povarchuk, V.Y.; Roguts’kyi, I.S.; Goushcha, A.O. Role of the intensity of high-temperature electron irradiation in accumulation of vacancy-oxygen defects in Cz n-Si. J. Mater. Res. 2021, 36, 1646–1656. [Google Scholar] [CrossRef]
  113. Pelenitsyn, V.; Korataev, P. First-principles study of radiation defects in silicon. Comp. Mater. Sci. 2022, 207, 111273. [Google Scholar] [CrossRef]
  114. Sueoka, K.; Kamiyama, E.; Spiewak, P.; Vanhellemont, J. Review—Properties of intrinsic point defects in Si and Ge assessed by density functional theory. ECS J. Solid State Sci. Technol. 2016, 5, P3176–P3195. [Google Scholar] [CrossRef]
  115. Chroneos, A.; Grimes, R.W.; Bracht, H. Impact of germanium on vacancy clustering in germanium-doped silicon. J. Appl. Phys. 2009, 105, 016102. [Google Scholar] [CrossRef]
  116. Rushton, M.J.D.; Chroneos, A.; Skinner, S.J.; Kilner, J.A.; Grimes, R.W. Effect of strain on the oxygen diffusion in yttria and gadolinia co-doped ceria. Solid State Ionics 2013, 230, 37–42. [Google Scholar] [CrossRef]
  117. Kelaidis, N.; Kordatos, A.; Christopoulos, S.R.G.; Chroneos, A. A roadmap of strain in doped anatase TiO2. Sci. Rep. 2018, 8, 12790. [Google Scholar] [CrossRef] [Green Version]
  118. Hussain, N.; Yao, Y.S.; Sagar, R.U.R.; Anwar, T.; Murtaza, M.; Huang, K.; Shehzad, K.; Wu, H.; Wang, Z.M. Quantum-confined blue photoemission in strain-engineered few-atomic-layer 2D germanium. Nano Energy 2021, 83, 105790. [Google Scholar] [CrossRef]
  119. Lee, M.L.; Fitzgerald, E.A. Strained Si, SiGe, and Ge channels for high-mobility metal-oxide-semiconductor field-effect transistors. J. Appl. Phys. 2005, 97, 011101. [Google Scholar] [CrossRef]
  120. Schichtel, N.; Korte, C.; Hesse, D.; Janek, J. Elastic strain at interfaces and its influence on ionic conductivity in nanoscaled solid electrolyte thin films- theoretical considerations and experimental studies. Phys. Chem. Chem. Phys. 2009, 11, 3043–3048. [Google Scholar] [CrossRef] [PubMed]
  121. Chiabrera, F.; Garbayo, I.; Lopez-Conesa, L.; Martin, G.; Ruiz-Caridad, A.; Walls, M.; Ruiz-Gonzalez, L.; Kordatos, A.; Nunez, M.; Morata, A.; et al. Engineering transport in manganites by tuning local nonstoichiometry in grain boundaries. Adv. Mater. 2019, 31, 1805360. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  122. Baiutti, F.; Chiabrera, F.; Acosta, M.; Diercks, D.; Parfitt, D.; Santiso, J.; Wang, X.; Cavallaro, A.; Morata, A.; Wang, H.; et al. A high-entropy manganite in an ordered nanocomposite for long-term application in solid oxide cells. Nat. Commun. 2021, 12, 2660. [Google Scholar] [CrossRef]
  123. Kuganathan, N.; Baiutti, F.; Tarancon, A.; Fleig, J.; Chroneos, A. Defects energetics in the SrTiO3-LaCrO3 system. Solid State Ionics 2021, 361, 115570. [Google Scholar] [CrossRef]
  124. Varotsos, P. Calculation of the migration volume of vacancies in ionic solids from macroscopic parameters. Phys. Stat. Sol. (A) 1978, 47, K133–K136. [Google Scholar] [CrossRef]
  125. Varotsos, P.; Alexopoulos, K. Thermodynamics of Point Defects and Their Relation with the Bulk Properties; North-Holland: Amsterdam, The Netherlands, 1986. [Google Scholar]
  126. Varotsos, P. Comparison of models that interconnect point defect parameters in solids with bulk properties. J. Appl. Phys. 2007, 101, 123503. [Google Scholar] [CrossRef]
  127. Murphy, S.T.; Chroneos, A.; Jiang, C.; Schwingenschlögl, U.; Grimes, R.W. Deviations from Vegard’s law in ternary III-V alloys. Phys. Rev. B 2010, 82, 073201. [Google Scholar] [CrossRef] [Green Version]
  128. Murphy, S.T.; Chroneos, A.; Grimes, R.W.; Jiang, C.; Schwingenschlögl, U. Phase stability and the arsenic vacancy defect in InxGa1-xAs. Phys. Rev. B 2011, 84, 184108. [Google Scholar] [CrossRef] [Green Version]
  129. Chroneos, A.; Vovk, R.V. Modeling self-diffusion in UO2 and ThO2 by connecting point defect parameters with bulk properties. Solid State Ionics 2015, 274, 1–3. [Google Scholar] [CrossRef]
  130. Cooper, M.W.D.; Grimes, R.W.; Fitzpatrick, M.E.; Chroneos, A. Modeling oxygen self-diffusion in UO2 under pressure. Solid State Ionics 2015, 282, 26–30. [Google Scholar] [CrossRef]
  131. Chroneos, A. Connecting point defect parameters with bulk properties to describe diffusion in solids. Appl. Phys. Rev. 2016, 3, 041304. [Google Scholar] [CrossRef] [Green Version]
  132. Saltas, V.; Chroneos, A.; Vallianatos, F.A. A thermodynamic approach of self- and hetero-diffusion in GaAs: Connecting point defect parameters with bulk properties. RSC Adv. 2016, 6, 53324–53330. [Google Scholar] [CrossRef]
  133. Magomedov, M.N. Parameters of the vacancy formation and self-diffusion in iron. J. Phys. Chem. Solids 2023, 172, 111084. [Google Scholar] [CrossRef]
  134. Jing, Y.; Zhang, X.; Wu, D.H.; Zhao, X.D.; Zhou, Z. High carrier mobility and pronounced light absorption in methyl-terminated germanene: Insights from first-principles. J. Phys. Chem. Lett. 2015, 6, 4252–4258. [Google Scholar] [CrossRef] [PubMed]
  135. Zhu, J.J.; Chroneos, A.; Schwingenschlögl, U. Silicene/germanene on MgX2 (X = Cl, Br, and I) for Li-ion batteries. Nanoscale 2016, 8, 7272–7277. [Google Scholar] [CrossRef]
  136. Kovalska, E.; Antonatos, N.; Luxa, J.; Sofer, Z. Edge-hydrogenated germanene by electrochemical decalcification-exfoliation of CaGe2: Germanene-enabled vapor sensor. ACS Nano 2021, 15, 16709–16718. [Google Scholar] [CrossRef]
  137. Zhao, F.L.; Feng, Y.Y.; Feng, W. Germanium-based monoelemental and binary two-dimensional materials: Theoretical and experimental investigations and promising applications. Infomat 2022, 4, e12365. [Google Scholar] [CrossRef]
  138. Liu, R.Q.; Kumar, A.; Chen, Z.Z.; Agrawal, A.; Sundararaghavan, V.; Choudhary, A. A predictive machine learning approach for microstructure optimization and materials design. Sci. Rep. 2015, 5, 22552. [Google Scholar] [CrossRef] [Green Version]
  139. Jay, E.E.; Rushton, M.J.D.; Chroneos, A.; Grimes, R.W.; Kilner, J.A. Genetics of superionic conductivity in lithium lanthanum titanates. Phys. Chem. Chem. Phys. 2015, 17, 178–183. [Google Scholar] [CrossRef]
  140. Mathew, J.; Parfitt, D.; Wilford, K.; Riddle, N.; Alamaniotis, M.; Chroneos, A.; Fitzpatrick, M.E. Reactor pressure vessel embrittlement: Insights from neural network modelling. J. Nucl. Mater. 2018, 502, 311–322. [Google Scholar] [CrossRef]
  141. Gubernatis, J.E.; Lookman, T. Machine learning in materials design and discovery: Examples from the present and suggestions for the future. Phys. Rev. Mater. 2018, 2, 120301. [Google Scholar] [CrossRef]
  142. Mathew, J.; Griffin, J.; Alamaniotis, M.; Kanarachos, S.; Fitzpatrick, M.E. Prediction of welding residual stresses using machine learning: Comparison between neural networks and neuro-fuzzy systems. Appl. Soft Comp. 2018, 70, 131–146. [Google Scholar] [CrossRef]
  143. Scappucci, G.; Kloeffel, C.; Zwanenburg, F.A.; Loss, D.; Myronov, M.; Zhang, J.J.; De Franceschi, S.; Katsaros, G.; Veldhorst, M. The germanium quantum information route. Nat. Rev. Mater. 2021, 6, 926–943. [Google Scholar] [CrossRef]
Applsci 12 11993 g001 550
Figure 1. Arrhenius plot for the diffusion coefficients of self-diffusion, n-type dopants (P, As, Sb) and p-type dopants (B, Al, Ga, In) in Ge [59].
Figure 1. Arrhenius plot for the diffusion coefficients of self-diffusion, n-type dopants (P, As, Sb) and p-type dopants (B, Al, Ga, In) in Ge [59].
Applsci 12 11993 g001
Applsci 12 11993 g002 550
Figure 2. The ring mechanism of diffusion in a Ge lattice [59].
Figure 2. The ring mechanism of diffusion in a Ge lattice [59].
Applsci 12 11993 g002
Applsci 12 11993 g003 550
Figure 3. A schematic representation of the AsnV clusters (n = 1–4). Cubes represent the vacancies, and white and black circles represent the Ge and As atoms, respectively [35].
Figure 3. A schematic representation of the AsnV clusters (n = 1–4). Cubes represent the vacancies, and white and black circles represent the Ge and As atoms, respectively [35].
Applsci 12 11993 g003
Applsci 12 11993 g004 550
Figure 4. The F4V cluster in Ge. The black circle represents the vacancy, the light blue circles F atoms and the yellow circles Ge atoms.
Figure 4. The F4V cluster in Ge. The black circle represents the vacancy, the light blue circles F atoms and the yellow circles Ge atoms.
Applsci 12 11993 g004
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Sgourou, E.N.; Daskalopulu, A.; Tsoukalas, L.H.; Stamoulis, G.; Vovk, R.V.; Chroneos, A. Seventy-Five Years since the Point-Contact Transistor: Germanium Revisited. Appl. Sci. 2022, 12, 11993. https://doi.org/10.3390/app122311993

AMA Style

Sgourou EN, Daskalopulu A, Tsoukalas LH, Stamoulis G, Vovk RV, Chroneos A. Seventy-Five Years since the Point-Contact Transistor: Germanium Revisited. Applied Sciences. 2022; 12(23):11993. https://doi.org/10.3390/app122311993

Chicago/Turabian Style

Sgourou, Efstratia N., Aspassia Daskalopulu, Lefteri H. Tsoukalas, George Stamoulis, Ruslan V. Vovk, and Alexander Chroneos. 2022. "Seventy-Five Years since the Point-Contact Transistor: Germanium Revisited" Applied Sciences 12, no. 23: 11993. https://doi.org/10.3390/app122311993

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop