Intuition and Symmetries in Electromagnetism: Eigenstates of Four Antennas
Abstract
1. Introduction
2. Problem Formulation
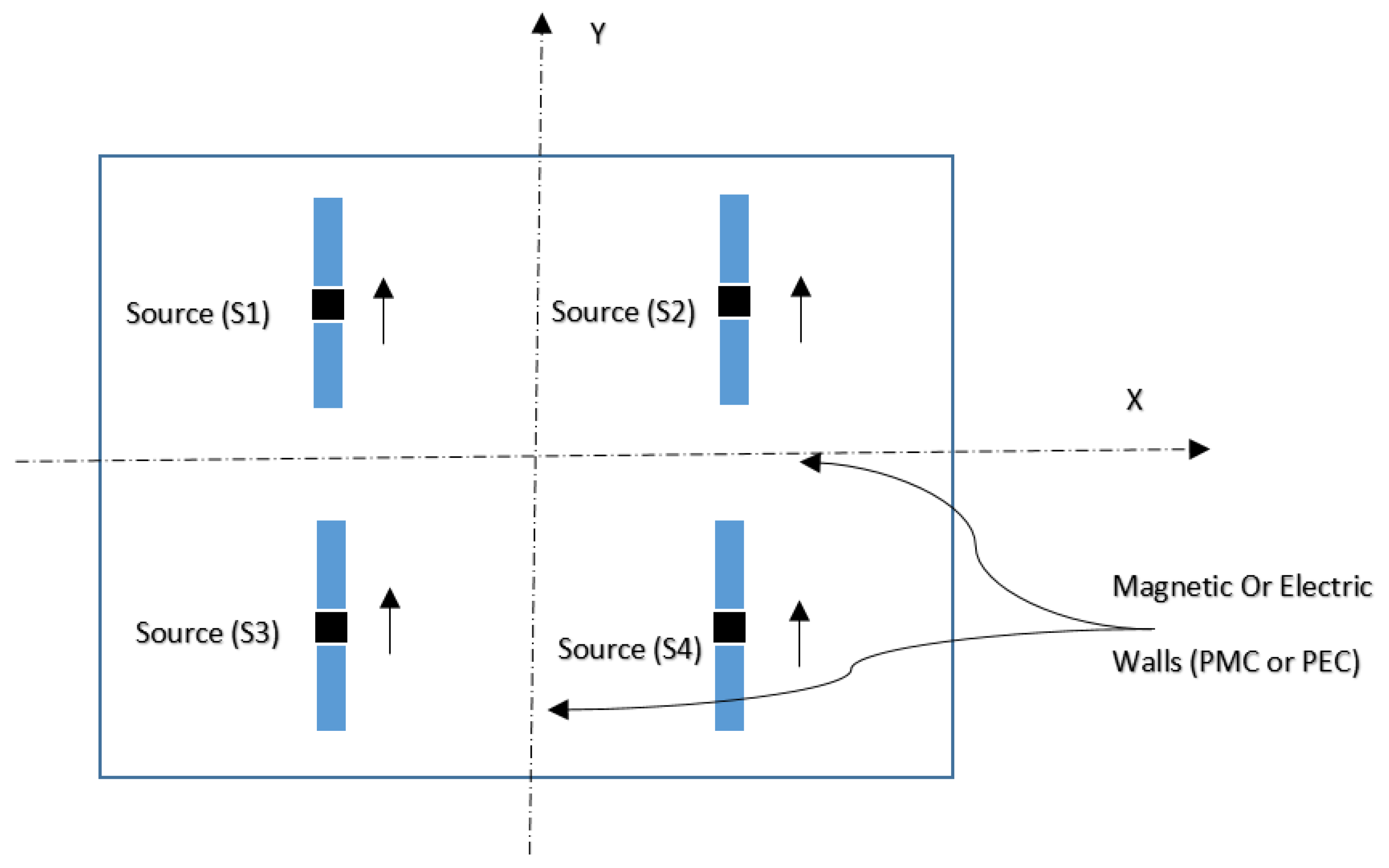
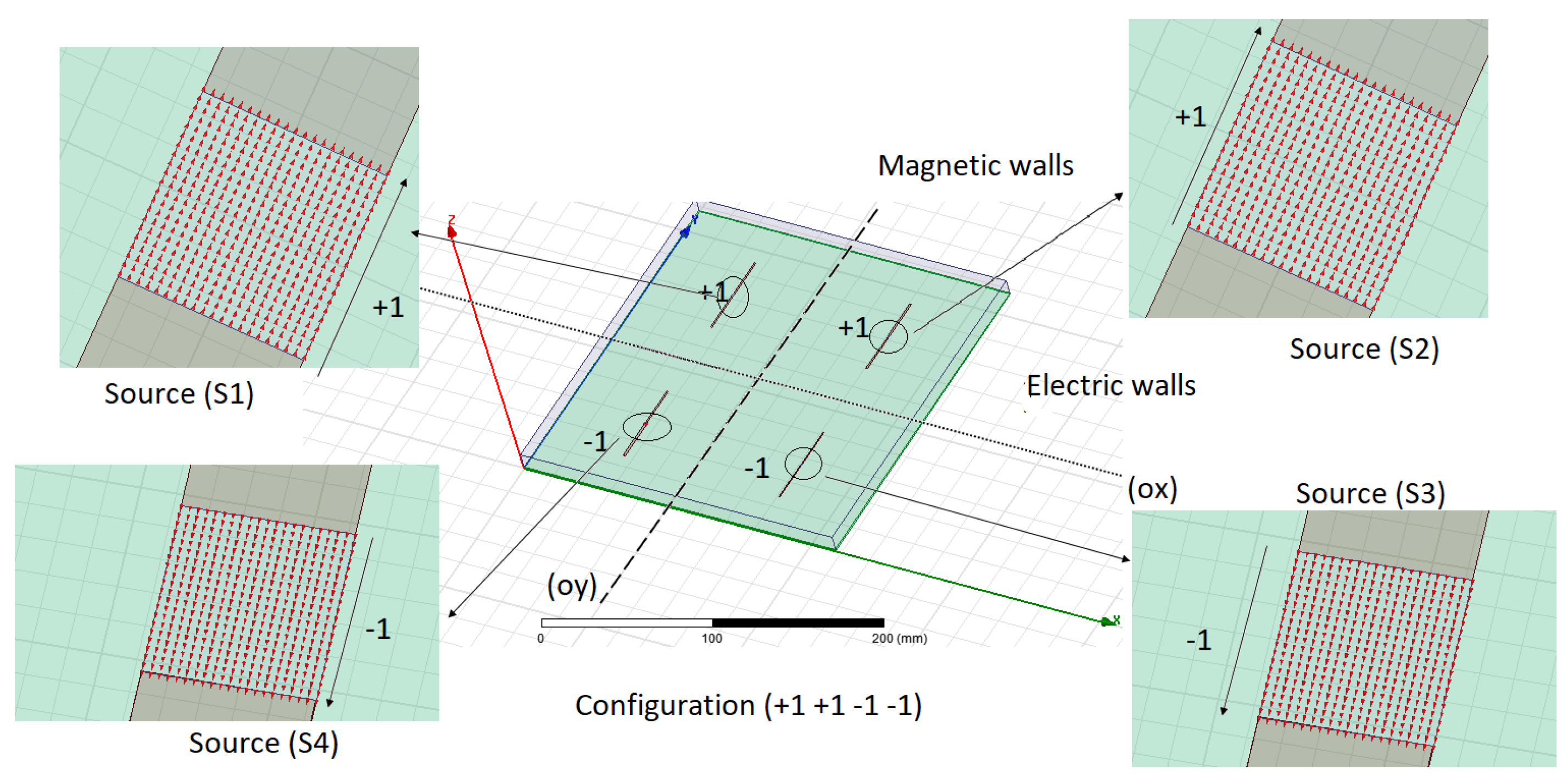
2.1. Setting Up of the Problem
| States | Walls | Amplitudes |
| of sources | ||
| 1 | electric (ox)∖magnetic (oy) | 1 1 1 1 |
| 2 | magnetic (ox)∖magnetic (oy) | 1 1 −1 −1 |
| 3 | electric (ox)∖electric (oy) | 1 −1 1 −1 |
| 4 | magnetic (ox)∖electric (oy) | 1 −1 −1 1 |
| States | E | ||||
| 1 | 1 | 1 | 1 | 1 | |
| 2 | 1 | 1 | −1 | −1 | |
| 3 | 1 | −1 | 1 | −1 | |
| 4 | 1 | −1 | −1 | 1 | |
2.2. Symmetries and Phases
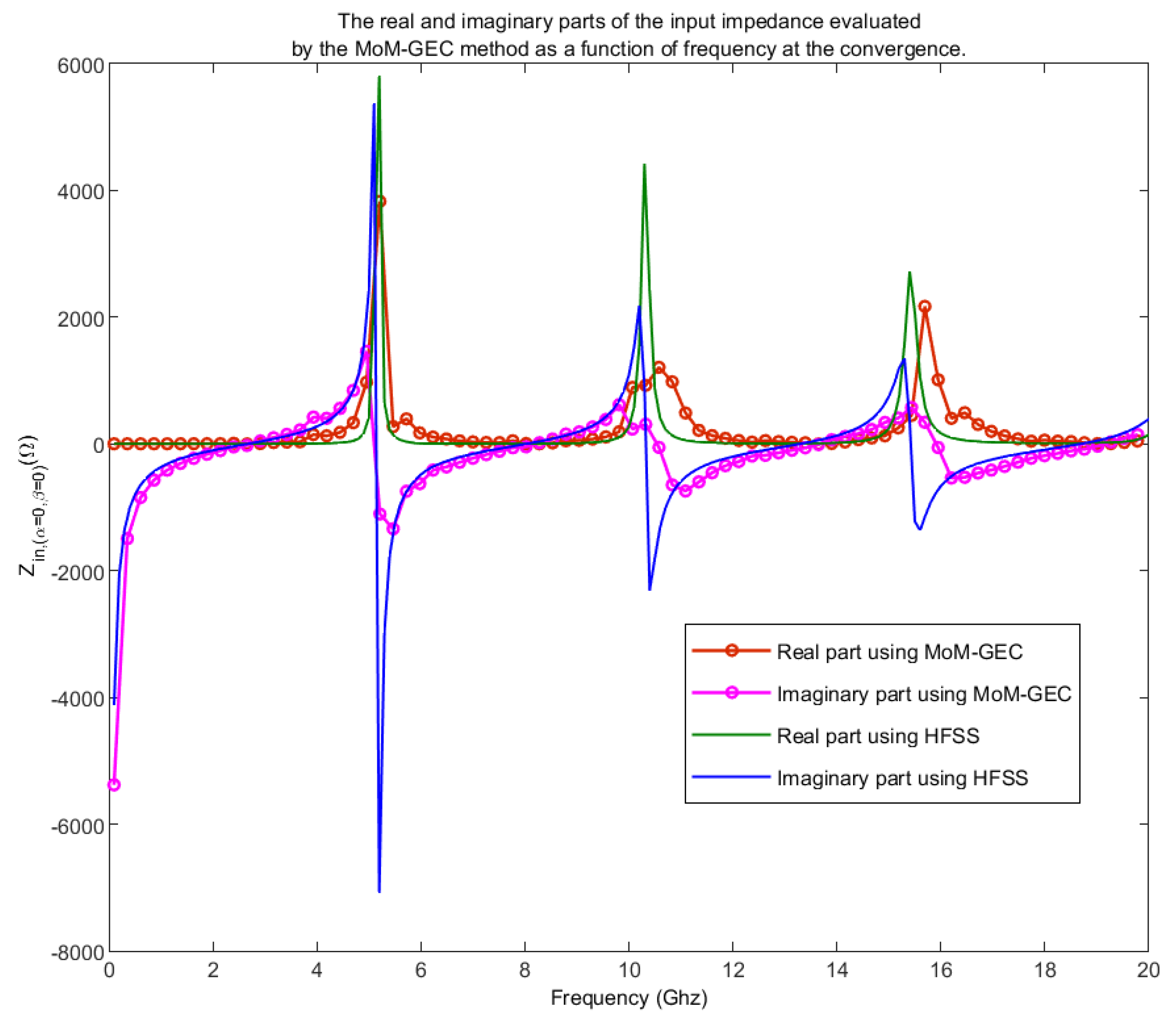
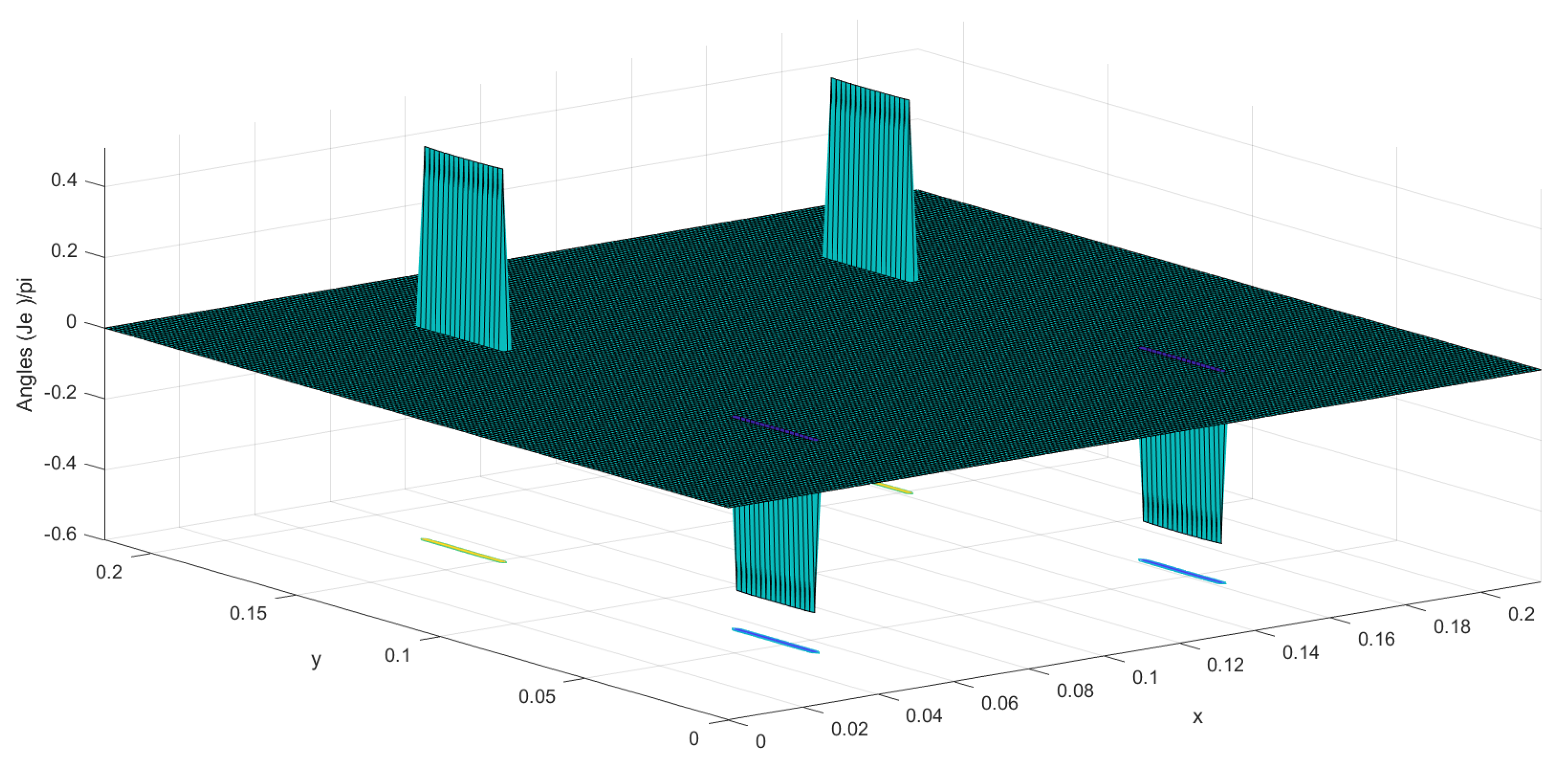
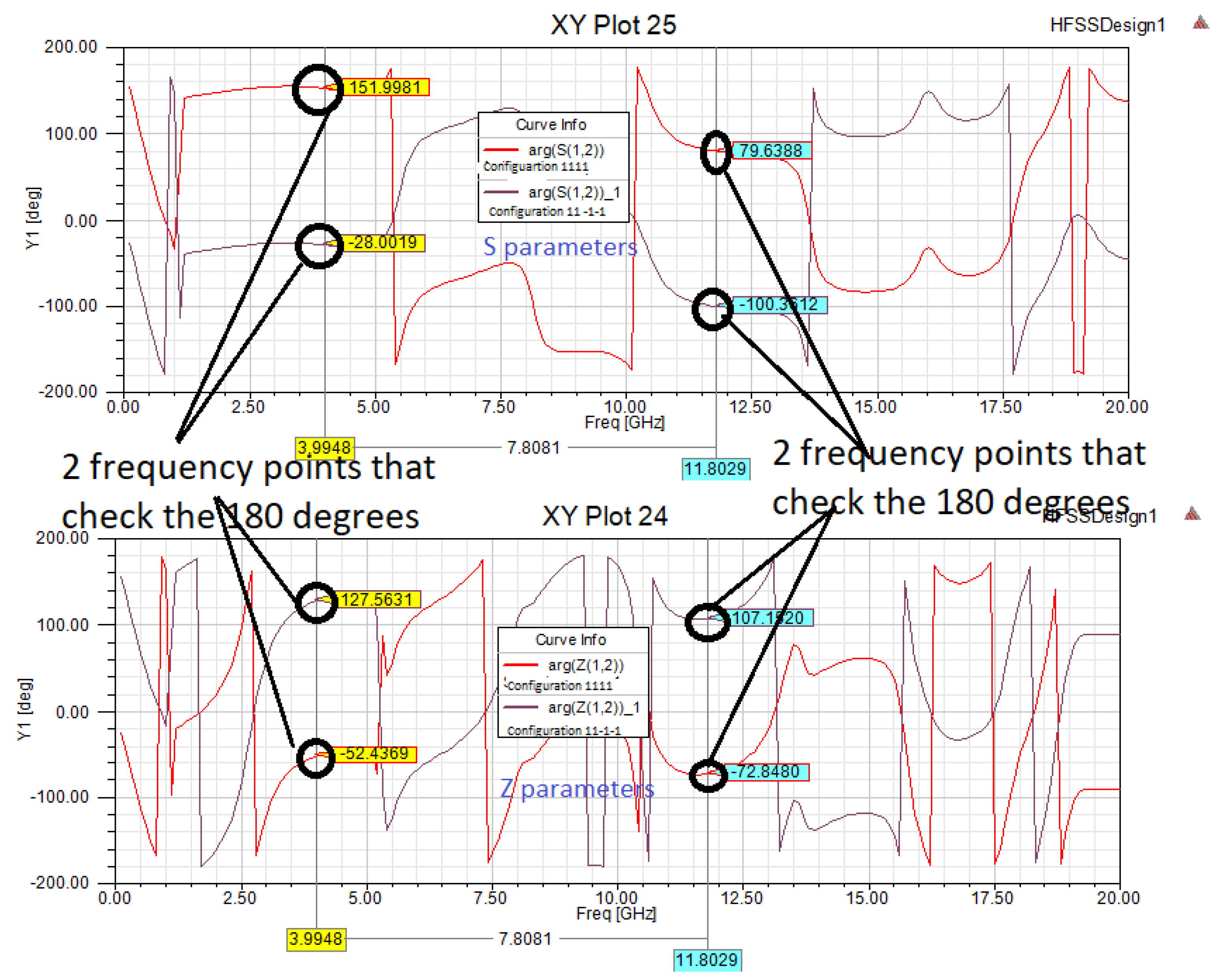
3. Results
4. Advantage of Symmetry
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MoM-GEC | Method of Moment combined with the Generalized Equivalent Circuits |
| HFSS | High-frequency structure simulator |
| CST | Computer Simulation Technology simulator |
| PEC | Perfect electric conductor |
| PMC | Perfect magnetic conductor |
| Symmetry point group of class |
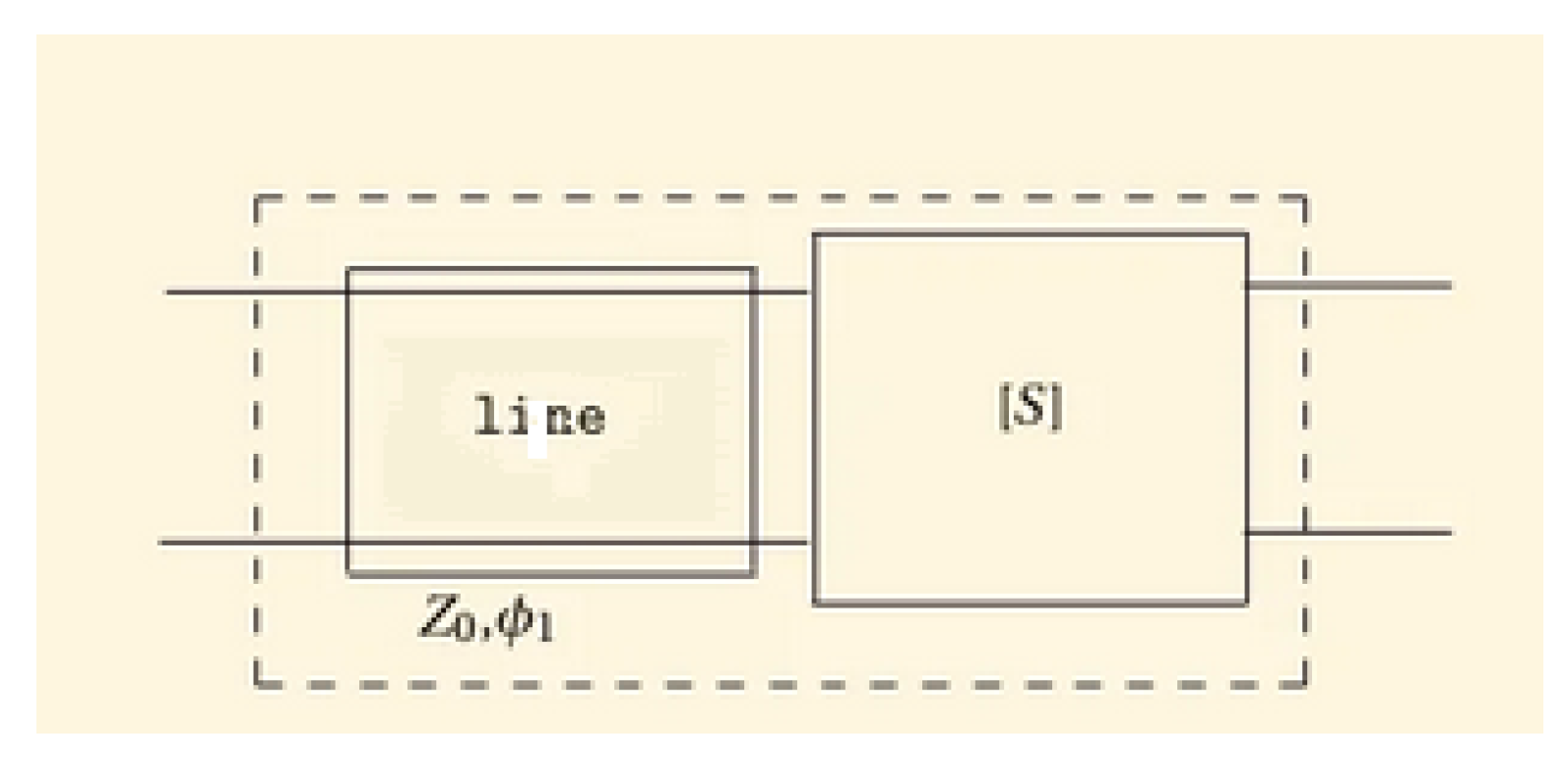
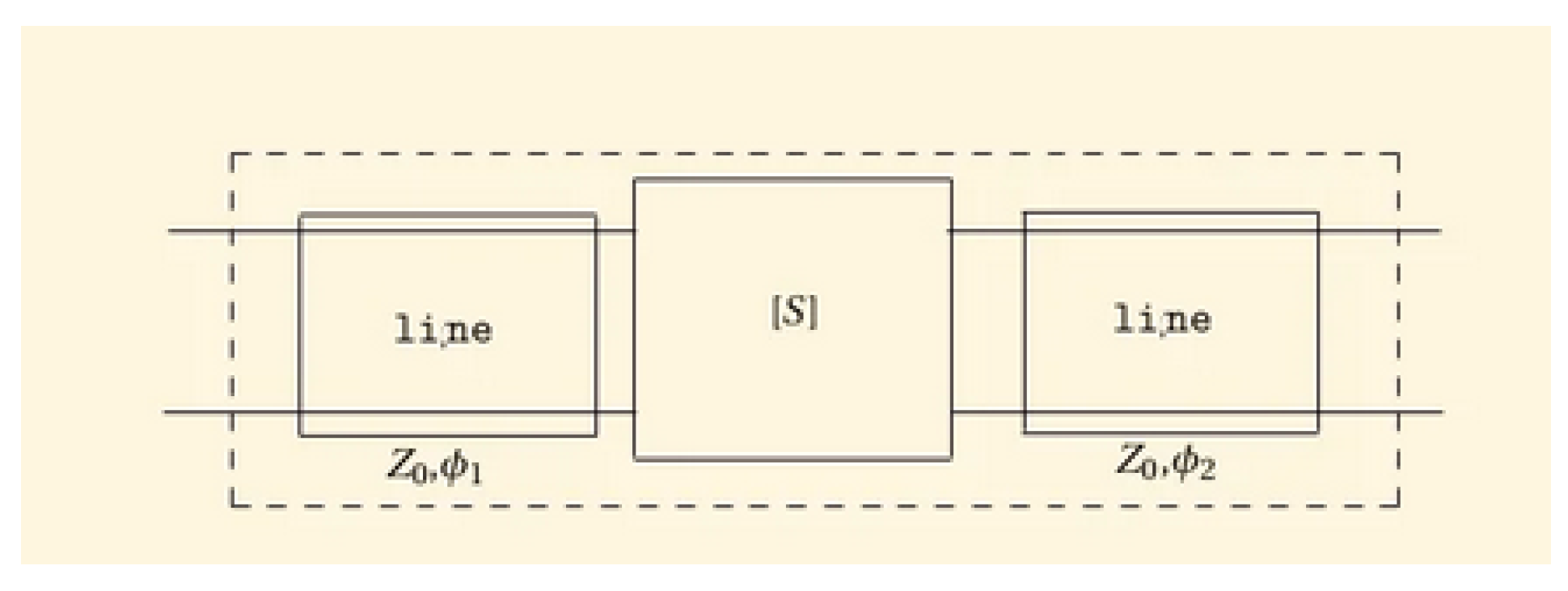
Appendix A. Technique to Count the Phase Shift between Two Sources (Particular Cases of Odd and Even Symmetries)
References
- Symmetric and ANTI-symmetric BCs in FDTD and MODE. Available online: https://support.lumerical.com/hc/en-us/articles/360034382694-Symmetri (accessed on 17 November 2022).
- Boundary Conditions-Symmetry Planes CST2013. Available online: https://space.mit.edu/RADIO/CST_online/mergedProjects/3D/special_solvopt/special_solvopt_boundary_conditions_symmetryplanes.htm (accessed on 17 November 2022).
- Symmetric Boundary Conditions in FEA. Available online: https://resources.system-analysis.cadence.com/blog/msa2022-symmetric-boundary-conditions-in-fea (accessed on 17 November 2022).
- Symmetry Plane Boundary Condition. Available online: https://edadocs.software.keysight.com/display/empro2010/Symmetry+Plane+Boundary+Condition (accessed on 17 November 2022).
- Exploiting Symmetry to Simplify Magnetic Field Modeling. Available online: https://www.comsol.fr/blogs/exploiting-symmetry-simplify-magnetic-field-modeling/ (accessed on 17 November 2022).
- PMC/PEC Boundary Conditions and Plane Wave Simulation. Available online: https://optiwave.com/optifdtd-manuals/fdtd-pmcpec-boundary-conditions-and-plane-wave-simulation/ (accessed on 17 November 2022).
- Dmitriev, V. Symmetry Principles and Group Theory in Electromagnetics. arXiv 2020, arXiv:2008.12644. [Google Scholar]
- Kritikos, H.N. Group Symmetries of Antenna Arrays. In Recent Advances in Electromagnetic Theory; Kritikos, H.N., Jaggard, D.L., Eds.; Springer: New York, NY, USA, 1990. [Google Scholar] [CrossRef]
- Sǒipusǒ, Z.; Bartolić, J.; Milin, Z. On symmetry in microstrip antenna analysis. Microw. Opt. Technol. Lett. 1994, 7, 464–466. [Google Scholar]
- Villain, J. Symétrie et théorie des groupes à travers la physique. arXiv 2009, arXiv:0906.3595. [Google Scholar]
- Xu, C.-W.; Zhu, F.; Liu, L.-N.; Niu, D.-P. Application of group theory in the problem of electromagnetic scattering of symmetry structures. Acta Phys. Sin. 2013, 62, 164102. [Google Scholar] [CrossRef]
- Hamdi, B.; Taoufik, A. Intuition and symmetries in electromagnetism: Eigen states of four antennas. Authorea Prepr. 2022. [Google Scholar] [CrossRef]
- Crouch, D. On the use of symmetry to reduce the computational requirements for FDTD analyses of finite phased arrays. Microw. Opt. Technol. Lett. 1996, 13, 123–128. [Google Scholar] [CrossRef]
- Crouch, D. Symmetry-Aided FDTD Analysis of Finite Phased Arrays. In Proceedings of the 12th Annual Review of Progress in Applied Computational Electromagnetics of the Naval Postgraduate School, Monterey, CA, USA, 18–22 March 1996; Volume I. [Google Scholar]
- George Mpantes: ‘Intuition and Symmetries in Electromagnetism’. Available online: https://www.academia.edu/40137899/Intuition_and_Symmetries_in_electromagnetism (accessed on 17 November 2022).
- Denton, R.E.; Hu, Y. Symmetry boundary conditions. J. Comput. Phys. 2009, 228, 4823–4835. [Google Scholar] [CrossRef]
- Laurent, CHUSSEAU Slides 23, 24 and 25 of Hyperfrequences-Parametres-S-Antennes. Available online: https://fr.slideshare.net/khaalidkk/37248247-courshyperfrequencesparametressantennes-1 (accessed on 17 November 2022).
- Bilel, H.; Aguili, T.; Baudrand, H. Floquet Modal Analysis to Modelize and Study 2 D Planar almost Periodic Structures in Finite and Infinite Extend with Coupled Motifs. Prog. Electromagn. Res. 2015, 62, 63–86. [Google Scholar]
- Hamdi, B.; Aguili, T. Multiscale Auxiliary Sources for Modeling Microwave Components. In Microwave Technologies; Kishk, A., Yeap, K.H., Eds.; IntechOpen: London, UK, 2022. [Google Scholar] [CrossRef]
- Tan, Z.; McDonald, K. Symmetries of Electromagnetic Fields Associated with a Plane Conducting Screen. 2012. Available online: http://kirkmcd.princeton.edu/examples/emsymmetry.pdf (accessed on 17 November 2022).
- Yao, C. Magnetism and mirror symmetry. Am. J. Phys. 1995, 63, 520–523. [Google Scholar] [CrossRef]
- Petzold, J.; Tkachenko, S.; Vick, R. Energy conserving coupling through small apertures in an infinite perfect conducting screen. Adv. Radio Sci. 2015, 13, 227–232. [Google Scholar] [CrossRef][Green Version]
- Ferrando, A.; García-March, M.Á. Symmetry in Electromagnetism. Symmetry 2020, 12, 685. [Google Scholar] [CrossRef]
- Cloete, J.H. On symmetry in engineering electromagnetics. In Proceedings of the 1998 South African Symposium on Communications and Signal Processing-COMSIG ’98 (Cat. No. 98EX214), Rondebosch, South Africa, 7–8 September 1998; pp. 379–380. [Google Scholar] [CrossRef]
- Harris, S.E. Symmetry of electromagnetism. IEE Proc.-Phys. Sci. Meas. Instrum. Manag.-Educ.-Rev. 1988, 135, 363–368. [Google Scholar] [CrossRef]
- Li, D.C.; Boone, F.; Bozzi, M.; Perregrini, L.; Wu, K. Concept of Virtual Electric/Magnetic Walls and its Realization With Artificial Magnetic Conductor Technique. IEEE Microw. Wirel. Components Lett. 2008, 18, 743–745. [Google Scholar] [CrossRef]
- Kishk, A.A.; Kildal, P.-S. Modelling of soft and hard surfaces using ideal perfect electric conducting/perfect magnetic conducting strip grids. IET Microwaves Antennas Propag. 2009, 3, 296–302. [Google Scholar] [CrossRef]
- Steer, M. Microwave and RF Design II—Transmission Lines; NC State University: Raleigh, NC, USA, 2021; Available online: https://repository.lib.ncsu.edu/handle/1840.20/36776 (accessed on 17 November 2022).
- Edelberg, S.; Oliner, A. Mutual coupling effects in large antenna arrays II: Compensation effects. Ire Trans. Antennas Propag. 1960, 8, 360–367. [Google Scholar] [CrossRef]
- Rodriguez-Pereyra, V.; Elsherbeni, A.Z.; Smith, C.E. Electromagnetic analysis of axi-symmetric structures. In Proceedings of the IEEE Southeastcon’99, Technology on the Brink of 2000 (Cat. No. 99CH36300), Lexington, KY, USA, 25–28 March 1999. [Google Scholar]
- Abdelghani, M.L. Étude et Conception d’Antennes Directives Large Bande à Base de Méta-Surfaces. Ph.D. Thesis, Université du Québec, Institut National de la Recherche Scientifique, Quebec City, QC, Canada, 2017. [Google Scholar]
- Baum, C.E.; Kritikos, H.N. Electromagnetic Symmetry (Electromagnetics Library); CRC Press: Boca Raton, FL, USA, 1995; 336p. [Google Scholar]
- Pigeon, M. Etude et Réalisation d’Antennes Ultra-Compactes à Base de Métamatériaux. Application à la Réalisation d’une Antenne GNSS Miniature. Ph.D. Thesis, Institut National Polytechnique de Toulouse INP Toulouse, Toulouse, France, 2011. [Google Scholar]
- Romier, M. Simulation Electromagnétique des Antennes Actives en Régime Non-Linéaire. Ph.D. Thesis, Institut National Polytechnique de Toulouse INP Toulouse, Toulouse, France, 2008. [Google Scholar]
- Solid Works Express, Tech Tips: ‘How to Use Symmetry and Anti-Symmetry Boundary Conditions’. Available online: https://www.clear.rice.edu/mech403/HelpFiles/CW_sym_anti-symmetry_BC.pdf (accessed on 17 November 2022).




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilel, H.; Taoufik, A. Intuition and Symmetries in Electromagnetism: Eigenstates of Four Antennas. Appl. Sci. 2022, 12, 12049. https://doi.org/10.3390/app122312049
Bilel H, Taoufik A. Intuition and Symmetries in Electromagnetism: Eigenstates of Four Antennas. Applied Sciences. 2022; 12(23):12049. https://doi.org/10.3390/app122312049
Chicago/Turabian StyleBilel, Hamdi, and Aguili Taoufik. 2022. "Intuition and Symmetries in Electromagnetism: Eigenstates of Four Antennas" Applied Sciences 12, no. 23: 12049. https://doi.org/10.3390/app122312049
APA StyleBilel, H., & Taoufik, A. (2022). Intuition and Symmetries in Electromagnetism: Eigenstates of Four Antennas. Applied Sciences, 12(23), 12049. https://doi.org/10.3390/app122312049





