Gray Image Denoising Based on Array Stochastic Resonance and Improved Whale Optimization Algorithm
Abstract
:1. Introduction
2. Array Stochastic Resonance Principle
2.1. Bistable Stochastic Resonance
2.2. Array Stochastic Resonance Theory
3. Improved Whale Optimization Algorithm
3.1. Whale Optimization Algorithm
3.2. Improve Whale Optimization Algorithm
3.2.1. Iterative Map Initialization
3.2.2. Nonlinear Convergence Factor and Variable Weight
3.2.3. Random Learning Strategy
3.2.4. Cauchy Mutation Strategy
4. Array Stochastic Resonance Strategy Based on Improved Whale Optimization Algorithm
4.1. Image Denoising Method by Array Stochastic Resonance
4.1.1. Image Dimension Reduction Coding
4.1.2. Modulation
4.1.3. Array Saturation Stochastic Resonance Process
4.1.4. Demodulation
4.2. Array Stochastic Resonance Strategy Based on Improved Whale Optimization Algorithm
4.3. Parameter Analysis of Improved Whale Optimization Algorithm
5. Image Denoising Based on Array Stochastic Resonance and Improved Whale Optimization Algorithm
5.1. Lena Image
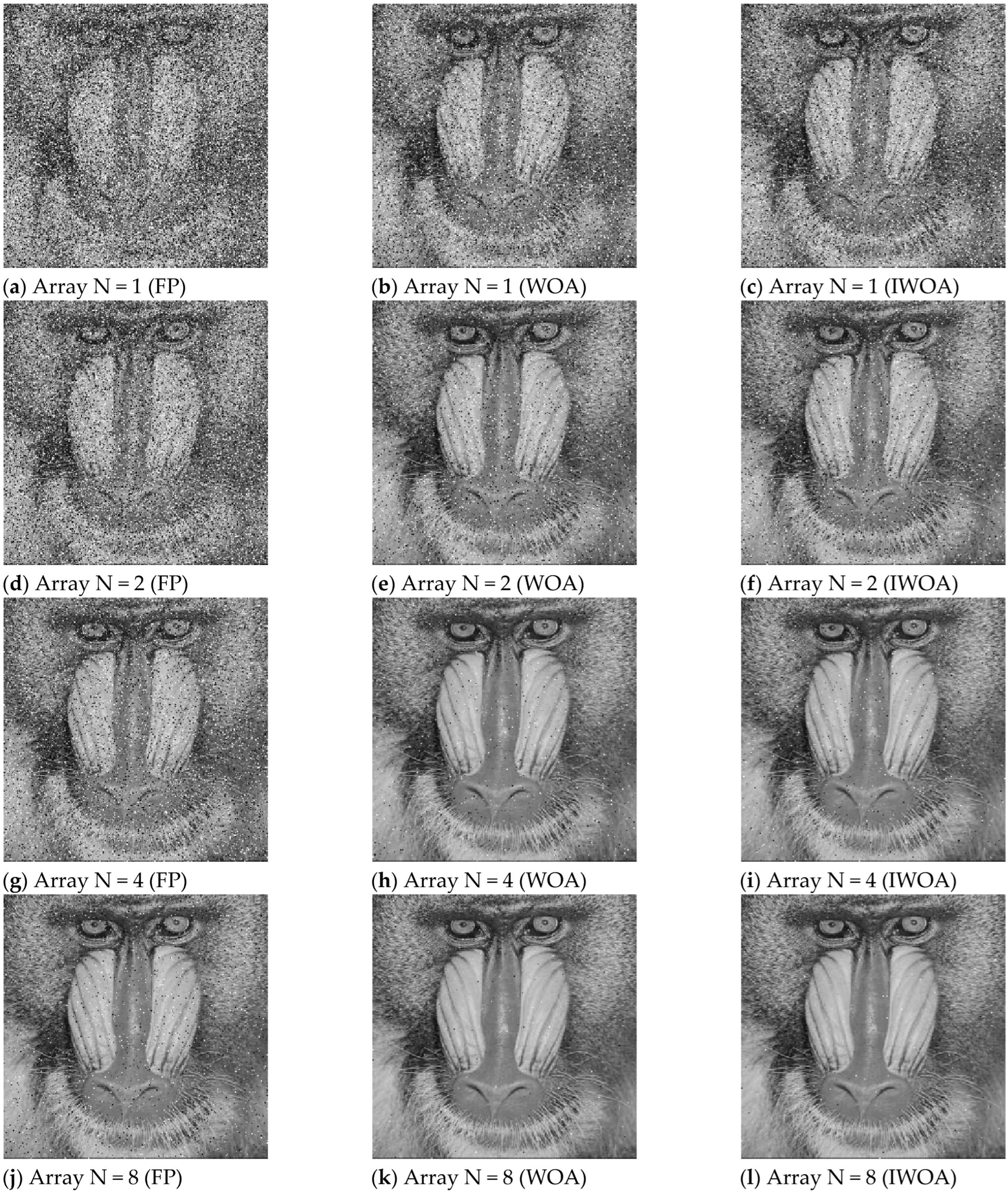
5.2. Baboon Image
5.3. Magnetic Resonance Imaging Image
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xue, H.Z.; Cui, H.W. Research on image restoration algorithms based on BP neural network. J. Vis. Commun. Image Represent. 2019, 59, 204–209. [Google Scholar] [CrossRef]
- Dastres, R.; Soori, M. Advanced Image Processing Systems. Int. J. Imaging Robot. 2021, 21, 27–44. [Google Scholar]
- Gong, S.; Kumar, R.; Kumutha, D. Design of Lighting Intelligent Control System Based on OpenCV Image Processing Technology. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2021, 29, 119–139. [Google Scholar] [CrossRef]
- John, A.; Christian, E.; Glenn, L. Onboard Image-Processing Algorithm for a Spacecraft Optical Navigation Sensor System. J. Spacecr. Rocket. 2012, 49, 337–352. [Google Scholar]
- Chandrasekhar, S.; Laxminarayana, G.; Chakrapani, Y. Novel Hybrid Segmentation Techniques for Cardiac Image Processing in Remote Health Care Monitoring Systems. J. Med. Imaging Health Inform. 2017, 7, 1153–1159. [Google Scholar] [CrossRef]
- Ma, L. Research on distance education image correction based on digital image processing technology. EURASIP J. Image Video Process. 2019, 2019, 18. [Google Scholar] [CrossRef] [Green Version]
- Arsenault, H.H.; Denis, M. Image processing in signal-dependent noise. Can. J. Phys. 1983, 61, 309–317. [Google Scholar] [CrossRef]
- Govinda, D.; Narayanankuttya, K.A.; Govinda, D. Image denoising using total variation wavelet galerkin method. Procedia Comput. Sci. 2018, 143, 481–492. [Google Scholar]
- Archana, K.S.; Sahayadhas, A. Comparison of various filters for noise removal in paddy leaf images. Int. J. Eng. Technol. 2018, 7, 372. [Google Scholar] [CrossRef] [Green Version]
- Awang, N.; Fauadi, M.H.F.M.; Noor, A.Z.M.; Idris, S.A.; Rosli, N.S. An improved image filtering method for weld bead inspection using Unsharp masking technique. J. Adv. Manuf. Technol. 2018, 12, 341–354. [Google Scholar]
- Xu, B.; Jiang, Z.-P.; Wu, X.; Repperger, D.W. Theoretical analysis of image processing using parameter-tuning stochastic resonance technique. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007. [Google Scholar]
- Yang, Y.B.; Jiang, Z.P.; Xu, B.H.; Daniel, W.R. An investigation of two-dimensional parameter-induced stochastic resonance and applications in nonlinear image processing. J. Phys. A Math. Theor. 2009, 42, 145207. [Google Scholar] [CrossRef]
- Benzi, R.; Parisi, G.; Vulpiani, S.A. A Theory of Stochastic Resonance in Climatic Change. SIAM J. Appl. Math. 1983, 43, 565–578. [Google Scholar] [CrossRef]
- Ye, Q.H.; Huang, H.N.; He, X.Y.; Zhang, C. A SR based radon transform to extra weak lines from noise images. In Proceedings of the 2003 International Conference on Image Processing, Barcelona, Spain, 14–17 September 2003; Volume 1, pp. 849–852. [Google Scholar]
- Liu, J.; Li, Z. Binary image enhancement based on aperiodic stochastic resonance. Image Process. Iet 2015, 9, 1033–1038. [Google Scholar] [CrossRef]
- Liu, J.; Hu, B.; Wang, Y.G. Optimum adaptive array stochastic resonance in noisy grayscale image restoration. Phys. Lett. A 2019, 383, 1457–1465. [Google Scholar] [CrossRef]
- Wu, C.Y.; Wu, C.J. Recovery and enhancement of unknown aperiodic binary signal by adaptive aperiodic stochastic resonance. Pramana 2021, 95, 36. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Yang, X.S.; Alavi, A.H. A novel improved accelerated particle swarm optimization algorithm for global numerical optimization. Eng. Comput. 2014, 31, 1198–1220. [Google Scholar] [CrossRef]
- Gao, K.P.; Xu, X.X.; Li, J.B.; Jiao, S.J.; Shi, N. Research on feature enhancement method of weak fault signal of rotating machinery based on adaptive stochastic resonance. J. Mech. Sci. Technol. 2022, 36, 553–563. [Google Scholar] [CrossRef]
- Chi, K.; Kang, J.S.; Tong, R.; Zhang, X.H. An adaptive stochastic resonance method based on multi-agent cuckoo search algorithm for bearing fault detection. J. Vibroengineering 2019, 21, 1296–1307. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, H.; Guo, J.; Zhu, L.; Lv, S. Research on mud pulse signal detection based on adaptive stochastic resonance. J. Pet. Sci. Eng. 2017, 157, 643–650. [Google Scholar] [CrossRef]
- Paniri, M.; Dowlatshahi, M.B.; Nezamabadi-pour, H. Ant-TD: Ant colony optimization plus temporal difference reinforcement learning for multi-label feature selection. Swarm Evol. Comput. 2021, 64, 100892. [Google Scholar] [CrossRef]
- Paniri, M.; Dowlatshahi, M.B.; Nezamabadi-pour, H. MLACO: A multi-label feature selection algorithm based on ant colony optimization. Knowl.-Based Syst. 2020, 192, 105285. [Google Scholar] [CrossRef]
- Liu, P.H.; Liu, J. Multi-leader PSO (MLPSO): A new PSO variant for solving global optimization problems. Appl. Soft Comput. 2017, 61, 256–263. [Google Scholar] [CrossRef]
- Dowlatshahi, M.B.; Nezamabadi-pour, H. GGSA: A Grouping Gravitational Search Algorithm for data clustering. Eng. Appl. Artif. Intell. 2014, 36, 114–121. [Google Scholar] [CrossRef]
- Serkan, D. A Novel Approach Based on Average Swarm Intelligence to Improve the Whale Optimization Algorithm. Arab. J. Sci. Eng. 2022, 47, 1763–1776. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, G.; Jiao, S.; Wang, J. Bearing Fault Diagnosis Based on Stochastic Resonance and Improved Whale Optimization Algorithm. Electronics 2022, 11, 2185. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–287. [Google Scholar] [CrossRef]
- Leng, Y.G. Mechanism of parameter-adjusted stochastic resonance based on Kramers rate. Acta Phys. Sin. 2009, 58, 5196–5200. [Google Scholar] [CrossRef]
- Duan, F.; Chapeau, B.F.; Abbottt, D. Noise enhanced SNR gain in parallel array of bistable oscillators. Electron. Lett. 2006, 42, 1008–1009. [Google Scholar] [CrossRef] [Green Version]
- Watkins, W.A.; Schevill, W.E. Aerial Observation of Feeding Behavior in Four Baleen Whales: Eubalaena glacialis, Balaenoptera borealis, Megaptera novaeangliae, and Balaenoptera physalus. J. Mammal. 1979, 60, 155–163. [Google Scholar] [CrossRef]
- Mehne, H.H.; Mirjalili, S. A parallel numerical method for solving optimal control problems based on whale optimization algorithm. Knowl.-Based Syst. 2018, 151, 114–123. [Google Scholar] [CrossRef]
- Bi, X.J.; Li, Y.; Chen, C.Y. A self-adaptive teaching-and-learning-based optimization algorithm with a mixed strategy. J. Harbin Eng. Univ. 2016, 37, 842–848. [Google Scholar]
- He, Q.; Lin, J.; Xu, H. Hybrid Cauchy Mutation and Uniform Distribution of Grasshopper Optimization Algorithm. Control. Decis. 2021, 36, 1558–1568. [Google Scholar]
- Wang, S.; Xu, X.-S. A New Algorithm of Hilbert Scanning Matrix and its MATLAB Program. J. Image Graph. 2006, 11, 119–122. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Processing Using Matlabtm. Digit. Image Process. Using Matlab. 2004, 21, 197–199. [Google Scholar]
- Zhao, J.; Ma, Y.; Pan, Z.; Zhang, H. Research on Image Signal Identification Based on Adaptive Array Stochastic Resonance. Syst. Sci. Complex. 2022, 35, 179–193. [Google Scholar] [CrossRef]









| Image Name | Size | Noisy Image | Mean | Median | Wiener | Gaussian |
|---|---|---|---|---|---|---|
| Lena | 256 × 256 | 8.7167 | 16.6138 | 13.3217 | 15.9101 | 16.6173 |
| Array Unit N = 1 | Array Unit N = 2 | Array Unit N = 4 | Array Unit N = 8 | |
|---|---|---|---|---|
| Fixed parameters | PSNR = 12.0409 a = 0.5; b = 1.5; h = 0.12 | PSNR = 13.7994 a = 0.5; b = 1.5; h = 0.12 | PSNR = 17.0191 a = 0.5; b = 1.5; h = 0.12 | PSNR = 22.9659 a = 0.5; b = 1.5; h = 0.12 |
| WOA optimization | PSNR = 15.5079 a = 0.53; b = 0.64; h = 0.06 | PSNR = 19.607 a = 0.5; b = 3.14; h = 0.03 | PSNR = 26.7732 a = 0.5; b = 0.86; h = 0.06 | PSNR = 40.5919 a = 0.5; b = 1.05; h = 0.06 |
| IWOA optimization | PSNR = 15.5679 a = 0.5; b = 1.21; h = 0.05 | PSNR = 26.4684 a = 0.57; b = 0.48; h = 0.08 | PSNR = 26.9934 a = 0.52; b = 1.17; h = 0.05 | PSNR = 41.1433 a = 0.5; b = 0.67; h = 0.07 |
| Image Name | Size | Noisy Image | Mean | Median | Wiener | Gaussian |
|---|---|---|---|---|---|---|
| Baboon | 256×256 | 8.6783 | 16.5892 | 12.9568 | 15.9909 | 16.6008 |
| Array Unit N = 1 | Array Unit N = 2 | Array Unit N = 4 | Array Unit N = 8 | |
|---|---|---|---|---|
| Fixed parameters | PSNR = 12.2744 a = 0.5; b = 1.5; h = 0.12 | PSNR = 13.9195 a = 0.5; b = 1.5; h = 0.12 | PSNR = 16.9321 a = 0.5; b = 1.5; h = 0.12 | PSNR = 22.9212 a = 0.5; b = 1.5; h = 0.12 |
| WOA optimization | PSNR = 15.3704 a = 0.5; b = 0.12; h = 0.12 | PSNR = 19.3184 a = 0.58; b = 0.80; h = 0.06 | PSNR = 25.926 a = 0.51; b = 0.19; h = 0.11 | PSNR = 41.6294 a = 0.5; b = 5.00; h = 0.03 |
| IWOA optimization | PSNR = 15.5307 a = 0.5; b = 1.37; h = 0.04 | PSNR = 19.4159 a = 0.61; b = 3.23; h = 0.03 | PSNR = 26.9586 a = 0.5; b = 4.88; h = 0.03 | PSNR = 41.6387 a = 0.51; b = 1.25; h = 0.05 |
| Image Name | Size | Noisy Image | Mean | Median | Wiener | Gaussian |
|---|---|---|---|---|---|---|
| Brain | 256 × 256 | 8.6885 | 15.6739 | 14.1595 | 14.9413 | 15.6747 |
| Array Unit N = 1 | Array Unit N = 2 | Array Unit N = 4 | Array Unit N = 8 | |
|---|---|---|---|---|
| Fixed parameters | PSNR = 11.5700 a = 0.5; b = 1.5; h = 0.12 | PSNR = 13.4826 a = 0.5; b = 1.5; h = 0.12 | PSNR = 16.7897 a = 0.5; b = 1.5; h = 0.12 | PSNR = 22.9187 a = 0.5; b = 1.5; h = 0.12 |
| WOA optimization | PSNR = 15.4988 a = 0.5; b = 0.99; h = 0.05 | PSNR = 19.6323 a = 0.5; b = 2.47; h = 0.03 | PSNR = 26.6149 a = 0.5; b = 0.31; h = 0.09 | PSNR = 41.1891 a = 0.5; b = 0.69; h = 0.07 |
| IWOA optimization | PSNR = 15.5083 a = 0.51; b = 0.60; h = 0.06 | PSNR = 19.6695 a = 0.5; b = 1.59; h = 0.04 | PSNR = 26.6260 a = 0.57; b = 0.49; h = 0.08 | PSNR = 42.3748 a = 0.64; b = 3.32;h = 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Zhang, G.; Jiao, S.; Wang, J. Gray Image Denoising Based on Array Stochastic Resonance and Improved Whale Optimization Algorithm. Appl. Sci. 2022, 12, 12084. https://doi.org/10.3390/app122312084
Huang W, Zhang G, Jiao S, Wang J. Gray Image Denoising Based on Array Stochastic Resonance and Improved Whale Optimization Algorithm. Applied Sciences. 2022; 12(23):12084. https://doi.org/10.3390/app122312084
Chicago/Turabian StyleHuang, Weichao, Ganggang Zhang, Shangbin Jiao, and Jing Wang. 2022. "Gray Image Denoising Based on Array Stochastic Resonance and Improved Whale Optimization Algorithm" Applied Sciences 12, no. 23: 12084. https://doi.org/10.3390/app122312084
APA StyleHuang, W., Zhang, G., Jiao, S., & Wang, J. (2022). Gray Image Denoising Based on Array Stochastic Resonance and Improved Whale Optimization Algorithm. Applied Sciences, 12(23), 12084. https://doi.org/10.3390/app122312084






