Autonomous Navigation Based on the Earth-Shadow Observation near the Sun–Earth L2 Point
Abstract
:1. Introduction
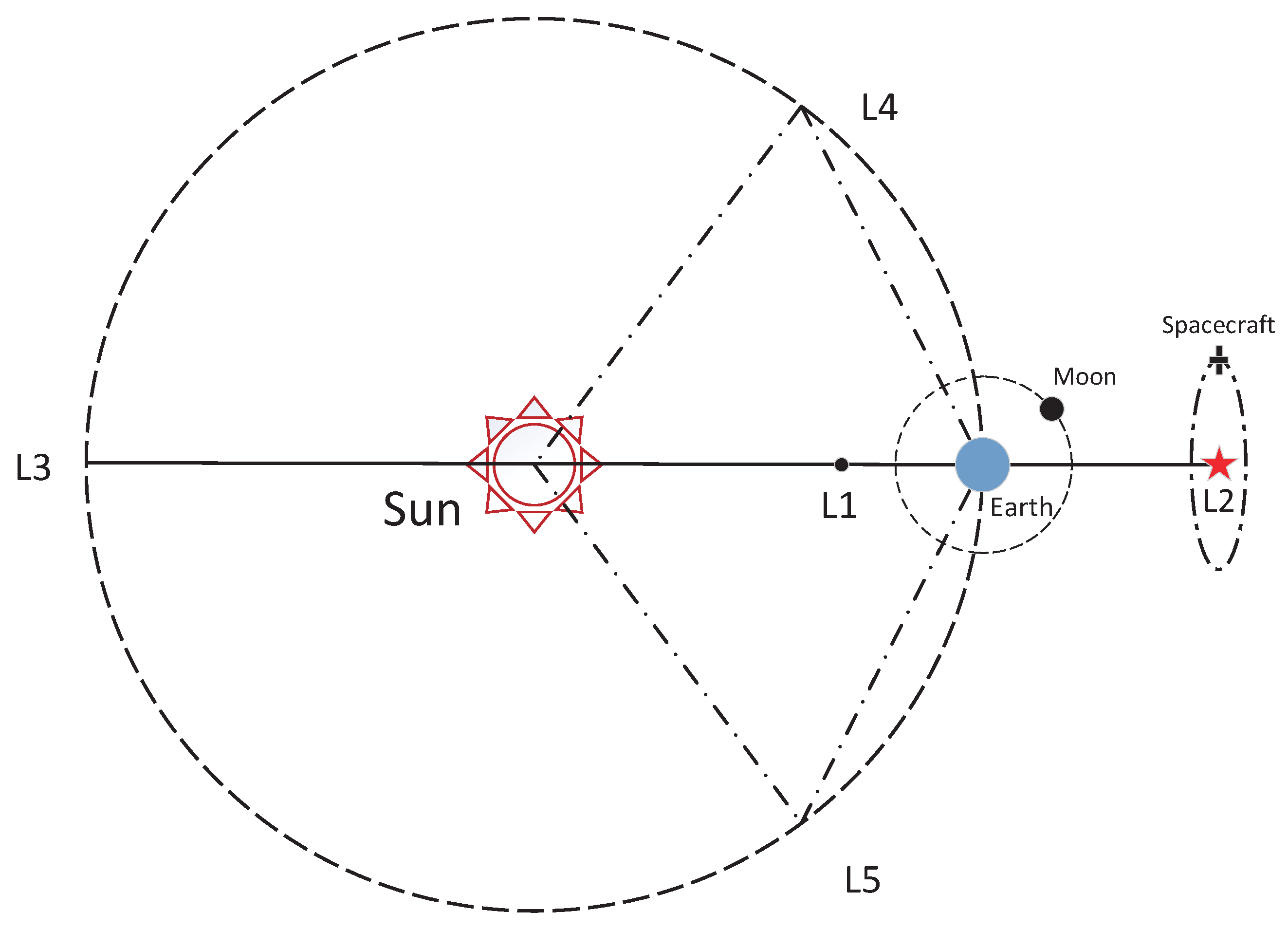
2. Design of Navigation System
2.1. Circular Restricted Three-Body Problem
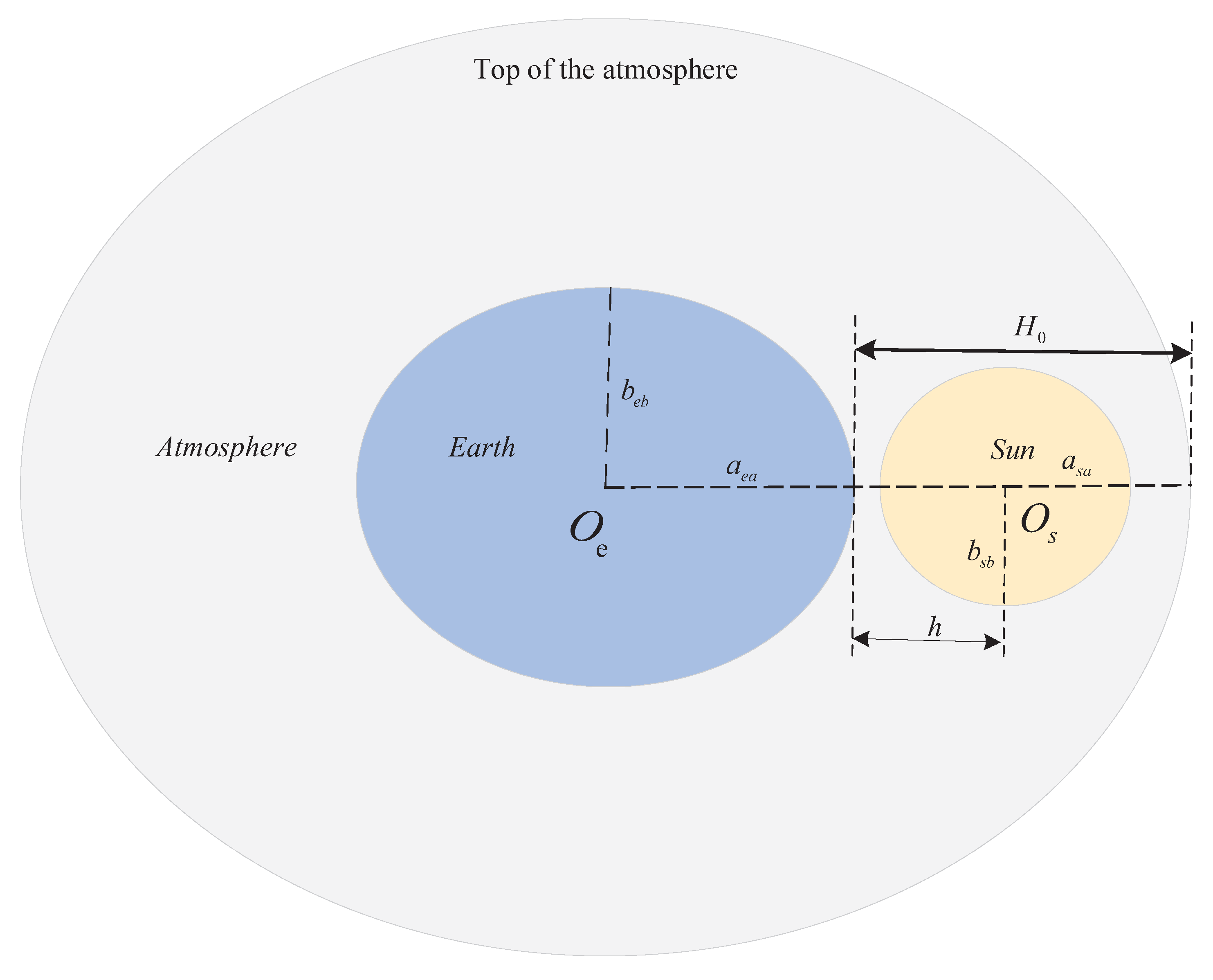
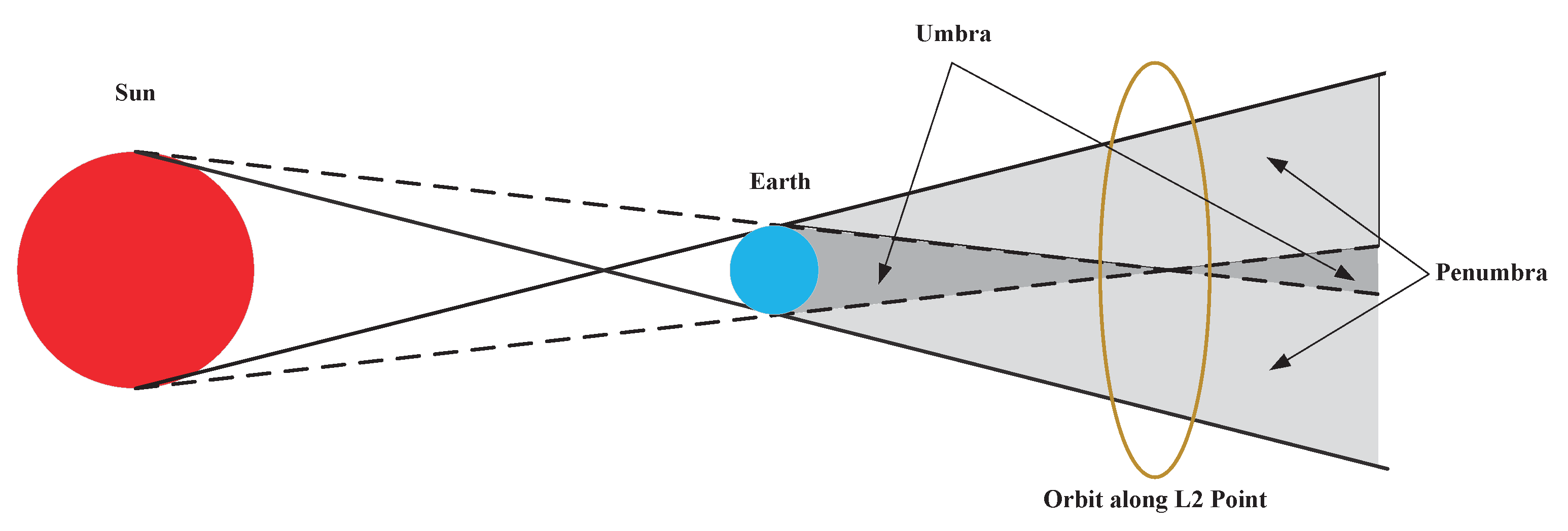
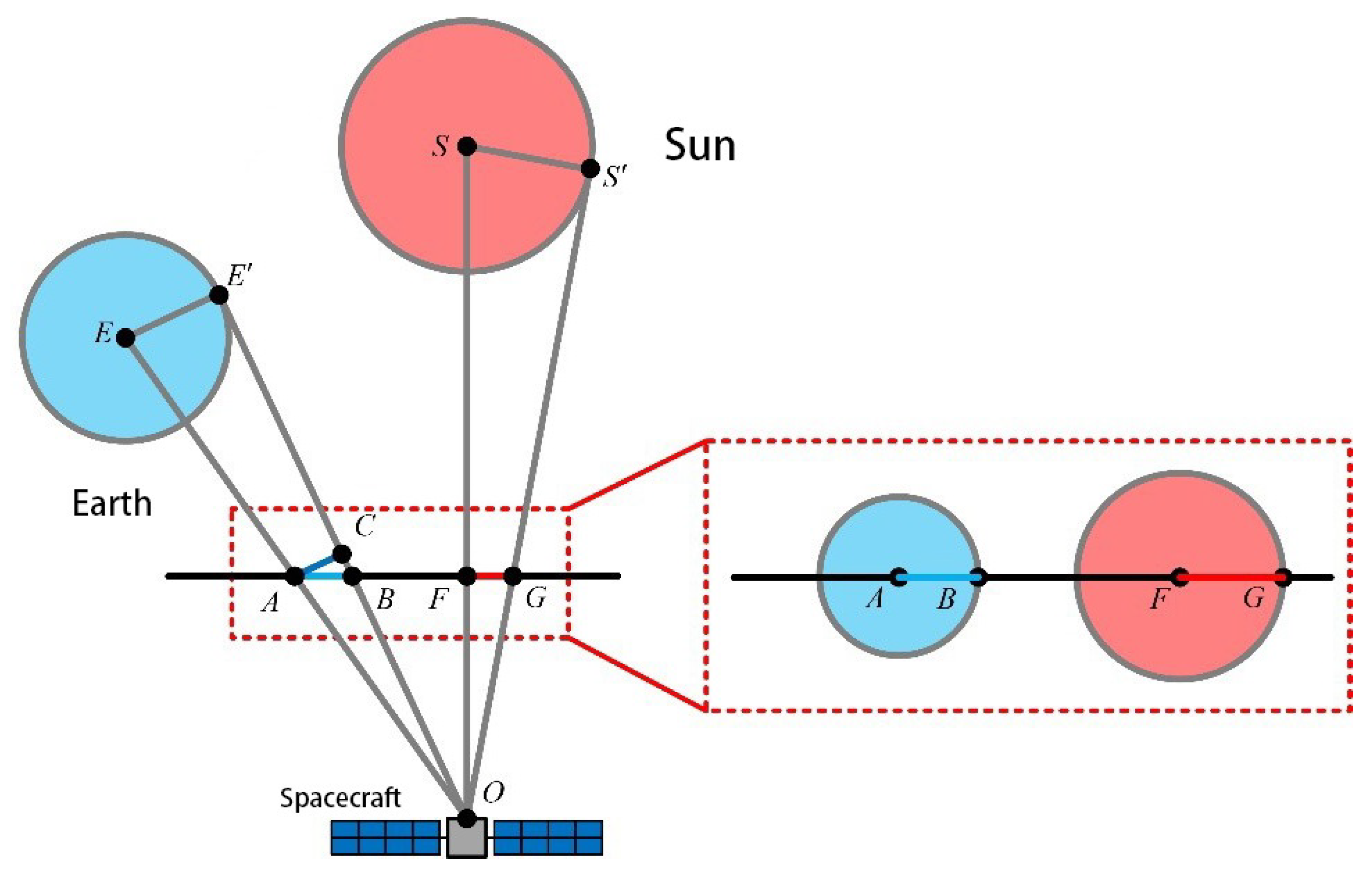
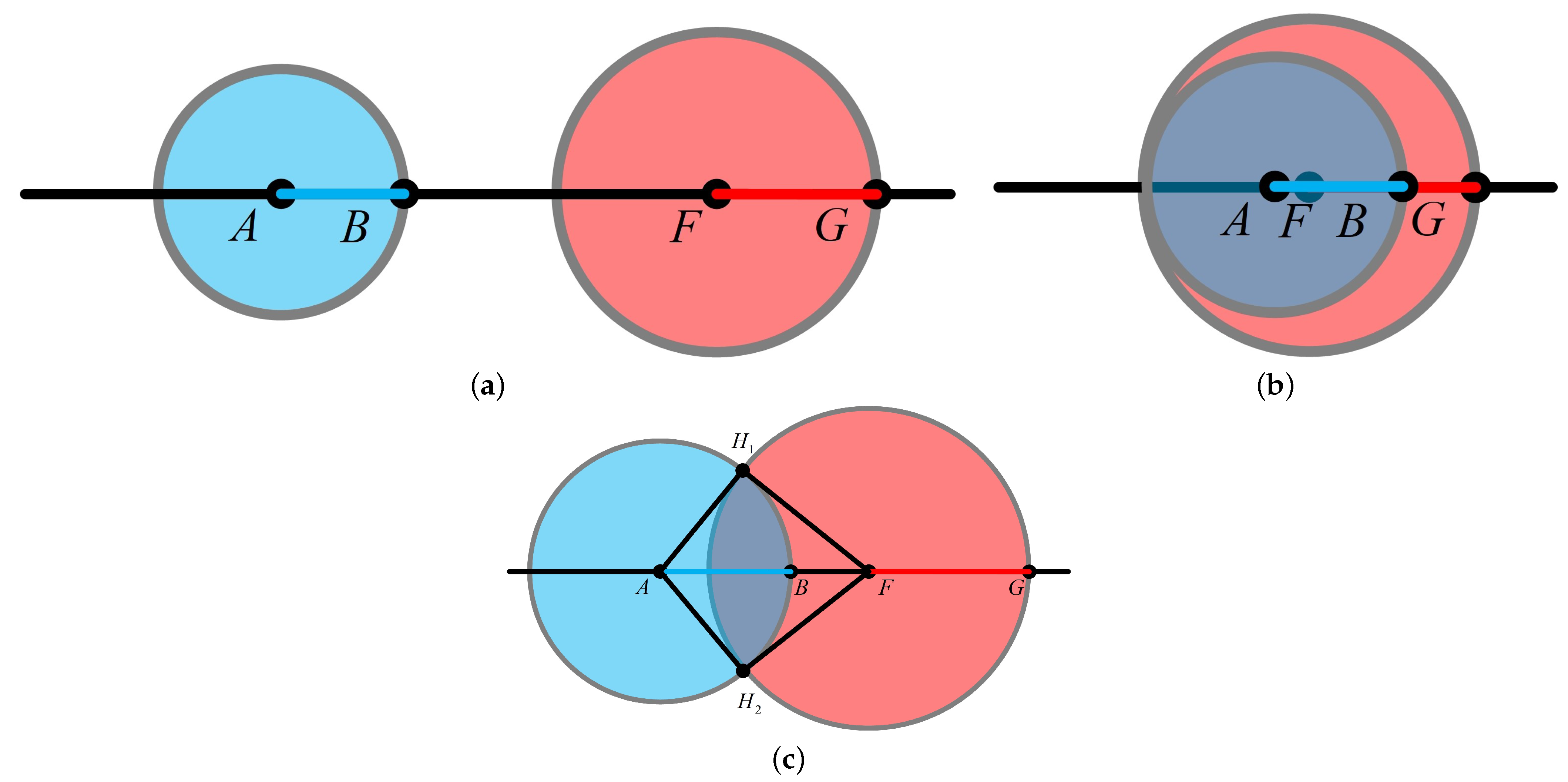
2.2. The Earth-Shadow Measurement Model
3. Design of the Navigation Filter Algorithm
3.1. Fifth-Order Spherical–Radial Rule
3.2. Fifth-Degree Cubature Kalman Filter
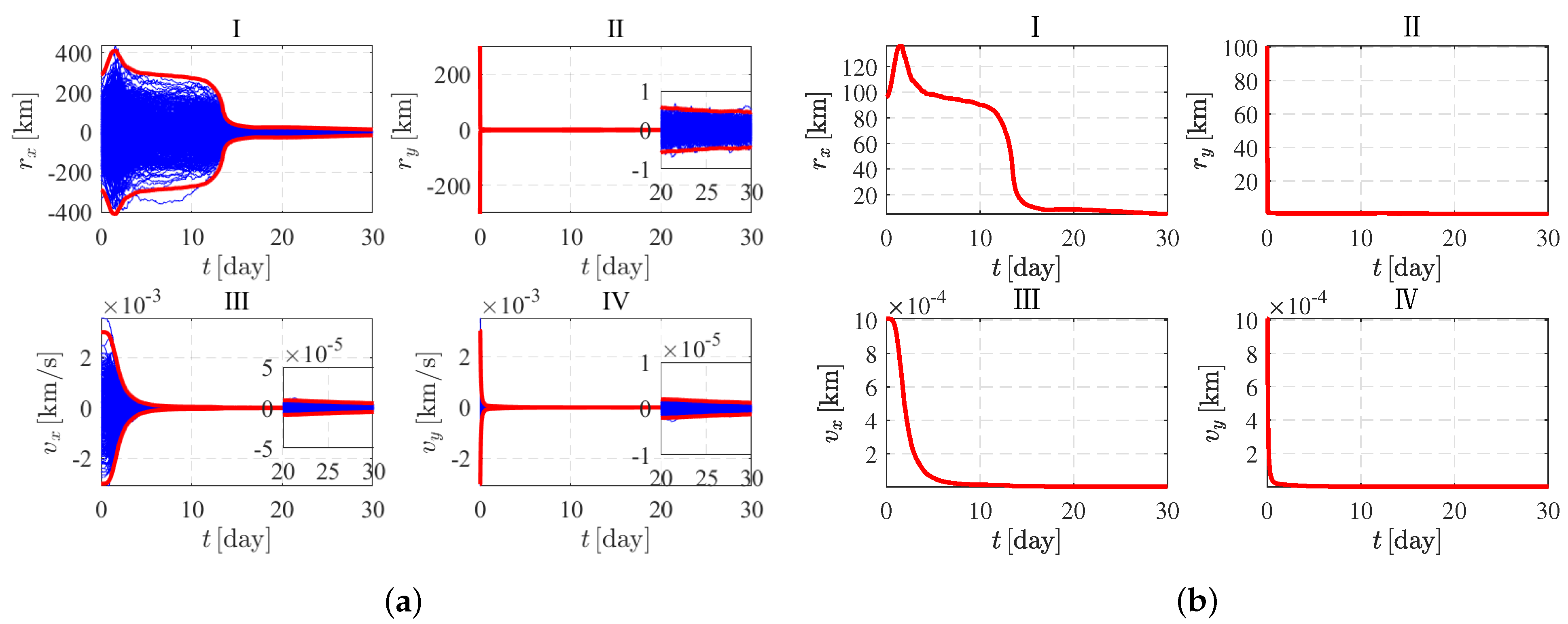
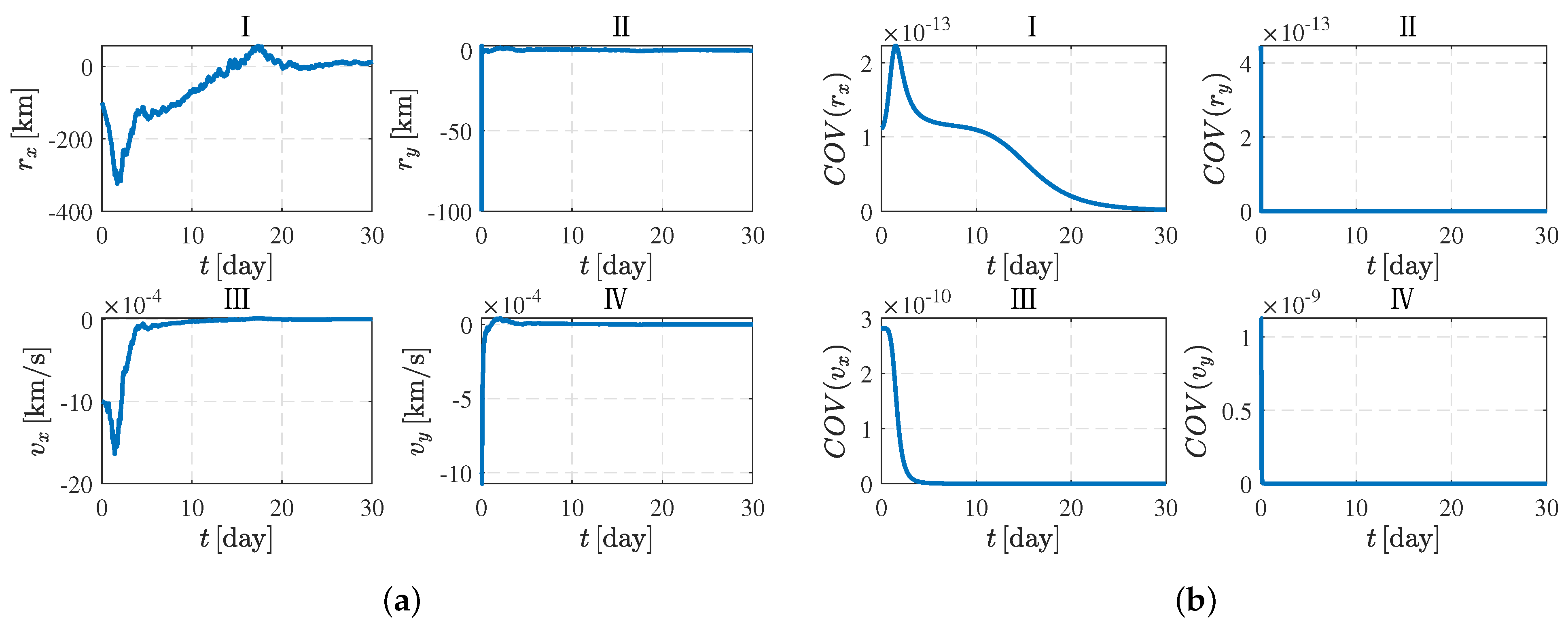
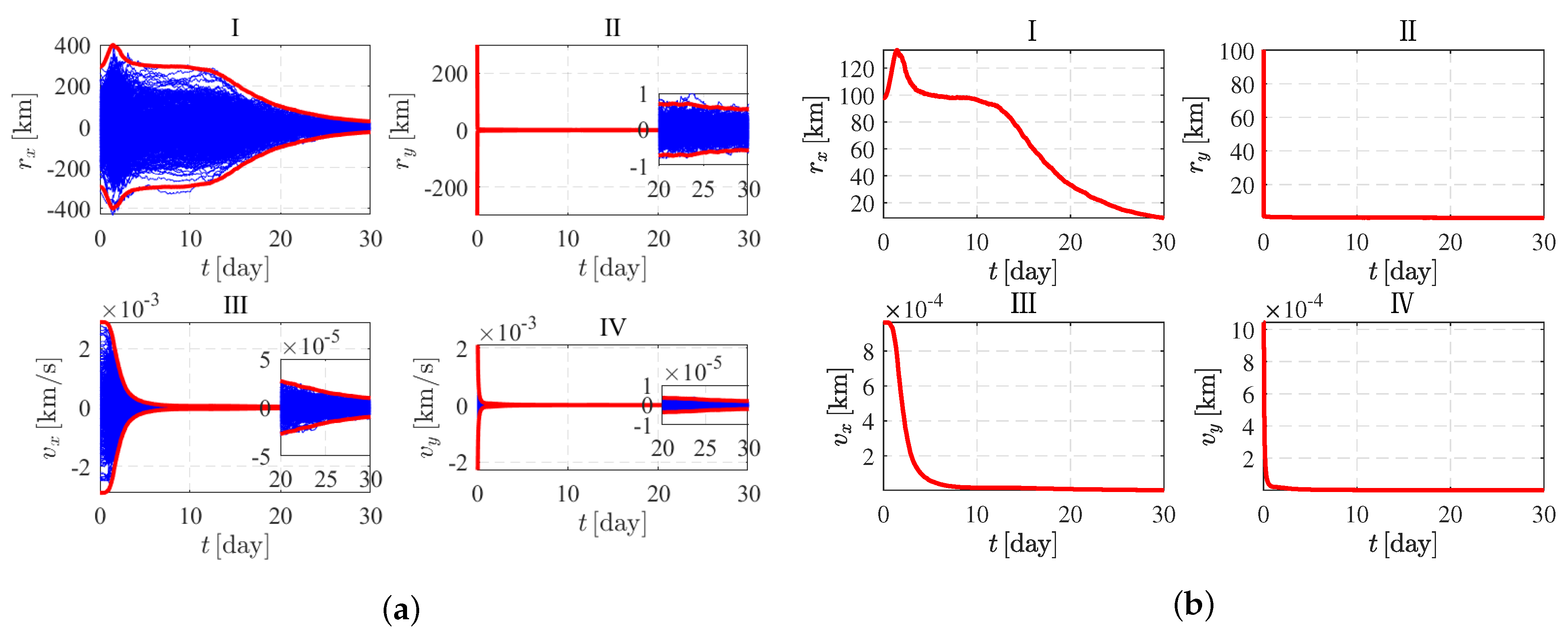
4. Simulation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Zuo, W.; Wen, W.; Zeng, X.; Gao, X.; Liu, Y.; Fu, Q.; Zhang, Z.; Su, Y.; Ren, X.; et al. Overview of the Chang’e-4 mission: Opening the frontier of scientific exploration of the lunar far side. Space Sci. Rev. 2021, 217, 1–32. [Google Scholar] [CrossRef]
- Wozniakiewicz, P.J.; Bridges, J.; Burchell, M.J.; Carey, W.; Carpenter, J.; Della Corte, V.; Dignam, A.; Genge, M.J.; Hicks, L.; Hilchenbach, M.; et al. A cosmic dust detection suite for the deep space Gateway. Adv. Space Res. 2021, 68, 85–104. [Google Scholar] [CrossRef]
- Cui, P.; Qin, T.; Zhu, S.; Liu, Y.; Xu, R.; Yu, Z. Trajectory curvature guidance for Mars landings in hazardous terrains. Automatica 2018, 93, 161–171. [Google Scholar] [CrossRef]
- Qin, T.; Zhu, S.; Cui, P.; Luan, E. Divert capability analysis and subsequent guidance design for mars landing. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MN, USA, 4–11 March 2018; pp. 1–15. [Google Scholar]
- Beckman, M. Orbit determination issues for libration point orbits. In Libration Point Orbits and Applications; World Scientific: Singapore, 2003; pp. 1–17. [Google Scholar]
- Cao, J.; Hu, S.; Huang, Y.; Liu, L. Orbit determination and analysis for chang’E-2 extended mission. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 1339–1343. [Google Scholar]
- Bobrinksy, N.; Maldari, P.; Schulz, K.J.; Sessler, G.; Mascaraque, Í. ESA’s Space Communication Architecture and Ground Station Evolution. In Proceedings of the SpaceOps 2008 Conference, Heidelberg, Germany, 12–16 May 2008; p. 3237. [Google Scholar]
- Barriot, J.; Serafini, J.; Sichoix, L. Calibration of the KA Band Tracking of the Bepi-Colombo Spacecraft (more Experiment). In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 9–13 December 2013; Volume 2013, p. P13A-1743. [Google Scholar]
- Huang, Y.; Li, P.; Fan, M. Orbit determination of CE-5T1 in Earth-Moon L2 libration point orbit with ground tracking data. 42nd COSPAR Sci. Assem. 2018, 42, B3-1. [Google Scholar] [CrossRef]
- Li, X.; Sanyal, A.K.; Warier, R.R.; Qiao, D. Landing of Hopping Rovers on Irregularly-shaped Small Bodies Using Attitude Control. Adv. Space Res. 2020, 65, 2674–2691. [Google Scholar] [CrossRef]
- Li, X.; Qiao, D.; Barucci, M. Analysis of equilibria in the doubly synchronous binary asteroid systems concerned with non-spherical shape. Astrodynamics 2018, 2, 133–146. [Google Scholar] [CrossRef]
- Zhou, X.; Cheng, Y.; Qiao, D.; Huo, Z. An adaptive surrogate model-based fast planning for swarm safe migration along halo orbit. Acta Astronaut. 2022, 194, 309–322. [Google Scholar] [CrossRef]
- Qin, T.; Zhu, S.; Cui, P.; Gao, A. An innovative navigation scheme of powered descent phase for Mars pinpoint landing. Adv. Space Res. 2014, 54, 1888–1900. [Google Scholar] [CrossRef]
- Luo, Y.; Qin, T.; Zhou, X. Observability Analysis and Improvement Approach for Cooperative Optical Orbit Determination. Aerospace 2022, 9, 166. [Google Scholar] [CrossRef]
- Zhou, X.; Qin, T.; Meng, L. Maneuvering Spacecraft Orbit Determination Using Polynomial Representation. Aerospace 2022, 9, 257. [Google Scholar] [CrossRef]
- Vasile, M.; Sironi, F.; Bernelli-Zazzera, F. Deep space autonomous orbit determination using CCD. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4818. [Google Scholar]
- Yim, J.R.; Crassidis, J.L.; Junkins, J.L. Autonomous orbit navigation of two spacecraft system using relative line of sight vector measurements. In Proceedings of the AAS Space Flight Mechanics Meeting, Maui, HI, USA, 8–12 February 2004. [Google Scholar]
- Chang, W.; Gan, Q.; Zhang, J.; Lu, B.; Ma, J. An orbit determination method using space-based angle measured data. Acta Astron. Sin. 2008, 49, 81–92. [Google Scholar]
- Zhang, J.; Cai, W.; Sun, C. Monocular vision-based relative motion parameter estimation for non-cooperative objects in space. Aerosp. Control Appl. 2010, 36, 31–35. [Google Scholar]
- Liu, G. Research on Non-Cooperative Target Tracking Algorithms and Related Technologies Using Space-Based Bearings-Only Measurements, Graduate School of National University of defence Technology; Graduate School of National University of Defense Technology: Singapore, 2011; pp. 26–30. [Google Scholar]
- Lu, R. Study on Autonomous Optical Navigation Technology for Deep Space Probe; Graduate School of Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2013. [Google Scholar]
- Wang, Y.; Zhang, Y.; Qiao, D.; Mao, Q.; Jiang, J. Transfer to near-Earth asteroids from a lunar orbit via Earth flyby and direct escaping trajectories. Acta Astronaut. 2017, 133, 177–184. [Google Scholar] [CrossRef]
- Cui, P.; Qiao, D.; Cui, H.; Luan, E. Target selection and transfer trajectories design for exploring asteroid mission. Sci. China Technol. Sci. 2010, 53, 1150–1158. [Google Scholar] [CrossRef]
- Silvestrini, S.; Piccinin, M.; Zanotti, G.; Brandonisio, A.; Lunghi, P.; Lavagna, M. Implicit Extended Kalman Filter for Optical Terrain Relative Navigation Using Delayed Measurements. Aerospace 2022, 9, 503. [Google Scholar] [CrossRef]
- Chen, J.; Jiao, W.; Ma, J.; Song, X. Autonav of navigation satellite constellation based on crosslink range and orientation parameters constraining. Geomat. Inf. Sci. Wuhan Univ. 2005, 30, 439–443. [Google Scholar]
- Li, X.; Qiao, D.; Li, P. Frozen orbit design and maintenance with an application to small body exploration. Aerosp. Sci. Technol. 2019, 92, 170–180. [Google Scholar] [CrossRef]
- Channumsin, S.; Jaturutd, S. Analysis of coupled attitude and orbit dynamics for uncontrolled re-entry satellite. In Proceedings of the 2019 7th International Electrical Engineering Congress (iEECON), Cha-am, Thailand, 6–8 March 2019; pp. 1–4. [Google Scholar]
- Li, X.; Warier, R.R.; Sanyal, A.K.; Qiao, D. Trajectory tracking near small bodies using only attitude control. J. Guid. Control. Dyn. 2019, 42, 109–122. [Google Scholar] [CrossRef]
- Tang, C.; Hu, X.; Zhou, S.; Liu, L.; Pan, J.; Chen, L.; Guo, R.; Zhu, L.; Hu, G.; Li, X.; et al. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with inter-satellite link measurements. J. Geod. 2018, 92, 1155–1169. [Google Scholar] [CrossRef]
- Wang, Y.; Qiao, D.; Cui, P. Design of optimal impulse transfers from the Sun–Earth libration point to asteroid. Adv. Space Res. 2015, 56, 176–186. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, X.; Guo, L. An autonomous navigation study of Walker constellation based on reference satellite and inter-satellite distance measurement. In Proceedings of the 2014 IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014; pp. 2553–2557. [Google Scholar]
- Qin, T.; Qiao, D.; Macdonald, M. Relative orbit determination using only intersatellite range measurements. J. Guid. Control. Dyn. 2019, 42, 703–710. [Google Scholar] [CrossRef]
- Edery, A. Earth Shadows and the SEV Angle of MAP’s Lissajous Orbit at L2. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4428. [Google Scholar]
- Adhya, S.; Sibthorpe, A.; Ziebart, M.; Cross, P. Oblate earth eclipse state algorithm for low-earth-orbiting satellites. J. Spacecr. Rocket. 2004, 41, 157–159. [Google Scholar] [CrossRef]
- Qiao, D.; Cui, P.; Cui, H. Proposal for a multiple-asteroid-flyby mission with sample return. Adv. Space Res. 2012, 50, 327–333. [Google Scholar] [CrossRef]
- Soto, G.; Savransky, D.; Gustafson, E.; Shapiro, J.; Keithly, D.; Della Santina, C. Navigation and Orbit Phasing of Modular Spacecraft for Segmented Telescope Assembly about Sun-Earth L2. In Proceedings of the American Astronomical Society Meeting Abstracts# 233, Seattle, WA, USA, 6–10 January; Volume 233, p. 157.20.
- Wang, Y.M.; Qiao, D.; Cui, P.Y. Design of low-energy transfer from lunar orbit to asteroid in the Sun-Earth-Moon system. Acta Mech. Sin. 2014, 30, 966–972. [Google Scholar] [CrossRef]
- Canalias, E.; Gomez, G.; Marcote, M.; Masdemont, J. Assessment of Mission Design Including Utilization of Libration Points and Weak Stability Boundaries; ESA Advanced Concept Team: Noordwijk, The Netherlands, 2004. [Google Scholar]
- Farquhar, R.W.; Dunham, D.W.; Guo, Y.; McAdams, J.V. Utilization of libration points for human exploration in the Sun–Earth–Moon system and beyond. Acta Astronaut. 2004, 55, 687–700. [Google Scholar] [CrossRef]
- Zhang, R.; Tu, R.; Zhang, P.; Liu, J.; Lu, X. Study of satellite shadow function model considering the overlapping parts of Earth shadow and Moon shadow and its application to GPS satellite orbit determination. Adv. Space Res. 2019, 63, 2912–2929. [Google Scholar] [CrossRef]
- Srivastava, V.K.; Yadav, S.; Kumar, J.; Kushvah, B.; Ramakrishna, B.; Ekambram, P. Earth conical shadow modeling for LEO satellite using reference frame transformation technique: A comparative study with existing earth conical shadow models. Astron. Comput. 2015, 9, 34–39. [Google Scholar] [CrossRef]
- Wang, Y.; Topputo, F. Indirect Optimization for Low-Thrust Transfers with Earth-Shadow Eclipses. In Proceedings of the 31st AAS/AIAA Space Flight Mechanics Meeting, Charlotte, NC, USA, 31 January–4 February 2021; pp. 1–17. [Google Scholar]
- Toulmonde, M. The diameter of the Sun over the past three centuries. Astron. Astrophys. 1997, 325, 1174–1178. [Google Scholar]
- Li, Z.; Ziebart, M.; Bhattarai, S.; Harrison, D. A shadow function model based on perspective projection and atmospheric effect for satellites in eclipse. Adv. Space Res. 2019, 63, 1347–1359. [Google Scholar] [CrossRef] [Green Version]




| Position/AU | Velocity/VU | ||||
|---|---|---|---|---|---|
| X | Y | X | Y | Time/h | |
| 1 | 1.01000070094259 | −3.34229357677352 × | 8.48460734682508 × | 0.000122175035008374 | 30 |
| 2 | 1.01000070094259 | 3.34229357677352 × | 0.000137596252572650 | 9.87543991711969 × | 30 |
| 3 | 1.01006754681413 | 3.34229357677352 × | −8.14563809519688 × | −0.000122288334314350 | 30 |
| 4 | 1.01006754681413 | −3.34229357677352 × | −0.000137785577674654 | −9.86025641499878 × | 30 |
| /km | /km | /(km/s) | /(km/s) | |
|---|---|---|---|---|
| Initial standard deviation | 95.924303 | 100.433111 | 0.001004 | 0.001005 |
| Terminal standard deviation | 4.858061 | 0.151765 | 0.000002 | 0.0000004 |
| Convergence percentage | 94.9355 | 99.8489 | 99.8008 | 99.9602 |
| /km | /km | /(km/s) | /(km/s) | |
|---|---|---|---|---|
| Initial standard deviation | 97.686914 | 99.763251 | 0.000961 | 0.001001 |
| Terminal standard deviation | 8.727596 | 0.187658 | 0.000003 | 0.000001 |
| Convergence percentage | 91.0657 | 99.8119 | 99.6878 | 99.9001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wang, Y.; Zhu, C.; Qin, T. Autonomous Navigation Based on the Earth-Shadow Observation near the Sun–Earth L2 Point. Appl. Sci. 2022, 12, 12154. https://doi.org/10.3390/app122312154
Li Q, Wang Y, Zhu C, Qin T. Autonomous Navigation Based on the Earth-Shadow Observation near the Sun–Earth L2 Point. Applied Sciences. 2022; 12(23):12154. https://doi.org/10.3390/app122312154
Chicago/Turabian StyleLi, Qian, Yamin Wang, Chunli Zhu, and Tong Qin. 2022. "Autonomous Navigation Based on the Earth-Shadow Observation near the Sun–Earth L2 Point" Applied Sciences 12, no. 23: 12154. https://doi.org/10.3390/app122312154





