Deep Compressed Sensing Generation Model for End-to-End Extreme Observation and Reconstruction
Abstract
1. Introduction
2. Related Background
2.1. Compressed Sensing
2.2. Compressed Sensing Using Generative Models
2.3. Deep Compressed Sensing
3. Method
3.1. Notation Explanation
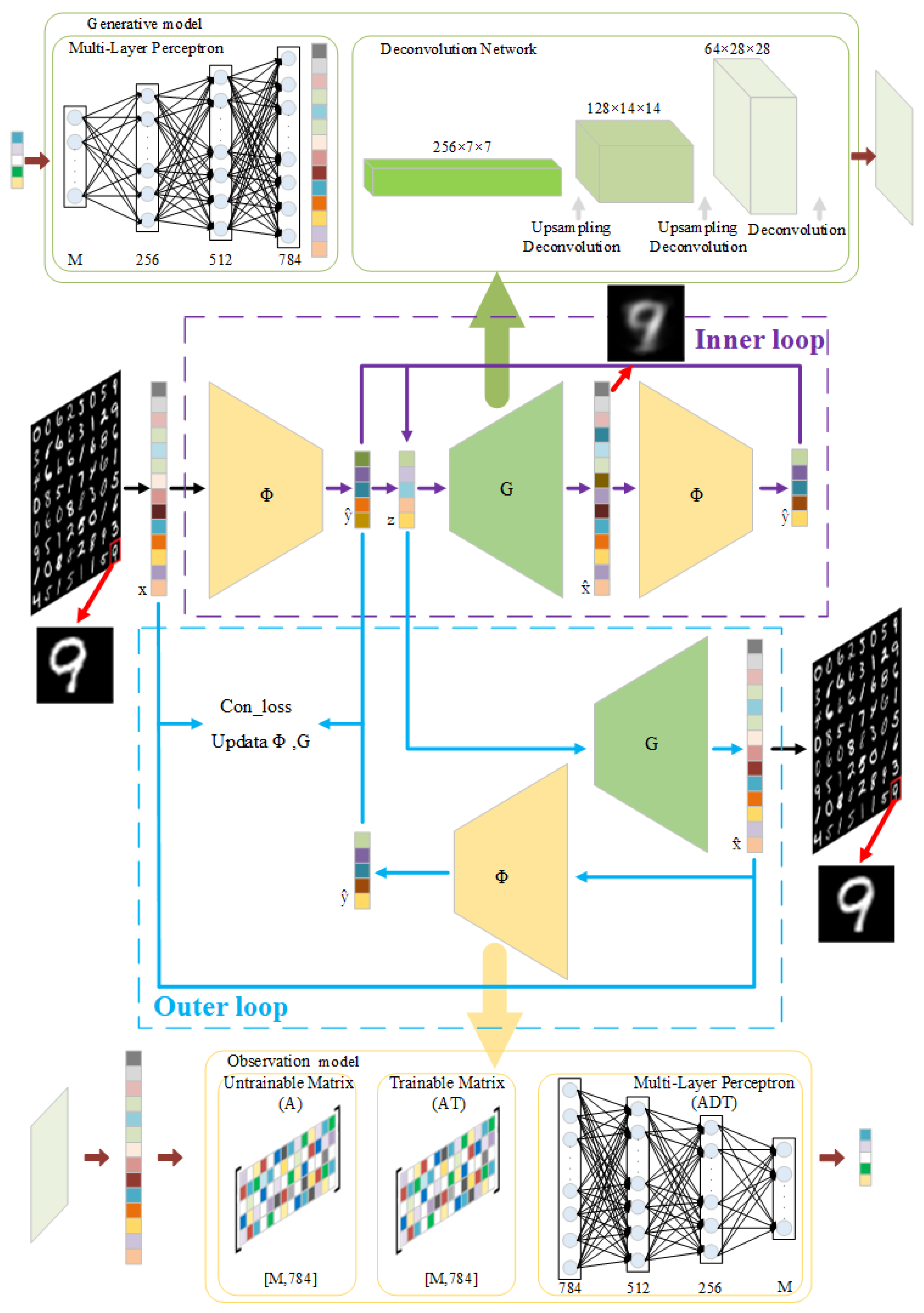
3.2. Model Structure
3.3. Algorithm Design
| Algorithm 1: The pseudo code of end-to-end deep compressed sensing generative model (E2E_DCSGM). |
| Input: : real samples x~P(T) N: Outer loop iteration T: Inner loop iteration |
| Training: |
| for i in range N//Outer loop iteration N times |
| //y is obtained by real data x |
| //real data observation vector normalization |
| for j in range T//Inner loop iteration T times |
| // is obtained by generation sample |
| //calculate the inner loop loss |
| //optimize input, the inner loop optimization rate α |
| end for//End the inner loop |
| //the joint loss of outer loop: |
| //optimize model, the outer loop optimization rate β |
| end for//End the outer loop |
| Output: : the generative model : the observation model : reconstruction samples |
4. Experiments and Results
4.1. Experimental Dataset
4.2. Experiment Operation Environment
4.3. Training Parameters and Evaluation Standards
4.4. MNIST Experiment and Analysis
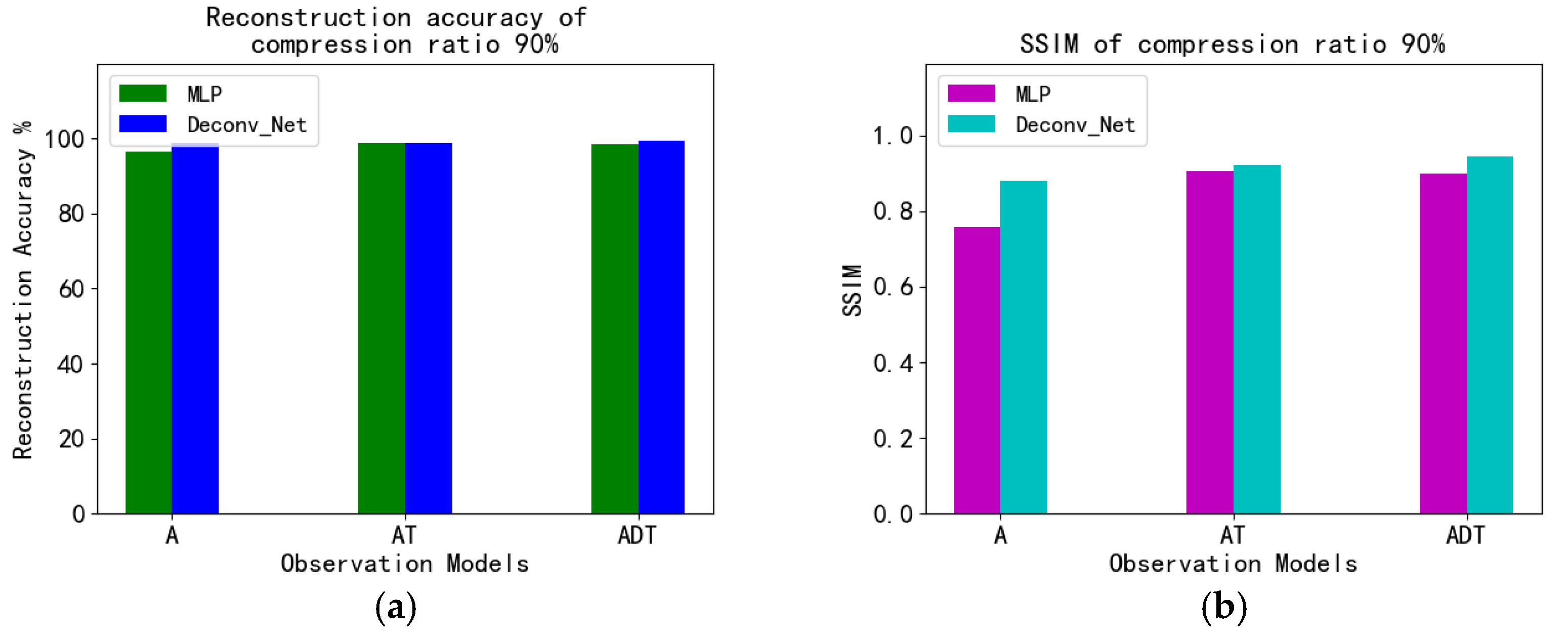
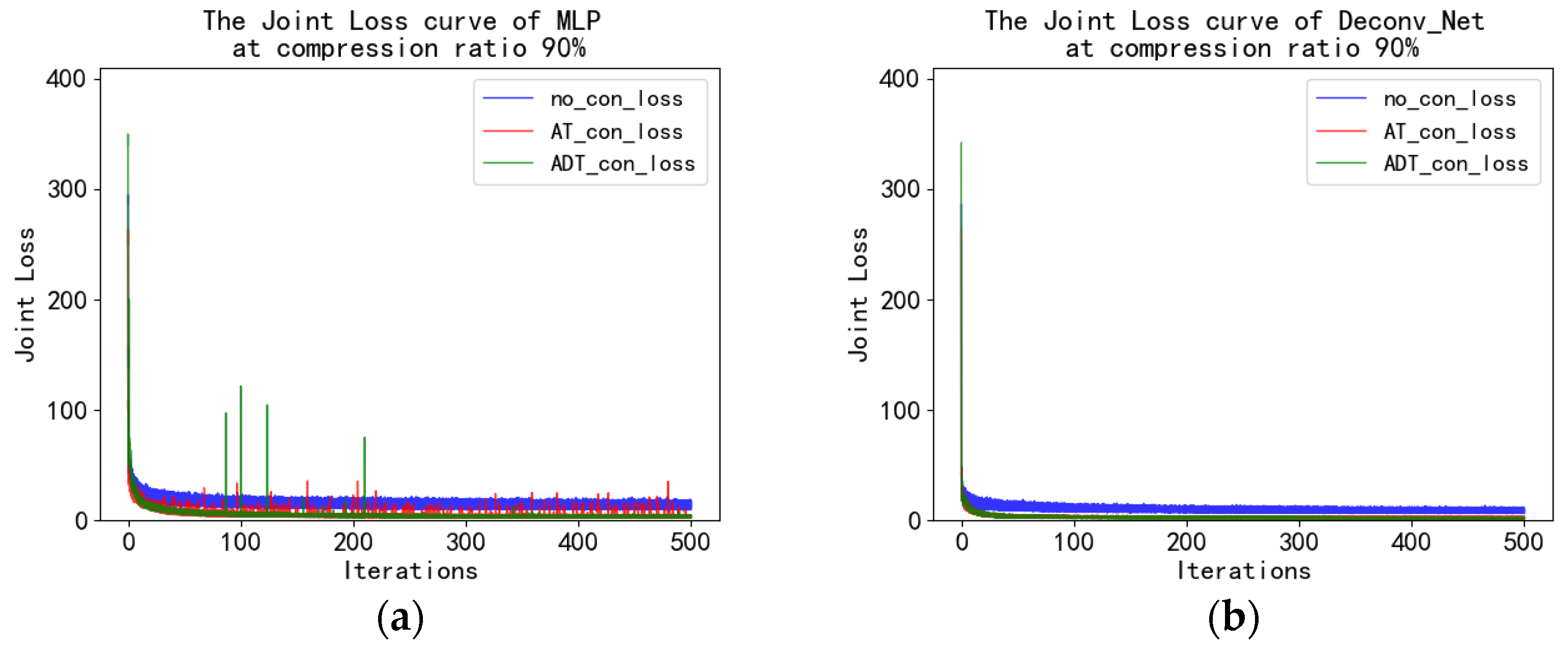
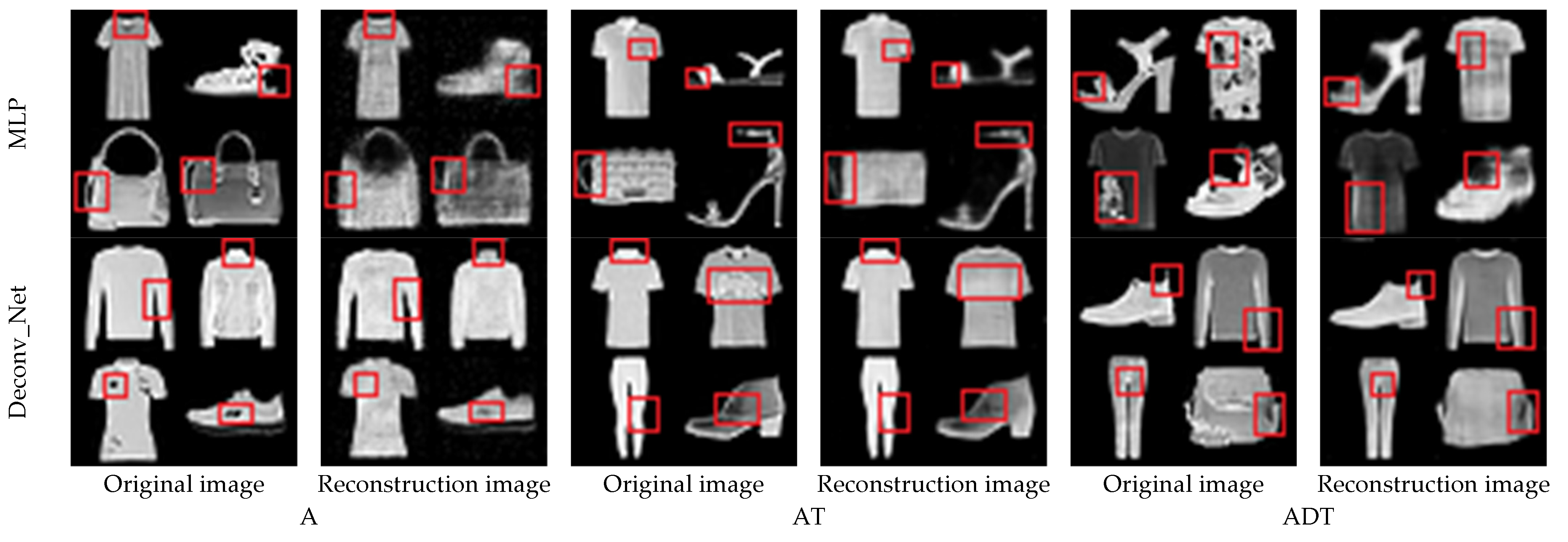
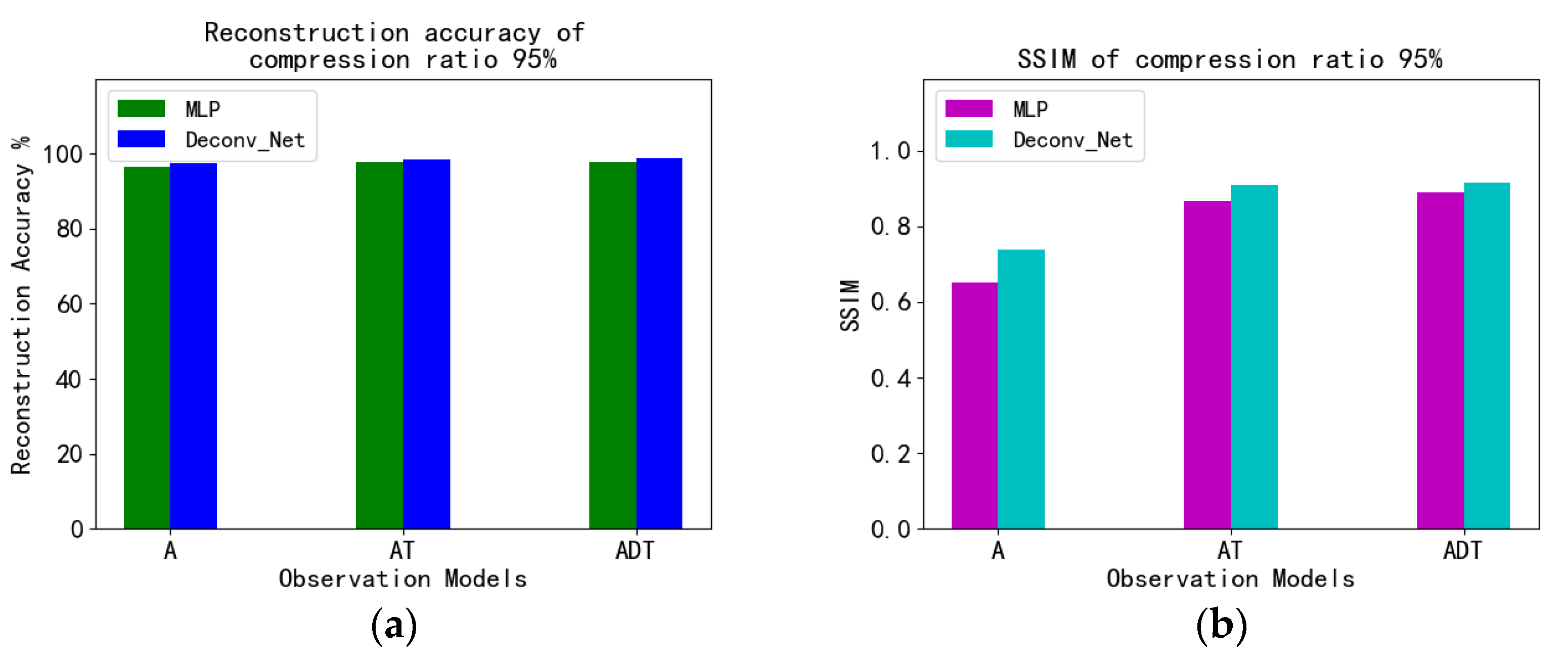
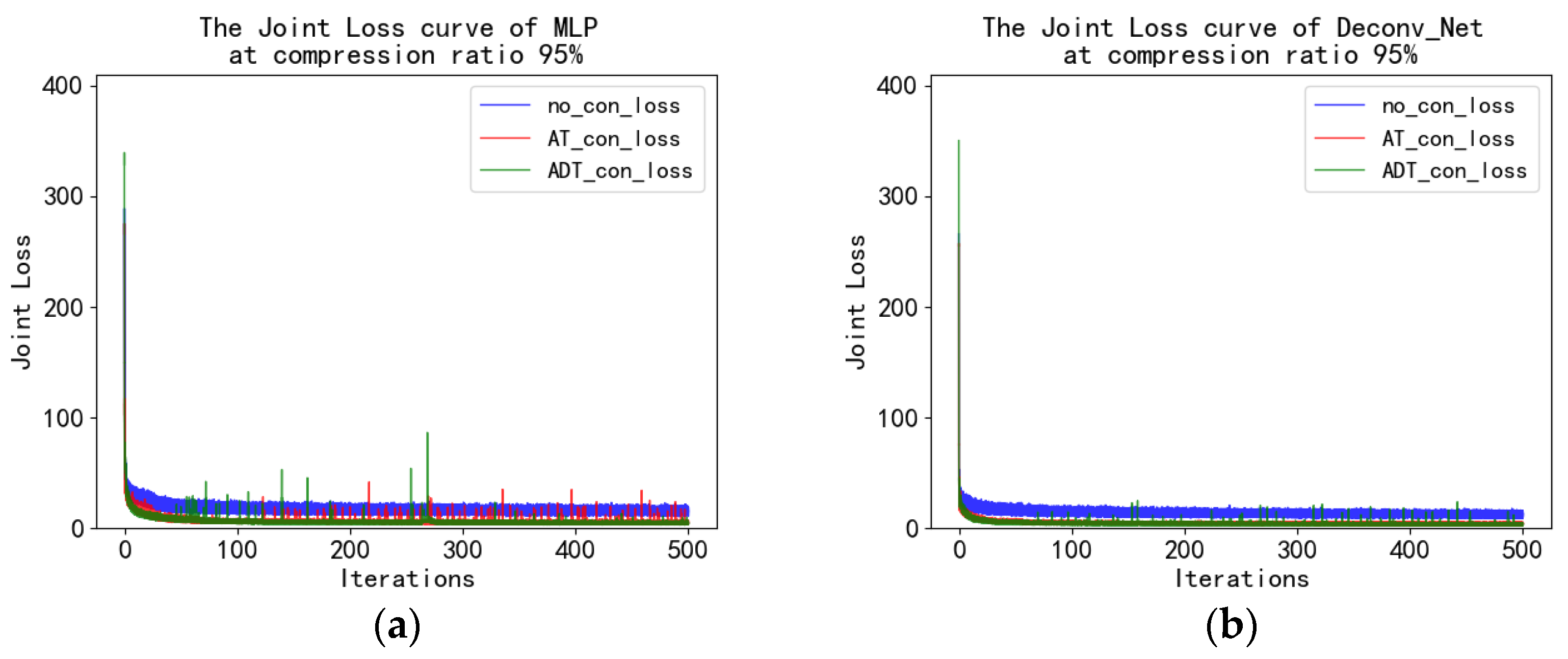
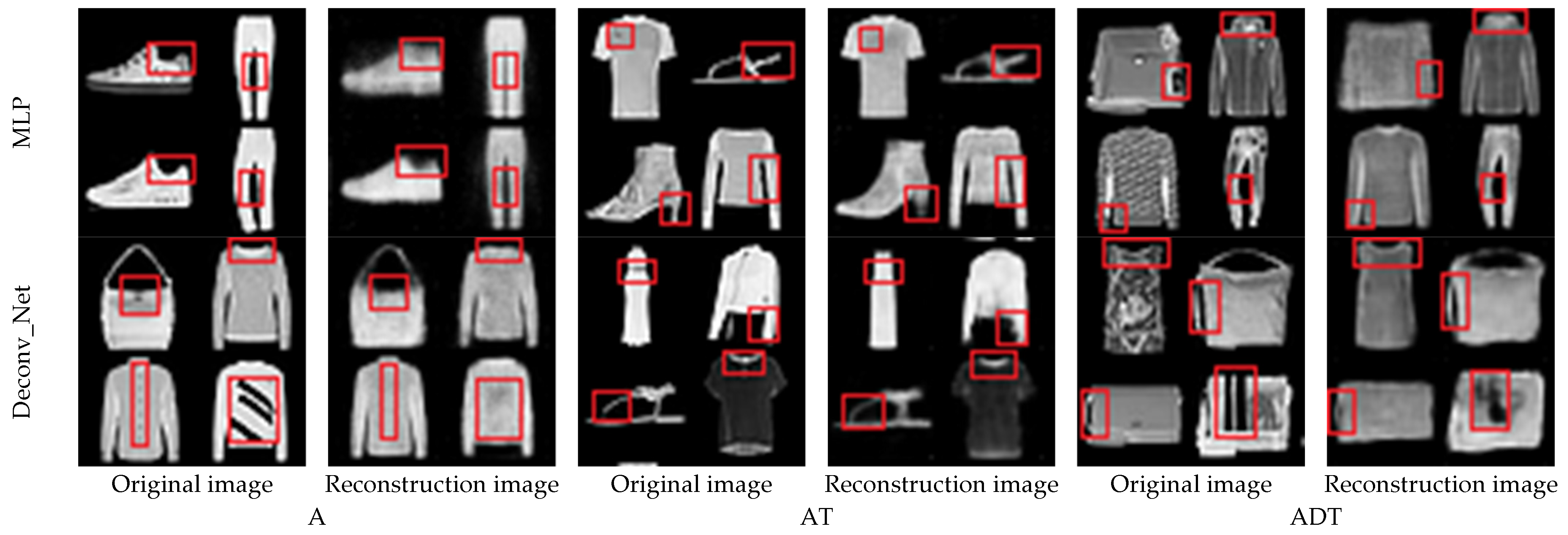
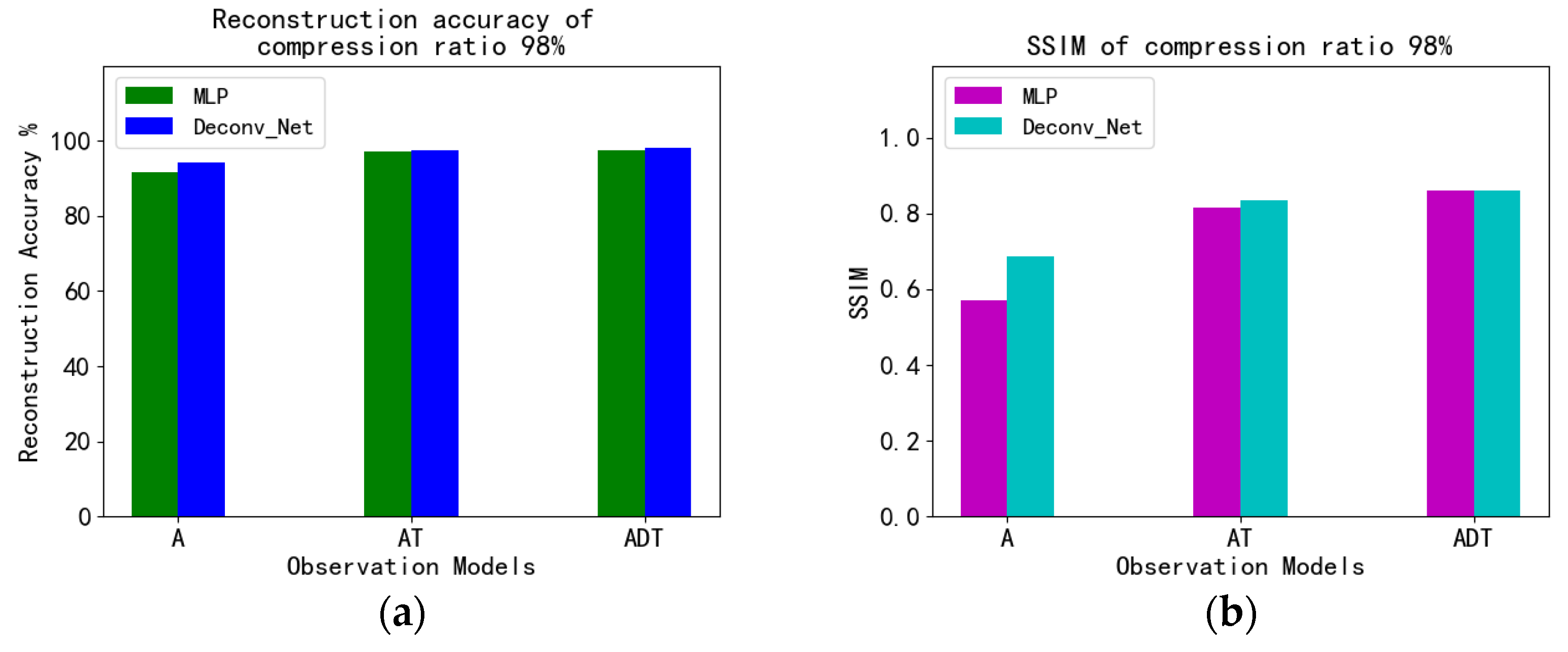
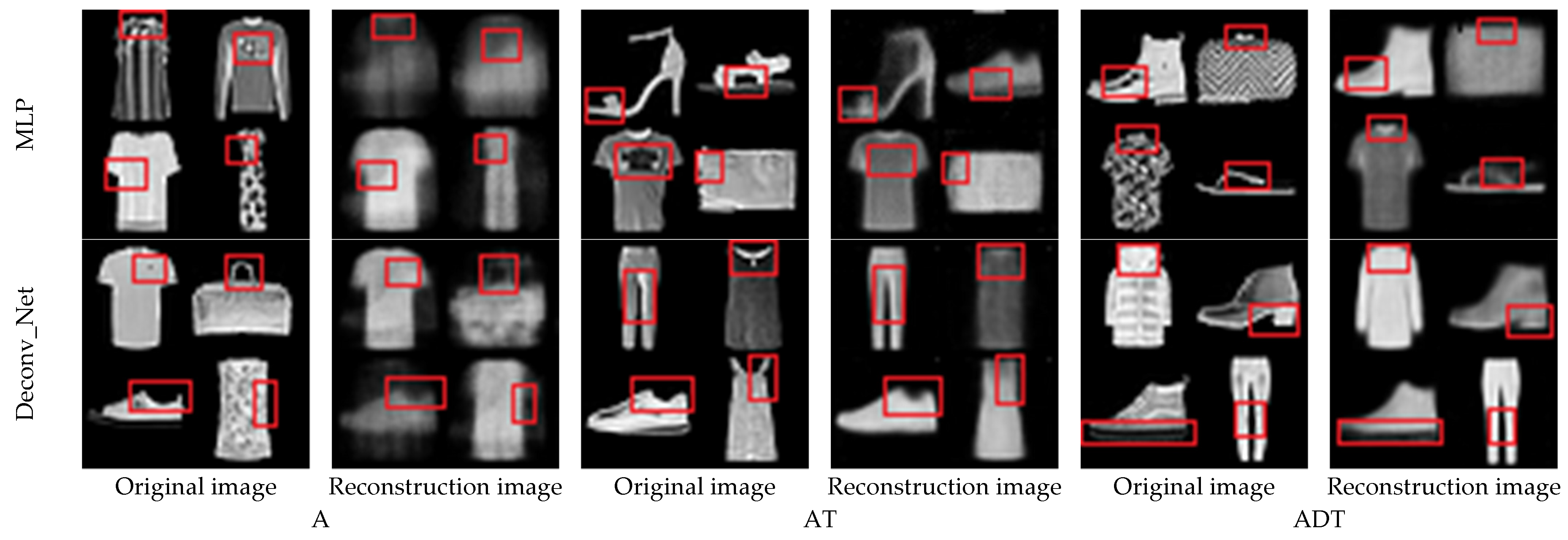
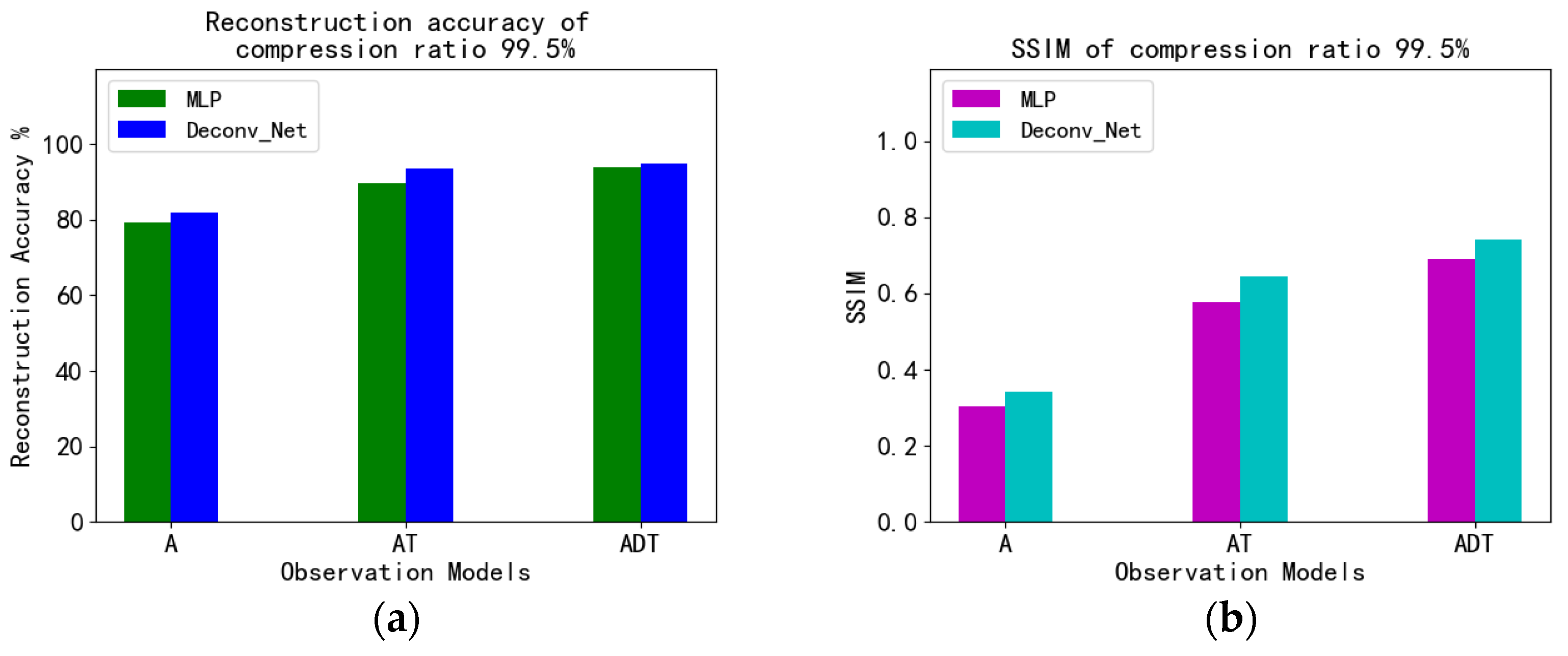
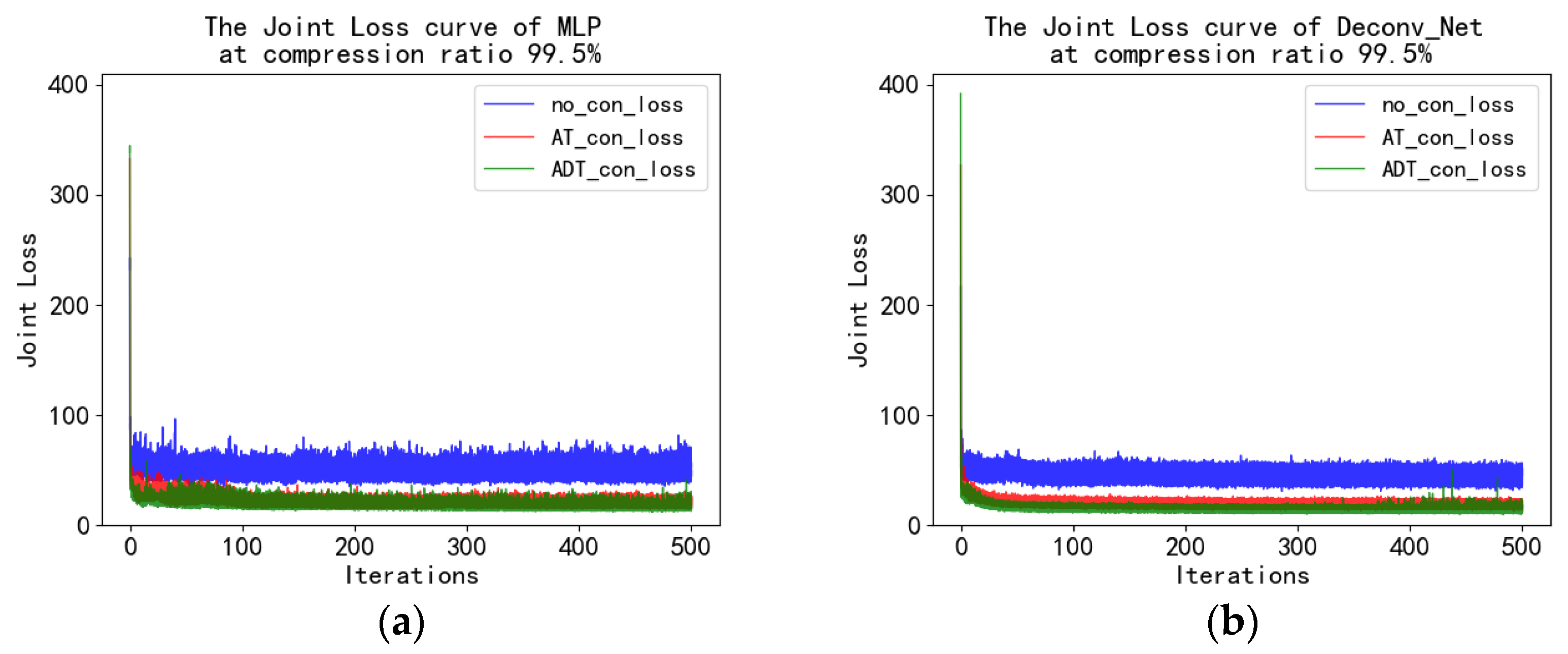
4.5. Fashion_MNIST Experiment and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, G.M.; Liu, D.H.; Gao, D.H.; Liu, Z.; Lin, J.; Wang, L.J. Advances in Theory and Application of Compressed Sensing. Acta Electron. Sin. 2009, 37, 1070–1081. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Zeng, C.Y.; Ye, J.X.; Wang, Z.F.; Wu, M. Survey of compressed sensing reconstruction algorithms in deep learning framework. Comput. Eng. Appl. 2019, 55, 1–8. [Google Scholar]
- Jiao, L.C.; Yang, S.Y.; Liu, F.; Hou, B. Development and Prospect of Compressive Sensing. Acta Electron. Sin. 2011, 39, 1651–1662. [Google Scholar]
- Tauböck, G.; Hlawatsch, F. A compressed sensing technique for OFDM channel estimation in mobile environments: Exploiting channel sparsity for reducing pilots. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 2885–2888. [Google Scholar]
- Bajwa, W.U.; Haupt, J.D.; Sayeed, A.M.; Nowak, R.D. Joint Source–Channel Communication for Distributed Estimation in Sensor Networks. IEEE Trans. Inf. Theory 2007, 53, 3629–3653. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.L.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef]
- Provost, J.; Lesage, F. The Application of Compressed Sensing for Photo-Acoustic Tomography. IEEE Trans. Med. Imaging 2009, 28, 585–594. [Google Scholar] [CrossRef]
- Jung, H.; Sung, K.; Nayak, K.S.; Kim, E.Y.; Ye, J.C. k-t FOCUSS: A general compressed sensing framework for high resolution dynamic MRI. Magn. Reson. Med. 2009, 61, 103–116. [Google Scholar] [CrossRef]
- Kim, Y.; Narayanan, S.S.; Nayak, K.S. Accelerated three-dimensional upper airway MRI using compressed sensing. Magn. Reson. Med. 2009, 61, 1434–1440. [Google Scholar] [CrossRef]
- Hu, S.; Lustig, M.; Chen, A.P.; Crane, J.C.; Kerr, A.B.; Kelley, D.A.; Hurd, R.E.; Kurhanewicz, J.; Nelson, S.J.; Pauly, J.M.; et al. Compressed sensing for resolution enhancement of hyperpolarized 13C flyback 3D-MRSI. J. Magn. Reson. 2008, 192, 258–264. [Google Scholar] [CrossRef]
- Herman, M.A.; Strohmer, T. High-Resolution Radar via Compressed Sensing. IEEE Trans. Signal Process. 2009, 57, 2275–2284. [Google Scholar] [CrossRef]
- Bobin, J.; Starck, J.; Ottensamer, R. Compressed Sensing in Astronomy. IEEE J. Sel. Top. Signal Process. 2008, 2, 718–726. [Google Scholar] [CrossRef]
- Shamsi, D.; Boufounos, P.T.; Koushanfar, F. Noninvasive leakage power tomography of integrated circuits by compressive sensing. In Proceedings of the 13th International Symposium on Low Power Electronics and Design (ISLPED ‘08), Bangalore, India, 11–13 August 2008; pp. 341–346. [Google Scholar]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust Face Recognition via Sparse Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef]
- Elad, M. Optimized Projections for Compressed Sensing. IEEE Trans. Signal Process. 2007, 55, 5695–5702. [Google Scholar] [CrossRef]
- Calderbank, R. Compressed Learning: Universal Sparse Dimensionality Reduction and Learning in the Measurement Domain; Technical Report; Rice University: Houston, TX, USA, 2009. [Google Scholar]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R. Single-Pixel Imaging via Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Bora, A.; Jalal, A.; Price, E.; Dimakis, A.G. Compressed Sensing using Generative Models. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y. Generative Adversarial Nets. In Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Mardani, M.; Gong, E.; Cheng, J.Y.; Vasanawala, S.S.; Zaharchuk, G.; Alley, M.T.; Thakur, N.; Han, S.; Dally, W.J.; Pauly, J.M.; et al. Deep Generative Adversarial Networks for Compressed Sensing Automates MRI. arXiv 2017, arXiv:1706.00051. [Google Scholar]
- Veen, D.V.; Jalal, A.; Price, E.; Vishwanath, S.; Dimakis, A.G. Compressed Sensing with Deep Image Prior and Learned Regularization. arXiv 2018, arXiv:1806.06438. [Google Scholar]
- Wu, Y.; Rosca, M.; Lillicrap, T.P. Deep Compressed Sensing. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019. [Google Scholar]
- Sun, Y.; Chen, J.; Liu, Q.; Liu, G. Learning image compressed sensing with sub-pixel convolutional generative adversarial network. Pattern Recognit. 2020, 98, 107051. [Google Scholar] [CrossRef]
- Sheykhivand, S.; Rezaii, T.Y.; Meshgini, S.; Makoui, S.; Farzamnia, A. Developing a Deep Neural Network for Driver Fatigue Detection Using EEG Signals Based on Compressed Sensing. Sustainability 2022, 14, 2941. [Google Scholar] [CrossRef]
- Islam, S.R.; Maity, S.P.; Ray, A.K.; Mandal, M. Deep learning on compressed sensing measurements in pneumonia detection. Int. J. Imaging Syst. Technol. 2022, 32, 41–54. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. arXiv 2017, arXiv:1703.03400. [Google Scholar]








| Notation | Meanings |
|---|---|
| the original signal | |
| the observation model | |
| the observed vector | |
| the generated signal | |
| the generative model | |
| the input of generative model from normalized the observed vector | |
| the input that is optimized | |
| the observed vector that is optimized | |
| the Euclidean norm | |
| the loss of generative model | |
| the loss of observation model | |
| the inner loop optimization rate | |
| the outer loop optimization rate | |
| the parameter of model | |
| T | the inner loop iteration |
| N | the outer loop iteration |
| the loss of inner loop | |
| the loss of outer loop |
| Method | Input | Models Combination | Type | Purpose |
|---|---|---|---|---|
| CSGM | Random input | MLP + A | Control Group | Random input control group |
| DCS | Random input | MLP + AT | Control Group | |
| DCS | MLP + ADT | |||
| We proposed | end-to-end | MLP + A | Experimental Group | Verify the feasibility of end-to-end reconstruction under the extreme observation |
| MLP + AT | ||||
| MLP + ADT | ||||
| end-to-end | Deconv_Net + A | Experimental Group | Verify the reconstruction effect of the improved generator on the extreme observation under the end-to-end case | |
| Deconv_Net + AT | ||||
| Deconv_Net + ADT |
| Network Layer | Related Hyperparameter Settings |
|---|---|
| Input | batch_size = 64 (batch_size, sensing_dim) |
| Hidden layer 1 | Linear(sensing_dim, 256) activation function: LeakyReLU |
| Hidden layer 2 | Linear(256, 512) activation function: LeakyReLU |
| Hidden layer 3 | Linear(512, 784) activation function: Tanh |
| output | (batch_size,1, 28, 28) |
| Network Layer | Related Hyperparameter Settings |
|---|---|
| Input | batch_size = 64 (batch_size, sensing_dim) |
| upsampling 1 | scale_factor: 2 |
| deconvolution layer 1 | kernel_size: (128, 3 × 3), stride_size: 1, padding_size: 1 activation function: LeakyReLU |
| upsampling 2 | scale_factor: 2 |
| deconvolution layer 2 | kernel_size: (64, 3 × 3), stride_size: 1, padding_size: 1 activation function: LeakyReLU |
| deconvolution layer 3 | kernel_size: (1, 3 × 3), stride_size: 1, padding_size: 1 activation function: Tanh |
| output | (batch_size, 1, 28, 28) |
| Network Layer | Related Hyperparameter Settings |
|---|---|
| Input | batch_size = 64 (batch_size,1, 28, 28) |
| Hidden layer 1 | Linear(784, 512) activation function: LeakyReLU |
| Hidden layer 2 | Linear(512, 256) activation function: LeakyReLU |
| Hidden layer 3 | Linear(256, sensing_dim) |
| output | (batch_size, sensing_dim) |
| Category | Versions |
|---|---|
| operating system | Windows10 |
| CPU | Core i5-10400 2.9 GHz |
| GPU | NVIDIA RTX2070SUPER 8G |
| Python | python3.8 |
| Pytorch | pytorch1.10 |
| CUDA | CUDA version10.2 |
| cuDNN | cuDNN7.6.5 |
| Compression Ratio (Number of Observations) | 75% (196) | 80% (157) | 85% (118) | 90% (78) | 95% (39) | 98% (16) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | SSIM | Accuracy | SSIM | Accuracy | SSIM | Accuracy | SSIM | Accuracy | SSIM | Accuracy | SSIM | |
| A | 99.76% | 0.9746 | 99.61% | 0.9710 | 99.54% | 0.9701 | 99.05% | 0.9217 | 97.96% | 0.5997 | 93.82% | 0.5901 |
| AT | 99.76% | 0.9829 | 99.67% | 0.9731 | 99.68% | 0.9784 | 99.60% | 0.9775 | 99.27% | 0.9659 | 97.91% | 0.9008 |
| ADT | 99.62% | 0.9794 | 99.72% | 0.9868 | 99.75% | 0.9859 | 99.60% | 0.9817 | 99.48% | 0.9775 | 98.45% | 0.9353 |
| Observation Model | A | AT | ADT | |
|---|---|---|---|---|
| Reconstruction accuracy | random input | 83.80% | 84.95% | 83.86% |
| end-to-end input | 87.07% | 89.54% | 91.61% | |
| SSIM | random input | 0.3491 | 0.3501 | 0.3803 |
| end-to-end input | 0.4517 | 0.5847 | 0.7032 | |
| Average loss | random input | 70.3399 | 53.0402 | 53.2837 |
| end-to-end input | 47.4702 | 33.8370 | 28.4777 | |
| Method | Compression Ratio (Number of Observations) | 90% (78) | 95% (39) | 98% (16) | 99.5% (4) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | SSIM | Accuracy | SSIM | Accuracy | SSIM | Accuracy | SSIM | ||
| CSGM | MLP + A | 96.57% | 0.7588 | 96.40% | 0.6518 | 91.63% | 0.5721 | 79.15% | 0.3026 |
| DCS | MLP + AT | 98.54% | 0.9061 | 97.75% | 0.8680 | 96.94% | 0.8139 | 89.58% | 0.5757 |
| DCS | MLP + ADT | 98.49% | 0.8980 | 97.65% | 0.8879 | 97.51% | 0.8602 | 93.88% | 0.6898 |
| We proposed | Conv + A | 98.60% | 0.8793 | 97.42% | 0.7365 | 94.10% | 0.6850 | 81.94% | 0.3430 |
| Conv + AT | 98.77% | 0.9206 | 98.45% | 0.9081 | 97.32% | 0.8340 | 93.40% | 0.6441 | |
| Conv + ADT | 99.23% | 0.9427 | 98.67% | 0.9152 | 98.00% | 0.8618 | 94.74% | 0.7405 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diao, H.; Lin, X.; Fang, C. Deep Compressed Sensing Generation Model for End-to-End Extreme Observation and Reconstruction. Appl. Sci. 2022, 12, 12176. https://doi.org/10.3390/app122312176
Diao H, Lin X, Fang C. Deep Compressed Sensing Generation Model for End-to-End Extreme Observation and Reconstruction. Applied Sciences. 2022; 12(23):12176. https://doi.org/10.3390/app122312176
Chicago/Turabian StyleDiao, Han, Xiaozhu Lin, and Chun Fang. 2022. "Deep Compressed Sensing Generation Model for End-to-End Extreme Observation and Reconstruction" Applied Sciences 12, no. 23: 12176. https://doi.org/10.3390/app122312176
APA StyleDiao, H., Lin, X., & Fang, C. (2022). Deep Compressed Sensing Generation Model for End-to-End Extreme Observation and Reconstruction. Applied Sciences, 12(23), 12176. https://doi.org/10.3390/app122312176




