Mechanical Strength Decay Evaluation of Excavation Unloaded Rock Mass under Freeze-Thaw Conditions
Abstract
:1. Introduction
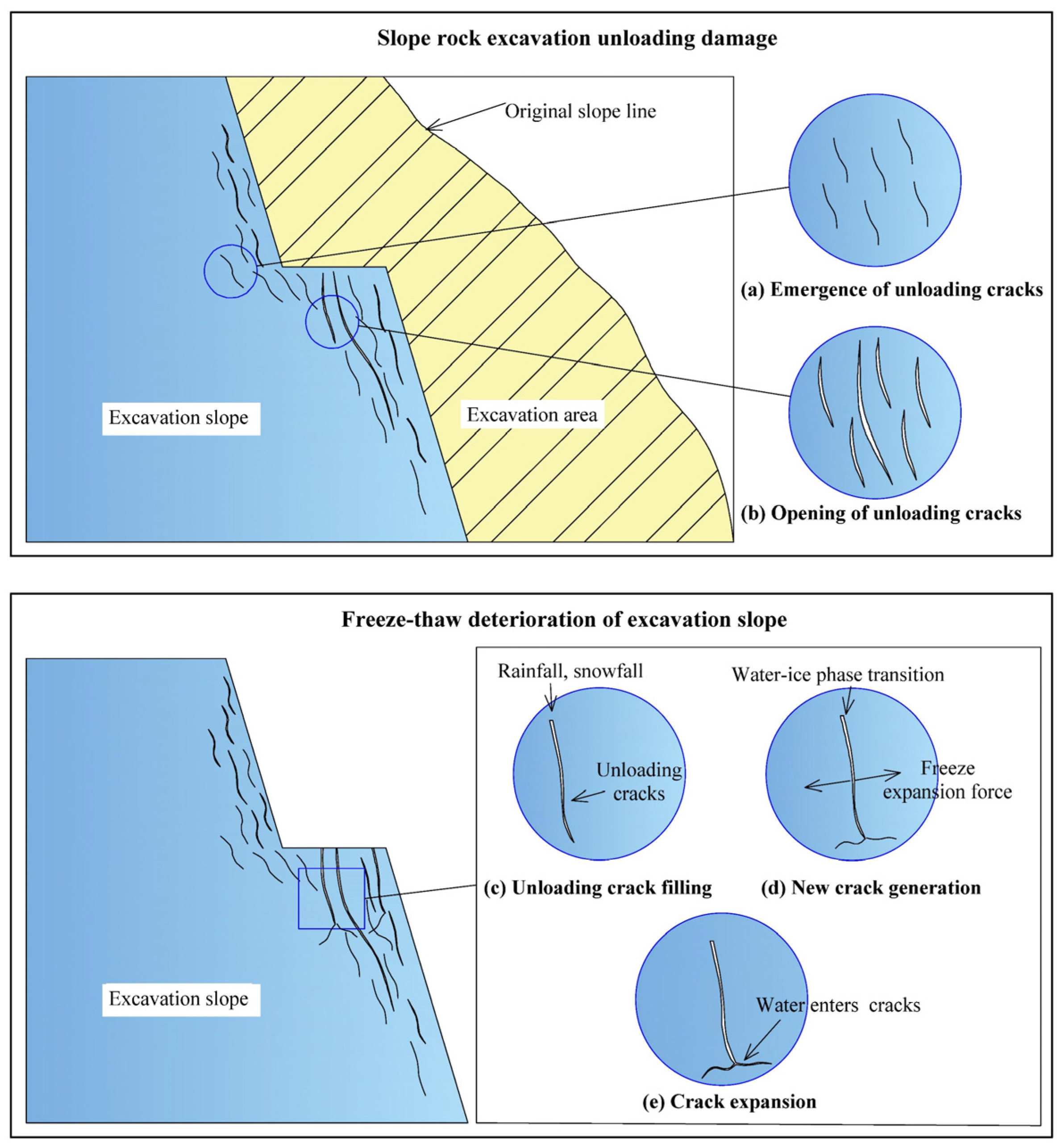
- The study of freeze-thaw degradation characteristics of excavated unloaded rock masses on steep and high slopes in cold regions is inadequate. The excavation unloading relaxation phenomenon on steep and high slopes is significant, and the damage and rupture of rock masses in a certain range in the excavation face provides a means of intervening in freeze-thaw erosion. Therefore, it is necessary to investigate the freeze-thaw erosion and deterioration of excavated and unloaded rock masses of steep and high slopes in regions with seasonal freezing by considering the indoor test program of the interaction between excavation disturbance and freeze-thaw cycles;
- Most of the studies on freeze-thaw strength decay models are based on the attenuation of uniaxial peak strength deterioration, while the rock body of the reservoir bank of the excavation and unloaded zone is still in a three-way stress state and has an inhibitory effect on freeze-thaw cycle erosion. Therefore, the established freeze-thaw strength decay model should be realistic and reflect the decay of freeze-thaw strength under the stress state of the rock body of the reservoir bank of the excavation and unloaded zone.
2. Test Overview
2.1. Sampling
2.2. Test Program
- Triaxial compression tests were carried out at three confining pressures (10 MPa, 15 MPa, and 20 MPa), and compressive strengths were obtained at specific circumferential pressures (130.25 MPa, 152.67 MPa, and 172.11 MPa);
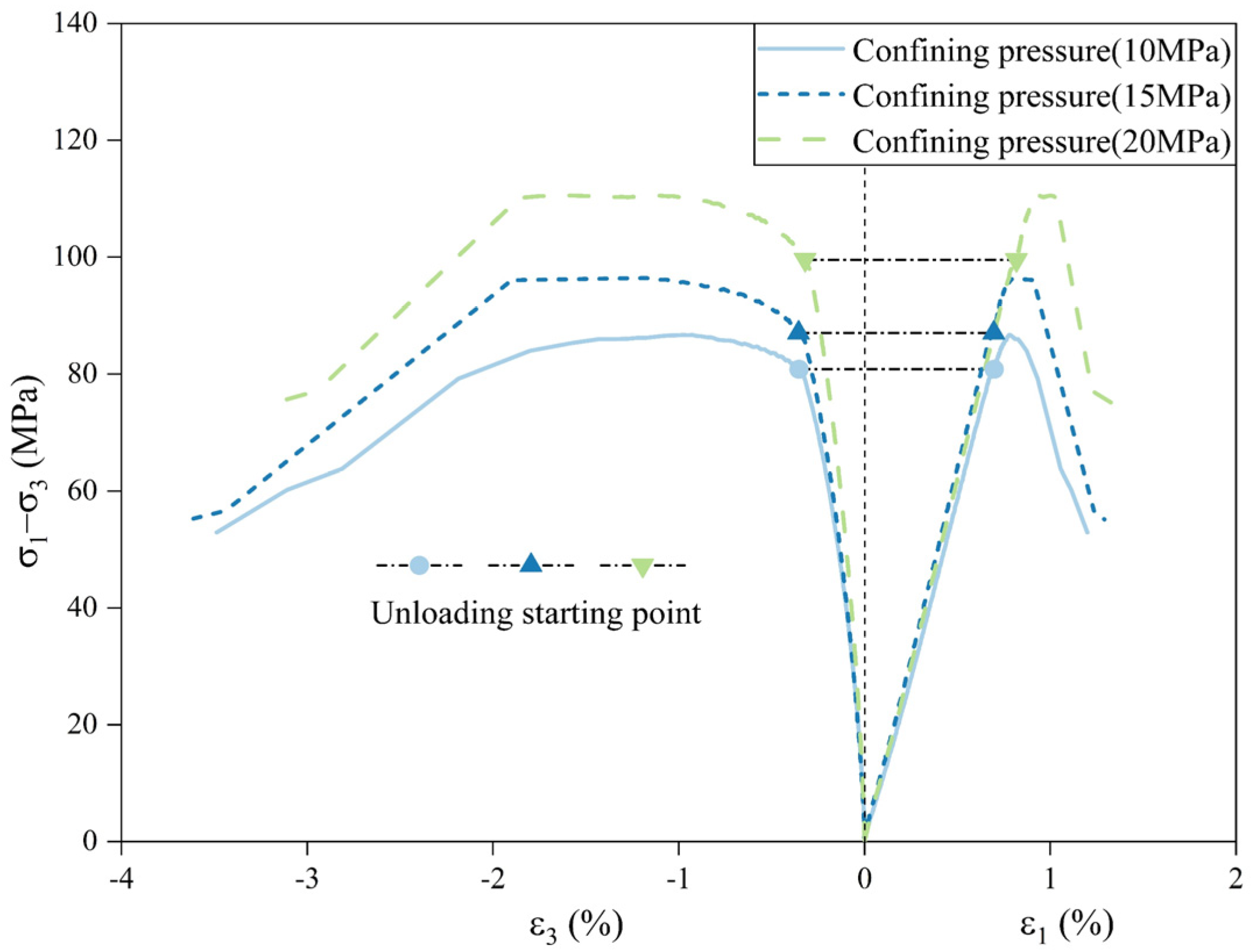
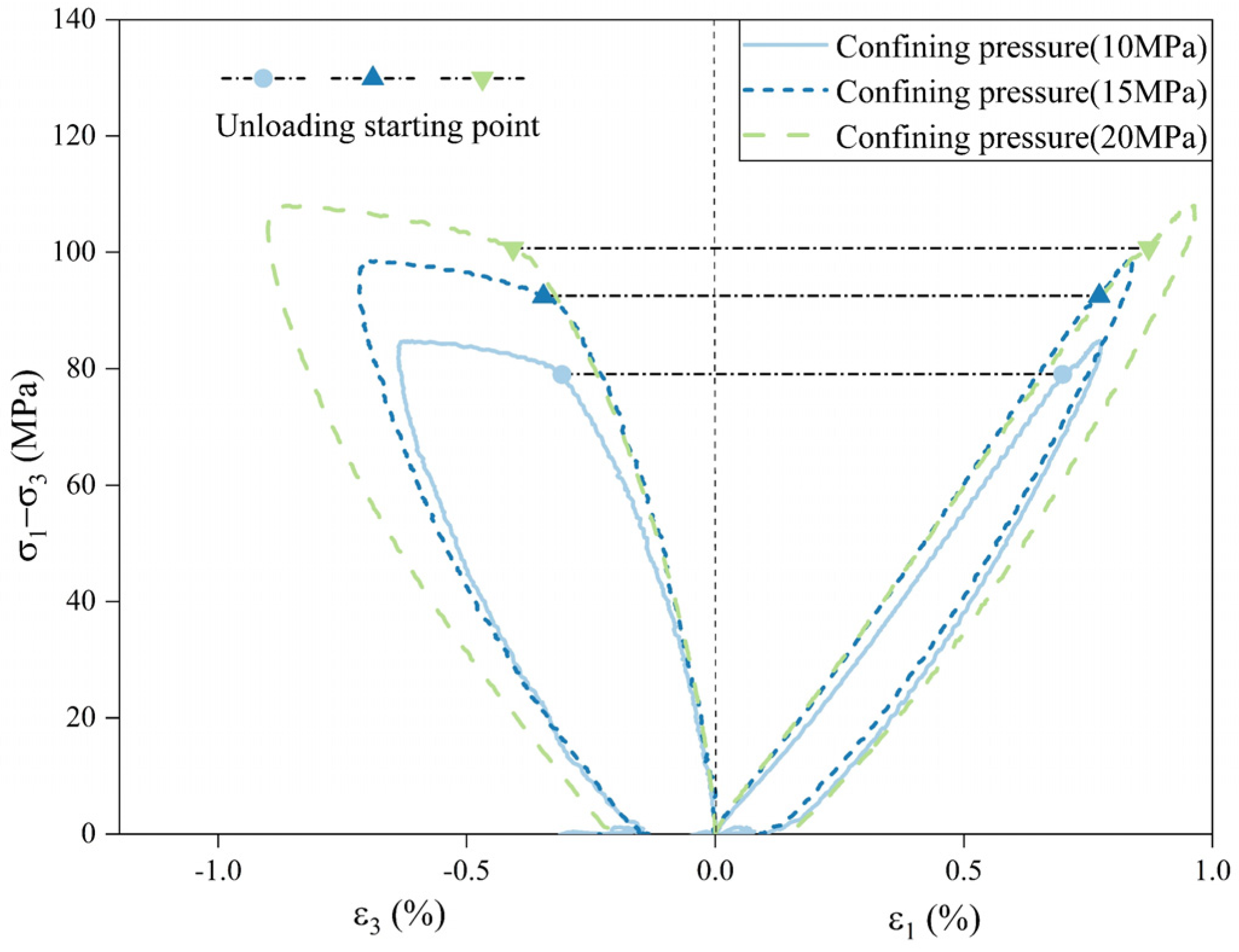
- The excavation unloading stress path of the slope rock in cold regions was simulated and triaxial unloading tests with constant axial pressure unloading of the confining pressure were performed in which the axial stress was loaded to 70% of the compressive strength at a specific surrounding pressure [19]. The confining pressure was then unloaded until the specimen was damaged. To investigate the evolution of the unloading damage process of the enclosing pressure and to obtain unloaded-damaged rock samples that still have a certain load-bearing capacity, the unloaded-damaged sample was prepared by using a stress path with constant unloading of the confining pressure to the target value;
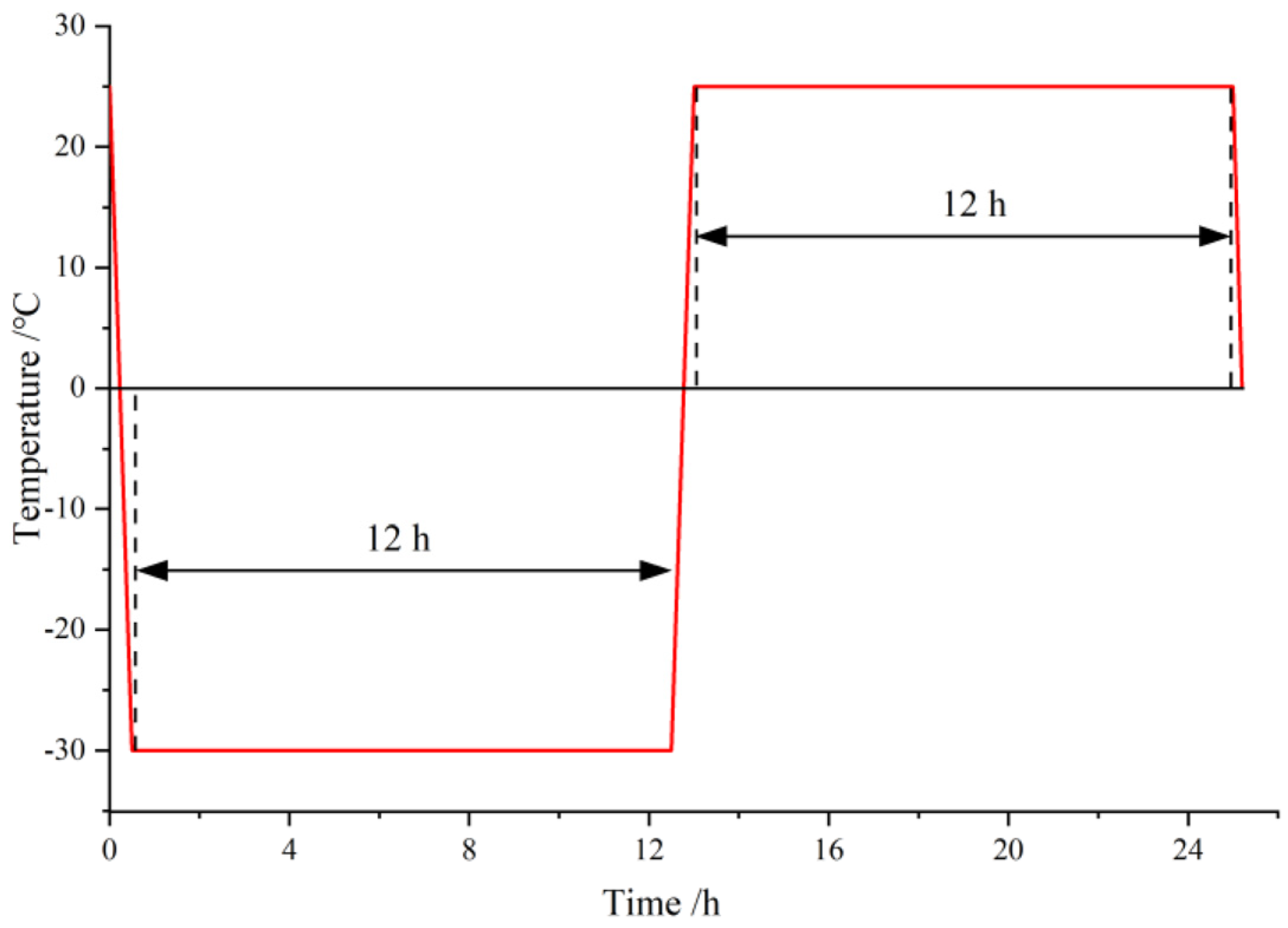
- The cold region bank slope excavation unloaded rock body is in a three-way force state, and the slope support causes the surface rock body to be affected by the restraint effect, and the freezing and thawing environment triggers the freezing and swelling force caused by the internal water-ice phase change of the rock body in the form of extended development and misalignment slip toward the internal fissures of the rock body. Using the unloaded-damaged sample rock sample as the object, a homemade rock freeze-thaw jig was used (as shown in Figure 2) and combined with the characteristics of the field temperature environment to perform an indoor freeze-thaw cycle test. The freezing temperature was set to −30 °C, the ablation temperature was set to 25 °C, and the sample experienced low-temperature freezing for 12 h followed by room-temperature ablation for 12 h (as shown in Figure 3). A freezing-thawing cycle pre-test was carried out on the unloaded-damaged sample until obvious macroscopic cracks appeared in the rock sample and the rock sample would be broken after the next freezing-thawing cycle. The maximum number of freezing-thawing cycles was measured to be eight times. Therefore, the number of freezing-thawing cycles was finally selected to be zero, two, four, six, and eight times.
- The unloaded-damaged samples were removed after each freeze-thaw cycle, and the mass, height, diameter, and porosity were recorded. After reaching the target number of freeze-thaw cycles, all rock samples were removed for uniaxial and triaxial reloading tests, in which the values of confining pressure for the triaxial reloading mechanics test were selected as the target values of confining pressure unloading in the preparation of the unloaded-damaged sample, which reflected the stress state after unloading and could better facilitate the investigation of the relationship between the stress state of excavation unloaded rock masses and freeze-thaw erosion.
3. Unloading-Damaged Test Procedure
3.1. Triaxial Unloading Test Analysis
3.2. Preparation of Unloaded-Damaged Samples
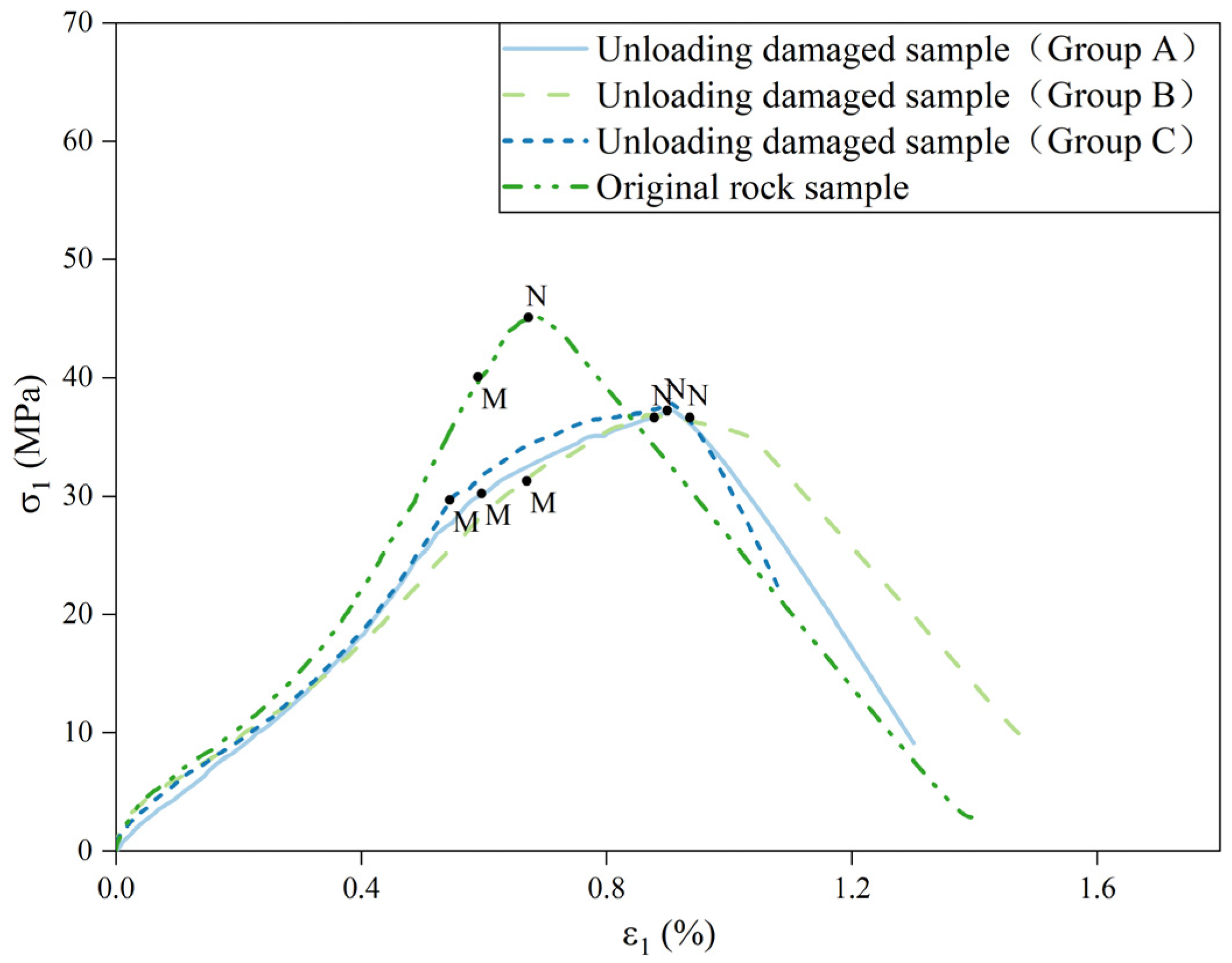
3.3. Mechanical Characteristics of the Unloaded-Damaged Samples
4. Freeze-Thaw Test Results and Analysis
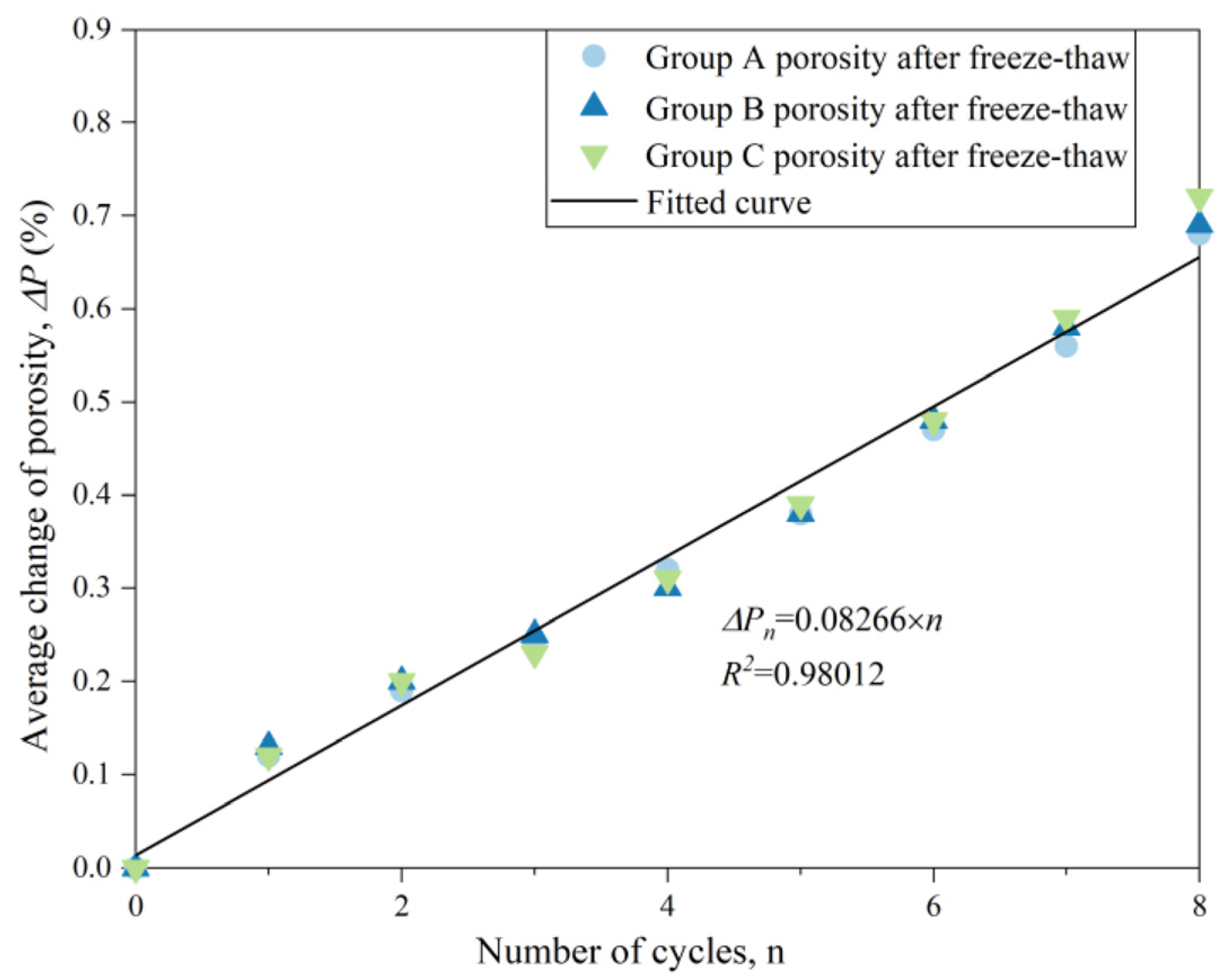
4.1. Porosity Variation Characteristics of Unloaded-Damaged Samples after Freeze-Thaw
4.2. Failure characteristics of Unloaded-Damaged Samples after Freeze-Thaw and Reloading
- After two and four freeze-thaw cycles, there is no significant change in the surface appearance of the sample, while after six and eight freeze-thaw cycles, transverse cracks appear on the surface and gradually develop and expand with the increase in the number of freeze-thaw cycles. The freeze-swelling force caused by the freezing of pore water acts on the pore wall, and this action is equivalent to the three-way tensile load on the rock sample. The unloaded-damaged samples are found to be mainly damaged in the axial direction by the apparent freeze-thaw deterioration characteristics, and transverse cracks develop and expand gradually;
- The uniaxial reloading damage pattern of the unloaded-damaged samples exhibits oblique penetration damage from top to bottom, and the number of ruptured blocks increases with the increase in the number of freeze-thaw cycles, indicating that the cycles trigger the development of internal pore fractures in the unloaded-damaged samples and induce macroscopic uniaxial reloading damage fragmentation;
- The triaxial reloading damage pattern shows an oblique penetration from the top to the bottom and multiple local damage cracks. The increase in the number of freeze-thaw cycles causes the development of multilinear local crack extension.
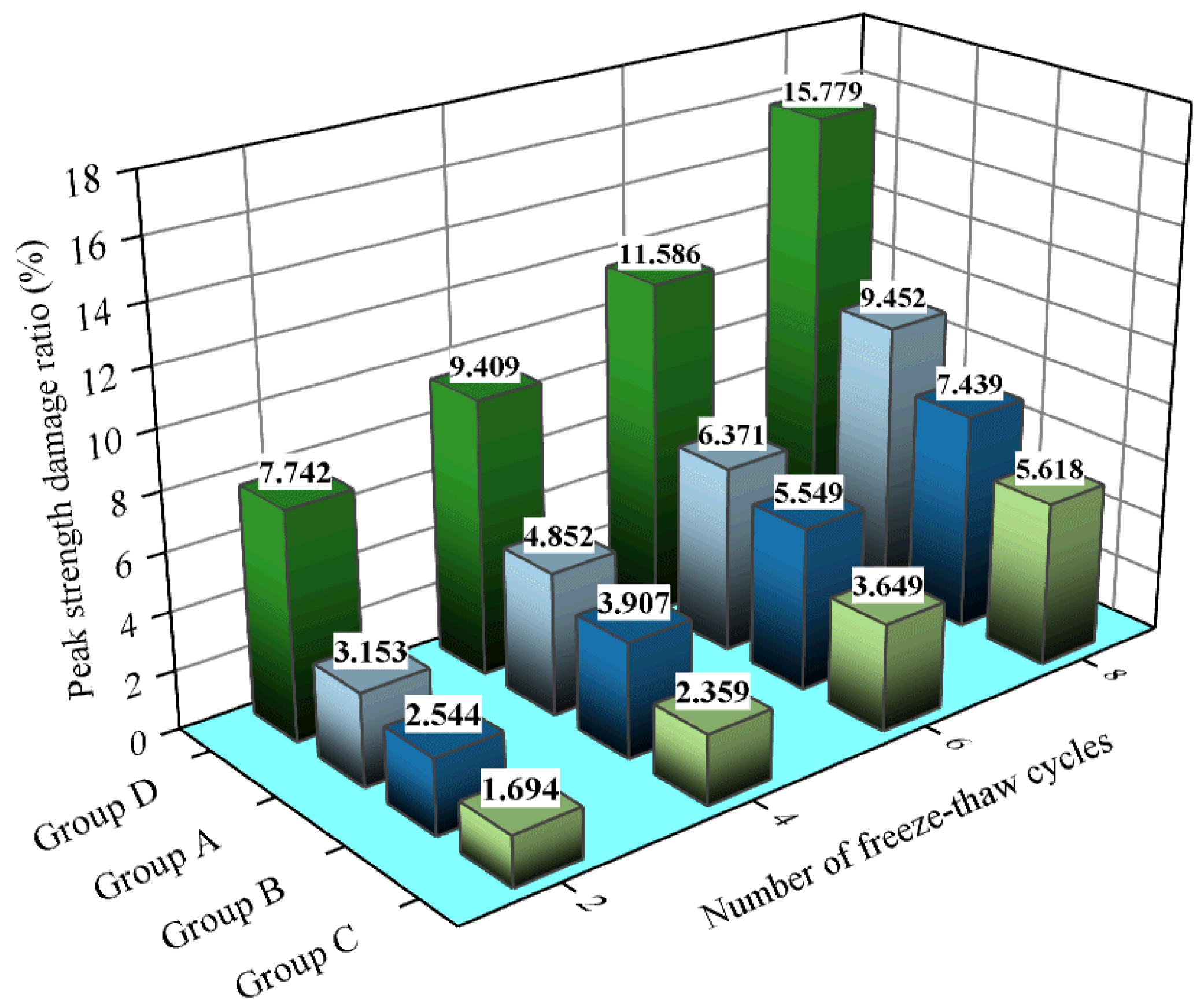
4.3. Analysis of Peak Strength Deterioration after Freeze-Thaw and Reloading of Unloaded-Damaged Samples
5. Freeze-Thaw Strength Decay Model
5.1. Strength Decay Model
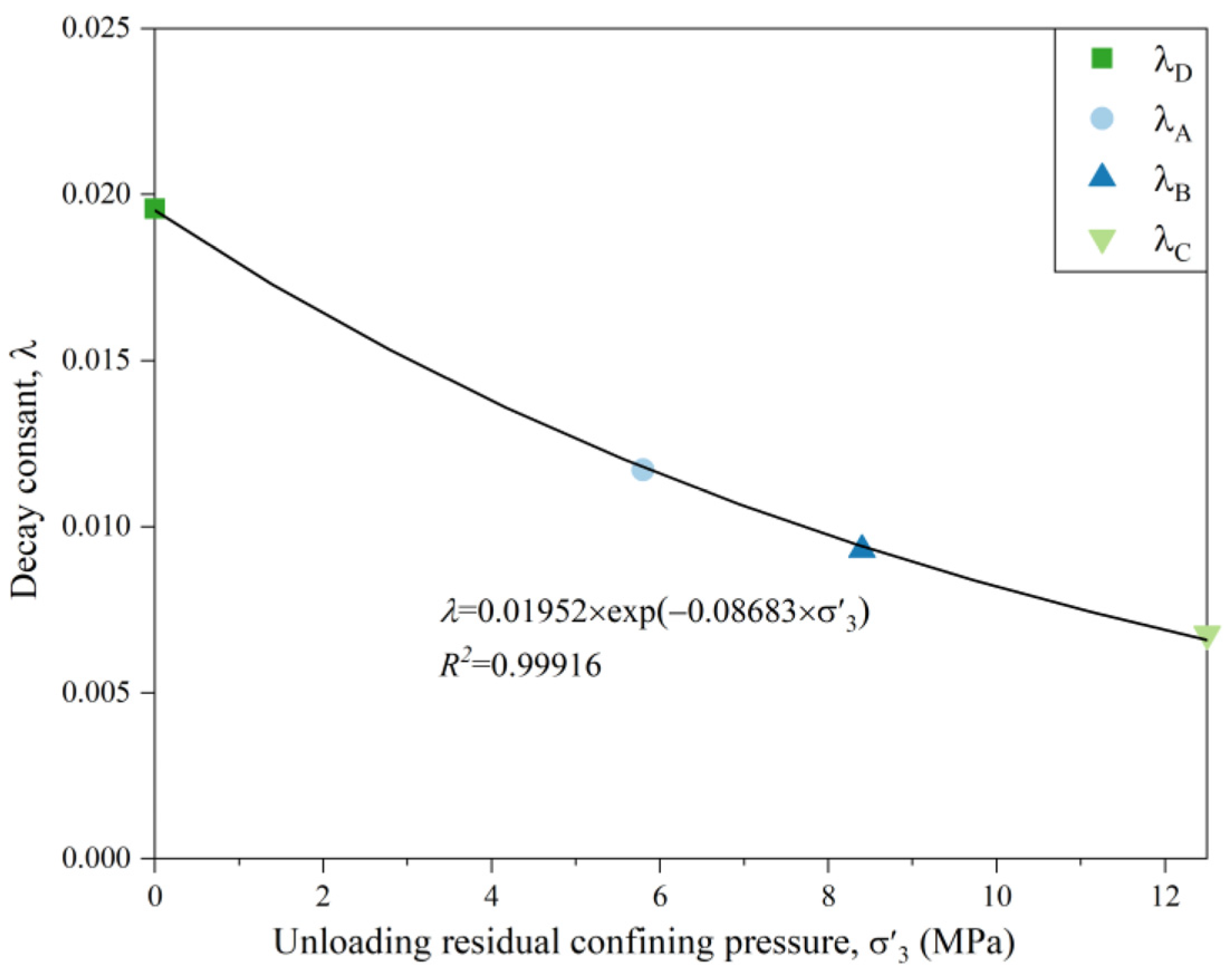
5.2. Parameter Determination
5.3. Verification
6. Conclusions
- In the process of unloading sandstone under different initial confining pressures, the evolution process of the amount of unloading on the deformation response of the rock sample is largely the same. Unloading quantities of 60% and 90% were used as the dividing points to create three stages: the slow section, uniform section, and accelerated section. A 60% unloading quantity is the dividing point for the opening and continuous expansion of microfractures induced by unloading inside the rock sample. The uniaxial strength of the unloaded-damaged samples under different initial confining pressures with 60% unloading is roughly the same, which is smaller than the uniaxial strength of the original sample, reflecting the feasibility and reasonableness of the abovementioned unloading quantity as the classification criterion of unloading damage and the unloading-damage test;
- The initial confining pressure of the three groups of unloaded-damaged samples is different, while the change in porosity with the number of freeze-thaw cycles and the value of change after freezing-thawing are constant across different initial confining pressures. This indicates that the degree and trend of freeze-thaw deterioration of unloaded-damaged samples with 60% unloading are largely the same, independent of the initial envelope pressure, so the average change in porosity can be used to measure the freeze-thaw deterioration of the unloaded-damaged samples;
- The peak strength damage rate of the unloaded-damaged samples after freeze-thaw reloading (both uniaxial and triaxial) increases with the increase in the number of freeze-thaw cycles. The unloading residual pressure value inhibits the increase; a larger value of unloading residual pressure leads to a more obvious degree of inhibition;
- Using the extended exponential attenuation model, the decay constant was modified by fitting the experimental data. The value of unloading residual confining pressure was introduced as the decay parameter and the freeze-thaw strength decay model was established with the easily determined average change in porosity. The values calculated by the model are largely consistent with the tested values. It is verified that the proposed model can reflect the decay of freeze-thaw strength using the average change in porosity after freeze-thaw cycles and can also consider the effect of unloading residual confining pressure. This reveals the micromechanical behavior induced by microstructure damage after freeze-thaw cycles of unloaded-damaged samples and predicts the decay in freeze-thaw strength. This provides some guidance for freeze-thaw hazard prediction of excavation and unloaded rock in cold regions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deprez, M.; De Kock, T.; De Schutter, G.; Cnudde, V. A review on freeze-thaw action and weathering of rocks. Earth-Sci. Rev. 2020, 203, 103143. [Google Scholar] [CrossRef]
- Li, J.; Wang, L. Theories of Unloading Rock Mass Mechanics and Its Engineering Practice; Science Press: Beijing, China, 2016. [Google Scholar]
- Huang, R. Mechanisms of large-scale landslides in China. Bull. Eng. Geol. Environ. 2011, 71, 161–170. [Google Scholar] [CrossRef]
- Deng, H.; Wang, Z.; Li, J.; Jiang, Q.; Zhang, H. Effect of unloading rate and pore water pressure on mechanical properties of sandstone. Chin. J. Geotech. Eng. 2017, 39, 1976–1983. [Google Scholar] [CrossRef]
- Ren, H.; Zhu, Y.; Wang, P.; Yu, W.; Li, P.; Zhang, Y. Experimental study on mechanical characteristics of unloaded damaged white sandstone before peak. Arab. J. Geosci. 2020, 13, 878. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Xu, W.; Qian, W. Investigation on mechanical behaviour of dacite under loading and unloading conditions. Géotech. Lett. 2019, 9, 130–135. [Google Scholar] [CrossRef]
- Meng, L.; Li, T.; Xu, J.; Chen, G.; Ma, H.; Yin, H. Deformation and failure mechanism of phyllite under the effects of THM coupling and unloading. J. Mt. Sci. 2012, 9, 788–797. [Google Scholar] [CrossRef]
- Li, X.-B.; Chen, Z.-H.; Weng, L.; Li, C.-J. Unloading responses of pre-flawed rock specimens under different unloading rates. Trans. Nonferrous Met. Soc. China 2019, 29, 1516–1526. [Google Scholar] [CrossRef]
- Xie, H.Q.; He, C.H. Study of the unloading characteristics of a rock mass using the triaxial test and damage mechanics. Int. J. Rock Mech. Min. Sci. 2004, 41, 74–80. [Google Scholar] [CrossRef]
- Feng, F.; Chen, S.; Wang, Y.; Huang, W.; Han, Z. Cracking mechanism and strength criteria evaluation of granite affected by intermediate principal stresses subjected to unloading stress state. Int. J. Rock Mech. Min. Sci. 2021, 143, 104783. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, B.; Li, C.; Cao, C.; Sui, Q.; Zhao, G.; Yu, W.; Chen, Z.; Wang, Y.; Liu, B.; et al. Experimental investigation on the spatio-temporal-energy evolution pattern of limestone fracture using acoustic emission monitoring. J. Appl. Geophys. 2022, 206, 104787. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Hou, X.; Elmo, D. Investigation of the spatial distribution pattern of 3D microcracks in single-cracked breakage. Int. J. Rock Mech. Min. Sci. 2022, 154, 105126. [Google Scholar] [CrossRef]
- Qiu, S.-L.; Feng, X.-T.; Xiao, J.-Q.; Zhang, C.-Q. An Experimental Study on the Pre-Peak Unloading Damage Evolution of Marble. Rock Mech. Rock Eng. 2013, 47, 401–419. [Google Scholar] [CrossRef]
- Li, D.; Sun, Z.; Xie, T.; Li, X.; Ranjith, P.G. Energy evolution characteristics of hard rock during triaxial failure with different loading and unloading paths. Eng. Geol. 2017, 228, 270–281. [Google Scholar] [CrossRef]
- Chen, X.; Tang, C.-A.; Yu, J.; Zhou, J.-F.; Cai, Y.-Y. Experimental investigation on deformation characteristics and permeability evolution of rock under confining pressure unloading conditions. J. Cent. South Univ. 2018, 25, 1987–2001. [Google Scholar] [CrossRef]
- Zhao, E.P.; Lu, B.; Jia, X.B. Disscusion on the Unloading—Seepage Coupled Model of Damaged Rock. Aer. Adv. Eng. Res. 2016, 75, 31–36. [Google Scholar] [CrossRef] [Green Version]
- Zhou, K.; Liu, T.; Hu, Z. Exploration of damage evolution in marble due to lateral unloading using nuclear magnetic resonance. Eng. Geol. 2018, 244, 75–85. [Google Scholar] [CrossRef]
- Weng, L.; Wu, Z.; Liu, Q. Evaluating Damage and Microcracking Behavior of Granite Using NMR Testing under Different Levels of Unconfined Compression. Int. J. Geomech. 2019, 19, 4018186. [Google Scholar] [CrossRef]
- Deng, H.; Assefa, E.; Xu, X.; Luo, Z.; Li, J.; Jiang, Q. Study on the Time-lag Failure of Sandstone with Different Degrees of Unloading Damage. Period. Polytech. Civ. Eng. 2019, 63, 206–214. [Google Scholar] [CrossRef] [Green Version]
- Manouchehrian, A.; Cai, M. Simulation of unstable rock failure under unloading conditions. Can. Geotech. J. 2016, 53, 22–34. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Li, J.; Deng, H.; Xu, X.; Chen, X. Mechanical Properties of Sandstones under Initial Unloading Damage. Adv. Civ. Eng. 2021, 2021, 6615846. [Google Scholar] [CrossRef]
- Zhu, Z.; Yu, L.; Li, J.; Su, H.; Zhang, Z.; Zhang, J. Research on acoustic emission characteristics of marble damaged by pre-peak unloading. IOP Conf. Ser. Earth Environ. Sci. 2020, 570, 32050. [Google Scholar] [CrossRef]
- Liang, Z.; Yu, Z.; Guo, L.; Huang, S.; Qin, N.; Wen, Z. Evaluation of white sandstone mechanical behaviour and the energy evolution of prepeak unloading damage. Sci. Rep. 2022, 12, 2793. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Liu, Q. Analysis of mechanism of rock failure due to freeze-thaw cycling and mechanical testing study on frozen-thawed rocks. Chin. J. Rock Mech. Eng. 2005, 24, 17. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, Z.; Li, J.; Tang, K.; Jin, J. The bedding sandstone unloading mechanical properties experimental study in the freeze-thaw cycle conditions. J. Glaciol. Geocryol. 2016, 38, 4. [Google Scholar] [CrossRef]
- Mahanta, B.; Tripathy, A.; Vishal, V.; Singh, T.N.; Ranjith, P.G. Effects of strain rate on fracture toughness and energy release rate of gas shales. Eng. Geol. 2017, 218, 39–49. [Google Scholar] [CrossRef]
- Martins, L.; Vasconcelos, G.; Lourenço, P.B.; Palha, C. Influence of the Freeze-Thaw Cycles on the Physical and Mechanical Properties of Granites. J. Mater. Civ. Eng. 2016, 28, 5. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhai, Y.; Meng, F.; Zhang, Y. Study on the Influence of Freeze-Thaw Weathering on the Mechanical Properties of Huashan Granite Strength. Rock Mech. Rock Eng. 2021, 54, 4741–4753. [Google Scholar] [CrossRef]
- Gao, J.; Xu, C.; Xi, Y.; Fan, L. Degradation of Mechanical Behavior of Sandstone under Freeze-Thaw Conditions with Different Low Temperatures. Appl. Sci. 2021, 11, 10653. [Google Scholar] [CrossRef]
- Huang, S.; Yu, S.; Ye, Y.; Ye, Z.; Cheng, A. Pore structure change and physico-mechanical properties deterioration of sandstone suffering freeze-thaw actions. Constr. Build. Mater. 2022, 330, 127200. [Google Scholar] [CrossRef]
- Li, X.; Peng, J.; Xie, Y.; Li, Q.; Zhou, T.; Wang, J.; Zheng, W.; Ao, S. Influence of High-Temperature Treatment on Strength and Failure Behaviors of a Quartz-Rich Sandstone under True Triaxial Condition. Lithosphere 2022, 2022, 3086647. [Google Scholar] [CrossRef]
- Kolay, E. Modeling the effect of freezing and thawing for sedimentary rocks. Environ. Earth Sci. 2016, 75, 210. [Google Scholar] [CrossRef]
- Mutlutürk, M.; Altindag, R.; Türk, G. A decay function model for the integrity loss of rock when subjected to recurrent cycles of freezing-thawing and heating-cooling. Int. J. Rock Mech. Min. Sci. 2004, 41, 237–244. [Google Scholar] [CrossRef]
- Aral, İ.F.; Boy, R.; Dinçer, A.R. Effects of freeze-thawing cycles on the physical and mechanical properties of basaltic and dolomitic rocks evaluated with a decay function model. Bull. Eng. Geol. Environ. 2021, 80, 2955–2962. [Google Scholar] [CrossRef]
- Jamshidi, A.; Nikudel, M.R.; Khamehchiyan, M. Evaluation of the durability of Gerdoee travertine after freeze-thaw cycles in fresh water and sodium sulfate solution by decay function models. Eng. Geol. 2016, 202, 36–43. [Google Scholar] [CrossRef]
- Eslami, J.; Walbert, C.; Beaucour, A.-L.; Bourges, A.; Noumowe, A. Influence of physical and mechanical properties on the durability of limestone subjected to freeze-thaw cycles. Constr. Build. Mater. 2018, 162, 420–429. [Google Scholar] [CrossRef]
- Wang, P.; Xu, J.; Liu, S.; Liu, S.; Wang, H. A prediction model for the dynamic mechanical degradation of sedimentary rock after a long-term freeze-thaw weathering: Considering the strain-rate effect. Cold Reg. Sci. Technol. 2016, 131, 16–23. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Xiong, X.; Zhou, K.; Li, J.-I.; Wenchao, S. Strength deterioration model of saturated sandstone under freeze-thaw cycles. Rock Soil Mech. 2019, 40, 3. [Google Scholar] [CrossRef]
- Xu, S.; Li, N.; Wang, X.; Xu, G.; Yuan, K.; Tian, Y.; Wang, L. Damage test and degradation model of saturated sandstone due to cyclic freezing and thawing of rock slopes of open-pit coal mine. Chin. J. Rock Mech. Eng. 2016, 35, 12. [Google Scholar] [CrossRef]
- Mousavi, S.Z.S.; Tavakoli, H.; Moarefvand, P.; Rezaei, M. Micro-structural, petro-graphical and mechanical studies of schist rocks under the freezing-thawing cycles. Cold Reg. Sci. Technol. 2020, 174, 103039. [Google Scholar] [CrossRef]
- Li, J.-L.; Zhou, K.-P.; Liu, W.-J.; Deng, H.-W. NMR research on deterioration characteristics of microscopic structure of sandstones in freeze-thaw cycles. Trans. Nonferrous Met. Soc. China 2016, 26, 2997–3003. [Google Scholar] [CrossRef]
- Wang, Y.; Han, J.Q.; Li, C.H. Acoustic emission and CT investigation on fracture evolution of granite containing two flaws subjected to freeze-thaw and cyclic uniaxial increasing-amplitude loading conditions. Constr. Build. Mater. 2020, 260, 119769. [Google Scholar] [CrossRef]
- Deng, H.; Zhang, H.; Li, J.; Wang, C.; Zhang, Y.; Hu, Y. Effect of water-rock interaction on unloading mechanical properties and microstructure of sandstone. Rock Soil Mech. 2018, 39, 2344–2352. [Google Scholar] [CrossRef]
- Qiu, S.; Feng, X.; Zhang, C.; Yang, J. Experimental research on mechanical properties of deep marble under different initial damage levels and unloading paths. Chin. J. Rock Mech. Eng. 2012, 31, 8. [Google Scholar] [CrossRef]
- Chen, X.; Chen, L.; Ma, B.; Zhang, X.; Du, W.; Wang, X.; Yang, C. Mechanical-characteristic evaluation of excavation unloading rock mass subject to high-temperature conditions. Eng. Fail. Anal. 2021, 130, 105757. [Google Scholar] [CrossRef]






| Number of Freeze-Thaw Cycles | Average Change of Porosity (%) | ||
|---|---|---|---|
| Group A | Group B | Group C | |
| 0 | 0.00 | 0.00 | 0.00 |
| 1 | 0.12 | 0.13 | 0.12 |
| 2 | 0.19 | 0.20 | 0.20 |
| 3 | 0.24 | 0.25 | 0.23 |
| 4 | 0.32 | 0.30 | 0.31 |
| 5 | 0.38 | 0.38 | 0.39 |
| 6 | 0.47 | 0.48 | 0.48 |
| 7 | 0.56 | 0.58 | 0.59 |
| 8 | 0.68 | 0.69 | 0.72 |
| Number of Freeze-Thaw Cycles | Triaxial Reloading Test | Uniaxial Reloading Test | ||||||
|---|---|---|---|---|---|---|---|---|
| Group A Peak Strength (MPa) | Strength Damage Rate (%) | Group B Peak Strength (MPa) | Strength Damage Rate (%) | Group C Peak Strength (MPa) | Strength Damage Rate (%) | Group D Peak Strength (MPa) | Strength Damage Rate (%) | |
| 0 | 110.66 | 0.000 | 125.41 | 0.000 | 145.79 | 0.000 | 37.20 | 0.000 |
| 2 | 107.17 | 3.153 | 122.22 | 2.544 | 143.32 | 1.694 | 34.32 | 7.742 |
| 4 | 105.29 | 4.853 | 120.51 | 3.907 | 142.35 | 2.359 | 33.70 | 9.409 |
| 6 | 103.61 | 6.371 | 118.45 | 5.549 | 140.47 | 3.649 | 32.89 | 11.586 |
| 8 | 100.10 | 9.452 | 116.08 | 7.439 | 137.60 | 5.618 | 31.33 | 15.779 |
| Fitting Parameter | Group A | Group B | Group C | Group D |
|---|---|---|---|---|
| F0 | 110.35915 | 125.06573 | 145.77302 | 36.59078 |
| λ | 0.01171 | 0.00931 | 0.00677 | 0.01957 |
| Average Change of Porosity (%) | Group A Reloading Peak Strength (MPa) | Group B Reloading Peak Strength (MPa) | Group C Reloading Peak Strength (MPa) | Group D Reloading Peak Strength (MPa) | ||||
|---|---|---|---|---|---|---|---|---|
| Calculated Values | Tested Values | Calculated Values | Tested Values | Calculated Values | Tested Values | Calculated Values | Tested Values | |
| 0.19 | 107.672 | 107.17 | 122.725 | 122.22 | 143.628 | 143.32 | 35.568 | 34.32 |
| 0.31 | 105.827 | 105.29 | 121.059 | 120.51 | 142.279 | 142.35 | 34.574 | 33.70 |
| 0.47 | 103.416 | 103.61 | 118.873 | 118.45 | 140.500 | 140.47 | 33.292 | 32.89 |
| 0.69 | 100.190 | 100.10 | 115.932 | 116.08 | 138.091 | 137.60 | 31.607 | 31.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Du, W.; Chen, L.; Ma, B.; Gong, S.; Jiang, H.; Wang, W. Mechanical Strength Decay Evaluation of Excavation Unloaded Rock Mass under Freeze-Thaw Conditions. Appl. Sci. 2022, 12, 12205. https://doi.org/10.3390/app122312205
Chen X, Du W, Chen L, Ma B, Gong S, Jiang H, Wang W. Mechanical Strength Decay Evaluation of Excavation Unloaded Rock Mass under Freeze-Thaw Conditions. Applied Sciences. 2022; 12(23):12205. https://doi.org/10.3390/app122312205
Chicago/Turabian StyleChen, Xingzhou, Wei Du, Lili Chen, Bin Ma, Sheng Gong, Hai Jiang, and Wenrui Wang. 2022. "Mechanical Strength Decay Evaluation of Excavation Unloaded Rock Mass under Freeze-Thaw Conditions" Applied Sciences 12, no. 23: 12205. https://doi.org/10.3390/app122312205
APA StyleChen, X., Du, W., Chen, L., Ma, B., Gong, S., Jiang, H., & Wang, W. (2022). Mechanical Strength Decay Evaluation of Excavation Unloaded Rock Mass under Freeze-Thaw Conditions. Applied Sciences, 12(23), 12205. https://doi.org/10.3390/app122312205










