1. Introduction
A gas-delayed blowback operation system is one of the design solutions [
1] applied in automatic firearms [
2]. It represents a development of the simple blowback operation system [
3] with a modification involving the use of additional components that slow down the movement of the recoiling assembly during the shot. In this solution (with the gas piston), a portion of the propellant gases flows out from the barrel bore through the gas port into the gas chamber and then presses down on the gas piston connected to the bolt (recoiling assembly). As a result, this method offers certain advantages, such as reduced recoil felt by the shooter, as well as the possibility of using a lighter recoiling assembly or ammunition with a higher muzzle energy. Thus, the modernization and improvement of the design of small arms with a gas-delayed blowback operation system seems to future-proof specified applications and it can be assumed that the novel weapons that use this method of working could be a useful extension to the solutions which are commonly used in the military.
Furthermore, the application of numerical methods, together with computer simulations, is justified during the development stage, with a view to reducing the duration and cost of experimental studies. To use the theoretical methods, the phenomena occurring in the firearm have to be described with both appropriate physical and mathematical models. Determination of the effect of certain individual weapon parameters on the output characteristics is one of the key stages of design optimization.
Data in the literature concerning the modeling of the gas-delayed blowback system are scarce. In study [
4], the authors made an attempt to theoretically model the action of a 9 mm pistol (probably the Heckler & Koch P7). However, after an analysis of the presented solution, it was found that many aspects raise doubts about their correctness, i.e., the construction parameters of the parts [
5] or results obtained. In addition, it seems reasonable to develop a mathematical model based on a NATO standardization document [
6]. All of these issues reinforce the assumption that it is worthwhile to undertake research to re-examine this small arms operation system solution with modern approaches.
In study [
7], the authors presented a preliminary formulation of the equations of the internal ballistic model of gas-delayed blowback operation firearms. An attempt was made to determine the effect of changing two parameters, which was a preliminary analysis of the operation of the system. In the analysis, the parameters were changed separately and the dependent influence of all parameters was not studied.
The automatic firearm action has also been analyzed in some papers [
8,
9,
10,
11] but they referred to other automatic systems (simple blowback operated, recoil operated and gas operated weapons). As was shown in studies [
12,
13], the values of time-varying interaction forces (projectile-barrel bore, projectile-cartridge case and cartridge case-cartridge chamber) are significant from the point of view of kinematic and ballistic characteristics in the considered system; therefore, it is necessary to implement them in the model.
It is important to note that many studies of the impact of individual factors on the output characteristics of weapons are conducted without consideration of the design of experimental methods (DoE). These methods are very beneficial tools and provide very informative and extensive outcomes with the possibility of reducing the research time and costs of experimental research [
14,
15,
16]. In this paper, the methods are applied to the analysis of the results of computer simulations. The simulations are based on a mathematical model describing the action of the gas-delayed blowback operation in small arms. Using the methods of the design of experiments (DoE), the significance of the effects of individual parameters on output characteristics is estimated making use of DoE methods, which is the main novelty of conducted investigations. The results created a basis for the design of a laboratory stand, designated for the validation of the theoretical model.
2. Materials and Methods
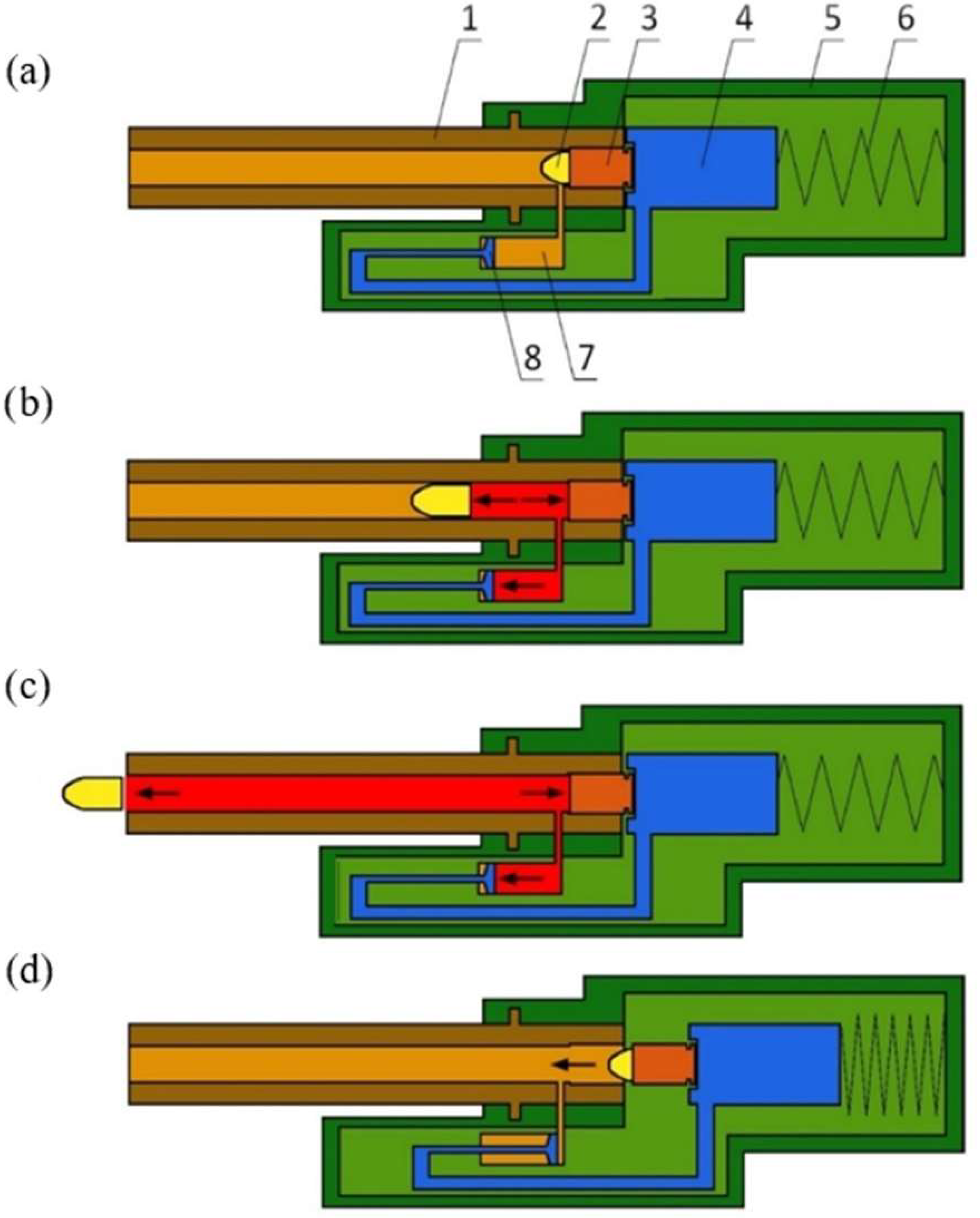
The description of the phenomena (the model of the interior ballistic) occurring in the system concerns a gas piston system in which some of the propellant gases are used to delay the recoiling assembly motion. When the shot is fired, the gases propel the projectile and, when it passes the gas port, some of the gases flow into the gas chamber and press on the front of the gas piston connected to the bolt. The scheme of the action of such a system is presented in
Figure 1.
The phenomena described in the presented mathematical model apply to the operation that starts when the propellant is ignited and completed when the pressure in the system (barrel bore and gas chamber) has the same value as the ambient pressure. The model presented in study [
7] required some improvements and, therefore—for the completeness of the description—an updated version is presented below. For the description of ballistic phenomena and kinematic equations occurring in the described model, the theory of internal ballistics and the thermodynamic approach proposed in a standardization document [
6] was mainly used. It is important that the model takes into account the forces of interaction between: the projectile and barrel bore, the projectile and cartridge case, and the cartridge case and chamber [
12,
13,
17,
18]. However, due to the preliminary quality of the model, some simplifying assumptions were accepted to solve this problem. Despite some shortcomings in comparison with distributed parameters multiphase models [
19] mainly based on finite volume approach—such as limited possibility of ignition process analysis—the lumped parameters models work well for short cartridge case systems [
13], and—with some modifications—with long cartridge case solutions [
20]. The main advantage of lumped parameters models is low computational cost of the simulation making use of numerical methods for ordinary differential equations [
21].
For this kind of system of small arms operation, the equations are as follows (the nomenclature is presented at the end of the paper):
- (a)
for the barrel bore:
the equation of the energy conservation:
- -
when the pressure in the barrel bore is higher than the pressure in the gas chamber:
considering that:
the equation describing the balance of the energy is:
- -
when the pressure in the barrel bore is lower than the pressure in the gas chamber:
considering that:
the equation describing the balance of the energy is:
- -
equation defining the barrel bore propellant gas density:
- -
equation of state of barrel bore propellant gas in the virial form:
- -
relative mass generation rate of gas produced by the combustion of the propellant:
- -
equation defining the relative mass flow rate of the propellant gases flowing between the barrel bore and the gas chamber—when the pressure in the barrel bore is higher than the pressure in the gas chamber:
- -
equation defining the relative mass flow rate of the propellant gases flowing between the barrel bore and the gas chamber—when the pressure in the barrel bore is lower than the pressure in the gas chamber:
- -
equation defining the relative mass flow rate of the propellant gases that flows to the environment (when the bullet passed the muzzle of the barrel bore):
- (b)
for the gas chamber:
the equation of the energy conservation:
- -
when the pressure in the barrel bore is higher than the pressure in the gas chamber:
considering that:
the equation describing the balance of the energy is:
- -
when the pressure in the barrel bore is lower than the pressure in the gas chamber:
taking into account the following relations:
the equation describing the balance of the energy is:
- -
equation defining the gas chamber propellant gas density:
- -
equation of the state of the gas chamber propellant gas:
- (c)
other equations:
- -
equation of the recoiling assembly motion:
- -
definition of the recoiling assembly velocity:
- -
equation of the bottom of the bullet pressure:
- -
equation of the bullet motion:
- -
definition of the bullet velocity:
Simulations were conducted for a system using 9 × 19 mm ammunition, since the designed laboratory stand will mainly be intended for such a cartridge.
Some of the significant results obtained or estimated in studies [
12,
13,
22] were used in the model. These were, primarily, the course of the dynamic vivacity (and other characteristics of propellant charge) and the interaction forces between the projectile, barrel bore, cartridge case and chamber.
Table 1 and
Table 2 show some parameters of the ammunition and weapon system used in the simulations.
Simulations were carried out using an original (own) program developed in MATLAB software, based on the above equations, definitions and data.
For the initial verification of the adopted model, some results (presented in
Table 3) reached adequate weapon specifications (including bolt mass, barrel length and recoil spring parameters) and were compared with those obtained in study [
2].
By comparing the results, it was concluded that the model seemed to be correct at this verification stage. Slight discrepancies may be caused due to the influence of some simplifications (especially concerning the ignition process or air resistance) or not taking into account the heat transfer process to the barrel [
13,
17], which is relatively negligible for fast-burning propellants applied in pistol ammunition [
22]. However, detailed verification and validation of the model in the area concerning gas flow through the gas port, between the barrel bore and the gas chamber, and the associated impact on the action of the recoiling assembly, could be carried out following the experimental tests performed on a newly designed laboratory stand.
3. Results
The purpose of this analysis is to determine the impact of individual parameters of a weapon on the kinematic characteristic of the weapon system and to identify the parameters which have a negligible influence on the analyzed output parameter. Eliminating these parameters from the set of parameters analyzed in the experimental studies will reduce the time and costs of the testing. Moreover, determining the character of the influence of a given parameter (linear or nonlinear) will be useful in the creation of an experimental plan.
Therefore, if there is a mathematical model of the object (which was described in the previous section) and the results of simulations of the model are known, we can determine the relationship between the measured value (recoiling assembly velocity) and the value of the factor to give the function of the object. To accomplish this objective, the design of experimental methods are very useful.
Then, it is necessary to define the input parameters (factors) and their levels (from chosen ranges of the values), as well as to choose the experimental plan (linking the levels in treatments). The choice of ranges was influenced by limitations resulting from the design of the laboratory stand. For example, the minimum value of the gas port position was determined by the necessity to locate the hole in front of the forward edge of the cartridge case and the minimum value of the recoiling assembly mass results from the minimum size of the bolt necessary to mount it in the stand and install the components on it.
The number of factors (N) is 5 and these factors are: gas port location, gas port diameter, recoiling assembly mass, gas chamber initial volume and recoil spring stiffness. The values of the factors are shown in
Table 4; for a better presentation of the plan, dimensionless values are also used.
The relation between coded and not coded values of factors is:
where:
i—serial number of a treatment,
xki/Xki—not coded/coded level of factor xk/Xk in the i-th treatment.
The complete plan can be used to provide all possible combinations of values of the factors. However, a major weakness in the complete plan is the high number of treatments; therefore, it is reasonable to apply the fractional plan, which consists of some selected treatments of the two-level complete plan [
23]. The chosen treatments are sufficient to determine the coefficients of the linear function which approximates the response surface.
The first plan is a two-level fractional plan. The chosen contrast value is: I = 1. The number of treatments is 8 and two generating relations are used:
The coded form of the plan is presented in
Table 5.
For the first fractional plan, the function describing the response surface is a linear function and is calculated as:
The values of the coefficients indicate that the influence of the factors
X1,
X2 and
X3 are significant; however, the influence of the factors
X4 and
X5 cannot be neglected.
Table 6 presents the results of simulations compared with the results approximated by the obtained function.
Comparing the results obtained from the numerical simulation and those approximated by the linear function, the differences between these results were found to be slight, with a maximum difference of 0.09 (approximately 2.05%). Therefore, it should be considered that the function of the object was calculated correctly. However, in order to be sure that the object can be considered to be linear (within the assumed range of parameters), one must perform the analysis for the two-level fractional plan in which one of the contrasts is equal to −1.
Therefore, for the second two-level fractional plan, the contrast for the fifth factor was changed to
I = (−1) and the other values remained unchanged. Furthermore, for this plan, the calculation of values using a linear function with coefficients calculated for the first plan was carried out—the results are shown in the ‘Approximation’ column in
Table 7. The function describing the response surface was calculated as:
Although the function gives a good estimation of the results from simulations, the maximum difference value is 0.09 (about 2.01%), the approximated values are significantly different. The recoiling assembly velocity values for the second plan, according to the coefficients determined for the first plan, compared to the values from the simulation show a discrepancy of 5.7%. It is also puzzling that the coefficient at X5 has changed its sign. Values of coefficients at other factors have not changed considerably. These findings may indicate that the influence of the parameters is not linear.
The third plan is formed by the connection of the first and second two-level fractional plan and so the number of treatments is 16 (
Table 8).
For the third plan, the function describing the response surface was calculated as:
For the third plan, the maximum difference value is 0.24 (about 4.13%). The functions of the object obtained for all three plans are summarized in
Table 9.
Based on the obtained functions, it can be concluded that the coefficient values for plan 3 are intermediate between those calculated for plan 1 and plan 2. However, the coefficient at the fifth factor (the recoil spring stiffness) is very small, which may indicate the possibility of neglecting the influence of this parameter, or the influence of some nonlinearities.
To verify the hypothesis, computations were carried out for the Bi plan [
23] and the results were approximated by a quadratic function. The plan consists of a core, in the form of a two-level fractional plan (or, optionally, a two-level complete plan) and star points with the star arm equal to 1. The center of the plan is not part of this plan. For five factors, the core of the plan comprised a minimum of 2
5−1 treatments. Therefore, the entire plan included 26 treatments (16 for the core and 10 star points), summarized in
Table 10.
For the Bi plan, the function describing the response surface is:
and the maximum relative error is 1.36%. Moreover, the values of the response for mean values of factors (for the center of the plan) were calculated using the obtained functions, and summarized in
Table 11. Thus, it is possible to check the correctness of the approximation, as well as to represent the graphs more accurately.
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6 show the functions of the object obtained for each plan when only one factor is changed and other factors have values for the center of the plan. In addition, the graphs indicate (with stars) the values of the recoil assembly velocity obtained from the simulation for the limiting values of the factor and for the center of the plan. In the first three graphs, the functions of plan 3 almost overlap with those of plan 1 and 2, which is why they are faintly visible.
4. Discussion
By analyzing the obtained results and graphs, it can be concluded that the dependence of the recoiling assembly velocity on the factors is not linear. However, the calculated and presented quadratic function approximation gives a very close estimation of the simulation results. The function obtained from plan Bi allows us to state that the strongest influences on the results are (in decreasing order): the recoiling assembly mass, the gas port location and the gas port diameter. Theoretically, increasing the recoiling assembly mass is the easiest way to reduce the recoiling assembly velocity (such a solution is characteristic of simple blowback weapons). The consequence of this is to primarily increase the weight of the entire firearm. Therefore, it was very significant to verify the influence of the other factors.
It is significant that the expected result was that the most advantageous solution—from the point of view of recoiling assembly braking—and is the shortest distance (for the starting position of the bullet—when the cartridge is in the chamber) of the bullet to the gas port. The minimum value of this distance is forced by the cartridge case length. Then, the largest coefficient in the quadratic function has this factor. This is justified by the fact that the location of the gas port, in close proximity to the front edge of the cartridge case, causes the propellant gases to have energy, which results in a significant decrease in recoiling assembly velocity. As the port is moved toward the muzzle of the barrel, much less gas flows into the gas chamber, and so the deceleration is increasingly negligible. This is largely due to the characteristics of pistol ammunition, in which a propellant charge is burned very dynamically.
As can be seen, the recoil spring stiffness has the least influence; it is practically insignificant in the assumed range (even though the maximum value is twice the minimum). The research reported in study [
24] also found negligibly small effects of this factor on recoiling assembly velocity; these results were for gas-operated small arms. Therefore, it was concluded that its impact would not be further investigated. This is very important when considering the cost and time-consuming nature of research.