Privacy-Preserved Image Protection Supporting Different Access Rights

Abstract

The boom in cloud computing and social networking has led to a large number of online users in the networks. It is necessary to use appropriate privacy protection mechanisms to prevent personal privacy leakage. In general, image privacy protection techniques proceed with the whole image. However, the image may contain multiple users’ information, and different people’s data may require different privacy protection. In addition, cloud servers are semi-trusted instead of trusted service providers due to unknown security vulnerabilities and the possibility of grabbing sensitive data from the cloud server. In order to provide image protection with different privacy-preserved access rights and to prevent the cloud server from retrieving sensitive information from the image, we propose a privacy-preserved scheme that supports different privacy-preserved access rights in a single image based on the difficulty of solving the factorization problem and the discrete logarithm problem. The cloud server performed the image management method without knowing the privacy information contained in the protected images. By working out the proposed scheme in detail, we experimentally validate the scheme and discuss various options of access rights in practice.

1. Introduction

With the emergence of digital technology, the world is continuously evolving and rapidly changing. Today, Internet communication has bridged the gap between people. Communication over the Internet ensures an instant connection between people on different sides of the world. Therefore, many cloud service companies offer a cloud-based platform, application, or storage services that allow people to share photos, videos, messages, locations, etc. Among these services, photo sharing and tagging friends in pictures have always been the most popular features of social networks. People like to share or post photos of themselves, family, friends, their life or special activities on their social networks. The photo sharing market is growing at a good clip, and hence we have recently seen an explosion of services that specifically revolve around sharing photos.

Visual cryptography [1,2,3,4,5,6] and information hiding [7,8,9,10,11,12,13,14,15] are proposed for image privacy protection. Social networks also provide some management to let image owners control photo permissions. Even though the account access permission limits only followers or who in the same group can see those photos, the photos could also be leaked by careless transmissions. We note that private information may become publicly available through illegal sources. It may threaten portrait rights and the personal privacy of people who also appeared in the same photo. The traditional mechanisms implement privacy protection only on the whole photo but not special regions and cannot set different privacy permission in one image. We should consider the different needs of protected privacy in different cases. Consequently, we need to develop a new mechanism to do privacy protection separately in a single photo on cloud-based services.

Nowadays, cloud computing is gaining popularity and confidence. Cloud computing has become a convenient and efficient way for companies to store, manage, and access data through the Internet instead of keeping the data on a local drive. Apart from being cost-effective, cloud computing provides elasticity and agility. Corporate cloud computing grows rapidly by more than 35% a year and reached $55.5 billion in Q4 of 2020 [16]. However, as the popularity of cloud computing grows, so will the potential security risks. We cannot completely trust cloud service providers (CSP) due to the fact that the success of accessing cloud services relies on network and authentication. Crashed network and unauthorized access disrupt the cloud-based services. Although CSPs are regulated by stringent regulations, assuming that the data owner and CSPs are in the same trusted domain may not be true since the CSPs may access sensitive information without authorization. Lapse in security risk management could lead to physical or financial harm.

Take celebrity photo leaks in 2014 [17], for example. Almost 500 private pictures of various celebrities were posted on the imageboard website, and later disseminated by other people on social networks. These photos were leaked via the online storage provided by Apple’s cloud services suite iCloud for automatically backing up photos from iOS devices [17]. Apple reported that the victims’ account information was cracked using brute-force attack in the Find My iPhone service which allowed hackers to make unlimited tries to guess victims’ passwords. Many celebrities pursued legal actions and claimed the leak to be a massive invasion of their privacy. It not only violated users’ privacy rights but damaged the company’s reputation.

Moreover, there were two serious data leaks caused by misconfigured Amazon Simple Storage Service (Amazon S3) [18]. One was found by Noah Rotem and Ran Locar [19]. The information of 1000 consultants and consulting firms was breached. The other data leak involved UK-based Fresh Film Productions, which exposed the sensitive data of crews, actors and collaborations [20]. Amazon S3 is a public object storage service that provides management features so that you can configure access to your data to meet your specific business requirements. However, the two leaks indicated that the owners did not define clearly and make the proper settings.

CSP may also have uncovered flaws. In 2020, an authentication problem on Google cloud platform (GCP) shell was found. It could make hackers gain root access to reconfigure any containers [21]. In 2021, Microsoft warned thousands of cloud computing customers that their Microsoft Azure Cosmos DB may have been exposed to intruders [22]. The research team Wiz found that the customers’ primary keys were long-lived and allowed full permission access to customer data [23]. As a result of these reports, we cannot rely on CSP completely.

CSP is semi-reliable; as a result, it is a challenge to accomplish a different permission of privacy protection in a single image. Almuflih et al. [24] proposed a key exchange method by using identity-based encryption in a multipath TCP environment. They also presented the feature-map-based detection for adversarial attacks [25]. Sultana [26] presented a privacy-preserved face image recognition system on MSB encrypted face images. Kumari et al. [27] proposed a secure biometrics-based multi-cloud-server authentication scheme. It used cloud storage and computing power while it did not let the cloud server know the content. They used an elliptic curve cryptosystem (ECC) to build keys among users, registration authorities and cloud servers, and proposed a biometric-based authentication system to make authentication much stricter. Registration authorities authenticate not only users but the cloud servers to make the whole process more secure.

In this paper, we present a privacy-preserved method that supports different access rights in a single image for privacy protection based on the difficulty of solving factoring problems and discrete logarithm problems. We use an access policy to decide who can decrypt the cipher blocks of the image to satisfy every privacy requirement in the original image. The privacy-preserved images with the access policy and authentication information are uploaded to the cloud server. When exploring the image, users follow the authentication information to confirm the blocks that are accessible in their permission to get a decryption key of the blocks to obtain the original image. With the designed strategy, the image management is executed by cloud servers such that cloud servers are not aware of the private information contained in the protected image.

To make this paper self-contained, in Section 2 we introduce the basic concepts of RSA public-key cryptography [28] and ElGamal public-key cryptography [29]. Section 3 explains the proposed scheme consisting of image protection method and image management method. Experimental results and their security analysis appear in Section 4. We also demonstrate how to perform different access rights in a single image for privacy protection. Finally, the paper is concluded in Section 5.

2. Related Works

We designed a privacy-preserved scheme which sets different permissions in a single image with the difficulty of solving the factoring problem and the difficulty of solving the discrete logarithm problem. Hence, we now review some elementary concepts and results from cryptography including RSA public-key cryptography [28] and ElGamal public-key cryptography [29] that are relevant for our paper.

2.1. RSA Public-Key Cryptography

RSA public-key cryptography was proposed by Rivest, Shamir, and Adleman [28] in 1978, and it is the first asymmetric cryptography algorithm in the world. Asymmetric cryptography means that RSA works on two different keys: public key and private key. Data can be encrypted via the public key but can only be decrypted by someone who knows the private key. RSA can be used for encryption and digital signatures. The security of RSA relies on the difficulty of solving the factoring problem, which is an open question about factoring the product of two large prime numbers. The applications of RSA are described as follows.

2.1.1. Key Generation

We assume that the user U₁ generates a public key and a private key. The keys for the RSA algorithm are generated as follows.

Step 1.

U₁ randomly chooses two large prime numbers p₁ and q₁ and computes n₁ = p₁ × q₁;

Step 2.

U₁ chooses an integer e₁ as a public key such that gcd(e₁, φ(n₁)) = 1 and φ(n₁) = (p₁ − 1) × (q₁ − 1);

Step 3.

U₁ computes the private key d₁ such that d₁ satisfies d₁ × e₁ ≡ 1 (mod φ(n₁));

Step 4.

U₁ publishes the public key (e₁, n₁) and keeps the private key d₁ secret.

The difficulty of solving factoring problem can be defined as follows. When n₁ is the product of two large prime numbers p₁ and q₁ only n₁ is known, it is hard to factor n₁ to find p₁ and q₁.

2.1.2. Encryption and Decryption

Assume that the user U₂ wants to send a message m to the user U₁. U₂ uses U₁’s public key (e₁, n₁) to encrypt m to generate the ciphertext ${C=m}^{e_1}{ \mathrm{mod} n}_1$, and sends it to U₁. When receiving C, U₁ can use U₁’s private key d₁ to recover the original message by computing ${m=C}^{d_1}{ \mathrm{mod} n}_1$.

2.1.3. Digital Signature

In order to verify the origin of messages, RSA can also be used for digital signatures. Assume that the user U₁ wants to send a signed message S to the user U₂. U₁ uses U₁’s private key d₁ to sign the message m and generates a digital signature $S=m^{d_1} \mathrm{mod} n_1$. When U₂ receives the signed message S and m, U₂ can use U₁’s public key (e₁, n₁) to authenticate whether S is generated by U₁ or not. U₂ computes $m^{\prime }=S^{e_1}{ \mathrm{mod} n}_1$ and compares m with m′. If m and m′ are the same, U₂ knows that S is the digital signature of m signed by U₁ and trusts that the message has not been tampered with since being sent.

2.2. ElGamal Public-Key Cryptography

ElGamal public-key cryptography is an asymmetric encryption algorithm, which was proposed by ElGamal [29] in 1985. Different from RSA, ElGamal encryption is probabilistic, meaning that one plaintext can be encrypted to many possible different ciphertexts. The security of ElGamal encryption depends upon the difficulty of solving the discrete logarithm problem. The applications of ElGamal encryption are described as follows.

2.2.1. Key Generation

System initially chooses two global parameters p and g, where p is a large prime number and g is the primitive root of p. The user U₁ generates a public key and a private key as follows.

Step 1.

U₁ arbitrarily chooses an integer x₁ as a private key;

Step 2.

U₁ computes the public key $y_1=g^{x_1} \mathrm{mod} p$;

Step 3.

U₁ publishes the public key y₁ and keeps the private key x₁ secret.

The difficulty of solving the discrete logarithm problem can be defined as follows. When $y_1=g^{x_1} \mathrm{mod} p$ and only y₁, p and g are known, it is hard to retrieve x₁.

2.2.2. Encryption and Decryption

Assume that the user U₂ wants to encrypt a message m to the user U₁. U₂ chooses a random number r and computes ${b=g}^r \mathrm{mod} p$ and ${c=m \times y}_1{}^r \mathrm{mod} p$. U₂ sends the ciphertext (b, c) to U₁. When receiving (b, c), U₁ can use U₁’s private key x₁ to recover the original message by computing ${m=c \times (b}^{x_1}{)}^{-1} \mathrm{mod} p$.

2.2.3. Digital Signature

Assume that the user U₁ wants to send a signed message to the user U₂. A message m is signed by U₁ as follows.

Step 1.

U₁ chooses a random number k such that gcd(k, p − 1) = 1;

Step 2.

U₁ computes r = g^k mod p;

Step 3.

U₁ finds s satisfying m= (x₁r + ks) mod (p − 1);

Step 4.

U₁ attaches the signature (r, s) to the message.

When U₂ receives the signed message (r, s) and m, U₂ can use U₁’s public key y₁ to authenticate the signed message. The signature is valid if and only if g^m ≡ y₁^rr^s (mod p).

3. Proposed Scheme

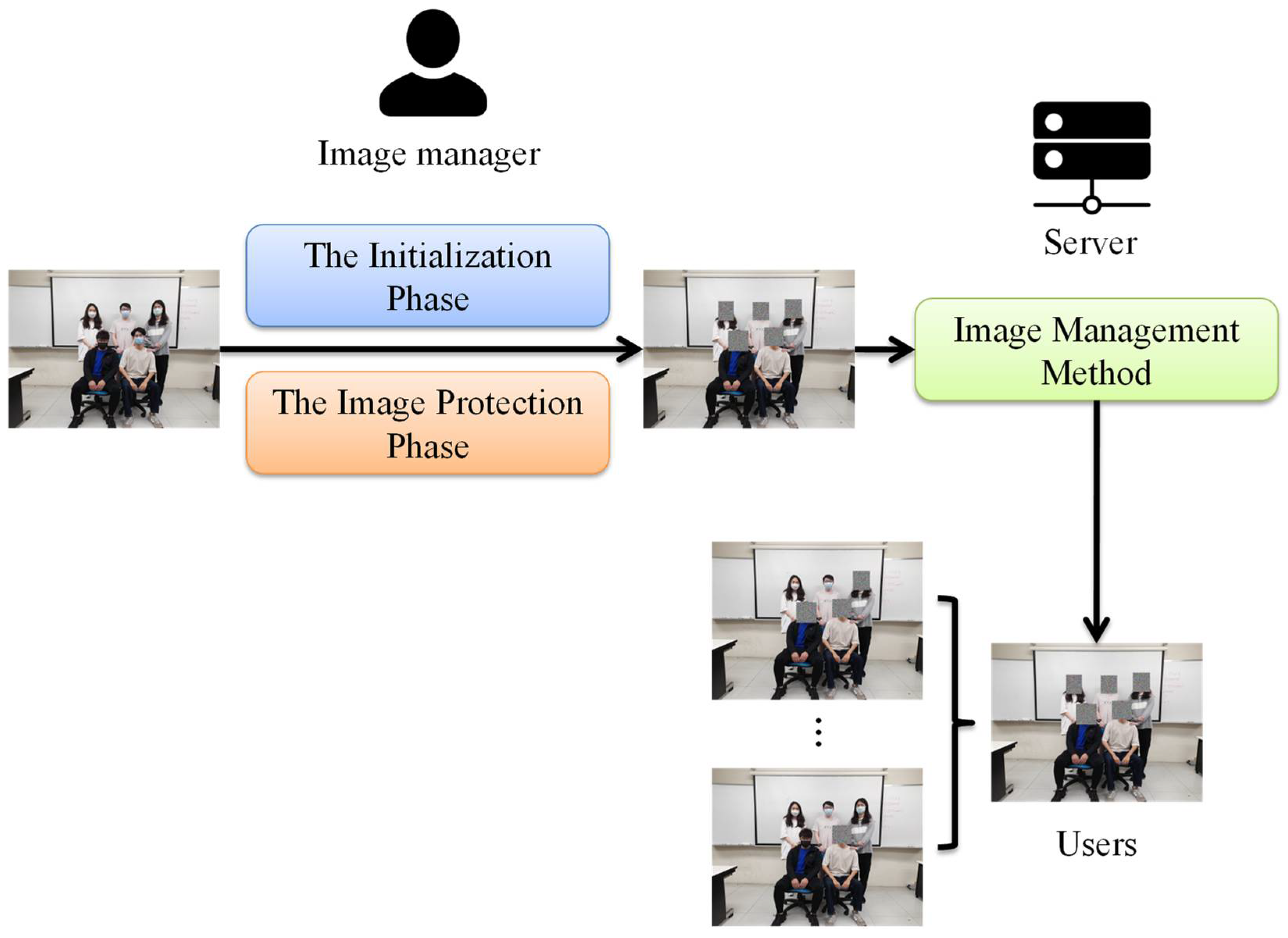
We propose a privacy-preserved scheme that supports different privacy-preserved access rights in a single image based on the difficulty of solving the factorization problem and the discrete logarithm problem. As shown in Figure 1, the image manager can formulate the access policy for specific users in the initialization phase. According to the access policy, specific users can read the original part of authorized blocks in a single image. To prevent private content from being exposed to unauthorized access, the image manager first encrypts the original image in the image protection phase before sending it to the cloud server. The protected images with the access policy will be uploaded to the cloud server. When a user performs image retrieval, the cloud server will provide the user with corresponding authorized images and authentication information according to the access policy. In the image management method, the authorized user can compute the decrypted keys to recover the original content of image blocks. The proposed schemes consisting of an image protection method and an image management method are described as follows.

3.1. Image Protection Method

The image protection method supporting different access rights in a single image for privacy protection is mainly composed of the initialization phase and image protection phase. In the initialization phase, the image manager can configure system parameters and generate keys for every user according to the access policy. In the image protection phase, the image in need of protection is set access rights on blocks to generate the corresponding encrypted image and authentication information. The initialization phase and the image protection phase are presented in the following.

3.1.1. The Initialization Phase

Based on the users’ intention, the image manager institutes the access policy T which comprises α disjoint authorized classes C_j for j = 1, 2, …, α. Each user U_i should belong to a single authorized class C_j, and each authorized class may contain one or several users. The access policy defines C_w ≤ C_r if C_r can access the data of C_w.

First, the image manager chooses two prime numbers p and q and g which is the primitive root modulo n, where n = p × q. Then, the image manager executes Key Generation Algorithm (Algorithm 1). After C_j generates a public key e_j, an encrypted key SK_j, a derivative key DK_j and partial authorized information PT_j, the image manager sends PT_j= {C_r |C_r ≤ C_j}, DK_j, and {e_r |C_r ≤ C_j and C_r ∈ {C₁, C₂,…, C_α}} to user U_i ∈ C_j through a secure channel. The image manager keeps SK_j secret and sends T and e_j to the cloud server. The initialization phase is given in Key Generation Algorithm (Algorithm 1).

Algorithm 1 Key Generation Algorithm.

Input: T

Output: ej, SKj, DKj, and PTj for j = 1, 2, …, α

Step 1. For j = 1, 2, …, α, choose ej, where gcd(ej, ϕ(n)) = 1 and er ≠ ew when r ≠ w; Step 2. For j = 1, 2, …, α, compute dj such that dj × ej ≡ 1 (mod ϕ(n)); Step 3. For j = 1, 2, …, α, compute SKj = $g^{d_j}\mathrm{mod}n$; Step 4. For j = 1, 2, …, α, compute DKj = $g^{{\displaystyle \prod }_{C_r\le C_j}{d}_r}\mathrm{mod}n$; Step 5. According to T, generate PTj = {Cr |Cr < Cj} for j = 1, 2, …, α.

3.1.2. The Image Protection Phase

In order to protect data privacy, the privacy-preserved image should be processed before sending to the cloud server. The image manager executes Image Protection Algorithm (Algorithm 2) to generate an encrypted image EI, image map IM, authentication information AI, and the number of authorized classes δ. Then, EI, IM, AI and δ are uploaded to the cloud server. The flowchart of the Image Protection Algorithm (Algorithm 2) is shown in Figure 2.

Image Protection Algorithm (Algorithm 2) consists of Image Map and Authentication Information Generation Algorithm (Algorithm 3), Coding Algorithm (Algorithm 4), and Image Encryption Algorithm Algorithm (Algorithm 5). First of all, the image manager defines the mapping between pixels and authorized classes. Image Map and Authentication Information Generation Algorithm (Algorithm 3) and Coding Algorithm (Algorithm 4) are then performed to compute the number of total authorized classes δ to generate the image map IM and the authentication information AI = {(C₁′, Code₁), (C₂′, Code₂), …, (C_δ′, Code_δ)}. The image map IM, authentication information AI, and the number of authorized classes δ are used to execute Image Encryption Algorithm (Algorithm 5) to obtain the encrypted image EI. Note that simple exclusive-or operation or symmetric encryption can be used for encryption in Image Encryption Algorithm (Algorithm 5). Using symmetric encryption for encryption is better due to the high-level security, however the fixed-length groups of bits are required in block cipher algorithms, such as AES and 3DES.

Algorithm 2 Image Protection Algorithm.

Input: An original image and SKj for j = 1, 2, …, α

Output: The encrypted image EI, image map IM, authentication information AI, the number δ of the involved access rights

Step 1. Define the protection pixels of the original image and the corresponding classes; Step 2. Execute Image Map and Authentication Information Generation Algorithm (Algorithm 3) with a protection-pixel-defined image and the corresponding classes as input to get image map IM, authentication information AI, and the number δ of the involved access rights, where AI = {(C1′, Code1), (C2′, Code2), …, (Cδ′, Codeδ)}; Step 3. Execute Image Encryption Algorithm (Algorithm 5) with the original image, IM, AI = {(C1′, Code1), (C2′, Code2), …, (Cδ′, Codeδ)}, and SKj′ of Cj′ for j = 1, 2, ..., δ as input to get the encrypted image EI.

Algorithm 3 Image Map and Authentication Information Generation Algorithm.

Input: A protection-pixel-defined image and the corresponding classes

Output: Image map IM, authentication information AI, and the number δ of the involved access rights

Step 1. Determine the number δ of the involved classes Cj′’s, where Cj′ ∈ {C1, C2, …, Cα}; Step 2. Compute φ = $\lceil {\log }_2(1+\delta )\rceil$; Step 3. Execute Coding Algorithm (Algorithm 4) to get (Cj′, Codej) for j = 1, 2, ..., δ; Step 4. Set AI = {(C1′, Code1), (C2′, Code2), …, (Cδ′, Codeδ)}; Step 5. With AI, read the protection-pixel-defined image pixel by pixel from left to right and from top to down, and generate a tile of φ bits in IM with the code of the related class for each read pixel. If the pixel does not need to be protected, the code for the tile will be 00...02 of φ bits.

Algorithm 4 Coding Algorithm.

Input: φ and δ involved classes Cj′ for j = 1, 2, ..., δ

Output: (Cj′, Codej) for j = 1, 2, ..., δ

For j = 1, 2, ..., δ, generate the code Codej of φ bits for Cj′ by setting Codej = j2, where j2 denotes the binary representation of j.

Algorithm 5 Image Encryption Algorithm.

Input: The original image, IM, AI = {(C1′, Code1), (C2′, Code2), …, (Cδ′, Codeδ)}, and SKj′ of Cj′ for j = 1, 2, ..., δ

Output: The encrypted image EI

Step 1. According to tiles in IM with Codej, get the corresponding pixels in the original image to form the bit string Plaintextj for j = 1, 2, ..., δ; Step 2. For j = 1, 2, ..., δ, encrypt Plaintextj with SKj′ to get Ciphertextj and replace Plaintextj in the original image with Ciphertextj; Step 3. Obtain EI.

3.2. Image Management Method

The cloud server can provide privacy-preserved image retrieval without knowing the data privacy. The user U_i (U_i ∈ C_w) sends a request to the cloud server to ask to see an encrypted image EI. The cloud server can determine whether the user has rights to access this image or not according to the access policy T. The user U_i has the access rights if C_j′ < C_w in T and then the cloud server will send EI, IM, AI and δ to U_i. Since the image manager sends PT_j= {C_r |C_r ≤ C_j}, DK_j, and {e_r |C_r ≤ C_j and C_r ∈ {C₁, C₂,…, C_α}} to user U_i ∈ C_j through a secure channel in the initialization phase of the image protection method, U_i can execute the following steps to recover the original content of accessible blocks.

Step 1.

For each accessible C_j′ in EI, U_i computes SK_j′ = $D{K}_w{}^{{\displaystyle \prod _{C_{\eta }\hspace{0.17em}\in \hspace{0.17em}P{T}_w-\left\{C_j{}^{\prime }\right\}}{e}_{\eta }}} \mathrm{mod}n$ according to PT_w;

Step 2.

For each accessible C_j′ in EI, U_i uses Code_j and IM to find the region of the authorized pixels in EI;

Step 3.

For the region of the authorized pixels of C_j′, U_i uses SK_j′ to decrypt the encrypted pixels to recover the original content.

4. Experimental Results

In this section, we conduct several experiments to evaluate the performance of our proposed scheme. The proposed scheme is implemented using python 3.10.4 and an open source pycryptodome 3.14.1 library on a PC with Intel Core i7-8750H 2.20 GHz CPU, 8 GB RAM, and 64-bits Windows 11 system. To make the process more secure and effective, an AES symmetric cryptosystem is used to encrypt the privacy-protected pixels with secret and derivative keys generated by RSA [28] and ElGamal [29]. The encrypted blocks can be decrypted by the derivative key and users’ public keys according to the access policy. To demonstrate the feasibility and effectiveness of our scheme for privacy protection, portrait images are used in the analysis.

4.1. Initialization

In the initialization phase, we take two large 128-bit prime numbers p and q validated by Miller Rabin Primality test [30] and then multiply them together to create a modulus n. As shown in Key Generation Algorithm (Algorithm 1), we use RSA cryptosystem to generate C_j’s public key e_j and private key d_j, and combine ElGamal cryptosystem to obtain secret key SK_j and derivative key DK_j. Let us assume that we compute n = 3602891806881971 and g = 29881307. The parameters of C_j used in the initialization phase are listed in

Table 1. The parameters of C_j.

Parameters	j = 1	j = 2	j = 3
ej	23185931	24590087	29512477
dj	3078401025127763	3107156642851655	2843269558133509
SKj	1616955632228291	3391708457587729	2316953048295578
DKj	1616955632228291	203896588144105	2683948244951649

.

4.2. Evaluation

We predetermine the privacy blocks that need to be protected to create the access policy. Let us assume that each user is in one class and each class has one access right in the access policy. According to the image map IM and authentication information AI, RGB layers of face region Plaintext_j are encrypted by AES with SK_j. Figure 3 shows the encrypted result of the test portrait image. We can see from Figure 3 that the distribution of encrypted pixel values is relatively uniform and it has no relationship with the original image.

The user sends a request to the cloud server to ask for seeing the encrypted image. The cloud server can determine if the user has rights to access this image or not according to access policy T. When receiving the derivative key DK_j and corresponding public keys, the user can compute SK_j′ to decrypt the encrypted blocks. Taking DK₂ and e₂ as an example, computing the SK₁′ of C₂ as ${DK}_2^{e_2}$ mod n = 203896588144105^24590087 mod 3602891806881971 = 1616955632228291 to decrypt the block of C₁. The decrypted results for different accessible classes C₁, C₂, and C₃ are shown in Figure 4. Note that the users cannot decrypt other privacy-protected blocks while they do not have access rights on them in access policy.

For adapting to different access policies, we try to encrypt three blocks for single class, and one block for different users in the same class, which is shown in Figure 5. The corresponding decryptions of multi-blocks are given in Figure 6. We can see that there is no difference between different users and a single user since encryption and decryption are dependent on authorized classes. Furthermore, we also notice that the quantity of blocks needed for a class does not lead to any encryption and decryption failure.

The above examples are considered as the hierarchical access control. We can see in Figure 7a that the class C₃ can access every class since it has a very high level of permissions. The class C₂ can access the class C₁, whereas it cannot access the class C₃. As a result, the hierarchical access control may have some restrictions on data access. To make the data access more flexible, the proposed method can provide a flexible access control as shown in Figure 7b. The class C₂ and class C₃ can access each other; however, only the class C₂ can access the class C₁. Figure 8 shows the result of the flexible access control. The parameters of C_j used for Figure 7b in the initialization phase are listed in

Table 2. The parameters of C_j for Figure 7b.

Parameters	j = 1	j = 2	j = 3
ej	18082907	33389011	18714097
dj	1421008669804883	3325689139217035	2183403614944417
SKj	2294561867680533	2547499887988133	1000342793147208
DKj	2294561867680533	117922932426603	2822790476719118

. For the class C₃, it can compute SK₂′ of C₃ as ${DK}_3^{e_3}$ mod n = 2822790476719118^18714097 mod 3602891806881971 = 2547499887988133 to decrypt the block of C₂. However, it cannot access the class C₁ since it cannot get SK₁′ by ${DK}_3^{e_3\times e_2}$ mod n = 2822790476719118^{(18714097×33389011)} mod 3602891806881971 = 29881307 ≠ 2294561867680533.

Therefore, the proposed method can support flexible access control in practice. The k out of n visual cryptography [1,2,3,4,5,6] can also be extended into a secret sharing scheme. Given a secret image, it will generate n transparencies so that the secret image is revealed if any k or more of them are stacked together but totally concealed if fewer than k transparencies are stacked together. It allows a secret image to be encrypted in such a way that the decrypted information appears as a visual image for human senses. To achieve this end, there is an expansion of space requirement in visual cryptography. The decrypted secret image is an enlarged visual image rather than a real secret image. Moreover, it can be used as a (k, n) threshold scheme, whereas it cannot be designed for a flexible access control for specific users.

We note that the image map IM must be communicated to the users along with the encrypted image for image decryption. The size of the image map depends on the number of authorized classes δ. For each pixel, we use log₂(1 + δ) bits to represent its corresponding authorized class. Figure 9 gives an image map example of three authorized classes. In Figure 9, three 10 × 10-pixel blocks B₁, B₂, and B₃ and their corresponding IM data are shown. For each pixel, “00” denotes the non-encryption pixel, “01” represents the class C₁, “10” represents the class C₂, and “11” represents the class C₃. As a result, the original color image is 24 bits per pixel (bpp) and its corresponding image map for three authorized classes is 2 bpp. We can see in Figure 9 that the runs of data that mean the same value occur in consecutive elements and can be used to further reduce the size by using lossless data compression algorithms, such as run-length encoding and modified Huffman coding. Thus, the overhead information that needs to be communicated to the users is small.

4.3. Security Analysis

For the purpose of promising safe privacy protection, RSA and ElGamal whose security rely on the difficulty of solving factoring problems and discrete logarithm problems are used in our key generation as described in Key Generation Algorithm (Algorithm 1). To see how the sensitive keys cannot be disclosed from the image protection algorithm, we simulate some scenarios where an adversary who has the advantage of calculation attempts to illegally access the private content.

4.3.1. Scenario 1

Let us assume that an adversary who has corresponding public keys {e′_r | C′_r ≤ C′_j and C′_r ∈ {C′₁, C′₂, …, C′_a}} attempts to get {d^*_r | C′_r ≤ C′_j and C′_r ∈ {C′₁, C′₂, …, C′_a}} to generate a temporary secret key SK^*_j for decrypting the encrypted image. The adversary will face the open problem about factoring the product of two large prime numbers in order to solve φ(n). Clearly, it is too hard to calculate appropriate d^*_r. Consequently, the adversary cannot generate the secret key to decrypt the encrypted image even though he has corresponding public keys.

4.3.2. Scenario 2

Suppose that an adversary who has SK^*_j wants to get other class’s secret keys SK^*_j+1. The adversary has to guess d^*_j+1 to obtain SK^*_j+1. Although he has always known n, g, and SK^*_j, it is indeed a very big challenge for him to calculate d^*_j+1 to get other class’s secret key due to the difficulty of solving the discrete logarithm problem.

4.4. Time Analysis

Encrypting the 128-bit data with AES encryption would take 68.45 nanoseconds (ns). Indeed, the AES encryption and decryption are pretty fast. Thus, the most time consuming part of the proposed scheme is calculating the decryption key. To see how long the decryption key calculation takes, let us take five authorized classes. Figure 10 shows an example of how fast the decryption key calculation with five authorized classes runs. We measured the average time taken to perform the decryption key calculation for 1000 times. We can see that it takes only 2.551 microseconds (μs) for C₁, and 112.997 μs for C₅ since C₁ computes one decryption key and C₅ computes five decryption keys. Longer calculation time could be taken by further increasing the number of authorized classes. Figure 10 also gives the average time of calculating one decryption key for each authorized class. We note that it would take approximately 5 μs for each additional decryption key calculation. Consequently, the proposed encryption and decryption are more computationally efficient, making the proposed scheme suitable for practical applications.

5. Conclusions

In this paper, we proposed a privacy protection scheme that supports different access rights in a single image based on the difficulty of solving factoring problems and discrete logarithm problems. The image manager can institute a different access policy in a single image for specific users. The access policy specifies who has access rights to read the original content of authorized regions. In the image protection method, the image in need of protection is set access rights on blocks to generate the corresponding encrypted image and authentication information. According to the access policy, we used different public keys and private keys built on RSA [28] to generate secret keys and derivative keys followed by ElGamal [29] to encrypt or decrypt the image blocks with AES. Moreover, the AES encryption and decryption are fast.

The encrypted images with the access policy will be uploaded to the cloud server. In the image management method, according to the access policy, the cloud server can determine whether the user has rights to access this image or not, without knowing the privacy information of images. The authorized users can read the original content of encrypted regions according to their access rights. The main benefit is that the proposed method allows users to securely share images across CSPs in semi-trusted cloud environments. Additionally, our method provides flexible access control in a single image for specific users making CSPs authenticate the image without accessing the privacy-preserved content. Performance evaluation results show that our method has no significant computation cost for CSPs and users. Security analysis shows that our image protection method based on the difficulty of solving factoring problems and discrete logarithm problems is secure, and our access control method can resist unauthorized access. Therefore, the proposed scheme not only provides image protection with different privacy-preserved access rights but also prevents the cloud server from leaking private information from the image.