Abstract
The fractional differential algorithm has a good effect on extracting image textures, but it is usually necessary to select an appropriate fractional differential order for textures of different scales, so we propose a novel approach for haptic texture rendering of two-dimensional (2D) images by using an adaptive fractional differential method. According to the fractional differential operator defined by the Grünvald–Letnikov derivative (G–L) and combined with the characteristics of human vision, we propose an adaptive fractional differential method based on the composite sub-band gradient vector of the sub-image obtained by wavelet decomposition of the image texture. We apply these extraction results to the haptic display system to reconstruct the three-dimensional (3D) texture force filed to render the texture surface of two-dimensional (2D) images. Based on this approach, we carry out the quantitative analysis of the haptic texture rendering of 2D images by using the multi-scale structural similarity (MS-SSIM) and image information entropy. Experimental results show that this method can extract the texture features well and achieve the best texture force file for 2D images.
1. Introduction
Haptic texture is a crucial cue to inform users of an interaction state with the surface texture, i.e., fine geometric surface features of an object. Haptic textures have received substantial attention in various fields [1,2,3]. Previous researchers have shown that the addition of haptic texture cues can greatly improve the realism of the virtual environment [4]. Therefore, the haptic texture rendering technique has several potential applications, such as virtual surgical simulation, haptic feedback teleoperation, on-line e-commerce, and aiding the visual impaired [5,6,7].
In general, there are three basic methods to render haptic textures. The first is the sample-based approach. S. Andrews introduced a system which is based on a tactile probe and a visual tracker for scanning and synthesizing tactile textures [8]. H. Vasudevan estimated the surface texture according to the frequency spectrum of vertical perturbations by dragging the tip of the tactile device on the object surface [9]. A. Song developed a PVDF-based haptic texture sensor by imitating human active texture perception to measure real object surface texture for haptic texture rendering in virtual reality [10]. V. Bove used holograms to record the surfaces and textures of objects in a holo–haptic system. The produced haptic images were felt and shaped by a handheld device [11]. The second is the procedural texture approach which uses mathematical functions to synthesize the surface texture of objects. Several related researchers were summarized in detail [12,13,14]. The third is the image-based approach. This method constructs a texture force field from 2D image data. Therefore, this kind of haptic texturing approach can also be considered as a type of VR [15]. L. M. Benjamin computed an elevation map based on the luminance coefficient for Texel images using four different techniques. These techniques were based on the fact that the height value of the pixel is proportional to the luminance value. Then, the elevation map is used to generate 3D bumps on the surface of the detected object, and calculate the corresponding tactile force for haptic rendering [16]. J. Wu and A. Song processed the 2D images with a Gaussian filter to obtain low-frequency components, and then subtracted the filtered image from the original image; the left components denote the texture information. The forces simulated from textures were applied to the user using a Delta haptic device [17]. S. Xu proposed an image-based haptic texture generation approach by replacing the Gaussian filter with an improved switching vector median filter for modeling the textured force and simulating the haptic stimuli [18]. Vasudevan used the conventional edge detection algorithms and proposed a design method of haptic mask to allow the user to feel the contours and textures of the image using haptic devices [19]. J. Lu and A. Song presented a haptic texture rendering method based on color temperature and luminance to construct 3D texture force fields of 2D color images [20]. E. R. Vimina and Divya proposed a fixed size descriptor based on local strength for texture calculation, and further expanded texture information by multi-channel color data collection [21].
Owing to the fact that the image-based haptic texture rendering approach has potential advantages of cost-effective realization, it has attracted substantial attention from researchers. However, the existing haptic texture rendering methods have problems in dealing with the images with fine geometric texture features.
In this paper, we propose a novel fractional differential method for image-based haptic texture rendering. Fractional differentiation is currently a new tool for image signal processing. Complex texture details will show highly self-similar fractal information in image signals, and the mathematical basis of fractal theory includes fractional differentiation [22,23]. Therefore, the features of complex texture in the image can be extracted by fractional differentiation and applied to the haptic texture reconstruction.
This paper introduces the Grünvald–Letnikov (G–L) definition of fractional differential in Euclidean space [24,25]. Based on the G–L definition, the isotropic m × n fractional differential mask is deduced. Then we propose a novel method to adaptively select the order of a fractional differential operator by using the composite sub-band gradient vector (CSGV) relate with the wavelet decomposition [26] and human visual characteristics [27,28]. Thirdly, we apply the approach in haptic texture rendering and give a quantitative analysis by using the image information entropy and multi-scale structural similarity (MS-SSIM). We apply these extraction results to the haptic display system to reconstruct the three-dimensional texture force filed to render the texture surface of 2D images. Finally, some experiments were carried out on different types of texture images. Experimental results show that the proposed haptic texture rendering method based on the adaptive fractional difference can extract texture features well and obtain an excellent texture force field of 2D images.
2. The Advantage of Fractional Differential
Fractional differential processing of signals can not only enhance the high-frequency components of a signal nonlinearly, but also enhance the intermediate frequency components of the signal nonlinearly to a certain extent, while retaining the low-frequency components of the signal nonlinearly [29,30]. Using this property of fractional differentiation, we can preserve the low-frequency contour information of digital images while nonlinearly augmenting high-frequency detailed texture patterns with wider gray distributions. Finally, the enhanced image is subtracted from the original image to obtain the texture extraction result.
The Grünvald–Letnikov (G–L) definition, Kaputo definition, and Riemann Liouville (RL) definition are three commonly used definitions of fractional differential under Euclidean Metric [29]. Recent research indicates that the implementation of differentials in digital image processing is almost always based on the G–L concept. The Tiansi operator mask that is constructed according to the definition of G–L will actually have inaccuracy in image processing, because it is discrete in digital images and is an approximate expression of functions, so the effect of image texture extraction is often unsatisfactory.
Therefore, we add adaptive augmentation to the G–L fractional differentiation definition, and find it is suitable for image texture acquisition.
The low-frequency components of the image can be well preserved under the fractional differential operator mask filtering. The output gradation value is dramatically enhanced for nearby pixels whose gray value fluctuates rapidly in the area (including picture borders and texture regions), showing that the fractional differential operator mask may significantly improve the original image’s high-frequency component.
3. Differential Order for Adaptive Selection Algorithm
Texture is one of the most essential image processing and analysis properties. Texture gives intuitive assessments of qualities, such as regularity, coarseness, and smoothness. The majority of texture analysis methods analyze the picture at a single scale. As revealed by J. Beck et al. [31], the visual cortex may be modeled as multiple channels, where each channel can perceive a specific direction and frequency tuning. Multi-scale texture analysis techniques are propelled by multichannel processing. Several multichannel texture analysis systems have been suggested [32,33]. In the past 10 years, the rapid development of wavelet theory has also brought new theories and methods to the field of image processing. I. Daubechies suggested a discretization approach for wavelet transform [34]. The relationship between multiresolution theory and wavelet transforms was further developed by S. G. Mallat [35]. Since then, wavelet theory has developed into a multi-scale (multi-resolution) mathematical tool in image analysis. The use of multi-scale methods in texture image analysis is based on the premise that lower resolution channels can better record “large” textures, while higher resolution channels can better record “small” textures.
The following describes the process involved. Apply wavelet and scaling filters to the image both horizontally and vertically, then sub-sample each output image by 2-1. This produces a coarse or approximate image Cj and three detail images with direction-selectivity Dj,k, where k = 1,2,3 and j represents the decomposition level. The same method is utilized to construct the following level of hierarchy resolution. Therefore, the hierarchical wavelet decomposition of the image is expressed as:
where C0 = I represents the original image, ↓1,2 means down-sampling every other pixel in the y direction, ↓2,1 means down-sampling every other pixel in the x direction, and * means the convolution operator. Gx and Hy and Gy and Hy represent high-pass and low-pass filters in the x and y directions, respectively. Therefore, the original image can be represented by a series of sub-images of multiple scales, {Cj, Dj, k} (j = 1, …, J; k = 1, 2, 3) is the multi-scale representation of image I at depth J. DAUB4 is used as the wavelet basis in this instance because of its superior average performance.
Gradient direction image may provide texture analysis with useful properties [36]. After the image is processed by the gradient operator, the change amplitude and direction of the pixel gray value can be obtained, and the image gradient describes the change trend of the image in different directions. A combination of a series of low-pass (H) and high-pass (G) filters enables wavelet decomposition, using multiple sets of filters for sampling, each set at half the sampling frequency of the previous set. Therefore, the original image can be processed to obtain four sub-images, namely:
- LL sub-image: low frequencies in both x and y directions.
- LH sub-image: low frequencies in the x direction and high frequencies in the y direction.
- HL sub-image: high frequencies in the x direction and low frequencies in the y direction.
- HH sub-image: high frequencies in both x and y directions.
LL, LH, HL, and HH are four sub-images obtained by wavelet decomposition. A gradient vector is constructed for each sub-image, denoted by , , , , respectively. We define , where is a “superimpose” operation. Therefore, CSGV can better describe the expression of image texture than the original gradient vector.
Studying the human visual characteristics reveals that the sensitivity of the human eye to the gray value in the range of 0~255 in the gray image is not constant. When the gray value is particularly high or low, it is difficult for the human eye to perceive the grayscale change of the intensity value. In the vicinity of gray level 0, the human eye can only feel the change of gray level 8, while in the vicinity of gray level 255, the human eye can only feel the change of gray level 3, and when the gray level is 128, the human eye can perceive changes in 2 gray levels [37]. In digital image research, the gradient size of a certain point in the image is calculated by the change rate of the gray value of the point. The above-mentioned gradient coincidence vector CSGV represents the gray value change rate of the image at multiple scales. Therefore, we regard the pixels with CSGV less than 2 as a region with constant grayscale, and the differential order is 0; the pixels with CSGV in the range of 2~128 are regarded as regions with small grayscale changes, and appropriately increasing the differential order can enhance the human eye’s perception of fine textures; while the pixels with CSGV greater than 128 are usually edge contour areas, it must have a correctly limited gradient interval, and the differential order should be appropriately reduced. From the above analysis, we have established the function of fractional derivative γ and CSGV:
Among them, is any positive number; is the maximum value of of all pixels in the image; is an artificially set, and its purpose is to enhance the effect of the center pixel on the neighboring pixels. The condition of should satisfy the following formula to ensure that the value of the differential order γ does not exceed 1:
When , , from Equation (3) , so take = 0.499. When , intended to use , , so take = 0.666. Therefore, the relationship between the differential order γ and CSGV is expressed as:
According to these equations, the gray value varies drastically along the image’s edge contour, and the CSGV is bigger, thus γ should be reduced accordingly. For densely textured areas, the grayscale variation and CSGV are small, so the fractional derivative γ obtained is appropriately increased. For areas where the gray value does not change or changes very little, γ is 0 and no processing is performed to maintain the gray value.
4. Texture Extraction Performance Evaluation
This section aims at demonstrating that the proposed adaptive algorithm based on CSGV has better capability using in the texture extraction.
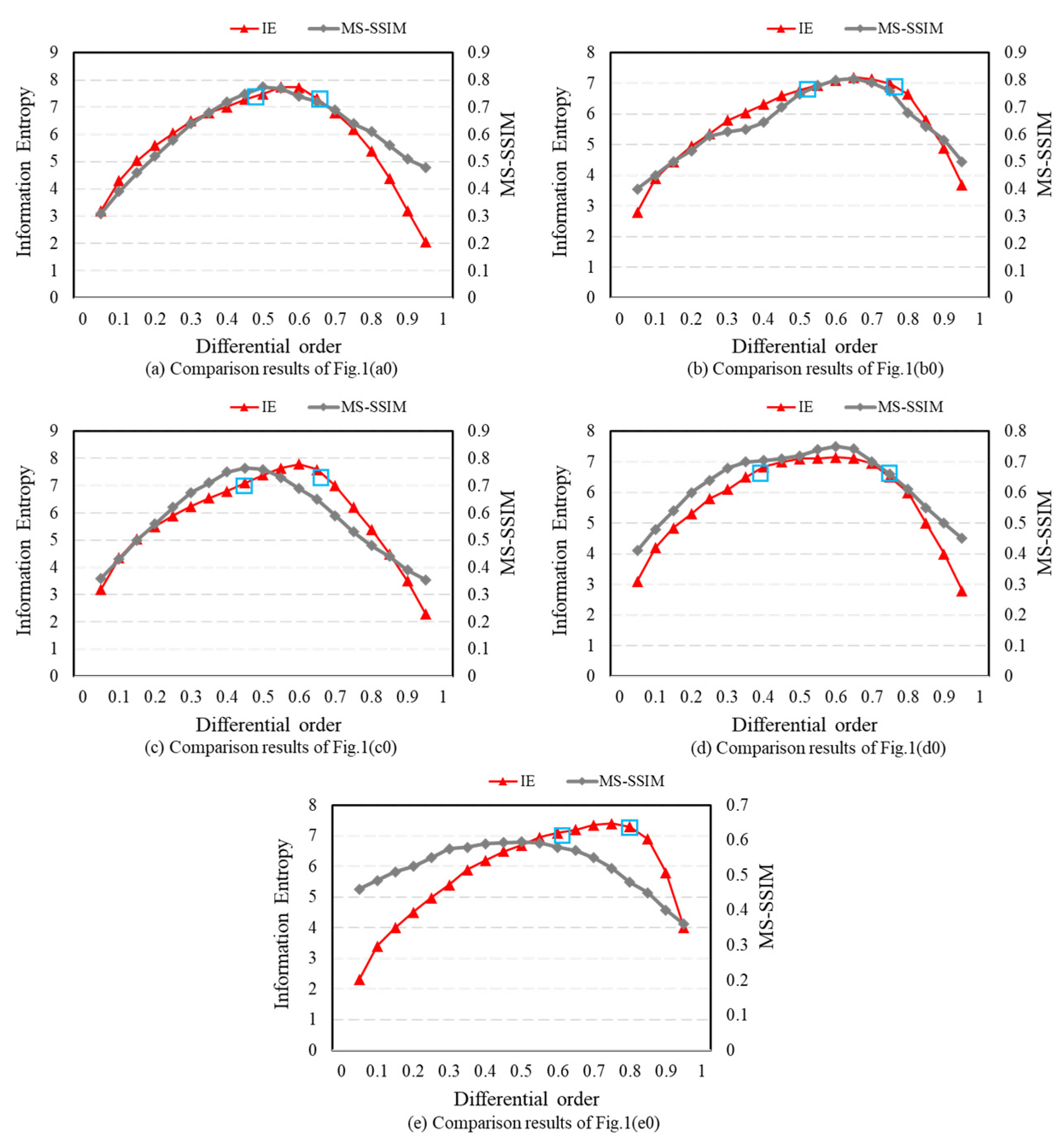
For fractional differential G–L, we set the 0.3, 0.55, and 0.7 as the fixed fractional differential order. In order to analyze and compare the differences in the ability to obtain texture information between the adaptive order differential and the specified fractional order differential, five groups of comparative experiments were conducted, and their results are shown in Figure 1. These results of five sets of comparative experiments show the advantages of fractional difference in extracting complex texture information. Although the 0.3-order differential extraction effect can preserve the detailed texture well, the texture extraction effect is too weak to be clearly displayed on the picture (as shown in Figure 1(a1,b1,c1,d1,e1). However, as the differential order increases (between 0 and 1), image enhancement promotes “large” textures to sharper images, but “small” textures are lost. The adaptive differential order selection algorithm adopted in this paper can retain almost all texture details to achieve the best texture extraction among five groups (as shown in Figure 1(a4,b4,c4,d4,e4).

Figure 1.
Texture extraction comparison tests: (a0–e0) are the original image; (a1–e1) are the 0.3-order fractional derivative; (a2–e2) are the 0.55-order fractional derivative; (a3–e3) are the 0.7th order fractional derivative; (a4–e4) are the adaptive fractional differentiation.
Multi-scale structural similarity and information entropy (MS-SSIM) is used as an evaluation criterion to evaluate the effect of texture information extraction in images [38,39]. Among them, information entropy can indirectly reflect the amount of information contained in grayscale images, and is very sensitive to images containing textures. Therefore, we adopt the calculation method of information entropy to analyze the amount of information in the image texture after extracting the image texture features. The information entropy is calculated as follows:
Because the human vision system is very suitable for extracting structural information from scenes, measurement results with similar structures can provide a reference for whether image quality is good for perception. The MS-SSIM value of an image is usually used to compare the quality of two images and is an objective evaluation method that replaces the human subjective perception [39]. We use it to compare the differences between the extraction results after using the adaptive method and the specified order differential method, thereby further verifying that the texture extraction effect of the adaptive method has obvious advantages.
A comparison method for structure, brightness, and contrast is given in Ref. [39]:
where , are two image patches extracted from the same spatial location from two images, respectively. And , and are the mean of , the variance of , and the covariance of and , respectively. C1, C2 and C3 are small constants given by
where L is the dynamic range of the pixel values (L = 255 for 8 bits/pixel gray scale images), and K1 << 1 and K2 << 1 are the two scalar constants.
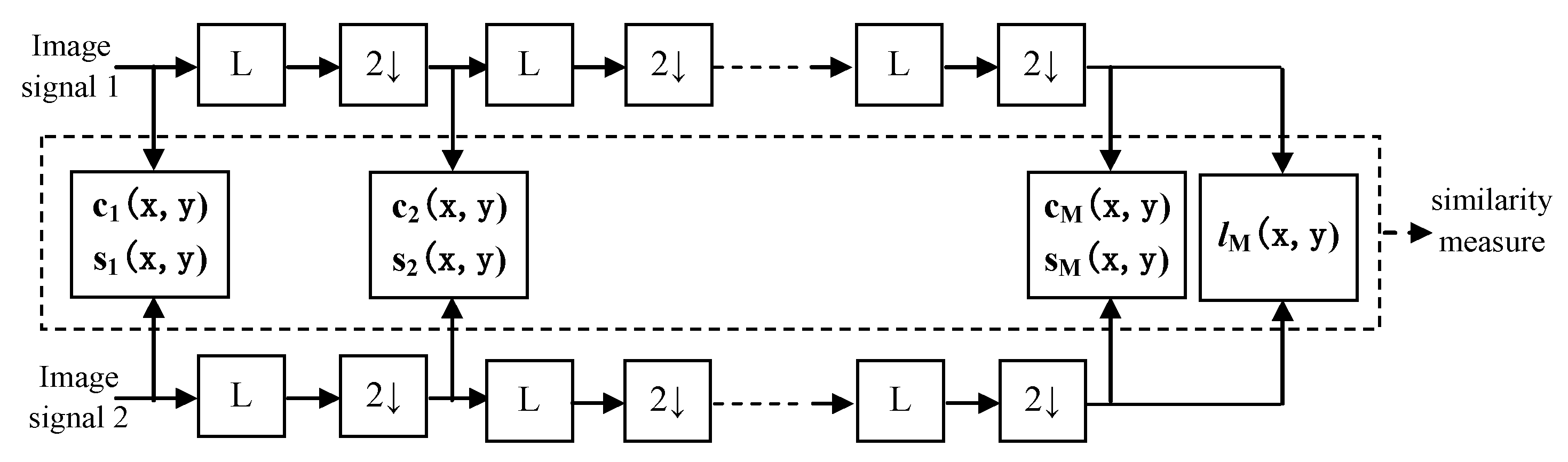
The procedure of the MS-SSIM method for image structural similarity assessment is illustrated in Figure 2. The two images to be compared are used as input signals, and then the low-pass filter is applied for iteration, and the filtered image is down sampled by factor 2. The original image index is scale 1, and the highest index is scale M. At the j-th scale, the contrast comparison and the structure comparison are calculated, respectively. The luminance comparison is computed only at scale M as . Thus, the MS-SSIM evaluation is obtained by combining the measurements at different scales using:
where , and are parameters to define the relative importance of the three components. To simplify parameter selection, we set = = = 1.
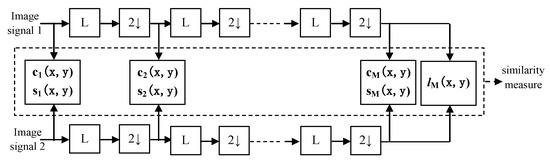
Figure 2.
Multi-scale structural similarity measurement procedure.
5. Texture Extraction Results Analysis
The analysis and comparison results are shown in Figure 3. The information entropy obtained by the adaptive method is marked in blue, and the red curve shows the information entropy obtained from order 0.05~0.95 (step length is 0.05 order). It can be seen that the result of the adaptive method is close to order 0.5~0.7, which is the fractional order interval with the best extraction effect. The grey curve shows the structural similarity of the adaptive results. When the MS-SSIM value of the extraction result of each specified order is closer to 1, it is closer to the adaptive result. From Figure 3, we find that the extraction results of order 0.5~0.7 are most similar to the results of the adaptive method. The comparison result of Figure 3 is the same as that of Figure 1. Quantitative analysis shows that the adaptive method can improve the effect of texture extraction with less losing of texture details.
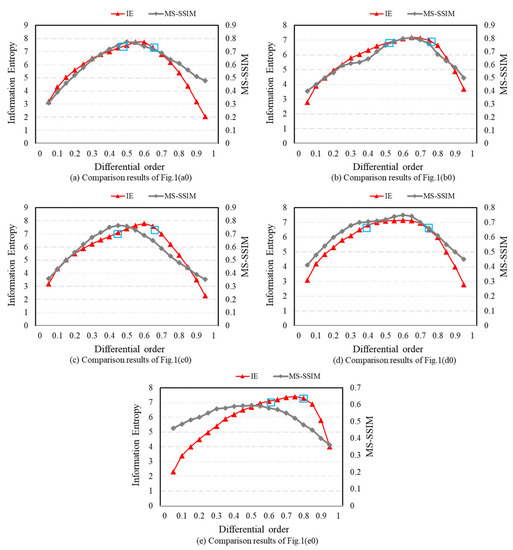
Figure 3.
Quantitative comparison between adaptive methods and different fractional orders.
Using the statistics constructed based on the gray level co-occurrence (GLCM) matrix to calculate the physical information of the texture image, and select four commonly used statistics (Set the offset to 1 and the direction to [0°, 45°, 90°, 135°]), as shown in Table 1, where the rows correspond to the pictures in Figure 1, and the columns correspond to the directions.

Table 1.
Physical information of the texture image.
AMS is a measure of the uniformity of image grayscale distribution and texture thickness. Entropy measures the randomness contained in an image and expresses the complexity of image texture. The contrast reflects the clarity of the image and the depth of the texture. The more obvious the “large” texture, the greater the contrast. The correlation reflects the consistency of the image texture.
After the texture image is processed by the adaptive fractional differential method, the “small” texture is significantly enhanced, so the values of AMS and entropy are increased. The gray value of the “small” texture is closer to that of the “large” texture than before, so the contrast value is reduced.
6. Haptic Texture Rendering Model
Haptic texture rendering is a method to reconstruct the surface attributes of virtual objects according to force fields or force vectors, so that users can feel the surface texture of virtual objects haptically by using haptic devices (such as Phantom, Force-Dimension Delta hand controller, etc.). In this section, we use the adaptive fractional differentiation method to provide a new tactile texture model based on the image texture extraction results.
The texture force vector at each pixel of an image can be modeled as the combination of normal force vector and tangential force vector as
The tangential force vector of the image is calculated based on the following assumption. There exists an interaction force between any two pixels in the gray image after processed by the proposed adaptive fractional differential method. The interaction force between any two pixels Pi and Pj is proportional to the absolute vale of the difference of the two pixel’s gray values, and inversely proportional to the distance between two pixels. The direction of interaction force vector is defined as from pixel with high luminance value to the pixel with low luminance value.
where is distance between two pixels and , and , are grey value of pixels and , respectively. denotes the direction from high luminance pixel to low luminance pixel.
If the distance between two pixels and is small, the difference of the two pixel’s gray values will cause a big interaction force, and vise versa. Thus, the force vector of the pixel can be defined as the vector sum of all interaction force vectors from pixels within n × n neighborhood N to the center pixel .
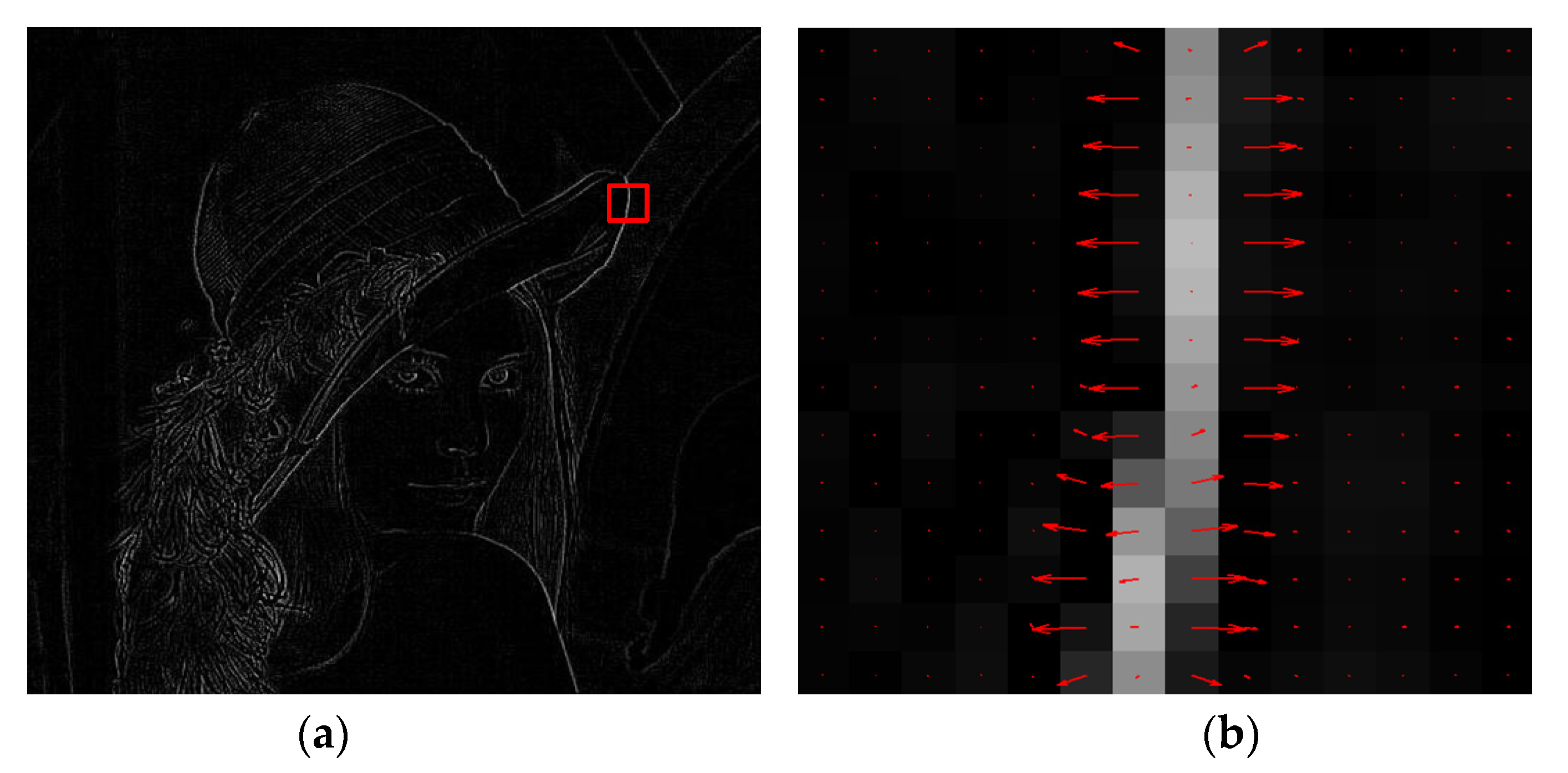
The force vector of each pixel is a two-dimensional vector associated with pixel grey change direction of image, as illustrated in Figure 4. Figure 4b is an amplified picture of the small red square area in Figure 4a, which shows the tangential force vectors of some pixels computed by Equation (11) with the 3 × 3 neighborhood N. Here, the arrow direction represents the direction of force vector while the arrow length represents the amplitude of force vector.
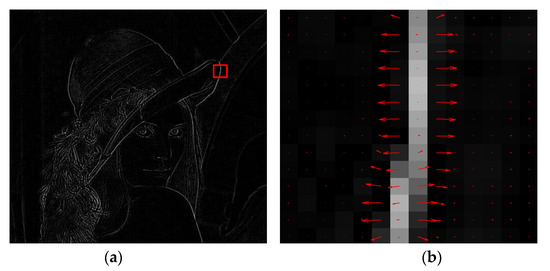
Figure 4.
Two-dimensional texture tangential force vectors of grey image. (a) texture feature extracted from “Lena” image using fractional differential method (v = 0.55); (b) texture tangential force vectors in amplified red square area in (a).
When the grey values of neighbor pixels change more greatly, the pixel force vector is larger, and vice versa. Since this pixel force vector is consistent with the texture information, it can be regarded as the texture tangential force component.
According to the psychological principle of the human sense of color and space, when a person observes the environment, he always feels the brighter object is closer to him than the darker object [40]. Therefore, we can define the normal force vector to be proportional to the image pixel gray value as
where c is a proportion factor, and fwall denotes the constraint force of the object surface. The above equation implies that if a portion of an image is brighter, then the rendered normal force is larger, which provides the user with feeling of bump when the virtual object is touched; and if the case is darker, then the rendered normal force is smaller, which expresses feelings of being shallow.
7. Experiment
The experimental system for haptic texture rendering of 2D images consists of a Phantom Omini haptic device and a computer, shown in Figure 5. The Phantom Omini haptic device has a six degrees of freedom position/attitude detection and a three degrees of freedom force feedback with the maximum force of 3.3 N. Its workspace is 160 mm width × 120 mm height × 70 mm depth with location accuracy 0.055 mm.

Figure 5.
The experimental system of haptic texture rendering of 2D image.
In this experimental system, we selected five images with 500 × 500 pixels from the Brodatz texture image database [41] and used the proposed adaptive fractional differential method to extract the texture features, shown in Table 2. Then, we used the proposed haptic texture rendering model to render the object surface based on the extracted texture. In order to verify the effect of our method, 20 volunteer subjects (10 male and 10 female, aged 21 to 31) is randomly selected to perform the texture perception experiments. The subject just haptically felt the surface of 25 2D images, which are stochastically produced by a computer one by one, and classified them into 5 types of images by using the Phantom Omini haptic device without any visual information of the 2D image.

Table 2.
Texture feature extracting of 2D images using adaptive fractional differential method.
The appearance of the original image and the texture image are hidden, and only the calculated texture force is mapped to a smooth virtual plane of 500 × 500 pixels. The calculation of the constraint force of the virtual plane is based on Hooke’s law. When the volunteers “groped” the “blank” virtual plane, the hand controller fed back the texture force of the image together with the constraint force of the virtual plane to the subject. Volunteers need to select the image to be reproduced by force/haptic sense of texture from five original images according to the perceived texture, and then count the correct rate of volunteers’ perception of each image.
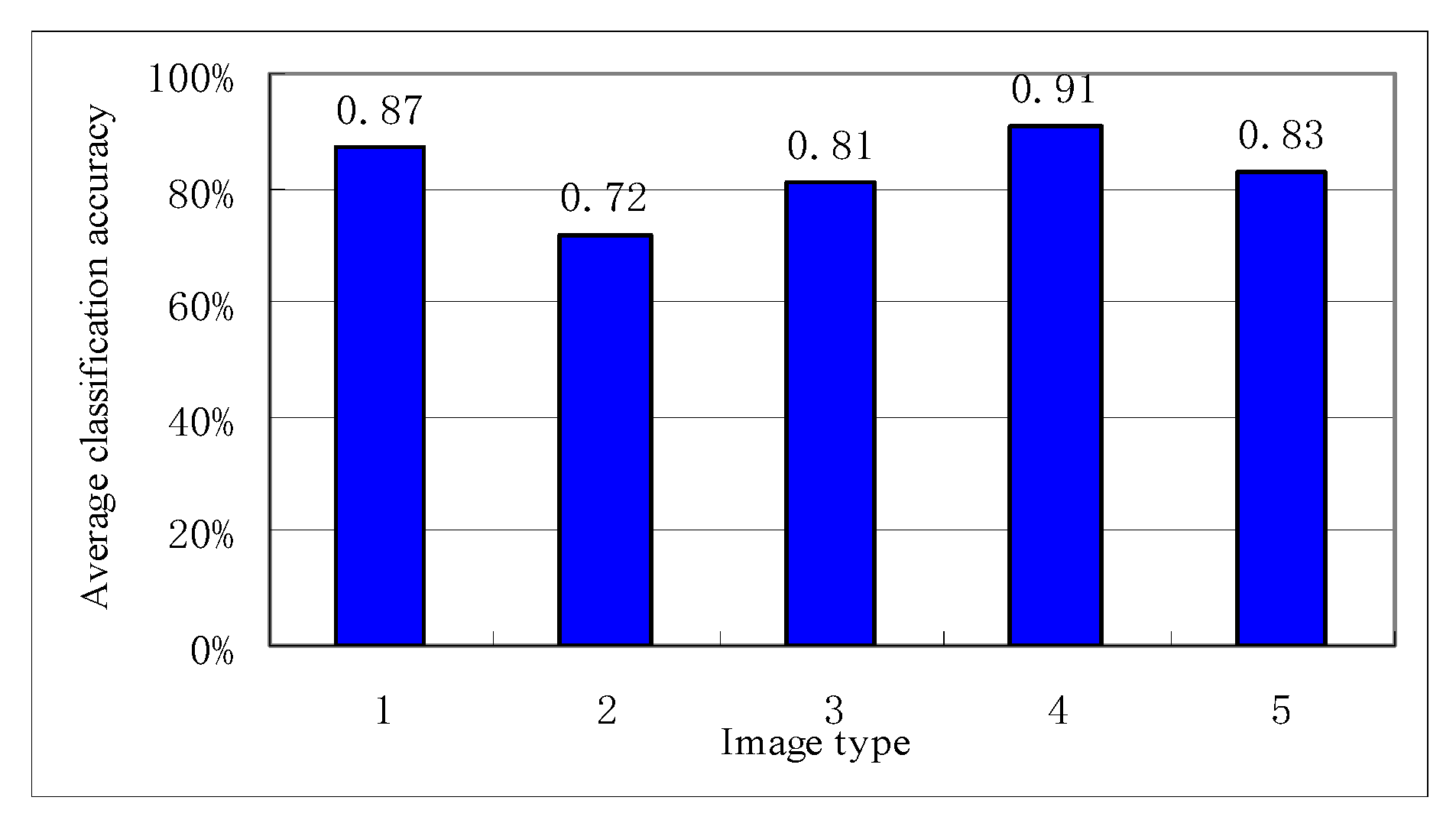
The experimental results show that the average classification accuracy of 5 types of images based on haptic feelings are 87%, 72%, 81%, 91%, and 83%, shown in Figure 6. It is obvious that the proposed haptic texture rendering method can help users understand the texture contents of the image. So, it is an effective approach of image-based haptic texture rendering.
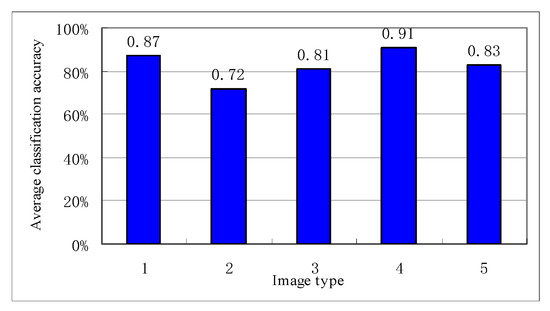
Figure 6.
Experiment results of image classification using haptic texture feeling.
Further, we conducted another group of experiments, we selected four 2D images, and extracted their texture features through the proposed adaptive algorithm, shown in Table 2. It can be seen from the extraction results that the image texture extracted by the adaptive fractional differentiation algorithm is clear and the details are retained completely, which indicate the excellent effect of the adaptive fractional differentiation algorithm in extracting the detail texture.
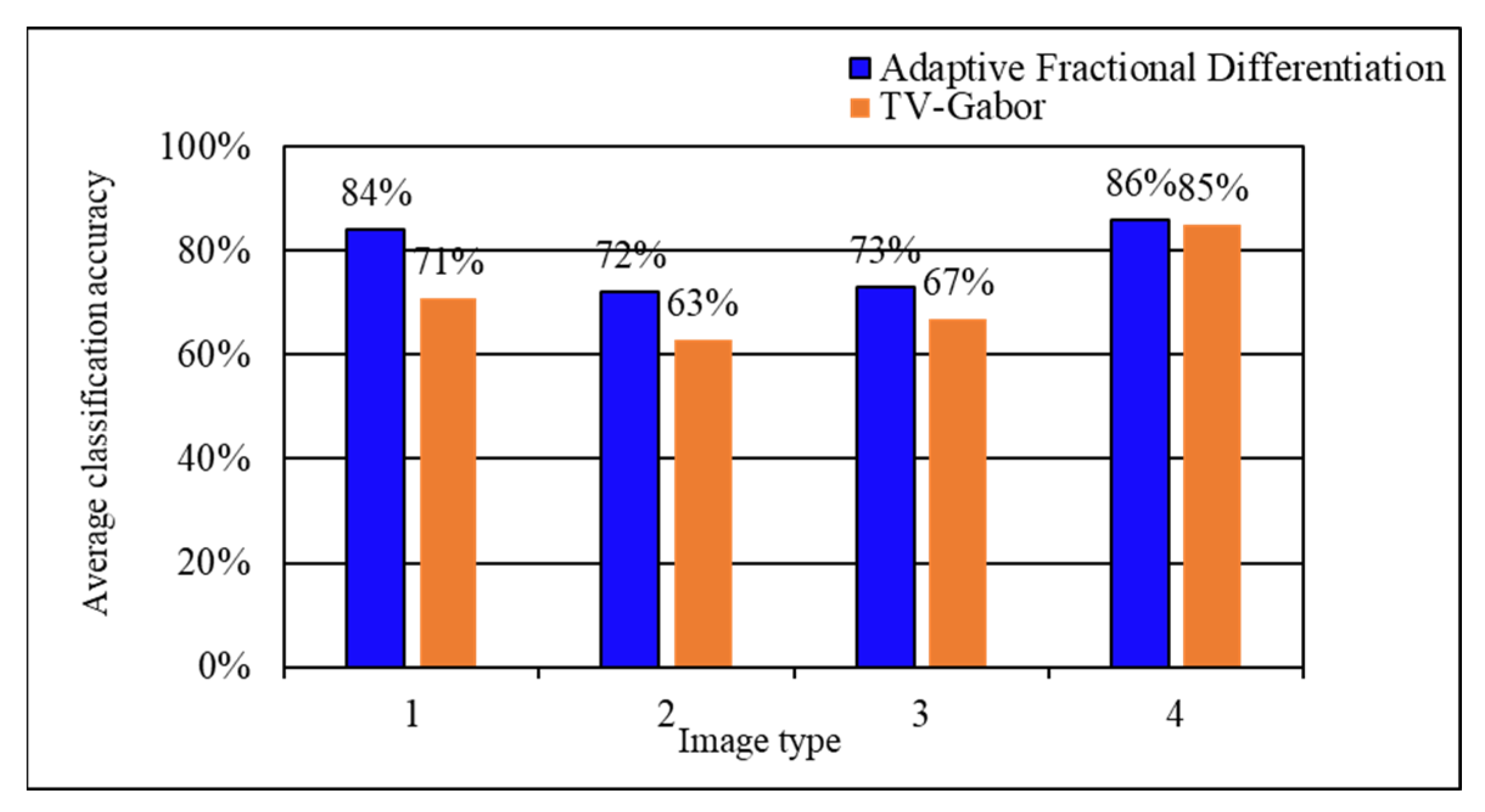
The TV-Gabor model is used for comparison (the TV-Gabor model decomposes the image by using the prior conditions of frequency and texture direction, so as to distinguish the contour shape of the image body from the texture part), and selected 4 real object images with textures, shown in Table 3. Similarly, we used the proposed Haptic texture rendering model to render the object surface based on the extracted texture. In the cases where the volunteers were blindfolded, we calculated the correct rate of each image recognition, shown in Figure 7. It is verified again that the texture feature outputs by the tactile texture rendering model conform to the more realistic perception of volunteers.

Table 3.
Comparison of image classification experiments with different haptic extraction algorithms.
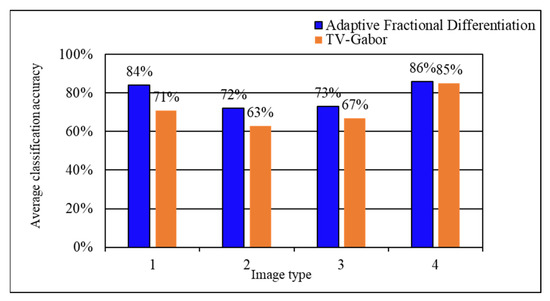
Figure 7.
Experimental results of image classification with different haptic extraction algorithms.
8. Conclusions
In this paper, a haptic texture rendering method for 2D images based on a novel adaptive fractional differentiation has been described. The optimal order of fractional differentiation operator has been adaptively selected by using the CSGV after wavelet decomposition and the human visual features. Additionally, the quantitative analysis method based on image information entropy and multi-scale structure similarity (MS-SSIM) has been proposed to evaluate the results of texture feature extraction. On this basis, we have provided a novel haptic texture model; these extraction results were used for reconstructing the three-dimensional texture force filed to render the texture surface of 2D images. The experimental results show an average classification accuracy improvement of 0.4dB compared to the established technique (TV-Gabor), and verify the proposed haptic texture rendering method based on this adaptive fractional differential can extract the texture features well and achieve the best texture force file for 2D images. It is an effective approach to enhance image texture and also can improve the human ability of haptic texture perception in image-based haptic display system.
Author Contributions
Conceptualization and methodology, A.S. and H.H.; formal analysis, A.S. and H.H.; supervision, A.S.; writing—original draft preparation, A.S.; writing and editing, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Shenzhen Virtual University Park Basic Research Project under grant no.2021Szvup025.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in https://www.ux.uis.no/~tranden/brodatz.html (accessed on 7 July 2020).
Acknowledgments
The authors would like to thank editor-in-chief, editor, and anonymous reviewers for their valuable reviews.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, S.; Tan, H.Z. An analysis of perceptual instability during haptic texture rendering. In Proceedings of the 10th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, Orlando, FL, USA, 24–25 March; pp. 129–136. [CrossRef]
- Jin, R.; Skedung, L.; Cazeneuve, C.; Chang, J.C.; Rutland, M.W.; Ruths, M.; Luengo, G.S. Bioinspired Self-Assembled 3D Patterned Polymer Textures as Skin Coatings Models: Tribology and Tactile Behavior. Biotribology 2020, 24, 100151. [Google Scholar] [CrossRef]
- Jarocka, E.; Pruszynski, J.A.; Johansson, R.S. Human Touch Receptors Are Sensitive to Spatial Details on the Scale of Single Fingerprint Ridges. J. Neurosci. 2021, 41, 3622–3634. [Google Scholar] [CrossRef] [PubMed]
- Hassan, A.W.; Abdulali, M.; Abdullah, S.C.; Jeon, A.S. Towards Universal Haptic Library: Library-Based Haptic Texture Assignment Using Image Texture and Perceptual Space. IEEE Trans. Haptics 2018, 11, 291–303. [Google Scholar] [CrossRef] [PubMed]
- Spillmann, S.J.; Harders, T.M. Adaptive space warping to enhance passive haptics in an arthroscopy surgical simulator. IEEE Trans. Vis. Comput. Graph. 2013, 19, 626–633. [Google Scholar] [CrossRef] [PubMed]
- Li, A.J.; Zhang, S.X. Image-based haptic texture rendering. In Proceedings of the 9th ACM SIGGRAPH Conference on Virtual-Reality Continuum and its Applications in Industry, Seoul, Republic of Korea, 12–13 December 2010; pp. 237–242. [Google Scholar]
- Janssen, M.J.; Huisman, M.; Van Dijk, J.P.M.; Ruijssenaars, W.A.J.J.M. Touching textures in different tasks by a woman with congenital deaf-blindness. J. Vis. Impair. Blind. 2012, 106, 739–745. [Google Scholar] [CrossRef]
- Andrews, S.; Lang, J. Haptic texturing based on real-world samples. In Proceedings of the IEEE International Workshop on Haptic Audio Visual Environments and Their Applications, Ottawa, ON, Canada, 22–23 October 2007; pp. 142–147. [Google Scholar]
- Vasudevan, H.; Manivannan, M. Recordable haptic textures. In Proceedings of the IEEE International Workshop on Haptic Audio Visual Environments and Their Applications, Ottawa, ON, Canada, 4–5 November 2006; pp. 130–133. [Google Scholar]
- Song, Y.A.; Han, H.; Tian, H.L.; Wu, J. Active perception-based haptic texture sensor. Sens. Mater. 2013, 25, 1–15. [Google Scholar]
- Bove, J.V.M.; Plesniak, W.J.; Quentmeyer, T.; Barabas, J. Real-time holographic video images with commodity PC hardware. Proc. SPIE 2005, 5664, 255–262. [Google Scholar]
- Lu, S.H.; Zheng, M.L.; Fontaine, M.C.; Nikolaidis, S.; Culbertson, H. Preference-Driven Texture Modeling through Interactive Generation and Search. IEEE Trans. Haptics 2022, 15, 508–520. [Google Scholar] [CrossRef]
- Halabi, O.; Khattak, G. Generating haptic texture using solid noise. Displays 2021, 69, 102048. [Google Scholar] [CrossRef]
- Friesen, R.F.; Klatzky, R.L.; Peshkin, M.A.; Colgate, J.E. Building a Navigable Fine Texture Design Space. IEEE Trans. Haptics 2021, 14, 897–906. [Google Scholar] [CrossRef]
- Kanade, T.; Narayanan, P.J.; Rander, P.W. Virtualized reality: Concepts and early results. In Proceedings of the IEEE Workshop on Representation of Visual Scenes, Cambridge, MA, USA, 24 June 1995; pp. 69–76. [Google Scholar]
- Benjamin, L.M.; Kheddar, A. A simple way of integrating texture in virtual environments for haptic rendering. In Proceedings of the 12th International Conference on Advanced Robotics, Seattle, WA, USA, 8–11 August 2005; pp. 755–760. [Google Scholar]
- Wu, A.J.; Song, C.; Zou, A. Novel haptic texture display based on image processing. In Proceedings of the 2007 IEEE International Conference on Robotics and Biomimetics, Sanya, China, 15–18 December 2007; pp. 1315–1320. [Google Scholar]
- Xu, S.; Li, C.; Hu, L.; Jiang, S.; Liu, X.P. An improved switching vector median filter for image-based haptic texture generation. In Proceedings of the 5th International Congress on Image and Signal Processing, Chongqing, China, 23–25 October 2012; pp. 1195–1199. [Google Scholar]
- Vasudevan, H.; Manivannan, M. Tangible images: Runtime generation of haptic textures from images. In Proceedings of the IEEE Symposium on Haptic interfaces for virtual environment and teleoperator systems, Reno, NV, USA, 13–14 March 2008; pp. 357–360. [Google Scholar]
- Li, J.; Song, A.; Zhang, X. Haptic texture rendering using single texture image. In Proceedings of the IEEE International Symposium on Computational Intelligence and Design, Washington, DC, USA, 29 October 2010; pp. 7–10. [Google Scholar]
- Vimina, E.R.; Divya, M.O. Maximal multi-channel local binary pattern with colour information for CBIR. Multimed. Tools Appl. 2020, 79, 25357–25377. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Falconer, K. Fractal Geometry—Mathematical Foundations and Applications, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Rakhshan, S.A.; Kamyad, A.V.; Effati, S. An efficient method to solve a fractional differential equation by using linear programming and its application to an optimal control problem. J. Vib. Control 2016, 22, 2120–2134. [Google Scholar] [CrossRef]
- Zou, Q.; Jin, Q.; Zhang, R. Design of fractional order predictive functional control for fractional industrial processes. Chemom. Intell. Lab. Syst. 2016, 152, 34–41. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Yang, L.J.; Li, Y. A Novel Adaptive Fractional Differential Active Contour Image Segmentation Method. Fractal Fract. 2022, 6, 579. [Google Scholar] [CrossRef]
- Coleman, S.A.; Suganthan, S.; Scotney, B.W. Gradient operators for feature extraction and characterization in range images. Pattern Recognit. Lett. 2010, 31, 1028–1040. [Google Scholar] [CrossRef]
- Fang, A.Q.; Zhao, X.B.; Yang, J.Q.; Zhang, Y.N.; Zheng, X. Non-linear and selective fusion of cross-modal images. Pattern Recognit. 2021, 119, 108042. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.A.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Wang, W.X.; Li, W.S.; Yu, X. Fractional differential algorithms for rock fracture images. Imaging Sci. J. 2012, 60, 103–111. [Google Scholar] [CrossRef]
- Beck, J.; Sutter, A.; Ivry, R. Spatial frequency channels and perceptual grouping in texture segregation. Comput. Vis. Graph. Image Process. 1987, 37, 299–325. [Google Scholar] [CrossRef]
- Bovik, A. Analysis of multichannel narrow band filters for image texture segmentation. IEEE Trans. Signal Process. 1991, 39, 2025–2043. [Google Scholar] [CrossRef]
- Jain, A.K. Learning texture discrimination masks. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 195–205. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Fountain, S.; Tan, T. Efficient rotation invariant texture features for content-based image retrieval. Pattern Recognit. 1998, 31, 1725–1732. [Google Scholar] [CrossRef]
- Liu, H.; Huang, K. A medical image processing method based on human eye visual property. Opto-Electron. Eng. 2001, 28, 38–41. [Google Scholar]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multi-scale structural similarity for image quality assessment. In Proceedings of the 37th IEEE Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 1398–1402. [Google Scholar]
- Zhu, B. Applied Psychology; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Brodatz Texture Database. Available online: http://www.ux.uis.no/~tranden/brodatz.html (accessed on 7 July 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).