Working Face Stability of Box Shield Tunneling under Non-Uniform Support Pressure
Abstract
:1. Introduction
2. Materials and Methods
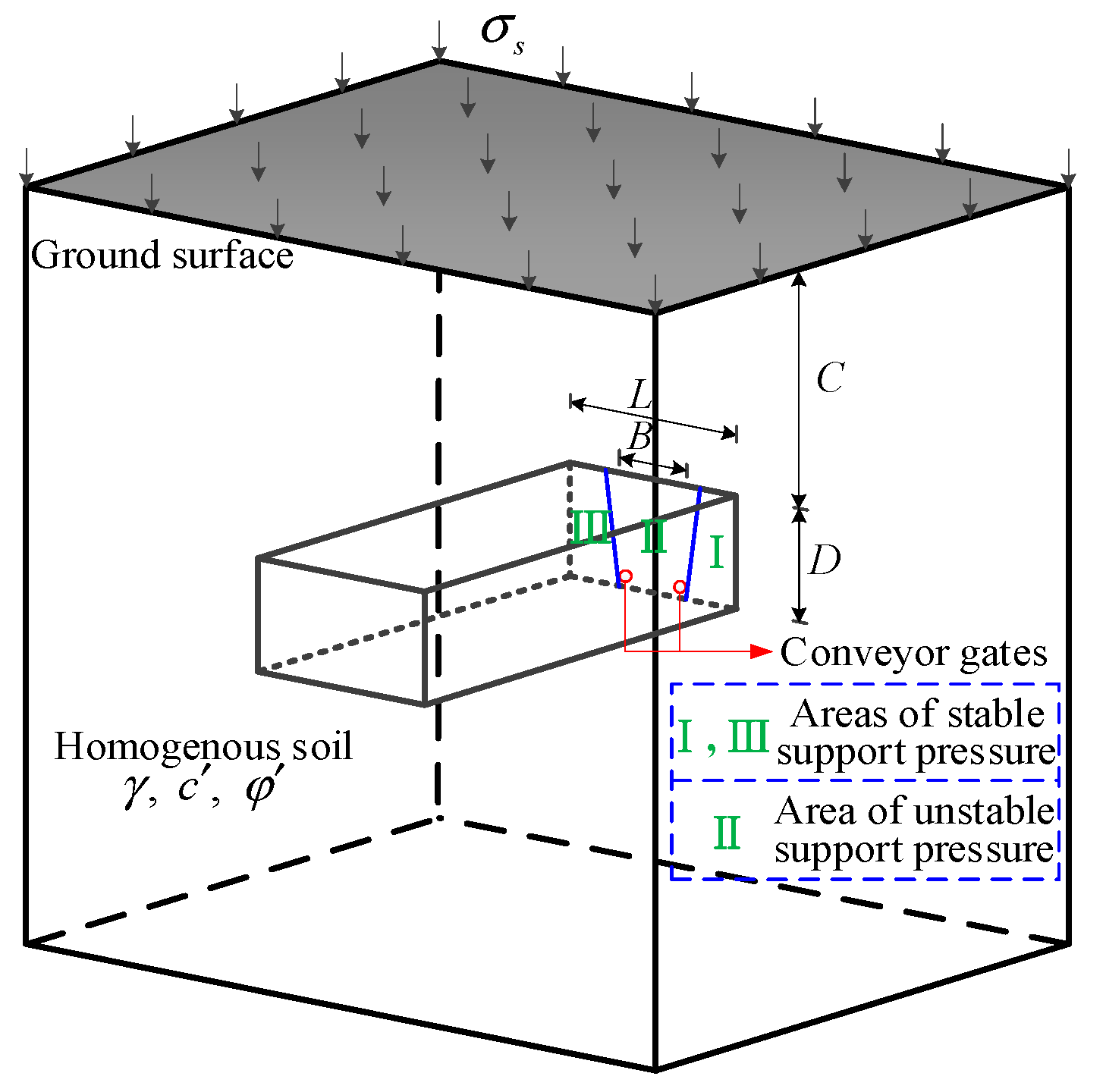
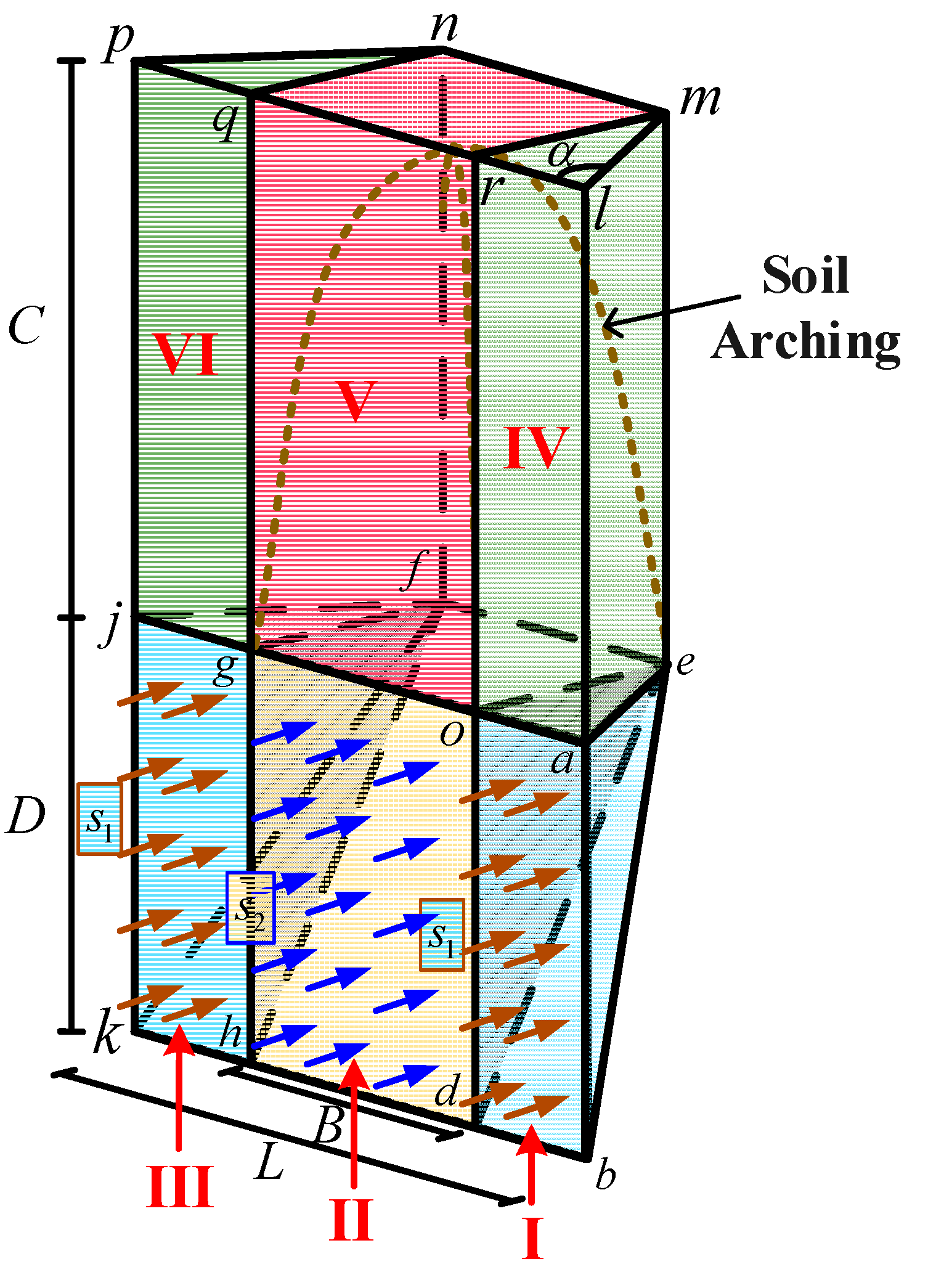
2.1. Distribution Characteristics of Support Pressure in Box Tunnels
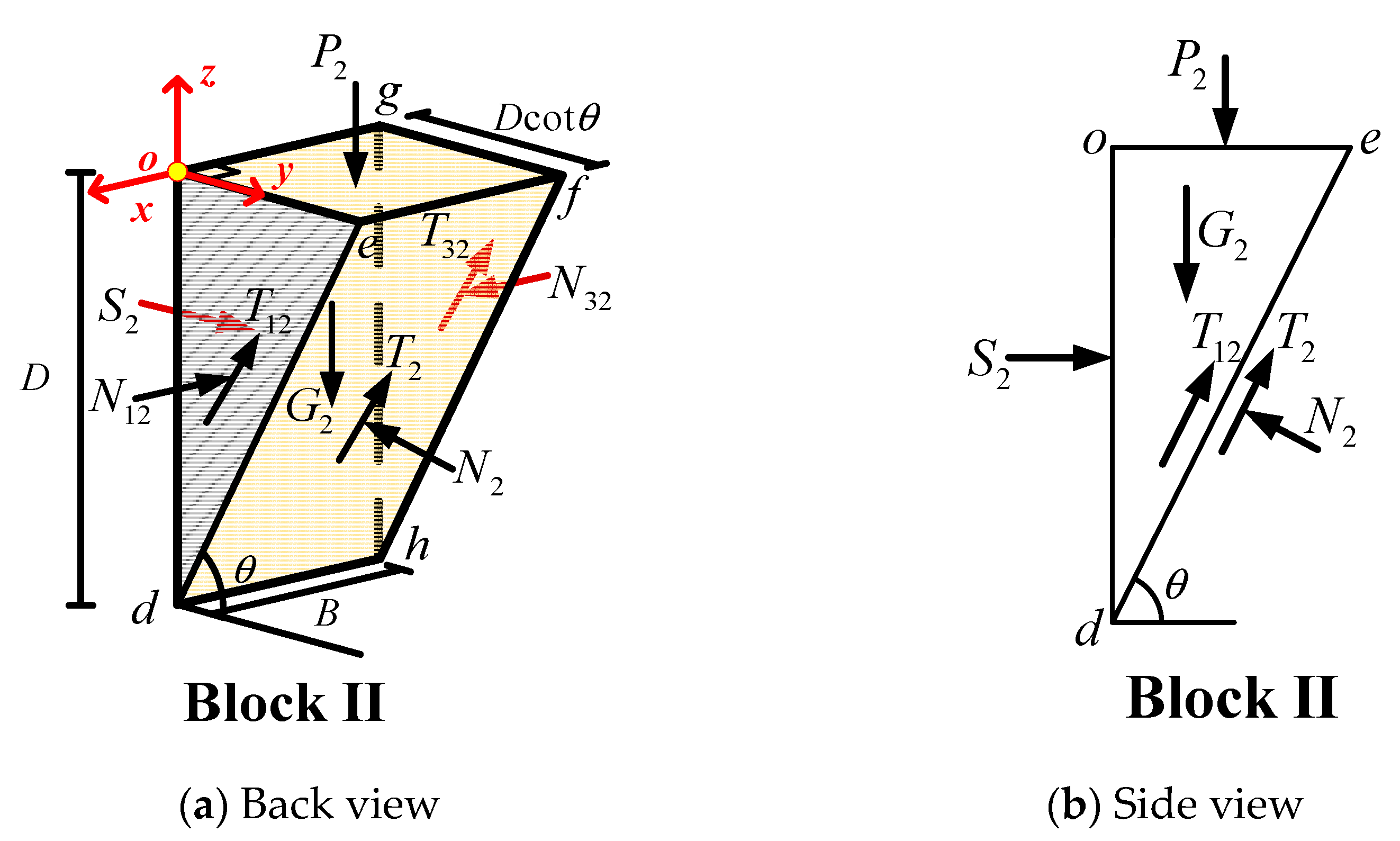
2.2. Modified Model
3. Results
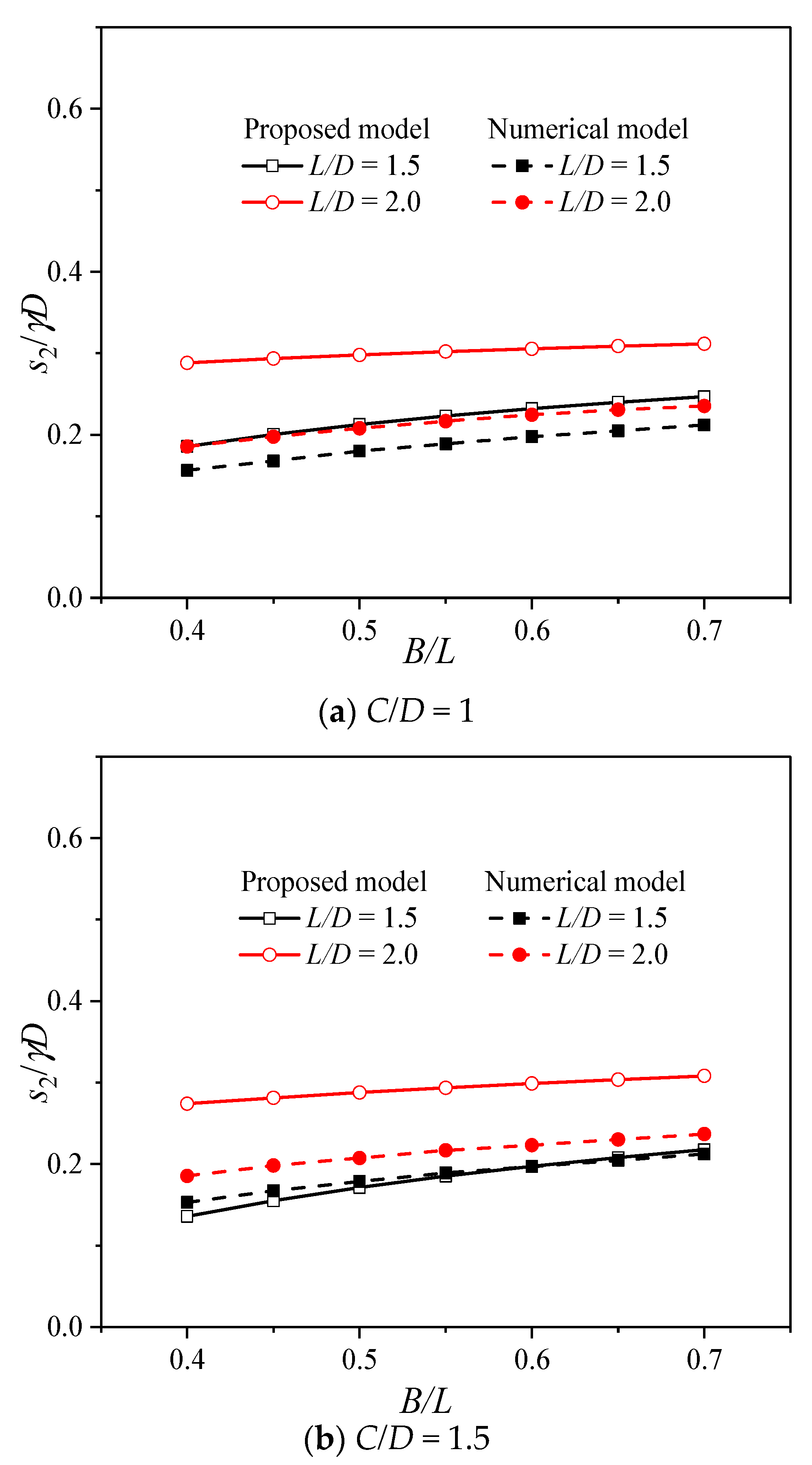
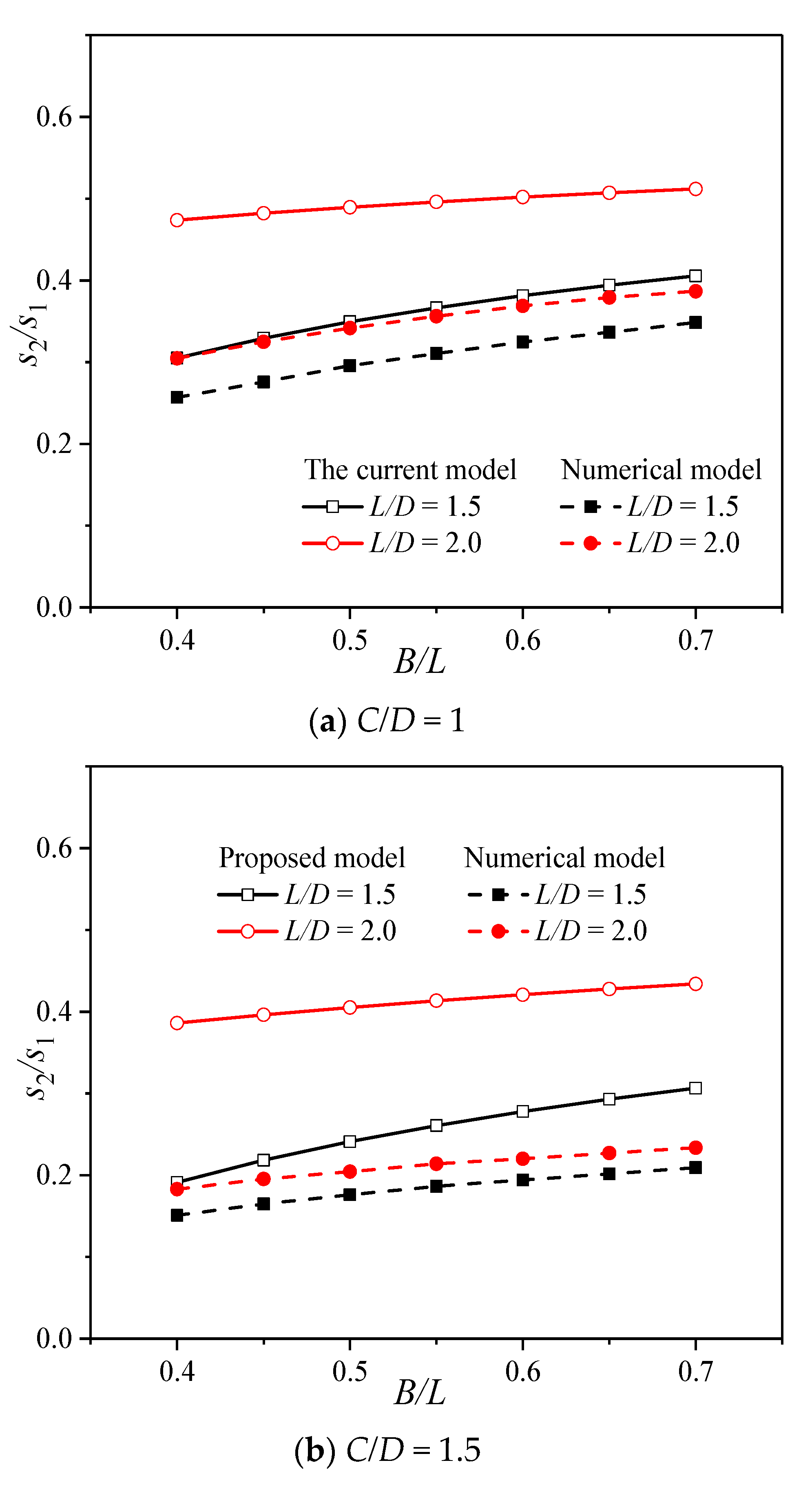
3.1. Comparisons of the Support Pressure
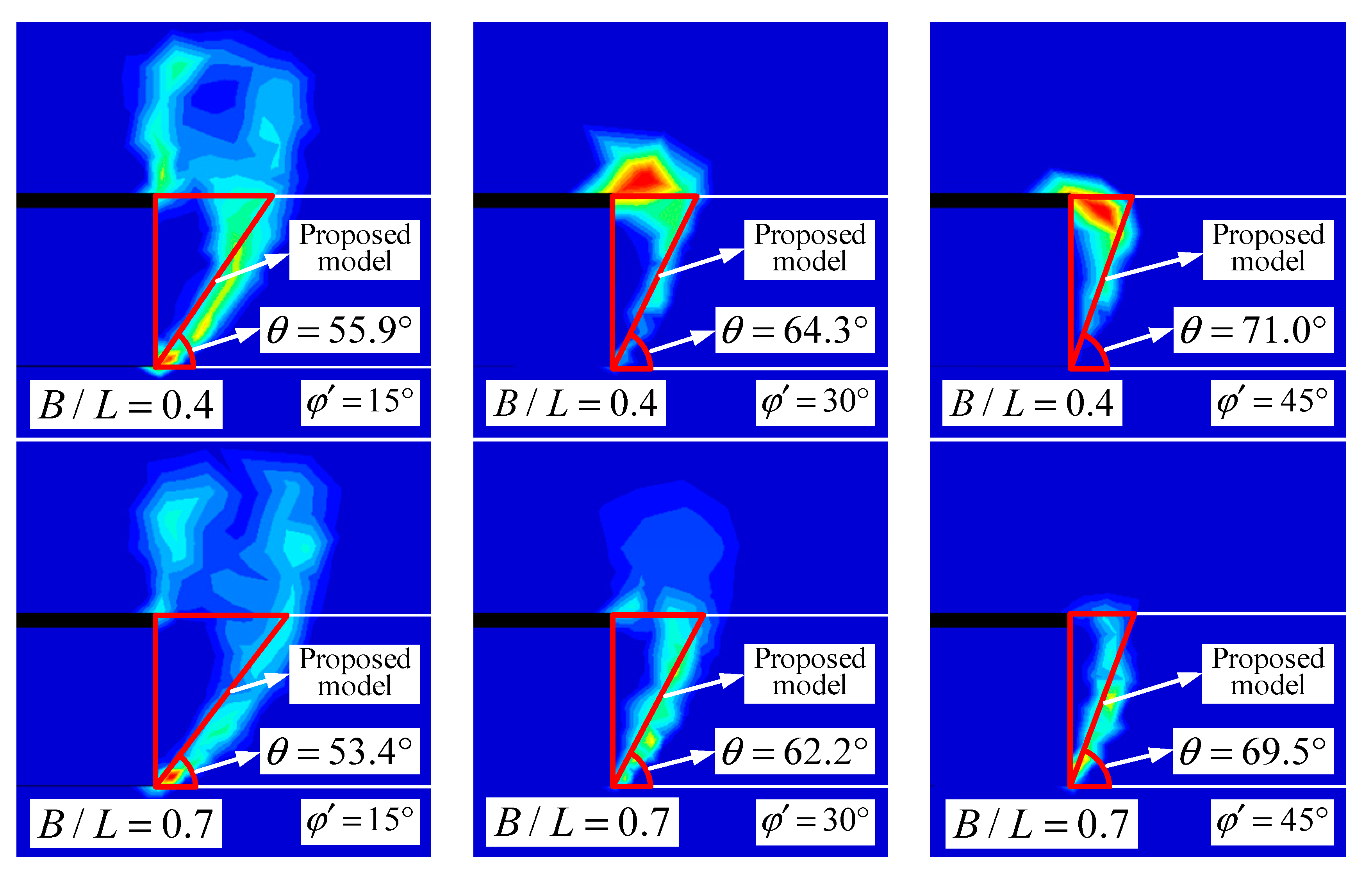
3.2. Comparisons of the Failure Geometry
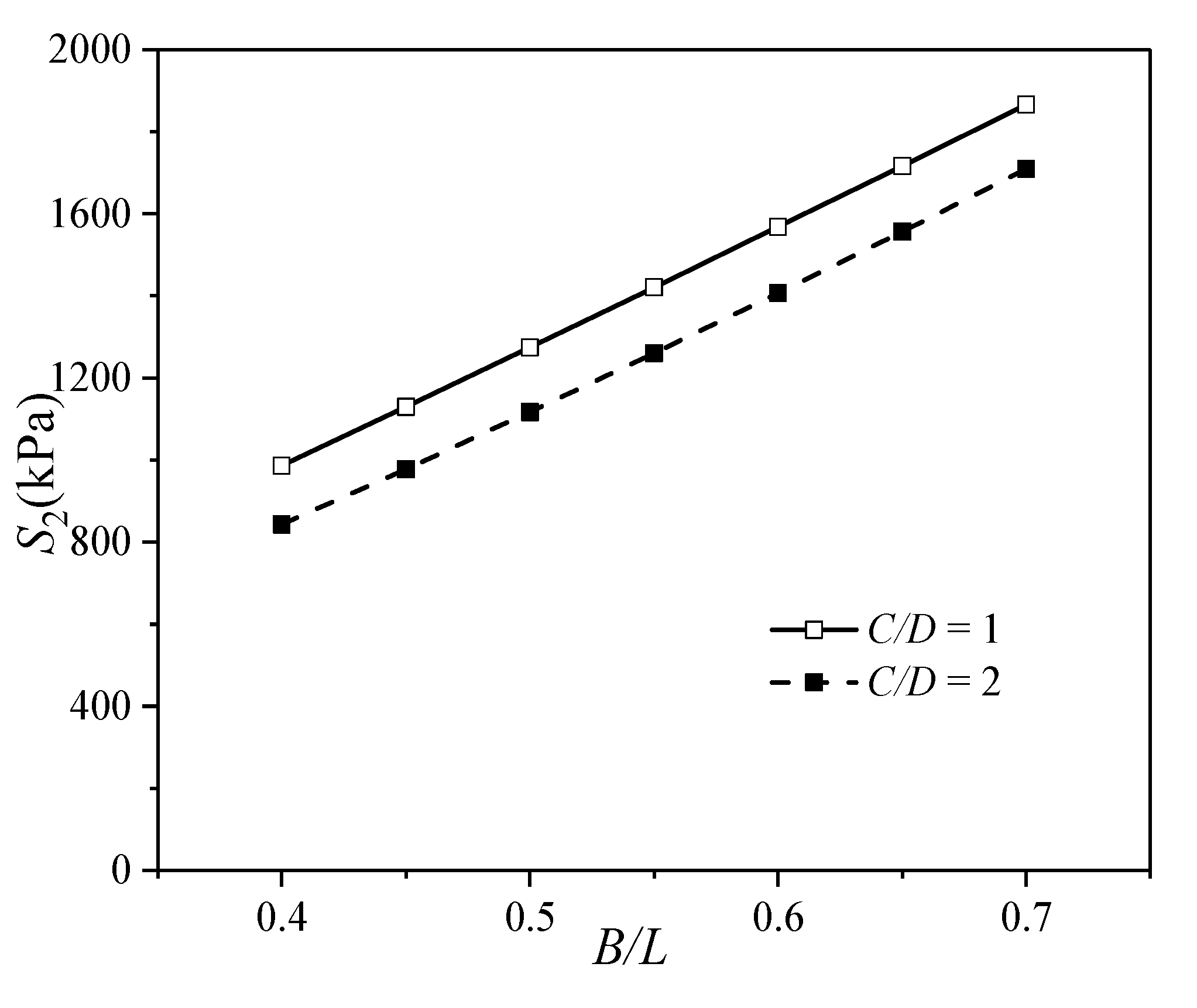
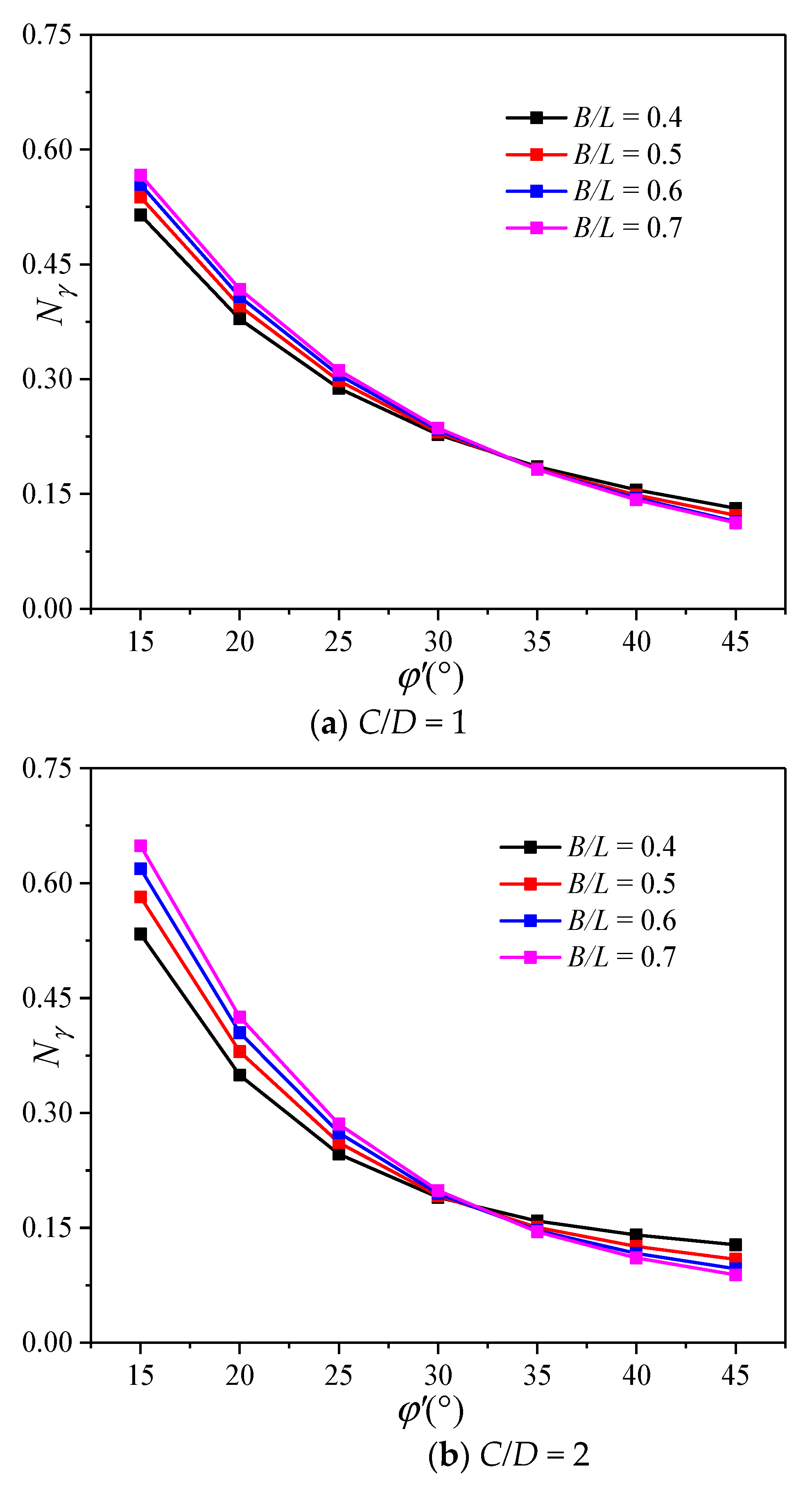
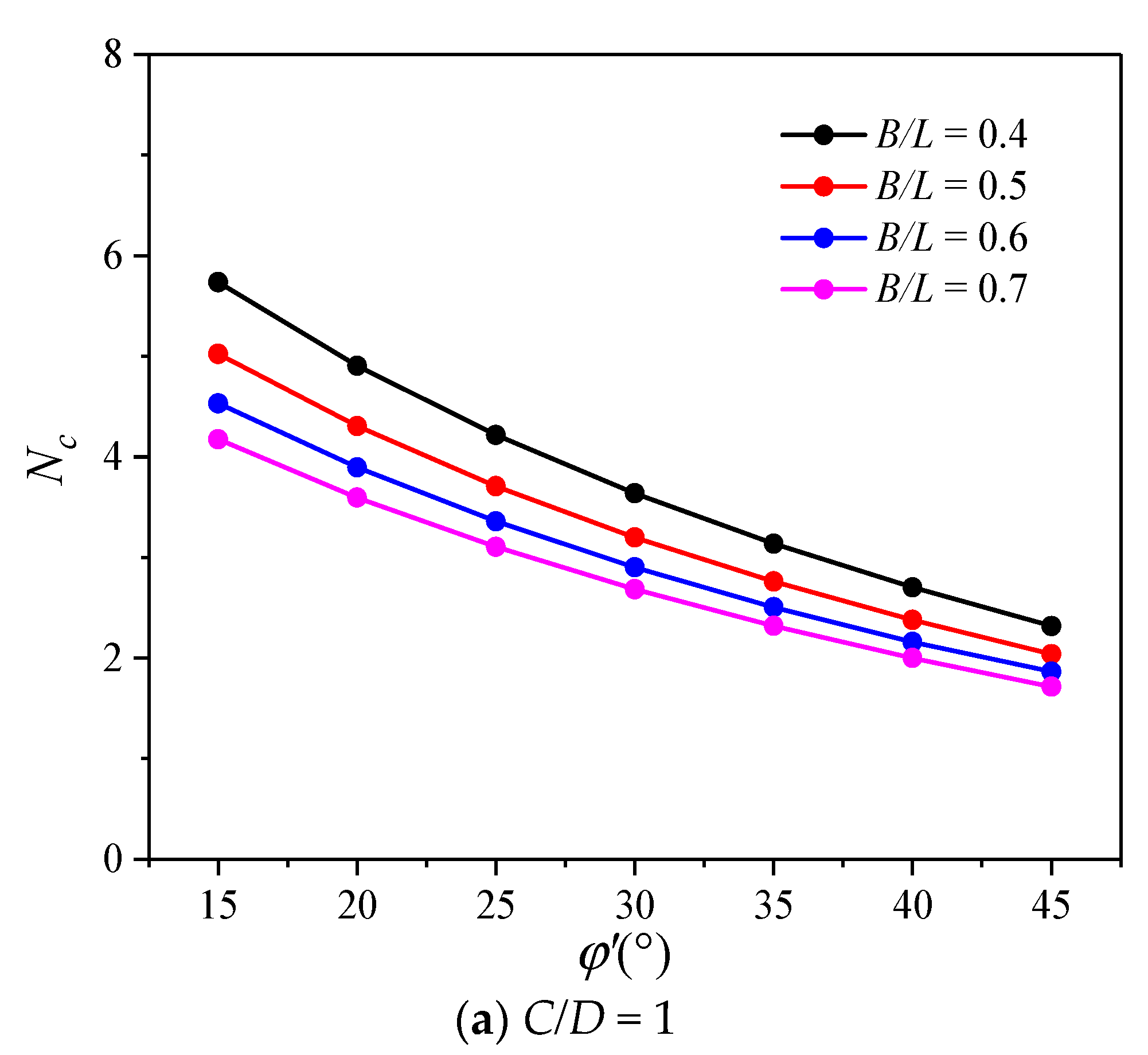
3.3. Parametric Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| height of tunnel | |
| width of tunnel | |
| cover depth | |
| width of partially supported area | |
| effective cohesion | |
| effective angle of internal friction | |
| the total unit weight | |
| ground surcharge | |
| support force acting on block I | |
| support force acting on block II | |
| wedge angle between slanted failure plane and the horizontal | |
| lateral stress coefficient | |
| active earth pressure coefficient | |
| ratio of the volume of the prism to its side area | |
| coefficient related to | |
| coefficient related to | |
| dimensionless coefficient | |
| dimensionless coefficient | |
| dimensionless coefficient |
References
- Davis, E.H.; Gunn, M.J.; Mair, R.J.; Seneviratne, H.N. The stability of shallow tunnels and underground openings in cohesive material. Géotechnique 1980, 30, 397–416. [Google Scholar] [CrossRef]
- Leca, E.; Dormieux, L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material. Géotechnique 1990, 40, 581–606. [Google Scholar] [CrossRef] [Green Version]
- Soubra, A.H.; Regenass, P. Three-dimensional passive earth pressures by kinematical approach. J. Geotech. Geoenviron. 2000, 126, 969–978. [Google Scholar] [CrossRef] [Green Version]
- Mollon, G.; Dias, D.; Soubra, A.H. Face Stability Analysis of Circular Tunnels Driven by a Pressurized Shield. J. Geotech. Geoenviron. 2010, 136, 215–229. [Google Scholar] [CrossRef] [Green Version]
- Mollon, G.; Dias, D.; Soubra, A.H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield. Int. J. Numer. Anal. Methods 2011, 35, 1363–1388. [Google Scholar] [CrossRef] [Green Version]
- Mollon, G.; Dias, D.; Soubra, A.H. Continuous velocity fields for collapse and blow-out of a pressurized tunnel face in purely cohesive soil. Int. J. Numer. Anal. Methods 2013, 37, 2061–2083. [Google Scholar] [CrossRef] [Green Version]
- Pan, Q.J.; Dias, D. Face Stability Analysis for a Shield-Driven Tunnel in Anisotropic and Nonhomogeneous Soils by the Kinematical Approach. Int. J. Geomech. 2015, 16, 04015076. [Google Scholar] [CrossRef]
- Pan, Q.J.; Dias, D. Upper-bound analysis on the face stability of a non-circular tunnel. Tunn. Undergr. Space Technol. 2017, 62, 96–102. [Google Scholar] [CrossRef]
- Pan, Q.J.; Dias, D. Three dimensional face stability of a tunnel in weak rock masses subjected to seepage forces. Tunn. Undergr. Space Technol. 2018, 71, 555–566. [Google Scholar] [CrossRef]
- Senent, S.; Yi, C.K.; Jimenez, R. An upper bound solution for tunnel face stability analysis considering the free span. Tunn. Undergr. Space Technol. 2020, 103, 103515. [Google Scholar] [CrossRef]
- Chen, G.H.; Zou, J.F.; Chen, J.Q. Shallow tunnel face stability considering pore water pressure in non-homogeneous and anisotropic soils. Comput. Geotech. 2019, 116, 103205. [Google Scholar] [CrossRef]
- Liu, W.; Shi, P.X.; Chen, L.J.; Tang, Q. Analytical analysis of working face passive stability during shield tunneling in frictional soils. Acta Geotech. 2020, 15, 781–794. [Google Scholar] [CrossRef]
- Liu, W.; Wu, B.; Shi, P.X.; Cai, G.Q. Upper bound analysis of working face passive failure in large-diameter shield tunneling based on a composite mechanism. Comput. Geotech. 2021, 138, 104362. [Google Scholar] [CrossRef]
- Liu, W.; Wu, B.; Shi, P.X.; Xu, X.Y. Analysis on face stability of rectangular cross-sectional shield tunneling based on an improved two-dimensional rotational mechanism. Acta Geotech. 2021, 16, 3725–3738. [Google Scholar] [CrossRef]
- Di, Q.G.; Li, P.F.; Zhang, M.J.; Wu, J. Influence of permeability anisotropy of seepage flow on the tunnel face stability. Undergr. Space 2022, 8, 1–14. [Google Scholar] [CrossRef]
- Jancsecz, S.; Steiner, W. Face support for a large mix-shield in heterogeneous ground conditions. In Proceedings of the Tunnelling 1994, London, UK, 5–7 July 1994; Springer: Boston, MA, USA, 1994; pp. 531–550. [Google Scholar]
- Broere, W. Tunnel Face Stability and New CPT Applications. Ph. D. Thesis, Delft University, Delft, The Netherlands, 2001. [Google Scholar]
- Anagnostou, G. The contribution of horizontal arching to tunnel face stability. Geotechnik 2012, 35, 34–44. [Google Scholar] [CrossRef]
- Xu, Y.J.; Liang, W.Z.; Liu, X.M.; Cui, G.Q.; Bai, X.G. Soil Mass Stability at the Working Face of a Rectangular Pipe-Jacking Tunnel with a Large Section. Mod. Tunn. Technol. 2017, 54, 70–85. (In Chinese) [Google Scholar]
- Cheng, C.; Zhao, W.; Cheng, C.N.; Li, F. Calculation on Active Limit Support Pressure of Shield Tunnel Excavation Face in Dry Cohesionless Soil. J. Northeast. Univ. (Nat. Sci.) 2018, 39, 1348–1352. (In Chinese) [Google Scholar]
- Yu, L.; Zhang, D.L.; Fang, Q.; Cao, L.Q.; Zhang, Y.; Xu, T. Face stability of shallow tunnelling in sandy soil considering unsupported length. Tunn. Undergr. Space Technol. 2020, 102, 103445. [Google Scholar] [CrossRef]
- Vu, M.N.; Broere, W.; Bosch, J. The impact of shallow cover on stability when tunnelling in soft soils. Tunn. Undergr. Space Technol. 2015, 50, 507–515. [Google Scholar] [CrossRef]
- Wei, G. Theoretical Study on Properties of Soil and Structure during Pipe Jacking Construction. Ph. D. Thesis, Zhejiang University, Hangzhou, China, 2005. [Google Scholar]
- Wei, G.; He, F. Calculation of minimal support pressure acting on shield face during pipe jacking in sandy soil. Chin. J. Undergr. Space Eng. 2007, 3, 903–908. (In Chinese) [Google Scholar]
- Sun, Z.Y.; Zhang, D.L.; Fang, Q.; Dui, G.S.; Tai, Q.M.; Sun, F.W. Analysis of the interaction between tunnel support and surrounding rock considering pre-reinforcement. Tunn. Undergr. Space Technol. 2021, 115, 104074. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Zhang, D.L.; Fang, Q.; Dui, G.S.; Chu, Z.F. Analytical solutions for deep tunnels in strain-softening rocks modeled by different elastic strain definitions with the unified strength theory. Sci. China Technol. Sci. 2022, 65, 2503–2519. [Google Scholar] [CrossRef]
- Zhang, D.L.; Sun, Z.Y.; Fang, Q. Scientific problems and research proposals for Sichuan-Tibet railway tunnel construction. Tunn. Undergr. Space 2022, 7, 419–439. [Google Scholar] [CrossRef]
- Liu, W.; Shi, P.X.; Yu, M.; Jia, P.J. Analysis of working face stability during obstruction removal from a box tunnel machine. Acta Geotech. 2022, 17, 4627–4639. [Google Scholar] [CrossRef]
- Li, C.D.; Zhang, W.; Wang, X.M.; Pan, B.; Zhu, H.H.; Spencer, B.F. Modeling dynamic responses of a cross-river road shield tunnel under stochastic vehicle loads. Tunn. Undergr. Space Technol. 2020, 102, 103432. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Zhou, Y.; Song, L.F. Seismic time-history response and system reliability analysis of slopes considering uncertainty of multi-parameters and earthquake excitations. Comput. Geotech. 2021, 136, 104245. [Google Scholar] [CrossRef]
- Chambon, P.; Corte, J. Shallow Tunnels in Cohesionless Soil: Stability of Tunnel face. Int. J. Geotech. Eng. 1994, 120, 1148–1165. [Google Scholar] [CrossRef]
- Chen, R.P.; Li, J.; Kong, L.G.; Tang, L.J. Experimental study on face instability of shield tunnel in sand. Tunn. Undergr. Space Technol. 2013, 33, 12–21. [Google Scholar] [CrossRef]
- Chen, R.P.; Li, J.; Chen, Y.M.; Kong, L.G. Large-scale tests on face stability of shield tunnelling in dry cohesionless soil. Chin. J. Geotech. Eng. 2011, 33, 117–122. (In Chinese) [Google Scholar]
- Chen, R.P.; Qi, L.Z.; Tang, L.J.; Zhou, B.S. Study of limit supporting force of excavation face’s passive failure of shield tunnels in sand strata. Chin. J. Rock Mech. Eng. 2013, 32, 2877–2882. (In Chinese) [Google Scholar]
- Chen, R.P.; Tang, L.J.; Yin, X.S.; Chen, Y.M.; Bian, X.C. An improved 3D wedge-prism model for the face stability analysis of the shield tunnel in cohesionless soils. Acta Geotech. 2015, 10, 683–692. [Google Scholar] [CrossRef]
- Wong, K.S.; Ng, C.W.W.; Chen, Y.M.; Bian, X.C. Centrifuge and numerical investigation of passive failure of tunnel face in sand. Tunn. Undergr. Space Technol. 2012, 28, 297–303. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Wong, K.S. Investigation of passive failure and deformation mechanisms due to tunnelling in clay. Can. Geotech. J. 2013, 50, 359–372. [Google Scholar] [CrossRef]
- Pan, Q.J.; Dias, D. The effect of pore water pressure on tunnel face stability. Int. J. Numer. Anal. Methods 2016, 40, 2123–2136. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, Y.; Shi, P.X.; Li, J.Y.; Gan, P.L. Face stability analysis of shield driven tunnels shallowly buried in dry sand using 1 g large-scale model tests. Acta Geotech. 2018, 13, 693–705. [Google Scholar] [CrossRef]
- Lu, X.L.; Zeng, S.; Zhao, Y.C.; Huang, M.S.; Ma, S.K.; Zhang, Z.G. Physical model tests and discrete element simulation of shield tunnel face stability in anisotropic granular media. Acta Geotech. 2020, 15, 3017–3026. [Google Scholar] [CrossRef]
- Lin, Q.T.; Lu, D.C.; Lei, C.M.; Tian, Y.; Gong, Q.M.; Du, X.L. Model test study on the stability of cobble strata during shield under-crossing. Tunn. Undergr. Space Technol. 2021, 110, 103807. [Google Scholar] [CrossRef]
- Zheng, H.B.; Li, P.F.; Ma, G.W.; Zhang, Q.B. Experimental investigation of mechanical characteristics for linings of twins tunnels with asymmetric cross-section. Tunn. Undergr. Space Technol. 2021, 119, 104209. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Zhang, D.L.; Li, A.; Lu, .S.; Tai, Q.M.; Chu, Z.F. Model test and numerical analysis for the face failure mechanism of large cross-section tunnels under different ground conditions. Tunn. Undergr. Space Technol. 2022, 130, 104735. [Google Scholar] [CrossRef]










| /kN/m3 | E/MPa | v | c’/kPa | /° |
|---|---|---|---|---|
| 19.8 | 30 | 0.25 | 0 | 15~45 |
| C/D = 1, L/D = 2 | ||||||
|---|---|---|---|---|---|---|
| /° | ||||||
| B/L = 0.5 | B/L = 0.6 | B/L = 0.7 | B/L = 0.5 | B/L = 0.6 | B/L = 0.7 | |
| 15 | 0.609 | 0.627 | 0.642 | 0.504 | 0.539 | 0.563 |
| 25 | 0.489 | 0.502 | 0.512 | 0.342 | 0.369 | 0.387 |
| 35 | 0.451 | 0.448 | 0.448 | 0.272 | 0.291 | 0.305 |
| 45 | 0.475 | 0.452 | 0.437 | 0.235 | 0.251 | 0.263 |
| C/D = 2, L/D = 2 | ||||||
| /° | (Proposed Model) | (Numerical Model) | ||||
| B/L = 0.5 | B/L = 0.6 | B/L = 0.7 | B/L = 0.5 | B/L = 0.6 | B/L = 0.7 | |
| 15 | 0.395 | 0.420 | 0.441 | 0.322 | 0.350 | 0.372 |
| 25 | 0.257 | 0.270 | 0.281 | 0.204 | 0.220 | 0.234 |
| 35 | 0.223 | 0.216 | 0.214 | 0.164 | 0.176 | 0.184 |
| 45 | 0.254 | 0.225 | 0.206 | 0.138 | 0.152 | 0.159 |
| /° | B/L = 0.4 | B/L = 0.7 | ||||
|---|---|---|---|---|---|---|
| /° | /° | /m3 | /° | /° | /m3 | |
| 15 | 55.9 | 48.5 | 117.1 | 53.4 | 68.0 | 144.5 |
| 20 | 58.99 | 45.1 | 104.2 | 56.5 | 65.6 | 128. 8 |
| 25 | 61.7 | 41.9 | 92.9 | 59.4 | 63.1 | 114.9 |
| 30 | 64.3 | 38. 7 | 83.0 | 62.2 | 60.4 | 102.5 |
| 35 | 66.7 | 35.6 | 74.3 | 64.8 | 57.5 | 91.5 |
| 40 | 69.0 | 32.7 | 66.5 | 67.2 | 54.5 | 81.6 |
| 45 | 71.0 | 29.8 | 59.4 | 69.5 | 51.2 | 72.6 |
| C/D = 2, L/D = 2 | ||||||
| /° | B/L= 0.4 | B/L= 0.7 | ||||
| /° | /° | /m3 | /° | /° | /m3 | |
| 15 | 55.7 | 48.6 | 117.7 | 51.6 | 69.3 | 154.2 |
| 20 | 59.5 | 44.5 | 101.8 | 55.6 | 66.3 | 132.9 |
| 25 | 62.8 | 40.6 | 88.8 | 59.4 | 63.1 | 115.0 |
| 30 | 65.7 | 37.0 | 78.1 | 62.8 | 59.7 | 99.9 |
| 35 | 68.2 | 33.7 | 69.1 | 65.8 | 56.2 | 87.3 |
| 40 | 70.4 | 30.7 | 61.4 | 68.5 | 52.7 | 76.6 |
| 45 | 72.4 | 27.9 | 54.8 | 70.8 | 49.2 | 67.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Liu, W.; Wu, B.; Yan, J.; Gan, P. Working Face Stability of Box Shield Tunneling under Non-Uniform Support Pressure. Appl. Sci. 2022, 12, 12360. https://doi.org/10.3390/app122312360
Yu M, Liu W, Wu B, Yan J, Gan P. Working Face Stability of Box Shield Tunneling under Non-Uniform Support Pressure. Applied Sciences. 2022; 12(23):12360. https://doi.org/10.3390/app122312360
Chicago/Turabian StyleYu, Miao, Wei Liu, Ben Wu, Jiajia Yan, and Penglu Gan. 2022. "Working Face Stability of Box Shield Tunneling under Non-Uniform Support Pressure" Applied Sciences 12, no. 23: 12360. https://doi.org/10.3390/app122312360




