Software Reliability Growth Model with Dependent Failures and Uncertain Operating Environments
Abstract
:1. Introduction
2. Software Reliability Growth Model
2.1. Poisson Processes
- (1)
- .
- (2)
- is an integer.
- (3)
- If .
- (4)
- When , represents the number of events within time interval .
2.2. Reliability Function
3. NHPP Software Reliability Growth Model (SRGM)
3.1. Model Formulation
3.2. Proposed Model
3.3. Existing NHPP Models
4. Numerical Example
4.1. Datasets
4.2. Criteria
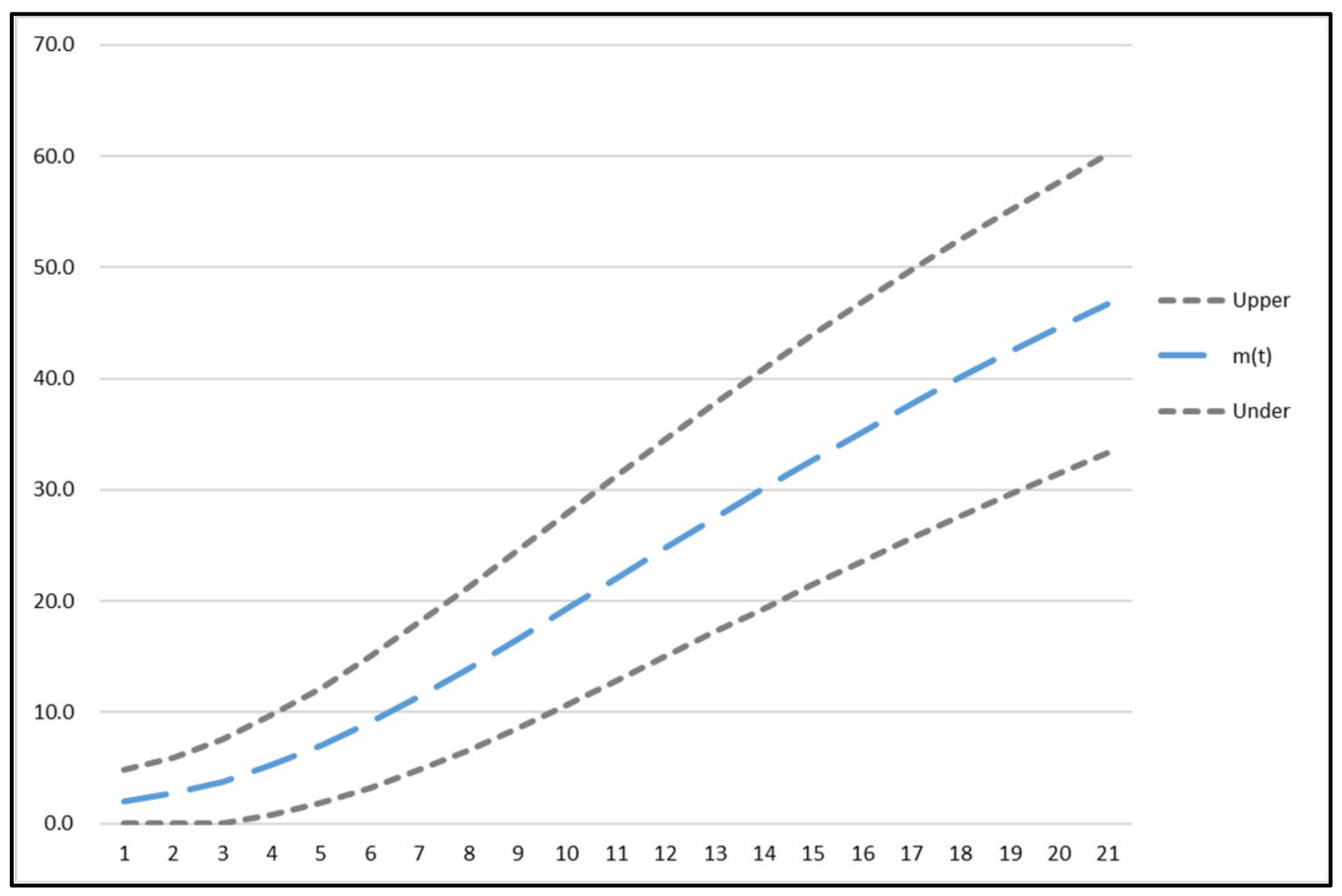
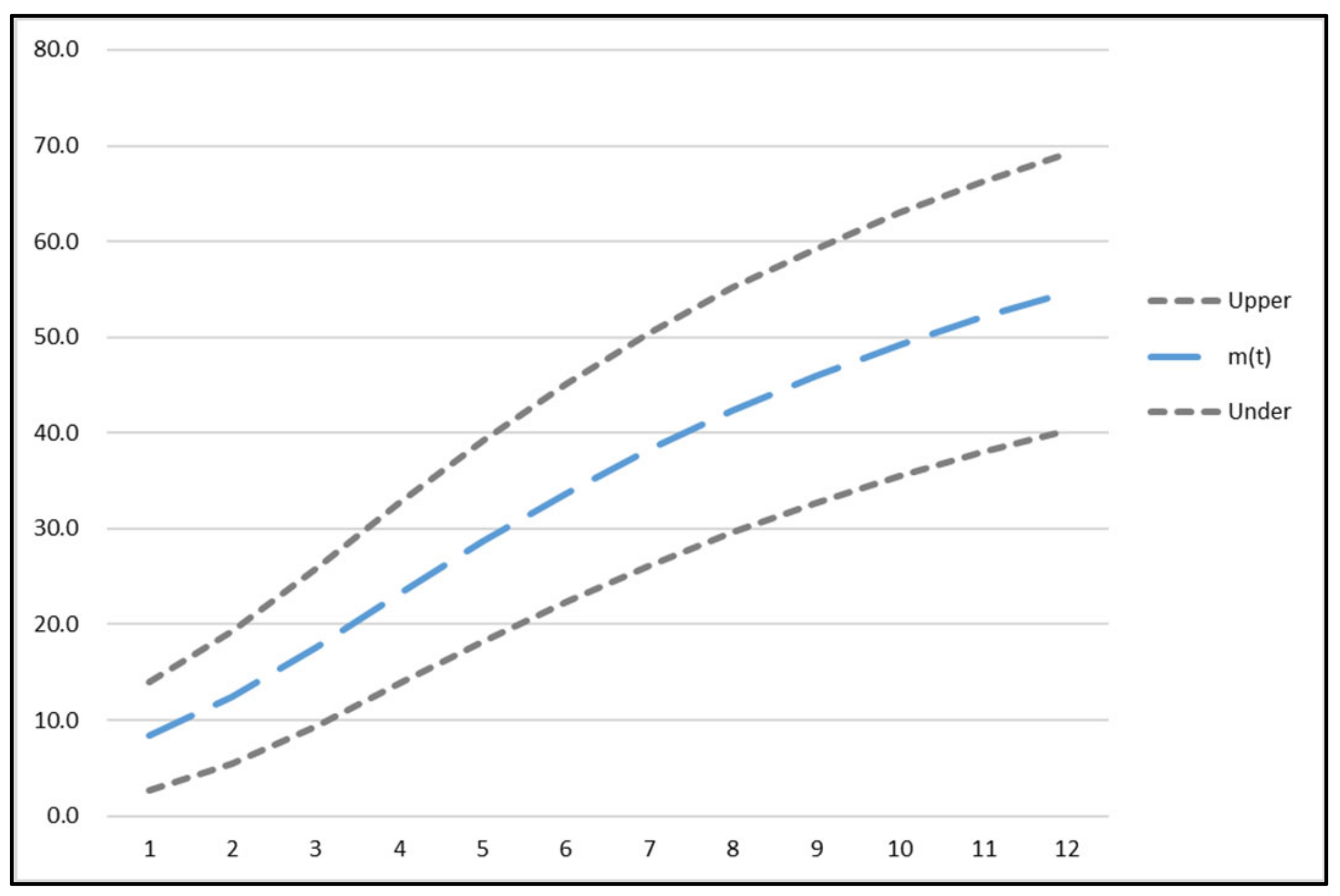
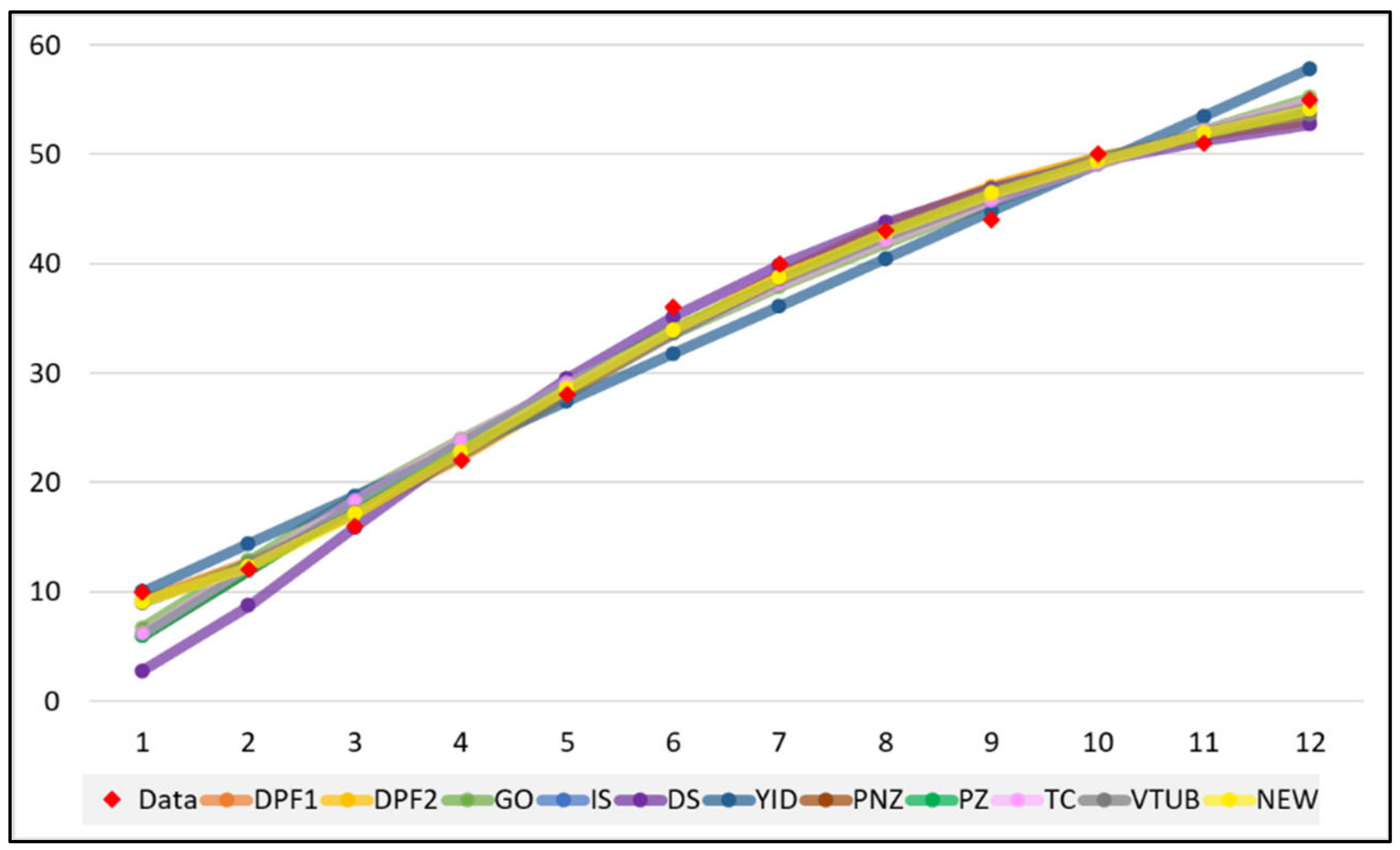
4.3. Results
5. Conclusions
6. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goel, A.L.; Okumoto, K. Time-dependent error-detection rate model for software reliability and other performance measures. IEEE Trans. Reliab. 1979, 28, 206–211. [Google Scholar] [CrossRef]
- Yamada, S.; Ohba, M.; Osaki, S. S-shaped software reliability growth models and their applications. IEEE Trans. Reliab. 1984, 33, 289–292. [Google Scholar] [CrossRef]
- Pham, H.; Zhang, X. An NHPP software reliability model and its comparison. Int. J. Reliab. Qual. Saf. Eng. 1997, 4, 269–282. [Google Scholar] [CrossRef]
- Pham, H.; Zhang, X. NHPP software reliability and cost models with testing coverage. Eur. J. Oper. Res. 2003, 145, 443–454. [Google Scholar] [CrossRef]
- Song, K.Y.; Chang, I.H.; Pham, H. A testing coverage model based on NHPP software reliability considering the software operating environment and the sensitivity analysis. Mathematics 2019, 7, 450. [Google Scholar] [CrossRef] [Green Version]
- Pham, H. A logistic fault-dependent detection software reliability model. J. Univers. Comput. Sci. 2018, 24, 1717–1730. [Google Scholar]
- Pham, H. Distribution function and its applications in software reliability. Int. J. Performability Eng. 2019, 15, 1306–1313. [Google Scholar] [CrossRef]
- Pradhan, V.; Kumar, A.; Dhar, J. Enhanced growth model of software reliability with generalized inflection S-shaped testing-effort function. J. Interdiscip. Math. 2022, 25, 137–153. [Google Scholar] [CrossRef]
- Erto, P.; Giorgio, M.; Lepore, A. The Generalized Inflection S-Shaped Software Reliability Growth Model. IEEE Trans. Reliab. 2020, 69, 228–244. [Google Scholar] [CrossRef]
- Saxena, P.; Ram, M. Two phase software reliability growth model in the presence of imperfect debugging and error generation under fuzzy paradigm. Math. Eng. Sci. Aerosp. (MESA) 2022, 13, 777–790. [Google Scholar]
- Haque, M.A.; Ahmad, N. An effective software reliability growth model. Saf. Reliab. 2021, 40, 209–220. [Google Scholar] [CrossRef]
- Nafreen, M.; Fiondella, L. Software Reliability Models with Bathtub-shaped Fault Detection. In Proceedings of the 2021 Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 24–27 May 2021; pp. 1–7. [Google Scholar]
- Song, K.Y.; Chang, I.H.; Pham, H. A three-parameter fault-detection software reliability model with the uncertainty of operating environments. J. Syst. Sci. Syst. Eng. 2017, 26, 121–132. [Google Scholar] [CrossRef]
- Song, K.Y.; Chang, I.H.; Pham, H. NHPP software reliability model with inflection factor of the fault detection rate considering the uncertainty of software operating environments and predictive analysis malignant. Symmetry 2019, 11, 521. [Google Scholar] [CrossRef] [Green Version]
- Zaitseva, E.; Levashenko, V. Construction of a Reliability Structure Function Based on Uncertain Data. IEEE Trans. Reliab. 2016, 65, 1710–1723. [Google Scholar] [CrossRef]
- Lee, D.H.; Chang, I.H.; Pham, H. Software reliability model with dependent failures and SPRT. Mathematics 2020, 8, 1366. [Google Scholar] [CrossRef]
- Kim, Y.S.; Song, K.Y.; Pham, H.; Chang, I.H. A software reliability model with dependent failure and optimal release time. Symmetry 2022, 14, 343. [Google Scholar] [CrossRef]
- Saxena, P.; Kumar, V.; Ram, M. A novel CRITIC-TOPSIS approach for optimal selection of software reliability growth model (SRGM). Qual. Reliab. Eng. Int. 2022, 38, 2501–2520. [Google Scholar] [CrossRef]
- Kumar, V.; Saxena, P.; Garg, H. Selection of optimal software reliability growth models using an integrated entropy–Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) approach. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Garg, R.; Raheja, S.; Garg, R.K. Decision Support System for Optimal Selection of Software Reliability Growth Models Using a Hybrid Approach. IEEE Trans. Reliab. 2022, 71, 149–161. [Google Scholar] [CrossRef]
- Yaghoobi, T. Selection of optimal software reliability growth model using a diversity index. Soft Comput. 2021, 25, 5339–5353. [Google Scholar] [CrossRef]
- Zhu, M. A new framework of complex system reliability with imperfect maintenance policy. Ann. Oper. Res. 2022, 312, 553–579. [Google Scholar] [CrossRef]
- Wang, L. Architecture-Based Reliability-Sensitive Criticality Measure for Fault-Tolerance Cloud Applications. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 2408–2421. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Yu, Q.; Zheng, Z. Learning the Evolution Regularities for BigService-Oriented Online Reliability Prediction. IEEE Trans. Serv. Comput. 2019, 12, 398–411. [Google Scholar] [CrossRef]
- Wang, L.; He, Q.; Gao, D.; Wan, J.; Zhang, Y. Temporal-Perturbation Aware Reliability Sensitivity Measurement for Adaptive Cloud Service Selection. IEEE Trans. Serv. Comput. 2022, 15, 2301–2313. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C. Software reliability prediction using a deep learning model based on the RNN encoder–decoder. Reliab. Eng. Syst. Saf. 2018, 170, 73–82. [Google Scholar] [CrossRef]
- San, K.K.; Washizaki, H.; Fukazawa, Y.; Honda, K.; Taga, M.; Matsuzaki, A. Deep Cross-Project Software Reliability Growth Model Using Project Similarity-Based Clustering. Mathematics 2021, 9, 2945. [Google Scholar] [CrossRef]
- Li, L. Software reliability growth fault correction model based on machine learning and neural network algorithm. Microprocess. Microsyst. 2021, 80, 103538. [Google Scholar] [CrossRef]
- Banga, M.; Bansal, A.; Singh, A. Implementation of machine learning techniques in software reliability: A framework. In Proceedings of the 2019 International Conference on Automation, Computational and Technology Management (ICACTM), London, UK, 24–26 April 2019; pp. 241–245. [Google Scholar] [CrossRef]
- Pham, H. System Software Reliability; Springer: London, UK, 2006. [Google Scholar]
- Pham, H.; Nordmann, L.; Zhang, Z. A general imperfect-software-debugging model with S-shaped fault-detection rate. IEEE Trans. Reliab. 1999, 48, 169–175. [Google Scholar] [CrossRef]
- Pham, H. A new software reliability model with Vtub-shaped fault-detection rate and the uncertainty of operating environments. Optimization 2014, 63, 1481–1490. [Google Scholar] [CrossRef]
- Yamada, S.; Tokuno, K.; Osaki, S. Imperfect debugging models with fault introduction rate for software reliability assessment. Int. J. Syst. Sci. 1992, 23, 2241–2252. [Google Scholar] [CrossRef]
- Chang, I.H.; Pham, H.; Lee, S.W.; Song, K.Y. A testing-coverage software reliability model with the uncertainty of operation environments. Int. J. Syst. Sci. Oper. Logist. 2014, 1, 220–227. [Google Scholar] [CrossRef]
- Ohba, M. Software reliability analysis models. IBM J. Res. Dev. 1984, 28, 428–443. [Google Scholar] [CrossRef]
- Song, K.Y.; Chang, I.H.; Pham, H. A software reliability model with a Weibull fault detection rate function subject to operating environments. Appl. Sci. 2017, 7, 983. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Pham, H. A testing-coverage software reliability model considering fault removal efficiency and error generation. PLoS ONE 2017, 12, e0181524. [Google Scholar] [CrossRef] [Green Version]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Okamura, H.; Dohi, T.; Osaki, S. Software reliability growth models with normal failure time distributions. Reliab. Eng. Syst. Saf. 2013, 116, 135–141. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Zhu, M.; Pham, H. A two-phase software reliability modeling involving with software fault dependency and imperfect fault removal. Comput. Lang. Syst. Struct. 2018, 53, 27–42. [Google Scholar] [CrossRef]
- Pillai, K.; Sukumaran Nair, V.S. A model for software development effort and cost estimation. IEEE Trans. Softw. Eng. 1997, 23, 485–497. [Google Scholar] [CrossRef]
- Anjum, M.; Haque, M.A.; Ahmad, N. Analysis and ranking of software reliability models based on weighted criteria value. Int. J. Inf. Technol. Comput. Sci. 2013, 5, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Gharaei, A.; Amjadian, A.; Shavandi, A. An integrated reliable four-level supply chain with multi-stage products under shortage and stochastic constraints. Int. J. Syst. Sci. Oper. Logist. 2021, 1–22. [Google Scholar] [CrossRef]
- Askari, R.; Sebt, M.V.; Amjadian, A. A Multi-product EPQ Model for Defective Production and Inspection with Single Machine, and Operational Constraints: Stochastic Programming Approach. In International Conference on Logistics and Supply Chain Management; Springer: Cham, Switzerland, 2021; pp. 161–193. [Google Scholar]
- Souza, R.L.C.; Ghasemi, A.; Saif, A.; Gharaei, A. Robust job-shop scheduling under deterministic and stochastic unavailability constraints due to preventive and corrective maintenance. Comput. Ind. Eng. 2022, 168, 108130. [Google Scholar] [CrossRef]
- Amjadian, A.; Gharaei, A. An integrated reliable five-level closed-loop supply chain with multi-stage products under quality control and green policies: Generalised outer approximation with exact penalty. Int. J. Syst. Sci. Oper. Logist. 2022, 9, 429–449. [Google Scholar] [CrossRef]
- Gharaei, A.; Almehdawe, E. Optimal sustainable order quantities for growing items. J. Clean. Prod. 2021, 307, 127216. [Google Scholar] [CrossRef]
- Gharaei, A.; Diallo, C.; Venkatadri, U. Optimal economic growing quantity for reproductive farmed animals under profitable by-products and carbon emission considerations. J. Clean. Prod. 2022, 374, 133849. [Google Scholar] [CrossRef]


| No. | Model | |
|---|---|---|
| 1 | DPF1 [16] | |
| 2 | DPF2 [17] | |
| 3 | DS [33] | |
| 4 | GO [1] | |
| 5 | IS [2] | |
| 6 | YID [33] | |
| 7 | PNZ [31] | |
| 8 | PZ [3] | |
| 9 | TC [34] | |
| 10 | VTUB [32] | |
| 11 | NEW |
| Time | Cumulative Failures | Time | Cumulative Failures | Time | Cumulative Failures |
|---|---|---|---|---|---|
| 1 | 2 | 8 | 12 | 15 | 31 |
| 2 | 3 | 9 | 19 | 16 | 37 |
| 3 | 4 | 10 | 21 | 17 | 38 |
| 4 | 5 | 11 | 22 | 18 | 41 |
| 5 | 7 | 12 | 24 | 19 | 42 |
| 6 | 9 | 13 | 26 | 20 | 45 |
| 7 | 11 | 14 | 30 | 21 | 46 |
| Time | Failures | Cumulative Failures | Time | Failures | Cumulative Failures |
|---|---|---|---|---|---|
| 1 | 10 | 10 | 7 | 4 | 40 |
| 2 | 2 | 12 | 8 | 3 | 43 |
| 3 | 4 | 16 | 9 | 1 | 44 |
| 4 | 6 | 22 | 10 | 6 | 50 |
| 5 | 6 | 28 | 11 | 1 | 51 |
| 6 | 8 | 36 | 12 | 4 | 55 |
| No | Criteria |
|---|---|
| 1 | Mean square error (MSE) [30] |
| 2 | Predictive ratio risk (PRR) [30] |
| 3 | Predictive power (PP) [30] |
| 4 | Sum of absolute error (SAE) [36] |
| 5 | R-square () [37] |
| 6 | Akaike’s information criterion (AIC) [38] |
| 7 | Bayesian information criterion (BIC) [39,40] |
| 8 | Bias [41] |
| 9 | Predicted relative variation (PRV) [42] |
| 10 | Root mean square prediction error (RMSPE) [42] |
| 11 | Mean absolute error (MAE) [43] |
| 12 | Mean error of prediction (MEOP) [43] |
| 13 | Theil statistic (TS) [43] |
| Model | |||||||
|---|---|---|---|---|---|---|---|
| DPF1 | 51.350 | 0.001 | - | - | - | 0.216 | 2.659 |
| DPF2 | 51.350 | 0.005 | - | - | - | 0.076 | 2.629 |
| DS | 77.253 | 0.0966 | - | - | - | - | - |
| GO | 14,264.000 | 0.0002 | - | - | - | - | - |
| IS | 58.943 | 0.170 | - | 8.386 | - | - | - |
| YID | 1.491 | 0.3068 | 1.7457 | - | - | - | - |
| PNZ | 29.875 | 0.192 | 0.045 | 4.900 | - | - | - |
| PZ | 59.316 | 0.1682 | 128.1029 | 8.2581 | - | 0.0005 | - |
| TC | 0.0191 | 1.567 | 839.1540 | 221.1735 | 78.7859 | - | - |
| VTUB | 1.9701 | 0.6892 | 0.2928 | 19.8529 | 87.2519 | - | - |
| NEW | - | 0.2470 | 2.355 | 1.968 | 126.140 | - | - |
| Model | |||||||
|---|---|---|---|---|---|---|---|
| DPF1 | 55.893 | 0.004 | - | - | - | 0.548 | 7.274 |
| DPF2 | 56.058 | 0.008 | - | - | - | 0.093 | 7.195 |
| DS | 57.478 | 0.344 | - | - | - | - | - |
| GO | 94.344 | 0.0733 | - | - | - | - | - |
| IS | 65.781 | 0.206 | - | 1.293 | - | - | - |
| YID | 5.749 | 52.415 | 0.756 | - | - | - | - |
| PNZ | 64.922 | 0.208 | 0.001 | 1.286 | - | - | - |
| PZ | 7.617 | 0.210 | 0.005 | 1.321 | - | 64.992 | - |
| TC | 0.005 | 1.075 | 2001.000 | 84.681 | 80.373 | - | - |
| VTUB | 5.0693 | 1.793 | 0.0181 | 0.0004 | 57.6685 | - | - |
| NEW | - | 0.316 | 1.326 | 1.142 | 91.500 | - | - |
| Model | MSE | PRR | PP | SAE | R2 | AIC | BIC | Bias | PRV | RMSPE | MAE | MEOP | TS (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
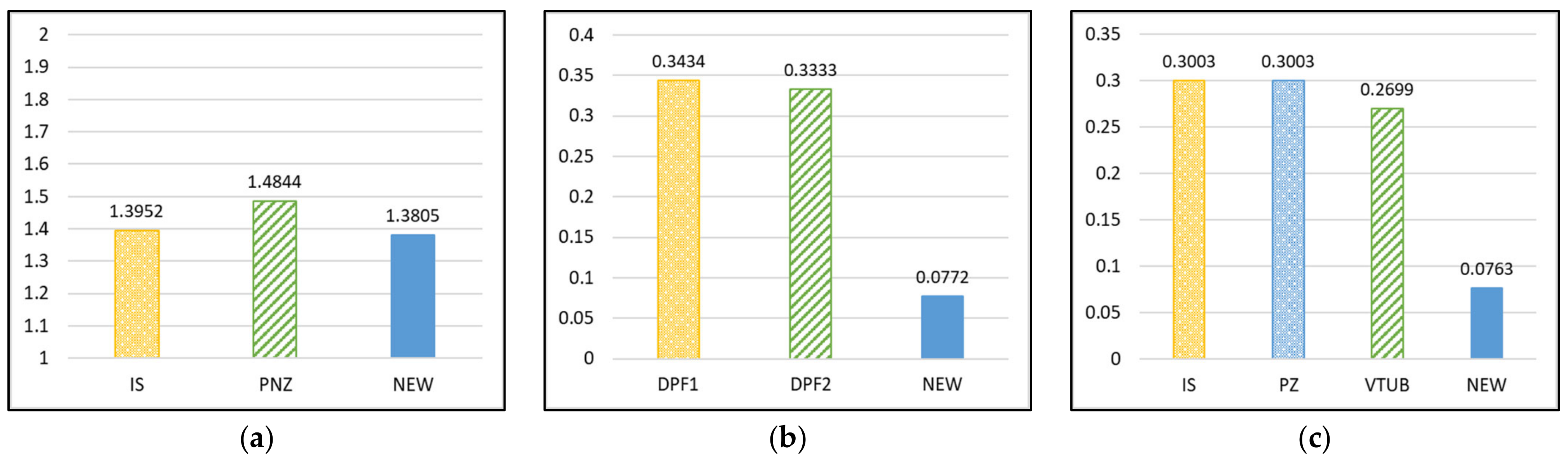
| DPF1 | 2.0159 | 0.3434 | 0.6026 | 20.5585 | 0.9924 | 78.8231 | 83.0012 | 0.1065 | 1.3044 | 1.3088 | 1.2093 | 1.1421 | 4.7409 |
| DPF2 | 2.0055 | 0.3333 | 0.5753 | 20.4606 | 0.9924 | 78.7999 | 82.9780 | 0.1006 | 1.3016 | 1.3054 | 1.2036 | 1.1367 | 4.7287 |
| DS | 1.6365 | 26.3229 | 1.2081 | 21.0349 | 0.9931 | 78.1184 | 80.2075 | −0.2326 | 1.2239 | 1.2458 | 1.1071 | 1.0517 | 4.5159 |
| GO | 6.6010 | 0.8080 | 1.8602 | 42.5436 | 0.9721 | 77.3351 | 79.4242 | 0.8913 | 2.3317 | 2.4962 | 2.2391 | 2.1272 | 9.0696 |
| IS | 1.3952 | 0.6991 | 0.3003 | 17.4495 | 0.9944 | 76.6925 | 79.8261 | −0.0325 | 1.1201 | 1.1205 | 0.9694 | 0.9184 | 4.0584 |
| YID | 1.7008 | 3.0656 | 0.6081 | 21.0606 | 0.9932 | 78.6624 | 81.7960 | −0.0548 | 1.2360 | 1.2372 | 1.1700 | 1.1085 | 4.4810 |
| PNZ | 1.4844 | 0.9578 | 0.3521 | 17.9074 | 0.9944 | 78.9419 | 83.1200 | −0.0504 | 1.1221 | 1.1232 | 1.0534 | 0.9949 | 4.0683 |
| PZ | 1.5697 | 0.6947 | 0.3003 | 17.5203 | 0.9944 | 80.7116 | 85.9342 | −0.0272 | 1.1203 | 1.1206 | 1.0950 | 1.0306 | 4.0586 |
| TC | 1.7268 | 5.9590 | 0.7580 | 19.4342 | 0.9939 | 82.5660 | 87.7886 | −0.0548 | 1.1740 | 1.1753 | 1.2146 | 1.1432 | 4.2568 |
| VTUB | 1.5438 | 0.5610 | 0.2699 | 17.5100 | 0.9945 | 80.6019 | 85.8245 | −0.0425 | 1.1105 | 1.1113 | 1.0944 | 1.0300 | 4.0250 |
| NEW | 1.3805 | 0.0772 | 0.0763 | 15.9817 | 0.9948 | 78.0915 | 82.2696 | −0.0021 | 1.0832 | 1.0832 | 0.9401 | 0.8879 | 3.9233 |
| Model | MSE | PRR | PP | SAE | R2 | AIC | BIC | Bias | PRV | RMSPE | MAE | MEOP | TS (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DPF1 | 2.8201 | 0.0276 | 0.0270 | 12.7389 | 0.9919 | 58.6958 | 60.6354 | 0.0103 | 1.4321 | 1.4321 | 1.5924 | 1.4154 | 3.6893 |
| DPF2 | 2.7946 | 0.0283 | 0.0275 | 12.7515 | 0.9919 | 58.6274 | 60.5670 | 0.0078 | 1.4256 | 1.4256 | 1.5939 | 1.4168 | 3.6726 |
| DS | 8.2096 | 7.3679 | 0.6177 | 20.9540 | 0.9704 | 69.6251 | 70.5950 | −0.7059 | 2.6305 | 2.7236 | 2.0954 | 1.9049 | 7.0377 |
| GO | 4.0245 | 0.2932 | 0.1627 | 19.4170 | 0.9855 | 57.7076 | 58.6775 | −0.0522 | 1.9120 | 1.9127 | 1.9417 | 1.7652 | 4.9275 |
| IS | 4.0555 | 0.4815 | 0.1905 | 17.0520 | 0.9868 | 60.1451 | 61.5998 | −0.1725 | 1.8126 | 1.8208 | 1.8947 | 1.7052 | 4.6926 |
| YID | 7.7536 | 0.0893 | 0.1027 | 24.4096 | 0.9748 | 58.2593 | 59.7140 | 0.0000 | 2.5187 | 2.5187 | 2.7122 | 2.4410 | 6.4885 |
| PNZ | 4.5632 | 0.4818 | 0.1906 | 17.0566 | 0.9868 | 62.1389 | 64.0786 | −0.1722 | 1.8128 | 1.8210 | 2.1321 | 1.8952 | 4.693 |
| PZ | 5.2153 | 0.4890 | 0.1917 | 17.0459 | 0.9868 | 64.1689 | 66.5934 | −0.1758 | 1.8125 | 1.8210 | 2.4351 | 2.1307 | 4.6931 |
| TC | 5.6420 | 0.4307 | 0.1888 | 18.3723 | 0.9857 | 64.2519 | 66.6765 | −0.1203 | 1.8906 | 1.8945 | 2.6246 | 2.2965 | 4.8813 |
| VTUB | 2.9516 | 0.0320 | 0.0296 | 12.6030 | 0.9925 | 59.5514 | 61.9760 | −0.0664 | 1.3688 | 1.3704 | 1.8004 | 1.5754 | 3.5306 |
| NEW | 2.7776 | 0.0606 | 0.0514 | 14.4914 | 0.9920 | 57.2427 | 59.1823 | −0.0070 | 1.4213 | 1.4213 | 1.8114 | 1.6102 | 3.6615 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.H.; Chang, I.H.; Pham, H. Software Reliability Growth Model with Dependent Failures and Uncertain Operating Environments. Appl. Sci. 2022, 12, 12383. https://doi.org/10.3390/app122312383
Lee DH, Chang IH, Pham H. Software Reliability Growth Model with Dependent Failures and Uncertain Operating Environments. Applied Sciences. 2022; 12(23):12383. https://doi.org/10.3390/app122312383
Chicago/Turabian StyleLee, Da Hye, In Hong Chang, and Hoang Pham. 2022. "Software Reliability Growth Model with Dependent Failures and Uncertain Operating Environments" Applied Sciences 12, no. 23: 12383. https://doi.org/10.3390/app122312383
APA StyleLee, D. H., Chang, I. H., & Pham, H. (2022). Software Reliability Growth Model with Dependent Failures and Uncertain Operating Environments. Applied Sciences, 12(23), 12383. https://doi.org/10.3390/app122312383





