Spatial Variability in Land Subsidence and Its Relation to Groundwater Withdrawals in the Choshui Delta
Abstract
:1. Introduction
2. Materials and Methods
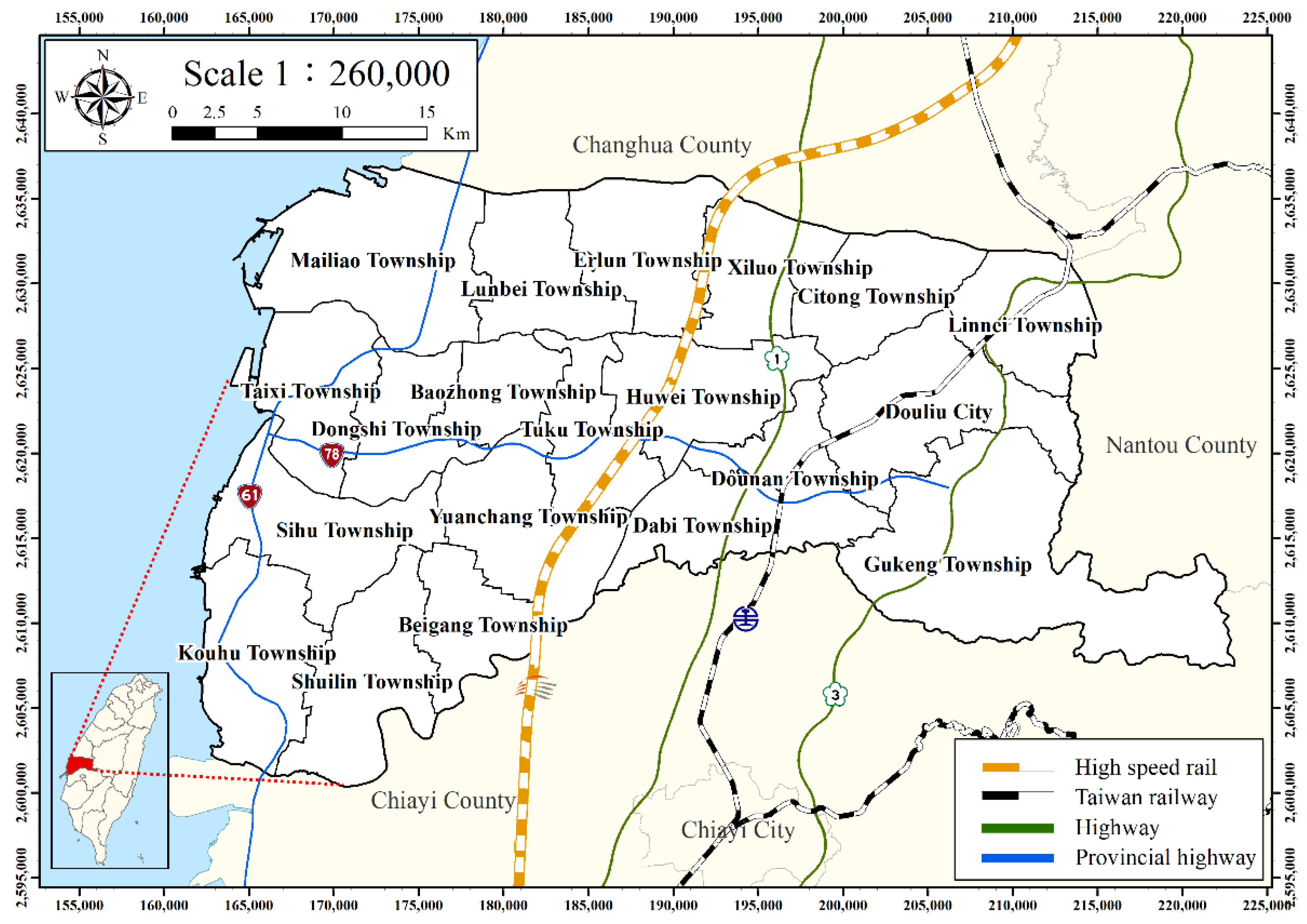
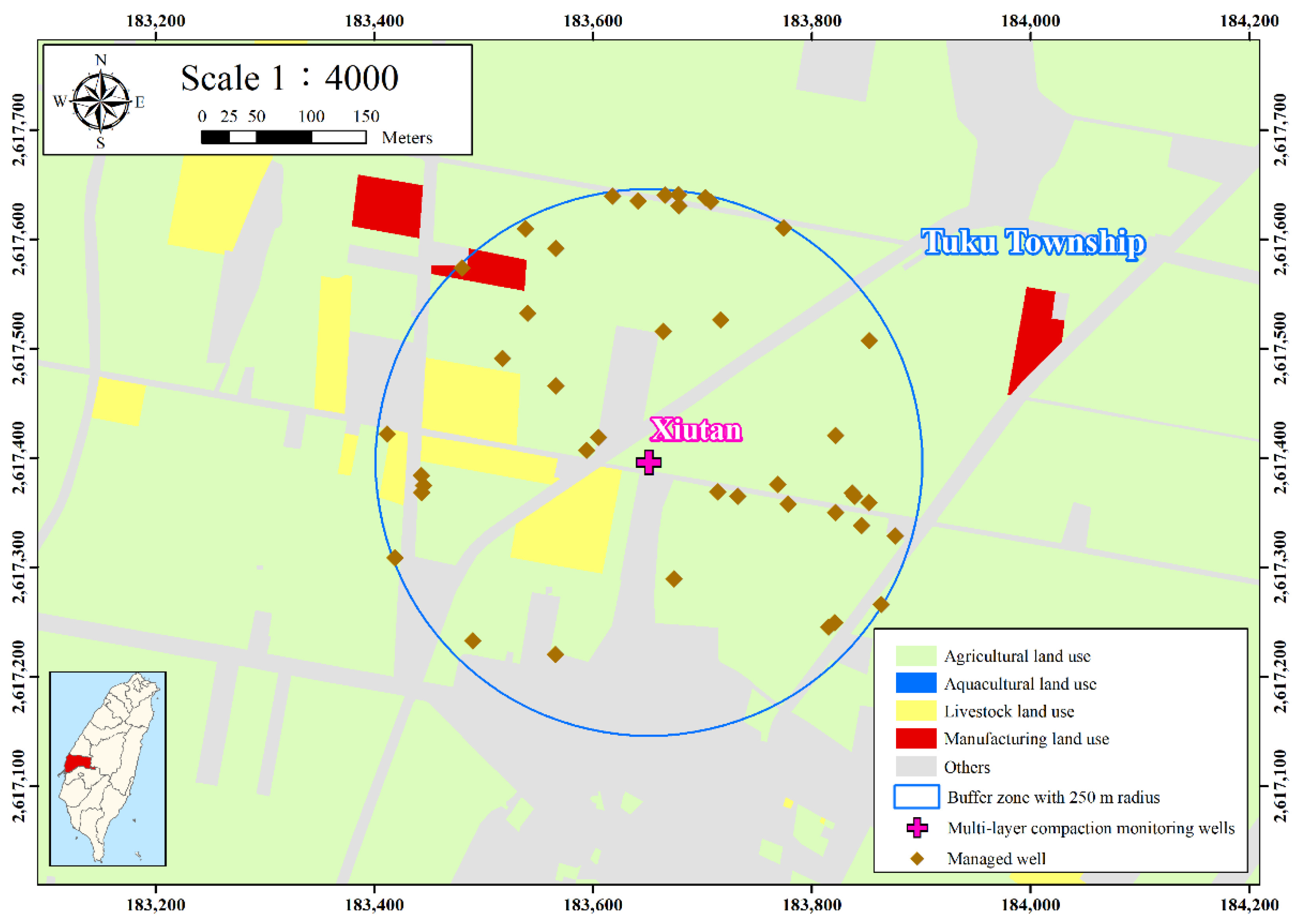
2.1. Study Area
2.2. Data Preparation and Geospatial Layer
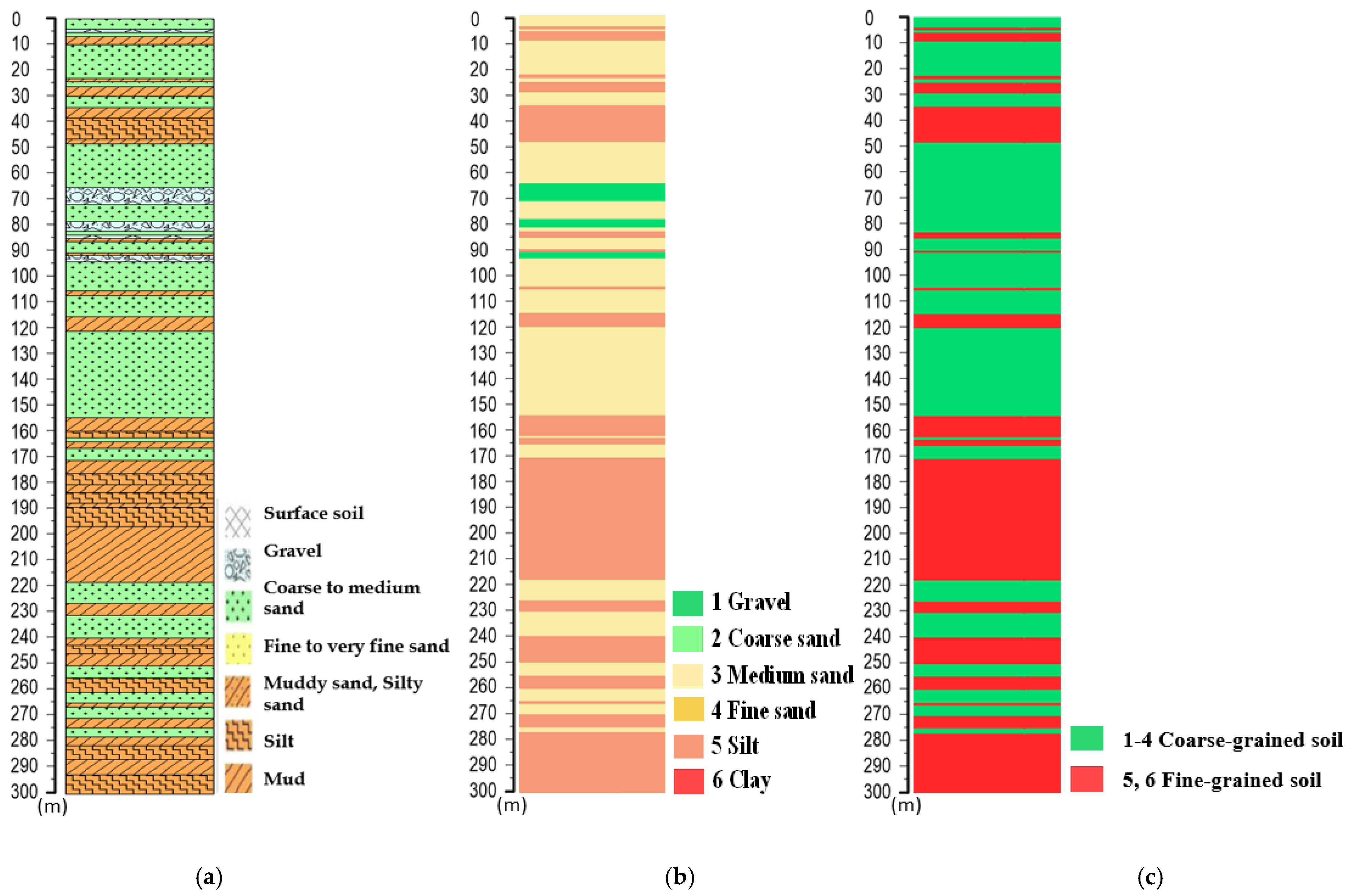
2.2.1. Percentage of Coarse-Grained Soil
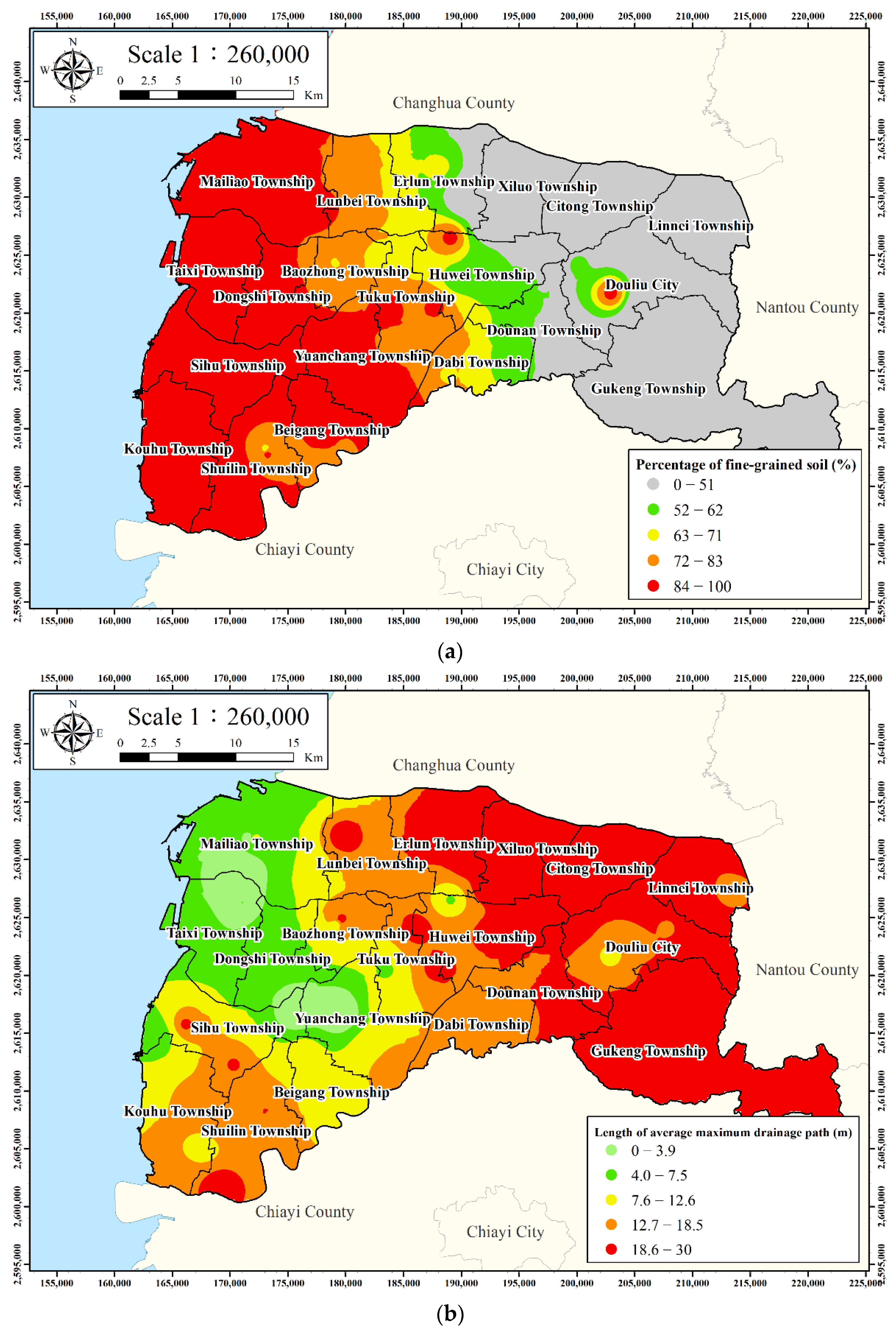
2.2.2. Percentage of Fine-Grained Soil
2.2.3. Length of Average Maximum Drainage Path
2.2.4. Percentage of Agricultural Land Use
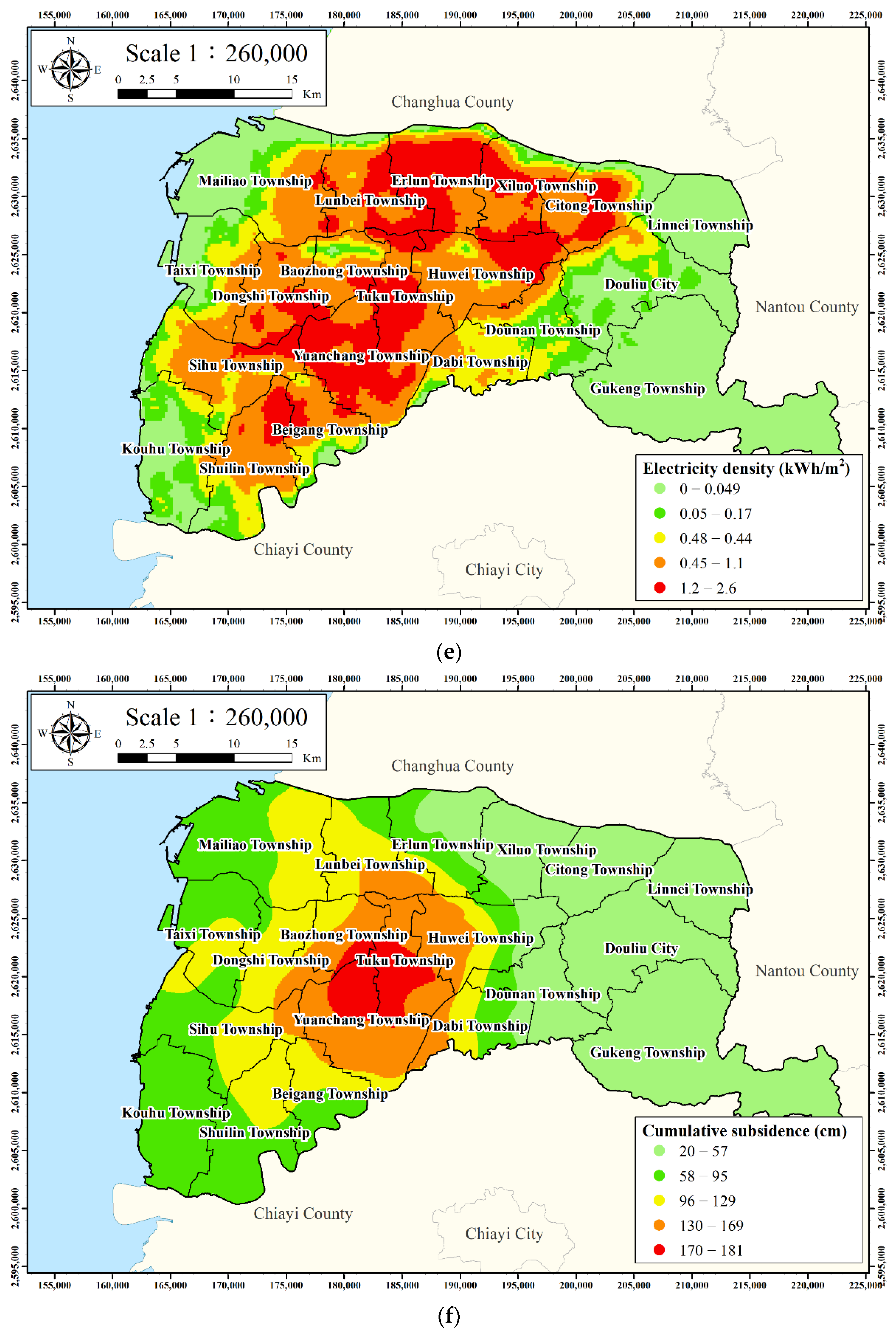
2.2.5. Electricity Consumption of Wells
2.2.6. Accumulated Subsidence Depth
2.3. Principal Component Analysis
3. Results
4. Discussion
5. Conclusions
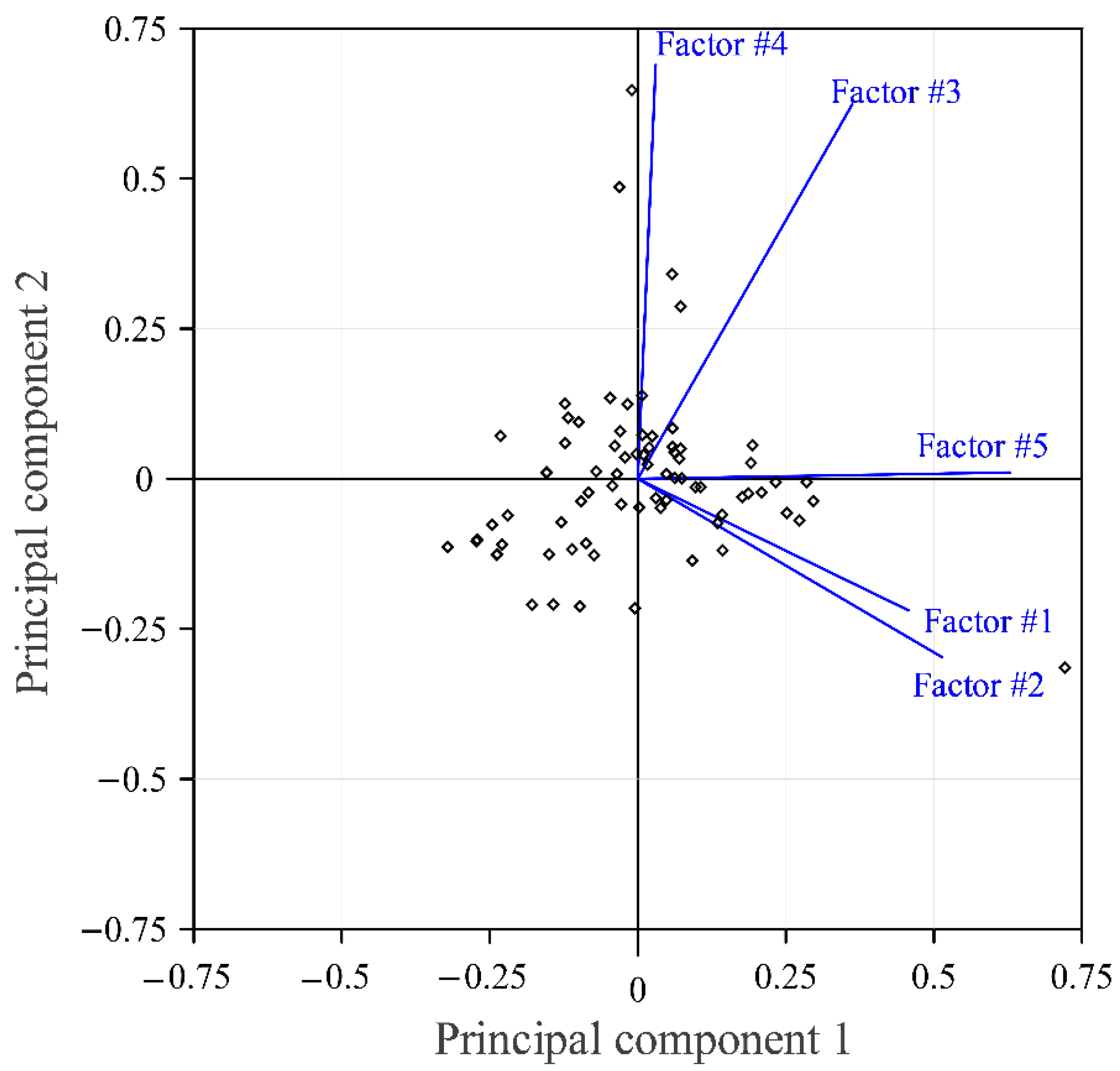
- To examine the influence of different environmental factors on land subsidence, the correlation coefficient was calculated. The results obtained show that factor #5 (accumulation depth of land subsidence from 2015 to 2020) is the cumulative subsidence factor, which is positively correlated with factor #1 (percentage of agricultural land use), factor #2 (electricity consumption of wells), and factor #3 (percentage of fine-grained soil). Furthermore, it was found that the correlation with factor #2 (electricity consumption of wells) is the highest, which is 0.46, indicating the high electricity consumption of the wells increases the accumulated land subsidence.
- The eigenvalues and contribution rates of factors demonstrate that the cumulative contribution of the first two principal components is 64.06%. It is found that the first two principal components can explain 64% of the data, which is representative to a certain extent. The contribution is 93.31%, which means that the first four principal components can explain almost all the data.
- From the PCA results, the largest subsidence rate was observed within the region that has both a high electricity consumption of wells and a large percentage of fine-grained soil. It appears that the electricity consumption of wells is highly correlated with the accumulated depth of land subsidence. The first principal component is the acquired factor causing land subsidence, such as the excessive withdrawal of groundwater. The second principal component is the congenital factor causing land subsidence, which corresponds to fine sand, silty, and clayey soils. The findings observed in this study may provide authorities with more information for planning future mitigation measures in significant land subsidence areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Faunt, C.C.; Sneed, M.; Traum, J.; Brandt, J.T. Water availability and land subsidence in the Central Valley, California, USA. Hydrogeol. J. 2016, 24, 675–684. [Google Scholar] [CrossRef] [Green Version]
- Sneed, M.; Galloway, D.L. Aquifer-System Compaction and Land Subsidence: Measurements, Analyses, and Simulations: The Holly Site, Edwards Air Force Base; (No. 4015); US Department of the Interior, US Geological Survey: Antelope Valley, CA, USA, 2000. [Google Scholar]
- Pang, S.C.; Yeh, T.K.; Hong, J.S.; Chen, C.H. Variability and climatology of precipitable water vapor from 12-year GPS observations in Taiwan. Adv. Space Res. 2021, 67, 2333–2346. [Google Scholar] [CrossRef]
- Ku, C.Y.; Liu, C.Y.; Su, Y.; Xiao, J.E.; Huang, C.C. Transient modeling of regional rainfall-triggered shallow landslides. Environ. Earth Sci. 2017, 76, 570. [Google Scholar] [CrossRef]
- Khoirunisa, N.; Ku, C.Y.; Liu, C.Y. A GIS-based artificial neural network model for flood susceptibility assessment. Int. J. Environ. Res. Public Health 2021, 18, 1072. [Google Scholar] [CrossRef]
- Liu, C.H.; Pan, Y.W.; Liao, J.J.; Huang, C.T.; Ouyang, S. Characterization of land subsidence in the Choshui River alluvial fan, Taiwan. Eng. Geol. 2004, 45, 1154–1166. [Google Scholar]
- Hung, W.C.; Hwang, C.; Chang, C.P.; Yen, J.Y.; Liu, C.H.; Yang, W.H. Monitoring severe aquifer-system compaction and land subsidence in Taiwan using multiple sensors: Yunlin, the southern Choushui River Alluvial Fan. Environ. Earth Sci. 2010, 59, 1535–1548. [Google Scholar] [CrossRef]
- Hung, W.C.; Hwang, C.; Liou, J.C.; Lin, Y.S.; Yang, H.L. Modeling aquifer-system compaction and predicting land subsidence in central Taiwan. Eng. Geol. 2012, 147, 78–90. [Google Scholar] [CrossRef]
- Castellazzi, P.; Arroyo-Domínguez, N.; Martel, R.; Calderhead, A.I.; Normand, J.C.; Gárfias, J.; Rivera, A. Land subsidence in major cities of Central Mexico: Interpreting InSAR-derived land subsidence mapping with hydrogeological data. Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 102–111. [Google Scholar] [CrossRef]
- Qiao, X.; Chu, T.; Tissot, P.; Louis, J.; Ali, I. Land subsidence estimation with tide gauge and satellite radar altimetry measurements along the Texas Gulf Coast, USA. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Li, A.; Tsai, F.T.C.; Yuill, B.T.; Wu, C. A three-dimensional stratigraphic model of the Mississippi River Delta, USA: Implications for river deltaic hydrogeology. Hydrogeol. J. 2020, 28, 2341–2358. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, H.; Gu, Z.; Wang, R.; Li, X.; Zhao, W. Characterization of land subsidence induced by groundwater withdrawals in the plain of Beijing city, China. Hydrogeol. J. 2014, 22, 397–409. [Google Scholar] [CrossRef]
- Smith, R.G.; Majumdar, S. Groundwater storage loss associated with land subsidence in Western United States mapped using machine learning. Water Resour. Res. 2020, 56, e2019WR026621. [Google Scholar] [CrossRef]
- Liu, C.; Shi, B.; Gu, K.; Zhang, T.; Tang, C.; Wang, Y.; Liu, S. Negative pore water pressure in aquitard enhances land subsidence: Field, laboratory, and numerical evidence. Water Resour. Res. 2022, 58, e2021WR030085. [Google Scholar] [CrossRef]
- Budhu, M.; Adiyaman, I. The influence of clay zones on land subsidence from groundwater pumping. Groundwater 2013, 51, 51–57. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.; Esaki, T.; Mori, J. GIS-based spatial and temporal prediction system development for regional land subsidence hazard mitigation. Environ. Geol. 2003, 44, 665–678. [Google Scholar] [CrossRef]
- Antonellini, M.; Giambastiani, B.M.S.; Greggio, N.; Bonzi, L.; Calabrese, L.; Luciani, P.; Perini, L.; Severi, P. Processes governing natural land subsidence in the shallow coastal aquifer of the Ravenna coast, Italy. Catena 2019, 172, 76–86. [Google Scholar] [CrossRef]
- Chu, H.J.; Lin, C.W.; Burbey, T.J.; Ali, M.Z. Spatiotemporal analysis of extracted groundwater volumes estimated from electricity consumption. Groundwater 2020, 58, 962–972. [Google Scholar] [CrossRef]
- Peng, Y.; Dong, D.; Chen, W.; Zhang, C. Stable regional reference frame for reclaimed land subsidence study in East China. Remote Sens. 2022, 14, 3984. [Google Scholar] [CrossRef]
- Xiao, B.; Zhao, J.; Li, D.; Zhao, Z.; Xi, W.; Zhou, D. The monitoring and analysis of land subsidence in Kunming (China) supported by time series InSAR. Sustainability 2022, 14, 12387. [Google Scholar] [CrossRef]
- Larson, K.J.; Başaǧaoǧlu, H.; Marino, M.A. Prediction of optimal safe ground water yield and land subsidence in the Los Banos-Kettleman City area, California, using a calibrated numerical simulation model. J. Hydrol. 2001, 242, 79–102. [Google Scholar] [CrossRef]
- Leake, S.A.; Galloway, D.L. Use of the SUB-WT Package for MODFLOW to simulate aquifer-system compaction in Antelope Valley, California, USA. In Land Subsidence, Associated Hazards and the Role of Natural Resources Development, Proceedings of the Eighth International Symposium on Land Subsidence, Queretaro, Mexico, 17–22 October 2010; International Association of Hydraulic Sciences: Queretaro, Mexico, 2010; pp. 61–67. [Google Scholar]
- Nadiri, A.A.; Habibi, I.; Gharekhani, M.; Sadeghfam, S.; Barzegar, R.; Karimzadeh, S. Introducing dynamic land subsidence index based on the ALPRIFT framework using artificial intelligence techniques. Earth Sci. Inform. 2022, 15, 1007–1021. [Google Scholar] [CrossRef]
- Nadiri, A.A.; Moazamnia, M.; Sadeghfam, S.; Barzegar, R. Mapping Risk to Land Subsidence: Developing a Two-Level Modeling Strategy by Combining Multi-Criteria Decision-Making and Artificial Intelligence Techniques. Water 2021, 13, 2622. [Google Scholar] [CrossRef]
- Sadeghfam, S.; Nourbakhsh Khiyabani, F.; Khatibi, R.; Daneshfaraz, R. A study of land subsidence problems by ALPRIFT for vulnerability indexing and risk indexing and treating subjectivity by strategy at two levels. J. Hydroinform. 2020, 22, 1640–1662. [Google Scholar] [CrossRef]
- Water Resources Agency, Ministry of Economic Affairs. Available online: https://data.gov.tw/dataset/41572 (accessed on 1 June 2022). (In Chinese)
- Central Geological Survey. Available online: https://geotech.moeacgs.gov.tw/imoeagis/Home/Supply (accessed on 1 June 2022). (In Chinese)
- National Land Surveying and Mapping Center (NLSC), Ministry of the Interior. Available online: https://maps.nlsc.gov.tw/homePage.action?in_type=mobile (accessed on 1 June 2022). (In Chinese)
- Indrawan, I.G.B.; Rahardjo, H.; Leong, E.C. Effects of coarse-grained materials on properties of residual soil. Eng. Geol. 2006, 82, 154–164. [Google Scholar] [CrossRef]
- Das, B.M. Principles of Geotechnical Engineering; Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Sridharan, A.; Gurtug, Y. Swelling behaviour of compacted fine-grained soils. Eng. Geol. 2004, 72, 9–18. [Google Scholar] [CrossRef]
- Daffertshofer, A.; Lamoth, C.J.; Meijer, O.G.; Beek, P.J. PCA in studying coordination and variability: A tutorial. Clin. Biomech. 2004, 19, 415–428. [Google Scholar] [CrossRef] [PubMed]
- Linhai Jing, Q.C.; Panahi, A. Principal component analysis with optimum order sample correlation coefficient for image enhancement. Int. J. Remote Sens. 2006, 27, 3387–3401. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Suthaharan, S. Machine learning models and algorithms for big data classification. Integr. Ser. Inf. Syst 2016, 36, 1–12. [Google Scholar]
- Kreyszig, E. Advanced Engineering Mathematics; John Wiley and Sons, Inc.: New York, NY, USA, 2008. [Google Scholar]
- Wang, Y.; Fan, Y.; Wang, Q.; Zhang, S.; Shi, Y.; Zheng, X. Response of Soil Fertility and Bacterial Community Composition to Vegetation Species in a Coal Mining Subsidence Area: A Survey After 20-Year Reclamation. Front. Environ. Sci. 2022, 10, 937688. [Google Scholar] [CrossRef]
- Shi, L.; Gong, H.; Chen, B.; Zhou, C. Land Subsidence Prediction Induced by Multiple Factors Using Machine Learning Method. Remote Sens. 2020, 12, 4044. [Google Scholar] [CrossRef]
- Hu, B.; Zhang, J.; Na, J.; Liu, D.; Xie, G. Temporal principal component analysis and synthetic aperture radar interference analysis of the spatial and temporal evolution of ground subsidence in the Los Angeles area. J. Appl. Remote Sens. 2022, 16, 044504. [Google Scholar] [CrossRef]

| No. | Factors | Source Data |
|---|---|---|
| 1 | Percentage of coarse-grained soil | Borehole data from the CGS and WRA of Taiwan |
| 2 | Percentage of fine-grained soil | |
| 3 | Length of average maximum drainage path | Borehole data from the CGS and WRA |
| 4 | Percentage of agricultural land use | Land use data from the NLSC |
| 5 | Electricity consumption of wells | Electricity consumption data from the WRA |
| 6 | Accumulated subsidence depth | Land subsidence data from the WRA |
| Soil Properties | Soil Type | Classification | Main Type |
|---|---|---|---|
| Gravel and coarse gravel | Gravel | 1 | Coarse-grained soil (Aquifer) |
| Grey coarse sand and coarse sand | Coarse sand | 2 | |
| Coarse to medium sand and medium sand | Medium sand | 3 | |
| Grey silty sand, grey fine sand, blue-gray silty sand, and fine to very fine sand | Fine sand | 4 | |
| Mud, muddy sand, sandy mud, silty sand, surface soil, silt, backfill sand, brown-gray sandy silt, and grey sandy silt | Silt | 5 | Fine-grained soil (Aquitard) |
| Grey silty clay, grey clay, and clay | Clay | 6 |
| No. | Factors | Data Source |
|---|---|---|
| 1 | Percentage of agricultural land use | Land use data from the NLSC |
| 2 | Electricity consumption of wells | Electricity consumption data from the WRA |
| 3 | Percentage of fine-grained soil | Borehole data from the CGS and WRA |
| 4 | Length of average maximum drainage path | Borehole data from the CGS and WRA |
| 5 | Accumulation depth of land subsidence from 2015 to 2020 | Land subsidence data from the WRA |
| Factor | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Factor | 1 | 1.00 | 0.31 | 0.06 | −0.04 | 0.33 |
| 2 | 0.31 | 1.00 | 0.02 | −0.08 | 0.46 | |
| 3 | 0.06 | 0.02 | 1.00 | 0.34 | 0.41 | |
| 4 | −0.04 | −0.08 | 0.34 | 1.00 | −0.06 | |
| 5 | 0.33 | 0.46 | 0.41 | −0.06 | 1.00 | |
| No. | Factor Definition | PC 1 | PC 2 | PC 3 | PC 4 |
|---|---|---|---|---|---|
| Factor #1 | Percentage of agricultural land use | 0.46 | −0.22 | 0.67 | −0.54 |
| Factor #2 | Electricity consumption of wells | 0.51 | −0.30 | 0.07 | 0.71 |
| Factor #3 | Percentage of fine-grained soil | 0.36 | 0.62 | −0.33 | −0.26 |
| Factor #4 | Length of average maximum drainage path | 0.03 | 0.69 | 0.54 | 0.37 |
| Factor #5 | Accumulation depth of land subsidence from 2015 to 2020 | 0.63 | 0.01 | −0.38 | −0.06 |
| Eigenvalue | Rate of Contribution (%) | Cumulative Contribution (%) | |
|---|---|---|---|
| Principal component 1 | 1.85 | 37.00 | 37.00 |
| Principal component 2 | 1.35 | 27.05 | 64.06 |
| Principal component 3 | 0.78 | 15.67 | 79.73 |
| Principal component 4 | 0.68 | 13.58 | 93.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, C.-Y.; Liu, C.-Y.; Lu, H.-C. Spatial Variability in Land Subsidence and Its Relation to Groundwater Withdrawals in the Choshui Delta. Appl. Sci. 2022, 12, 12464. https://doi.org/10.3390/app122312464
Ku C-Y, Liu C-Y, Lu H-C. Spatial Variability in Land Subsidence and Its Relation to Groundwater Withdrawals in the Choshui Delta. Applied Sciences. 2022; 12(23):12464. https://doi.org/10.3390/app122312464
Chicago/Turabian StyleKu, Cheng-Yu, Chih-Yu Liu, and Hsueh-Chuan Lu. 2022. "Spatial Variability in Land Subsidence and Its Relation to Groundwater Withdrawals in the Choshui Delta" Applied Sciences 12, no. 23: 12464. https://doi.org/10.3390/app122312464
APA StyleKu, C.-Y., Liu, C.-Y., & Lu, H.-C. (2022). Spatial Variability in Land Subsidence and Its Relation to Groundwater Withdrawals in the Choshui Delta. Applied Sciences, 12(23), 12464. https://doi.org/10.3390/app122312464








