New Statistical Results of Partial Sums of Ordered Gamma-Distributed RVs for Performance Evaluation of Wireless Communication Systems
Abstract
1. Introduction
1.1. Related Works
1.2. Contributions and Novelty
2. System and Channel Model
3. Methodology: Statistics of the Combined Received SNR
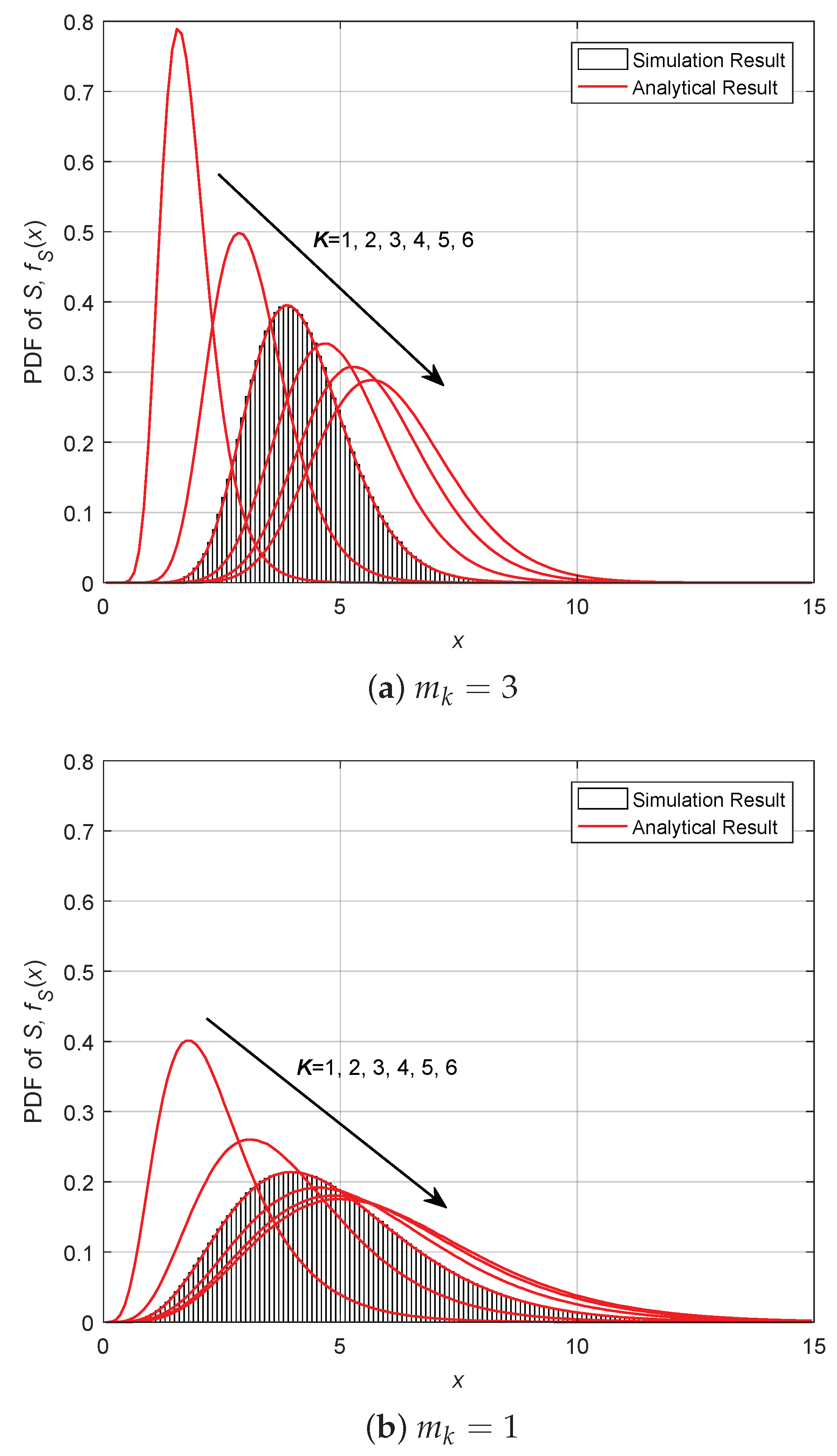
4. Numerical Results and Discussion
5. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivations of (14) and (15)
Appendix B. Derivations of (16)
References
- David, H.A. Order Statistics, 1st ed.; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Yang, H.C.; Alouini, M.S. Order Statistics in Wireless Communications: Diversity, Adaptation, and Scheduling in MIMO and OFDM Systems, 1st ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Balakrishnan, N.; Rao, C.R. Handbook of Statistics 17: Order Statistics: Applications, 2nd ed.; North-Holland/Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Goldsmith, A. Wireless Communications; Cambridge Univ. Press: New York, NY, USA, 2005. [Google Scholar]
- Fu, X.; Wang, Y.; Yang, Y.; Postolache, O. Analysis on cascading reliability of edge-assisted Internet of Things. Reliab. Eng. Syst. Saf. 2022, 223, 108463. [Google Scholar] [CrossRef]
- Fu, X.; Pace, P.; Aloi, G.; Li, W.; Fortino, G. Cascade failures analysis of Internet of Things under global/local routing mode. IEEE Sens. J. 2022, 22, 1705–1719. [Google Scholar] [CrossRef]
- Lo, T.K.Y. Maximum ratio transmission. IEEE Trans. Commun. 1999, 47, 1458–1461. [Google Scholar] [CrossRef]
- Cavers, J.K. Single-user and multiuser adaptive maximal ratio transmission for Rayleigh channels. IEEE Trans. Veh. Technol. 2000, 49, 2043–2050. [Google Scholar] [CrossRef]
- Kim, K.J.; Khan, T.A.; Orlik, P.V. Performance analysis of cooperative systems with unreliable backhauls and selection combining. IEEE Trans. Veh. Technol. 2017, 66, 2448–2461. [Google Scholar] [CrossRef]
- Liang, Y.C.; Leon, W.S.; Zeng, Y.; Xu, C. Design of cyclic delay diversity for single carrier cyclic prefix (SCCP) transmissions with block-iterative GDFE (BI-GDFE) receiver. IEEE Trans. Wirel. Commun. 2008, 7, 677–684. [Google Scholar] [CrossRef]
- Kwon, U.K.; Im, G.H. Cyclic delay diversity with frequency domain turbo equalization for uplink fast fading channels. IEEE Commun. Lett. 2009, 13, 184–186. [Google Scholar] [CrossRef]
- Mehana, A.H.; Nosratinia, A. Single-carrier frequency-domain equalizer with multi-antenna transmit diversity. IEEE Trans. Wirel. Commun. 2013, 12, 388–397. [Google Scholar] [CrossRef]
- Li, Q.; Yan, Q.; Teh, K.C.; Li, K.H.; Hu, Y. A multi-relay-selection scheme with cyclic delay diversity. IEEE Commun. Lett. 2013, 17, 349–352. [Google Scholar] [CrossRef]
- Wen, M.; Lin, S.; Kim, K.J.; Ji, F. Cyclic delay diversity with index modulation for green internet of things. IEEE Trans. Green Commun. Netw. 2021, 5, 600–610. [Google Scholar] [CrossRef]
- IEEE Standard 802.11ac-2013; Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications—Amendment 4: Enhancements for Very High Throughput for Operation in Bands Below 6 GHz. IEEE: Piscataway, NJ, USA, 2009.
- IEEE Standard 802.11n-2009; Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications—Amendment 5: Enhancements for Higher Throughput. IEEE: Piscataway, NJ, USA, 2009.
- 3GPP TS 36.211 V8.9.0 (2009-12); Technical Specification Group Radio Access Network, Evolved Universal Terrestrial Radio Access (E-UTRA): Physical Channels and Modula tion (Release 8). IEEE: Piscataway, NJ, USA, 2009.
- Kato, S.; Harada, H.; Funada, R.; Baykas, T.; Sum, C.S.; Wang, J.; Rahman, M.A. Single carrier transmission for multi-gigabit 60-GHz WPAN systems. IEEE J. Select. Areas Commun. 2009, 27, 1466–1478. [Google Scholar] [CrossRef]
- Iradukunda, N.; Nguyen, H.T.; Hwang, W.J. On cyclic delay diversity-based single-carrier scheme in spectrum sharing systems. IEEE Commun. Lett. 2019, 23, 1069–1072. [Google Scholar] [CrossRef]
- Eghbali, H.; Muhaidat, S.; Al-Dhahir, N. A novel receiver design for single-carrier frequency domain equalization in broadband wireless networks with amplify-and-forward relaying. IEEE Trans. Wirel. Commun. 2011, 10, 721–727. [Google Scholar] [CrossRef]
- Mheidat, H.; Uysal, M.; Al-Dhahir, N. Equalization techniques for distributed space-time block codes with amplify-and-forward relaying. IEEE Trans. Signal Process. 2007, 55, 1839–1852. [Google Scholar] [CrossRef]
- Kim, K.J.; Duong, T.Q.; Poor, H.V. Outage probability of single-carrier cooperative spectrum sharing systems with decode-and-forward relaying and selection combining. IEEE Trans. Wirel. Commun. 2013, 12, 806–817. [Google Scholar] [CrossRef]
- Kim, K.J.; Di Renzo, M.; Liu, H.; Orlik, P.V.; Poor, H.V. Performance analysis of distributed single carrier systems with distributed cyclic delay diversity. IEEE Trans. Commun. 2017, 65, 5514–5528. [Google Scholar] [CrossRef]
- Kim, K.J.; Liu, H.; Ding, Z.; Orlik, P.V.; Poor, H.V. Diversity gain analysis of distributed CDD systems in non-identical fading channels. IEEE Trans. Commun. 2020, 68, 7218–7231. [Google Scholar] [CrossRef]
- Tellambura, C. Bounds on the distribution of a sum of correlated lognormal random variables and their application. IEEE Trans. Commun. 2008, 56, 1241–1248. [Google Scholar] [CrossRef]
- Rached, N.B.; Botev, Z.; Kammoun, A.; Alouini, M.S.; Tempone, R. Importance Sampling Estimator of Outage Probability under Generalized Selection Combining Model. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, Alberta, 15–20 April 2018; pp. 3909–3913. [Google Scholar] [CrossRef][Green Version]
- Ben Rached, N.; Botev, Z.; Kammoun, A.; Alouini, M.S.; Tempone, R. On the sum of order statistics and applications to wireless communication systems performances. IEEE Trans. Wirel. Commun. 2018, 17, 7801–7813. [Google Scholar] [CrossRef]
- Li, G.; Xu, X.; Gu, Y. Lower bound for RIP constants and concentration of sum of top order statistics. IEEE Trans. Signal Process. 2020, 68, 3169–3178. [Google Scholar] [CrossRef]
- Alouini, M.S.; Simon, M. An MGF-based performance analysis of generalized selection combining over Rayleigh fading channels. IEEE Trans. Commun. 2000, 48, 401–415. [Google Scholar] [CrossRef]
- Yang, H.C. New results on ordered statistics and analysis of minimum-selection generalized selection combining (GSC). IEEE Trans. Wirel. Commun. 2006, 5, 1876–1885. [Google Scholar] [CrossRef]
- Ko, Y.C.; Yang, H.C.; Eom, S.S.; Alouini, M.S. Adaptive modulation with diversity combining based on output-threshold MRC. IEEE Trans. Wirel. Commun. 2007, 6, 3728–3737. [Google Scholar] [CrossRef]
- Nuttall, A.H. An Integral Solution for the Joint PDF of Order Statistics and Residual Sum; Technical Report; NUWC-NPT: Middletown, RI, USA, 2001. [Google Scholar]
- Nuttall, A.H. Joint Probability Density Function of Selected ORDER Statistics and the Sum of the Remaining Random Variables; Technical Report; NUWC-NPT: Middletown, RI, USA, 2002. [Google Scholar]
- Nuttall, A.H.; Baggenstoss, P.M. Joint Distributions for Two Useful Classes of Statistics, with Applications to Classification and Hypothesis Testing; Technical Report; NUWC-NPT: Middletown, RI, USA, 2002. [Google Scholar]
- Nam, S.S.; Alouini, M.S.; Yang, H.C. An MGF-based unified framework to determine the joint statistics of partial sums of ordered random variables. IEEE Trans. Inform. Theory 2010, 56, 5655–5672. [Google Scholar] [CrossRef][Green Version]
- Nam, S.S.; Yang, H.C.; Alouini, M.S.; Kim, D.I. An MGF-based unified framework to determine the joint statistics of partial sums of ordered i.n.d. random variables. IEEE Trans. Signal Process. 2014, 62, 4270–4283. [Google Scholar] [CrossRef][Green Version]
- Nakagami, M. The m-Distribution—A General Formula of Intensity Distribution of Rapid Fading. In Statistical Methods in Radio Wave Propagation; Hoffman, W., Ed.; Pergamon: Oxford, UK, 1960; pp. 3–36. [Google Scholar] [CrossRef]
- Suzuki, H. A statistical model for urban radio propagation. IEEE Trans. Commun. 1977, 25, 673–680. [Google Scholar] [CrossRef]
- Sheikh, A.; Abdi, M.; Handforth, M. Indoor mobile radio channel at 946 MHz: Measurements and modeling. In Proceedings of the IEEE 43rd Vehicular Technology Conference, Secaucus, NJ, USA, 18–20 May 1993; pp. 73–76. [Google Scholar] [CrossRef]
- Ben Issaid, C.; Ben Rached, N.; Kammoun, A.; Alouini, M.S.; Tempone, R. On the efficient simulation of the distribution of the sum of Gamma–Gamma variates with application to the outage probability evaluation over fading channels. IEEE Trans. Commun. 2017, 65, 1839–1848. [Google Scholar] [CrossRef]
- Nam, S.S.; Ko, Y.C.; Alouini, M.S. New closed-form results on ordered statistics of partial sums of gamma random variables and its application to performance evaluation in the presence of Nakagami fading. IEEE Access 2017, 5, 12820–12832. [Google Scholar] [CrossRef]
- Nguyen, B.C.; The Dung, L.; Hoang, T.M.; Tran, X.N.; Kim, T. Impacts of imperfect CSI and transceiver hardware noise on the performance of full-duplex DF relay system with multi-antenna terminals over Nakagami-m fading channels. IEEE Trans. Commun. 2021, 69, 7094–7107. [Google Scholar] [CrossRef]
- Truong, V.T.; Vo, V.N.; Ha, D.B.; So-In, C. On the system performance of mobile edge computing in an uplink NOMA WSN with a multiantenna access point over Nakagami-m fading. IEEE/CAA J. Autom. Sin. 2022, 9, 668–685. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Abolhassani, B.; Razavizadeh, S.M.; Nguyen, H.H. User clustering and resource allocation in hybrid NOMA-OMA systems under Nakagami-m fading. IEEE Access 2022, 10, 38709–38728. [Google Scholar] [CrossRef]
- Kim, K.J.; Orlik, P.V.; Khan, T.A. Performance analysis of finite-sized co-operative systems with unreliable backhauls. IEEE Trans. Wirel. Commun. 2016, 15, 5001–5015. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, Corrected and Enlarged ed.; Academic: San Diego, CA, USA, 1994. [Google Scholar]
- Exponential Integral Function. Available online: https://functions.wolfram.com/06.34.07.0001.01 (accessed on 1 July 2022).
- Stüber, G.L. Principles of Mobile Communication, 2nd ed.; Kluwer Academic Publishers: Norwell, MA, USA, 2001. [Google Scholar]
- Simon, M.K.; Alouini, M.S. Digital Communication over Fading Channels, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
- Nam, S.S.; Yang, H.C.; Alouini, M.S.; Kim, D.I. Impact of interference on the performance of selection based parallel multiuser scheduling. IEEE Trans. Wirel. Commun. 2012, 11, 531–536. [Google Scholar] [CrossRef]
- Kim, S.W.; Ha, D.; Reed, J. Minimum selection GSC and adaptive low-power rake combining scheme. In Proceedings of the 2003 IEEE International Symposium on Circuits and Systems (ISCAS), Bangkok, Thailand, 25–28 May 2003; Volume 4, p. IV. [Google Scholar] [CrossRef]
- Choi, S.; Alouini, M.S.; Qaraqe, K.A.; Yang, H.C. Finger replacement method for Rake receivers in the soft handover region. IEEE Trans. Wirel. Commun. 2008, 7, 1152–1156. [Google Scholar] [CrossRef]
- Choi, S.; Alouini, M.S.; Qaraqe, K.A.; Yang, H.C. Finger replacement schemes for RAKE receivers in the soft handover region with multiple base stations. IEEE Trans. Veh. Technol. 2008, 57, 2114–2122. [Google Scholar] [CrossRef]
- Nam, S.S.; Hasna, M.O.; Alouini, M.S. Joint statistics of partial sums of ordered exponential variates and performance of GSC RAKE receivers over Rayleigh fading channel. IEEE Trans. Commun. 2011, 59, 2241–2253. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Choi, S.; Ko, Y.C. Performance of selection MIMO systems with generalized selection criterion over Nakagami-m fading channels. IEICE Trans. Commun. 2006, E89-B, 3467–3470. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, S.; Hwang, D.; Nam, S.S. New Statistical Results of Partial Sums of Ordered Gamma-Distributed RVs for Performance Evaluation of Wireless Communication Systems. Appl. Sci. 2022, 12, 12485. https://doi.org/10.3390/app122312485
Choi S, Hwang D, Nam SS. New Statistical Results of Partial Sums of Ordered Gamma-Distributed RVs for Performance Evaluation of Wireless Communication Systems. Applied Sciences. 2022; 12(23):12485. https://doi.org/10.3390/app122312485
Chicago/Turabian StyleChoi, Seyeong, Duckdong Hwang, and Sung Sik Nam. 2022. "New Statistical Results of Partial Sums of Ordered Gamma-Distributed RVs for Performance Evaluation of Wireless Communication Systems" Applied Sciences 12, no. 23: 12485. https://doi.org/10.3390/app122312485
APA StyleChoi, S., Hwang, D., & Nam, S. S. (2022). New Statistical Results of Partial Sums of Ordered Gamma-Distributed RVs for Performance Evaluation of Wireless Communication Systems. Applied Sciences, 12(23), 12485. https://doi.org/10.3390/app122312485






