Interplay between Binary and Three-Body Interactions and Enhancement of Stability in Trapless Dipolar Bose–Einstein Condensates
Abstract
:1. Introduction
2. The Model
3. The Variational Method
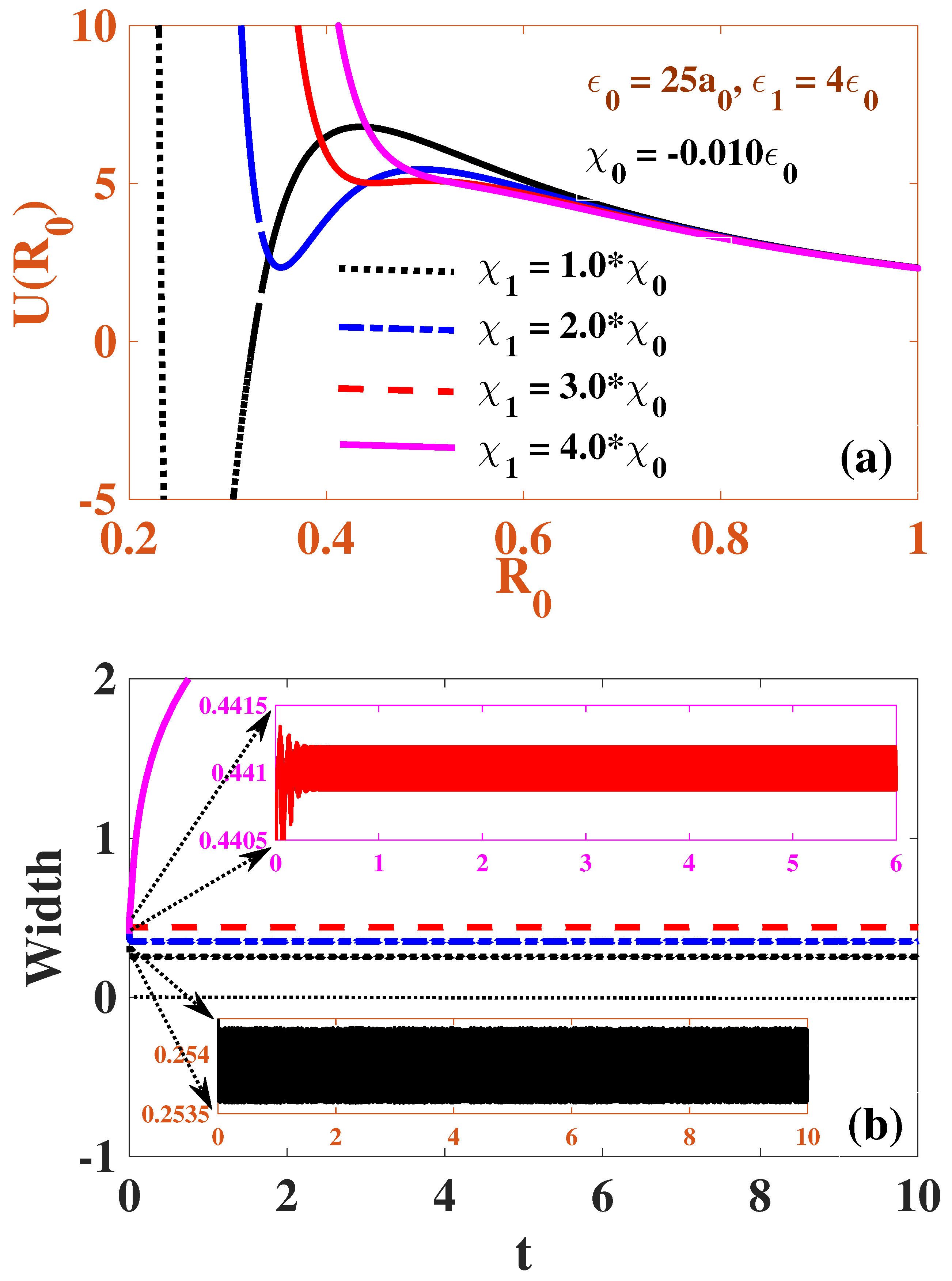
4. Three-Dimensional Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koch, T.; Tobias, L.; Thierry, M.; Jonas, F.; Bernd, G.; Axel, P.A. Stabilization of a purely dipolar quantum gas against collapse. Nat. Phys. 2008, 4, 218. [Google Scholar] [CrossRef] [Green Version]
- Lahaye, T.; Menotti, C.; Santos, L.; Lewenstein, M.; Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 2009, 72, 126401. [Google Scholar] [CrossRef]
- Lu, M.; Burdick, N.Q.; Youn, S.H.; Lev, B.L. Strongly Dipolar Bose–Einstein Condensate of Dysprosium. Lev. Phys. Rev. Lett. 2011, 107, 190401. [Google Scholar] [CrossRef] [PubMed]
- Youn, S.H.; Lu, M.; Ray, U.; Lev, B.L. Dysprosium magneto-optical traps. Phys. Rev. A 2010, 82, 043425. [Google Scholar] [CrossRef] [Green Version]
- Aikawa, K.; Frisch, A.; Mark, M.; Baier, S.; Rietzler, A.; Grimm, R.; Ferlaino, F. Bose–Einstein Condensation of Erbium. Phys. Rev. Lett. 2012, 108, 210401. [Google Scholar] [CrossRef] [Green Version]
- Baranov, M. Theoretical progress in many-body physics with ultracold dipolar gases. Phys. Rep. 2008, 464, 71. [Google Scholar] [CrossRef]
- Santos, L.; Shlyapnikov, G.V.; Lewenstein, M. Roton-Maxon Spectrum and Stability of Trapped Dipolar Bose–Einstein Condensates. Phys. Rev. Lett. 2003, 90, 250403. [Google Scholar] [CrossRef] [Green Version]
- Goral, K.; Santos, L. Ground state and elementary excitations of single and binary Bose–Einstein condensates of trapped dipolar gases. Phys. Rev. A 2002, 66, 023613. [Google Scholar] [CrossRef] [Green Version]
- Wilson, R.M.; Ronen, S.; Bohn, J.L. Critical Superfluid Velocity in a Trapped Dipolar Gas. Phys. Rev. Lett. 2010, 104, 094501. [Google Scholar] [CrossRef] [Green Version]
- Ticknor, C.; Wilson, R.M.; Bohn, J.L. Anisotropic Superfluidity in a Dipolar Bose Gas. Phys. Rev. Lett. 2011, 106, 065301. [Google Scholar] [CrossRef] [Green Version]
- Tieleman, O.; Lazarides, A.; Smith, C.M. Supersolid phases of dipolar bosons in optical lattices with a staggered flux. Phys. Rev. A 2011, 83, 013627. [Google Scholar] [CrossRef] [Green Version]
- Zhou, K.; Liang, Z.; Zhang, Z. Quantum phases of a dipolar Bose–Einstein condensate in an optical lattice with three-body interaction. Phys. Rev. A 2010, 82, 013634. [Google Scholar] [CrossRef] [Green Version]
- Mulkerin, B.C.; van Bijnen, R.M.W.; O’Dell, D.H.J.; Martin, A.M.; Parker, N.G. Anisotropic and Long-Range Vortex Interactions in Two-Dimensional Dipolar Bose Gases. Phys. Rev. Lett. 2013, 111, 170402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martin, A.M.; Marchant, N.G.; O’Dell, D.H.J.; Parker, N.G. Vortices and vortex lattices in quantum ferrofluids. J. Phys. Cond. Matt. 2017, 29, 103004. [Google Scholar] [CrossRef] [Green Version]
- Sabari, S. Vortex formation and hidden vortices in dipolar Bose–Einstein condensates. Phys. Lett. A 2017, 381, 3062. [Google Scholar]
- Sabari, S.; Kishor Kumar, R. Effect of an oscillating Gaussian obstacle in a dipolar Bose–Einstein condensate. Eur. Phys. J. D 2018, 72, 48. [Google Scholar] [CrossRef]
- Tikhonenkov, I.; Malomed, B.A.; Vardi, A. Anisotropic Solitons in Dipolar Bose–Einstein Condensates. Phys. Rev. Lett. 2008, 100, 090406. [Google Scholar] [CrossRef] [Green Version]
- Köberle, P.; Zajec, D.; Wunner, G.; Malomed, B.A. Creating two-dimensional bright solitons in dipolar Bose–Einstein condensates. Phys. Rev. A 2012, 85, 023630. [Google Scholar] [CrossRef] [Green Version]
- Ferrier-Barbut, I.; Kadau, H.; Schmitt, M.; Wenzel, M.; Pfau, T. Observation of Quantum Droplets in a Strongly Dipolar Bose Gas. Phys. Rev. Lett. 2016, 116, 215301. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, M.; Wenzel, M.; Büttcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chomaz, L.; Baier, S.; Petter, D.; Mark, M.J.; Wachtler, F.; Santos, L.; Ferlaino, F. Quantum-Fluctuation-Driven Crossover from a Dilute Bose–Einstein Condensate to a Macrodroplet in a Dipolar Quantum Fluid. Phys. Rev. X 2016, 6, 041039. [Google Scholar] [CrossRef]
- Cuevas, J.; Malomed, B.A.; Kevrekidis, P.G.; Frantzeskakis, D.J. Solitons in quasi-one-dimensional Bose–Einstein condensates with competing dipolar and local interactions. Phys. Rev. A 2009, 79, 053608. [Google Scholar] [CrossRef] [Green Version]
- Muruganandam, P.; Adhikari, S.K. Numerical and variational solutions of the dipolar Gross–Pitaevskii equation in reduced dimensions. Las. Phys. 2012, 22, 813. [Google Scholar] [CrossRef]
- Lahaye, T.; Metz, J.; Frohlich, B.; Koch, T.; Meister, M.; Griesmaier, A.; Pfau, T.; Saito, H.; Kawaguchi, Y.; Ueda, M. d-Wave Collapse and Explosion of a Dipolar Bose–Einstein Condensate. Phys. Rev. Lett. 2008, 101, 080401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kishor Kumar, R.; Young, L.E.; Vudragović, D.; Balaž, A.; Muruganandam, P.; Adhikari, S.K. Fortran and C programs for the time-dependent dipolar Gross–Pitaevskii equation in an anisotropic trap. Comput. Phys. Commun. 2015, 195, 117. [Google Scholar] [CrossRef] [Green Version]
- Strecker, K.E.; Partridge, G.B.; Truscott, A.G.; Hulet, R.G. Formation and propagation of matter-wave soliton trains. Nature 2002, 417, 150. [Google Scholar] [CrossRef]
- Khaykovich, L.; Schreck, F.; Ferrari, G.; Bourdel, T.; Cubizolles, J.; Carr, L.; Castin, Y.; Salomon, C. Formation of a Matter-Wave Bright Soliton. Science 2002, 296, 1290. [Google Scholar] [CrossRef] [Green Version]
- Krolikowski, W.; Bang, O.; Rasmussen, J.J.; Wyller, J. Modulational instability in nonlocal nonlinear Kerr media. Phys. Rev. E 2001, 64, 016612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bang, O.; Krolikowski, W.; Wyller, J.; Rasmussen, J.J. Collapse arrest and soliton stabilization in nonlocal nonlinear media. Phys. Rev. E 2002, 66, 046619. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landau, L.; Lifshitz, E.M. Mechanics; Pergamon: Oxford, UK, 1960. [Google Scholar]
- Towers, I.; Malomed, B.A. Stable (2+1)-dimensional solitons in a layered medium with sign-alternating Kerr nonlinearity. J. Opt. Soc. Am. B 2002, 19, 537. [Google Scholar] [CrossRef]
- Abdullaev, F.K.; Caputo, J.G.; Kraenkel, R.A.; Malomed, B.A. Controlling collapse in Bose–Einstein condensates by temporal modulation of the scattering length. Phys. Rev. A 2003, 67, 013605. [Google Scholar] [CrossRef] [Green Version]
- Saito, H.; Ueda, M. Dynamically Stabilized Bright Solitons in a Two-Dimensional Bose–Einstein Condensate. Phys. Rev. Lett. 2003, 90, 040403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adhikari, S.K. Stabilization of bright solitons and vortex solitons in a trapless three-dimensional Bose–Einstein condensate by temporal modulation of the scattering length. Phys. Rev. A 2004, 69, 063613. [Google Scholar] [CrossRef] [Green Version]
- Malomed, B.A. Soliton Management in Periodic Systems; Springer: New York, NY, USA, 2006. [Google Scholar]
- Sabari, S.; Raja, R.V.J.; Porsezian, K.; Muruganandam, P. Stability of trapless Bose–Einstein condensates with two-and three-body interactions. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 125302. [Google Scholar] [CrossRef] [Green Version]
- Sabari, S.; Porsezian, K.; Muruganandam, P. Dynamical stabilization of two-dimensional trapless Bose–Einstein condensates by three-body interaction and quantum fluctuations. Chaos Solitons Fractals 2017, 103, 232. [Google Scholar] [CrossRef] [Green Version]
- Tamil Thiruvalluvar, R.; Sabari, S.; Porsezian, K. Stabilization of repulsive trapless Bose–Einstein condensates. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 165202. [Google Scholar]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Kartashov, Y.V.; Malomed, B.A.; Torner, L. Solitons in nonlinear lattices. Rev. Mod. Phys. 2011, 83, 247. [Google Scholar] [CrossRef]
- Zeng, J.; Malomed, B.A. Stabilization of one-dimensional solitons against the critical collapse by quintic nonlinear lattices. Phys. Rev. A 2012, 85, 023824. [Google Scholar] [CrossRef] [Green Version]
- Sakaguchi, H.; Malomed, B.A. Matter-wave solitons in nonlinear optical lattices. Phys. Rev. E 2005, 72, 046610. [Google Scholar] [CrossRef]
- Abdullaev, F.K.; Garnier, J. Propagation of matter-wave solitons in periodic and random nonlinear potentials. Phys. Rev. A 2005, 72, 061605. [Google Scholar] [CrossRef] [Green Version]
- Abdullaev, F.K.; Kamchatnov, A.M.; Konotop, V.V.; Brazhnyi, V.A. Adiabatic Dynamics of Periodic Waves in Bose–Einstein Condensates with Time Dependent Atomic Scattering Length. Phys. Rev. Lett. 2003, 90, 230402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perez-Garcia, V.; Konotop, V.; Brazhnyi, V.A. Feshbach Resonance Induced Shock Waves in Bose–Einstein Condensates. Phys. Rev Lett. 2004, 92, 220403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Konotop, V.V.; Pacciani, P. Collapse of Solutions of the Nonlinear Schrödinger Equation with a Time-Dependent Nonlinearity: Application to Bose–Einstein Condensates. Phys. Rev Lett. 2005, 94, 240405. [Google Scholar] [CrossRef] [Green Version]
- Belmonte-Beitia, J.; Pérez-García, V.M.; Vekslerchik, V.; Torres, P.J. Localized Nonlinear Waves in Systems with Time- and Space-Modulated Nonlinearities. Phys. Rev. Lett. 2008, 100, 164102. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.-S.; Hu, X.-H.; Liu, W.M. Localized nonlinear matter waves in two-component Bose–Einstein condensates with time- and space-modulated nonlinearities. Phys. Rev. A 2010, 82, 023612. [Google Scholar] [CrossRef] [Green Version]
- Sabari, S.; Jisha, C.P.; Porsezian, K.; Brazhnyi, V.A. Dynamical stability of dipolar Bose–Einstein condensates with temporal modulation of the s-wave scattering length. Phys. Rev. E 2015, 92, 032905. [Google Scholar] [CrossRef]
- Tamilthiruvalluvar, R.; Sabari, S. Stabilization of trapless Bose– Einstein condensates without any management. Phys. Lett. A 2019, 383, 2033. [Google Scholar]
- Sabari, S.; Biswajyoti, D. Stabilization of trapless dipolar Bose–Einstein condensates by temporal modulation of the contact interaction. Phys. Rev. E 2018, 98, 042203. [Google Scholar] [CrossRef] [Green Version]
- Keltoum, R.; Boudjemaa, A. Dipolar Bose gas with three-body interactions in weak disorder. Eur. Phys. J. D 2019, 73, 115. [Google Scholar] [CrossRef] [Green Version]
- Boudjemaa, A. Dipolar Bose gas with three-body interactions at finite temperature. J. Phys. B: At. Mol. Opt. Phys. 2018, 51, 025203. [Google Scholar] [CrossRef] [Green Version]
- Blakie, P.B. Properties of a dipolar condensate with three-body interactions. Phys. Rev. A 2016, 93, 033644. [Google Scholar] [CrossRef] [Green Version]
- Xi, K.-T.; Saito, H. Droplet formation in a Bose–Einstein condensate with strong dipole-dipole interaction. Phys. Rev. A 2016, 93, 011604. [Google Scholar] [CrossRef] [Green Version]
- Bisset, R.N.; Blakie, P.B. Crystallization of a dilute atomic dipolar condensate. Phys. Rev. A 2015, 92, 061603. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.-K.; Li, Y.; Petrov, D.S.; Shlyapnikov, G.V. Stable Dilute Supersolid of Two-Dimensional Dipolar Bosons. Phys. Rev. Lett. 2015, 115, 075303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bulgac, A. Dilute Quantum Droplets. Phys. Rev. Lett. 2002, 89, 050402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Braaten, E.; Hammer, H.W.; Mehen, T. Dilute Bose–Einstein Condensate with Large Scattering Length. Phys. Rev. Lett. 2002, 88, 040401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gammal, A.; Frederico, T.; Tomio, L.; Chomaz, P. Atomic Bose–Einstein condensation with three-body interactions and collective excitations. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 4053. [Google Scholar] [CrossRef] [Green Version]
- Fibich, G. The Nonlinear Schrödinger Equation: Singular Solutions and Optical Collapse; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Mihalache, D.; Mazilu, D.; Crasovan, L.-C.; Towers, I.; Malomed, B.A.; Buryak, A.V.; Torner, L.; Lederer, F. Stable three-dimensional spinning optical solitons supported by competing quadratic and cubic nonlinearities. Phys. Rev. E 2002, 66, 016613. [Google Scholar] [CrossRef] [Green Version]
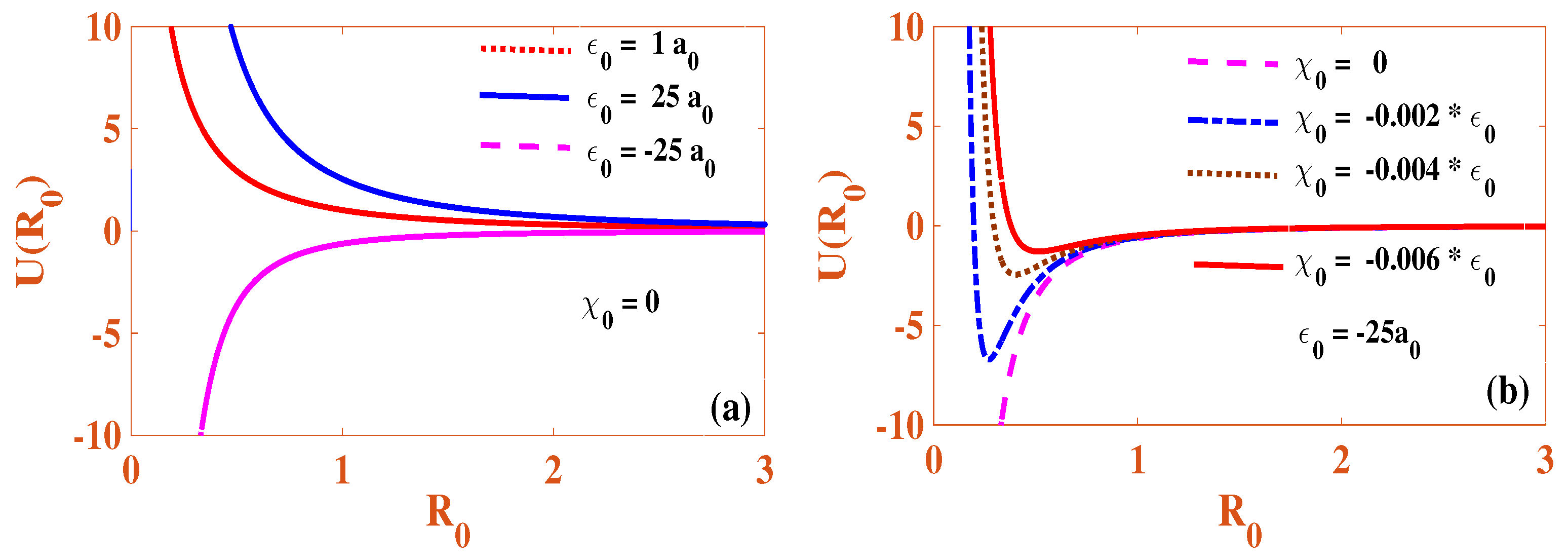
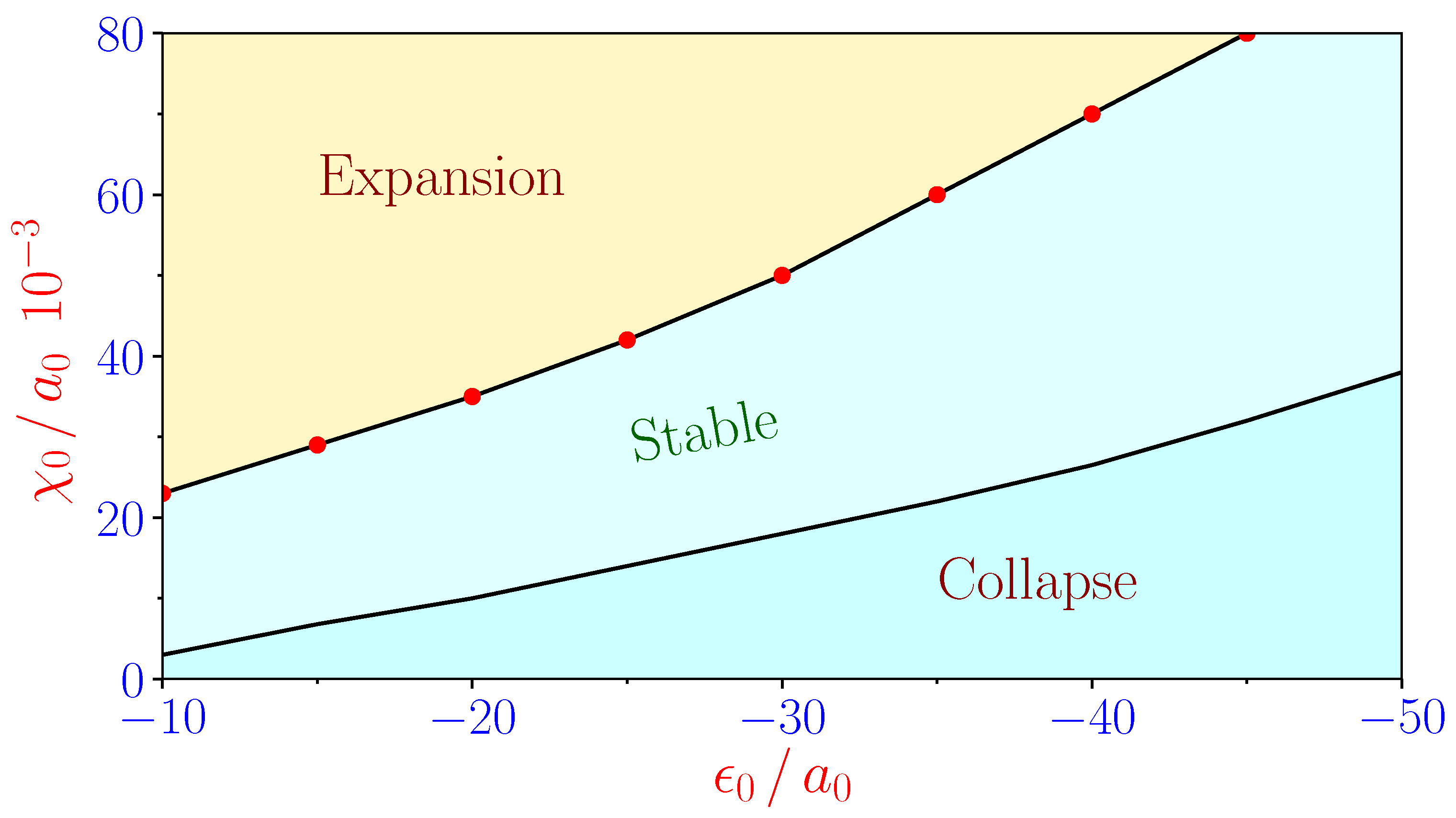
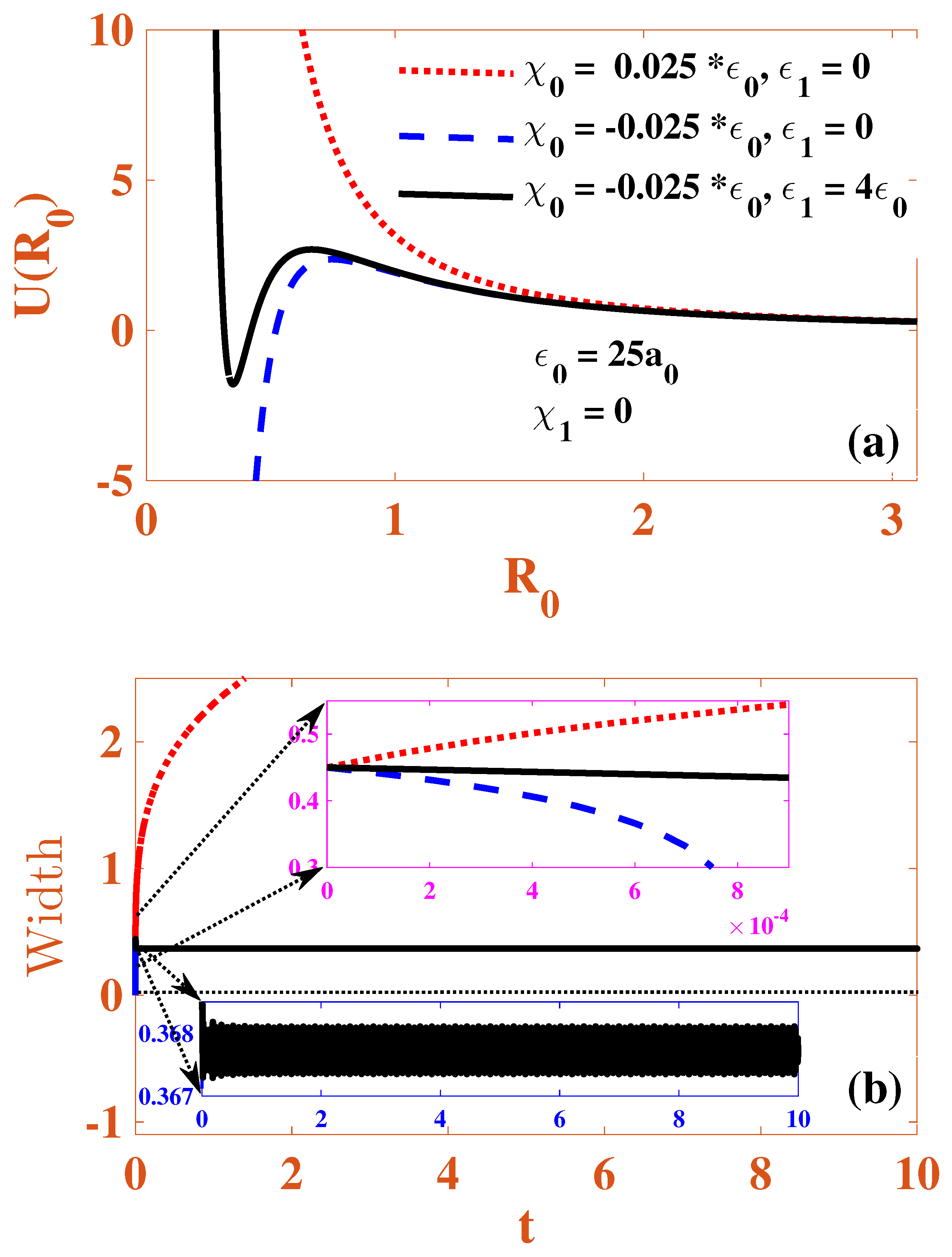
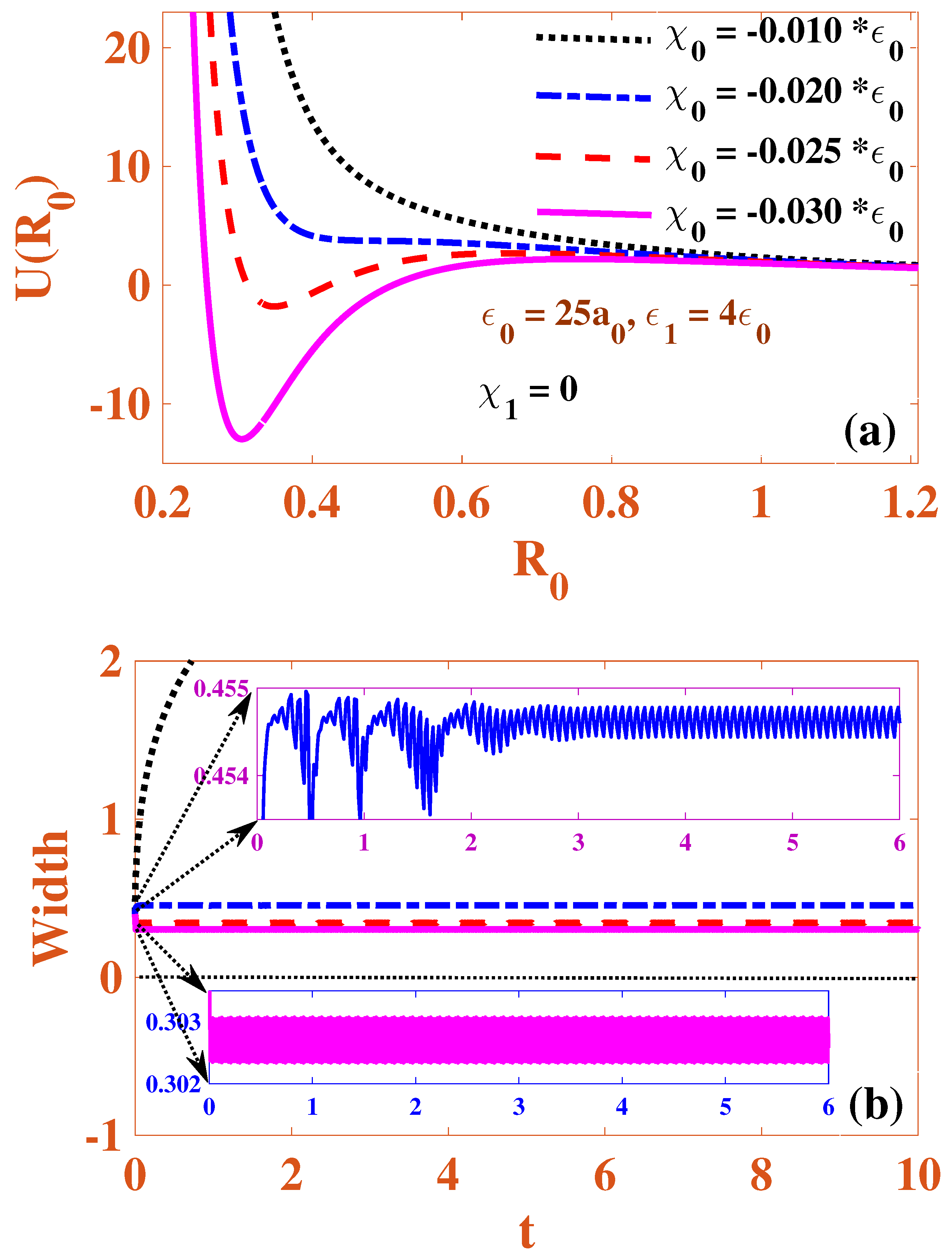

| Minimum | Inference | ||||
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | No | Unstable |
| (Expansion) | |||||
| 25 | 0 | 0 | 0 | No | Unstable |
| (Expansion) | |||||
| −25 | 0 | 0 | 0 | No | Unstable |
| (Collapse) | |||||
| 0 | 0 | Yes | Stable | ||
| (−25) | (−0.002) | ||||
| 0 | 0 | No | Unstable | ||
| (25) | (−0.025 ) | (Collapse) | |||
| 0 | Yes | Stable | |||
| (25) | (4 ) | (−0.025 ) | |||
| Yes | Stable | ||||
| (25) | (4 ) | (−0.01) | (2) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subramaniyan, S.; Ramavarmaraja, K.K.; Ramaswamy, R.; Malomed, B.A. Interplay between Binary and Three-Body Interactions and Enhancement of Stability in Trapless Dipolar Bose–Einstein Condensates. Appl. Sci. 2022, 12, 1135. https://doi.org/10.3390/app12031135
Subramaniyan S, Ramavarmaraja KK, Ramaswamy R, Malomed BA. Interplay between Binary and Three-Body Interactions and Enhancement of Stability in Trapless Dipolar Bose–Einstein Condensates. Applied Sciences. 2022; 12(3):1135. https://doi.org/10.3390/app12031135
Chicago/Turabian StyleSubramaniyan, Sabari, Kishor Kumar Ramavarmaraja, Radha Ramaswamy, and Boris A. Malomed. 2022. "Interplay between Binary and Three-Body Interactions and Enhancement of Stability in Trapless Dipolar Bose–Einstein Condensates" Applied Sciences 12, no. 3: 1135. https://doi.org/10.3390/app12031135
APA StyleSubramaniyan, S., Ramavarmaraja, K. K., Ramaswamy, R., & Malomed, B. A. (2022). Interplay between Binary and Three-Body Interactions and Enhancement of Stability in Trapless Dipolar Bose–Einstein Condensates. Applied Sciences, 12(3), 1135. https://doi.org/10.3390/app12031135







