Wide-Aperture Bimorph Deformable Mirror for Beam Focusing in 4.2 PW Ti:Sa Laser
Abstract
:1. Introduction
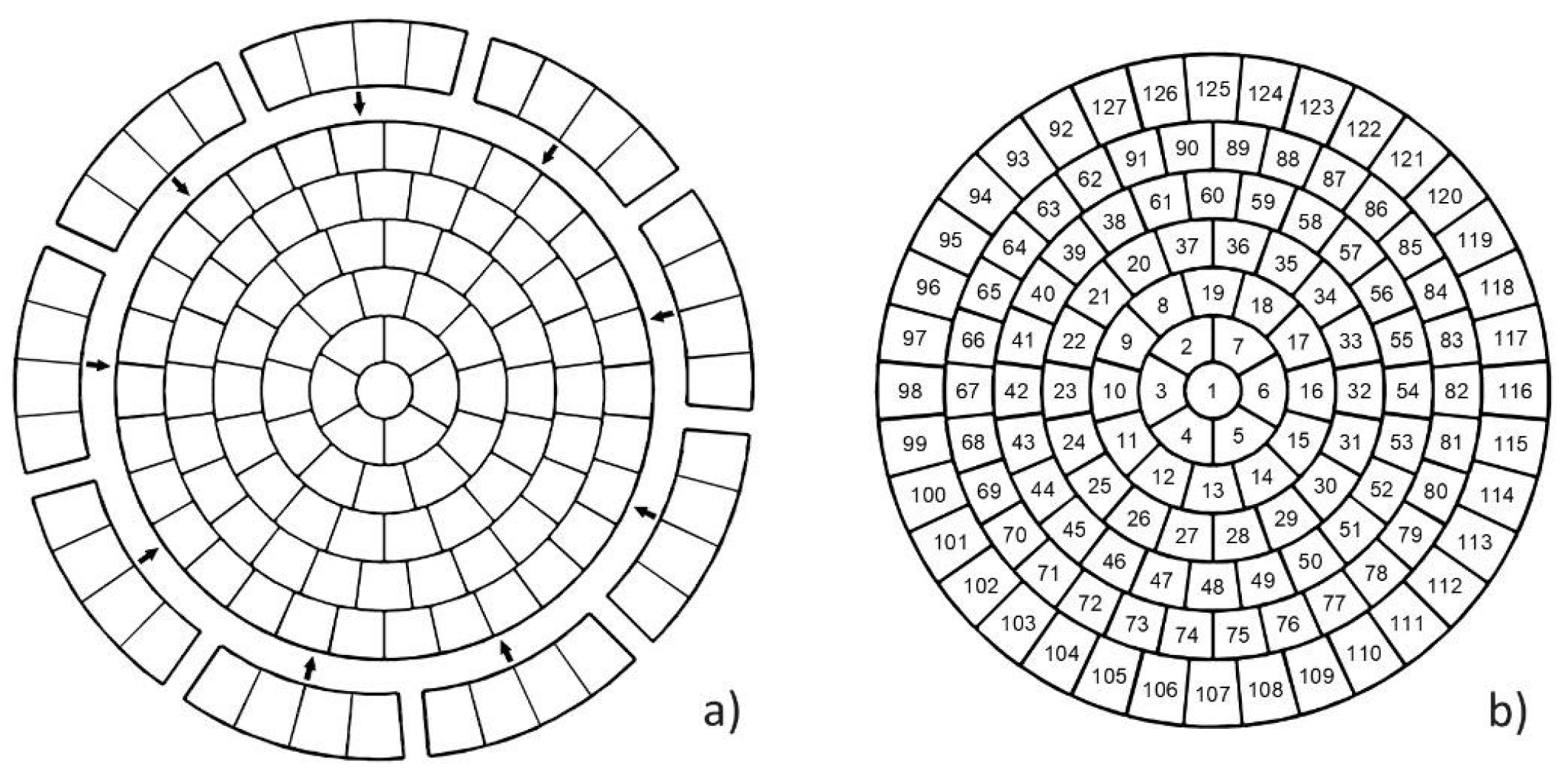
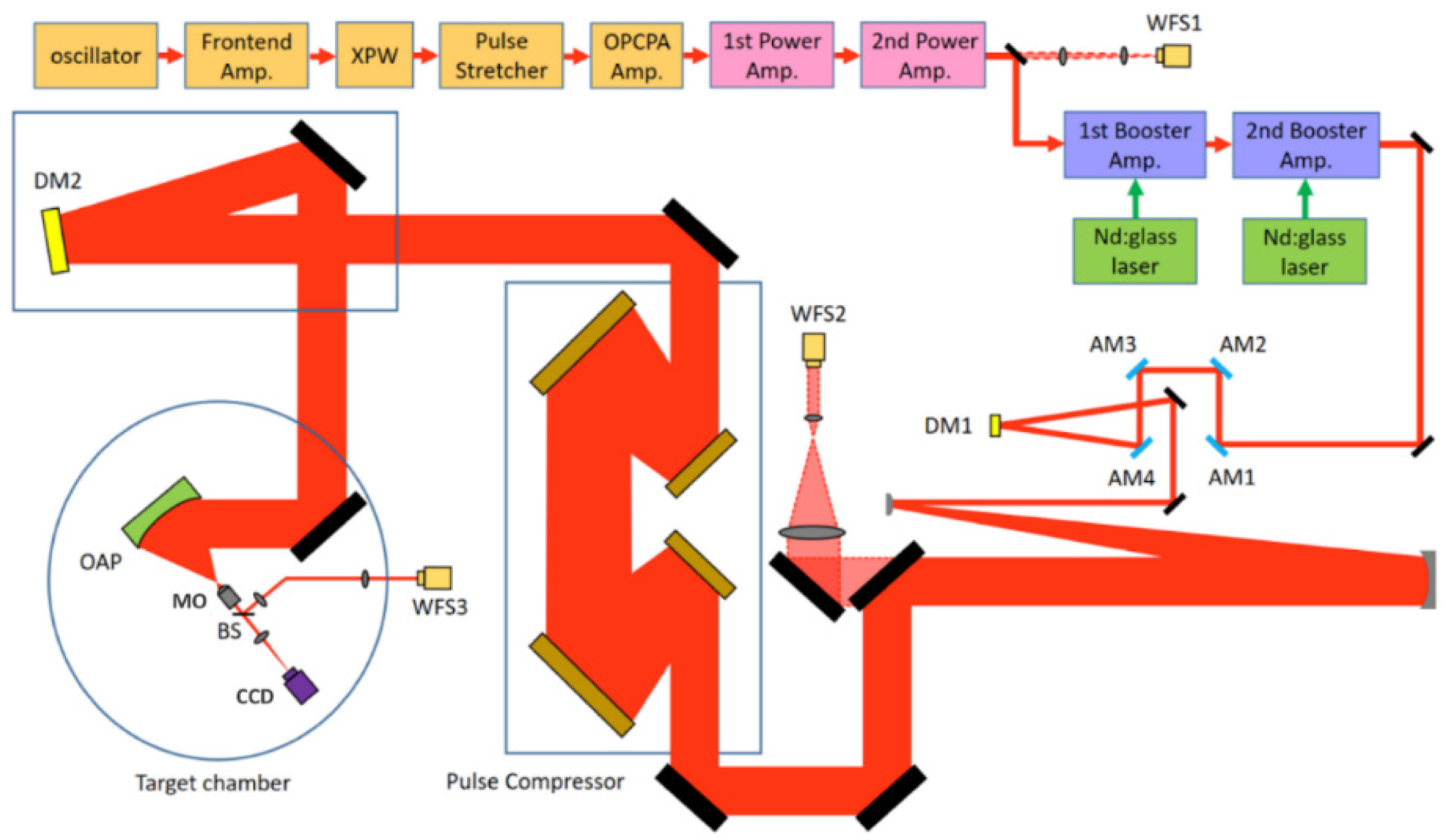
2. Materials and Methods (Design of a 320 mm Bimorph Deformable Mirror)
3. Results
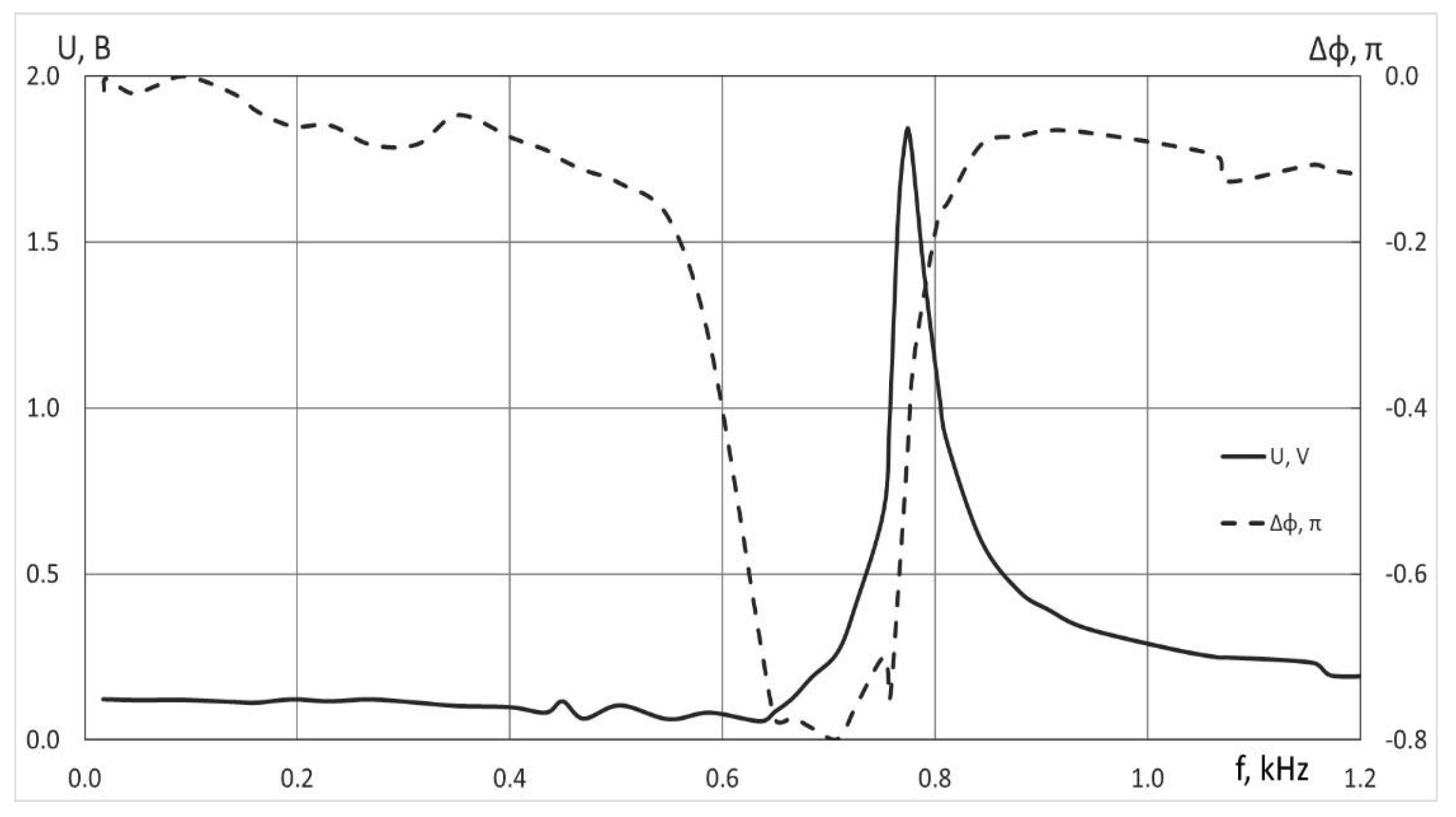
3.1. Investigations of the Deformable Mirror
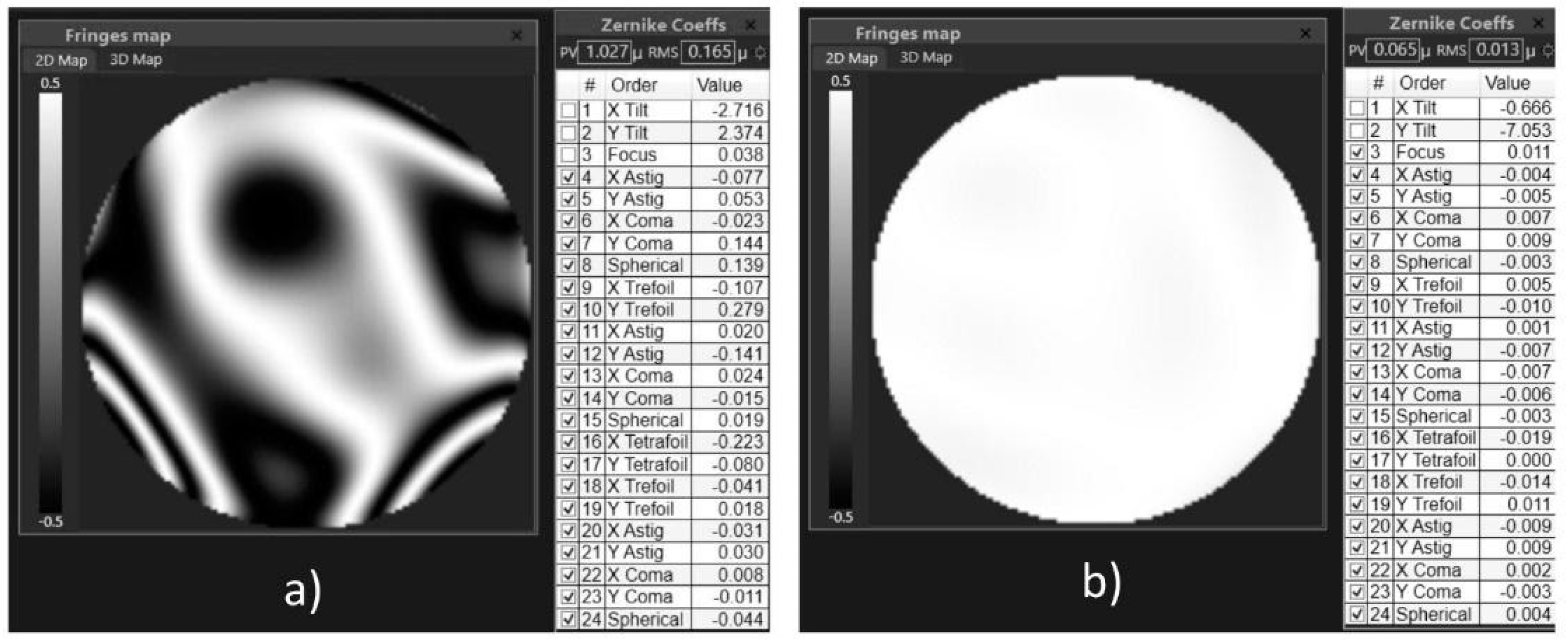
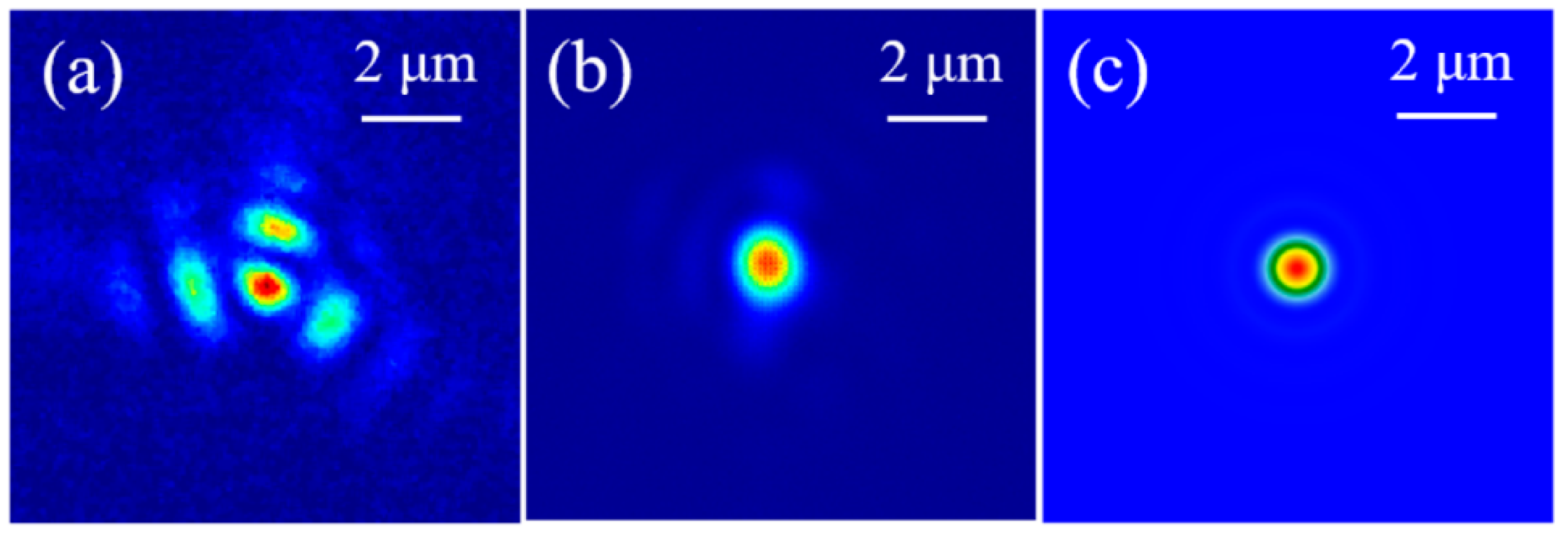
3.2. Wavefront Correction in a 4.2-Petawatt Ti: Sa Laser
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Danson, C.N.; Haefner, C.; Bromage, J.; Butcher, T.; Chanteloup, J.C.-F.; Chowdhury, E.A.; Galvanauskas, A.; Gizzi, L.A.; Hein, J.; Hillier, D.I.; et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Eng. 2019, 7, e54. [Google Scholar] [CrossRef]
- Chu, Y.; Gan, Z.; Liang, X.; Yu, L.; Lu, X.; Wang, C.; Wang, X.; Xu, L.; Lu, H.; Yin, D.; et al. High-energy large-aperture Ti:sapphire amplifier for 5 PW laser pulses. Opt. Lett. 2015, 40, 5011–5014. [Google Scholar] [CrossRef]
- Sung, J.H.; Lee, H.W.; Yoo, J.Y.; Yoon, J.W.; Lee, C.W.; Yang, J.M.; Son, Y.J.; Jang, Y.H.; Lee, S.K.; Nam, C.H. 4.2 PW, 20 fs Ti:sapphire laser at 0.1 Hz. Opt. Lett. 2017, 42, 2058–2061. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.T.; Pathak, V.B.; Pae, K.H.; Lifschitz, A.; Sylla, F.; Shin, J.H.; Hojbota, C.; Lee, S.K.; Sung, J.H.; Lee, H.W.; et al. Stable multi-GeV electron accelerator driven by waveform-controlled PW laser pulses. Sci. Rep. 2017, 7, 10203. [Google Scholar] [CrossRef] [PubMed]
- Di Piazza, A.; Müller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177. [Google Scholar] [CrossRef] [Green Version]
- Wattellier, B.; Fuchs, J.; Zou, J.P.; Abdeli, K.; Haefner, C.; Pépin, H. High-Power Short-Pulse Laser Repetition Rate. Improvement by Adaptive Wave Front Correction. Rev. Sci. Instrum. 2004, 75, 5186–5192. [Google Scholar] [CrossRef] [Green Version]
- Soloviev, A.A.; Kotov, A.V.; Perevalov, S.E.; Esyunin, M.; Starodubtsev, M.; Alexandrov, A.; Galaktionov, I.; Samarkin, V.; Kudryashov, A.; Ginzburg, V.; et al. Adaptive system for wavefront correction of the PEARL laser facility. Quantum Electron. 2020, 50, 1115–1122. [Google Scholar] [CrossRef]
- Sueda, K.; Jitsuno, T.; Morio, N.; Matsuo, S.; Kawanaka, J.; Miyanaga, N. Waveform control and wavefront correction of a large-aperture high-energy glass laser system. Plasma Phys. Fusion Technol.–Laser Soc. Jpn. 2009, 37, 455–460. [Google Scholar]
- Yoon, J.W.; Jeon, C.; Shin, J.; Lee, S.K.; Lee, H.W.; Choi, I.W.; Kim, H.T.; Sung, J.H.; Nam, C.H. Achieving the laser intensity of 5.5 × 1022 W/cm2 with a wavefront-corrected multi-PW laser. Opt. Express 2019, 27, 20412–20420. [Google Scholar] [CrossRef]
- Yoon, J.W.; Kim, Y.G.; Choi, I.W.; Sung, J.H.; Lee, H.W.; Lee, S.K.; Nam, C.H. Realization of laser intensity over 1023 W/cm2. Optica 2021, 8, 630–635. [Google Scholar] [CrossRef]
- Spaeth, M.L.; Manes, K.R.; Widmayer, C.C.; Williams, W.H.; Whitman, P.K.; Henesian, M.A.; Stowers, I.F.; Honig, J. National Ignition Facility wavefront requirements and optical architecture. Opt. Eng. 2004, 43, 2854–2865. [Google Scholar] [CrossRef]
- Aleksandrov, A.G.; Zavalova, V.E.; Kudryashov, A.V.; Rukosuev, A.; Sheldakova, J.; Samarkin, V.V.; Romanov, P.N. Shack-Hartmann wavefront sensor to measure high power lasers. Quantum Electron. 2010, 40, 321. [Google Scholar] [CrossRef]
- Grosset-Grange, C.; Barnier, J.-N.; Chappuis, C.; Cortey, H. Design principle and first results on the LMJ deformable mirror prototype. Proc. SPIE 2007, 6584, 658403. [Google Scholar]
- Lefaudeux, N.; Levecq, X.; Dovillaire, G.; Ballesta, J.; Lavergne, E.; Sauvageot, P.; Escolano, L. Development of a new technology of deformable mirror for ultra intense laser applications. Nucl. Instrum. Methods Phys. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2011, 653, 164–167. [Google Scholar] [CrossRef]
- Bokalo, S.Y.; Garanin, S.G.; Grigorovich, S.V.; Zhupanov, V.G.; Koltygin, M.O.; Kulikov, S.M.; Lyakhov, D.M.; Manachinckii, A.N.; Mizin, P.P.; Ogorodnikov, A.V.; et al. Deformable mirror based on piezoelectric actuators for the adaptive system of the Iskra-6 facility. Quantum Electron. 2007, 37, 691–696. [Google Scholar] [CrossRef]
- Toporovskiy, V.V.; Kudryashov, A.V.; Samarkin, V.V.; Sheldakova, J.; Rukosuev, A.; Skvortsov, A.; Pshonkin, D. Bimorph deformable mirror with a high density of electrodes to correct for atmospheric distortions. Appl. Opt. 2019, 58, 6019–6026. [Google Scholar] [CrossRef]
- Fourmaux, S.; Payeur, S.; Alexandrov, A.G.; Serbanescu, C.; Martin, F.; Ozaki, T.; Kudryashov, A.; Kieffer, J.C. Laser beam wavefront correction for ultra high intensities with 100 TW laser system at the Advanced Laser Light Source. Opt. Express 2008, 16, 11987. [Google Scholar] [CrossRef]
- Aleksandrov, A.G.; Zavalova, V.E.; Kudryashov, A.V.; Rukosuev, A.; Samarkin, V.V. Adaptive Correction of a High-Power Titanium-Sapphire Laser Radiation. J. Appl. Spectrosc. 2005, 72, 744–750. [Google Scholar] [CrossRef]
- Akahane, Y.; Ma, J.; Fukuda, Y.; Aoyoma, M.; Kiriyama, H.; Sheldakova, J.V.; Kudryashov, A.V.; Yamakawa, K. Characterization of wave-front corrected 100 TW, 10 Hz laser pulses with peak intensities greater than 1020 W/cm2. Rev. Sci. Instrum. 2006, 77, 023102. [Google Scholar] [CrossRef]
- Kokorowski, S.J. Analysis of adaptive optical elements made from piezolectric bimorphs. J. Opt. Soc. Am. 1979, 69, 181–187. [Google Scholar] [CrossRef]
- Steinhaus, E.; Lipson, S.G. Bimorph piezoelectric flexible mirror. J. Opt. Soc. Am. 1979, 69, 478–481. [Google Scholar] [CrossRef]
- Samarkin, V.V.; Aleksandrov, A.G.; Jitsuno, T.; Romanov, P.N.; Rukosuev, A.L.; Kudryashov, A. Study of a wide-aperture combined deformable mirror for high-power pulsed phosphate glass lasers. Quantum Electron. 2015, 45, 1086–1087. [Google Scholar] [CrossRef]
- Nikitin, A.N.; Sheldakova, J.V.; Kudryashov, A.V.; Borsoni, G.; Denisov, D.; Karasik, V.; Sakharov, A. A device based on the Shack-Hartmann wave front sensor for testing wide aperture optics. Proc. SPIE 2016, 9754, 97540K. [Google Scholar]
- Toporovsky, V.V.; Samarkin, V.V.; Sheldakova, J.V.; Rukosuev, A.; Kudryashov, A. Water-cooled stacked-actuator flexible mirror for high-power laser beam correction. Opt. Laser Technol. 2021, 144, 107427. [Google Scholar] [CrossRef]
- Shanin, O.I. Adaptive Optical Systems in High Power Pulsed Laser Facilities; Technosphera: Moscow, Russia, 2012; 200p. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samarkin, V.; Alexandrov, A.; Galaktionov, I.; Kudryashov, A.; Nikitin, A.; Rukosuev, A.; Toporovsky, V.; Sheldakova, J. Wide-Aperture Bimorph Deformable Mirror for Beam Focusing in 4.2 PW Ti:Sa Laser. Appl. Sci. 2022, 12, 1144. https://doi.org/10.3390/app12031144
Samarkin V, Alexandrov A, Galaktionov I, Kudryashov A, Nikitin A, Rukosuev A, Toporovsky V, Sheldakova J. Wide-Aperture Bimorph Deformable Mirror for Beam Focusing in 4.2 PW Ti:Sa Laser. Applied Sciences. 2022; 12(3):1144. https://doi.org/10.3390/app12031144
Chicago/Turabian StyleSamarkin, Vadim, Alexander Alexandrov, Ilya Galaktionov, Alexis Kudryashov, Alexander Nikitin, Alexey Rukosuev, Vladimir Toporovsky, and Julia Sheldakova. 2022. "Wide-Aperture Bimorph Deformable Mirror for Beam Focusing in 4.2 PW Ti:Sa Laser" Applied Sciences 12, no. 3: 1144. https://doi.org/10.3390/app12031144
APA StyleSamarkin, V., Alexandrov, A., Galaktionov, I., Kudryashov, A., Nikitin, A., Rukosuev, A., Toporovsky, V., & Sheldakova, J. (2022). Wide-Aperture Bimorph Deformable Mirror for Beam Focusing in 4.2 PW Ti:Sa Laser. Applied Sciences, 12(3), 1144. https://doi.org/10.3390/app12031144









