Image Reconstruction Using Autofocus in Single-Lens System
Abstract
:1. Introduction
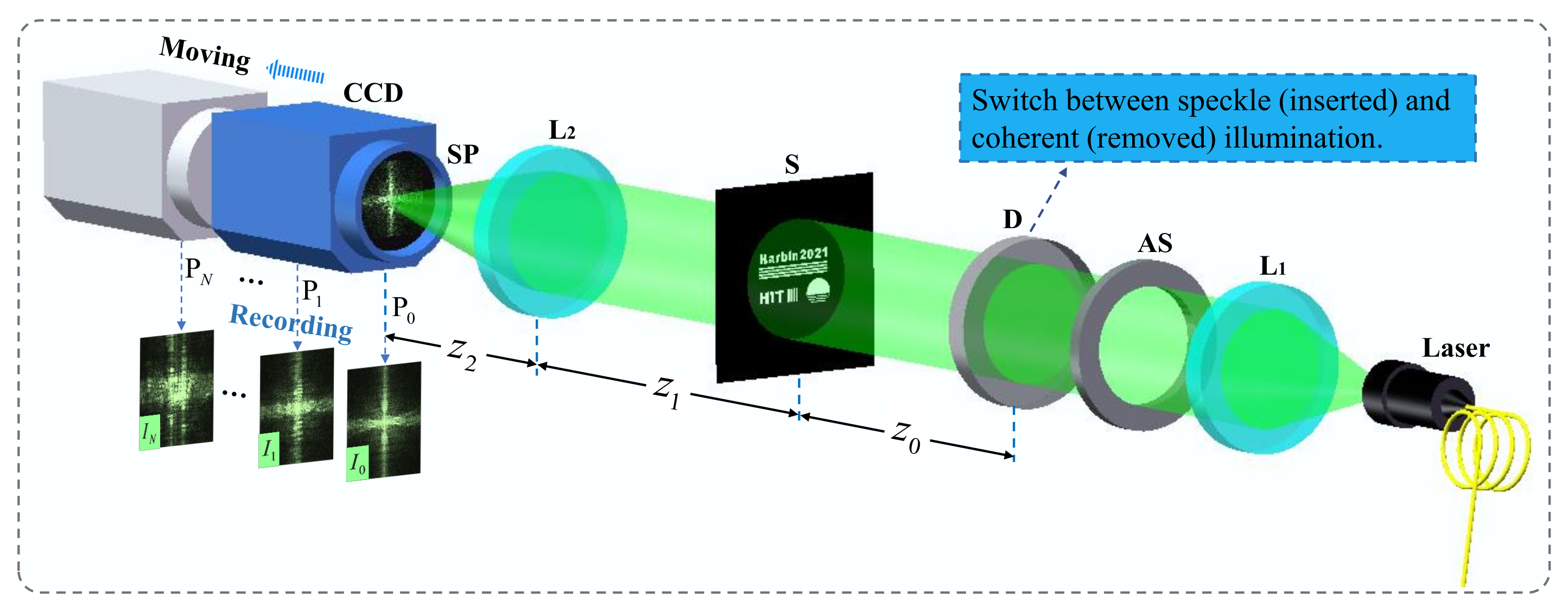
2. Methodology
2.1. Autofocus and Iterative Algorithm
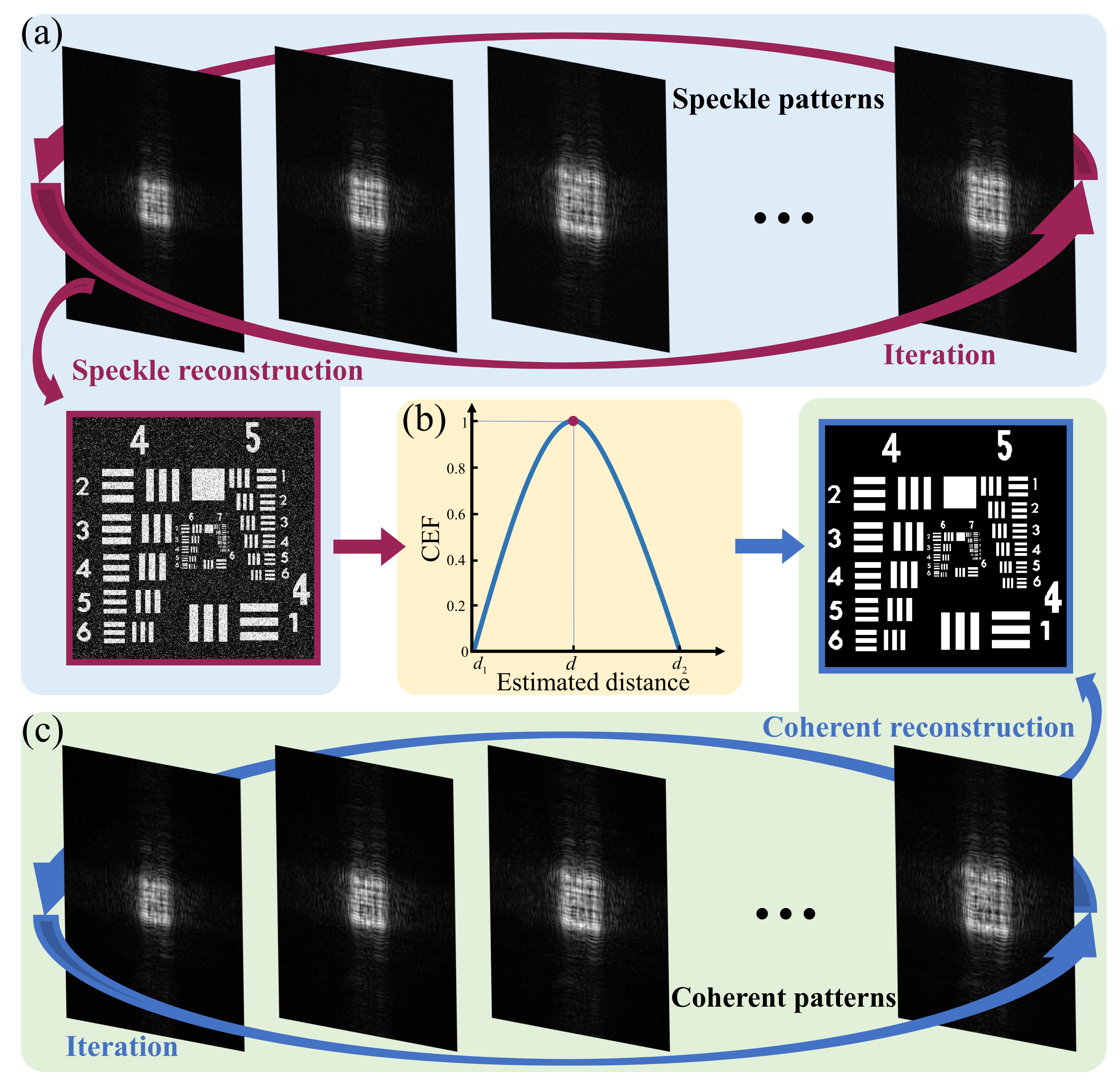
- Reconstruction of the scattered out-of-focus dataset by using the intensity patterns under speckle illumination.
- Clarity evaluation of reconstructed speckle images, and curve drawing between estimated distances and clarity results.
- Reconstruction of coherent patterns by using the quasi-focus distance in step 2.
2.2. Clarity Evaluation Function
2.3. Image Reconstruction
- (1)
- represents the pattern of scattered illumination on n-th imaging plane recorded by CCD. represents the k-th complex-value guess when the image is on the n-th plane.
- (2)
- The light field functions of two adjacent imaging surfaces are propagated by the angular spectrum method aswhere is forward angular spectrum propagation operator with a distance d. During the iteration, the real part of k-th complex-value guess on the plane is replaced by the root of measured intenisty . The intervals between the adjacent detecting positions are equal in simulations and experiments.
- (3)
- When the iteration runs on the last diffraction plane , the synthesized complex amplitude propagates backward to the first plane . And, represents the backforward angular spectrum propagation operator. The complex amplitude at the plane is replaced withSteps (2) and (3) will be implemented iteratively.
- (4)
- Convergence evaluation criteria in the current loop is achieved by the function
- (i)
- A specific range for object distance is selected for covering the actual distance.
- (ii)
- Supposing that is the complex amplitude at the plane after M iterations, the complex amplitude of sample is obtained by back propagation and is expressed aswhere and are complex amplitudes at the plane and the sample plane, respectively. The function is the phase of the lens .
- (iii)
- By changing the distance , several recovered complex amplitudes of sample are obtained with at the distance , which is given aswhere and represent starting distance and interval.
2.4. Speckle Model
3. Simulation and Experiments
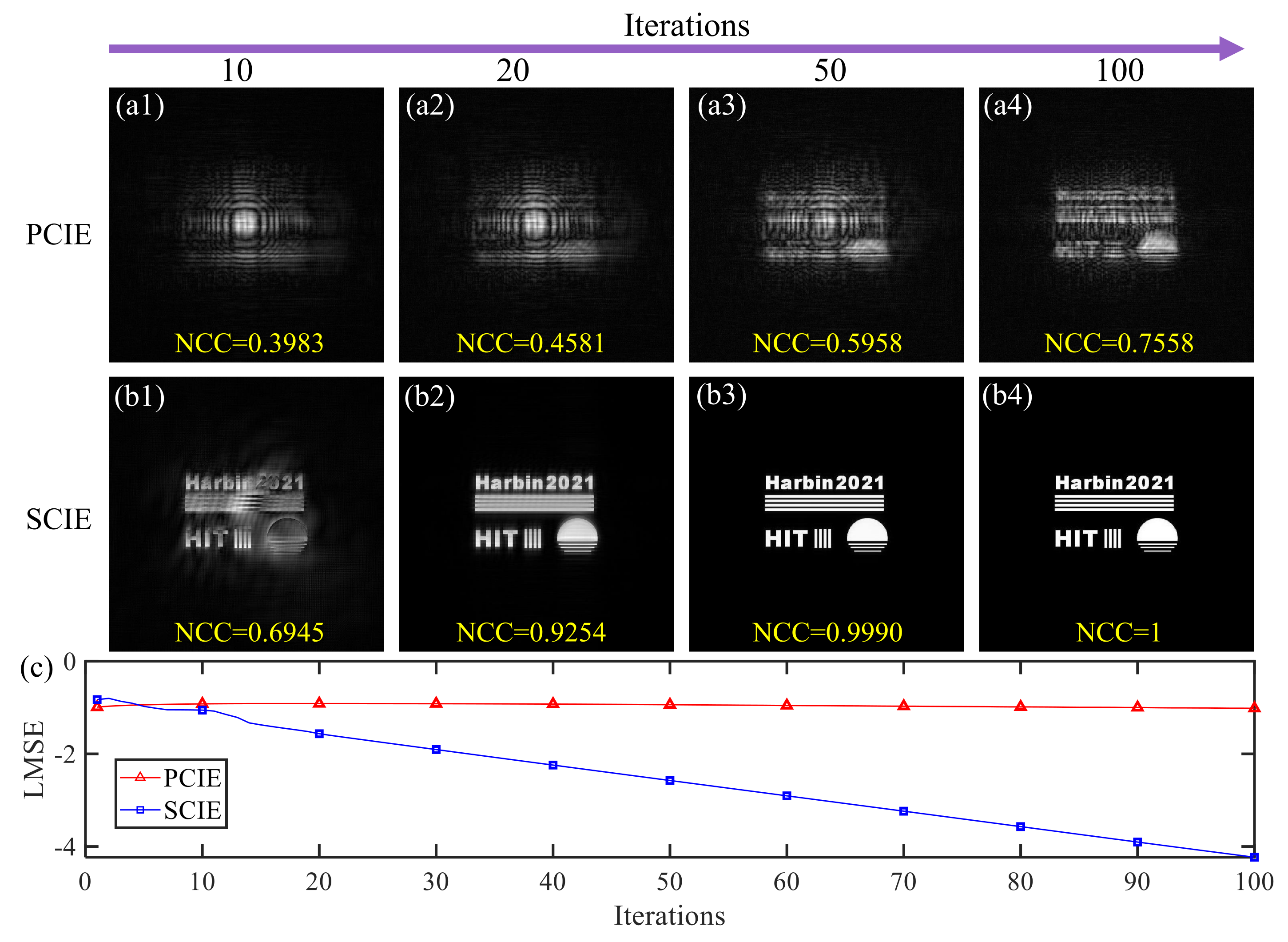
3.1. Comparison of the Two Iteration Methods
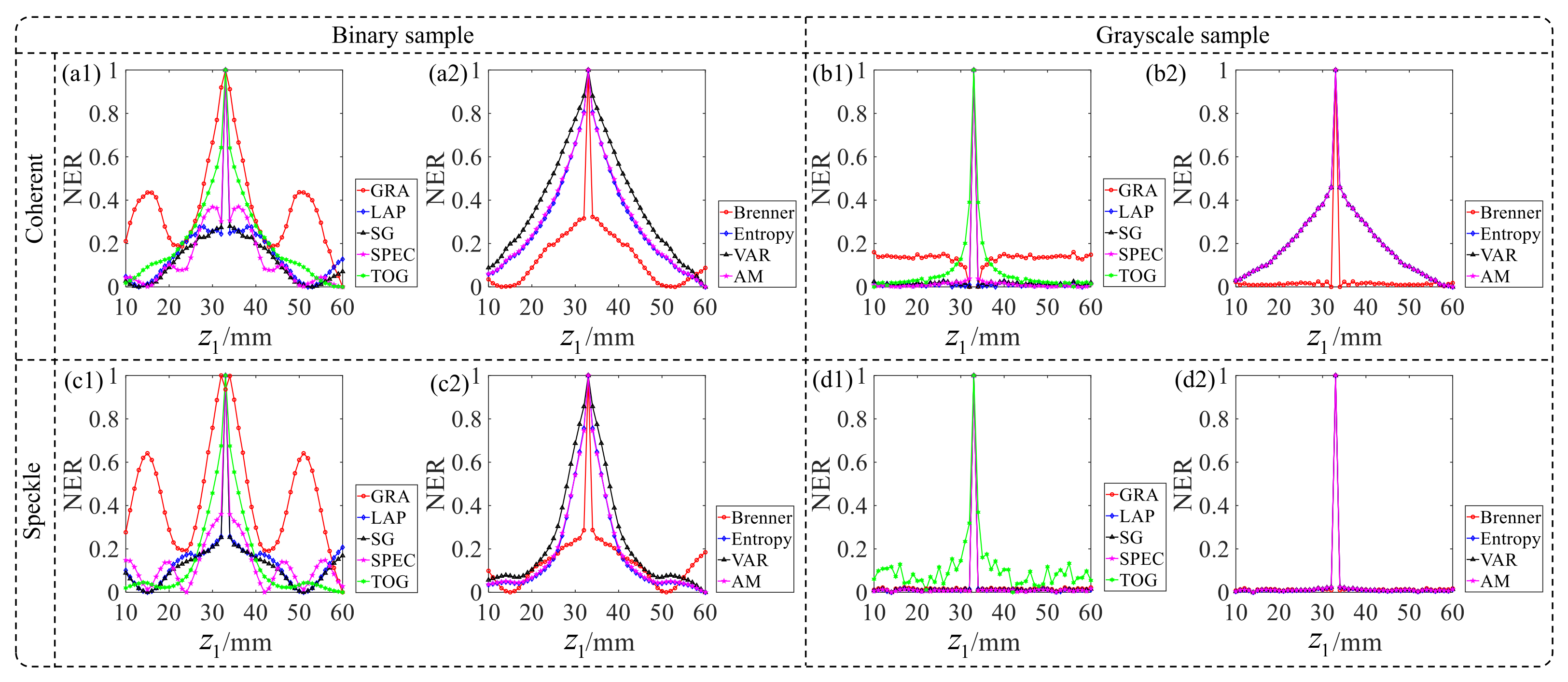
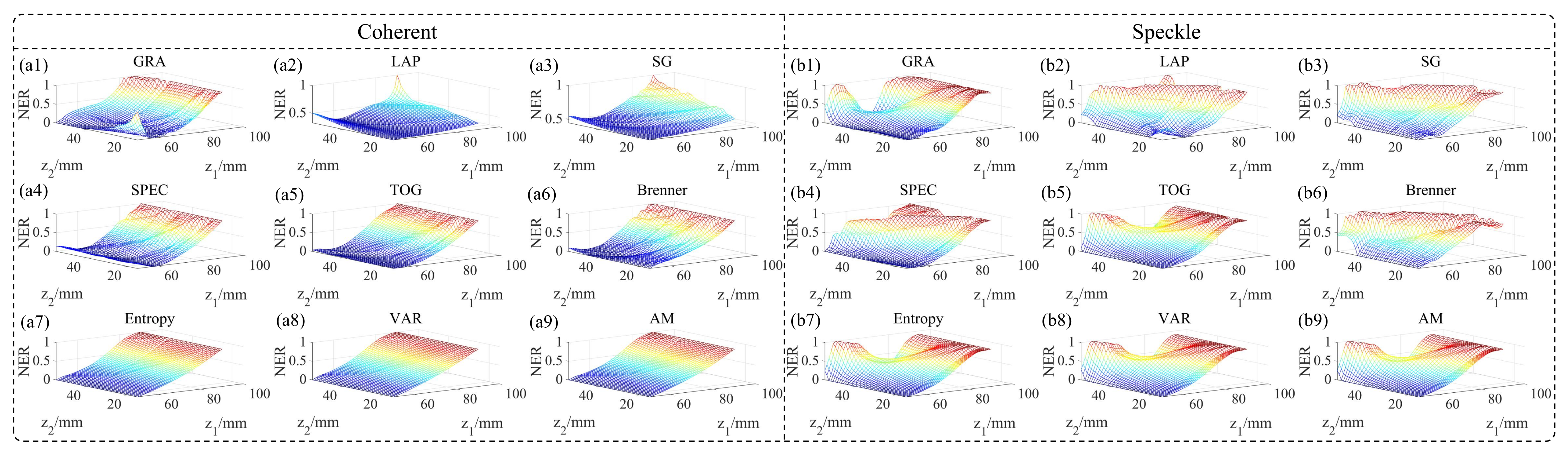
3.2. Autofocus for Object Distance
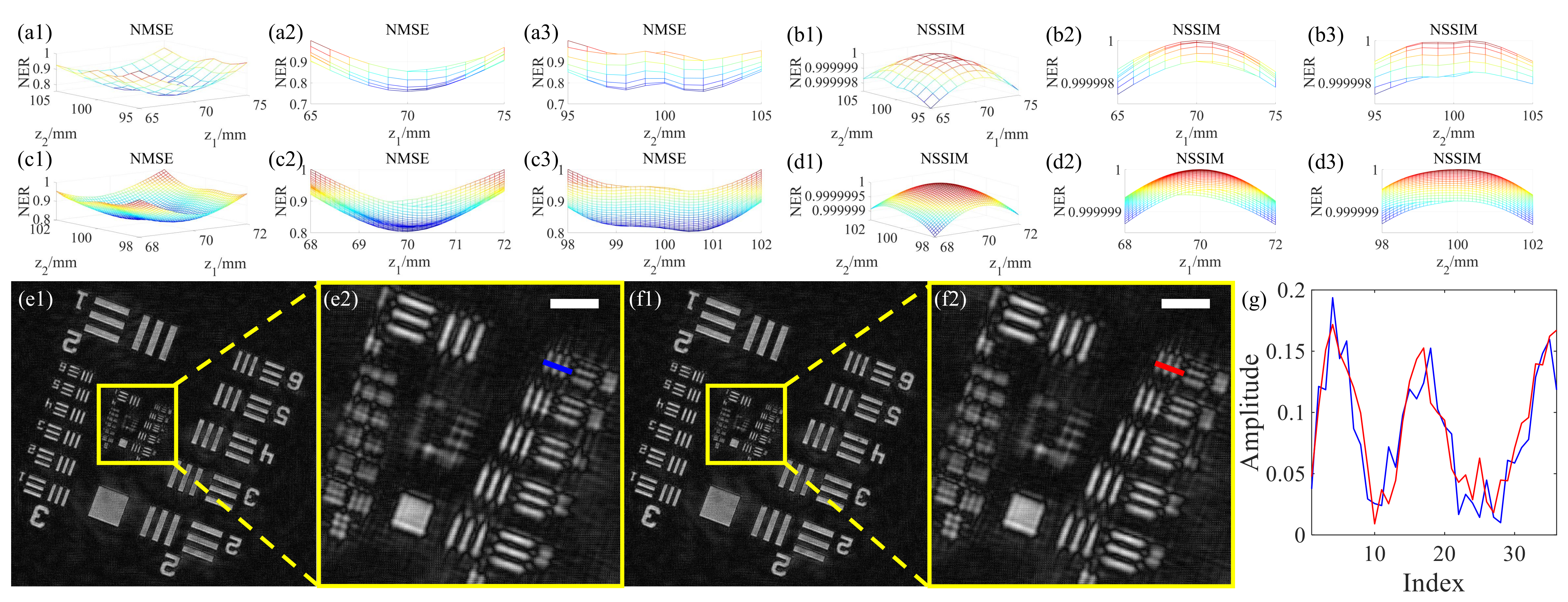
3.3. Autofocus for Object Distance and Image Distance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, F.X.; Yan, W.; Peng, F.P.; Wang, S.M.; Du, J.L. Enhanced phase retrieval method based on random phase modulation. Appl. Sci. 2020, 10, 1184. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.S.; Ye, Q.; Hoorfar, A.; Meng, G.X. Extrapolative phase retrieval based on a hybrid of PhaseCut and alternating projection techniques. Opt. Lasers Eng. 2019, 121, 96–103. [Google Scholar] [CrossRef]
- Shan, M.G.; Liu, L.; Zhong, Z.; Liu, B.; Zhang, Y.B. Direct phase retrieval for simultaneous dual-wavelength off-axis digital holography. Opt. Lasers Eng. 2019, 121, 246–251. [Google Scholar] [CrossRef]
- Sun, M.J.; Zhang, J.M. Phase retrieval utilizing geometric average and stochastic perturbation. Opt. Lasers Eng. 2019, 120, 1–5. [Google Scholar] [CrossRef]
- Tsuruta, M.; Fukuyama, T.; Tahara, T.; Takaki, Y. Fast image reconstruction technique for parallel phase-shifting digital holography. Appl. Sci. 2021, 11, 11343. [Google Scholar] [CrossRef]
- Guo, C.; Shen, C.; Tan, J.B.; Bao, X.J.; Liu, S.T.; Liu, Z.J. A robust multi-image phase retrieval. Opt. Lasers Eng. 2018, 101, 16–22. [Google Scholar] [CrossRef]
- Bao, P.; Zhang, F.C.; Pedrini, G.; Osten, W. Phase retrieval using multiple illumination wavelengths. Opt. Lett. 2008, 33, 309–311. [Google Scholar] [CrossRef]
- Kühn, J.; Colomb, T.; Montfort, F.; Charrière, F.; Emery, Y.; Cuche, E.; Marquet, P.; Depeursinge, C. Real-time dual-wavelength digital holographic microscopy with a single hologram acquisition. Opt. Express 2007, 15, 7231–7242. [Google Scholar] [CrossRef]
- Pedrini, G.; Osten, W.; Zhang, Y. Wave-front reconstruction from a sequence of interferograms recorded at different planes. Opt. Lett. 2005, 30, 833–835. [Google Scholar] [CrossRef]
- Geng, Y.; Tan, J.B.; Guo, C.; Shen, C.; Ding, W.Q.; Liu, S.T.; Liu, Z.J. Computational coherent imaging by rotating a cylindrical lens. Opt. Express 2018, 26, 22110–22122. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Guo, C.; Geng, Y.; Tan, J.B.; Liu, S.T.; Liu, Z.J. Noise-robust pixel-super-resolved multi-image phase retrieval with coherent illumination. J. Opt. 2018, 20, 115703. [Google Scholar] [CrossRef]
- Guo, C.; Li, Q.; Tan, J.B.; Liu, S.T.; Liu, Z.J. A method of solving tilt illumination for multiple distance phase retrieval. Opt. Lasers Eng. 2018, 106, 17–23. [Google Scholar] [CrossRef]
- Guo, C.; Zhao, Y.X.; Tan, J.B.; Liu, S.T.; Liu, Z.J. Multi-distance phase retrieval with a weighted shrink-wrap constraint. Opt. Lasers Eng. 2019, 113, 1–5. [Google Scholar] [CrossRef]
- Luo, W.; Zhang, Y.; Feizi, A.; Göröcs, Z.; Ozcan, A. Pixel super-resolution using wavelength scanning. Light Sci. Appl. 2016, 5, e16060. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.J.; Guo, C.; Tan, J.B.; Wu, Q.; Pan, L.Q.; Liu, S.T. Iterative phase-amplitude retrieval with multiple intensity images at output plane of gyrator transforms. J. Opt. 2015, 17, 025701. [Google Scholar] [CrossRef]
- Jin, X.; Ding, X.M.; Tan, J.B.; Shen, C.; Liu, S.T.; Liu, Z.J. Wavefront reconstruction of a non-coaxial diffraction model in a lens system. Appl. Opt. 2018, 57, 1127–1133. [Google Scholar] [CrossRef]
- Shen, C.; Tan, J.B.; Wei, C.; Liu, Z.J. Coherent diffraction imaging by moving a lens. Opt. Express 2016, 24, 16520–16529. [Google Scholar] [CrossRef]
- Almoro, P.F.; Gundu, P.N.; Hanson, S.G. Numerical correction of aberrations via phase retrieval with speckle illumination. Opt. Lett. 2009, 34, 521–523. [Google Scholar] [CrossRef]
- Zhu, F.P.; Lu, R.Z.; Bai, P.X.; Lei, D. A novel in situ calibration of object distance of an imaging lens based on optical refraction and two-dimensional DIC. Opt. Lasers Eng. 2019, 120, 110–117. [Google Scholar] [CrossRef]
- Wang, X.Z.; Liu, L.; Du, X.H.; Zhang, J.; Ni, G.M.; Liu, J.X. GMANet: Gradient mask attention network for finding clearest human fecal microscopic image in autofocus process. Appl. Sci. 2021, 11, 10293. [Google Scholar] [CrossRef]
- Yang, C.P.; Chen, M.H.; Zhou, F.F.; Li, W.; Peng, Z.M. Accurate and rapid auto-focus methods based on image quality assessment for telescope observation. Appl. Sci. 2020, 10, 658. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.B.; Wang, H.D.; Wu, Y.C.; Tammamitsu, M.; Ozcan, A. Edge sparsity criterion for robust holographic autofocusing. Opt. Lett. 2017, 42, 3824–3827. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Duthaler, S.; Nelson, B.J. Autofocusing algorithm selection in computer microscopy. In Proceedings of the 2005 IEEE RSJ International Conference on Intelligent Robots Systems, Edmonton, Alta, 2–6 August 2005; pp. 70–76. [Google Scholar]
- Santos, A.; Solórzano, C.O.; Vaquero, J.J.; Peña, J.M.; Malpica, N.; Pozo, F. Evaluation of autofocus functions in molecular cytogenetic analysis. J. Microsc. 1997, 188, 264–272. [Google Scholar] [CrossRef] [Green Version]
- Brenner, J.F.; Dew, B.S.; Horton, J.B.; King, J.B.; Neirath, P.W.; Sellers, W.D. An automated microscope for cytologic research a preliminary evaluation. J. Histochem. Cytochem. 1976, 24, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Yeo, T.T.E.; Ong, S.H.; Sinniah, R. Autofocusing for tissue microscopy. Image Vision Comput. 1993, 11, 629–639. [Google Scholar] [CrossRef]
- Dwivedi, P.; Konijnenberg, A.P.; Pereira, S.F.; Urbach, H.P. Lateral position correction in ptychography using the gradient of intensity patterns. Ultramicroscopy 2018, 192, 29–36. [Google Scholar] [CrossRef]
- Langehanenberg, P.; Kemper, B.; Dirksen, D.; Bally, G.V. Autofocusing in digital holographic phase contrast microscopy on pure phase objects for live cell imaging. Appl. Opt. 2008, 47, D176–D182. [Google Scholar] [CrossRef] [PubMed]
- Vollath, D. The influence of the scene parameters and of noise on the behavior of automatic focusing algorithms. J. Microsc. 1988, 151, 133–146. [Google Scholar] [CrossRef]
- Shenfield, A.; Rodenburg, J.M. Evolutionary determination of experimental parameters for ptychographical imaging. J. Appl. Phys. 2011, 109, 124510. [Google Scholar] [CrossRef] [Green Version]
- Guo, C.; Zhao, Y.X.; Tan, J.B.; Liu, S.T.; Liu, Z.J. Adaptive lens-free computational coherent imaging using autofocusing quantification with speckle illumination. Opt. Express 2018, 26, 14407–14420. [Google Scholar] [CrossRef] [PubMed]
- Yazdanfar, S.; Kenny, K.B.; Tasimi, K.; Corwin, A.D.; Dixon, E.L.; Filkins, R.J. Simple and robust image-based autofocusing for digital microscopy. Opt. Express 2008, 12, 8670–8677. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Duthaler, S.; Nelson, B.J. Autofocusing in computer microscopy: Selecting the optimal focus algorithm. Microsc. Res. Techniq. 2004, 65, 139–149. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.S.; Lee, S.J. Three-dimensional volumetric measurement of red blood cell motion using digital holographic microscopy. Appl. Opt. 2009, 48, 2983–2990. [Google Scholar] [CrossRef]
- Yang, Y.; Kang, B.S.; Choo, Y.J. Application of the correlation coefficient method for determination of the focal plane to digital particle holography. Appl. Opt. 2008, 47, 817–824. [Google Scholar] [CrossRef] [Green Version]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts and Company Publishers: Greenwood Village, CO, USA, 2004; pp. 154–162. [Google Scholar]
- Hardin. Centers for Disease Control and Prevention. Available online: https://phil.cdc.gov/Details.aspx?pid=22920 (accessed on 25 October 2021).
- Freund, I.; Rosenbluh, M.; Feng, S.C. Memory effects in propagation of optical waves through disordered media. Phys. Rev. Lett. 1988, 61, 2328–2331. [Google Scholar] [CrossRef]
- Bertolotti, J. Multiple scattering: Unravelling the tangle. Nat. Phys. 2015, 11, 622–623. [Google Scholar] [CrossRef]
- Wen, X.; Geng, Y.; Guo, C.; Zhou, X.Y.; Tan, J.B.; Liu, S.T.; Tan, C.M.; Liu, Z.J. A parallel ptychographic iterative engine with a co-start region. J. Opt. 2020, 22, 1–11. [Google Scholar] [CrossRef]
- Wen, X.; Geng, Y.; Zhou, X.Y.; Tan, J.B.; Liu, S.T.; Tan, C.M.; Liu, Z.J. Ptychography imaging by 1-D scanning with a diffuser. Opt. Express 2020, 28, 22658–22668. [Google Scholar] [CrossRef]
- Zhang, F.L.; Guo, C.; Zhai, Y.L.; Tan, J.B.; Liu, S.T.; Tan, C.M.; Chen, H.; Liu, Z.J. A noise-robust multi-intensity phase retrieval method based on structural patch decomposition. J. Opt. 2020, 22, 075706. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, Z.P.; Wang, H.J.; Gong, Q.; Zhou, N.R. Robust information encryption diffractive-imaging-based scheme with special phase retrieval algorithm for a customized data container. Opt. Lasers Eng. 2018, 105, 118–124. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Wen, X.; Ji, Y.; Li, Y.; Liu, S.; Liu, Z. Image Reconstruction Using Autofocus in Single-Lens System. Appl. Sci. 2022, 12, 1378. https://doi.org/10.3390/app12031378
Zhou X, Wen X, Ji Y, Li Y, Liu S, Liu Z. Image Reconstruction Using Autofocus in Single-Lens System. Applied Sciences. 2022; 12(3):1378. https://doi.org/10.3390/app12031378
Chicago/Turabian StyleZhou, Xuyang, Xiu Wen, Yu Ji, Yutong Li, Shutian Liu, and Zhengjun Liu. 2022. "Image Reconstruction Using Autofocus in Single-Lens System" Applied Sciences 12, no. 3: 1378. https://doi.org/10.3390/app12031378
APA StyleZhou, X., Wen, X., Ji, Y., Li, Y., Liu, S., & Liu, Z. (2022). Image Reconstruction Using Autofocus in Single-Lens System. Applied Sciences, 12(3), 1378. https://doi.org/10.3390/app12031378






