Analytical Model for Enhancing the Adoptability of Continuous Descent Approach at Airports
Abstract
:Featured Application
Abstract
1. Introduction
2. Preliminaries and Process Description
2.1. Structure of Airspace around Airports
2.2. Description of the Aircraft Descent and Approach Process at Airports
2.2.1. Descent and Approach Operations
2.2.2. Step-Down Descent Approach (SDA)
2.2.3. Comparison between CDA and SDA
3. CDA Adoptability and Aircraft Descent Times
3.1. Factors Impacting CDA Adoptability and Aircraft Descent Time
Factors Impacting CDA Adoptability and Aircraft Descent Times
3.2. Estimation of Aircraft Descent Time
3.2.1. Aircraft Velocity and Lift Model
3.2.2. Drag Model
3.2.3. Thrust Model
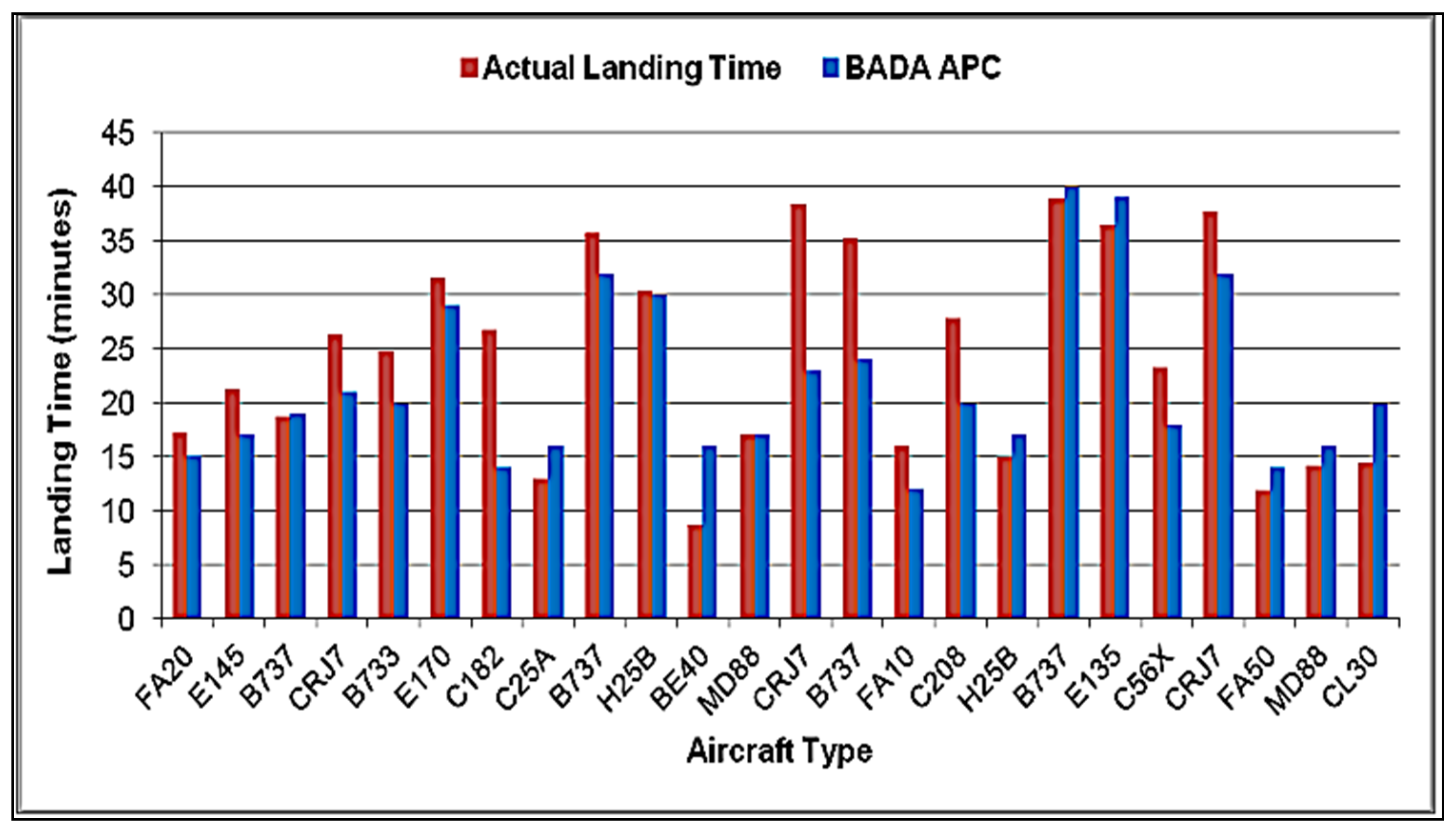
3.3. Evaluation of Aircraft Estimated Descent Time
4. Model Development
4.1. Background on Queueing Theory
4.2. Adopting Queueing Theory to Our Model
4.2.1. Assumptions and Parameters of the Model
- The space available for stacking aircraft arrivals in the TMA is considered as the maximum number of aircrafts (customers) that are permitted in the queue, and
- the longitudinal separation distance between aircrafts conducting CDA are greater than the distance between aircrafts not conducting CDA
4.2.2. Capacity of the Stacking Space for Aircraft Arrivals
5. The Applied Queueing Model
5.1. Traffic Intensity
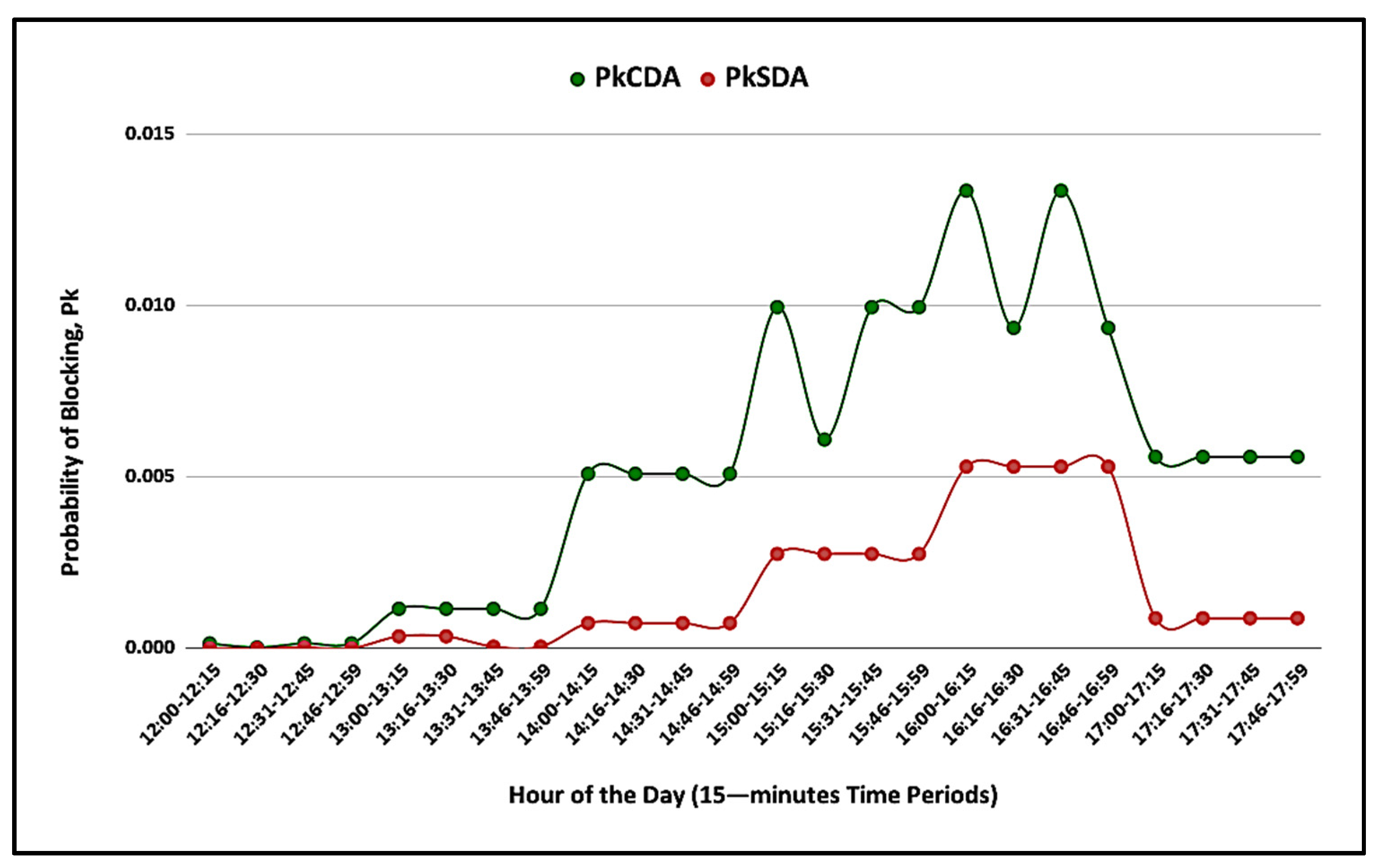
5.2. Probability of Aircraft Blocking
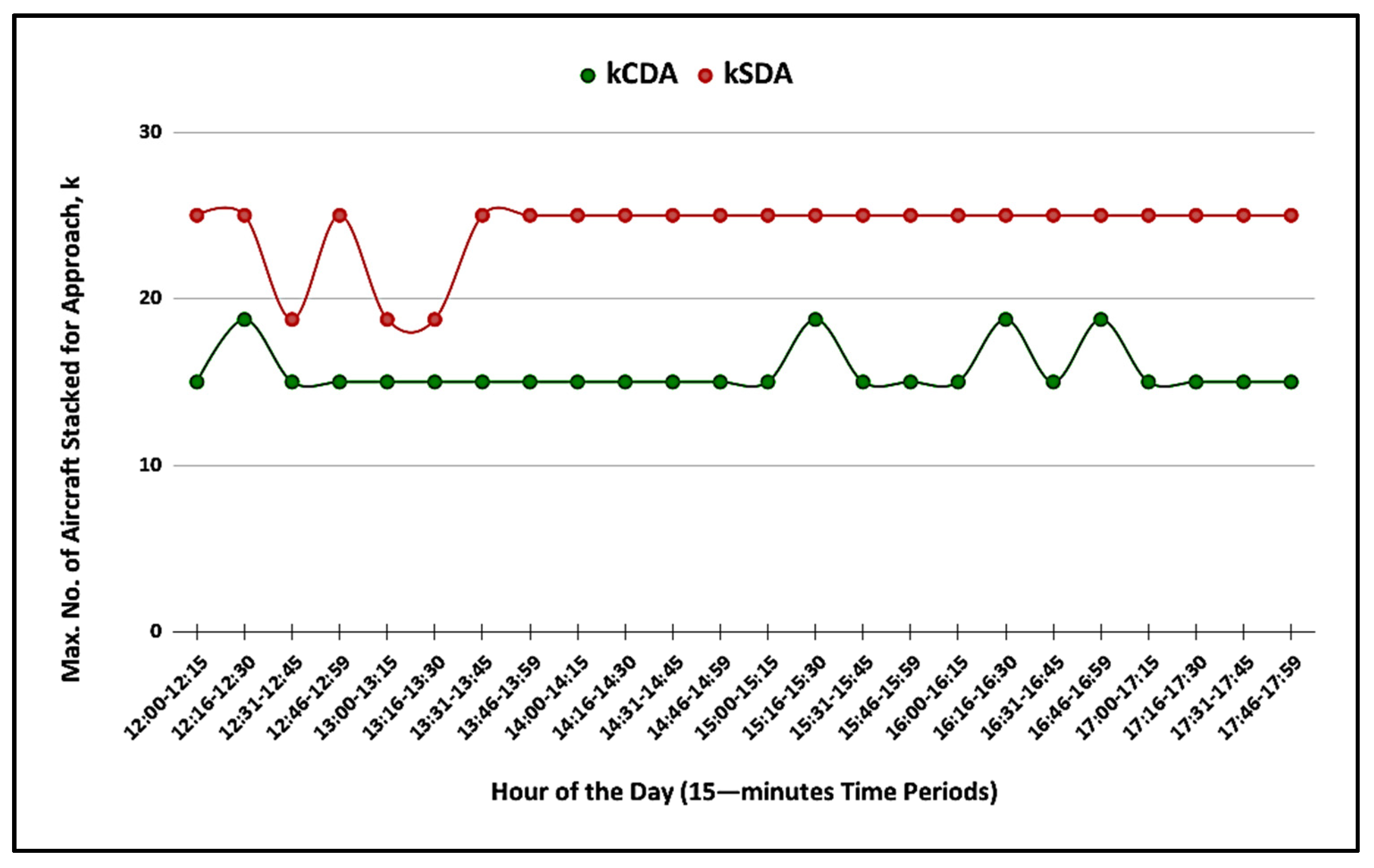
6. Numerical Results to Illustrate the Model
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- IATA. IATA Forecasts Passenger Demand to Double Over 20 Years. 2016. Available online: http://www.iata.org/pressroom/pr/Pages/2016-10-18-02.aspx (accessed on 10 March 2020).
- EPA. EPA Determines That Aircraft Emissions Contribute to Climate Change Endangering Public Health and the Environment. 2016. Available online: https://archive.epa.gov/epa/newsreleases/epa-determines-aircraft-emissions-contribute-climate-change-endangering-public-health-0.html (accessed on 10 March 2020).
- European, C. Reducing Emissions from Aviation. 2017. Available online: https://ec.europa.eu/clima/policies/transport/aviation_en (accessed on 11 March 2020).
- Dillingham, G.L.; Martin, B. Aviation and the Environment: Results from a Survey of the Nation’s 50 Busiest Commercial Service Airports; US General Accounting Office: Washington, DC, USA, 2000.
- Basner, M.; Babisch, W.; Davis, A.; Brink, M.; Clark, C.; Janssen, S.; Stansfeld, S. Auditory and non-auditory effects of noise on health. Lancet 2013, 383, 1325–1332. [Google Scholar] [CrossRef] [Green Version]
- Clarke, J.-P.B.; Ho, N.T.; Ren, L.; Brown, J.A.; Elmer, K.R.; Tong, K.-O.; Wat, J.K. Continuous Descent Approach: Design and Flight Test for Louisville International Airport. J. Aircr. 2004, 41, 1054–1066. [Google Scholar] [CrossRef]
- Coppenbarger, R.A.; Mead, R.W.; Sweet, D.N. Field Evaluation of the Tailored Arrivals Concept for Datalink-Enabled Continuous Descent Approach. J. Aircr. 2009, 46, 1200–1209. [Google Scholar] [CrossRef]
- McNulty, M. Airbus Says Jets Flying Close Behind Each Other Could Reduce Fuel Costs by 10 Percent. 2019. Available online: https://www.foxbusiness.com/lifestyle/airbus-jets-flying-close-reduce-fuel-costs (accessed on 29 November 2019).
- Turgut, E.T.; Usanmaz, O.; Canarslanlar, A.O.; Sahin, O. Energy and emission assessments of continuous descent approach. Aircr. Eng. Aerosp. Technol. 2010, 82, 32–38. [Google Scholar] [CrossRef]
- Morrell, P.S. Moving Boxes by Air: The Economics of International Air Cargo; Ashgate: Farnham, UK, 2011. [Google Scholar]
- Girvin, R. Aircraft noise-abatement and mitigation strategies. J. Air Transp. Manag. 2009, 15, 14–22. [Google Scholar] [CrossRef]
- Postorino, M.N.; Mantecchini, L. A systematic approach to assess the effectiveness of airport noise mitigation strategies. J. Air Transp. Manag. 2016, 50, 71–82. [Google Scholar] [CrossRef]
- Schroeder, J. A perspective on NASA Ames air traffic management research. In Proceedings of the 9th AIAA Aviation Technology, Integration, and Operations Conference (ATIO) and Aircraft Noise and Emissions Reduction Symposium (ANERS), Hilton Head, SC, USA, 21–23 September 2009. [Google Scholar]
- Stibor, J.; Nyberg, A. Implementation of continuous descent approaches at Stockholm Arlanda airport, Sweden. In Proceedings of the 2009 IEEE/AIAA 28th Digital Avionics Systems Conference, Orlando, FL, USA, 23–29 October 2009; pp. 2.C.1-1–2.C.1-13. [Google Scholar] [CrossRef]
- Arnaldo Valdés, R.; Pérez Sanz, V.G.C.L. Modeling Advanced Continuous Descent Approach Procedures in Congested Airports. Int. Rev. Aerosp. Eng. 2009, 2, 304–314. [Google Scholar]
- Cao, Y.; Rathinam, S.; Sun, D. A Rescheduling Method for Conflict-free Continuous Descent Approach. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar] [CrossRef]
- Robinson, J.; Kamgarpour, M. Benefits of Continuous Descent Operations in High-Density Terminal Airspace Under Scheduling Constraints. In Proceedings of the 10th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Fort Worth, TX, USA, 13–15 September 2010. [Google Scholar]
- Weitz, L.A.; Hurtado, J.E.; Barmore, B.E.; Krishnamurthy, K. An Analysis of Merging and Spacing Operations with Continuous Descent Approaches. In Proceedings of the IEEE 24th Digital Avionics Systems Conference, Washington, DC, USA, 30 October–3 November 2005. [Google Scholar] [CrossRef]
- Wilson, I.; Hafner, F. Benefit Assessment of Using Continuous Descent Approaches at Atlanta. In Proceedings of the IEEE 24th Digital Avionics Systems Conference, Washington, DC, USA, 30 October–3 November 2005. [Google Scholar] [CrossRef]
- Khardi, S. Mathematical Model for Advanced CDA and Takeoff Procedures Minimizing Aircraft Environmental Impact. Int. Math. Forum 2010, 5, 1747–1774. [Google Scholar]
- Sáez, R.; Polishchuk, T.; Schmidt, C.; Hardell, H.; Smetanová, L.; Polishchuk, V.; Prats, X. Automated sequencing and merging with dynamic aircraft arrival routes and speed management for continuous descent operations. Transp. Res. Part C Emerg. Technol. 2021, 132, 103402. [Google Scholar] [CrossRef]
- De Jong, P.M.A.; de Gelder, N.; Verhoeven, R.P.M.; Bussink, F.J.L.; Kohrs, R.; van Paassen, R.; Mulder, M. Time and Energy Management During Descent and Approach: Batch Simulation Study. J. Aircr. 2015, 52, 190–203. [Google Scholar] [CrossRef]
- Itoh, E.; Wickramasinghe, N.K.; Hirabayashi, H.; Uejima, K.; Fukushima, S. Analyzing Feasibility of Continuous Descent Operation Following Fixed-flight Path Angle from Oceanic Route to Tokyo International Airport. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, San Diego, CA, USA, 4–8 January 2016; p. 0168. [Google Scholar] [CrossRef]
- Fricke, H.; Seiß, C.; Herrmann, R. Fuel and Energy Benchmark Analysis of Continuous Descent Operations. Air Traffic Control Q. 2015, 23, 83–108. [Google Scholar] [CrossRef]
- Zhao, W.; Alam, S.; Abbass, H.A. Evaluating ground–air network vulnerabilities in an integrated terminal maneuvering area using co-evolutionary computational red teaming. Transp. Res. Part C Emerg. Technol. 2013, 29, 32–54. [Google Scholar] [CrossRef]
- Jafari, S.; Nikolaidis, T. Thermal Management Systems for Civil Aircraft Engines: Review, Challenges and Exploring the Future. Appl. Sci. 2018, 8, 2044. [Google Scholar] [CrossRef] [Green Version]
- Lai, Y.-C.; Ting, W.O. Design and Implementation of an Optimal Energy Control System for Fixed-Wing Unmanned Aerial Vehicles. Appl. Sci. 2016, 6, 369. [Google Scholar] [CrossRef] [Green Version]
- Wubben, F.; Busink, J. Environmental Benefits of Continuous Descent Approaches at Schiphol Airport Compared with Conventional Approach Procedures. 2000. Available online: http://www.conforg.fr/internoise2000/cdrom/data/articles/000281.pdf (accessed on 21 January 2022).
- Alam, S.; Nguyen, M.H.; Abbass, H.A.; Lokan, C.; Ellejmi, M.; Kirby, S. A dynamic continuous descent approach methodology for low noise and emission. In Proceedings of the 29th Digital Avionics Systems Conference, Salt Lake City, UT, USA, 3–7 October 2010. [Google Scholar]
- Belobaba, P.; Odoni, A.; Barnhart, C. The Global Airline Industry; John Wiley & Sons: West Sussex, UK, 2015. [Google Scholar]
- Nolan, M.S. Fundamentals of Air Traffic Control; Brooks/Cole Company: Pacific Grove, CA, USA, 1999. [Google Scholar]
- FAA. Instrument Procedures Handbook; U.S. Department of Transportation: Washington, DC, USA, 2015.
- Alharbi, E. Airspace Analysis for Greener Operations: Towards More Adoptability and Predictability of Continuous Descent Approach (CDA); Mechanical and Industrial Engineering Department, New Jersey Institute of Technology: Newark, NJ, USA, 2017. [Google Scholar]
- FAA. FAA Order JO 7210.3Z—Facility Operation and Administration; U.S. Department of Transportation: Washington, DC, USA, 2015.
- De Neufville, R.; Odoni, A.R.; Belobaba, P.P.; Reynolds, T.G. Airport Systems: Planning, Design and Management; McGraw Hill Education: New York, NY, USA, 2013. [Google Scholar]
- ICAO (International Civil Aviation Organization). Documentation 4444—Procedures for Air Navigation Services: Air Traffic Management, 16th ed.; ICAO: Montreal, QC, Canada, 2016. [Google Scholar]
- DeLaura, R.A.; Ferris, R.F.; Robasky, F.M.; Troxel, S.W.; Underhill, N.K. Initial Assessment of Wind Forecasts for Airport Acceptance Rate (AAR) and Ground Delay Program (GDP) Planning; Project Reprt ATC-414; MIT Lincoln Laboratory: Lexington, MA, USA, 2014. [Google Scholar]
- Wei, P.; Chen, J.-T.; Andrisani, D.; Sun, D. Routing Flexible Traffic into Metroplex. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar]
- Ramanujam, V.; Balakrishnan, H. Data-Driven Modeling of the Airport Configuration Selection Process. IEEE Trans. Hum.-Mach. Syst. 2015, 45, 490–499. [Google Scholar] [CrossRef] [Green Version]
- Nuic, A.; Poles, D.; Mouillet, V. BADA: An advanced aircraft performance model for present and future ATM systems. Int. J. Adapt. Control Signal Process. 2010, 24, 850–866. [Google Scholar] [CrossRef]
- Nuic, A. User Manual for the Base of aircraft data (BADA) revision 3.11. Atmosphere 2010, 2010, 1. [Google Scholar]
- Hillier, F.S.; Lieberman, G.J. Introduction to Operations Research; McGraw-Hill Higher Education: New York, NY, USA, 2010. [Google Scholar]
- Shortle, J.F.; Thompson, J.M.; Gross, D.; Harris, C.M. Fundamentals of Queueing Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Taha, H.A. Operations Research: An Introduction; Pearson Education, Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Chen, H.; Solak, S. Lower Cost Arrivals for Airlines: Optimal Policies for Managing Runway Operations under Optimized Profile Descent. Prod. Oper. Manag. 2014, 24, 402–420. [Google Scholar] [CrossRef]






| Comparison Criteria | CDA | SDA |
|---|---|---|
| Operational Benefits | Reduces noise, emissions, and flight time and improves fuel efficiency. | May expedite air traffic during high volumes of arrivals. |
| Facilitation | Tactical radar vectoring, published arrival procedures (STAR), or a combination of these. | Subject to standard radar vectors with speed and altitude control. |
| Approach Type Based on Vertical Navigation | Performance path computed by the FMS using idle or near-idle thrust from the TOD point to the first waypoint. | Geometric path computed by the FMS between two constrained waypoints. |
| Sequencing and Separation of Air Traffic | Requires more spacing between aircrafts during radar vectoring and early sequencing that may require advanced sequencing tools. | Follows separation minima standards based on the sequencing method. |
| Impact on Airport Capacity | May reduce airport capacity. | No reduction in airport capacity |
| Descent Initiation | The pilot initiates descent from a TOD point that is as close to the airport as possible. | Normally, the pilot initiates descent from the TOD point at cruise altitude further from the airport than with CDA. |
| Aircraft Performance: Airspeed | Smooth speed profile, although the pilot may occasionally adjust speed at the controller’s request to account or to balance the rate of descent. | Fluctuating speed profile as the pilot decelerates before level-off and accelerates to resume descent from a level. |
| Trailing Aircraft | ||||||
|---|---|---|---|---|---|---|
| Leading Aircraft | Separation in Distance (nmi) | Separation in Time (s) | ||||
| Heavy | Medium | Light | Heavy | Medium | Light | |
| Heavy | 4 | 5 | 6 | 105 | 131 | 158 |
| Medium | 3 | 4 | 79 | 105 | ||
| Light | 3 | 79 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharbi, E.A.; Abdel-Malek, L.L.; Milne, R.J.; Wali, A.M. Analytical Model for Enhancing the Adoptability of Continuous Descent Approach at Airports. Appl. Sci. 2022, 12, 1506. https://doi.org/10.3390/app12031506
Alharbi EA, Abdel-Malek LL, Milne RJ, Wali AM. Analytical Model for Enhancing the Adoptability of Continuous Descent Approach at Airports. Applied Sciences. 2022; 12(3):1506. https://doi.org/10.3390/app12031506
Chicago/Turabian StyleAlharbi, Emad A., Layek L. Abdel-Malek, R. John Milne, and Arwa M. Wali. 2022. "Analytical Model for Enhancing the Adoptability of Continuous Descent Approach at Airports" Applied Sciences 12, no. 3: 1506. https://doi.org/10.3390/app12031506
APA StyleAlharbi, E. A., Abdel-Malek, L. L., Milne, R. J., & Wali, A. M. (2022). Analytical Model for Enhancing the Adoptability of Continuous Descent Approach at Airports. Applied Sciences, 12(3), 1506. https://doi.org/10.3390/app12031506






