Verification of 3D AE Source Location Technique in Triaxial Compression Tests Using Pencil Lead Break Sources on a Cylindrical Metal Specimen
Abstract
:1. Introduction
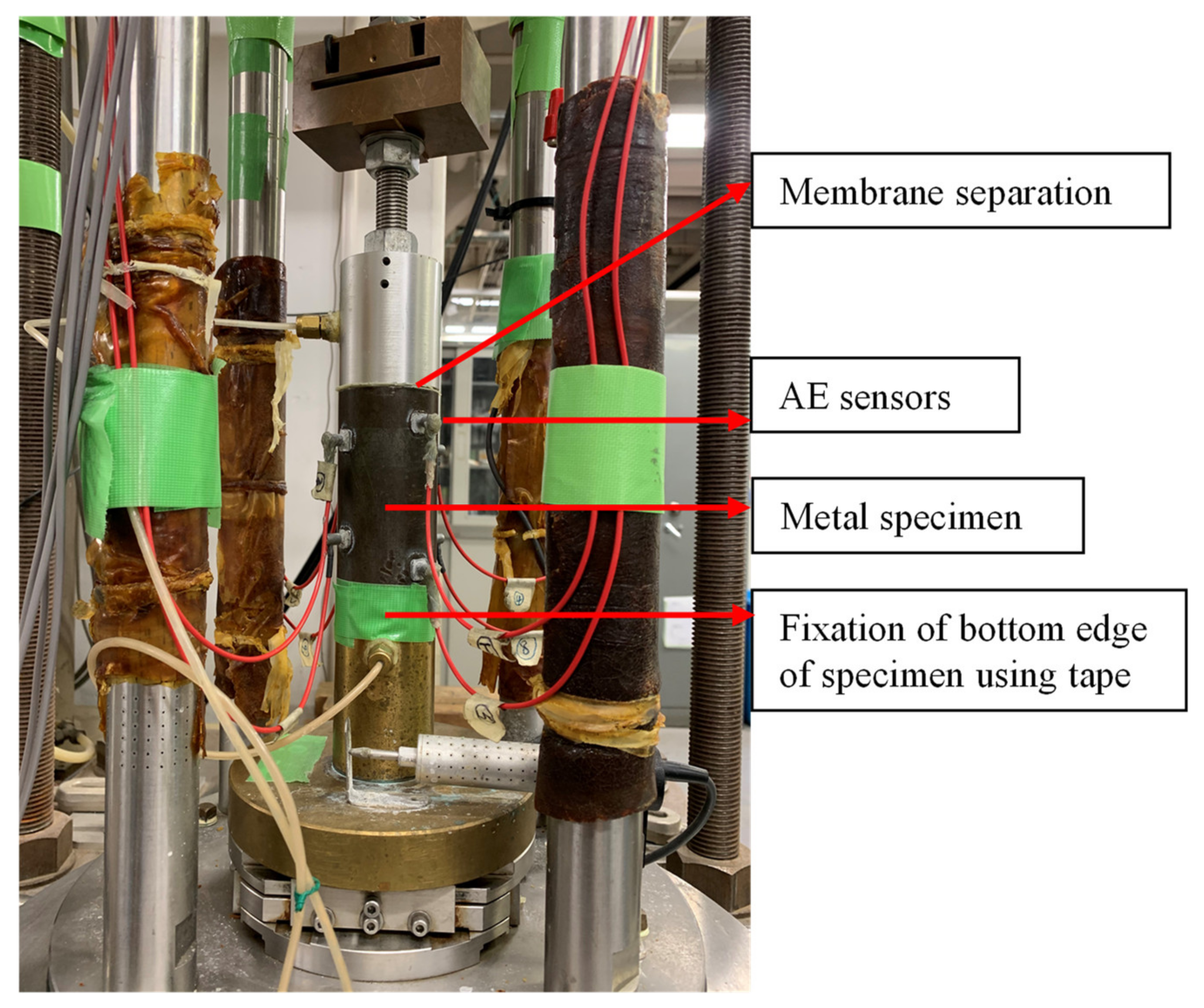
2. Experimental Design
2.1. Set-Up
2.2. Experimental Method
2.2.1. PLB Tests
2.2.2. Noise Check Test
3. Principle of the AE Source Location Technique
3.1. Time Difference of Arrival (TDOA)
3.2. P-wave Velocity Measurement for a Metal Specimen
4. Results
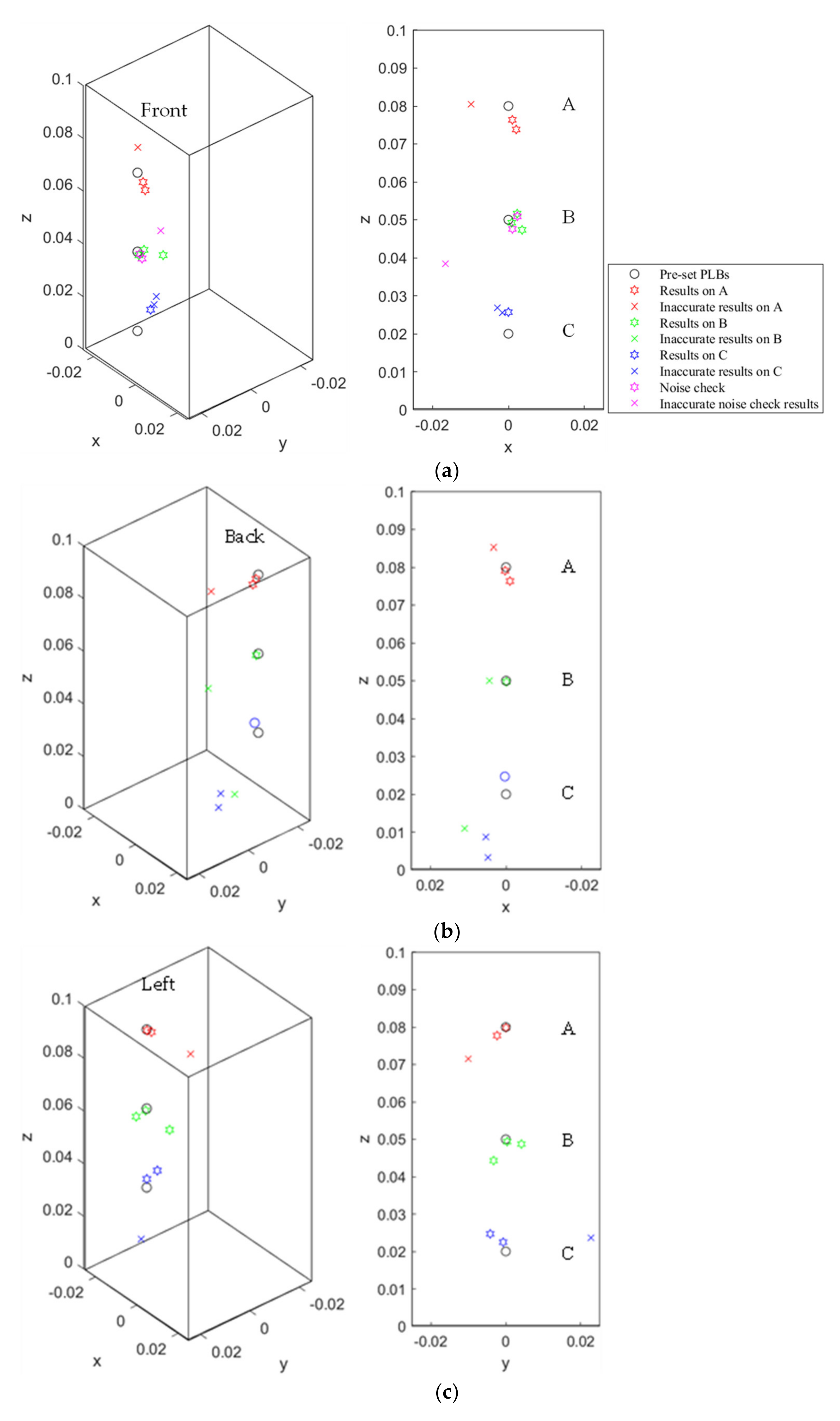
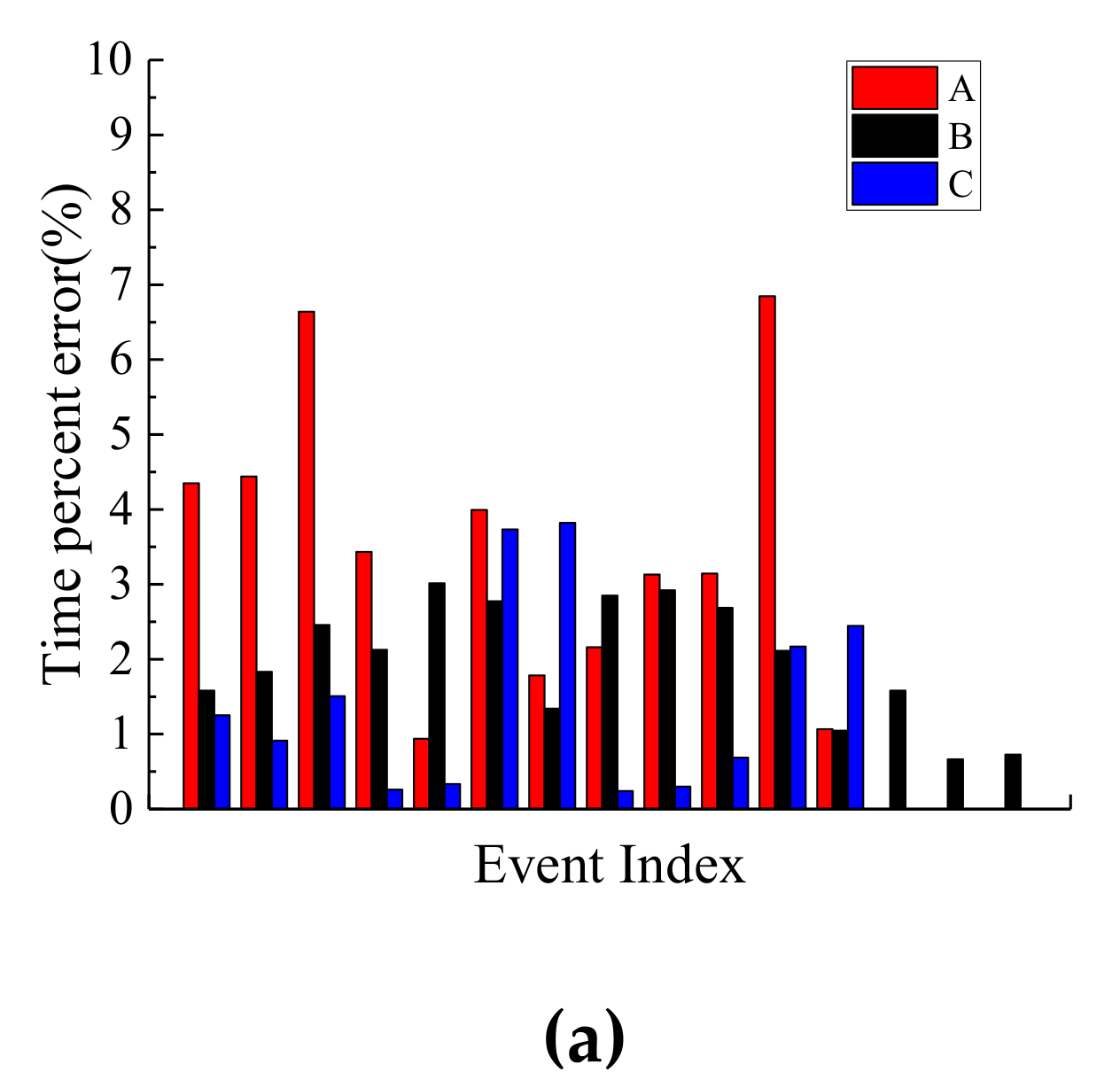
4.1. Analysis Method and Results
4.2. Noise Check Test Results
5. Conclusions
- (a)
- The validity of the developed AE source location technique was verified by PLB tests. The existing method was proven to have the least error in terms of distance from the coordinate origin but with some errors along the x, y, and z axes. When the PLB sources originate in the middle part of the specimen, the calculated result had higher accuracy, as compared to the other positions. Moreover, the calculated AE sources tended to be concentrated on the central part, with some errors.
- (b)
- The outside man-made noise, i.e., a hammer hit noise, had virtually no effect on this AE source location technique.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ASTM E1316-14e; Standard terminology for nondestructive examinations. The American Society for Testing and Materials: West Conshohocken, PA, USA, 2015.
- Hasan, A.; Alshibli, K.A. Experimental assessment of 3D particle-to-particle interaction within sheared sand using synchrotron microtomography. Géotechnique 2010, 60, 369–379. [Google Scholar] [CrossRef]
- Koseki, J. Several challenges in advanced laboratory testing of geomaterials with emphasis on unconventional types of liquefaction tests. Geomech. Energy Environ. 2021, 27, 100157. [Google Scholar] [CrossRef]
- Mao, W.; Hei, L.; Yang, Y. Advances on the acoustic emission testing for monitoring of granular soils. Measurement 2021, 185, 110110. [Google Scholar] [CrossRef]
- Ohtsu, M.; Okamoto, T.; Yuyama, S. Moment tensor analysis of acoustic emission for cracking mechanisms in concrete. ACI Struct. J. 1998, 95, 87–95. [Google Scholar]
- Kurz, J.H.; Grosse, C.U.; Reinhardt, H.W. Strategies for reliable automatic onset time picking of acoustic emissions and of ultrasound signals in concrete. Ultrasonics 2005, 43, 538–546. [Google Scholar] [CrossRef] [PubMed]
- Shah, H.R.; Weiss, J. Quantifying shrinkage cracking in fiber reinforced concrete using the ring test. Mater. Struct. 2006, 39, 887–899. [Google Scholar] [CrossRef]
- Carpinteri, A.; Xu, J.; Lacidogna, G.; Manuello, A. Reliable onset time determination and source location of acoustic emissions in concrete structures. Cem. Concr. Compos. 2012, 34, 529–537. [Google Scholar] [CrossRef]
- Cadman, J.D.; Goodman, R.E. Landslide noise. Science 1967, 158, 1182–1184. [Google Scholar] [CrossRef] [PubMed]
- Mao, W.; Aoyama, S.; Towhata, I. A study on particle breakage behavior during pile penetration process using acoustic emission source location. Geosci. Front. 2020, 11, 413–427. [Google Scholar] [CrossRef]
- Lin, W.; Mao, W.; Liu, A.; Koseki, J. Application of an acoustic emission source-tracing method to visualise shear banding in granular materials. Géotechnique 2021, 71, 925–936. [Google Scholar] [CrossRef]
- Li, X.; Lin, W.; Mao, W.; Koseki, J. Acoustic emission source location of saturated dense coral sand in triaxial compression tests. Jpn. Geotech. Soc. Spec. Publ. 2020, 8, 331–334. [Google Scholar] [CrossRef]
- Kundu, T. Acoustic source localization. Ultrasonics 2014, 54, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory; Akademiai Kiado: Budapest, Hungary, 1973; pp. 267–287. [Google Scholar]
- Ben-Israel, A. A Newton-Raphson method for the solution of systems of equations. J. Math. Anal. Appl. 1966, 15, 243–252. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, V.S.; Kuzmin, Y.O. The Influence of Fracturing of the Rocks and Model Materials on P-Wave Propagation Velocity: Experimental Studies. Izv. Phys. Solid Earth 2020, 56, 470–480. [Google Scholar] [CrossRef]
- Hamaguchi, H.; Mao, W.; Koseki, J. Model tests on application of AE tomography method to observe microscopic phenomena during pile penetration in sand. Jpn. Geotech. J. 2020, 15, 623–634. (In Japanese) [Google Scholar] [CrossRef]
- Li, X. Experimental Study on Acoustic Emission of Granular Materials under Triaxial Compression. Ph.D. Thesis, The University of Tokyo, Tokyo, Japan, 2021. [Google Scholar]





| Sensor No. | x/m | y/m | z/m |
|---|---|---|---|
| S1 | 0.018 | 0.018 | 0.085 |
| S2 | −0.018 | −0.018 | 0.085 |
| S3 | −0.018 | 0.018 | 0.075 |
| S4 | 0.018 | −0.018 | 0.075 |
| S5 | 0.018 | 0.018 | 0.015 |
| S6 | −0.018 | −0.018 | 0.015 |
| S7 | −0.018 | 0.018 | 0.025 |
| S8 | 0.018 | −0.018 | 0.025 |
| Tests | Location | x0/m | y0/m | z0/m | d0/m | |
|---|---|---|---|---|---|---|
| PLB | A | 0.000 | 0.025 | 0.080 | 0.084 | |
| Front | B | 0.000 | 0.025 | 0.050 | 0.056 | |
| C | 0.000 | 0.025 | 0.020 | 0.032 | ||
| A | 0.000 | −0.025 | 0.080 | 0.084 | ||
| Back | B | 0.000 | −0.025 | 0.050 | 0.056 | |
| C | 0.000 | −0.025 | 0.020 | 0.032 | ||
| A | −0.025 | 0.000 | 0.080 | 0.084 | ||
| Left | B | −0.025 | 0.000 | 0.050 | 0.056 | |
| C | −0.025 | 0.000 | 0.020 | 0.032 | ||
| A | 0.025 | 0.000 | 0.080 | 0.084 | ||
| Right | B | 0.025 | 0.000 | 0.050 | 0.056 | |
| C | 0.025 | 0.000 | 0.020 | 0.032 | ||
| Noise check | Front | B | 0.000 | 0.025 | 0.050 | 0.056 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Naqi, A.; Maqsood, Z.; Koseki, J. Verification of 3D AE Source Location Technique in Triaxial Compression Tests Using Pencil Lead Break Sources on a Cylindrical Metal Specimen. Appl. Sci. 2022, 12, 1603. https://doi.org/10.3390/app12031603
Li X, Naqi A, Maqsood Z, Koseki J. Verification of 3D AE Source Location Technique in Triaxial Compression Tests Using Pencil Lead Break Sources on a Cylindrical Metal Specimen. Applied Sciences. 2022; 12(3):1603. https://doi.org/10.3390/app12031603
Chicago/Turabian StyleLi, Xianfeng, Ali Naqi, Zain Maqsood, and Junichi Koseki. 2022. "Verification of 3D AE Source Location Technique in Triaxial Compression Tests Using Pencil Lead Break Sources on a Cylindrical Metal Specimen" Applied Sciences 12, no. 3: 1603. https://doi.org/10.3390/app12031603
APA StyleLi, X., Naqi, A., Maqsood, Z., & Koseki, J. (2022). Verification of 3D AE Source Location Technique in Triaxial Compression Tests Using Pencil Lead Break Sources on a Cylindrical Metal Specimen. Applied Sciences, 12(3), 1603. https://doi.org/10.3390/app12031603








