Approaching the Attosecond Frontier of Dynamics in Matter with the Concept of X-ray Chronoscopy
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
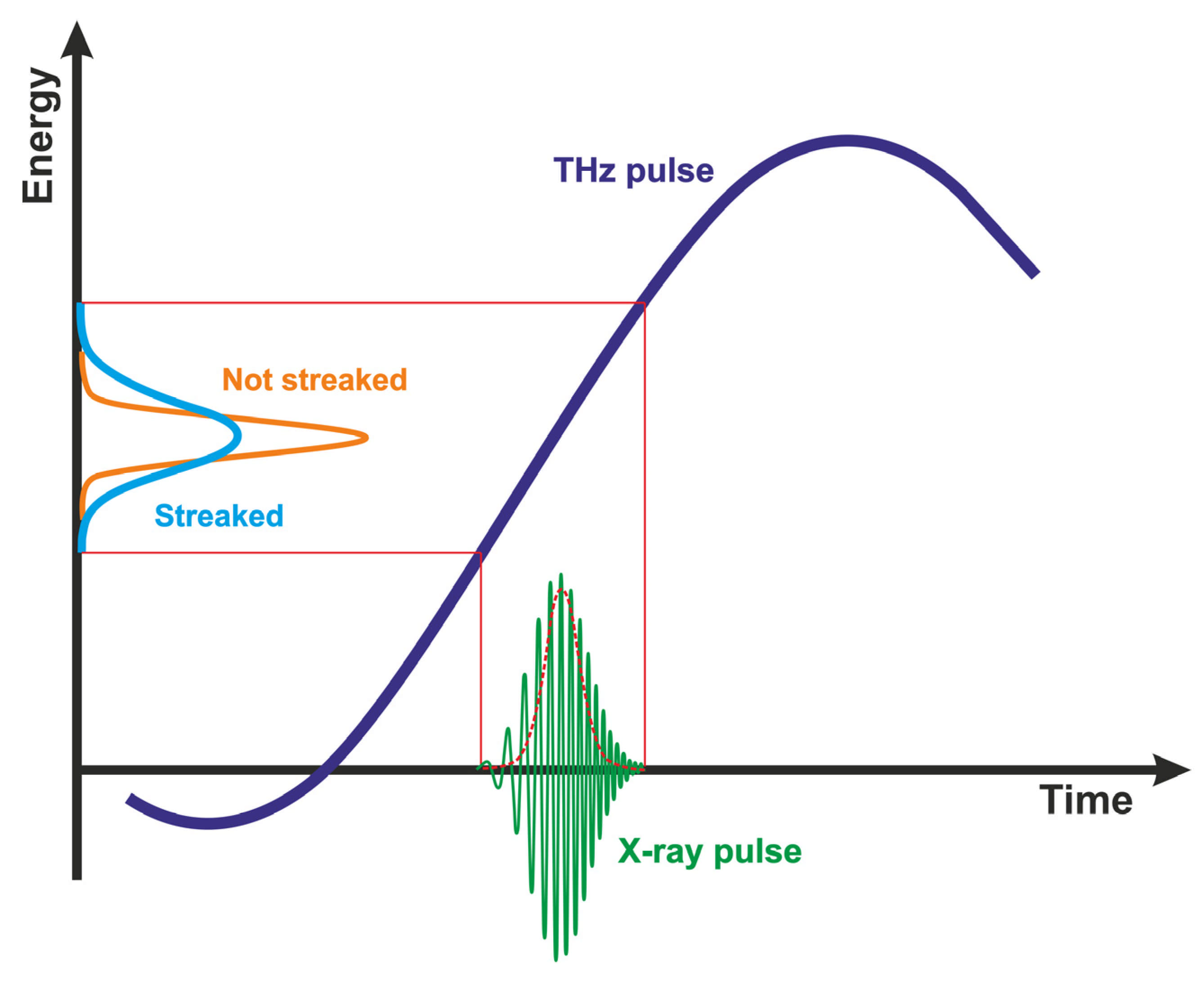
2.1. Principle of THz Streaking for Time-Dependent X-ray Pulse Analysis
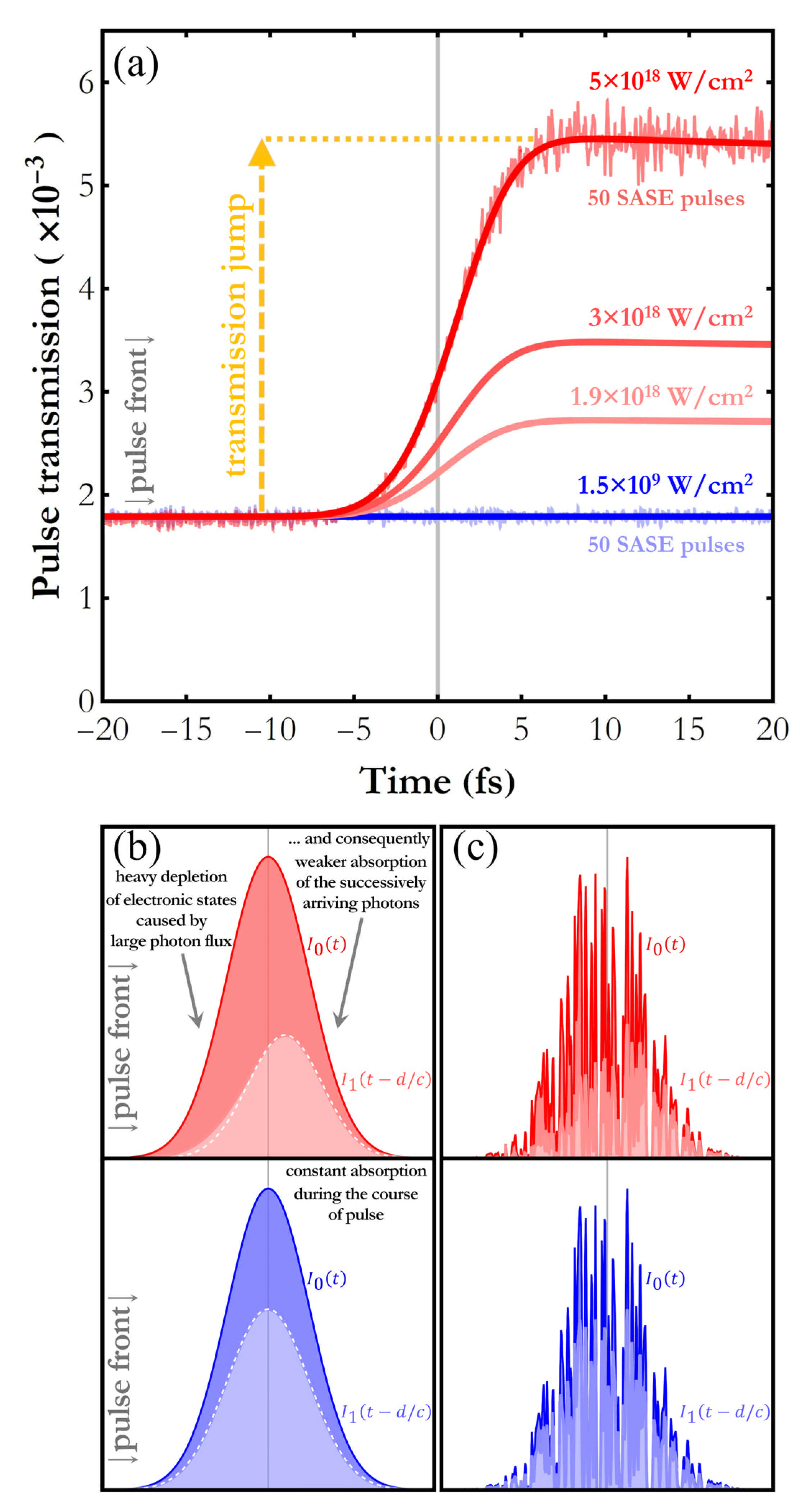
2.2. Time-Dependent Studies of Saturable Absorption at Hard X-ray Energies
3. X-ray Pulse Transmission in Saturable Absorption Conditions
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bressler, C.; Chergui, M. Molecular Structural Dynamics Probed by Ultrafast X-ray Absorption Spectroscopy. Annu. Rev. Phys. Chem. 2010, 61, 263. [Google Scholar] [CrossRef] [PubMed]
- Van Bokhoven, J.A.; Lamberti, C. X-ray Absorption and X-ray Emission Spectroscopy; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Renner, O.; Rosmej, F.B. Challenges of X-ray spectroscopy in investigations of matter under extreme conditions. Matter Radiat. Extrem. 2019, 4, 024201. [Google Scholar] [CrossRef] [Green Version]
- Milne, C. SwissFEL: The Swiss X-ray Free Electron Laser. Appl. Sci. 2017, 7, 720. [Google Scholar] [CrossRef]
- Gorgisyan, I. THz streak camera method for synchronous arrival time measurement of two-color hard X-ray FEL pulses. Opt. Express 2017, 25, 2080. [Google Scholar] [CrossRef] [PubMed]
- Inoue, I. Atomic-Scale Visualization of Ultrafast Bond Breaking in X-ray-Excited Diamond. Phys. Rev. Lett. 2021, 126, 117403. [Google Scholar] [CrossRef] [PubMed]
- McNeil, B.W.J.; Thompson, N.R. X-ray free electron lasers. Nat. Photonics 2010, 4, 814. [Google Scholar] [CrossRef]
- Amann, J. Demonstration of self-seeding in a hard-X-ray free-electron laser. Nat. Photonics 2012, 6, 693. [Google Scholar] [CrossRef]
- Huang, S.; Ding, Y.; Huang, Z.; Qiang, J. Generation of stable subfemtosecond hard X-ray pulses with optimized nonlinear bunch compression. J. Phys. Rev. ST Accel. Beams 2014, 17, 120703. [Google Scholar] [CrossRef] [Green Version]
- Duris, J. Tunable isolated attosecond X-ray pulses with gigawatt peak power from a free-electron laser. Nat. Photonics 2020, 14, 30. [Google Scholar] [CrossRef] [Green Version]
- Maroju, P.K. Attosecond pulse shaping using a seeded free-electron laser. Nature 2020, 578, 386. [Google Scholar] [CrossRef]
- Malyzhenkov, A. Single-and two-color attosecond hard x-ray free-electron laser pulses with nonlinear compression. Phys. Rev. Res. 2020, 2, 042018. [Google Scholar] [CrossRef]
- Rossi, T.P.; Erhart, P.; Kuisma, M. Hot-Carrier Generation in Plasmonic Nanoparticles: The Importance of Atomic Structure. ACS Nano 2020, 14, 9963. [Google Scholar] [CrossRef] [PubMed]
- Condon, E.U. Nuclear Motions Associated with Electron Transitions in Diatomic Molecules. Phys. Rev. 1928, 32, 858. [Google Scholar] [CrossRef]
- Bradley, D.J. Picosecond X-ray chronoscopy. Opt. Commun. 1975, 15, 231. [Google Scholar] [CrossRef]
- Cavalieri, A.L. Clocking Femtosecond X-rays. Phys. Rev. Lett. 2005, 94, 114801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frühling, U. Single-shot terahertz-field-driven X-ray streak camera. Nat. Photonics 2009, 3, 523. [Google Scholar] [CrossRef]
- Grguraš, I. Ultrafast X-ray pulse characterization at free-electron lasers. Nat. Photonics 2012, 6, 852. [Google Scholar] [CrossRef]
- Zhao, L. Terahertz Streaking of Few-Femtosecond Relativistic Electron Beams. Phys. Rev. X 2018, 8, 021061. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, N. Attosecond time–energy structure of X-ray free-electron laser pulses. Nat. Photonics 2018, 12, 215. [Google Scholar] [CrossRef]
- Wieland, M. Deriving X-ray pulse duration from center-of-energy shifts in THz-streaked ionized electron spectra. Opt. Express 2021, 29, 32739. [Google Scholar] [CrossRef]
- Hentschel, M. Attosecond metrology. Nature 2001, 414, 509. [Google Scholar] [CrossRef]
- Drescher, M.; Hentschel, M.; Kienberger, R.; Tempea, G.; Spielmann, C.; Reider, G.A.; Corkum, P.B.; Krausz, F. X-ray Pulses Approaching the Attosecond Frontier. Science 2001, 291, 1923. [Google Scholar] [CrossRef] [PubMed]
- Gorgisyan, I.; Ischebeck, R.; Prat, E.; Reiche, S.; Rivkin, L.; Juranić, P. Simulation of FEL pulse length calculation with THz streaking method. J. Synchrotron Radiat. 2016, 23, 643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coffee, R.N.; Cryan, J.P.; Duris, J.; Helml, W.; Li, S.; Marinelli, A. Development of ultrafast capabilities for X-ray free-electron lasers at the linac coherent light source. Philos. Trans. R. Soc. A 2019, 377, 20180386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Helml, W. Measuring the temporal structure of few-femtosecond free-electron laser X-ray pulses directly in the time domain. Nat. Photonics 2014, 8, 950. [Google Scholar] [CrossRef]
- Juranić, P.N. High-precision X-ray FEL pulse arrival time measurements at SACLA by a THz streak camera with Xe clusters. Opt. Express 2014, 22, 30004. [Google Scholar] [CrossRef] [Green Version]
- Frühling, U. Light-field streaking for FELs. J. Phys. B 2011, 44, 243001. [Google Scholar] [CrossRef]
- Gaumnitz, T.; Jain, A.; Pertot, Y.; Huppert, M.; Jordan, I.; Ardana-Lamas, F.; Wörner, H.J. Streaking of 43-attosecond soft-X-ray pulses generated by a passively CEP-stable mid-infrared driver. Opt. Express 2017, 25, 27506. [Google Scholar] [CrossRef]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Emma, P. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641. [Google Scholar] [CrossRef]
- Haynes, D.C. Clocking Auger electrons. Nat. Phys. 2021, 17, 512. [Google Scholar] [CrossRef]
- Young, L. Femtosecond electronic response of atoms to ultra-intense X-rays. Nature 2010, 466, 56. [Google Scholar] [CrossRef] [PubMed]
- Vinko, S.M. Investigation of femtosecond collisional ionization rates in a solid-density aluminium plasma. Nat. Commun. 2015, 6, 6397. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tamasaku, K. X-ray two-photon absorption competing against single and sequential multiphoton processes. Nat. Photonics 2014, 8, 313. [Google Scholar] [CrossRef]
- Beye, M.; Schreck, S.; Sorgenfrei, F.; Trabant, C.; Pontius, N.; Schüßler-Langeheine, C.; Wurth, W.; Föhlisch, A. Stimulated X-ray emission for materials science. Nature 2013, 501, 191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glover, T.E. Controlling X-rays with light. Nat. Phys. 2010, 6, 69. [Google Scholar] [CrossRef]
- Yoneda, H. Saturable absorption of intense hard X-rays in iron. Nat. Commun. 2014, 5, 5080. [Google Scholar] [CrossRef]
- Rackstraw, D.S. Saturable Absorption of an X-ray Free-Electron-Laser Heated Solid-Density Aluminum Plasma. Phys. Rev. Lett. 2015, 114, 015003. [Google Scholar] [CrossRef] [Green Version]
- Nagler, B. Turning solid aluminium transparent by intense soft X-ray photoionization. Nat. Phys. 2009, 5, 693. [Google Scholar]
- Bostedt, C. Experiments at FLASH. Nucl. Instr. Meth. Phys. Res. 2009, 601, 108. [Google Scholar] [CrossRef]
- Kayser, Y. Core-level nonlinear spectroscopy triggered by stochastic X-ray pulses. Nat. Commun. 2019, 10, 4761. [Google Scholar] [CrossRef]
- Parnis, J.M.; Oldham, K.B. Beyond the Beer–Lambert law: The dependence of absorbance on time in photochemistry. J. Photochem. Photobiol. A 2013, 267, 6. [Google Scholar] [CrossRef]
- Schoonjans, T.; Brunetti, A.; Golosio, B.; del Rio, M.S.; Solé, V.A.; Ferrero, C.; Vincze, L. The xraylib library for X-ray–matter interactions. Recent developments. Spectrochim. Acta Part B 2011, 66, 776. [Google Scholar] [CrossRef]
- Li, K.; Labeye, M.; Ho, P.J.; Gaarde, M.B.; Young, L. Resonant propagation of x rays from the linear to the nonlinear regime. Phys. Rev. A 2020, 102, 053113. [Google Scholar] [CrossRef]
- Sun, Y.-P.; Liu, J.-C.; Wang, C.-K.; Gel’mukhanov, F. Propagation of a strong x-ray pulse: Pulse compression, stimulated Raman scattering, amplified spontaneous emission, lasing without inversion, and four-wave mixing. Phys. Rev. A 2010, 81, 013812. [Google Scholar] [CrossRef]
- Durbin, S.M. X-ray pump optical probe cross-correlation study of GaAs. Nat. Photonics 2012, 6, 111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sumida, D.S.; Fan, T.Y. Effect of radiation trapping on fluorescence lifetime and emission cross section measurements in solid-state laser media. Opt. Lett. 1994, 19, 1343. [Google Scholar] [CrossRef]
- Błachucki, W. Inception of electronic damage of matter by photon-driven post-ionization mechanisms. Struct. Dyn. 2019, 6, 024901. [Google Scholar] [CrossRef]
- Jurek, Z.; Son, S.-K.; Ziaja, B.; Santra, R. XMDYN and XATOM: Versatile simulation tools for quantitative modeling of X-ray free-electron laser induced dynamics of matter. J. Appl. Cryst. 2016, 49, 1048. [Google Scholar] [CrossRef]
- Szlachetko, J. Establishing nonlinearity thresholds with ultraintense X-ray pulses. Sci. Rep. 2016, 6, 33292. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Błachucki, W.; Wach, A.; Czapla-Masztafiak, J.; Delcey, M.; Arrell, C.; Fanselow, R.; Juranić, P.; Lundberg, M.; Milne, C.; Sá, J.; et al. Approaching the Attosecond Frontier of Dynamics in Matter with the Concept of X-ray Chronoscopy. Appl. Sci. 2022, 12, 1721. https://doi.org/10.3390/app12031721
Błachucki W, Wach A, Czapla-Masztafiak J, Delcey M, Arrell C, Fanselow R, Juranić P, Lundberg M, Milne C, Sá J, et al. Approaching the Attosecond Frontier of Dynamics in Matter with the Concept of X-ray Chronoscopy. Applied Sciences. 2022; 12(3):1721. https://doi.org/10.3390/app12031721
Chicago/Turabian StyleBłachucki, Wojciech, Anna Wach, Joanna Czapla-Masztafiak, Mickaël Delcey, Christopher Arrell, Rafał Fanselow, Pavle Juranić, Marcus Lundberg, Christopher Milne, Jacinto Sá, and et al. 2022. "Approaching the Attosecond Frontier of Dynamics in Matter with the Concept of X-ray Chronoscopy" Applied Sciences 12, no. 3: 1721. https://doi.org/10.3390/app12031721








