Atrial Fibrillation and Anterior Cerebral Artery Absence Reduce Cerebral Perfusion: A De Novo Hemodynamic Model †
Abstract
:1. Introduction
2. Methods
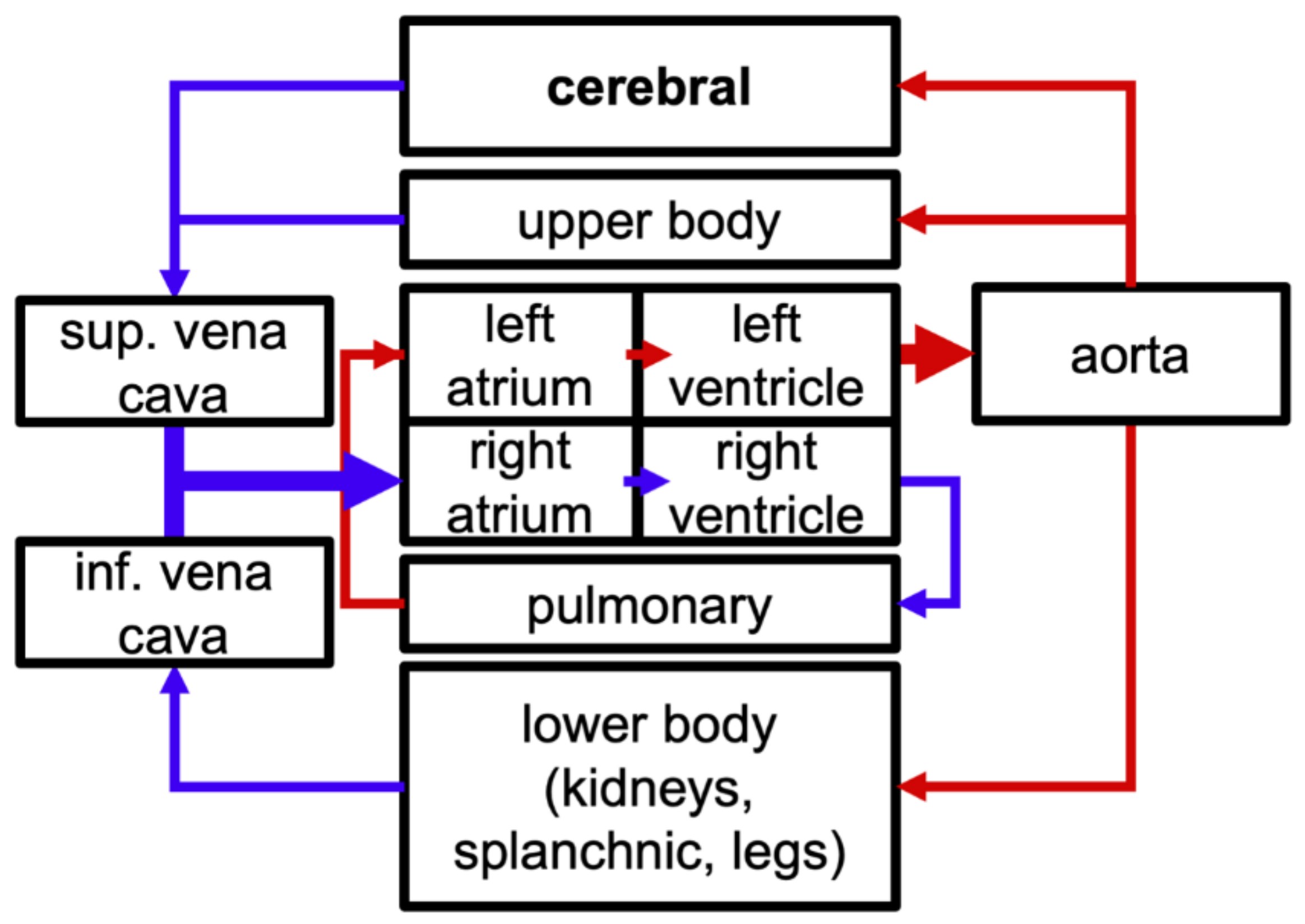
2.1. Model Components
2.2. Atrial Fibrillation
2.3. Computational Methods
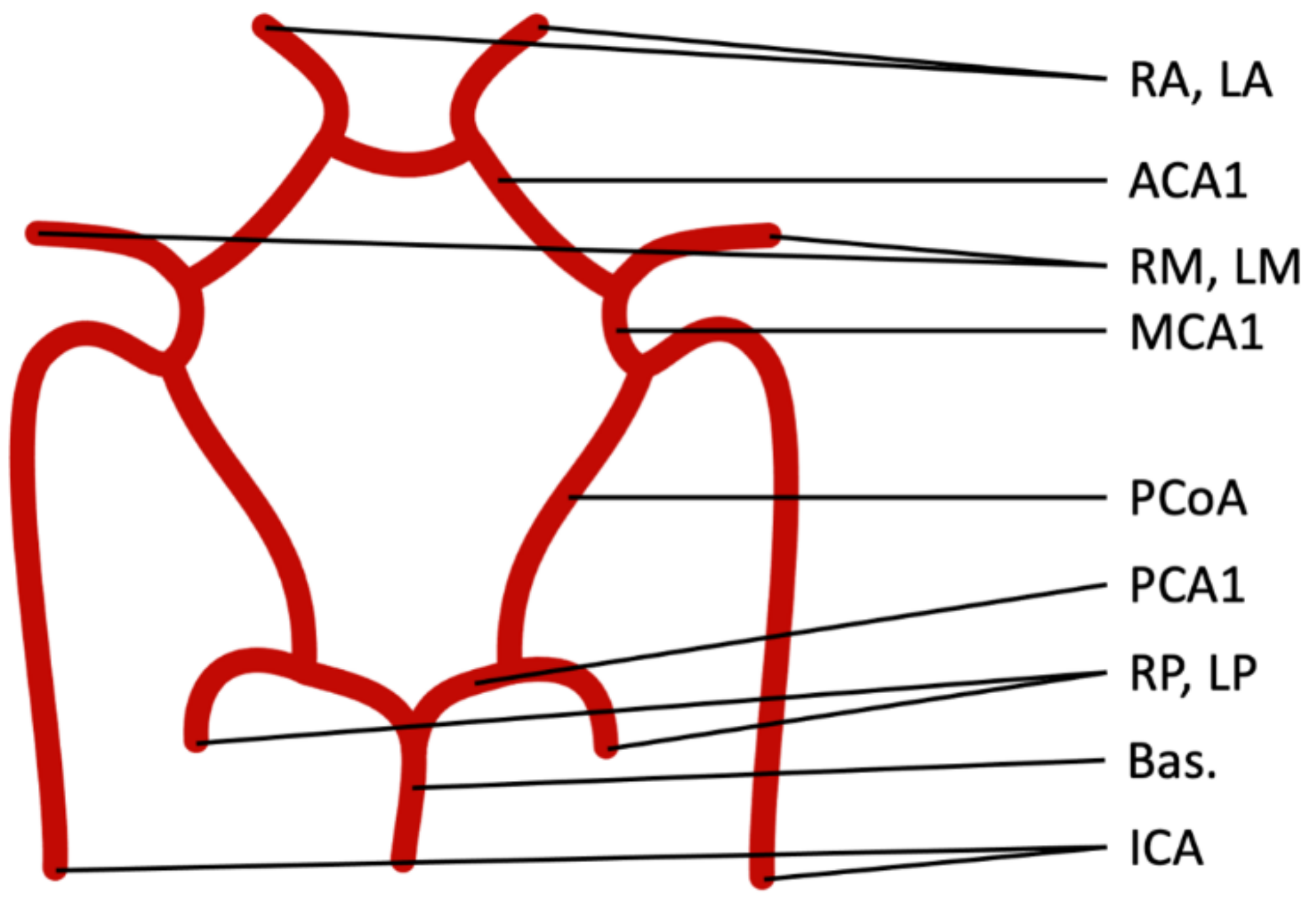
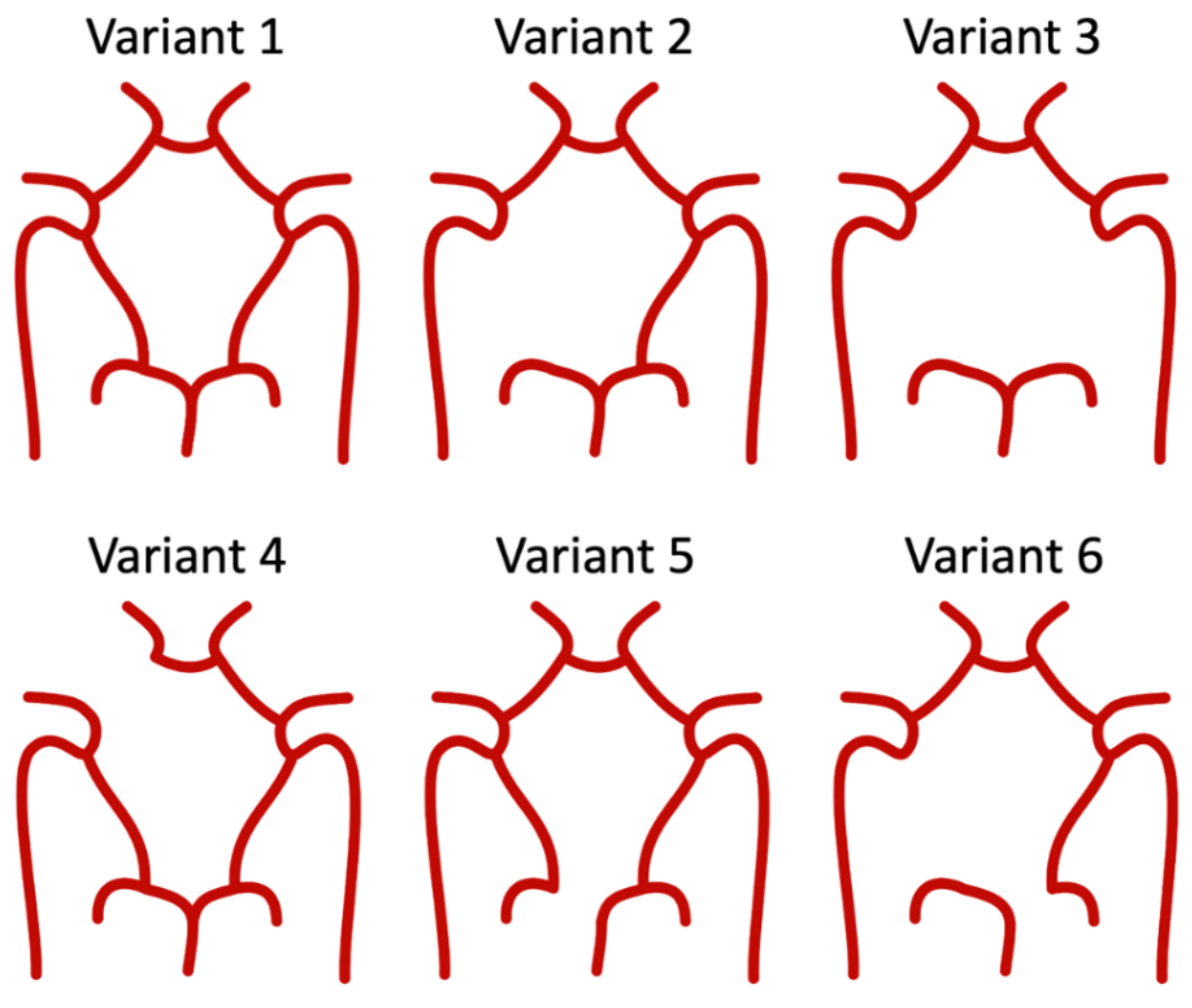
2.4. Hemodynamic Differences in CoW Variants
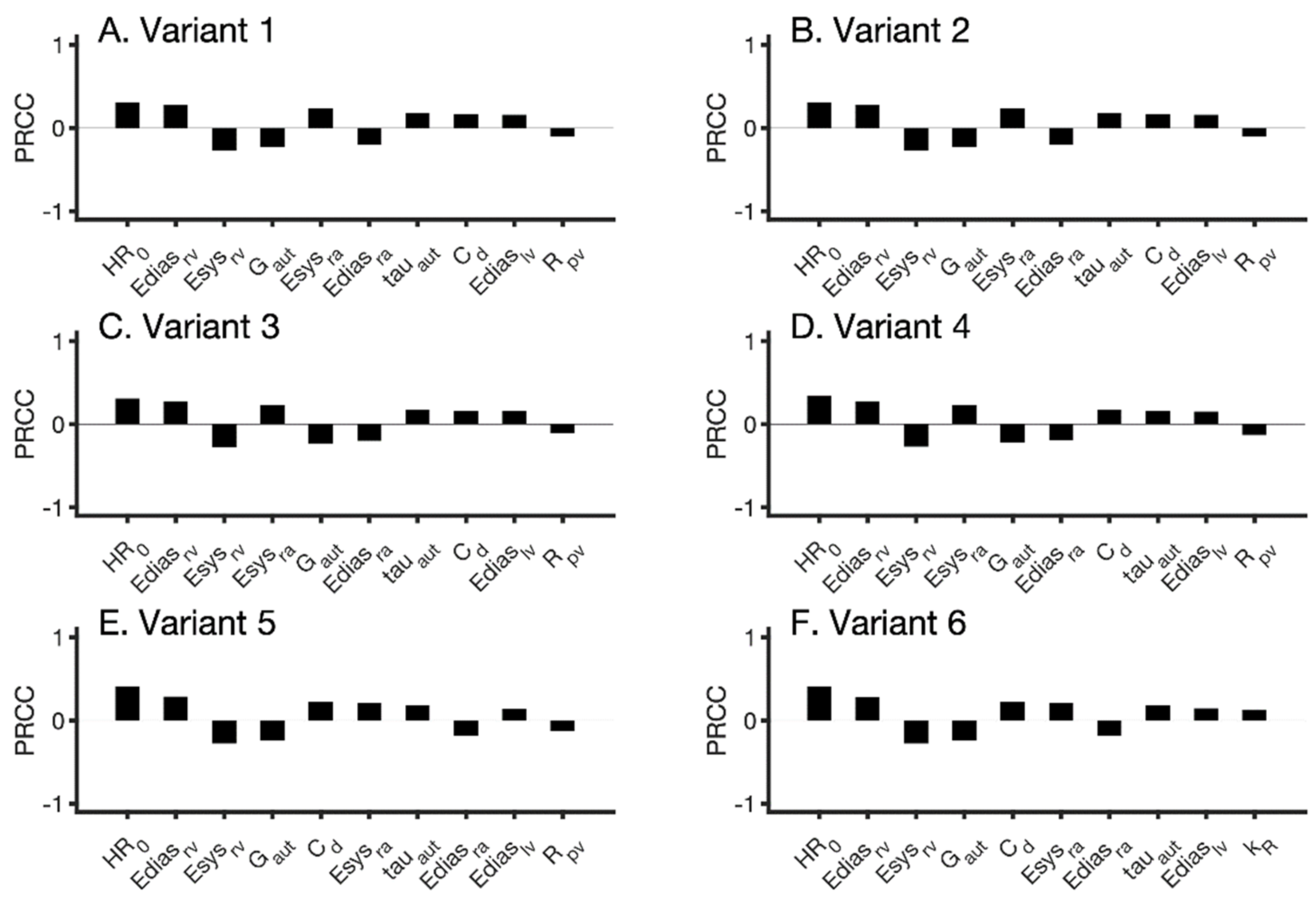
2.5. Sensitivity Analysis
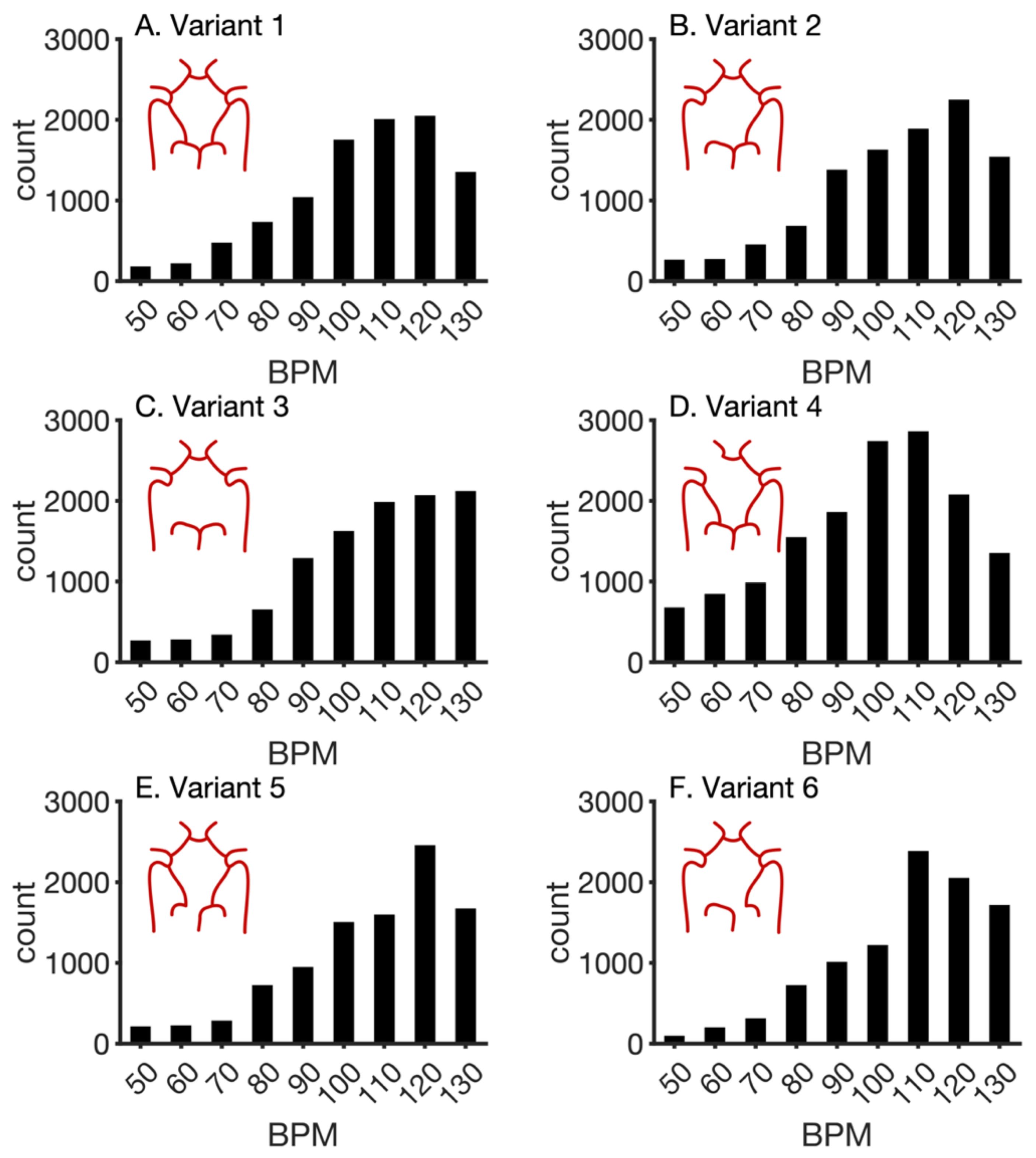
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hunter, T.J.; Joseph, J.J.; Anazodo, U.; Kharche, S.R.; McIntyre, C.W.; Goldman, D. Computational modelling of the role of atrial fibrillation on cerebral blood perfusion. In Functional Imaging and Modeling of the Heart; Ennis, D.B., Perotti, L.E., Wang, V.Y., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 12738 LNCS, pp. 679–686. [Google Scholar]
- De Bruijn, R.F.A.G.; Heeringa, J.; Wolters, F.J.; Franco, O.H.; Stricker, B.H.C.; Hofman, A.; Koudstaal, P.J.; Ikram, M.A. Association Between Atrial Fibrillation and Dementia in the General Population. JAMA Neurol. 2015, 72, 1288–1294. [Google Scholar] [CrossRef] [PubMed]
- Gardarsdottir, M.; Sigurdsson, S.; Aspelund, T.; Rokita, H.; Launer, L.J.; Gudnason, V.; Arnar, D.O. Atrial fibrillation is associated with decreased total cerebral blood flow and brain perfusion. EP Eur. 2018, 20, 1252–1258. [Google Scholar] [CrossRef] [PubMed]
- Anselmino, M.; Scarsoglio, S.; Saglietto, A.; Gaita, F.; Ridolfi, L. Transient cerebral hypoperfusion and hypertensive events during atrial fibrillation: A plausible mechanism for cognitive impairment. Sci. Rep. 2016, 6, 8635. [Google Scholar] [CrossRef]
- Anazodo, U.C.; Shoemaker, J.K.; Suskin, N.; St. Lawrence, K.S. An investigation of changes in regional gray matter volume in cardiovascular disease patients, pre and post cardiovascular rehabilitation. Neuroimage 2013, 3, 388. [Google Scholar] [CrossRef] [Green Version]
- Steinman, D.A.; Poepping, T.L.; Tambasco, M.; Rankin, R.N.; Holdsworth, D.W. Flow Patterns at the Stenosed Carotid Bifurcation: Effect of Concentric versus Eccentric Stenosis. Ann. Biomed. Eng. 2000, 28, 415–423. [Google Scholar] [CrossRef] [Green Version]
- Alastruey, J.; Parker, K.H.; Peiró, J.; Byrd, S.M.; Sherwin, S.J. Modelling the circle of Willis to assess the effects of anatomical variations and occlusions on cerebral flows. J. Biomech. 2007, 40, 1794–1805. [Google Scholar] [CrossRef] [PubMed]
- Antiga, L.; Piccinelli, M.; Botti, L.; Ene-Iordache, B.; Remuzzi, A.; Steinman, D.A. An image-based modeling framework for patient-specific computational hemodynamics. Med. Biol. Eng. Comput. 2008, 46, 1097–1112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lan, H.; Updegrove, A.; Wilson, N.M.; Maher, G.D.; Shadden, S.C.; Marsden, A.L. A Re-Engineered Software Interface and Workflow for the Open-Source SimVascular Cardiovascular Modeling Package. J. Biomech. Eng. 2018, 140, 024501. [Google Scholar] [CrossRef] [Green Version]
- Altamirano-Diaz, L.; Kassay, A.D.; Serajelahi, B.; McIntyre, C.W.; Filler, G.; Kharche, S.R. Arterial Hypertension and Unusual Ascending Aortic Dilatation in a Neonate with Acute Kidney Injury: Mechanistic Computer Modeling. Front. Physiol. 2019, 10, 1391. [Google Scholar] [CrossRef]
- Joseph, J.J.; Hunter, T.J.; Sun, C.; Goldman, D.; Kharche, S.R.; McIntyre, C.W. Using a Human Circulation Mathematical Model to Simulate the Effects of Hemodialysis and Therapeutic Hypothermia. Appl. Sci. 2021, 12, 307. [Google Scholar] [CrossRef]
- Saglietto, A.; Scarsoglio, S.; Ridolfi, L.; Gaita, F.; Anselmino, M. Higher ventricular rate during atrial fibrillation relates to increased cerebral hypoperfusions and hypertensive events. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Van Gelder, I.C.; Groenveld, H.F.; Crijns, H.J.G.M.; Tuininga, Y.S.; Tijssen, J.G.P.; Alings, A.M.; Hillege, H.L.; Bergsma-Kadijk, J.A.; Cornel, J.H.; Kamp, O.; et al. Lenient versus Strict Rate Control in Patients with Atrial Fibrillation. N. Engl. J. Med. 2010, 362, 1363–1373. [Google Scholar] [CrossRef] [Green Version]
- Heldt, T. Computational Models of Cardiovascular Response to Orthostatic Stress. Ph.D. Dissertation, Massacheusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Lin, J.; Ngwompo, R.F.; Tilley, D.G. Development of a cardiopulmonary mathematical model incorporating a baro-chemoreceptor reflex control system. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2012, 226, 787–803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ursino, M.; Giannessi, M. A model of cerebrovascular reactivity including the circle of Willis and cortical anastomoses. Ann. Biomed. Eng. 2010, 38, 955–974. [Google Scholar] [CrossRef]
- Hennig, T.; Maass, P.; Hayano, J.; Heinrichs, S.; Hennig, T.; Maass, P.; Hayano, J.; Heinrichs, S. Exponential Distribution of Long Heart Beat Intervals During Atrial Fibrillation and Their Relevance for White Noise Behaviour in Power Spectrum. J. Biol. Phys. 2006, 32, 383–392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scarsoglio, S.; Guala, A.; Camporeale, C.; Ridolfi, L. Impact of atrial fibrillation on the cardiovascular system through a lumped-parameter approach. Med. Biol. Eng. Comput. 2014, 52, 905–920. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anselmino, M.; Scarsoglio, S.; Saglietto, A.; Gaita, F.; Ridolfi, L. A computational study on the relation between resting heart rate and atrial fibrillation hemodynamics under exercise. PLoS ONE 2017, 12, e0169967. [Google Scholar] [CrossRef] [PubMed]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Tange, O. GNU Parallel 2018. Available online: https://zenodo.org/record/1146014#.YgJqUerMKUl (accessed on 31 December 2021). [CrossRef]
- Pianelli, M.; Scaglione, M.; Anselmino, M.; Caponi, D.; Garcia, P.; Cesarani, F.; Toso, E.; Raimondo, C.; Halimi, F.; Leclercq, J.F.; et al. Delaying cardioversion following 4-week anticoagulation in case of persistent atrial fibrillation after a transcatheter ablation procedure to reduce silent cerebral thromboembolism: A single-center pilot study. J. Cardiovasc. Med. 2011, 12, 785–789. [Google Scholar] [CrossRef]
- Kharche, S.R.; Mironova, G.Y.; Goldman, D.; McIntyre, C.W.; Welsh, D.G. Sensitivity analysis of a smooth muscle cell electrophysiological model. In Functional Imaging and Modeling of the Heart; Ennis, D.B., Perotti, L.E., Wang, V.Y., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 12738 LNCS, pp. 540–550. [Google Scholar]
- Matsumoto, M.; Nishimura, T. Mersenne twister. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef] [Green Version]
- Malone, B.P.; Minansy, B.; Brungard, C. Some methods to improve the utility of conditioned Latin hypercube sampling. PeerJ 2019, 7, e6451. [Google Scholar] [CrossRef] [PubMed]
- Kharche, S.; Lüdtke, N.; Panzeri, S.; Zhang, H. A global sensitivity index for biophysically detailed cardiac cell models: A computational approach. In Functional Imaging and Modeling of the Heart; Ayache, N., Delingette, H., Sermesant, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 366–375. [Google Scholar]
- Hamby, D.M. A comparison of sensitivity analysis techniques. Health Phys. 1995, 68, 195–204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zarrinkoob, L.; Ambarki, K.; Wåhlin, A.; Birgander, R.; Eklund, A.; Malm, J. Blood flow distribution in cerebral arteries. J. Cereb. Blood Flow Metab. 2015, 35, 648–654. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joseph, J.J.; Lee, T.-Y.; Goldman, D.; McIntyre, C.W.; Kharche, S.R. The role of extra-coronary vascular conditions that affect coronary fractional flow reserve estimation. In Functional Imaging and Modeling of the Heart; Ennis, D.B., Perotti, L.E., Wang, V.Y., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 12738 LNCS, pp. 595–604. [Google Scholar]
- Grande Gutierrez, N. Hemodynamic Based Thrombotic Risk Stratification in Kawasaki Disease Patients with Coronary Artery Aneurysms. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, 2019. [Google Scholar]



| Parameter | Description | Baseline Value |
|---|---|---|
| Whole-body circulation | ||
| HR0 | Intrinsic heart rate | 75 bpm |
| Ediasrv | Right ventricular diastolic elastance. | 0.07 (mmHg ml−1) |
| Esysrv | Right ventricular systolic elastance. | 1.3 (mmHg ml−1) |
| Esysra | Right atrial systolic elastance. | 0.74 (mmHg ml−1) |
| Ediasra | Right atrial diastolic elastance. | 0.3 (mmHg ml−1) |
| Ediaslv | Left ventricular diastolic elastance. | 0.13 (mmHg ml−1) |
| Rpv | Pulmonary venous resistance. | 0.01 (mmHg s ml−1) |
| Cerebral circulation | ||
| Gaut | Autoregulation function gain. | 0.9 (unitless) |
| tauaut | Autoregulation function time constant. | 20 (s) |
| Cd | Distal cerebral arterial compliance. | 200 (ml mmHg−1) |
| kR | Distal cerebral resistance scaling term. | 13,100 (mmHg−3 s ml−1) |
| Output Name | Output Values | |
|---|---|---|
| NSR | AF | |
| Pa,sys (mmHg) | 117.44 ± 21.35 | 119.51 ± 17.45 |
| Pa,dias (mmHg) | 77.81 ± 15.85 | 78.95 ± 16.64 |
| QACA (ml s−1) | 0.99 ± 0.37 | 0.95 ± 0.45 |
| QMCA (ml s−1) | 3.68 ± 1.21 | 3.64 ± 1.37 |
| QPCA (ml s−1) | 1.47 ± 0.52 | 1.44 ± 0.59 |
| CBF (ml s−1) | 12.54 ± 4.24 | 12.31 ± 4.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hunter, T.J.; Joseph, J.J.; Anazodo, U.; Kharche, S.R.; McIntyre, C.W.; Goldman, D. Atrial Fibrillation and Anterior Cerebral Artery Absence Reduce Cerebral Perfusion: A De Novo Hemodynamic Model. Appl. Sci. 2022, 12, 1750. https://doi.org/10.3390/app12031750
Hunter TJ, Joseph JJ, Anazodo U, Kharche SR, McIntyre CW, Goldman D. Atrial Fibrillation and Anterior Cerebral Artery Absence Reduce Cerebral Perfusion: A De Novo Hemodynamic Model. Applied Sciences. 2022; 12(3):1750. https://doi.org/10.3390/app12031750
Chicago/Turabian StyleHunter, Timothy J., Jermiah J. Joseph, Udunna Anazodo, Sanjay R. Kharche, Christopher W. McIntyre, and Daniel Goldman. 2022. "Atrial Fibrillation and Anterior Cerebral Artery Absence Reduce Cerebral Perfusion: A De Novo Hemodynamic Model" Applied Sciences 12, no. 3: 1750. https://doi.org/10.3390/app12031750
APA StyleHunter, T. J., Joseph, J. J., Anazodo, U., Kharche, S. R., McIntyre, C. W., & Goldman, D. (2022). Atrial Fibrillation and Anterior Cerebral Artery Absence Reduce Cerebral Perfusion: A De Novo Hemodynamic Model. Applied Sciences, 12(3), 1750. https://doi.org/10.3390/app12031750







