A Two-Step Surface Reconstruction Method Using Signed Marching Cubes
Abstract
:1. Introduction
2. Method
2.1. Radial Basis Functions Interpolation
2.2. Signed Fast Multipole Method
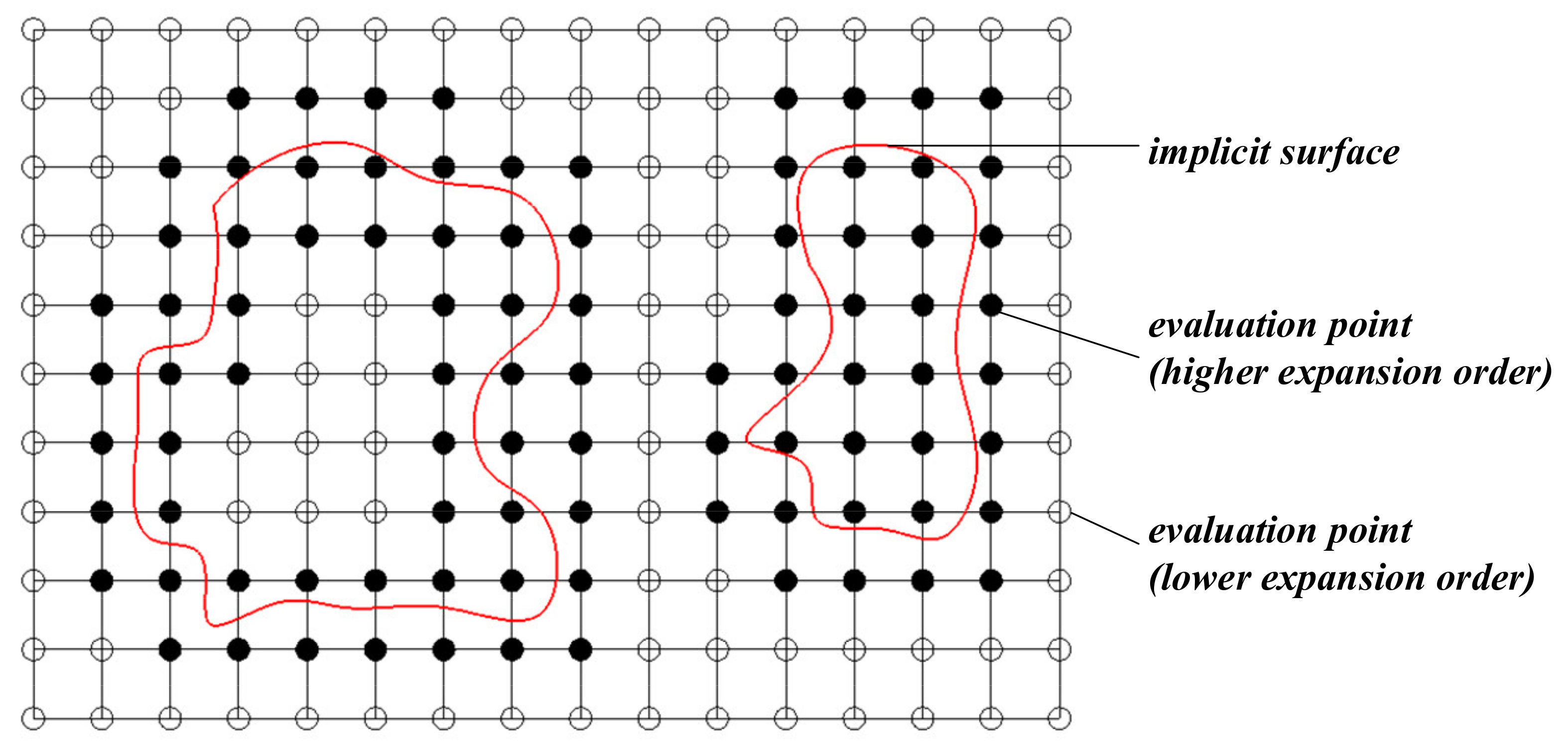
2.3. Two-Step Surface Reconstruction Method
3. Results
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cowan, E.J.; Beatson, R.K.; Ross, H.J.; Fright, W.R.; McLennan, T.J.; Evans, T.R.; Carr, J.C.; Lane, R.G.; Bright, D.V.; Gillman, A.J.; et al. Practical implicit geological modelling. In Proceedings of the 5th International Mining Geology Conference, Bendigo, Australia, 17–19 November 2003; pp. 89–99. [Google Scholar]
- Rolo, R.M.; Radtke, R.; Costa, J.F.C.L. Signed distance function implicit geologic modeling. REM Int. Eng. J. 2017, 70, 221–229. [Google Scholar] [CrossRef] [Green Version]
- Martin, R.; Boisvert, J.B. Iterative refinement of implicit boundary models for improved geological feature reproduction. Comput. Geosci. 2017, 109, 1–15. [Google Scholar] [CrossRef]
- Goncalves, I.G.; Kumaira, S.; Guadagnin, F. A machine learning approach to the potential-field method for implicit modeling of geological structures. Comput. Geosci. 2017, 103, 173–182. [Google Scholar] [CrossRef]
- Hillier, M.; de Kemp, E.; Schetselaar, E. Implicitly Modelled Stratigraphic Surfaces using Generalized Interpolation. In Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM), Rhodes, Greece, 23–29 September 2015. [Google Scholar]
- Pellerin, J.; Levy, B.; Caumon, G.; Botella, A. Automatic surface remeshing of 3D structural models at specified resolution: A method based on Voronoi diagrams. Comput. Geosci. 2014, 62, 103–116. [Google Scholar] [CrossRef] [Green Version]
- Clausolles, N.; Collon, P.; Caumon, G. Generating variable shapes of salt geobodies from seismic images and prior geological knowledge. Interpretation 2019, 7, T829–T841. [Google Scholar] [CrossRef]
- Sherbrooke, E.C.; Patrikalakis, N.M. Computation of solution of non-linear polynomial systems. Comput. Aided Geom. Des. 1993, 5, 379–405. [Google Scholar] [CrossRef] [Green Version]
- Mourrain, B.; Pavone, J.-P. Subdivision methods for solving polynomial equations. J. Symb. Comput. 2009, 3, 292–306. [Google Scholar] [CrossRef] [Green Version]
- Fuhrmann, S.; Kazhdan, M.; Goesele, M. Accurate Isosurface Interpolation with Hermite Data. In Proceedings of the 2015 International Conference on 3D Vision (ENS), Lyon, France, 19–22 October 2015; pp. 256–263. [Google Scholar]
- Cuno, A.; Esperanca, C.; Oliveira, A.; Cavalcanti, P.R. Fast polygonization of variational implicit surfaces. In Proceedings of the 17th Brazilian Symposium on Computer Graphics and Image Processing/2nd Ibero-American Symposium on Computer Graphics, Curitiba, Brazil, 17–20 October 2004; pp. 258–265. [Google Scholar]
- Fournier, M. Automatic Grid Resolution and Efficient Triangulation of Implicit Vector Field. Siam J. Imaging Sci. 2010, 3, 564–577. [Google Scholar] [CrossRef]
- Engwer, C.; Nuessing, A. Geometric Reconstruction of Implicitly Defined Surfaces and Domains with Topological Guarantees. Acm Trans. Math. Softw. 2017, 44, 1–20. [Google Scholar] [CrossRef]
- Congote, J.; Moreno, A.; Barandiaran, I.; Barandiaran, J.; Posada, J.; Ruiz, O. Marching cubes in an unsigned distance field for surface reconstruction from unorganized point sets. In Proceedings of the 5th International Conference on Computer Graphics Theory and Applications (GRAPP 2010), Univ Angers, Angers, France, 17–21 May 2010; pp. 143–147. [Google Scholar]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. In Seminal Graphics: Pioneering Efforts that Shaped the Field; Association for Computing Machinery: New York, NY, USA, 1998; pp. 347–353. [Google Scholar]
- Lorensen, W.E. History of the Marching Cubes Algorithm. IEEE Comput. Graph. Appl. 2020, 40, 8–15. [Google Scholar] [CrossRef]
- Zhao, T.; Alliez, P.; Boubekeur, T.; Buse, L.; Thiery, J.-M. Progressive Discrete Domains for Implicit Surface Reconstruction. Comput. Graph. Forum 2021, 40, 143–156. [Google Scholar] [CrossRef]
- D’Otreppe, V.; Boman, R.; Ponthot, J.-P. Generating smooth surface meshes from multi-region medical images. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 642–660. [Google Scholar] [CrossRef]
- Peiro, J.; Sherwin, S.J.; Giordana, S. Automatic reconstruction of a patient-specific high-order surface representation and its application to mesh generation for CFD calculations. Med. Biol. Eng. Comput. 2008, 46, 1069–1083. [Google Scholar] [CrossRef]
- Jamin, C.; Alliez, P.; Yvinec, M.; Boissonnat, J.-D. CGALmesh: A Generic Framework for Delaunay Mesh Generation. Acm Trans. Math. Softw. 2015, 41, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Garanzha, V.A.; Kudryavtseva, L.N. Generation of Three-Dimensional Delaunay Meshes from Weakly Structured and Inconsistent Data. Comput. Math. Math. Phys. 2012, 52, 427–447. [Google Scholar] [CrossRef]
- Dietrich, C.A.; Scheidegger, C.E.; Schreiner, J.; Comba, J.L.D.; Nedel, L.P.; Silva, C.T. Edge Transformations for Improving Mesh Quality of Marching Cubes. IEEE Trans. Vis. Comput. Graph. 2009, 15, 150–159. [Google Scholar] [CrossRef] [Green Version]
- Raman, S.; Wenger, R. Quality isosurface mesh generation using an extended marching cubes lookup table. Comput. Graph. Forum 2008, 27, 791–798. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Han, C.-Y.; Wee, W.G. On surface reconstruction: A priority driven approach. Comput. -Aided Des. 2009, 41, 626–640. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Plantinga, S.; Vegter, G. Certified meshing of Radial Basis Function based isosurfaces. Vis. Comput. 2012, 28, 445–462. [Google Scholar] [CrossRef] [Green Version]
- Zhong, D.; Zhang, J.; Wang, L. Fast Implicit Surface Reconstruction for the Radial Basis Functions Interpolant. Appl. Sci. 2019, 9, 5335. [Google Scholar] [CrossRef] [Green Version]
- Muneeswaran, V.; Rajasekaran, M.P. Performance Evaluation of Radial Basis Function Networks Based on Tree Seed Algorithm. In Proceedings of the IEEE International Conference on Circuit, Power and Computing Technologies (ICCPCT), Kanyakumari, India, 18–19 March 2016. [Google Scholar]
- Macedo, I.; Gois, J.P.; Velho, L. Hermite Radial Basis Functions Implicits. Comput. Graph. Forum 2011, 30, 27–42. [Google Scholar] [CrossRef]
- Li, X.; Micchelli, C.A. Approximation by radial bases and neural networks. Numer. Algorithms 2000, 25, 241–262. [Google Scholar] [CrossRef]
- Buchau, A.; Rucker, W.M. Preconditioned fast adaptive multipole boundary-element method. IEEE Trans. Magn. 2002, 38, 461–464. [Google Scholar] [CrossRef]
- Buchau, A.; Hafla, W.; Groh, F.; Rucker, W.M. Fast multipole boundary element method for the solution of 3D electrostatic field problems. In Proceedings of the 26th World Conference on Boundary Elements and other Mesh Reduction Methods, Bologna, Italy, 19–21 April 2004; pp. 369–379. [Google Scholar]
- Of, G. An efficient algebraic multigrid preconditioner for a fast multipole boundary element method. Computing 2008, 82, 139–155. [Google Scholar] [CrossRef]
- Kurzak, J.; Mirkovic, D.; Pettitt, B.M.; Johnsson, S.L. Automatic generation of FFT for translations of multipole expansions in spherical harmonics. Int. J. High Perform. Comput. Appl. 2008, 22, 219–230. [Google Scholar] [CrossRef] [Green Version]
- Koc, S.; Song, J.M.; Chew, W.C. Error analysis for the numerical evaluation of the diagonal forms of the scalar spherical addition theorem. Siam J. Numer. Anal. 1999, 36, 906–921. [Google Scholar] [CrossRef] [Green Version]
- Powell, M. The theory of radial basis function approximation in 1990. In Advances in Numerical Analysis; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Sertel, K.; Volakis, J.L. Multilevel fast multipole method solution of volume integral equations using parametric geometry modeling. IEEE Trans. Antennas Propag. 2004, 52, 1686–1692. [Google Scholar] [CrossRef]
- Fong, W.; Darve, E. The black-box fast multipole method. J. Comput. Phys. 2009, 228, 8712–8725. [Google Scholar] [CrossRef]






| p | Ne | ||
|---|---|---|---|
| 10,000 | 100,000 | 1,000,000 | |
| 12 | 2.93 × 10−9 | 3.92 × 10−9 | 3.83 × 10−9 |
| 11 | 2.03 × 10−8 | 2.16 × 10−8 | 2.64 × 10−8 |
| 10 | 1.29 × 10−7 | 1.91 × 10−7 | 1.56 × 10−7 |
| 9 | 9.30 × 10−7 | 1.38 × 10−6 | 1.54 × 10−6 |
| 8 | 8.27 × 10−6 | 8.18 × 10−6 | 9.25 × 10−6 |
| 7 | 1.04 × 10−4 | 8.60 × 10−5 | 8.80 × 10−5 |
| 6 | 9.92 × 10−4 | 8.61 × 10−4 | 1.06 × 10−3 |
| 5 | 7.60 × 10−1 | 9.20 × 10−1 | 7.40 × 10−1 |
| p | Ne | ||
|---|---|---|---|
| 10,000 | 100,000 | 1,000,000 | |
| 12 | 3.92 × 10−9 | 5.94 × 10−9 | 5.65 × 10−9 |
| 11 | 3.17 × 10−8 | 4.64 × 10−8 | 3.54 × 10−8 |
| 10 | 2.88 × 10−7 | 3.32 × 10−7 | 4.54 × 10−7 |
| 9 | 4.83 × 10−6 | 5.50 × 10−6 | 4.47 × 10−6 |
| 8 | 2.94 × 10−5 | 2.50 × 10−5 | 2.55 × 10−5 |
| 7 | 1.66 × 10−4 | 1.65 × 10−4 | 1.58 × 10−4 |
| 6 | 3.24 × 10−3 | 2.62 × 10−3 | 3.02 × 10−3 |
| 5 | 9.88 × 10−3 | 7.78 × 10−3 | 1.00 × 10−2 |
| Models | N | |||||
|---|---|---|---|---|---|---|
| Figure 6a | 10,704 | 5 | 2.75 × 107 | 2.75 × 107 | 2.65 × 105 | 0.96% |
| 10 | 3.45 × 106 | 3.45 × 106 | 6.61 × 104 | 1.92% | ||
| 20 | 4.37 × 105 | 4.37 × 105 | 1.59 × 104 | 3.64% | ||
| Figure 6b | 6999 | 2 | 1.57 × 105 | 1.57 × 105 | 1.59 × 104 | 10.07% |
| 5 | 1.09 × 104 | 1.09 × 104 | 2.45 × 103 | 22.53% | ||
| 8 | 2.65 × 103 | 2.65 × 103 | 9.14 × 102 | 34.54% | ||
| Figure 6c | 3735 | 10 | 1.20 × 106 | 1.20 × 106 | 7.05 × 104 | 5.88% |
| 15 | 3.62 × 105 | 3.62 × 105 | 3.12 × 104 | 8.61% | ||
| 30 | 4.65 × 104 | 4.65 × 104 | 7.51 × 103 | 16.16% | ||
| Figure 6d | 1767 | 5 | 2.15 × 106 | 2.15 × 106 | 1.01 × 105 | 4.69% |
| 10 | 2.72 × 105 | 2.72 × 105 | 2.52 × 104 | 9.26% | ||
| 20 | 3.44 × 104 | 3.44 × 104 | 6.13 × 103 | 17.81% | ||
| Figure 6e | 3747 | 5 | 4.13 × 105 | 4.13 × 105 | 3.01 × 104 | 7.28% |
| 10 | 5.32 × 104 | 5.32 × 104 | 6.67 × 103 | 12.54% | ||
| 15 | 1.64 × 104 | 1.64 × 104 | 2.65 × 103 | 16.18% | ||
| Figure 6f | 3735 | 5 | 8.93 × 105 | 8.93 × 105 | 2.27 × 104 | 2.55% |
| 10 | 1.16 × 105 | 1.16 × 105 | 4.96 × 103 | 4.29% | ||
| 12 | 6.70 × 104 | 6.70 × 104 | 3.37 × 103 | 5.03% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhong, D.; Wang, L. A Two-Step Surface Reconstruction Method Using Signed Marching Cubes. Appl. Sci. 2022, 12, 1792. https://doi.org/10.3390/app12041792
Zhang J, Zhong D, Wang L. A Two-Step Surface Reconstruction Method Using Signed Marching Cubes. Applied Sciences. 2022; 12(4):1792. https://doi.org/10.3390/app12041792
Chicago/Turabian StyleZhang, Ju, Deyun Zhong, and Liguan Wang. 2022. "A Two-Step Surface Reconstruction Method Using Signed Marching Cubes" Applied Sciences 12, no. 4: 1792. https://doi.org/10.3390/app12041792
APA StyleZhang, J., Zhong, D., & Wang, L. (2022). A Two-Step Surface Reconstruction Method Using Signed Marching Cubes. Applied Sciences, 12(4), 1792. https://doi.org/10.3390/app12041792







