Anisotropic Effective Elastic Properties for Multi-Dimensional Fractured Models

Featured Application

The proposed method in the paper has significance in calculating the effective elastic properties of multi-dimensional fracture models and interaction mechanisms.

Abstract

The size, distribution, and orientation of fractures are generally multiscale and multi-dimensional in nature, leading to complex anisotropic characteristics. Theoretical or semi-analytical methods to determine the effective elastic properties depend on several assumptions, including the absence of the stress interaction and idealized fractures. On the basis of finite-element models, we conduct numerical oscillatory relaxation tests for determining the effective elastic properties of fractured rocks. The numerical approach for calculating equivalent stiffness tensors in two-dimensions is compared to the theoretical models for different fracture densities. Due to fracture interactions at high fracture densities, the suggested model makes a physical prediction. The effective elastic properties obtained from the application to a real fractured model, established from an outcrop, obviously disperse at different frequencies, which can be used to investigate fracture interactions and dynamic stress disturbances. The algorithm is extended to three-dimensional cases and also validated by using conventional effective medium theories. It is found that the fracture density obviously impacts the effective anisotropy properties, and the proposed method gives a reasonable prediction for high-fracture density. This work is significant because it enables the calculation of effective elastic properties of multi-dimensional fractured models and the fracture interaction mechanism.

1. Introduction

Cracks are the key factor in determining the deformability of rocks, properties of fluid movement, and tectonic history. We need to enhance ways for detecting and characterizing fractures. Due to the fact that natural fractures in geological formations frequently have a complicated shape and distribution, their interactions cause the complex anisotropic features of effective elastic properties. Thus, knowing the natural fractures’ elastic behavior is essential for interpreting and predicting seismic responses in terms of rock properties and enables us to bridge the gaps in the spatial and temporal scale [1,2]. The overall effective elastic coefficient of a fractured rock is frequently composed of the stiffness tensor of the background host rock and fractures [3], which attract considerable attention because of their contribution to the elastic property. The theoretical medium models (TMM) have been widely applied to calculate the effective elastic properties of fractured rocks analytically [4,5,6,7,8]. However, due to the dilute assumption of fracture densities, these models ignore fracture interactions. The second-order Hudson’s model takes into account the pair-wise interaction among cracks [9]. Chapman [10] proposed an equivalent-media theory that was sensitive to fracture length and studied the frequency-dependent anisotropy of fractured porous rocks using the squirt flow mechanism. Guo et al. [11] united linear-slip theory and anisotropic Gassmann equations to analyze equivalent stiffness coefficients. The self-consistent approximation (SCA) and differential effective medium (DEM) were applied to control the concentration of fractures to investigate the consequences of fracture interactions [12,13,14]. Jakobsen et al. [15] applied the T-matrix method to characterize the pores–fracture interaction. Meanwhile, the idealization and oversimplification of real rock severely limit the utility of theoretical or semi-analytical models.

In an attempt to circumvent certain assumptions inherent in effective medium theories [16,17,18,19,20,21,22,23], numerical simulations have been extensively applied for studying the elastic properties of complex rocks. Numerical methods can be used to characterize real fractures with different shapes, sizes, partial interconnections, and intersections, as well as provide independent validation of theoretical methods and laboratory measurements as an efficient means of determining their general applicability. Masson et al. [24] used numerical experiments to analyze the correlation between material structure and seismic attenuation anisotropy in porous media. Rubino et al. [25,26] employed 2D numerical oscillatory relaxation experiments to study the frequency-dependent effective stiffness matrix using the least-squares optimal approach. The method is used to characterize the frequency- and incidence-angle- dependent attenuation and velocity dispersion in cracked porous media for the P wave [27,28,29] and P-SV wave [30]. Jian et al. [31] expanded Rubino’s relaxation tests to a three-dimensional (3D) case for computing the equivalent stiffness matrix.

We apply Rubino’s numerical method to explore the elastic and seismic anisotropy characteristics of real fractures in this paper. Particular attention should be paid to the anisotropy variation of fractures generated by different frequencies and crack densities. The following is the outline. In the first part of the technique, we demonstrate the novel form of Rubino’s 2D algorithm using three oscillatory relaxation tests with different fracture densities. Additionally, six oscillatory relaxation tests are used to spread Rubino’s algorithm to three-dimensional fractured media. Following that, the effective stiffness of the 2D numerical method is compared with that of the classical Hudson’s model and the Eshelby–Cheng model with different fracture densities. Then, 3D fractured media are compared with TMM in elastic responses to different fracture densities. Three 2D fracture models are presented to illustrate the primary mechanism of stress interreaction and their effects on the entire effective elasticity. Finally, the method is applied to a real fractured medium generated from an outcrop, demonstrating that frequency influences the stiffness tensor anisotropy. The anisotropic effective elastic properties have been discovered to have a direct effect on fracture density. This study aims to analyze the anisotropic effective elastic properties of multi-dimensional (2D and 3D) fracture models at different fracture densities.

2. Methodology

This section mainly introduces the methodology of studying anisotropic effective elastic properties of multi-dimensional fracture models. The entire modeling methodology is illustrated in Figure 1. First, we demonstrate the simulation equations and three oscillatory relaxation tests. Next, the 2D equivalent stiffness matrix is calculated by solving the simulation equations using the finite-element method (FEM). Following that, the effective stiffness of the 2D numerical method is compared with that of Hudson’s model and the Eshelby–Cheng model with different fracture densities. Additionally, six oscillatory relaxation tests are used to spread to three-dimensional fractured media.

2.1. Anisotropic Effective Elastic Properties for 2D Fractured Models

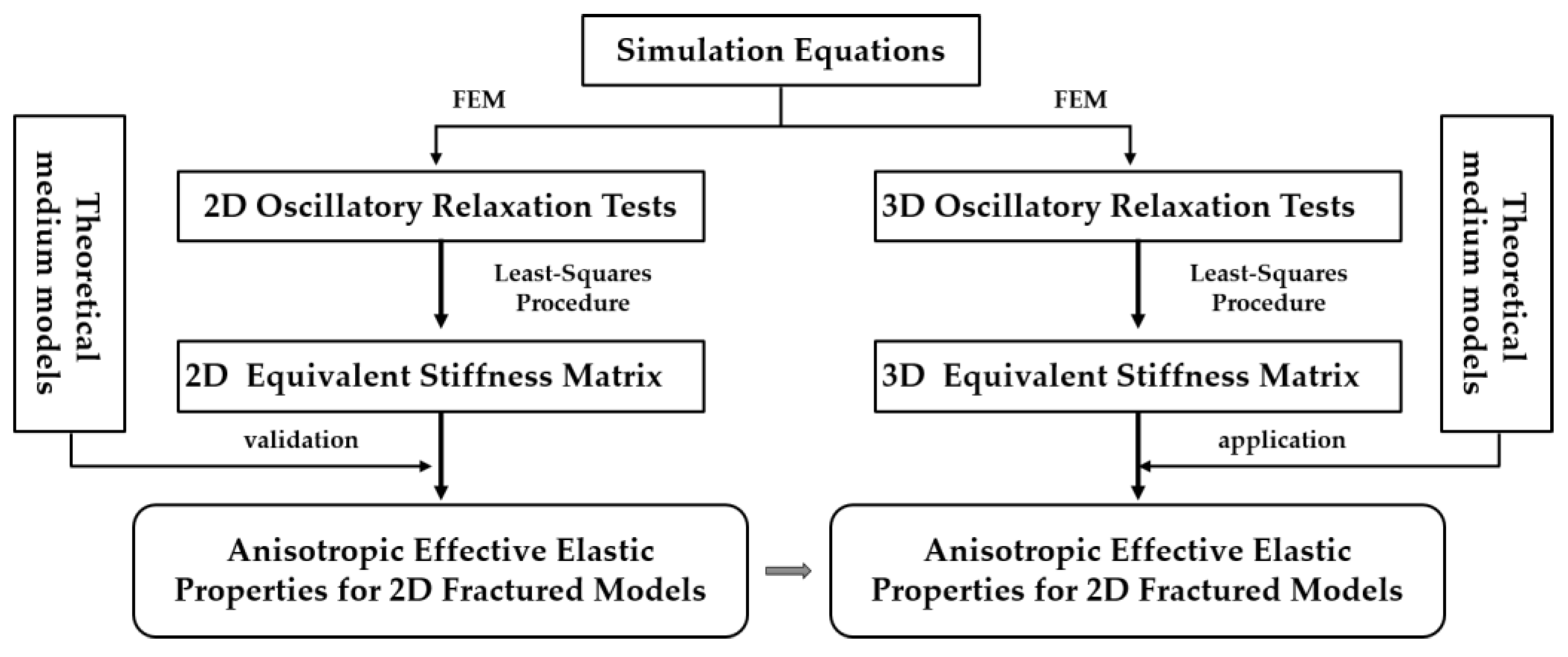
2.1.1. Simulation Equations

We have to use numerical methods because the TMM for predicting the elasticity of multi-scale real intersecting cracks is limited by its own assumptions. We here apply Rubino’s 2D numeric upscaling procedure in an attempt to pattern natural cracks. Biot’s consolidation system of equations in the space-frequency domain is expressed as [26].

$$\nabla ·\mathit{\sigma }=\mathbf{0},$$

(1)

$$\nabla P_f=-i\omega \frac{\eta }{\kappa }\mathbf{W}.$$

(2)

where $\nabla$ represents the spatial derivatives; $\mathit{\sigma }\equiv \left({\sigma }_{ij}\right)$ is total stress tensor; P_f denotes the fluid pressure, $\kappa$ the permeability and $\omega$ the angular frequency; and W denotes average relative fluid–solid displacement tensor. $\eta$ indicates the viscosity of pore fluid. Thus, the stress–strain relationships [32] state that

$${\sigma }_{ij}=2\mu e_{ij}+{\delta }_{ij}\left({\lambda }_u\nabla \cdot U-\alpha N\xi \right),$$

(3)

$$e_{ij}=\frac{1}{2}\left(\partial U_i/\partial x_j+\partial U_j/\partial x_x\right),$$

(4)

$$P_f=-\alpha N\nabla \cdot U+N\xi ,$$

(5)

where δ_ij is the Kronecker delta, and $\xi =-\nabla \cdot W$ denotes the measurement of the local variations in the fluid content. U is the solid displacement vector; e_ij denotes strain tensor; and $\mu$ denotes the shear modulus of the rock with saturated water, which is equivalent to that of a dry frame ${\mu }_m$. The Biot constant $\alpha$, fluid storage coefficient N, and Lame parameter ${\lambda }_u$ are expressed as

$$N={\left(\frac{\alpha -\varphi }{K_s}+\frac{\varphi }{K_f}\right)}^{-1},$$

(6)

$${\lambda }_u=K_m+{\alpha }^{2}N-\frac{2}{3}{\mu }_m,$$

(7)

$$\alpha =1-\frac{K_m}{K_s},$$

(8)

where $\varphi$ is the porosity; K_s denotes the bulk moduli of solid grains; K_m is the bulk moduli of dry frame; and K_f denotes the bulk moduli of fluid phase.

Substituting Equation (7) to Equation (3) and taking Equation (5), we have a new form of 2D/3D total stress tensor in porous fractured medium

$${\sigma }_{ij}=2\mu e_{ij}+{\delta }_{ij}\left(\lambda \nabla \cdot U-\alpha P_f\right),$$

(9)

where $\lambda =K_m-2{\mu }_m/3$. When $i,j=x,y$, it is the 2D case. When $i,j=x,y,z$, it is the 3D case. Substituting $\xi =-\nabla \cdot W$ into Equation (5), we have

$$P_f=-\alpha N\nabla \cdot U-N\nabla \cdot W,$$

(10)

Taking Equations (2) and (10), the P_f is given by

$$P_f=-\alpha N\nabla \cdot U-N\nabla \cdot \left(\frac{ik}{\eta \omega }\nabla P_f\right).$$

(11)

In order to obtain the solid displacement fields, we conduct relaxation tests and solve Equations (1) and (11) with the corresponding boundary conditions applying the finite-element method (FEM).

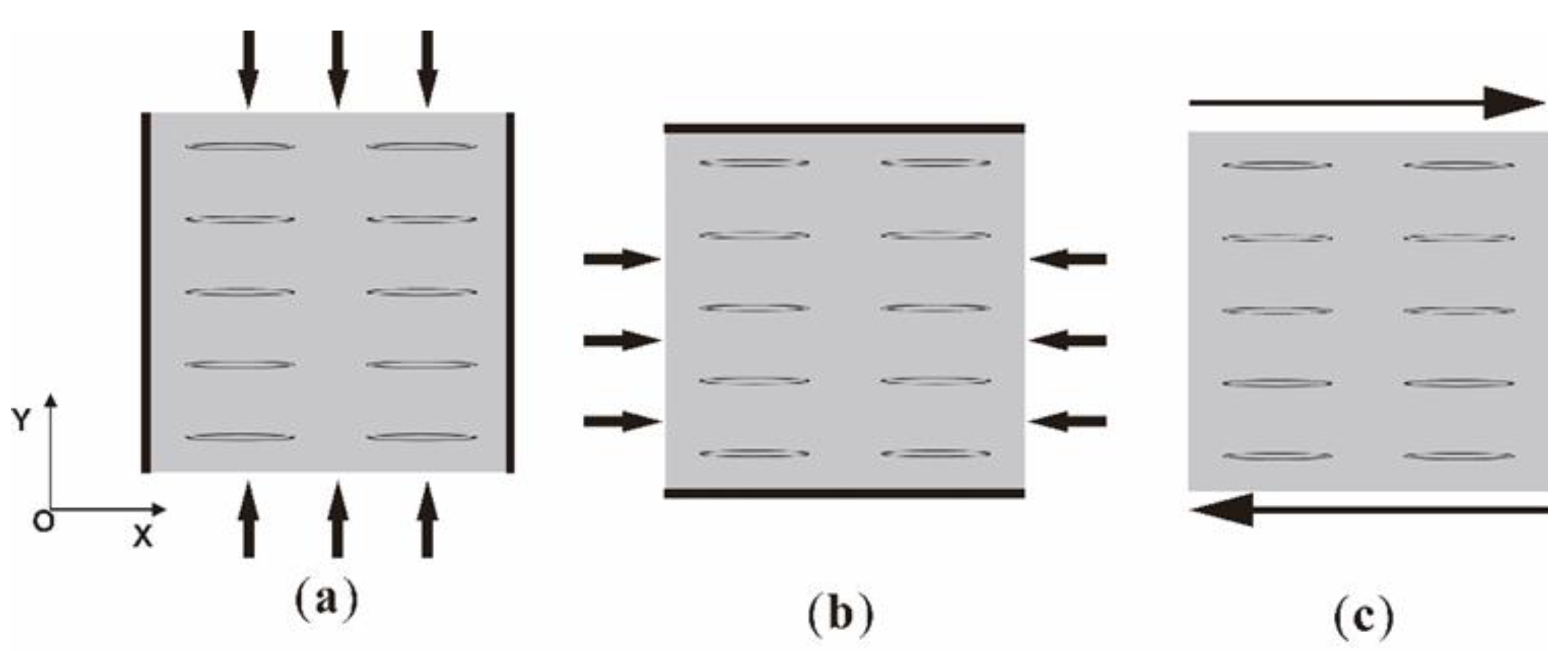
2.1.2. 2D Oscillatory Relaxation Tests

As shown in Figure 2, we need to conduct three simulation oscillatory relaxation tests for calculating the elements of an equivalent stiffness tensor of a 2D sample of interest according to the 2D stress–strain correlation. Let $D=\left(0,L_x\right)\times \left(0,L_y\right)$ be an area that represents the interest model. Performing the first oscillatory relaxation test (see Figure 2a), a uniform vertical displacement is imposed on the bottom and top boundaries, with two lateral boundaries being confined and no shear stress being applied. As a result, the x- and y-directions’ boundary conditions are as follows:

$$\{\begin{array}{l}U·\mathsf{\nu }=-\mathsf{\Delta }U, \left(x,y\right)\in {\Gamma }^b\cup {\Gamma }^t,\hfill \\ U·\mathsf{\nu }=0, \left(x,y\right)\in {\Gamma }^l\cup {\Gamma }^r,\hfill \\ \left(\sigma \nu \right)·\mathsf{\chi }=0, \left(x,y\right)\in \Gamma ,\hfill \end{array}$$

(12)

where U is the solid displacement; $\mathsf{\Delta }$U is the displacement shift; $\sigma$ represents the total stress tensor; Γ is the model boundary; Γ^b, Γ^t, Γ^l, and Γ^r are the bottom, top, left, and right boundary, respectively, on Γ; $\chi$ is a unit tangent; and $\nu$ is the unit outer normal so that {$\nu$,$\chi$} is an orthonormal system on Γ.

Figure 2b illustrates the second test that is analogous to the first, but with a uniform horizontal displacement to the right and left boundaries and the two other boundaries confined. Thus, the corresponding boundary conditions are expressed as

$$\{\begin{array}{l}U·\mathsf{\nu }=-\mathsf{\Delta }U, \left(x,y\right)\in {\Gamma }^l\cup {\Gamma }^r,\hfill \\ U·\mathsf{\nu }=0, \left(x,y\right)\in {\Gamma }^b\cup {\Gamma }^t\hfill \\ \left(\mathsf{\sigma }\nu \right)·\mathsf{\chi }=0, \left(x,y\right)\in \Gamma ,\hfill \end{array},$$

(13)

Figure 2c shows the third test, a shear test, applied to the interested model, where the top and bottom boundaries are loaded with displacement. The corresponding boundary conditions are

$$\{\begin{array}{l}U·\mathsf{\chi }=-\mathsf{\Delta }U, \left(x,y\right)\in {\Gamma }^b\cup {\Gamma }^t,\hfill \\ U·\mathsf{\chi }=0, \left(x,y\right)\in {\Gamma }^l\cup {\Gamma }^r\hfill \\ \left(\mathsf{\sigma }\nu \right)·\mathsf{\nu }=0, \left(x,y\right)\in \Gamma .\hfill \end{array},$$

(14)

2.1.3. Calculation of 2D Equivalent Stiffness Matrix

After computing the displacement field, the stress and strain components of each element are computed using Equations (3) and (4). The corresponding stress and strain average over the model’s volume can be calculated using these parameters

$$\overline{e_{ij}^m}=\frac{1}{S}{\int }_D{e}_{ij}^{m}dS,$$

(15)

$$\overline{{\sigma }_{ij}^m}=\frac{1}{S}{\int }_D{\sigma }_{ij}^{m}dS,$$

(16)

where m = 1–3 denotes the mth test, and S is the surface of domain D.

Taking the prerequisite that an equivalent homogeneous anisotropic elastic solid can stand for the average response of the interest model, the average stress and strain components can be related through the Voigt stiffness matrix M ≡ M_ij. In the case of general anisotropy and under plane strain conditions, this relation is given by

$$\left(\begin{array}{c}\overline{{\sigma }_{xx}^m}\\ \overline{{\sigma }_{yy}^m}\\ \overline{{\sigma }_{xy}^m}\end{array}\right)\equiv \left(\begin{array}{ccc}{M}_{11}& M_{12}& M_{16}\\ M_{12}& M_{22}& M_{26}\\ M_{16}& M_{26}& M_{66}\end{array}\right)\left(\begin{array}{c}\overline{e_{xx}^m}\\ \overline{e_{yy}^m}\\ 2\overline{e_{xy}^m}\end{array}\right)$$

(17)

where $\overline{{\sigma }_{ij}^m}$ and $\overline{e_{ij}^m}$ are cells of the averaging stress and strain vector, respectively, and m = 1–3 denotes the mth simulation test. It is worthy to note that the matrix M considers the greatest extent of anisotropy.

Thus, the six unknown components of the stiffness matrix possibly are calculated utilizing a least-squares procedure. That is, the components of equivalent stiffness matrix M_ij can be obtained by minimizing the cost function F₁ (M) as follows:

$$\frac{\partial F_1\left(M\right)}{\partial M_{ij}}=0.$$

(18)

We can solve the linear system of six equations yielded by Equation (18) to obtain the equivalent stiffness tensor M_ij; see Appendix A for more details.

2.2. Anisotropic Effective Elastic Properties for 3D Fractured Models

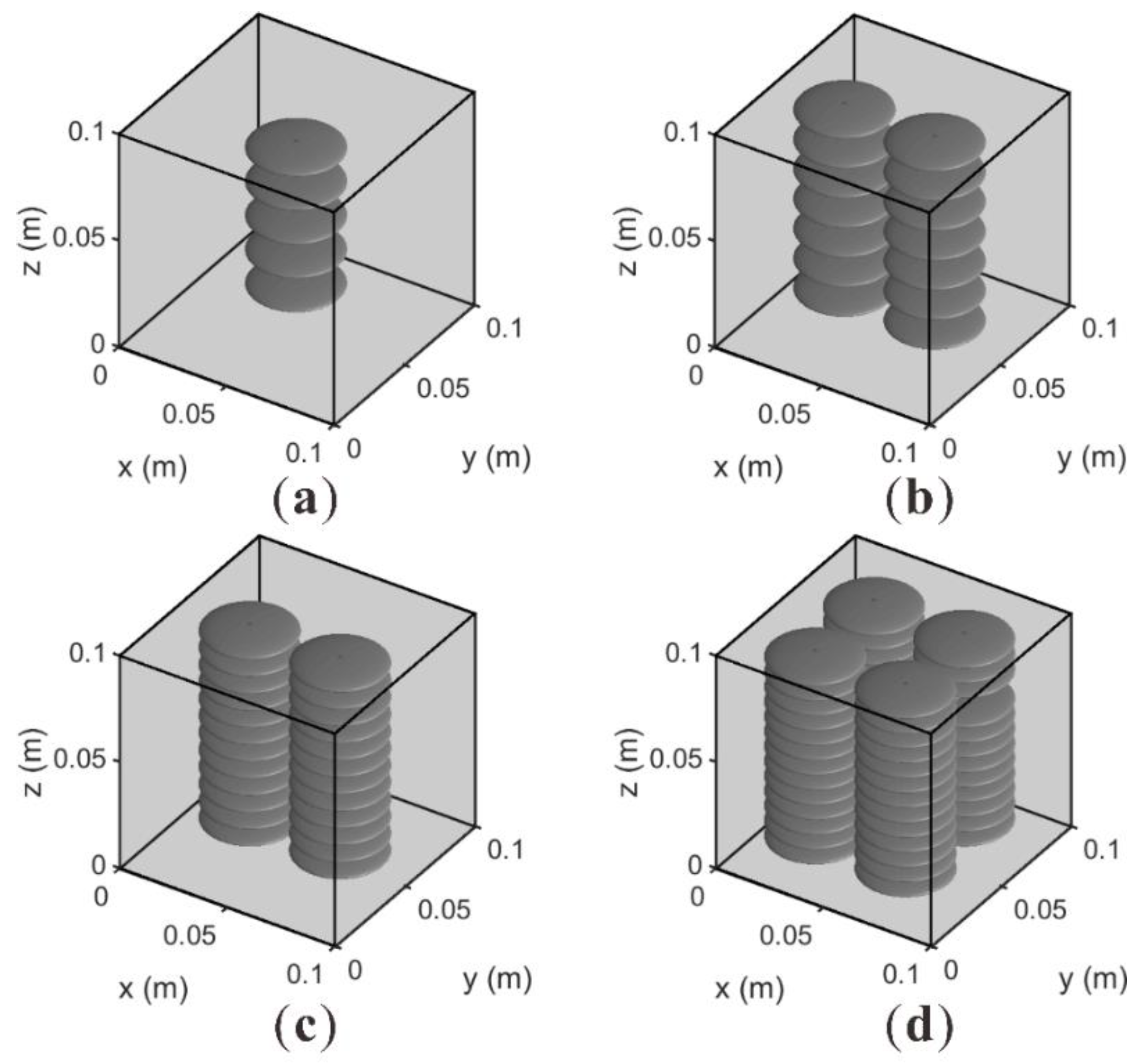
2.2.1. 3D Oscillatory Relaxation Tests

In this part, we apply Rubino’s 2D method to a 3D cracked medium [30]. The governing Equations (1)–(11) would remain the same. As illustrated in Figure 3, we need to conduct six simulation oscillatory relaxation tests for calculating the elements of an equivalent stiffness matrix for a 3D probed model according to the 3D stress–strain correlation.

Set $\mathsf{\Omega }=\left(0,L_x\right)\times \left(0,L_y\right)\times \left(0,L_z\right)$ as a domain that represents a 3D interest model. Figure 3a displays the first oscillatory relaxation test in which a uniform vertical displacement along the x-direction (blue arrow) is applied to the model’s red side, with the other sides employing periodic boundary conditions. The opposing side (gray side) is confined, and no shear stress is applied. Thus, the boundary conditions of the x-, y-, and z- directions are imposed as follows:

$$\{\begin{array}{l}\begin{array}{l}\begin{array}{l}U·\mathsf{\nu }=-\mathsf{\Delta }U, \left(x,y,z\right)\in A^r,\hfill \\ U·\mathsf{\nu }=0, \left(x,y,z\right)\in A^l,\hfill \end{array}\hfill \\ \left(\mathsf{\sigma }\nu \right)·\mathsf{\chi }=0, \left(x,y,z\right)\in A,\hfill \end{array}\hfill \\ U_{dst}=U_{src}, \left(x,y,z\right)\in A^f\cup A^k,\hfill \\ {\mathbf{U}}_{dst}=U_{src}, \left(x,y,z\right)\in A^t\cup A^b,\hfill \end{array}$$

(19)

where $\sigma$ represents the total stress tensor; $U$ denotes the solid displacement; $\mathsf{\Delta }U$ denotes the displacement shift; $U_{src}$ denotes the source displacement field; $U_{dst}$ denotes the displacement field of the target boundary; A is its side boundaries; A^f, A^k, A^l, A^r, A^t, and A^b are the left, right, front, back, top, and bottom boundaries, respectively; $\chi$ is a unit tangent; and $\nu$ denotes the unit outer normal on A, so that {$\nu$,$\chi$} is an orthonormal system.

Figure 3b illustrates the second test that is analogous to the first, but with a uniform horizontal displacement applied to the red side from the y-direction and the opposing side fixed and periodical boundary conditions applied to the other surfaces. So, we have

$$\begin{array}{l}\begin{array}{l}\begin{array}{l}U·\chi =-\Delta U, \left(x,y,z\right)\in A^f,\hfill \\ U·\text{χ}=0, \left(x,y,z\right)\in A^k,\hfill \end{array}\hfill \\ \left(\mathsf{\sigma }\nu \right)·\text{ν}=0, \left(x,y,z\right)\in A,\hfill \end{array}\hfill \\ U_{dst}=U_{src}, \left(x,y,z\right)\in A^l\cup A^r,\hfill \\ U_{dst}=U_{src}, \left(x,y,z\right)\in A^t\cup A^b,\hfill \end{array}$$

(20)

Figure 3c–f shows the third to sixth tests whose loaded direction of solid displacement and the relevant boundary conditions are given by

$$\begin{array}{l}\begin{array}{l}\begin{array}{l}U·\mathsf{\nu }=-\mathsf{\Delta }U, \left(x,y,z\right)\in A^t,\hfill \\ U·\mathsf{\nu }=0, \left(x,y,z\right)\in A^b,\hfill \end{array}\hfill \\ \left(\mathsf{\sigma }\nu \right)·\mathsf{\chi }=0, \left(x,y,z\right)\in A,\hfill \end{array}\hfill \\ U_{dst}=U_{src}, \left(x,y,z\right)\in A^f\cup A^k,\hfill \\ U_{dst}=U_{src}, \left(x,y,z\right)\in A^r\cup A^l,\hfill \end{array}$$

(21)

for the third test,

$$\begin{array}{l}\begin{array}{l}\begin{array}{l}U·\mathsf{\chi }=-\mathsf{\Delta }U, \left(x,y,z\right)\in A^f,\hfill \\ U·\mathsf{\chi }=0, \left(x,y,z\right)\in A^k,\hfill \end{array}\hfill \\ \left(\mathsf{\sigma }\nu \right)·\mathsf{\nu }=0, \left(x,y,z\right)\in A,\hfill \end{array}\hfill \\ U_{dst}=U_{src}, \left(x,y,z\right)\in A^l\cup A^r,\hfill \\ U_{dst}=U_{src}, \left(x,y,z\right)\in A^t\cup A^b,\hfill \end{array}$$

(22)

for the fourth test,

$$\begin{array}{l}\begin{array}{l}\begin{array}{l}U·\mathsf{\chi }=-\mathsf{\Delta }U, \left(x,y,z\right)\in A^t,\hfill \\ U·\mathsf{\chi }=0, \left(x,y,z\right)\in A^b,\hfill \end{array}\hfill \\ \left(\mathsf{\sigma }\nu \right)·\mathsf{\nu }=0, \left(x,y,z\right)\in A,\hfill \end{array}\hfill \\ U_{dst}=U_{src}, \left(x,y,z\right)\in A^f\cup A^k,\hfill \\ U_{dst}=U_{src}, \left(x,y,z\right)\in A^r\cup A^l,\hfill \end{array}$$

(23)

for the fifth test, and

$$\begin{array}{l}\begin{array}{l}\begin{array}{l}U·\mathsf{\chi }=\mathsf{\Delta }U, \left(x,y,z\right)\in A^r,\hfill \\ U·\mathsf{\chi }=0, \left(x,y,z\right)\in A^l,\hfill \end{array}\hfill \\ \left(\mathsf{\sigma }\nu \right)·\mathsf{\nu }=0, \left(x,y,z\right)\in A,\hfill \end{array}\hfill \\ U_{dst}=U_{src}, \left(x,y,z\right)\in A^f\cup A^k,\hfill \\ {\mathbf{U}}_{dst}=U_{src}, \left(x,y,z\right)\in A^t\cup A^b.\hfill \end{array}$$

(24)

for the sixth test.

2.2.2. Calculation of 3D Equivalent Stiffness Matrix

We solve Equations (1) and (11) by applying the FEM to obtain the corresponding displacement field, which promotes the stress and strain components for every element to be obtained using Equations (3) and (4). Then, parameters allow us to estimate the corresponding average over the sample’s volume:

$$\overline{e_{ij}^r}=\frac{1}{V}{\int }_{\mathsf{\Omega }}{e}_{ij}^{r}dV,$$

(25)

And

$$\overline{{\sigma }_{ij}^r}=\frac{1}{V}{\int }_{\mathsf{\Omega }}{\sigma }_{ij}^{r}dV,$$

(26)

where V is the volume of $\mathsf{\Omega }$, with r = 1–6 denoting the rth simulation oscillatory relaxation test described in Figure 3, respectively.

As in the case of 2D, we use a second-order equivalent Voigt stiffness matrix M≡M_ij to relate the averaging stress and strain components of 3D models. In the case of general anisotropy and under plane strain conditions, this relation is given by

$$\left(\begin{array}{c}\overline{{\sigma }_{xx}^r}\\ \overline{{\sigma }_{yy}^r}\\ \overline{{\sigma }_{zz}^r}\\ \overline{{\sigma }_{yz}^r}\\ \overline{{\sigma }_{zx}^r}\\ \overline{{\sigma }_{xy}^r}\end{array}\right)\equiv (\begin{array}{cccccc}{M}_{11}& M_{12}& M_{13}& M_{14}& M_{15}& M_{16}\\ M_{12}& M_{22}& M_{23}& M_{24}& M_{25}& M_{26}\\ M_{13}& M_{23}& M_{33}& M_{34}& M_{35}& M_{36}\\ M_{14}& M_{24}& M_{34}& M_{44}& M_{45}& M_{46}\\ M_{15}& M_{25}& M_{35}& M_{45}& M_{55}& M_{56}\\ M_{16}& M_{26}& M_{36}& M_{46}& M_{56}& M_{66}\end{array}\left)\right(\begin{array}{c}\overline{e_{xx}^r}\\ \overline{e_{yy}^r}\\ \overline{e_{zz}^r}\\ 2\overline{e_{yz}^r}\\ \begin{array}{c}2\overline{e_{zx}^r}\\ 2\overline{e_{xy}^r}\end{array}\end{array})$$

(27)

where M_ij is the equivalent stiffness components in the 3D media, and $\overline{{\sigma }_{ij}^r}$ and $\overline{e_{ij}^r}$ are cells of the average stress and strain vector, respectively. In general, the matrix M takes into account the highest degree of anisotropy for a 3D case. Like in the 2D case, we can obtain 21 unknown stiffness tensors by applying the least-squares procedure to minimize the following cost function F₂ (M),

$$\frac{\partial F_2\left(M\right)}{\partial M_{ij}}=0.$$

(28)

We can solve the linear system of twenty-one equations yielded by Equation (28) to obtain the equivalent stiffness matrix M_ij, seeing Appendix B for more niceties.

3. Results

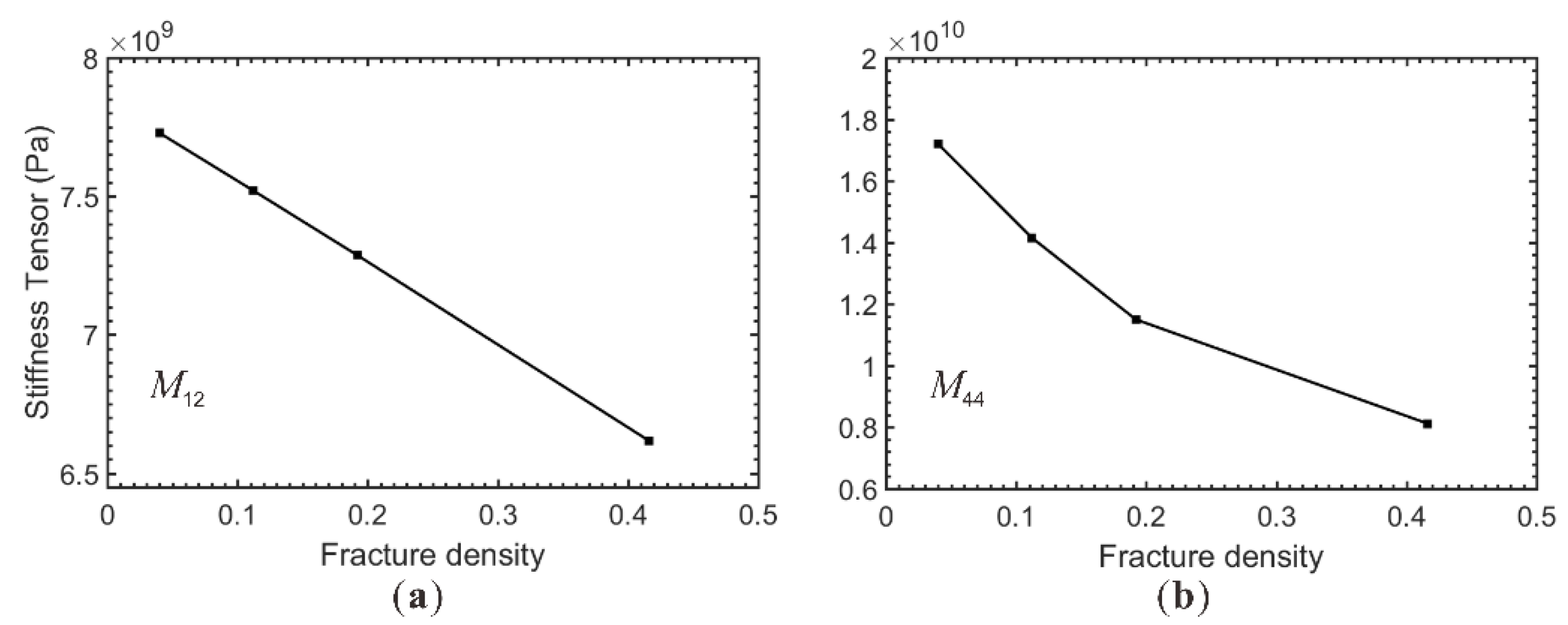
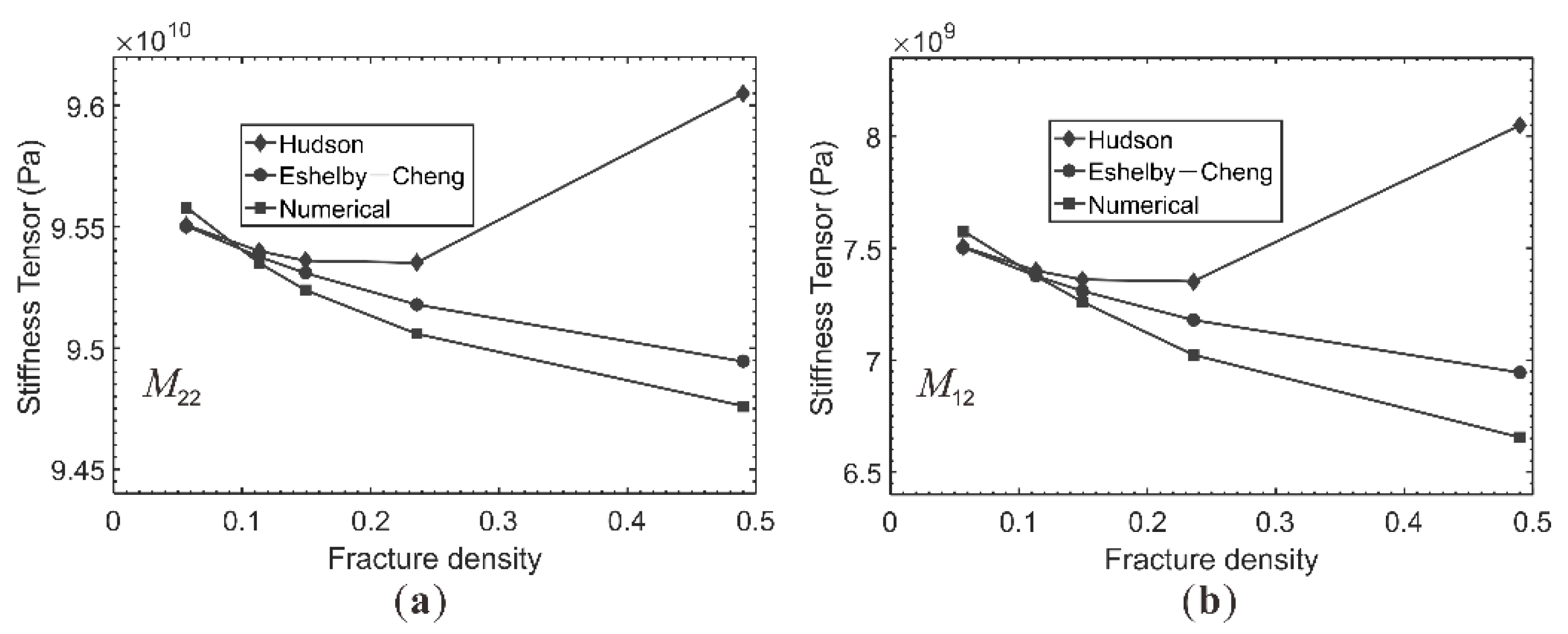
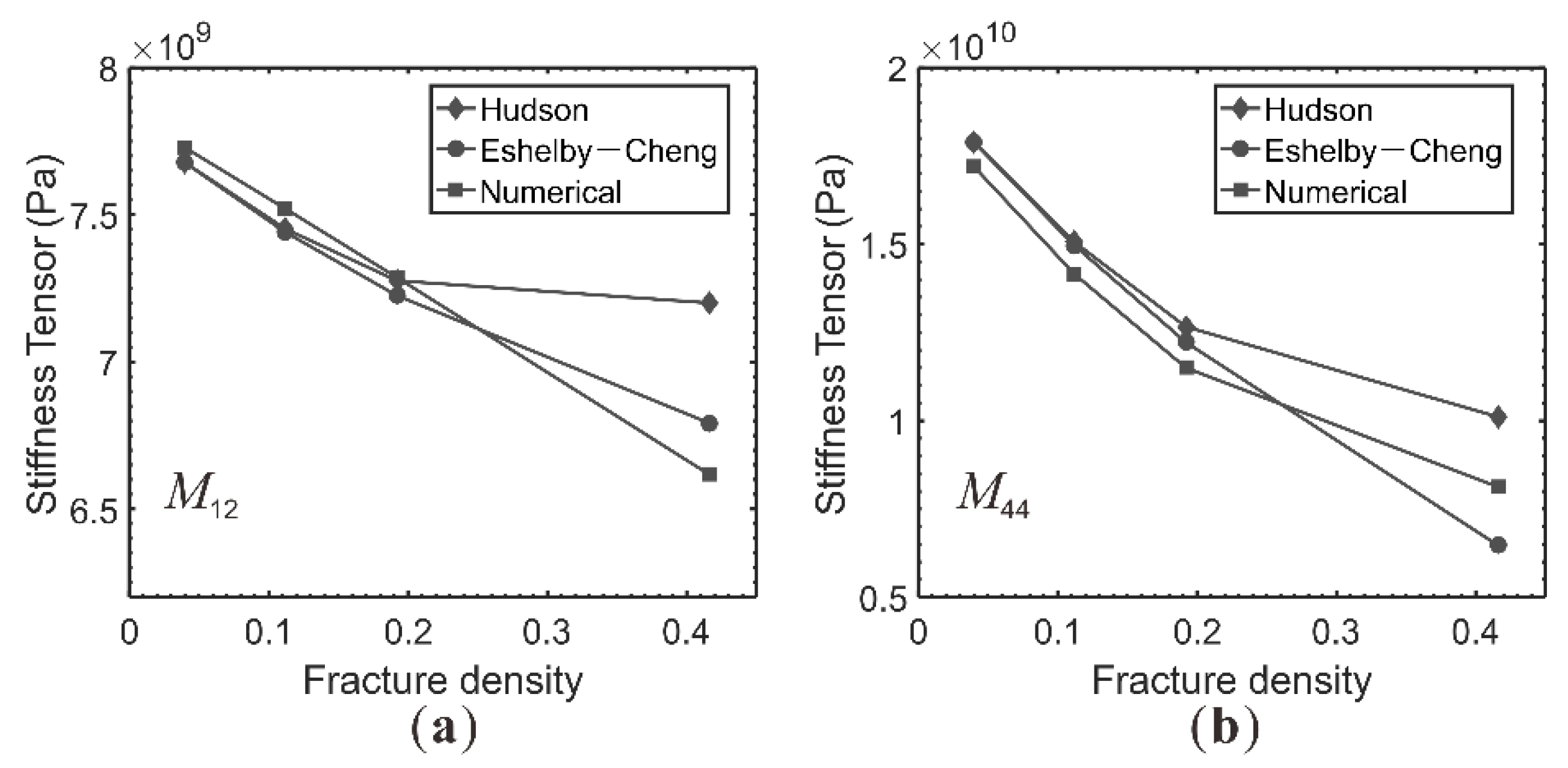
3.1. Stiffness Tensors for 2D Fractured Model

As a 2D case, a fractured model with sides of 0.1 m contains small, isolated, and penny-shaped elliptical cracks along the x-axis. Every elliptical fracture has an x-semiaxis of 1.5 cm and y-semiaxis of 0.08 cm. The following formula is used to define the fracture density [13].

$$\mathsf{\zeta }=\frac{N{a}^2}{s}$$

(29)

where N and a denote the fracture numbers and major semiaxis, respectively; s is the area of the model. Five group parameters are designed with different fracture densities of 0.056, 0.11, 0.149, 0.23, and 0.49 in the horizontal direction.

Table 1. Simulation parameters for multi-dimensional cracked models.

Parameters	Phase
Matrix
Grain Bulk moduli, ks (GPa)	37.0
$\mathrm{Grain} \mathrm{Density}, {\mathsf{\rho }}_s$ (g/cm3)	2.65
$\mathrm{Porosity}$ ϕ	0.1
Bulk modulus, km (GPa)	26
$\mathrm{Shear} \mathrm{modulus}, \mu$ or ${\mu }_m$ (GPa)	31.0
$\mathrm{Permeability}$κ (m2)	1 × 10−15
Fractures
Grain Bulk moduli, ks (GPa)	37.0
$\mathrm{Grain} \mathrm{Density}, {\mathsf{\rho }}_s$ (g/cm3)	2.65
$\mathrm{Porosity}$ ϕ	0.8
Bulk modulus, km (GPa)	0.04
$\mathrm{Shear} \mathrm{modulus}, \mu$ or ${\mu }_m$ (GPa)	0.02
$\mathrm{Permeability}$ κ (m2)	1 × 10−10
Brine
Bulk modulus, kf (GPa)	2.25
$\mathrm{Density}, {\mathsf{\rho }}_s$ (g/cm3)	1.09
$\mathrm{Viscosity}, \mathsf{\eta }$(Pa.s)	0.01

shows the physical parameters of fluid parameters, fractures with saturated brine, and the embedding background matrix.

We solve Equations (1) and (11) using the relaxation experiments with FEM. Once the stress and strain fields are obtained, the stiffness tensor is calculated by the least-squares method. Figure 4 shows the resulting equivalent stiffness tensors M₂₂ and M_12. With increasing fracture density, the equivalent stiffness tensors M₂₂ and M₁₂ have a similar decreasing trend.

3.2. Stiffness Tensors for 3D Fractured Model

In the 3D case, as shown in Figure 5, we build four models, each being a cube of 0.1 m on all sides for validating the 3D numerical oscillatory relaxation tests. These models include penny-shaped ellipsoidal cracks along the horizontal direction, and x-, y-, and z-semiaxes of 0.02 m, 0.02 m, and 0.003 m, respectively, with different fracture densities.

As with 2D, the four fracture densities are set to 0.04, 0.112, 0.192, and 0.416, respectively, according to the basic definition,

$$\mathsf{\zeta }=\frac{N{a}^3}{v}$$

(30)

where v is the volume of the cube. The same physical parameters in Table 1 are applied to the 3D models, and the relaxation tests are conducted at a frequency of 20 Hz.

Equations (1) and (11) are also solved by the relaxation experiments with FEM. Once the stress and strain fields are obtained, the stiffness tensor is calculated by the least-squares method. Figure 6 shows the resulting equivalent stiffness tensors M₁₂ and M₄₄. With increasing fracture density, the equivalent stiffness tensors M₁₂ and M₄₄ tend to decrease.

3.3. Validation of Numerical Method

3.3.1. Validation of 2D Numerical Method

To validate the finite-element numerical simulation, the classical second-order Hudson’s model and the Eshelby–Cheng model are used. Specific formulas are included in Appendix C.

Figure 7 compares the resulting equivalent stiffness tensors M₂₂ and M₁₂ calculated from the 2D numerical oscillatory relaxation tests for a frequency of 20 Hz with the Hudson model and the Eshelby–Cheng model. As expected, the solutions obtained using the different methods are almost comparable for low fracture densities but significantly different for high crack densities. We see that the second-order Hudson model for pair-wise interactions between cracks produces an unreasonable result at a high crack density that is over the dilution to make the assumption invalid. Both the equivalent stiffness matrix M₁₁ and M₁₂ by the Eshelby–Cheng model keep a good trend close to the numerical results, but their difference becomes large with increasing crack densities.

3.3.2. Numerical Analysis of 3D Fractured Model

As illustrated in Figure 8, the resulting effective stiffness coefficients M₁₂ and M₄₄ are compared to the theoretical solutions obtained using the Hudson and Eshelby–Cheng models. As expected, these predictions exhibit a similar trend as facture densities increase. As illustrated in Figure 8a,b, there is a substantially better agreement between the numerical M₁₂ and M₄₄ and their theoretical counterpart solutions, especially at low crack densities. We also see that the numerical results closely match the Eshelby–Cheng model, with some minor departures between them at higher crack densities due to limited accuracies in the Eshelby–Cheng model. The simulation method provides a physical prediction at high fracture densities that control the overall elastic properties of rocks. We can analyze the fracture-induced anisotropy using these equivalent stiffness tensors.

4. Discussion

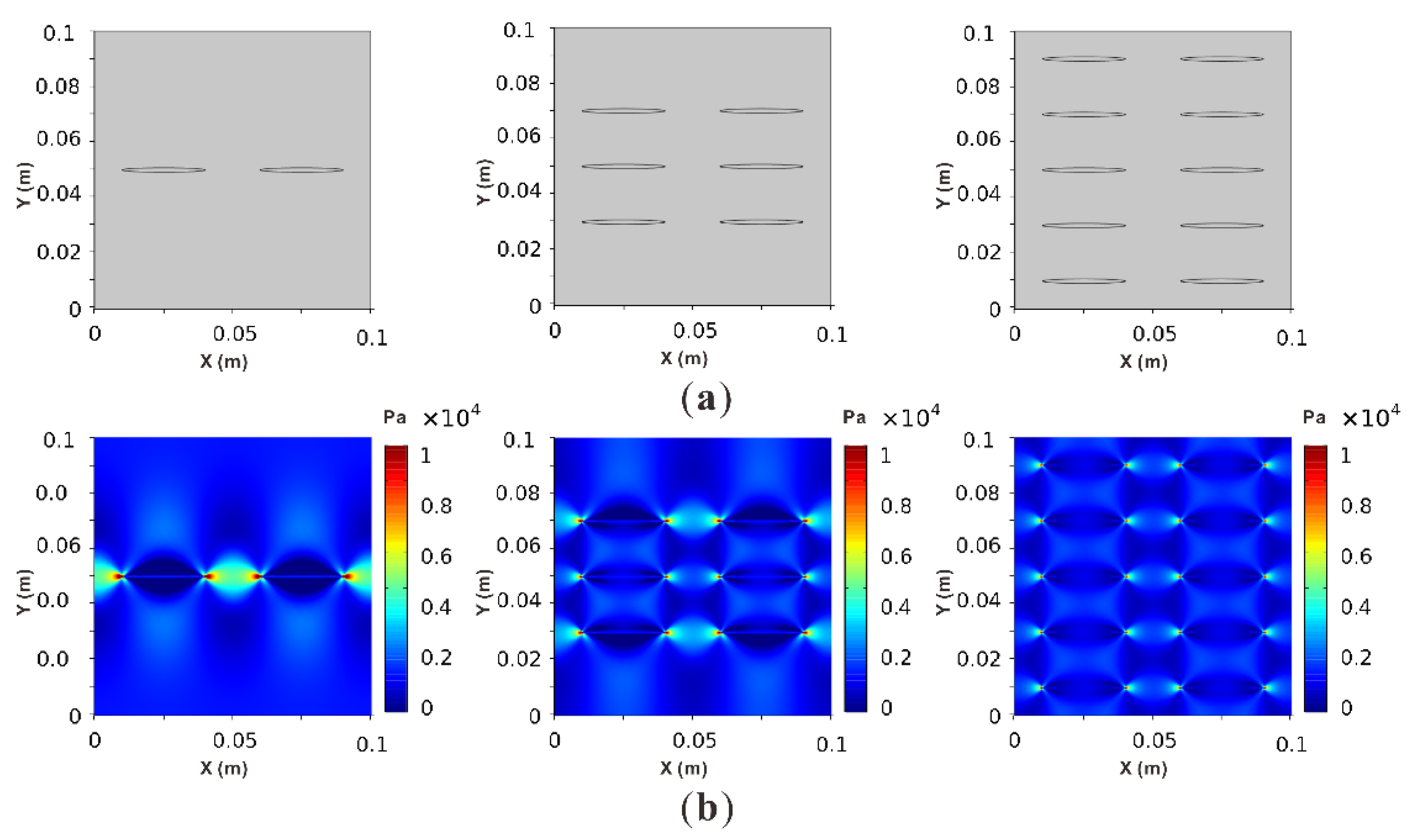
4.1. Stress Distribution Induced on Crack Interaction

Stress interactions (stress amplification and dilution) produced by fractures have a substantial effect on the anisotropic characteristics of cracks. To better illustrate the stress interactions across cracks at different fracture densities, we did numerical tests with three 2D simple fracture models (Figure 9). As shown in Figure 9a, each model (0.01 m²) contains two, six, and ten elliptic inclusions (fractures). Allow each fracture to have a main semiaxis and an aspect ratio of 0.015, and 0.053, respectively. The fractures are completely saturated with water. Table 1 contains the simulation parameters.

We repeated the numerical test in Figure 2a with the corresponding boundaries, this time using the model in Figure 9a. As illustrated in Figure 9b, the stress distributions of the models vary. The fractures alter the stress distribution in their neighborhood. The stress dilution and concentration occurring near the face (central part) and tip of a fracture in Figure 9b. The stress distribution with a high fracture density contributes a broader range of effects to the background than the low fracture density. Additionally, when fracture density increases, the stress concentrations around the tips decrease. On the basis of the foregoing, it is possible to explain in Figure 7 and Figure 8 that the elastic matrix with a high fracture density is lower than the theoretical method.

4.2. Anisotropy Properties for Real Fractures

Combined with Figure 7 and Figure 8, we see that different fracture densities can induce elastic anisotropy, which can be quantitatively characterized using the equivalent stiffness tensors. We apply 2D anisotropic finite-element modeling to a real crack for anisotropy properties at this part. Figure 10a illustrates an outcrop from the Ordovician carbonate formation in the Tarim Basin, northwest China. Multistage tectonic movements result in a complicated fracture network in the formation [33]. From the Cambrian to the Middle Ordovician, strike-slip faults with numerous fractures were formed by the joint action of north–south and north–east stresses [34]. These secondary fractures are considered as both migration channels and fracture reservoir spaces for hydrocarbon. The outcrop is selected because its fracture characteristics are similar to those of subsurface strata over 7 km, and a complicated fracture network satisfies the simulation scale. Due to the complexity of natural fractures, modeling of irregular geometries and anisotropic features are challenging. The outcrop picture is simplified into a model consisting of background media and superimposed fractures with different shapes, sizes, and orientations to facilitate research on the anisotropy properties of fractures and their stress interaction, as illustrated in Figure 10b.

We investigate the cracked model’s density and dip-angle. For calculating fracture density, we use the method developed by reference [35,36], which employs a circular scanning window to calculate the number of total fractures by counting the number of endpoints of complete visible fractures within the window. An equal-area rose diagram instead of the histogram of fracture length is used since it provides an indirect orientation distribution (see reference [37] for more details). Figure 10c,d shows the geometric properties of the real model, which clearly exhibits a range of densities and orientations in different areas.

We use a numerical approach combined with finite-element modeling to study the anisotropic properties of the real fracture model at different frequencies. The same physical parameters in Table 1 are used, and oscillatory relaxation tests at frequencies of 0.01, 1, 10, 100, and 1000 Hz are applied.

The resultant real parts of the effective stiffness coefficients M₁₁ are illustrated in Figure 11. As we see in Figure 11, the real parts of the stiffness matrix of M₁₁ (red circle and red dotted line) show an increasing tendency with increasing frequency, which is not as regular as the simple models in reference [26]. The pictures indicated by the shallow green arrow represent the stress (${\sigma }_{xx}$) distributions at different frequencies. Additionally, we observe that they change slowly at the beginning, then rapidly, and tend to be flat at high frequency, as the difference between protolith and faults affecting the stiffening of the fluid becomes smaller [38]. The stress (${\sigma }_{xx}$) occurs an obvious difference between high frequency (100 and 1000 Hz) and low frequency, and the interaction becomes more intense as the frequency increases. The resultant anisotropies of effective elastic properties under the different frequencies can be used to characterize fracture interactions and dynamic stress disturbances. We can characterize the velocity anisotropy and seismic attenuation using these equivalent stiffness tensors.

The existence of fractures surely affects the overall elasticity, as shown in Figure 4 and Figure 6. In the geophysical community, conventional analytical methods, such as the Hudson model and Eshelby–Cheng model, have been widely used to study the effective elastic properties of rocks, but they are limited to their assumption that fracture geometries are idealized [19,22] and hardly characterize the elastic properties of complex and irregular natural fracture networks. We see that the numerical results keep a good trend with the analytical methods at low crack density, while the difference between them becomes larger with the increase of fracture density (Figure 7 and Figure 8) in that the numerical method explicitly simulates the influence of fractures distribution and their interaction (Figure 9). It proves that our method can accurately simulate the equivalent stiffness tensors with different frequencies and low fracture density.

When the fracture density is very high, Figure 7 and Figure 8 show that the decreasing trend may change because the solution of the simulation equation may be unstable. Some non-dilute crack theories should be used; for example, non-dilute crack theories established successfully based on the inclusion model DEM theory [39]. Additionally, we need to consider that fractures in nature can be too large to satisfy the simulation conditions. Therefore, further investigation on effective stiffness tensors of arbitrary complex multi-dimensional fracture should also consider these elements and laboratory measurements.

5. Conclusions

Numerical methods must be used to determine the effective elasticity of genuine fractures. We modify Rubino’s numeric FEM for real fractures. For 2D simple fracture models with different fracture densities, the 2D technique is compared to theoretical models (Hudson’s model and Eshelby–Cheng model). The results closely match the theoretical predictions at low fracture densities. The simulation method provides a physical prediction at high fracture densities that controls the overall elastic properties of rocks.

When applied to a sample of natural fractures extracted from an outcrop at different frequencies, the stress interactions between cracks become highly complex. The stiffness matrix of M₁₁ shows a trend as the frequency increases. With increasing frequency, the stress concentration spreads quickly to cover the network’s high fracture density, intensifying the interactions and becoming intense. The effective elastic properties of the resulting real fractured model can be altered to understand fracture interactions and dynamic stress disturbances.

The 2D finite-element numerical method is extended to 3D fractured media using the 3D stress–strain relationship defined by the six oscillatory relaxation simulation tests. A least-squares approach can be used to solvethe relevant equations for unknown stiffness tensors. The 3D fractured media are compared to effective medium theories in terms of their elastic responses to different fracture densities. The fracture density is found to have an obvious effect on the anisotropic effective properties, and the proposed method gives a physical prediction for high fracture densities. This work has significance calculating the effective elastic properties of multi-dimensional fracture models and fracture interaction mechanisms.