Global Vibration Intensity Assessment Based on Vibration Source Localization on Construction Sites: Application to Vibratory Sheet Piling
Abstract
:1. Introduction
2. Numerical Simulations of Vibratory Sheet Pile Driving
2.1. Simulation Model
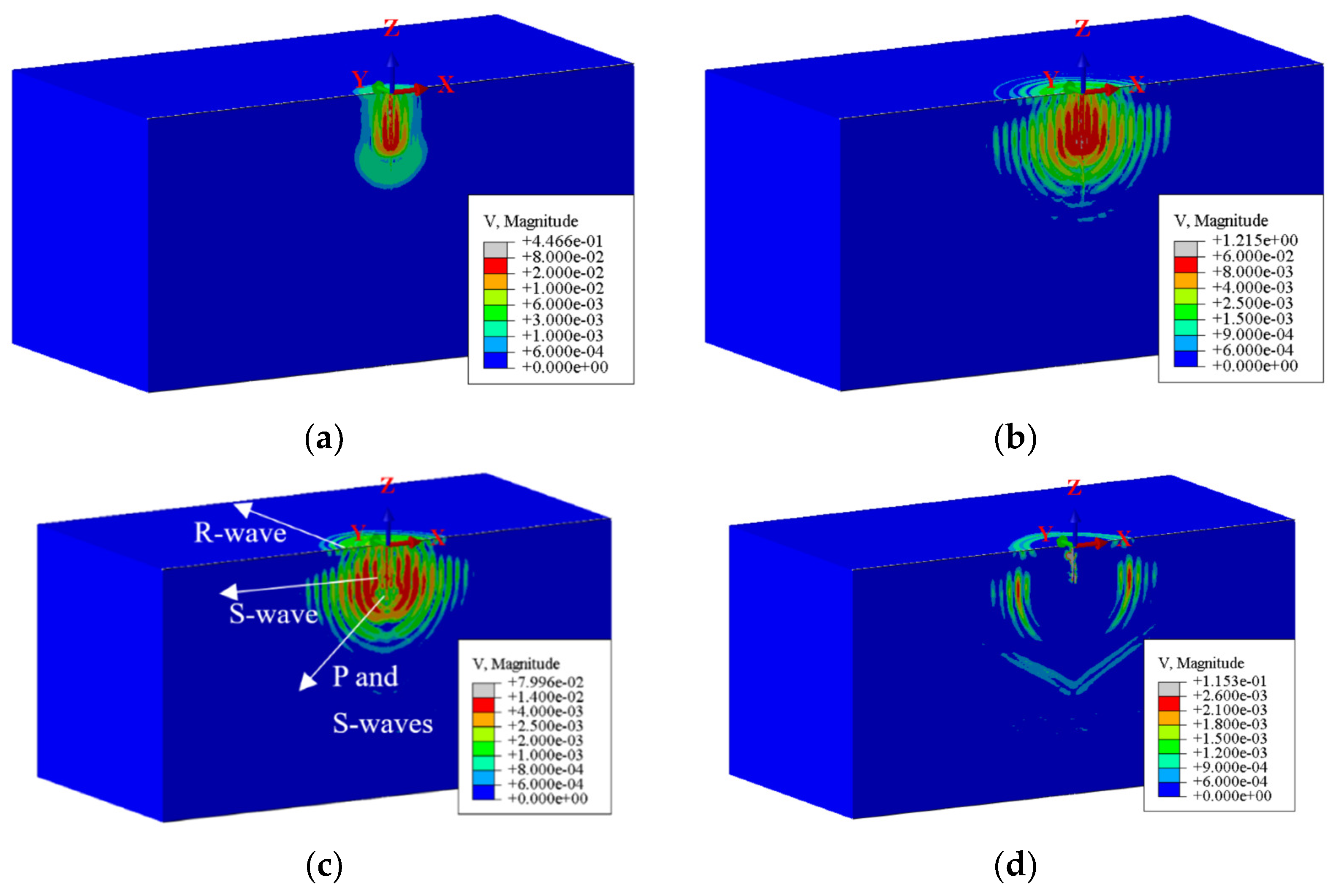
2.2. Numerical Simulation Results
3. Time-Based Localization Method and Localization Performance in Numerical Examples
3.1. Time-Based Localization Method
3.2. Localization Performance in Numerical Examples
4. Field Validation Tests and Global Vibration Intensity Prediction
4.1. Field Validation Tests
4.2. Global Vibration Intensity Prediction
5. Conclusions
- For vibratory sheet pile driving at a certain depth, surface waves dominate the ground surface vibrations, while cylindrical shear waves from the pile shaft dominate the underground vibrations within the range of the pile shaft, and spherical body waves from the pile toe dominate underground vibrations at depths below the pile toe.
- The time-based localization method assuming the single surface wave content along the ground surface is proved to be effective in localizing a vibratory driving source (e.g., vibratory sheet pile diving) on construction sites under different ground and construction conditions.
- The layout of monitoring points has a notable effect on the localization performance. Both numerical simulations and field tests of vibratory sheet pile driving show that using a layout of monitoring points deployed in both directions surrounding the driving location can achieve a better localization performance.
- The localized driving location and the estimated vibration attenuation formula can jointly estimate vibration intensity in the entire surrounding area rather than at a few monitored points, and then realize a global vibration impact assessment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- BS ISO 4866; Mechanical Vibration and Shock, Vibration of Fixed Structures, Guidelines for the Measurement of Vibrations and Evaluation of Their Effects on Structures. BSI Group: London, UK, 2010.
- BS 5228-2; Code of Practice for Noise and Vibration Control on Construction and Open Sites, Part 2: Vibration. European Committee for Standardization: Brussels, Belgium, 2009.
- Jim, A.; David, B.; Harjodh, G.; Wesley, L. Transportation and Construction Vibration Guidance Manual; CT-HWANP-RT-13-069.25.3; California Department of Transportation Division of Environmental Analysis Environmental Engineering Hazardous Waste, Air, Noise, and Paleontology Office: Sacramento, CA, USA, 2013.
- DIN 4150-3; Structural vibration—Part 3: Effects of Vibration on Structures. German Institute for Standardisation: Berlin, Germany, 1999.
- Deckner, F.; Viking, K.; Hintze, S. Ground vibrations due to pile and sheet pile driving: Prediction models of today. In Proceedings of the 22nd European Young Geotechnical Engineers Conference, Gothenburg, Sweden, 26–29 August 2012; pp. 107–112. [Google Scholar]
- Richart, F.E.; Hall, J.R.; Woods, R.D. Vibrations of Soils and Foundations; Prentice Hall: Englewood Cliffs, NJ, USA, 1970; pp. 60–92. [Google Scholar]
- Wiss, J.F. Construction vibrations: State-of-the-art. J. Geotech. Eng. Div. 1981, 107, 167–181. [Google Scholar] [CrossRef]
- Attewell, P.B.; Selby, A.R.; O’Donnell, L. Estimation of ground vibration from driven piling based on statistical analyses of recorded data. Geotech. Geol. Eng. 1992, 10, 41–59. [Google Scholar] [CrossRef]
- Ramshaw, C.L.; Selby, A.R.; Bettess, P. Computer Ground Waves Due to Piling. In Proceedings of the Geotechnical Earthquake Engineering and Soil Dynamics III, Seattle, WA, USA, 3–6 August 1998; pp. 1484–1495. [Google Scholar]
- Masoumi, H.R.; François, S.; Degrande, G. A non-linear coupled finite element-boundary element model for the prediction of vibrations due to vibratory and impact pile driving. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 245–274. [Google Scholar] [CrossRef]
- Khoubani, A.; Ahmadi, M.M. Numerical study of ground vibration due to impact pile driving. Proc. Inst. Civ. Eng. Geotech. Eng. 2014, 167, 28–39. [Google Scholar] [CrossRef]
- Rooz, A.F.H.; Hamidi, A. Numerical analysis of factors affecting ground vibrations due to continuous impact pile driving. Int. J. Geomech. 2017, 17, 04017107. [Google Scholar] [CrossRef]
- Jongmans, D. Prediction of ground vibrations caused by pile driving: A new methodology. Eng. Geol. 1996, 42, 25–36. [Google Scholar] [CrossRef]
- Svinkin, M.R. Predicting soil and structure vibrations from impact machines. J. Geotech. Geoenviron. Eng. 2002, 128, 602–612. [Google Scholar] [CrossRef]
- Athanasopoulos, G.A.; Pelekis, P.C. Ground vibrations from sheetpile driving in urban environment: Measurement, analysis and effects on buildings and occupants. Soil Dyn. Earthq. Eng. 2000, 19, 371–387. [Google Scholar] [CrossRef]
- Zhu, S.; Shi, X.; Leung, R.C.; Cheng, L.; Ng, S.; Zhang, X.; Wang, Y. Impact of construction-induced vibration on vibration-sensitive medical equipment: A case study. Adv. Struct. Eng. 2014, 17, 907–920. [Google Scholar] [CrossRef]
- Dowding, C.H. Construction Vibrations; Prentice Hall: Englewood Cliffs, NJ, USA, 1996; pp. 425–453. [Google Scholar]
- Svinkin, M.R. Minimizing construction vibration effects. Pract. Period. Struct. Des. Constr. 2004, 9, 108–115. [Google Scholar] [CrossRef]
- Manvell, D. Noise and vibration monitoring around construction sites-examples of standards and practice from around the world. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Hong Kong, China, 27–30 August 2017; Institute of Noise Control Engineering: Washington, DC, USA, 2017; Volume 255, pp. 5046–5054. [Google Scholar]
- Zhang, M.; Tao, M.; Gautreau, G.; Zhang, Z.D. Statistical approach to determining ground vibration monitoring distance during pile driving. Pract. Period. Struct. Des. Constr. 2013, 18, 196–204. [Google Scholar] [CrossRef]
- Lemke, J. Remote vibration monitoring system using wireless internet data transfer. In Proceedings of the SPIE’s 5th Annual International Symposium on Nondestructive Evaluation and Health Monitoring of Aging Infrastructure, Newport Beach, CA, USA, 9 June 2000; pp. 436–445. [Google Scholar] [CrossRef]
- Veggeberg, K. Wireless Noise and Vibration Management System for Construction Sites. Struct. Dyn. 2011, 3, 1553–1557. [Google Scholar] [CrossRef]
- Meng, Q.; Zhu, S. Developing IoT sensing system for construction-induced vibration monitoring and impact assessment. Sensors 2020, 20, 6120. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhu, S. Impact source localization and vibration intensity prediction on construction sites. Measurement 2021, 175, 109148. [Google Scholar] [CrossRef]
- Zerwer, A.; Cascante, G.; Hutchinson, J. Parameter estimation in finite element simulations of Rayleigh waves. J. Geotech. Geoenviron. Eng. 2002, 128, 250–261. [Google Scholar] [CrossRef]
- Hibbitt, D.; Karlsson, B.; Sorensen, P. Abaqus User’s Manual, version 6.13; Hibbitt, Karlsson and Sorensen Inc.: Providence, RI, USA, 2013. [Google Scholar]
- BS EN 10248; Hot Rolled Sheet Piling of Non-Alloy Steels. Technical Delivery Conditions. BSI Group: London, UK, 1996.
- Novotny, J.W.; Perkins, W.W.; Price, J.N.; Watts, R.L.; Wheeler, H.C. NAVFAC (CHESDIV) (Naval Facilities Engineering Command) (Chesapeake Division) Standards and Criteria Program, Phase 1A, Volume 1; Naval Undersea Center: San Diego, CA, USA, 1975.
- Woods, R.D. Dynamic Effects of Pile Installations on Adjacent Structures; National Academy Press: Washington, DC, USA, 1997; pp. 11–15. [Google Scholar]
- Kim, D.S.; Lee, J.S. Propagation and attenuation characteristics of various ground vibrations. Soil Dyn. Earthq. Eng. 2000, 19, 115–126. [Google Scholar] [CrossRef]
- Branch, M.A.; Grace, A. Matlab Optimization Toolbox; The Mathworks Inc.: Natick, MA, USA, 1996. [Google Scholar]
- Deckner, F.; Viking, K.; Hintze, S. Wave patterns in the ground: Case studies related to vibratory sheet pile driving. Geotech. Geol. Eng. 2017, 35, 2863–2878. [Google Scholar] [CrossRef] [Green Version]
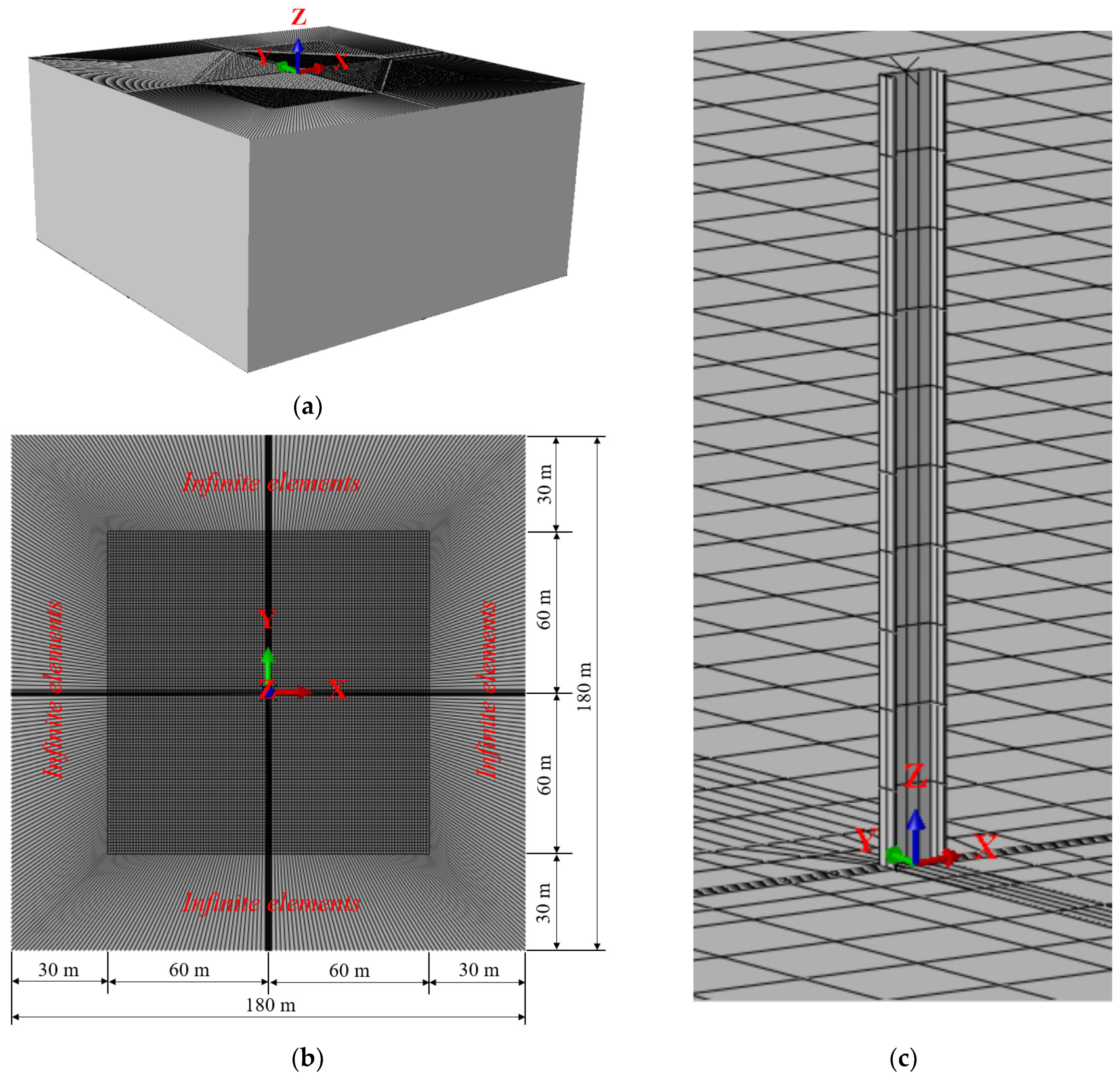
















| Pile Type | U-Type Dimensions b (m)–h (m)–t (m) | Length (m) | Mass (kg/m) |
|---|---|---|---|
| Steel sheet | 0.4–0.17–0.016 | 15 | 76.1 |
| Soil Type | Density (kg/m3) | Modulus of Elasticity (MPa) | Poisson’s Ratio | Friction Angle (Degrees) | Cohesion (kPa) |
|---|---|---|---|---|---|
| Sandy clay | 2000 | 80 | 0.4 | 25 | 15 |
| Actual Vibratory Sheet Pile Driving Locations | Pile Toe on the Ground Surface | Pile Toe 10 m below the Ground Surface | ||||
|---|---|---|---|---|---|---|
| Linear Layout | Linear Layout | Square Layout | ||||
| X (%) | Y (%) | X (%) | Y (%) | X (%) | Y (%) | |
| S1 | 1.85 | 0.02 | 2.67 | 0.02 | 1.00 | 0.02 |
| S2 | 1.70 | 0.02 | 3.33 | 0.02 | 0.67 | 0.02 |
| S3 | 2.00 | 0.02 | 3.00 | 0.02 | 1.75 | 0.02 |
| S4 | 0.92 | 0.08 | 1.75 | 0.12 | 0.92 | 0.10 |
| S5 | 1.67 | 0.02 | 3.33 | 0.02 | 1.33 | 0.02 |
| S6 | 1.38 | 0.08 | 2.22 | 0.08 | 1.38 | 0.14 |
| S7 | 1.50 | 0.17 | 2.25 | 0.19 | 1.42 | 0.15 |
| S8 | 1.50 | 0.08 | 4.00 | 0.09 | 1.50 | 0.09 |
| S9 | 2.08 | 0.19 | 1.67 | 0.19 | 1.58 | 0.17 |
| Mean | 1.62 | 0.08 | 2.69 | 0.08 | 1.28 | 0.08 |
| Max. | 2.08 | 0.19 | 4.00 | 0.19 | 1.75 | 0.17 |
| Investigated Parameters | Mean | Max. | |||
|---|---|---|---|---|---|
| X (%) | Y (%) | X (%) | Y (%) | ||
| Shear wave velocity (when f0 = 20 Hz, μ = 0.25) | vs = 60 m/s | 2.52 | 0.08 | 4.17 | 0.25 |
| vs = 120 m/s | 2.69 | 0.08 | 4.00 | 0.19 | |
| vs = 250 m/s | 3.56 | 0.07 | 4.78 | 0.25 | |
| Vibratory driving frequency (when vs = 120 m/s, μ = 0.25) | f0 = 20 Hz | 2.69 | 0.08 | 4.00 | 0.19 |
| f0 = 40 Hz | 2.71 | 0.06 | 3.68 | 0.17 | |
| f0 = 60 Hz | 3.73 | 0.07 | 5.30 | 0.21 | |
| Pile–soil friction coefficient (when vs = 120 m/s, f0 = 20 Hz) | μ = 0.1 | 3.35 | 0.09 | 5.07 | 0.17 |
| μ = 0.25 | 2.69 | 0.08 | 4.00 | 0.19 | |
| μ = 0.4 | 1.75 | 0.07 | 3.08 | 0.25 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhu, S. Global Vibration Intensity Assessment Based on Vibration Source Localization on Construction Sites: Application to Vibratory Sheet Piling. Appl. Sci. 2022, 12, 1946. https://doi.org/10.3390/app12041946
Wang S, Zhu S. Global Vibration Intensity Assessment Based on Vibration Source Localization on Construction Sites: Application to Vibratory Sheet Piling. Applied Sciences. 2022; 12(4):1946. https://doi.org/10.3390/app12041946
Chicago/Turabian StyleWang, Shiguang, and Songye Zhu. 2022. "Global Vibration Intensity Assessment Based on Vibration Source Localization on Construction Sites: Application to Vibratory Sheet Piling" Applied Sciences 12, no. 4: 1946. https://doi.org/10.3390/app12041946
APA StyleWang, S., & Zhu, S. (2022). Global Vibration Intensity Assessment Based on Vibration Source Localization on Construction Sites: Application to Vibratory Sheet Piling. Applied Sciences, 12(4), 1946. https://doi.org/10.3390/app12041946






