Deep Graph Reinforcement Learning Based Intelligent Traffic Routing Control for Software-Defined Wireless Sensor Networks
Abstract
:1. Introduction
- We proposed a deep graph reinforcement learning (DGRL)-based framework for intelligent traffic control in SDWSN systems. By learning and optimizing the data forwarding policy, the SDN controller can provide adaptive and effective routing control for dynamic traffic patterns and network topologies.
- We designed an actor–critic network architecture for the DRGL model, which takes into account both graph convolutional networks and deterministic policy gradient. Reward functions for the reinforcement learning and training method were developed for the DRGL model.
- Compared with traditional routing protocols, the proposed DGRL traffic control mechanism can effectively reduce the probability of network congestion, especially in the case of high concurrent traffic intensity. Simulation experiments based on the Omnet++ platform show that, compared with existing traffic routing algorithms for SDWSNs, the proposed intelligent routing control method can effectively reduce packet transmission delay, increase PDR (Packet Delivery Ratio), and reduce the probability of network congestion.
2. Related Works
3. System Design
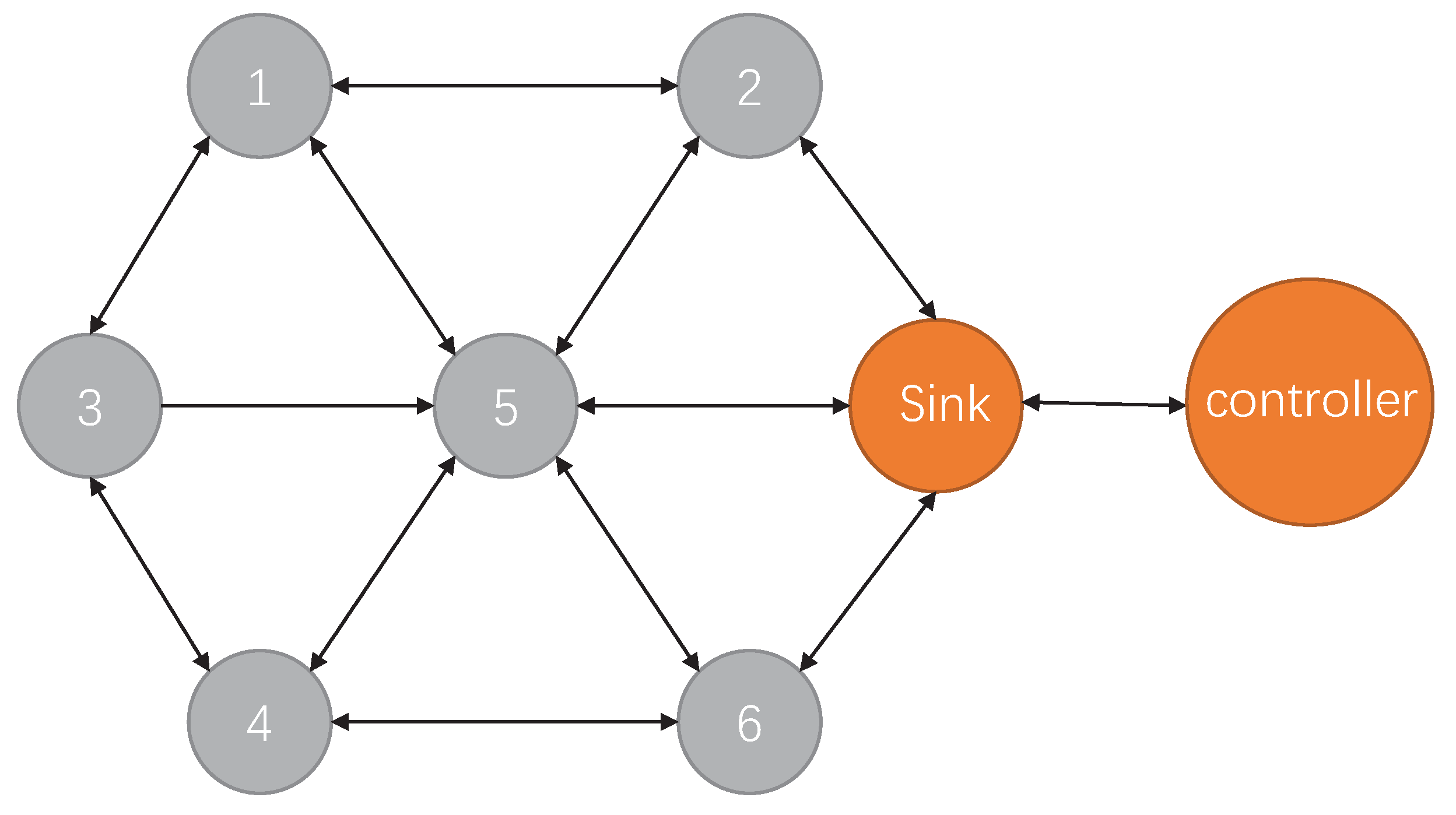
3.1. Problem Statement and Notations
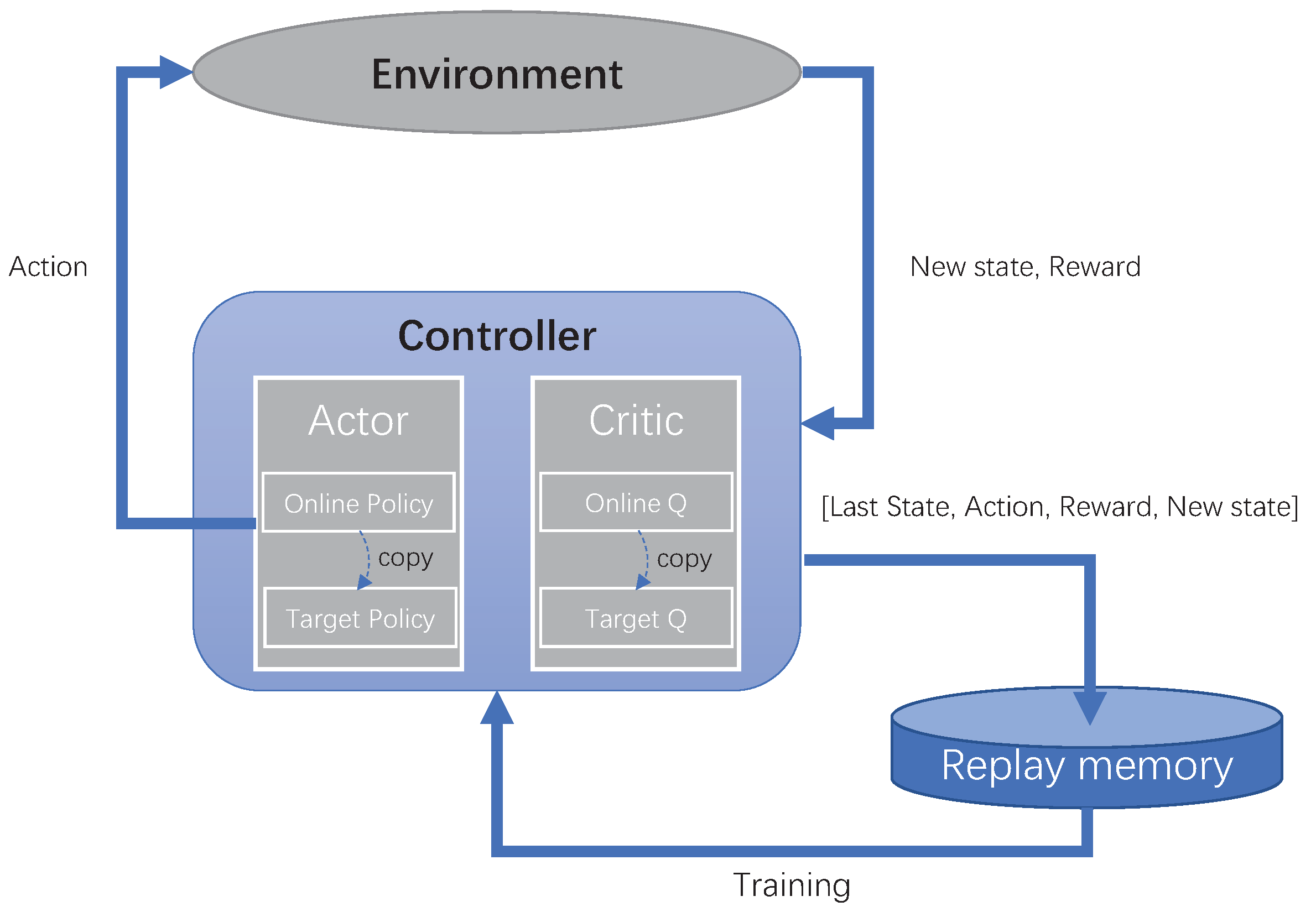
3.2. System Framework of DGRL
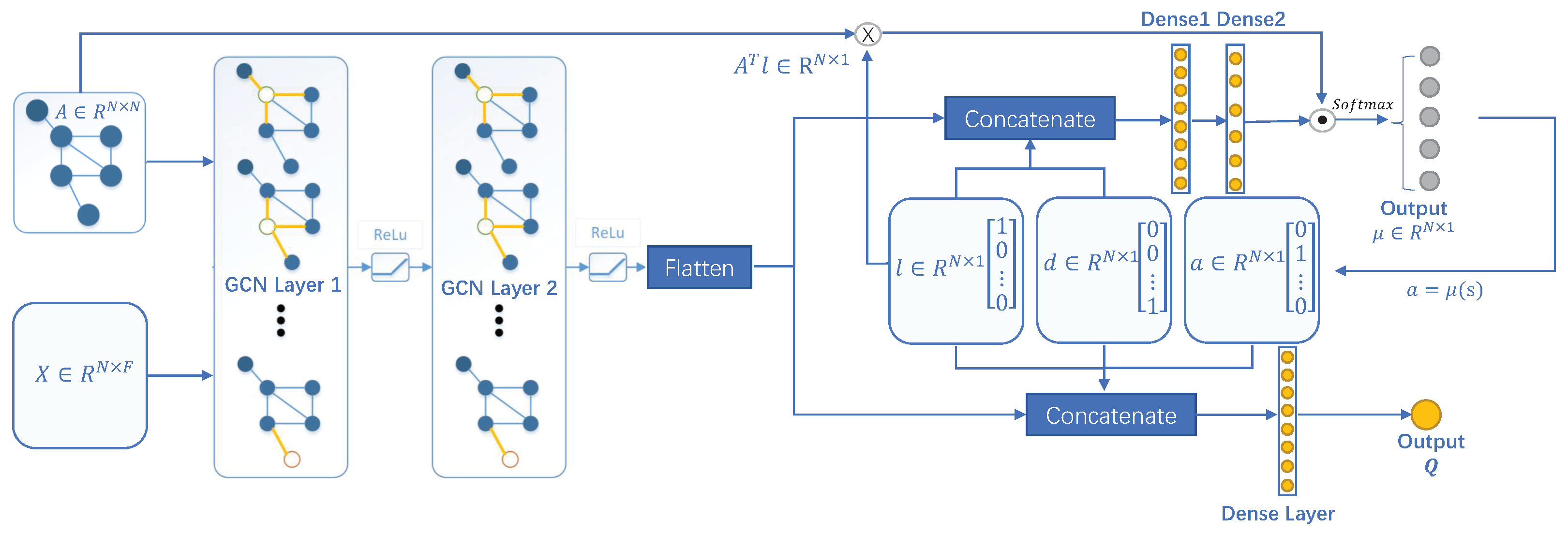
3.3. Feedforward Processes for Actor and Critic Models
3.3.1. Feedforward Calculation of Actor Neural Network
3.3.2. Feedforward Calculation of Critic Neural Network
3.4. Design of DGRL Training Method, Controller Node Features and Reward Function
3.4.1. The Training Method of DGRL
3.4.2. Design of Node Characteristics and Reward Function
3.5. Traffic Control Based on Deep Graph Reinforcement Learning
| Algorithm 1 Running phase |
| Input: batch size, Load the weights: for target Actor model
|
| Algorithm 2 Training phase |
Input: Adjacency matrix A of the SDN, Experience Replay,
|
4. Evaluation
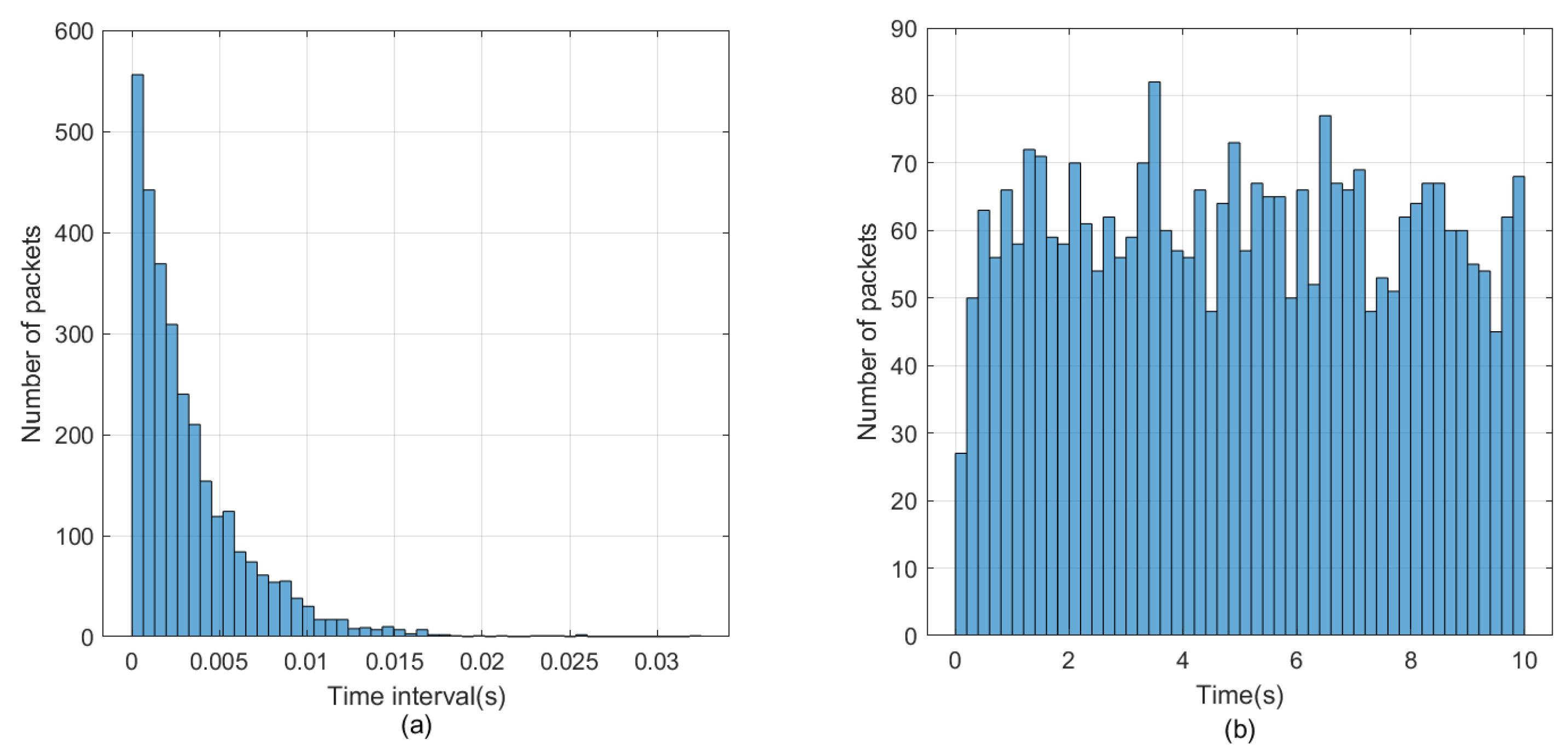
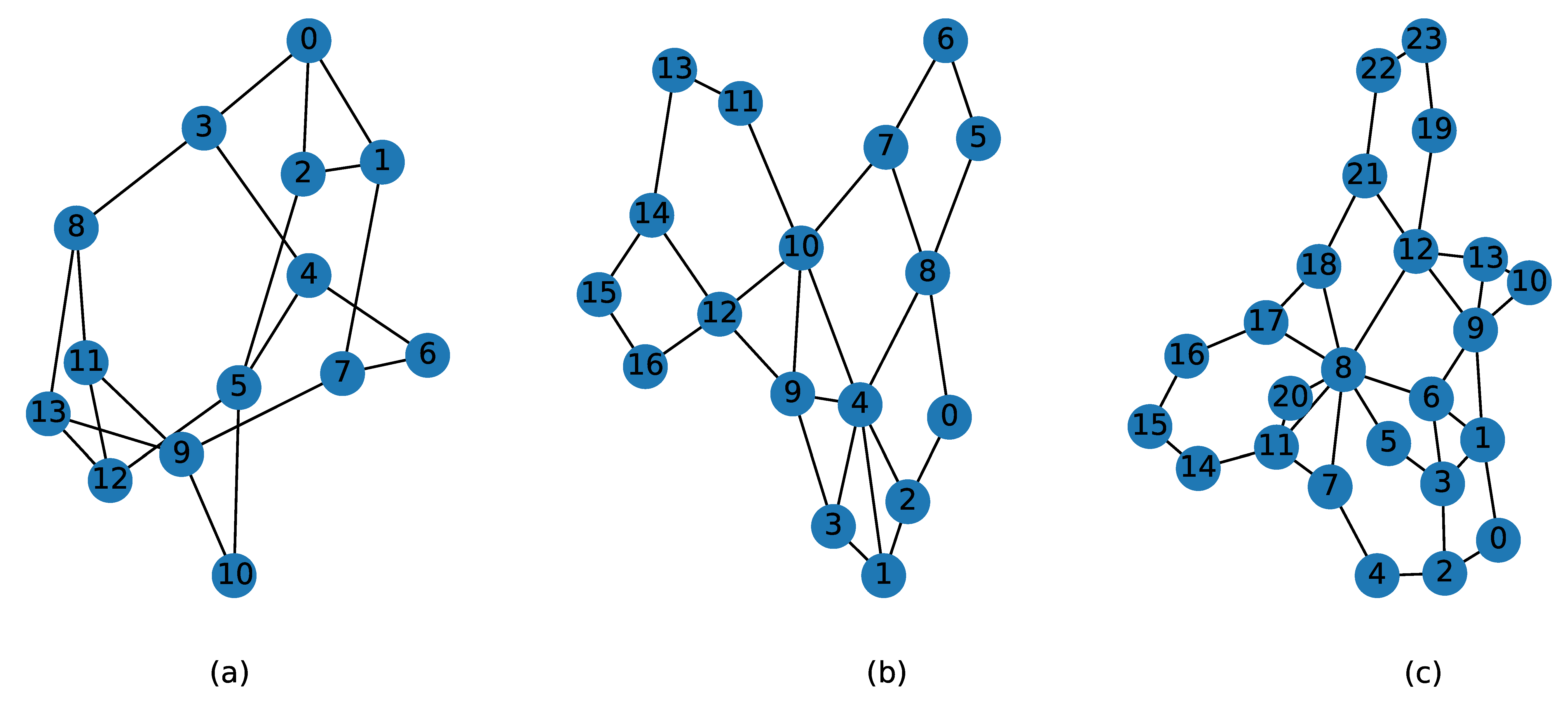
4.1. Simulation Environment
4.1.1. Operation Platform
4.1.2. Parameter Setting
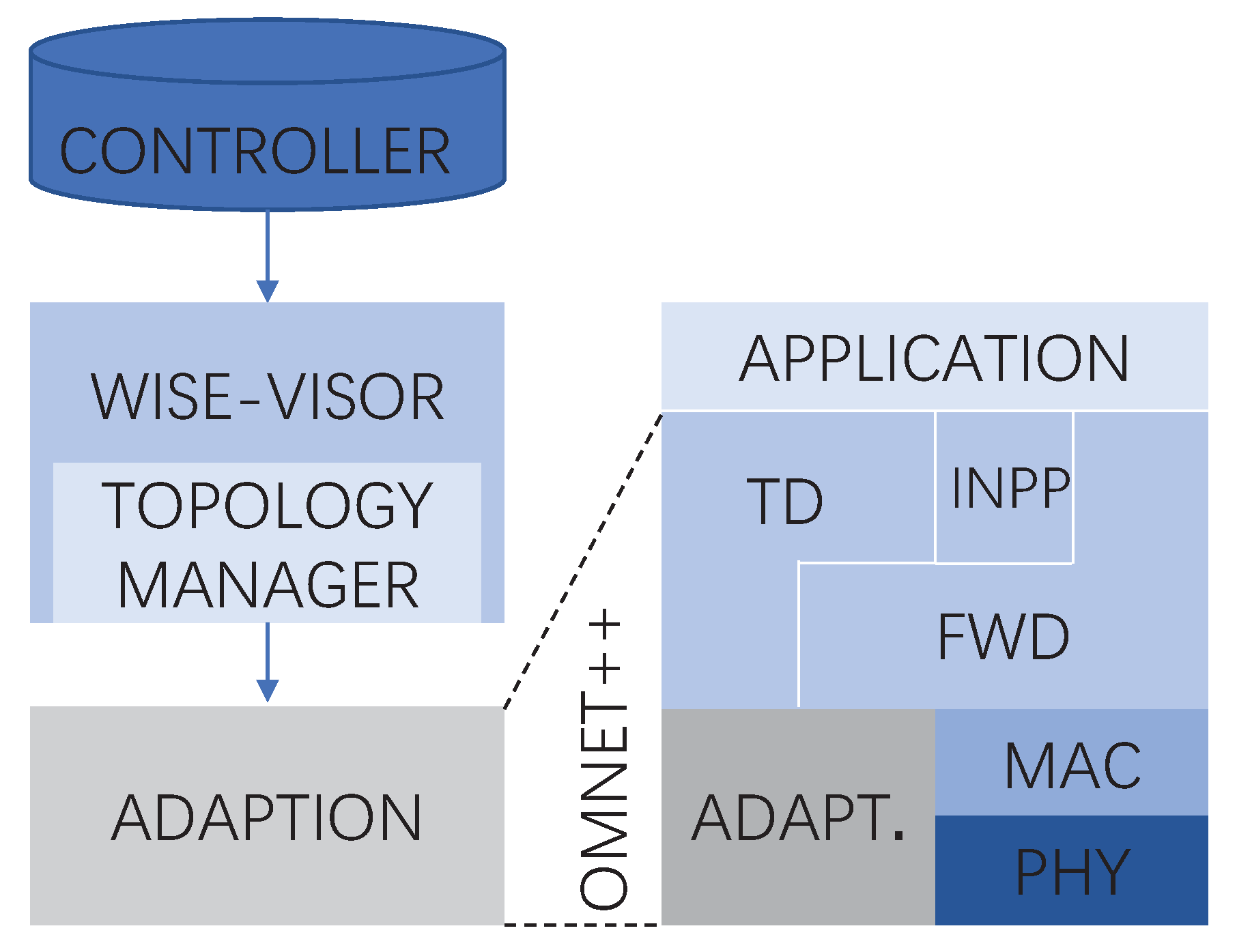
4.1.3. Protocol Architecture
4.2. Compared Algorithm Models
- 1.
- Open Shortest Path First (OSPF): According to the directed graph of the network topology, the algorithm generates a shortest path tree as a static routing table. Nodes will forward packets based on the flow table generated by this static routing table.
- 2.
- Deep Reinforcement Learning-Optimized Routing (DRL-OR) [35]: The model contains two fully connected layers and uses the traffic features of nodes to represent the network state. The dimension of state is 182. Its Actor and Critical models are two-layer perceptron structures, and the dimensions of perceptron are [91,42].
- 3.
- Deep Reinforcement Learning-Full Connect (DGRL-FC): All GCN layers of the proposed DGRL model are removed, and only the perceptron layers of each model are retained. The other neural network parameters are completely consistent with DGRL.
4.3. Performance Evaluation Metrics
4.3.1. Average Network Delay
4.3.2. PDR
4.3.3. Dispersion of Routing Load
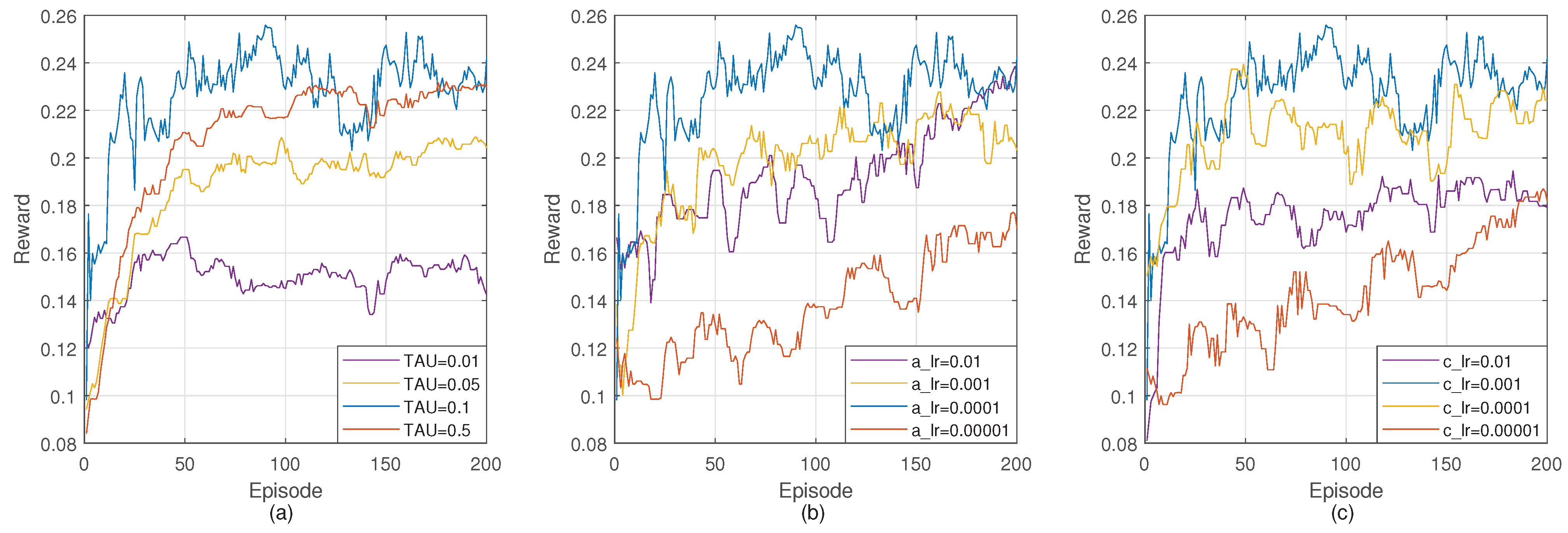
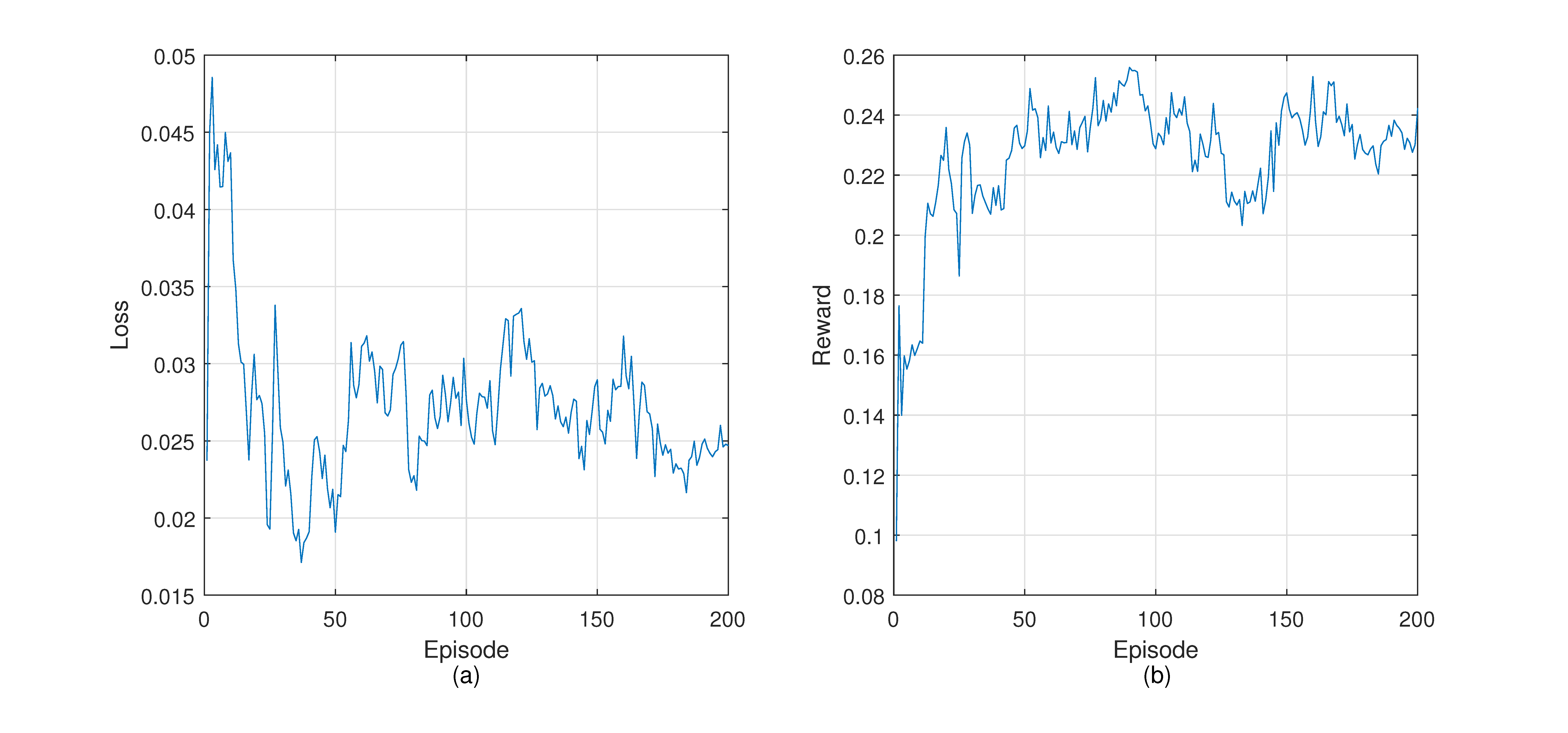
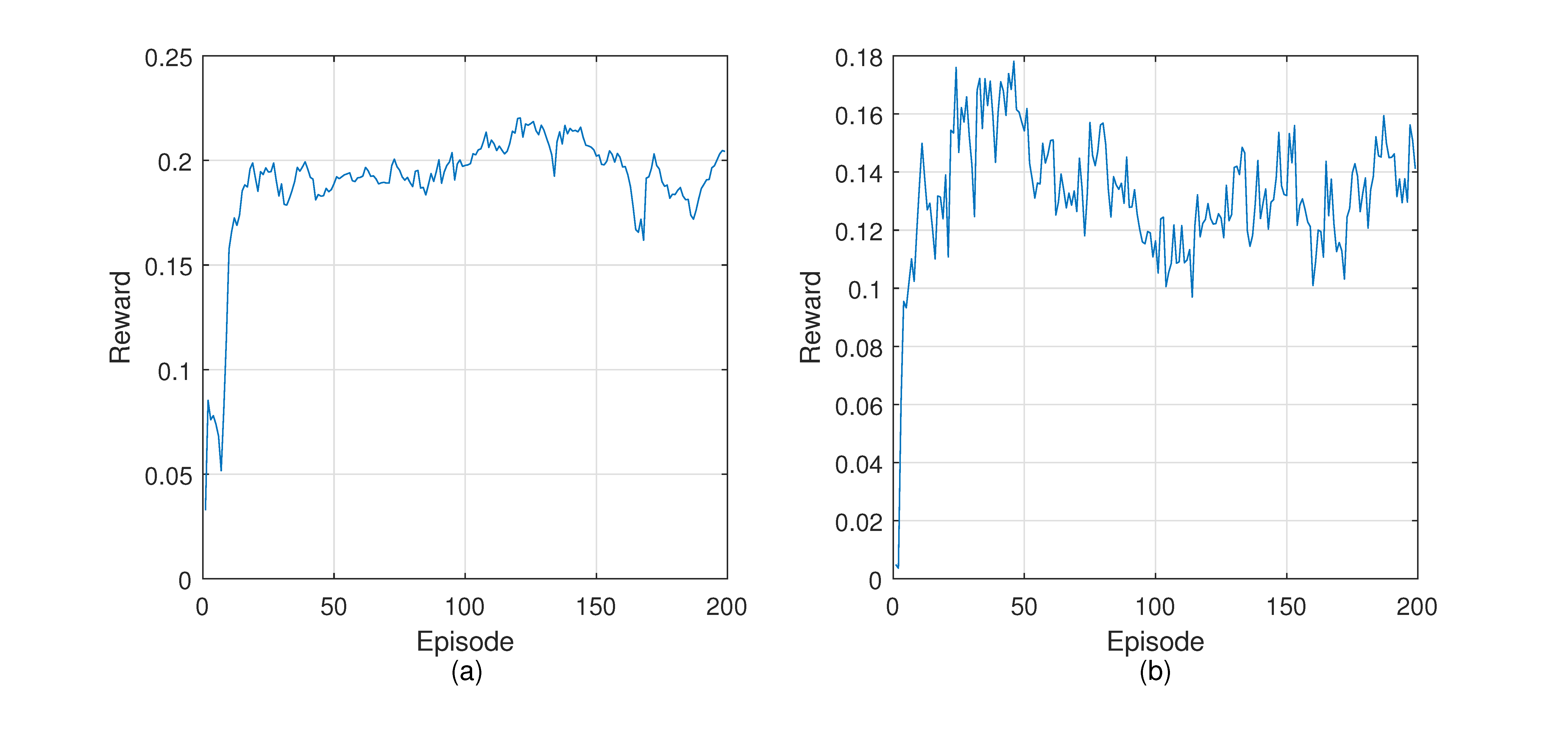
4.4. Training DGRL
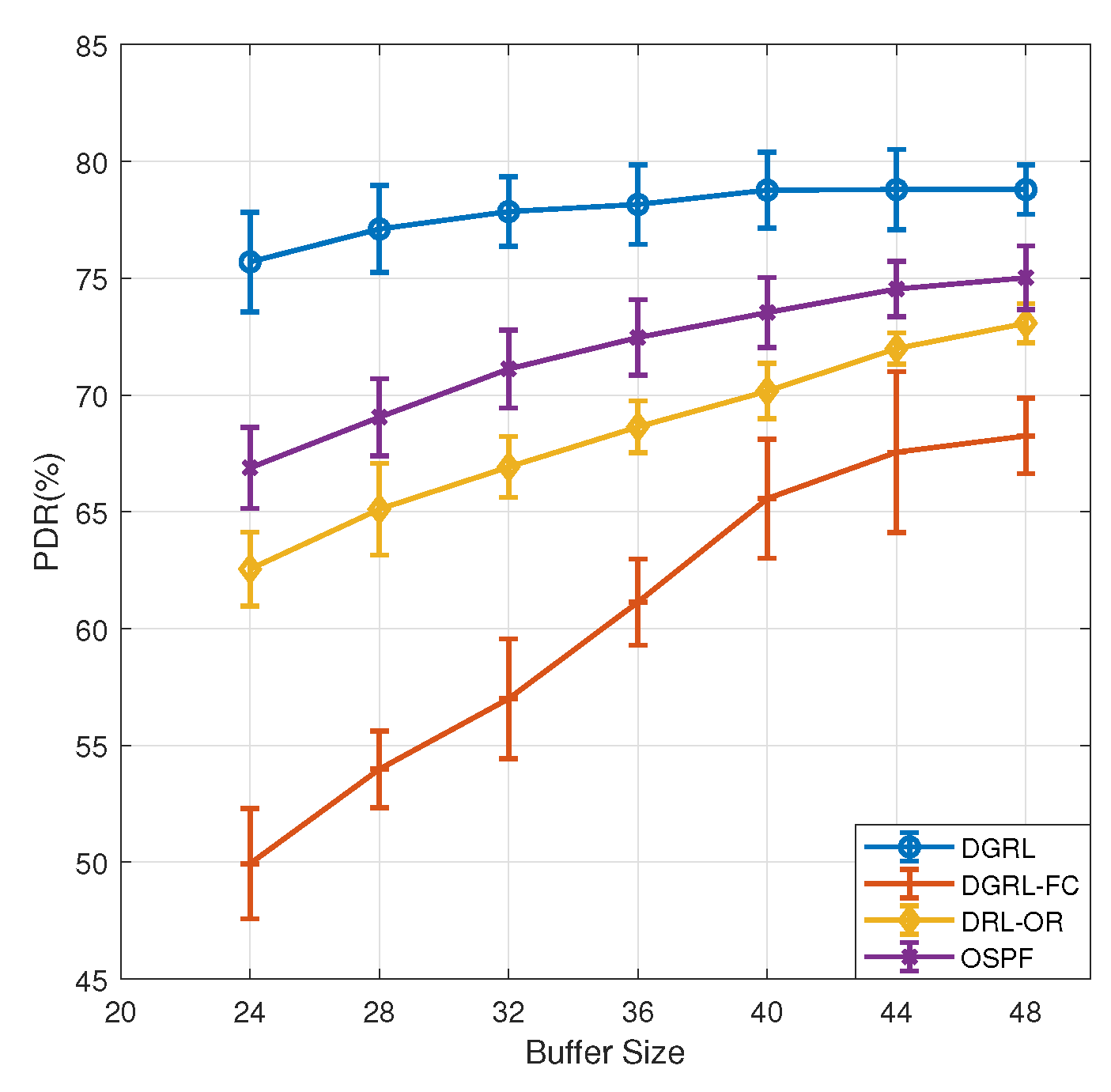
4.5. Evaluation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kibria, M.G.; Nguyen, K.; Villardi, G.P.; Zhao, O.; Ishizu, K.; Kojima, F. Big data analytics, machine learning, and artificial intelligence in next-generation wireless networks. IEEE Access 2018, 6, 32328–332338. [Google Scholar] [CrossRef]
- Qin, Z.; Denker, G.; Giannelli, C.; Bellavista, P.; Venkatasubramanian, N. A software defined networking architecture for the internet-of-things. In Proceedings of the 2014 IEEE network operations and management symposium (NOMS), Krakow, Poland, 5–9 May 2014; pp. 1–9. [Google Scholar]
- Kalkan, K.; Zeadally, S. Securing internet of things with software defined networking. IEEE Commun. Mag. 2017, 56, 186–192. [Google Scholar] [CrossRef]
- Galluccio, L.; Milardo, S.; Morabito, G.; Palazzo, S. Sdn-wise: Design, prototyping and experimentation of a stateful sdn solution for wireless sensor networks. In Proceedings of the 2015 IEEE Conference on Computer Communications (INFOCOM), Hong Kong, China, 26 April–1 May 2015; pp. 513–521. [Google Scholar]
- Margi, C.B.; Alves, R.C.; Segura, G.A.N.; Oliveira, D.A. Software-defined wireless sensor networks approach: Southbound protocol and its performance evaluation. Open J. Internet Things (OJIOT) 2018, 4, 99–108. [Google Scholar]
- Guo, Y.; Wang, Z.; Yin, X.; Shi, X.; Wu, J. Traffic engineering in sdn/ospf hybrid network. In Proceedings of the 2014 IEEE 22nd International Conference on Network Protocols, Raleigh, NC, USA, 21–24 October 2014; pp. 563–568. [Google Scholar]
- Shanmugapriya, S.; Shivakumar, M. Context based route model for policy based routing in wsn using sdn approach. In Proceedings of the BGSIT National Conference on Emerging Trends in Electronics and Communication, Karnataka, India, 5 May 2015. [Google Scholar]
- Younus, M.U.; Khan, M.K.; Anjum, M.R.; Afridi, S.; Arain, Z.A.; Jamali, A.A. Optimizing the lifetime of software defined wireless sensor network via reinforcement learning. IEEE Access 2020, 9, 259–272. [Google Scholar] [CrossRef]
- Mousavi, S.S.; Schukat, M.; Howley, E. Deep reinforcement learning: An overview. In Proceedings of the SAI Intelligent Systems Conference, London, UK, 21–22 September 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 426–440. [Google Scholar]
- Bao, K.; Matyjas, J.D.; Hu, F.; Kumar, S. Intelligent software-defined mesh networks with link-failure adaptive traffic balancing. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 266–276. [Google Scholar] [CrossRef]
- Huang, R.; Chu, X.; Zhang, J.; Hu, Y.H. Energy-efficient monitoring in software defined wireless sensor networks using reinforcement learning: A prototype. Int. J. Distrib. Sens. Netw. 2015, 11, 360428. [Google Scholar] [CrossRef]
- Bi, Y.; Han, G.; Lin, C.; Peng, Y.; Pu, H.; Jia, Y. Intelligent quality of service aware traffic forwarding for software-defined networking/open shortest path first hybrid industrial internet. IEEE Trans. Ind. Inform. 2019, 16, 1395–1405. [Google Scholar] [CrossRef]
- Al-Jawad, A.; Trestian, R.; Shah, P.; Gemikonakli, O. Baprobsdn: A probabilistic-based qos routing mechanism for software defined networks. In Proceedings of the 2015 1st IEEE Conference on Network Softwarization (NetSoft), London, UK, 13–17 April 2015; pp. 1–5. [Google Scholar]
- Shrestha, A.; Mahmood, A. Review of deep learning algorithms and architectures. IEEE Access 2019, 7, 53040–53065. [Google Scholar] [CrossRef]
- Tang, F.; Mao, B.; Fadlullah, Z.M.; Kato, N.; Akashi, O.; Inoue, T.; Mizutani, K. On removing routing protocol from future wireless networks: A real-time deep learning approach for intelligent traffic control. IEEE Wirel. Commun. 2017, 25, 154–160. [Google Scholar] [CrossRef]
- Mao, B.; Fadlullah, Z.M.; Tang, F.; Kato, N.; Akashi, O.; Inoue, T.; Mizutani, K. Routing or computing? the paradigm shift towards intelligent computer network packet transmission based on deep learning. IEEE Trans. Comput. 2017, 66, 1946–1960. [Google Scholar] [CrossRef]
- Huang, R.; Ma, L.; Zhai, G.; He, J.; Chu, X.; Yan, H. Resilient routing mechanism for wireless sensor networks with deep learning link reliability prediction. IEEE Access 2020, 8, 64857–64872. [Google Scholar] [CrossRef]
- Tang, F.; Fadlullah, Z.M.; Mao, B.; Kato, N. An intelligent traffic load prediction-based adaptive channel assignment algorithm in sdn-iot: A deep learning approach. IEEE Internet Things J. 2018, 5, 5141–5154. [Google Scholar] [CrossRef]
- Tang, F.; Mao, B.; Fadlullah, Z.M.; Liu, J.; Kato, N. St-delta: A novel spatial-temporal value network aided deep learning based intelligent network traffic control system. IEEE Trans. Sustain. Comput. 2019, 5, 568–580. [Google Scholar] [CrossRef]
- Sanagavarapu, S.; Sridhar, S. Sdpredictnet-a topology based sdn neural routing framework with traffic prediction analysis. In Proceedings of the 2021 IEEE 11th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 27–30 January 2021; pp. 0264–0272. [Google Scholar]
- Mao, B.; Tang, F.; Fadlullah, Z.M.; Kato, N.; Akashi, O.; Inoue, T.; Mizutani, K. A novel non-supervised deep-learning-based network traffic control method for software defined wireless networks. IEEE Wirel. Commun. 2018, 25, 74–81. [Google Scholar] [CrossRef]
- Chen, Y.-R.; Rezapour, A.; Tzeng, W.-G.; Tsai, S.-C. Rl-routing: An sdn routing algorithm based on deep reinforcement learning. IEEE Trans. Netw. Sci. Eng. 2020, 7, 3185–3199. [Google Scholar] [CrossRef]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Hu, T.; Fei, Y. Qelar: A machine-learning-based adaptive routing protocol for energy-efficient and lifetime-extended underwater sensor networks. IEEE Trans. Mob. Comput. 2010, 9, 796–809. [Google Scholar]
- Huang, R.; Chu, X.; Zhang, J.; Hu, Y.H.; Yan, H. A machine-learning-enabled context-driven control mechanism for software-defined smart home networks. Sens. Mater. 2019, 31, 2103–2129. [Google Scholar] [CrossRef]
- Razzaque, M.A.; Ahmed, M.H.U.; Hong, C.S.; Lee, S. Qos-aware distributed adaptive cooperative routing in wireless sensor networks. Ad Hoc Netw. 2014, 19, 28–42. [Google Scholar] [CrossRef]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In International Conference on Machine Learning; PMLR: Beijing, China, 22–24 June 2014; pp. 387–395. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.-X. Intelligent routing based on deep reinforcement learning in software-defined data-center networks. In Proceedings of the 2019 IEEE Symposium on Computers and Communications (ISCC), Barcelona, Spain, 29 June–3 July 2019; pp. 1–6. [Google Scholar]
- Yu, C.; Lan, J.; Guo, Z.; Hu, Y. Drom: Optimizing the routing in software-defined networks with deep reinforcement learning. IEEE Access 2018, 6, 64533–64539. [Google Scholar] [CrossRef]
- Abbasloo, S.; Yen, C.-Y.; Chao, H.J. Classic meets modern: A pragmatic learning-based congestion control for the internet. In Proceedings of the Annual conference of the ACM Special Interest Group on Data Communication on the Applications, Technologies, Architectures, and Protocols for Computer Communication, New York, NY, USA, 10–14 August 2020; pp. 632–647. [Google Scholar]
- Meng, Z.; Wang, M.; Bai, J.; Xu, M.; Mao, H.; Hu, H. Interpreting deep learning-based networking systems. In Proceedings of the Annual conference of the ACM Special Interest Group on Data Communication on the Applications, Technologies, Architectures, and Protocols for Computer Communication, New York, NY, USA, 10–14 August 2020; pp. 154–171. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the brownian motion. Phys. Rev. 1930, 36, 823. [Google Scholar] [CrossRef]
- Stampa, G.; Arias, M.; Sánchez-Charles, D.; Muntés-Mulero, V.; Cabellos, A. A deep-reinforcement learning approach for software-defined networking routing optimization. arXiv 2017, arXiv:1709.07080. [Google Scholar]


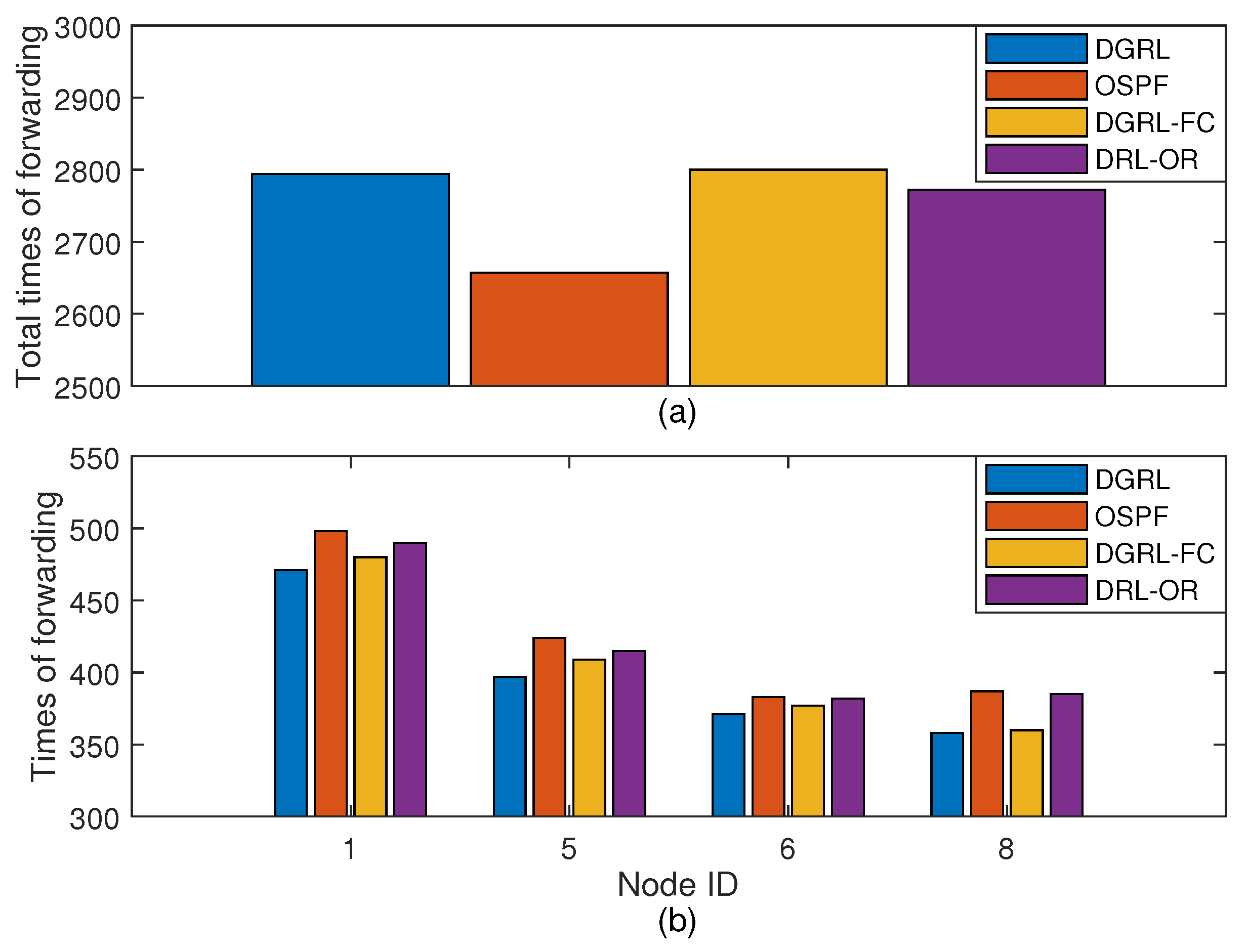
| Reference | Metrics | Experimental Platform | Drawbacks |
|---|---|---|---|
| Chen et al. [22] | Reward, file transmission time, utilization rate | Simulations:Mininet | Fixed traffic patterns |
| Younus et al. [8] | Lifetime | Real-tested: Raspberry Pi 3 | Limited metrics |
| Hu et al. [24] | Energy consumption, delivery rate | Simulations:NS2 | Limited scenarios |
| Huang et al. [25] | Energy consumption | Simulations:NS3 | Lack metrics |
| Razzaque et al. [26] | Delay, delivery ratio, energy consumption, overhead, lifetime | Simulations:NS2 | Limited scenarios |
| Liu et al. [30] | Flow completion time, throughput, link load | Simulations:OMNet++ | Very light traffic |
| Yu et al. [31] | Delay, throughput | Simulations:OMNet++ | Limited scenarios |
| Abbasloo et al. [32] | Throughput | Real-world scenarios | Limited metrics, heavyweight to deploy |
| Meng et al. [33] | Criticality of path | Own testbed Simulations | Lack comparisons and metrics |
| Symbol | Description |
|---|---|
| N | The number of nodes in the network |
| A | The adjacency matrix of the network |
| X | The feature matrix of all nodes |
| l | One-hot coding of current node |
| d | One-hot coding of target node |
| F | The number of features of nodes |
| The output action decision vector of the Actor model | |
| J | The number of packets that received by its destination node |
| The time when packet j sent by its source node | |
| The time when packet j received by its destination node | |
| The number of packets received at node as a destination | |
| The number of packets dropped at node | |
| The ratio of the number of packets forwarded by node to the total number of packets forwarded in the network | |
| The average of |
| Parameters | Setting |
|---|---|
| Number of nodes | 14 |
| Channel rate | 8 kbps |
| Average channel delay | 58.0014521 ms |
| Average packet length | 1026.28 bit |
| Buffer length | 24, 28, 32, 36, 40, 44, 48 |
| Parameters | Setting |
|---|---|
| Soft replacement | |
| Reward discount | |
| Learning rate for the Actor model | |
| Learning rate for the Critic model | |
| Initial random exploration rate | |
| Final random exploration rate |
| Model Name | Layer Name | Parameter Details | ||
|---|---|---|---|---|
| Hidden Units | Activation | Trainable Weights | ||
| Actor model | GCN1 | 256 | ReLU | 10,774 |
| GCN2 | 8 | ReLU | ||
| Denses1 | 64 | ReLU | ||
| Denses2 | N | Linear | ||
| Output | 1 | Softmax | ||
| Critic model | GCN1 | 256 | ReLU | 10,113 |
| GCN2 | 8 | ReLU | ||
| Dense layer | 64 | ReLU | ||
| Output | 1 | Linear | ||
| Topology | Method | PDR(%) | Delay (s) | Dispersion |
|---|---|---|---|---|
| GBN topology | DGRL | 73.11 | 6.97 | 0.049 |
| OSPF | 66.92 | 7.18 | 0.058 | |
| GEANT2 topology | DGRL | 68.65 | 7.26 | 0.051 |
| OSPF | 62.82 | 7.41 | 0.062 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, R.; Guan, W.; Zhai, G.; He, J.; Chu, X. Deep Graph Reinforcement Learning Based Intelligent Traffic Routing Control for Software-Defined Wireless Sensor Networks. Appl. Sci. 2022, 12, 1951. https://doi.org/10.3390/app12041951
Huang R, Guan W, Zhai G, He J, Chu X. Deep Graph Reinforcement Learning Based Intelligent Traffic Routing Control for Software-Defined Wireless Sensor Networks. Applied Sciences. 2022; 12(4):1951. https://doi.org/10.3390/app12041951
Chicago/Turabian StyleHuang, Ru, Wenfan Guan, Guangtao Zhai, Jianhua He, and Xiaoli Chu. 2022. "Deep Graph Reinforcement Learning Based Intelligent Traffic Routing Control for Software-Defined Wireless Sensor Networks" Applied Sciences 12, no. 4: 1951. https://doi.org/10.3390/app12041951
APA StyleHuang, R., Guan, W., Zhai, G., He, J., & Chu, X. (2022). Deep Graph Reinforcement Learning Based Intelligent Traffic Routing Control for Software-Defined Wireless Sensor Networks. Applied Sciences, 12(4), 1951. https://doi.org/10.3390/app12041951






