Designing the Controller-Based Urban Traffic Evaluation and Prediction Using Model Predictive Approach

Abstract

As society grows, the urbanized population proliferates, and urbanization accelerates. Increasing traffic problems affect the normal process of the city. The urban transportation system is vital to the effective functioning of any city. Science and technology are critical elements in improving traffic performance in urban areas. In this paper, a novel control strategy based on selecting the type of traffic light and the duration of the green phase to achieve an optimal balance at intersections is proposed. This balance should be adaptable to fixed behavior of time and randomness in a traffic situation; the goal of the proposed method is to reduce traffic volume in transportation, the average delay for each vehicle, and control the crashing of cars. Due to the distribution of urban traffic and the urban transportation network among intelligent methods for traffic control, the multi-factor system has been designed as a suitable, intelligent, emerging, and successful model. Intersection traffic control is checked through proper traffic light timing modeled on multi-factor systems. Its ability to solve complex real-world problems has made multiagent systems a field of distributed artificial intelligence that is rapidly gaining popularity. The proposed method was investigated explicitly at the intersection through an appropriate traffic light timing by sampling a multiagent system. It consists of many intersections, and each of them is considered an independent agent that shares information with each other. The stability of each agent is proved separately. One of the salient features of the proposed method for traffic light scheduling is that there is no limit to the number of intersections and the distance between intersections. In this paper, we proposed method model predictive control for each intersection’s stability; the simulation results show that the predictive model controller in this multi-factor model predictive system is more valuable than scheduling in the fixed-time method. It reduces the length of vehicle queues.

1. Introduction

Traffic signal control is one of the essential topics in recent world developments. Due to the growing population in cities, the demand for transportation has increased, and heavy road traffic has been known to be a big issue for some time. Controlling traffic and the direct effects of urban transportation systems on traffic are big problems. For example, Mexico City, with the rank of $66\%$, is the first in the world in terms of traffic congestion. This country’s population of 21 million is one of the traffic congestion reasons, which makes the people waste at least 1 hour a day in city traffic. One of the city’s main plans is to reduce traffic congestion by developing public transportation [1,2,3]. Additionally, among the big cities, Istanbul has the highest traffic volume after Mexico City. However, in recent years, traffic congestion has decreased significantly [4]. Over the years, city officials have expanded public transportation to reduce traffic congestion. At the same time, they plan to extend metro lines to decrease traffic congestion in the city. In Istanbul, drivers face the worst traffic congestion in the country and the worst in Europe [5]. It is difficult to get around Istanbul, especially at night. The city’s direct economic effects, such as delays in transporting goods and materials due to traffic congestion leading to severe traffic congestion, are expected [6,7,8,9].

There are equations in the paper for period green phase time queue length; it has been done using fixed time and intelligent technique methods [10]. The intelligent method has been used to adjust signal timing; nowadays, this technique is used for urban traffic control plans. The intelligent methods started in 1990, for which Scoot and Scats are prototypes of intelligent transportation systems [11]. The urban transportation system requires adequate solution methodologies. Traffic signal timing optimization is one of the quickest, most efficient ways to reduce overcrowding at intersections and develop traffic flow in urban traffic [12,13]. There are approaches for solving traffic issues below, such as:

• Compulsory migration for urban dwellers.
• Development of urban transport infrastructure.
• Improving the use of available infrastructure.

For the first approach, if we do not want to be irrational, we have to say that it removes the problem form. The second approach is a vital issue, but this approach comes with hardship and cost in crowded areas like city centers. The third approach seems more straightforward, and it improves how to use transport infrastructure and improves traffic flow. Therefore, to date, traffic control methods have primarily been introduced to classical control methods through data and experiments. Finally, in this research, the parameters desired are adjusted in the form of the optimal and specific level of control. This level of accountability in traffic systems for high complexity of the structure includes sections such as control, communications, computer, and a high volume of implementation and maintenance costs, in research related to traffic control. It has to have a proper and complete understanding and completion of the traffic system. This article aims to provide an intelligent solution for traffic control. Urban traffic is a complex system for controlling traffic issues, consisting of continuous and discrete solutions. Parameters important for controlling traffic include input flow speed to the lines and intersection, adjusting traffic light signals, reducing the effect of noise generated like accidents, stopping unnecessarily, etc. In this work, with attention to the problem, the agents’ approach is studied. We suggest minimizing the number of vehicles at intersections by predicting the green time using urban traffic control strategies [14,15,16]. The system is linear in condition evolution equations, yet links predict queuing dynamics. In the model predictive control approach, linearity is essential, since the objective is to solve optimization problems with near-optimal control techniques repeatedly. We employ only linear dynamics in the proposed model predictive control framework to achieve this [17,18,19]. Multiagents are modeled as a sequence of queues with nonuniform features, and connections at intersections are contacted.

Problem Statement

There are many problems related to traffic congestion in the big city. It generates environmental pollution, hinders transportation, impairs the daily lives of humans, and causes material losses. Researchers are trying to solve this by analyzing various aspects in every country based on the traffic situation. In this work, a traffic light controller was designed using model predictive with MATLAB. Mathematically, at first we used a dynamic model from an intersection, and proposed to improve a single intersection to 8 intersections. Then, for connecting intersections together, we suggested a multiagent model. Eventually, we further proposed a model predictive control for stability proof. The purpose of this research is summarized as follows:

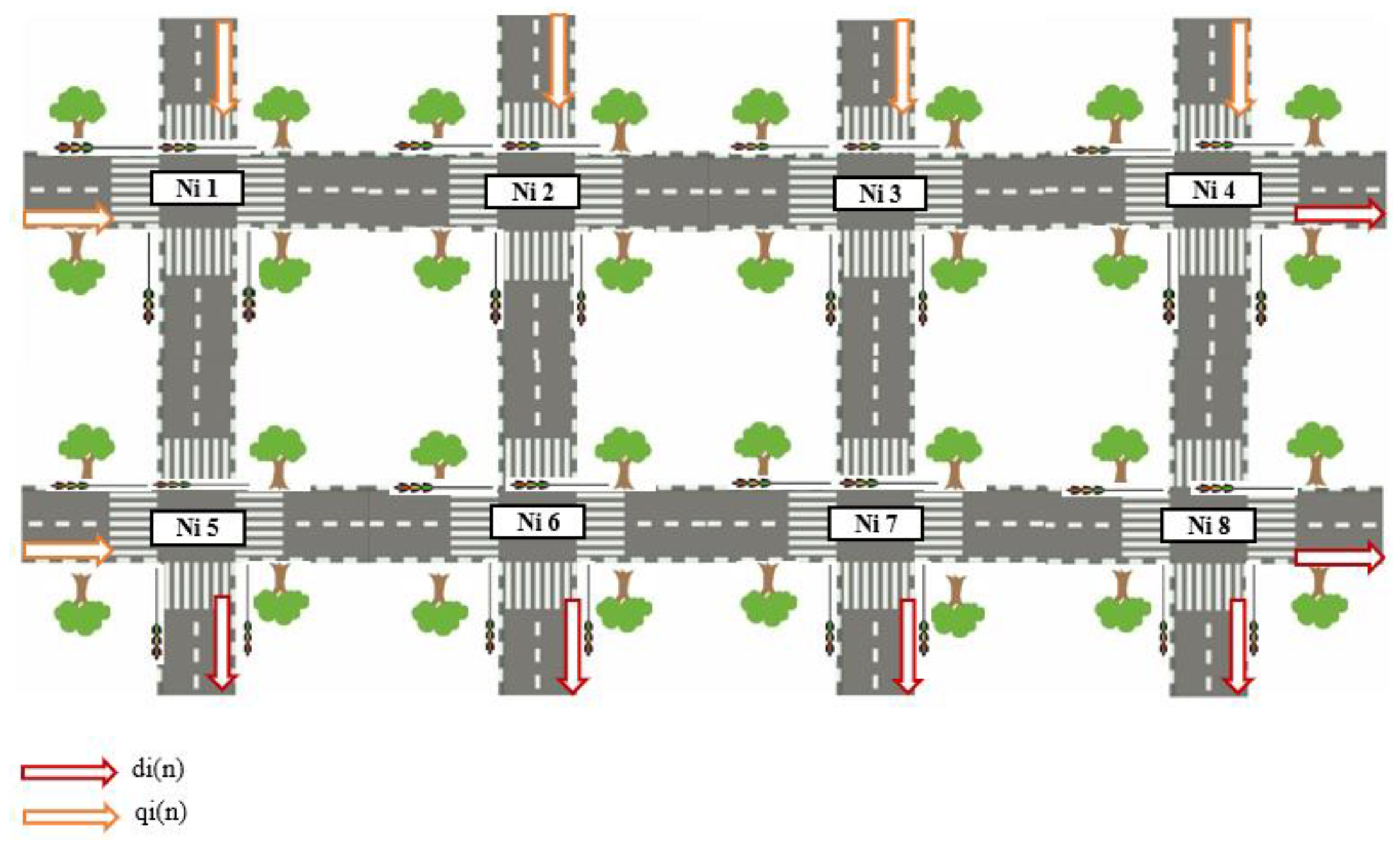
• Linking eight intersections in urban traffic with the use of multiagents.
• Proof and stability of the proposed model.
• Design model predictive controller reduces the number of vehicles in the queue.
• Evaluate the average number of cars queued in the two models with and without a controller.

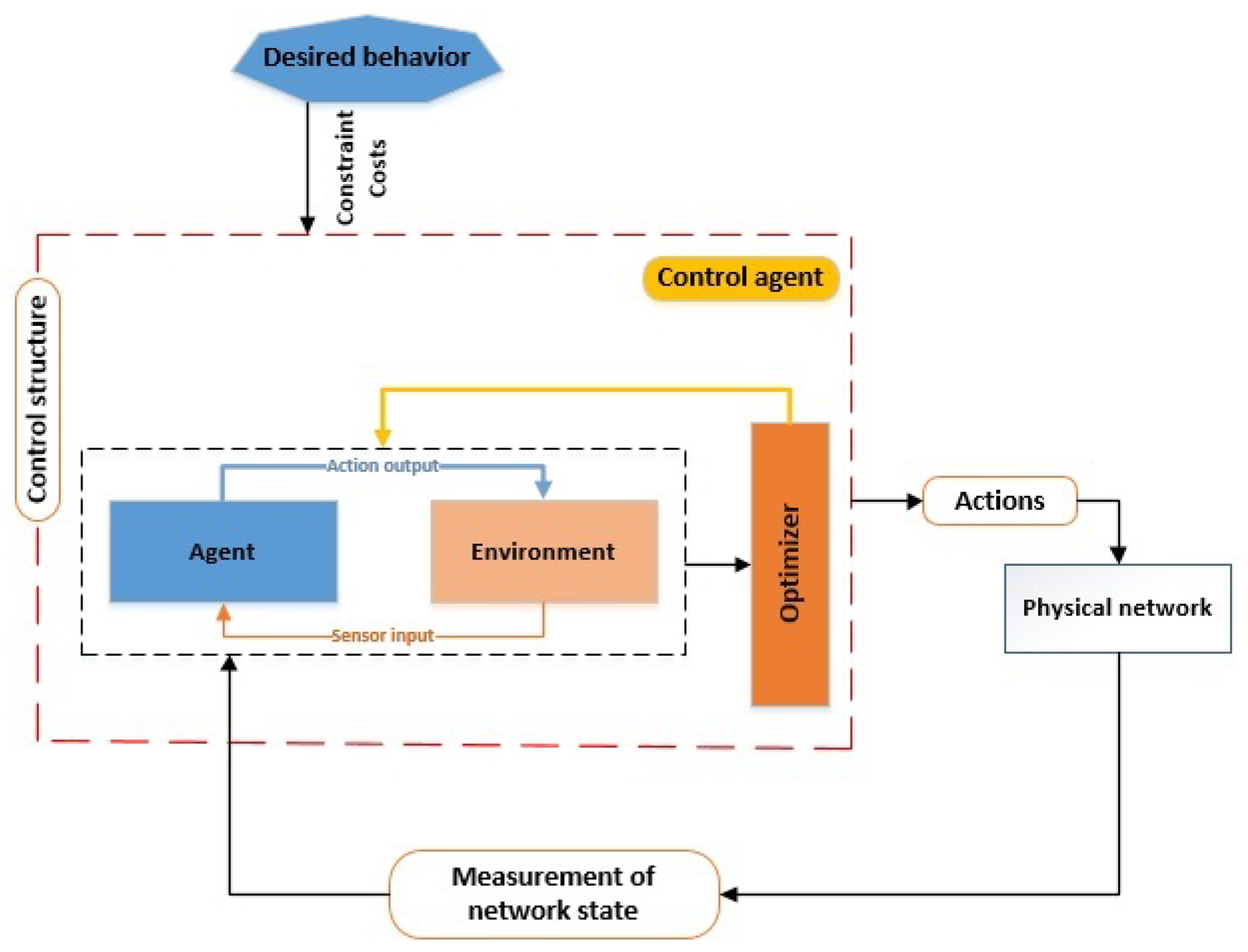
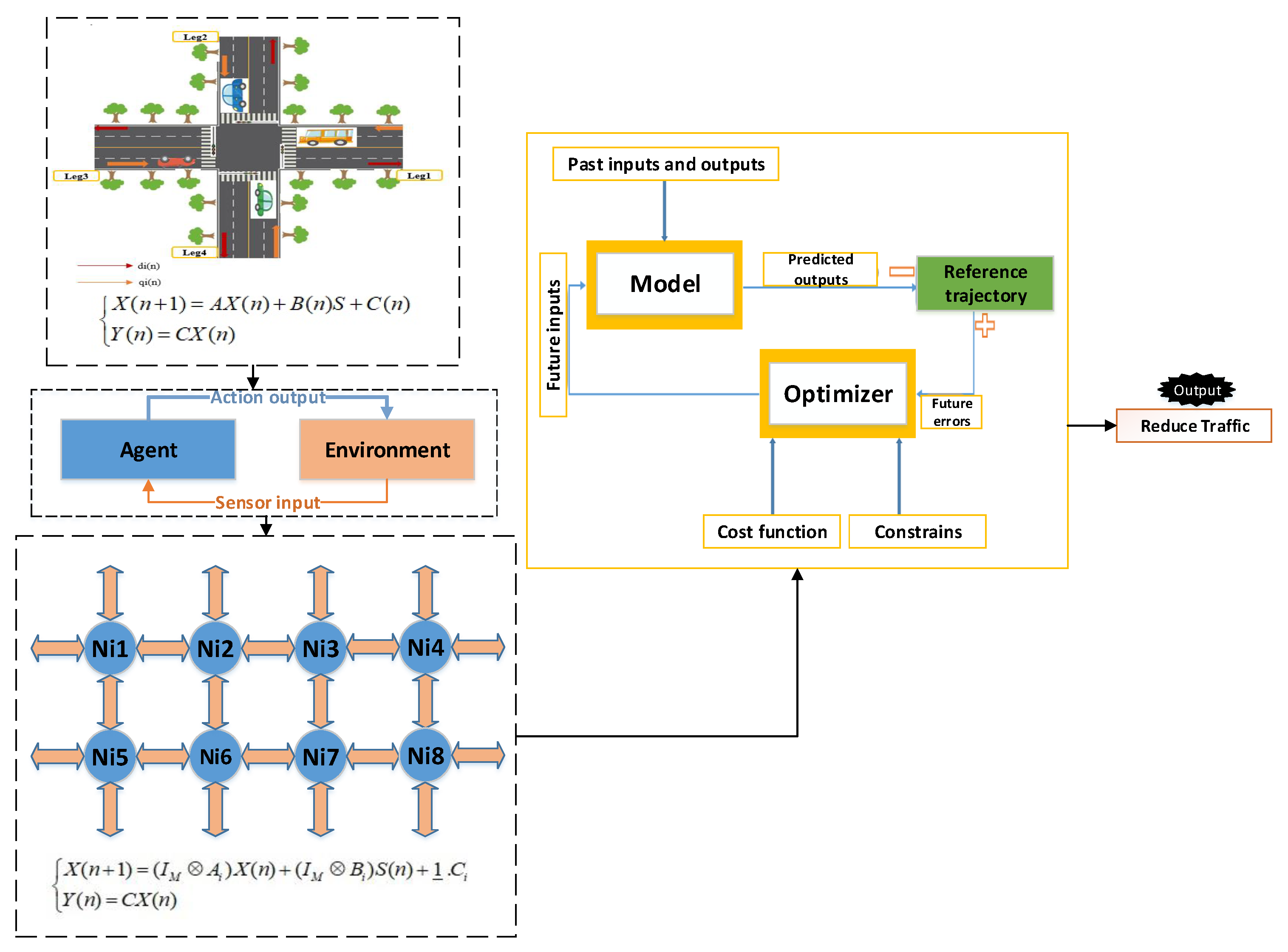
The rest of this paper is categorized as follows. Section 2 introduces related work. Section 3 suggested a building model system for designing model predictive control for intersections with multiple agents. Mathematical models of intersections are described. The stability analysis is mentioned in Section 4. In Section 5, designation of the predictive controller is described in detail. Simulation results are mentioned in Section 6. They are followed by Section 7, which concludes this paper.

2. Related Works

A kind of traffic flow is a fundamental diagram used in urban traffic because of its ability to predict the capability of a road system as it can consider inputs and speed limits with applying regulation. A low-scatter relationship between traffic accumulation can determine traffic accumulation and trip completion rate for urban networks. For example, there is a traffic control strategy for a single urban congested region [20]. This research has presented a macroscopic traffic flow model for the condition to achieve a stable traffic flow. There is congestion in urban overcrowding problems in city roads. However, it is frequently the first point of reference [21]. In [22], the use of Cell Transmission Model (CTM) at a macroscopic model proposed to increase the accuracy and prediction of the trip period at the visible model. The main goal is to create a general structure in urban traffic networks. In [23], they developed an agent-based networked traffic-management system to achieve flexible and intelligent control of traffic and transportation systems. The agent-based control decomposes a complicated control algorithm into simple task-oriented agents which are distributed over a network. This study proposes a fuzzy intelligent controller to achieve an optimal balance at nine intersections. Recently, numerous researchers have applied fuzzy logic in the field of traffic signal control.

2.1. Urban Traffic Control with Multi-Agent

Due to its geographically dispersed nature, many subjects have introduced multiagent system technology in transportation and transport; over the past few years, there has been a dramatic increase in intermittent use and idle running features. One of the most intelligent methods is the Multi-Factor Systems method, which can use multiple intelligent agents to solve problems that interact with each other for controlling urban traffic [24]. The general framework and working methods of forecasting control include process models, cost functions, and organizational strategies; different choices for each element lead to other structures. Predictive control is the first model from which critical processes can be derived [25]. This study examines the intelligent control of consensus control with multiple systems. Control thresholds are introduced for individual systems via event-based, static, flexible, and collaboration methods. It is also rated [26]. An integrated multi-factor deep scalable and scalable local method has been successfully implemented to improve traffic light control for existing traffic systems [27]. This has recently demonstrated a technique that combines Artificial Intelligence and Internet-of-Things, defined as AI-powered Internet-of-Things, which has been processing large amounts of generated data. Then, with the use of multiagent, Q learning, queue lengths, waiting time at intersections, this has improved the throughput efficiency of the all-over control system [28]. The authors of this [29] suggest that a multiagent system (MAS) helps transport operators determine the best transportation strategies to deal with non-urban road accidents. Agents are applied to both systems using the Java Agent Development (JADE) Framework. This paper has used a mathematical method for timing traffic signals at an intersection to deal with travel and improve speed cars by the multiagent system at urban signal traffic; it has been done with the Matlab program [30].

2.2. Urban Traffic by Using Predictive Model Control

Model predictive control was presented in 1970. It is a new model in which a control is based on model prediction [31]. In [32], traffic congestion on major urban roads and highway control to regulate and improve the economy by monitoring the forecast range based on macro base maps was first proposed. The main goal of this system is to use a predictive model for improving traffic signals at urban way traffic, management rights, and finding optimal methods. Currently, the urban transport community is one of the biggest problems [33].

This paper’s primary function is to model and minimize the queue length and the oscillation of green time in urban traffic using predictive model control and neural networks in a genetic algorithm [34].

This article presents a participatory control approach to a bright urban environment based on information from pollution, and urban traffic control engineering models have been used to adjust the length of traffic lights cycles using [35].

Table 1. Existing studies of urban traffic.

Author	Model	Advantages	Limitation
Haber et al. [36]	Cooperative control of urban subsystems	Improve the performance	Urban traffic networks
Pallavi et al. [37]	Deep reinforcement learning	Decision-making capabilities	Region-based traffic flow
Sulaiman et al. [38]	Deep learning-based	Prediction	Framework urban traffic flow
Fan et al. [39]	Spatial- temporal Ordinary Differential Equations	Prediction accuracy and computational efficiency	Multi-city traffic flow
Yiling et al. [40]	Multi-task learning	Prediction, multi-task learning	Control signal traffic, traffic control
Miletić et al. [41]	Fuzzy logic	Reduce traffic	Traffic signal
Tuo et al. [42]	Machine learning, genetic algorithms	Fast, training parameter, minimize	Traffic signal
Hong et al. [43]	Adaptive linear quadratic	Reduced traffic delay and energy consumption	Urban traffic control operations
Radja et al. [44]	Particle Swarm Optimization	Reducing fuel consumption and pollutant emissions, optimal signal timing	Urban traffic networks with course determination
Ting et al. [45]	Data-driven model free	Improve the performance	Urban traffic management
Bartosz et al. [46]	Dynamic Radio Frequency IDentification identification	Identification	Traffic lights under the universe
Cang et al. [47]	Fuzzy logic	Reduce and improve, optimal	Traffic light control for heterogeneous, traffic systems
Yanmei et al. [48]	Multi-objective linear programming	Guarantees the interests of passengers, reduce carbon emissions, minimize	Traffic light control for heterogeneous traffic systems
Hoang et al. [49]	Distributed control strategy	Optimal and minimize	Large-scale urban network
Mahdiyeh et al. [50]	Multiple linear regression model	Multiple linear regression model	Modeling traffic noise level in intersection
Zongtao et.al. [51]	Deep hybrid network	Prediction	Urban traffic flow
Alvaro et al. [52]	Weighted multi-map strategies	Traffic management	Urban traffic

demonstrates a summary of the technologies used in the direction system with a classification of a different model in the urban traffic. As shown, the primary goals are the used model and the kind of advantages they have used—the spatial term in their suggested system and the research work’s main scenario. Overall, a summary of the presented strategy with other related work shows various control techniques utilized to improve the system’s performance based on urban traffic.

3. Multi-Agent and Model Predictive Control

All predictive control structures include general predictive control frameworks and operation models, cost functions, and organizational methods. Different choices for each element lead to other facilities. Model predictive control is the first model from which an essential process can be derived. Predicting future production based on current values and future control methods are recommended. The optimizer calculates this by considering the cost function and constraints. Specific models are easy to understand and implement; more information is explained in [53].

Here, the actions performed within an agent system in a structure affect the sub-net network and the subsidiary network. In a design, an agent control adjusts points and also enables other agents. There is an agent in a structure control multiagent, and this control causes changes in how other agents select another agent. It causes adjusted system performance at the high layer. Additionally, all information in the structuring agent is used. Using this method reduces the load on the computer. Agents can communicate with other agents and work together to provide a better solution. Factor cycle control using general prediction control has a current mode system and maximum efficiency.

The framework of multiagents with model predictive control is as follows:

• In a system model, the selected can be a hierarchical system.
• The control issue adjusts to minimize the hierarchical cost function.
• A hierarchical control problem can be solved using hierarchical architecture.
• Agents must communicate in the model predictive multiagent system. The centralized system and control problem are separated, and they become smaller problems dependent upon each other.

Effects on business agent evolution. The system is connected to its subsystem. Agents are not reviewed in a multiagent environment, however they can only have sensors and actuators. There is uncertainty in the subsystem, which was used out of connection to reduce this uncertainty. That is why conscious consumers value their plans: a proxy recurrence account and local contact for each control cycle. Figure 1 shows communication between multiagents and a model predictive control and how to combine. Each model prediction control tool cycle includes this form cycle: the advantage of system behavior and actions. The system behavior and system input and output in this process are limited.

There is information about future glitches. The primary purpose of this data is to improve the system’s behavior and is a sign that costs are being kept to a minimum. The control agent used model predictive control to predict the system’s behavior to get the best performance. This figure has the supervisory control layer, which considers the dynamics of both a lower and underlying physical network. This physical network has been controlled with several control layers to control the network.

4. Mathematical Models in Intersections

Our study elaborates on a network control process consisting of several junctions that control all the traffic lights. The aim of achieving an optimal balance at intersections has been proposed in this algorithm based on selecting a kind of traffic light and the duration of the green phase. This intersection consists of many independent agents that exchange information with each other, and the stability of each agent is proved separately. This article investigates eight isolated intersections; the four phases are shown in Figure 2. We used a dynamic model from a single intersection at the first step. After that, with attention to the dynamic model intersection, we prove stability, then we get a new equation. To expand an intersection to 8 intersections, we proposed a multiagent method to connect intersections. Here, Figure 2 shows the presented multiagent model, which has been used for eight intersections in traffic control and reducing the queue length using a model predictive control. Finally, we want to reduce the queue length created at the intersections by the proposed model.

In this section, mathematical equations and several connecting intersections have been mentioned. The stability of an intersection has been mentioned in [53]. For more explanation, there are two phases at an intersection, Leg 1, Leg 3, and Leg 2, Leg 4. Here, a vehicle’s queue length is one of the main parameters in the equation of traffic flow at each intersection in the Equation (1).

$$Q_i(n+1)=Q_i\left(n\right)+q_i\left(n\right)-d_i\left(n\right)s_i\left(n\right)$$

(1)

In this case, $i=1,2,3,\dots ,n$ is the leg index that enters the intersection. In addition, $n=0,1,2,\dots ,N-1$ is the discrete-time interval index. $Q_i\left(n\right)$ represents the length of the queue of vehicles, $q_i\left(n\right)$ represents the number of leaving cars, $d_i\left(n\right)$ represents the number of entering vehicles and $s_i\in [0,1]$ represents the traffic light status in the legs of the simulation. As long as T has been considered as a discretized time interval, and can be assumed uniform in every time interval, a uniform arrival of vehicles is presumed for every time interval, resulting in the calculation of the overall waiting time as Equation (2).

$$W_i(n+1)=W_i+TQi\left(n\right)+q_i\left(n\right)-d_i\left(n\right)s_i\left(n\right)1/2q_i\left(n\right)l$$

(2)

For further details, state-space equations for a single intersection are as below:

$$\left\{\begin{array}{c}X(n+1)=AX\left(n\right)+B\left(n\right)S+C\left(n\right)\\ Y\left(n\right)=CX\left(n\right)\end{array}\right.$$

(3)

We used Equation (2) for proving the stability of eight intersections. At this Equation, $X_i\left(n\right),W_i\left(n\right)$ are control variables. Additionally, Equation (3) shows other matrices of coefficients and vectors, for example A,B,C,D, as follows:

$$C=\left[\begin{array}{cc}{I}_M& 0\\ 0& I_M\end{array}\right]$$

(4)

$$A=\left[\begin{array}{cc}{I}_M& 0\\ T{I}_M& I_M\end{array}\right]$$

(5)

$$B\left(n\right)=-\left[\begin{array}{cccccc}{d}_1\left(n\right)& 0& .& .& .& 0\\ 0& d_2\left(n\right)& .& .& .& 0\\ .& .& .& .& .& .\\ .& .& .& .& .& .\\ .& .& .& .& .& .\\ 0& .& .& .& .& d_M\left(n\right)\\ 1/2T{d}_1\left(n\right)& 0& .& .& .& 0\\ 0& 1/2T{d}_2\left(n\right)& 0& 0& 0& 0\\ .& .& .& .& .& .\\ .& .& .& .& .& .\\ .& .& .& .& .& .\\ 0& 0& .& .& .& 1/2T{d}_M\left(n\right)\end{array}\right]$$

(6)

$$C_n={[q_1\left(n\right)q_2\left(n\right)\dots q_M\left(n\right)1/2T{q}_1\left(n\right)1/2T{q}_2\left(n\right)\dots 1/2T{q}_M\left(n\right)]}^T$$

(7)

These are:

$$X\left(n\right)={[Q_1\left(n\right)Q_2\left(n\right)\dots Q_M\left(n\right)W_1\left(n\right)W_2\left(n\right)\dots 1/2T{q}_M\left(n\right)]}^T$$

(8)

These variables refer to state variables and queue lengths and delays of $Q_i\left(n\right)$.

Mathematical Model of Multi-Agent Intersections

Figure 3 shows multi-agent intersections linked to each other.

When the intersections are connected to each other, all the parameters of $Q_i\left(n\right),W_i\left(n\right)$ all the matrices of the coefficients are similar to the intersection. Their only difference is in the state-space equations based on the Kronecker product as Equation (9). The most important feature used in the multiagent systems of Kronecker mathematics is a Kronecker multiplier. It is displayed as ⊗. This multiplication factor is on two matrices of optional size.

The interrelationships between agents have been represented in a multi-factorial system in Figure 3. Each factor of the graph is equal to the presence of one element, and the information exchanged between the agents depends on the connection of each path.

Table 2. The parameters used in this article.

Component	Description
$Q_i\left(n\right)$	Queue length
$q_i\left(n\right)$	The number of vehicles that enter the queue
$d_i\left(n\right)$	The number of vehicles that have left the queue
$S_i\left(n\right)$	Control signal
$W_i\left(n\right)$	Waiting time
T	Sampling time
X(n)	Model variable vector
S(n)	Control signal
$I_M$	Identity matrix
$A_i,B_i,C_i$	Metrics
J	Cost function
y(n)	New output
y’(n)	Output
H	Hamilton equation
⊗	Kronecker

shows the parameters using notations in the predictive model based on the proposed method.

$$\left\{\begin{array}{c}X(n+1)=\left(I_M\otimes A_i\right)X\left(n\right)+\left(I_M\otimes B_i\right)S\left(n\right)+\underline{1}·C_i\hfill \\ Y\left(n\right)=CX\left(n\right)\hfill \end{array}\right.$$

(9)

5. Designing Stable Predictive Controller for Multi-Agent Intersections

The cost function according to an intersection model using a multiagent system is described as follows:

$$J=X^T(n+1)(I_N\otimes Q)X(n+1)+\Delta S^T\left(n\right)(I_N\otimes W)\Delta S\left(n\right)$$

(10)

The model predictive control determines control signals by having a process model and receiving future signals based on optimization. This act minimizes the difference between the predicted outputs and the reference signals.

Theorem 1.

The dynamic system in Equation (9) limits and finalizes the overall system. In counting, all signals of the closed-loop system have been limited.

The proof: Typically, in urban intersections, the control signal is a traffic light that is green or red, and if it is green, vehicles can enter or leave, and during the red phase, the vehicles only can enter the queue.

$$\left[\begin{array}{c}\Delta X(n+1)\\ Y\left(n\right)\end{array}\right]=\left[\begin{array}{cc}(I_M\otimes A_i)& 0\\ \underline{1}.C_i& I\end{array}\right]\left[\begin{array}{c}\Delta X\left(n\right)\\ Y\left(n\right)\end{array}\right]+\left[\begin{array}{c}(I_M\otimes B_i)\\ Y\left(n\right)\end{array}\right]S\left(n\right)+\left[\begin{array}{c}I\\ 0\end{array}\right]\Delta C\left(n\right)$$

(11)

The new output will be as follows:

$$y^{\prime }\left(n\right)=\left[\begin{array}{c}\xi \end{array}\right]\left(\begin{array}{c}\Delta X\left(n\right)\\ Y\left(n\right)\end{array}\right)$$

(12)

Now, for proving the stability of the general system, the suitable Hamiltonian function with the goal of strength should be presented in this Theorem. Since the equations are discrete, then in this paper, Equation (13) is the Hamiltonian function.

$$H=y^{\prime T}y+\Delta S^{T}R\Delta S$$

(13)

Equation (13) causes the cost function to minimize. This equation is a new output on the based cost function at a general system, totaling the previous output with the control and reference signals. Then, via putting relation $\Delta X$ in relation Equation (13), the above equation can be written as follows:

$$H={(\xi \Delta X(n+1))}^T(\xi \Delta X(n+1))+\Delta S^{T}R\Delta S$$

(14)

where $\xi$ = [1 1 1 1 0 0 0 0] and by placement:

$$\Delta X(n+1)=A\Delta X+B\Delta S+C$$

(15)

With assuming that:

$$\begin{gathered} A=(I_M\otimes A_i)x\left(n\right) \\ B=(I_M\otimes B_i)x\left(n\right) \\ C=\underline{1}.C_i \end{gathered}$$

(16)

Additionally, $I_M=q$ has been defined as input at the general system. Using Equation (17) and via putting relation, Equations (17) and (18) can be rewritten as follows:

$$\begin{array}{c}H={(\xi (I_M\otimes A_i)X\left(n\right)+(I_M\otimes B_i)S\left(n\right)+\underline{1}.C_i)}^T\\ (\xi (I_M\otimes A_i)X\left(n\right)+(I_M\otimes B_i)S\left(n\right)+\underline{1}.C_i+\Delta S^{T}R\Delta S\end{array}$$

(17)

According to Equation (17), $\xi$ affects each parameter, written as the Hamiltonian equation below.

$$\begin{array}{c}H={(\xi (I_M\otimes A_i)X\left(n\right)+\xi (I_M\otimes B_i)S\left(n\right)+\xi \underline{1}.C_i)}^T\\ (\xi (I_M\otimes A_i)X\left(n\right)+\xi (I_M\otimes B_i)S\left(n\right)+\xi \underline{1}.C_i)+\Delta S^{T}R\Delta S\end{array}$$

(18)

After some mathematical manipulations, such as with attention, considering the Equation (14) and placing it in Equation (18), the following Equation is obtained:

$$\begin{array}{c}H=(\Delta X^T{(I_M\otimes A_i)}^T{\xi }^T+\Delta S^T{(I_M\otimes B_i)}^T{\xi }^T+\underline{1}.C_i^T{\xi }^T)\\ (\xi (I_M\otimes A_i)\Delta X+\xi (I_M\otimes B_i)\Delta S+\xi C_i)+\Delta S^{T}R\Delta S\end{array}$$

(19)

At this step, using ${\left(AB\right)}^T=B^T{A}^{T}and{(A\otimes B)}^T=B^T\otimes A^T$ applying some mathematical operations, we get the following Equation (20):

$$\begin{array}{c}H=\Delta X^T{(I_M\otimes A_i)}^T{\xi }^T\xi (I_M\otimes A_i)\Delta X+\Delta X^T{(I_M\otimes A_i)}^T{\xi }^T\xi (I_M\otimes B_i)\Delta S+\\ \Delta X^T{(I_M\otimes A_i)}^T{\xi }^T\xi \underline{1}.C_i+\Delta S^T{(I_M\otimes B_i)}^T{\xi }^T\xi (I_M\otimes A_i)\Delta X+\Delta S^T(I_M\otimes \\ B_i{)}^T{\xi }^T\xi (I_M\otimes B_i)\Delta S+\Delta S^T{(I_M\otimes B_i)}^T{\xi }^T\xi C_i+\underline{1}.C_i{\xi }^T\xi (I_M\otimes A_i)\Delta X+\\ \underline{1}.C_i{\xi }^T\xi (I_M\otimes B_i)\Delta S+\underline{1}.C_i^T{\xi }^T\xi C_i+\Delta S^{T}R\Delta S\end{array}$$

(20)

Finally, calculating the general system can create a Hamiltonian equation, which derives the cost function ratio to the control effort by equalizing it with zero. The Hamiltonian Equation (21) obtained the following:

$$\frac{\partial H}{\partial \Delta S}=0$$

(21)

Then Equation (22) obtained:

$$\begin{array}{c}\frac{\partial H}{\partial \Delta S}=\Delta X^T{(I_M\otimes A_i)}^T{\xi }^T\xi (I_M\otimes B_i)+\Delta X^T{(I_M\otimes A_i)}^T{\xi }^T\xi (I_M\otimes B_i)+\Delta S^T\\ {(I_M\otimes B_i)}^T{\xi }^T\xi (I_M\otimes B_i)+C_i^T{\xi }^T\xi (I_M\otimes B_i)+C_i^T{\xi }^T\xi (I_M\otimes B_i)+\Delta S^{T}R\Delta S=0\end{array}$$

(22)

At result:

$$\begin{array}{c}\Delta S^T((I_M\otimes B_i){\xi }^T\xi (I_M\otimes B_i)+R+R^T)=\\ -2(\Delta X^T{(I_M\otimes A_i)}^T{\xi }^T\xi (I_M\otimes B_i)+C_i^T{\xi }^T\xi (I_M\otimes B_i))\end{array}$$

(23)

Therefore, the above relation after differentiating can be expressed as follows:

$$\begin{array}{c}\Delta S^T=-2(\Delta X^T{(I_M\otimes A_i)}^T{\xi }^T\xi (I_M\otimes B_i)+C_i^T{\xi }^T\xi (I_M\otimes B_i))\\ {({(I_M\otimes B_i)}^T{\xi }^T\xi (I_M\otimes B_i)+R+R^T)}^{-1}\end{array}$$

(24)

This completes the proof. In this section, we first presented a dynamic equation in which the main parameter has been obtained from a single intersection then has considered several intersections as a multi-factorial system, connected by agents; it was shown communication between agents as a graph. Additionally, considering dynamics for several intersections has been proved stable using model predictive control.

6. Simulation Results

In the simulation, the quadruple length reduction criterion is used in both fixed time and the proposed model predictive control, and sampling time $T=0.1$ s is utilized, which draws attention to the values of different traffic conditions. The parameters $q_i$ and $d_i$ are random and distributed in the predictive model. The results of this example are shown in visual form. Below, we explain the proposed model without a controller. Then, in fixed-time control, the simulation results for the number of vehicles in the queue without controller actions are shown in the following figures.

The number of vehicles in the first intersection using fixed-time control improves using the model predictive control. The length of the queue of vehicles on the fourth leg is higher than on the other leg, and the number of cars per leg is monitored with timing. In the first phase, the number of cars is almost constant and has not increased. However, the volume of traffic at the third leg is higher than at the second and fourth leg at this intersection, as shown in Figure 4.

The volume of vehicles that cars produce increases in the first and third legs, and in the second leg with fixed time increasing. The length of the queue of vehicles in the fourth leg is more than in another leg in the intersection, as shown in Figure 5.

Figure 6 shows the number of vehicles at the third intersection. The number of cars on the first leg shows that the number of vehicles increases. However, the number of cars in the third leg will be fixed after a while. The traffic volume in the fourth leg is more than the other legs after. It will be fixed for a time.

The vehicle queue length in the fourth intersection at the first leg and the second is fixed and does not fluctuate. Then, the number of vehicles in the third leg will stabilize and decrease over time. Additionally, the volume of traffic in the fourth leg is more than the other legs trend; it has an increase, as shown in Figure 7.

This Figure 8 shows the traffic at the fifth intersection. The number of vehicles has increased in the first phase using fixed-time control, so as you can see, the number of vehicles will be proved after a while in the third phase. However, the traffic volume on the fourth leg is higher than the other legs, increasing.

Figure 9 shows the length of the vehicle queue at the sixth intersection of the controller without a predictive model. In the first phase, the number of vehicles increased, and in the fourth phase, traffic volume decreased. Additionally, as you see, the vehicle queue length in the second leg and the third is fixed and does not fluctuate.

Figure 10 shows the queue vehicle in the seventh intersection without the predictive controller; the queue length of cars is fixed in the first leg, the second leg shows results with the fix-time controller, which has been proven after a while. The number of vehicles at the third leg increases. Additionally, the traffic volume in the fourth leg first increases and then decreases.

The eighth intersection in Figure 11 has been shown. In the first and third legs, we have seen the increasing trend of traffic, which we expect to decrease by applying predictive model control. However, the number of legs decreases after a while in the second and fourth leg, but traffic is still seen in it.

Figure 12 shows control variables indicating green or red traffic lights. Similarly, the vehicle’s queue length has been shown at other intersections, which has improved by using a predictive controller. The proposed controller is designed based on equations. The output of the predictive controller as the control variable $S_i$ of the traffic system was demonstrated as follows. The proposed model is explained using model predictive control in the below figures:

Figure 13 shows the number of vehicles in the first queue of intersection; there was no change in the queue of vehicles at the first stop compared to the case without a controller. In the second phase, we see a reduction in the length of the number of vehicles in traffic. In the third phase, there was a significant reduction in the number of vehicles compared to the uncontrollable mode. Finally, the length of the queue on the fourth leg has been changed drastically. This indicates the excellent performance of the designed controller.

The following figures further show the queue length of vehicles at additional intersections with the model predictive control that has been given.

According to the results of the decreasing trend of the queue length in Figure 14, it is seen at all the legs of the second intersection.

Figure 15 shows that the length of the queue of cars in the first leg has not changed compared to the case without a controller; in the second leg, the length of the queue of cars has been reduced. However, in the fourth leg in this intersection queue, length first increases and then decreases. At the third intersection, the length of the car queue in the third leg has been fixed, and in the other legs, relative to without the controller has been improved.

It shows the fourth intersection at Figure 16. The queue length of vehicles in the first leg was initially constant and then had an increasing trend, and eventually decreased. Additionally, in the second leg, the queue length of vehicles has been reduced. In the third and fourth legs, the number of vehicles decreased significantly. As a result, model predictive controller has had good performance in the intersection.

Figure 17 shows how a predictive model can be used to control the queue length of vehicles. The number of vehicles at intersection 5 decreased with a suggested model in legs 1 and 3, while the volume of traffic used by the proposed method in the second and fourth legs significantly reduced to zero.

The sixth intersection is shown in Figure 18 at the start, where the queue length of cars has increased then decreased.

The length of the queue for the third leg did not change significantly. In addition, however, the queue length of cars in the intersection has been reduced in the second and fourth. Meanwhile, the number of vehicles at this third-leg intersection increased.

Figure 19 shows the number of vehicles in the seventh intersection using model predictive control. The length of the car queue has decreased in the second and fourth legs, and we have seen a much better result. In the third leg, we are also facing a decrease in the length of the car queue.

The eighth intersection, which in the second and fourth legs means there are reduced queue lengths more than the first and third legs, is shown in Figure 20.

In this chapter, first, several intersections are considered a multi-factor system. The relationship between the factors are shown in graphs, proving that the dynamics considered for several intersections are stable. Moreover, according to the simulation results, it can be said that by using a predictive controller, the queue length of cars in each leg has been decreased compared to the fixed time control. Continuing, we compared results in the length of the queue of vehicles using a model predictive control according to the simulation results in the corresponding

Table 3. The comparison of results in length of queue of vehicles using model predictive control.

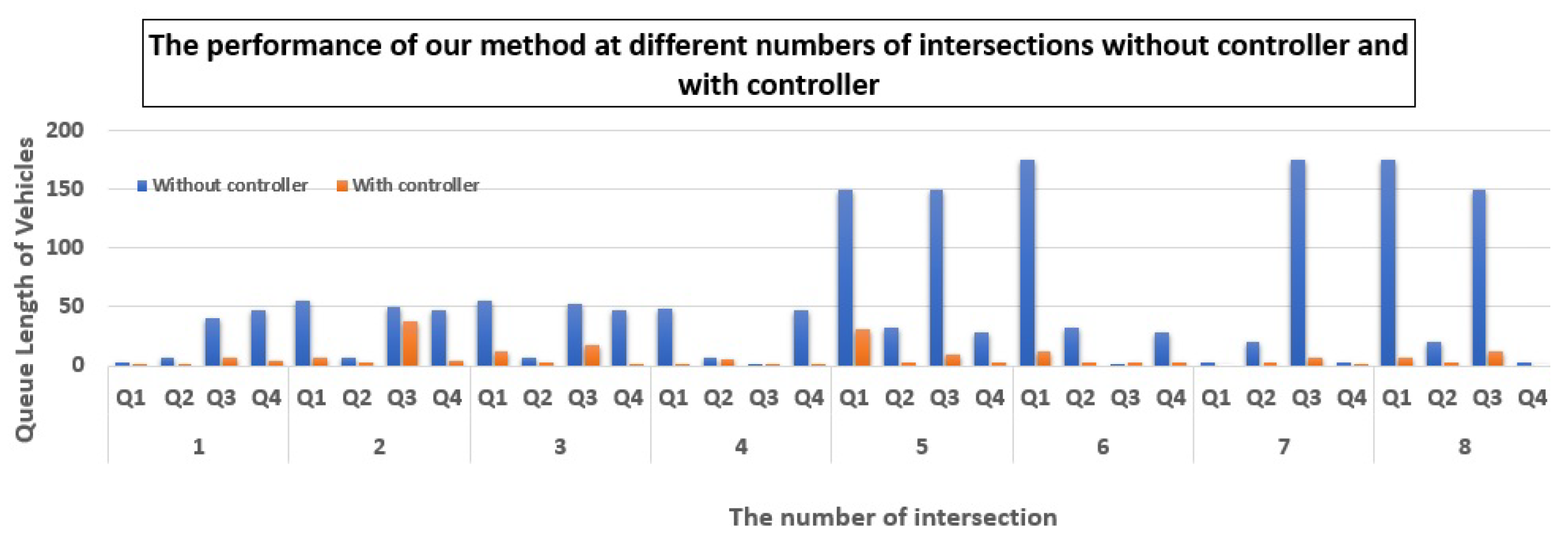
Queue Length of Vehicles	Intersection	Without Controller	With Controller	Improvement (%)
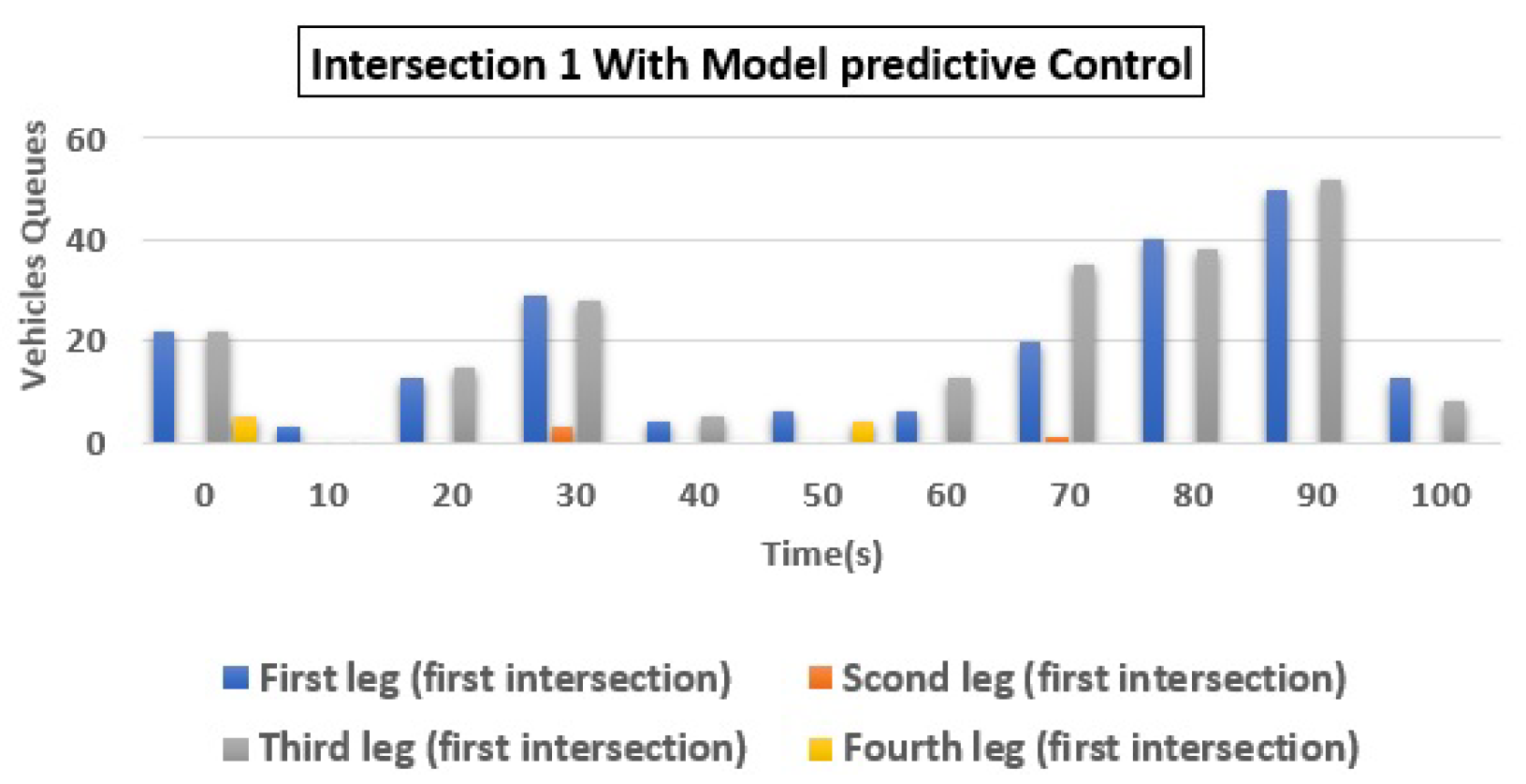
1	(a) Q1	3	1	66.67
	(b) Q2	7	1	85.71
	(c) Q3	40	7	82.50
	(d) Q4	47	4	91.49
Total		97	13	86.60
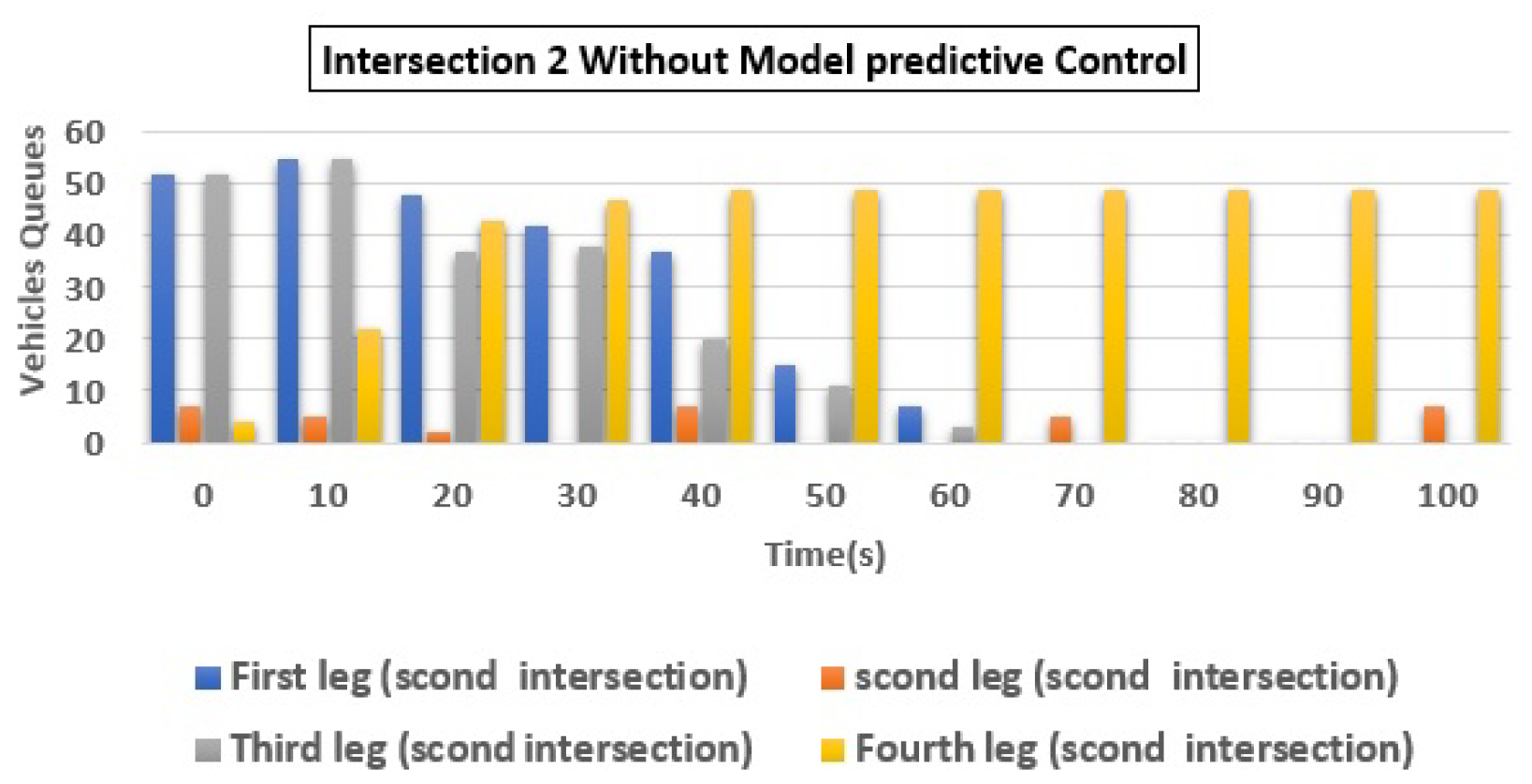
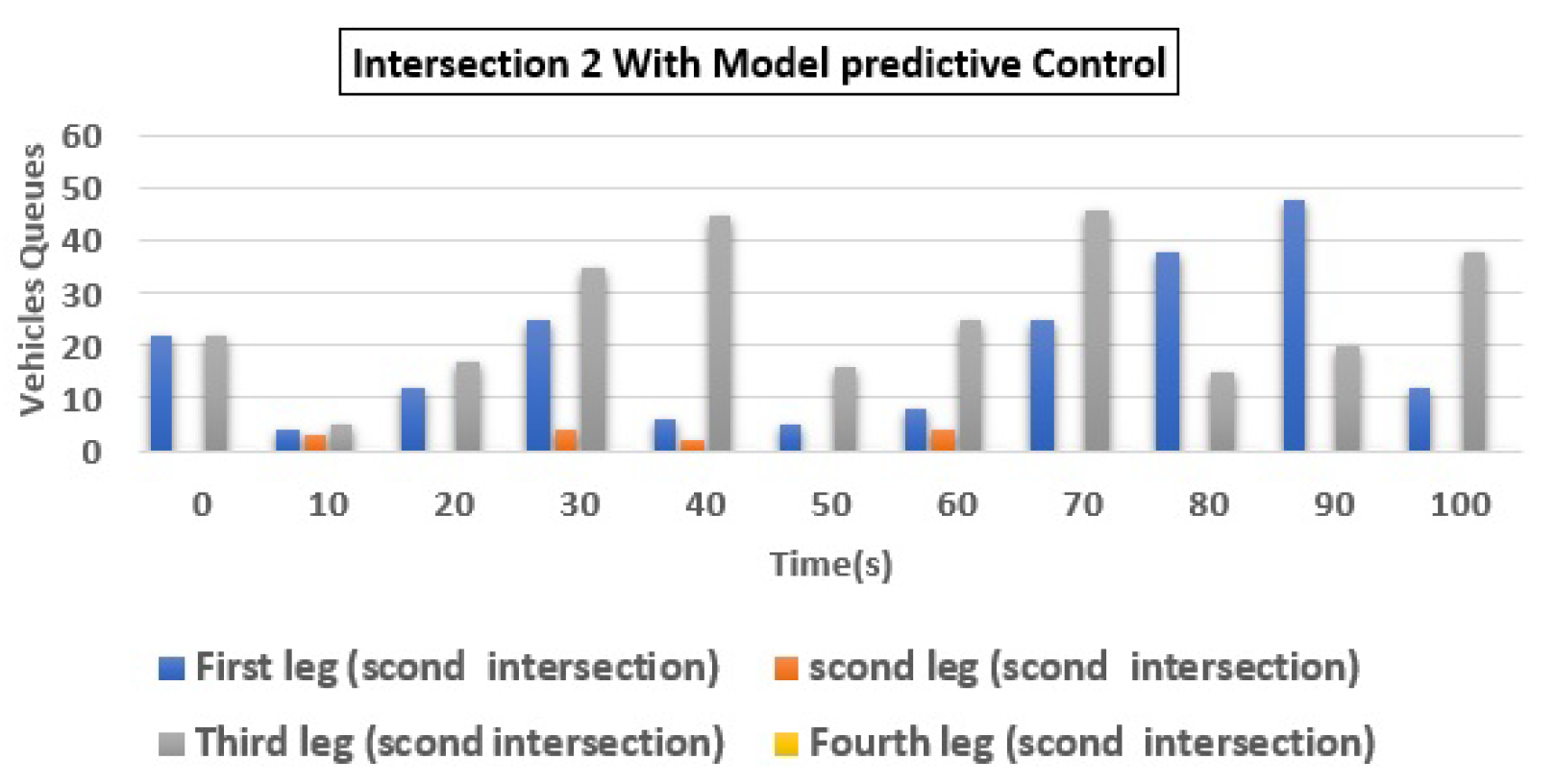
2	(a) Q1	55	7	87.27
	(b) Q2	7	3	57.14
	(c) Q3	50	38	24.00
	(d) Q4	47	4	91.49
Total		159	52	67.30
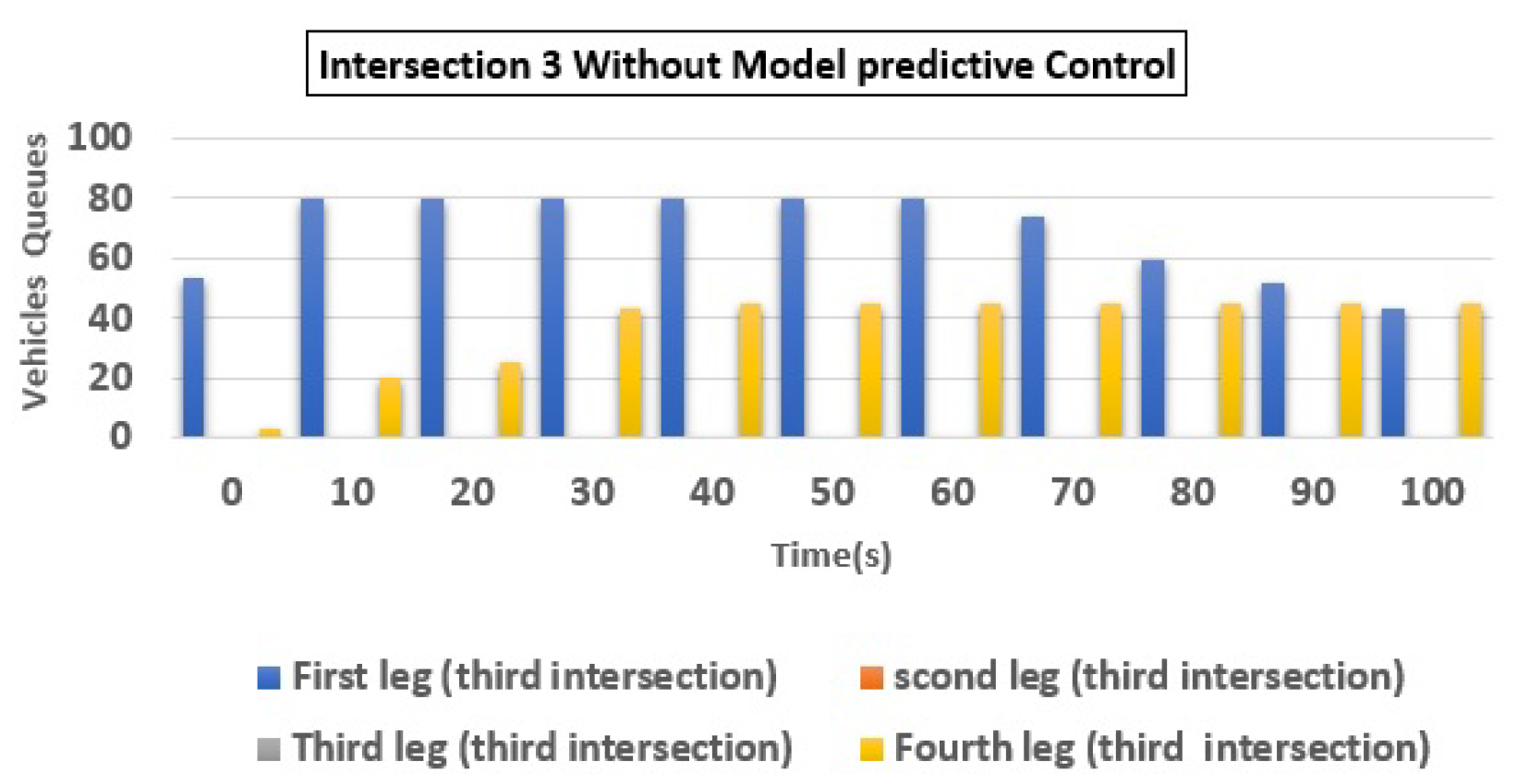
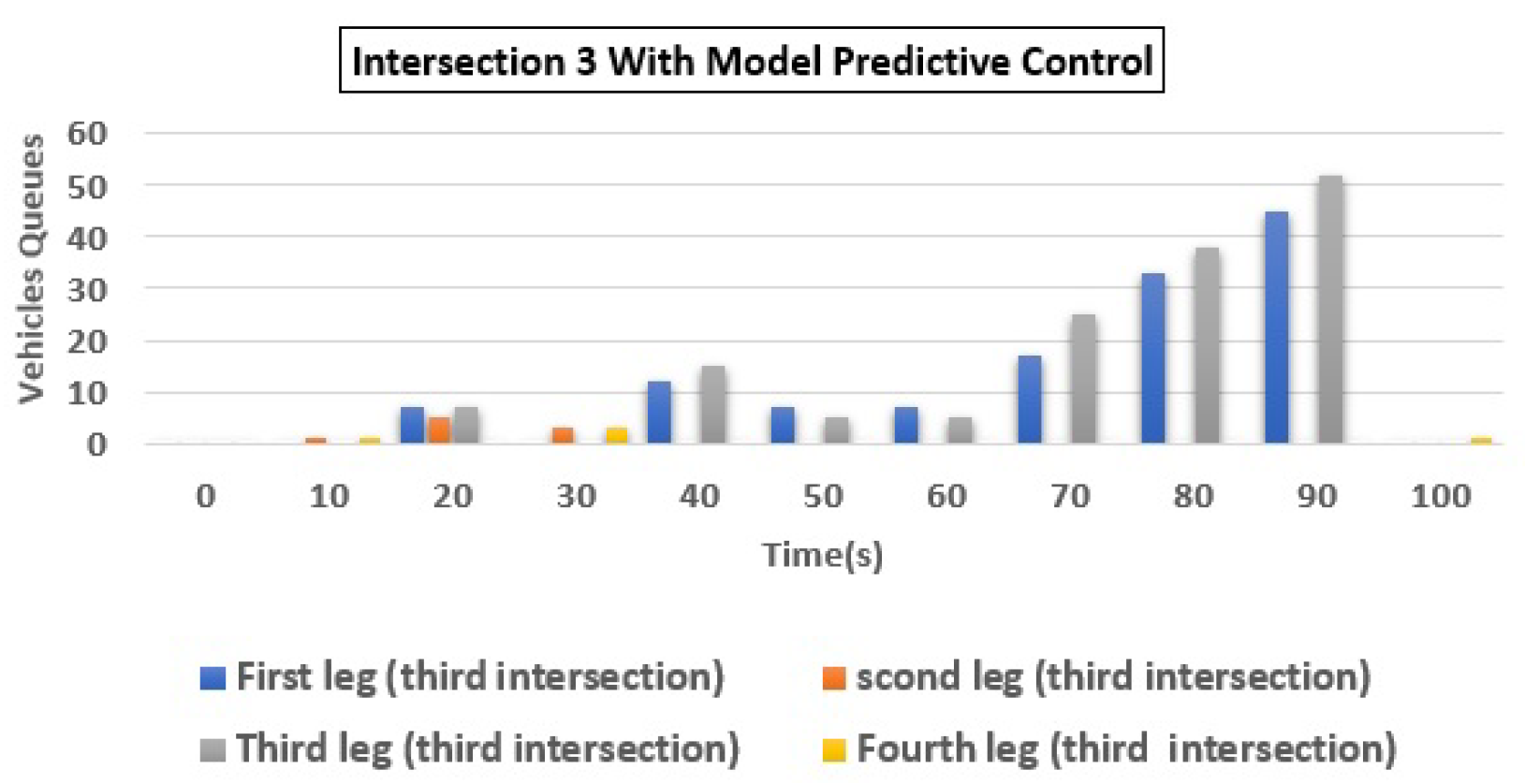
3	(a) Q1	55	12	78.18
	(b) Q2	7	3	57.14
	(c) Q3	53	17	67.92
	(d) Q4	47	1	97.87
Total		162	33	79.63
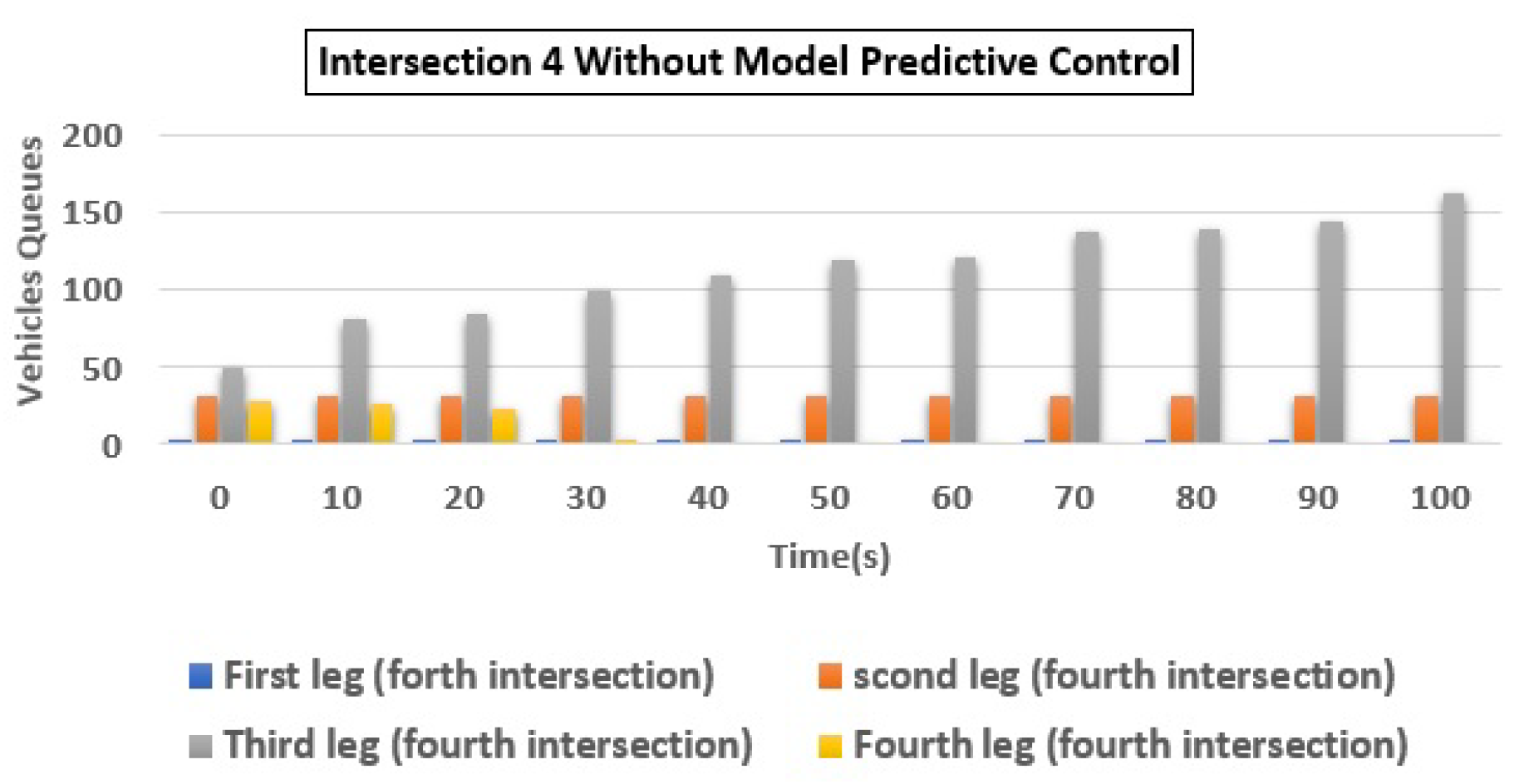
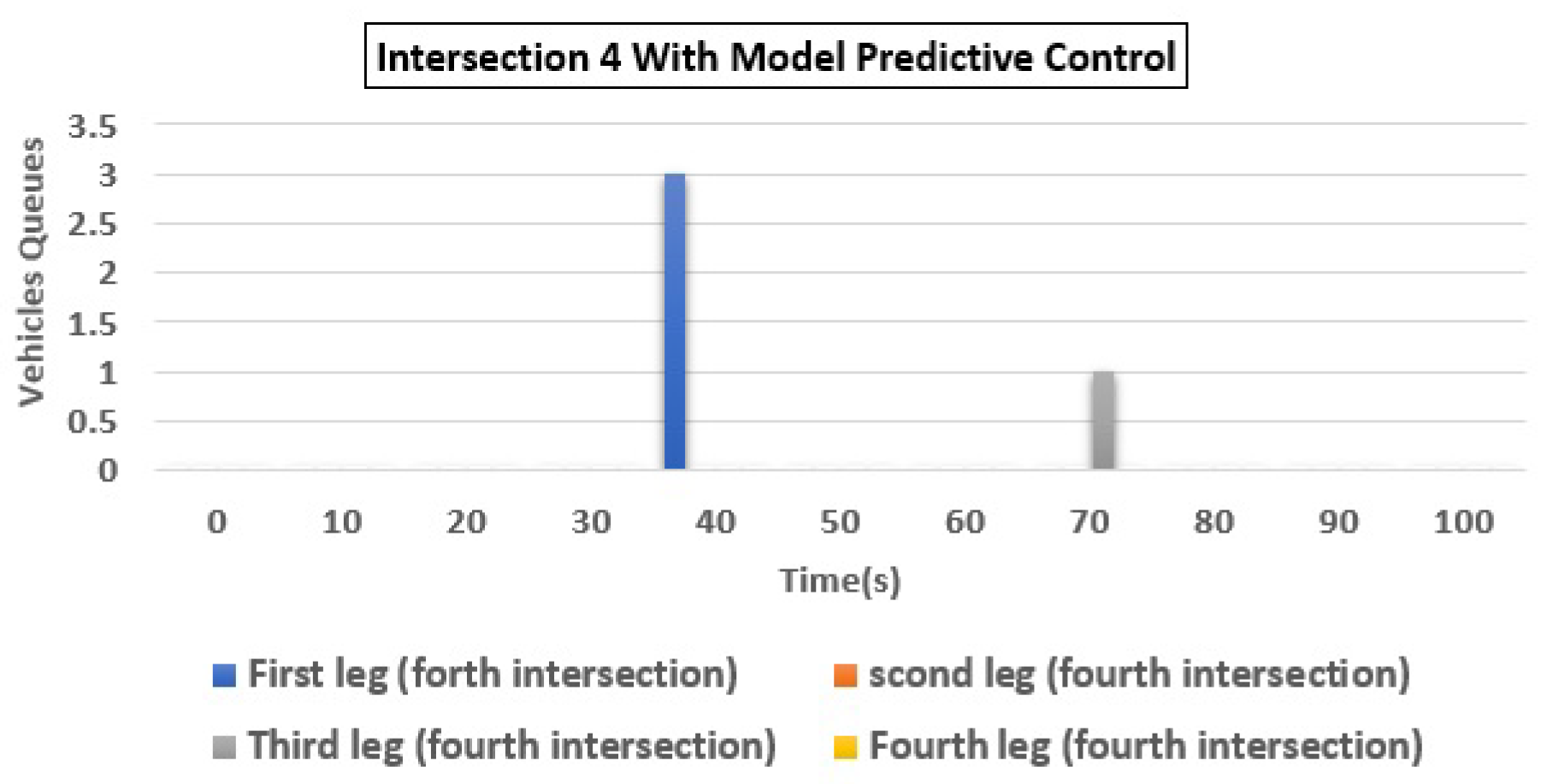
4	(a) Q1	49	1	97.96
	(b) Q2	7	6	14.29
	(c) Q3	2	1	50.00
	(d) Q4	47	1	97.87
Total		105	9	91.43
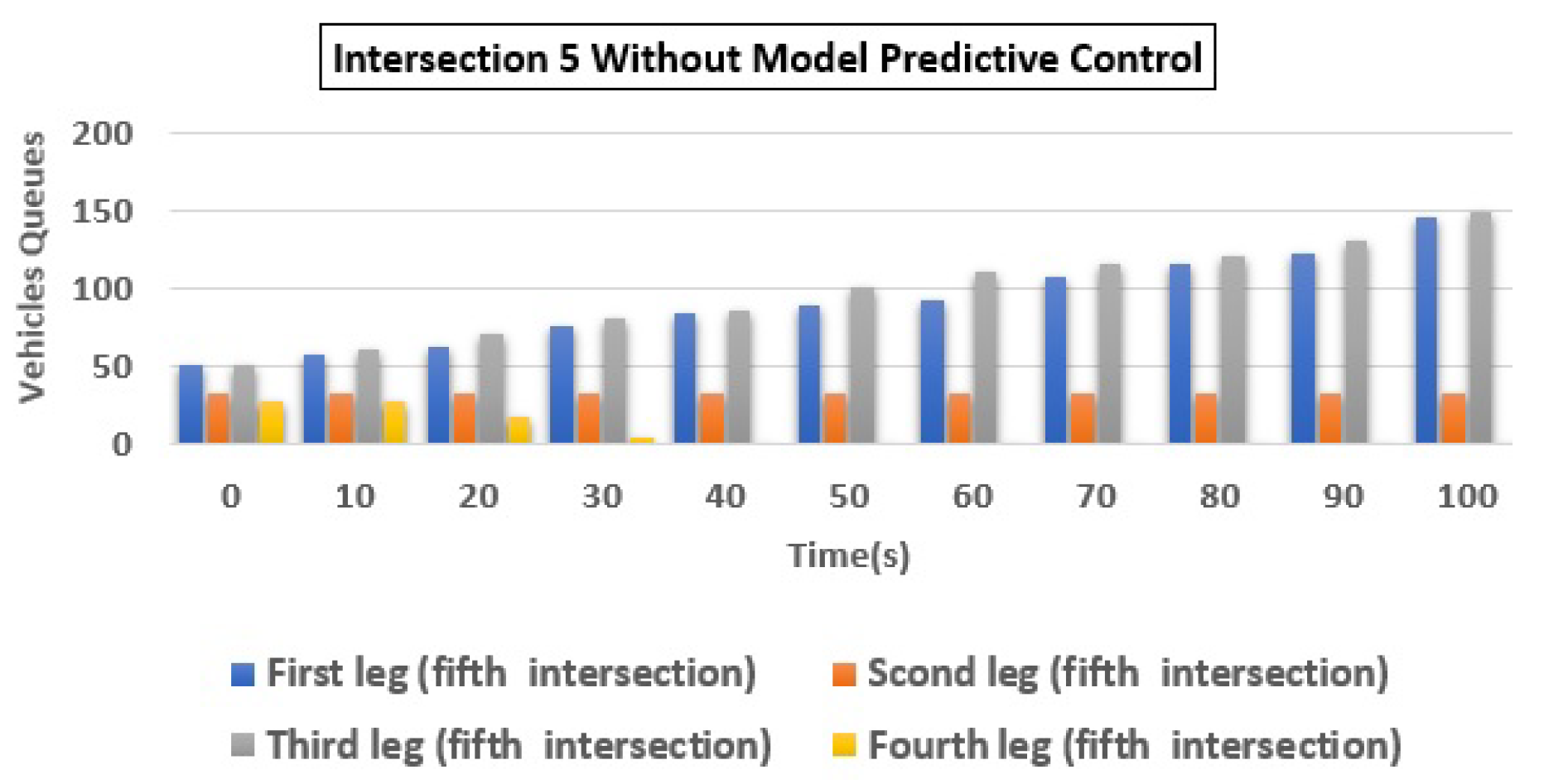
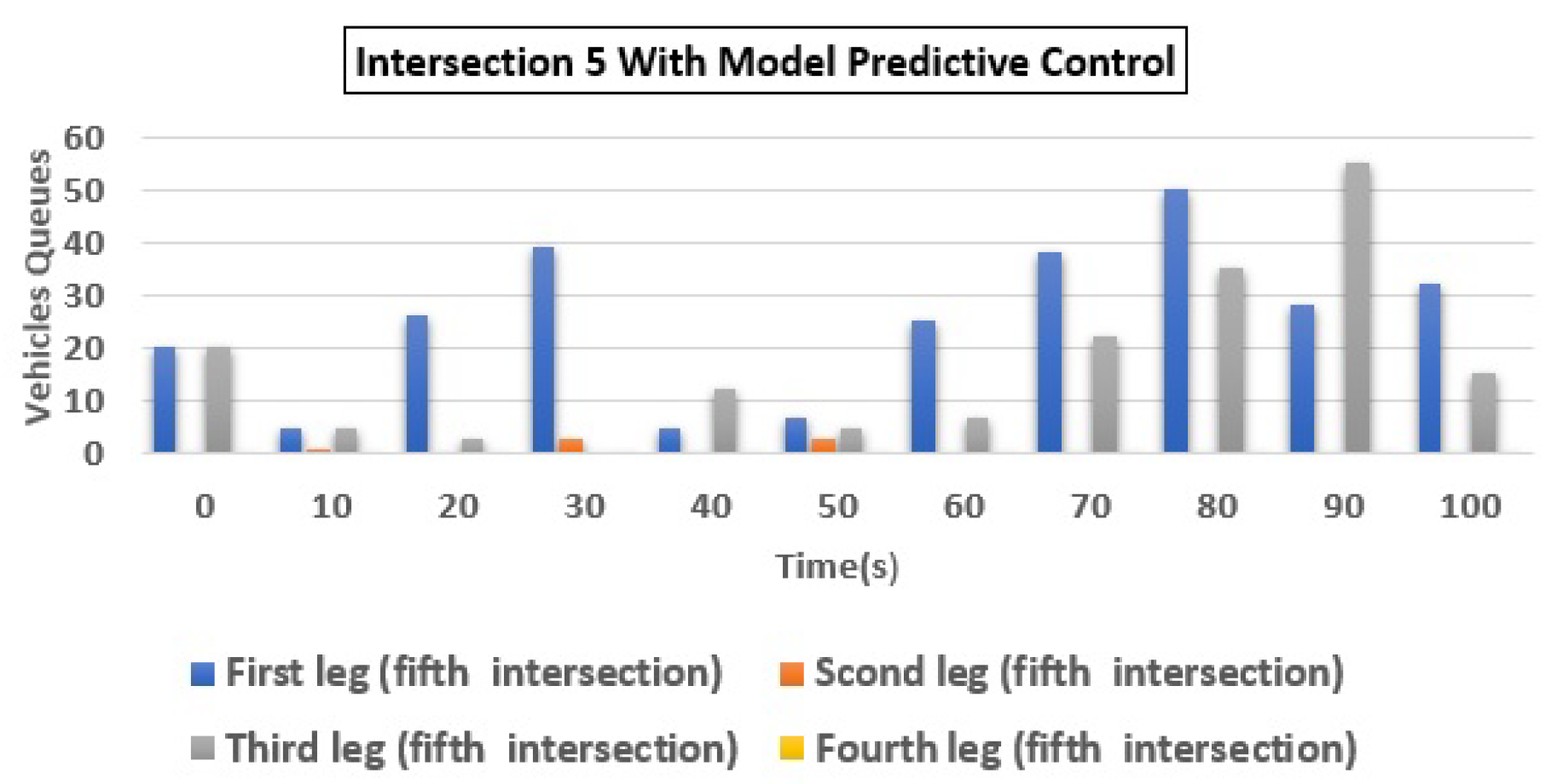
5	(a) Q1	150	31	79.33
	(b) Q2	32	3	90.63
	(c) Q3	150	10	93.33
	(d) Q4	28	3	89.29
Total		360	47	86.94
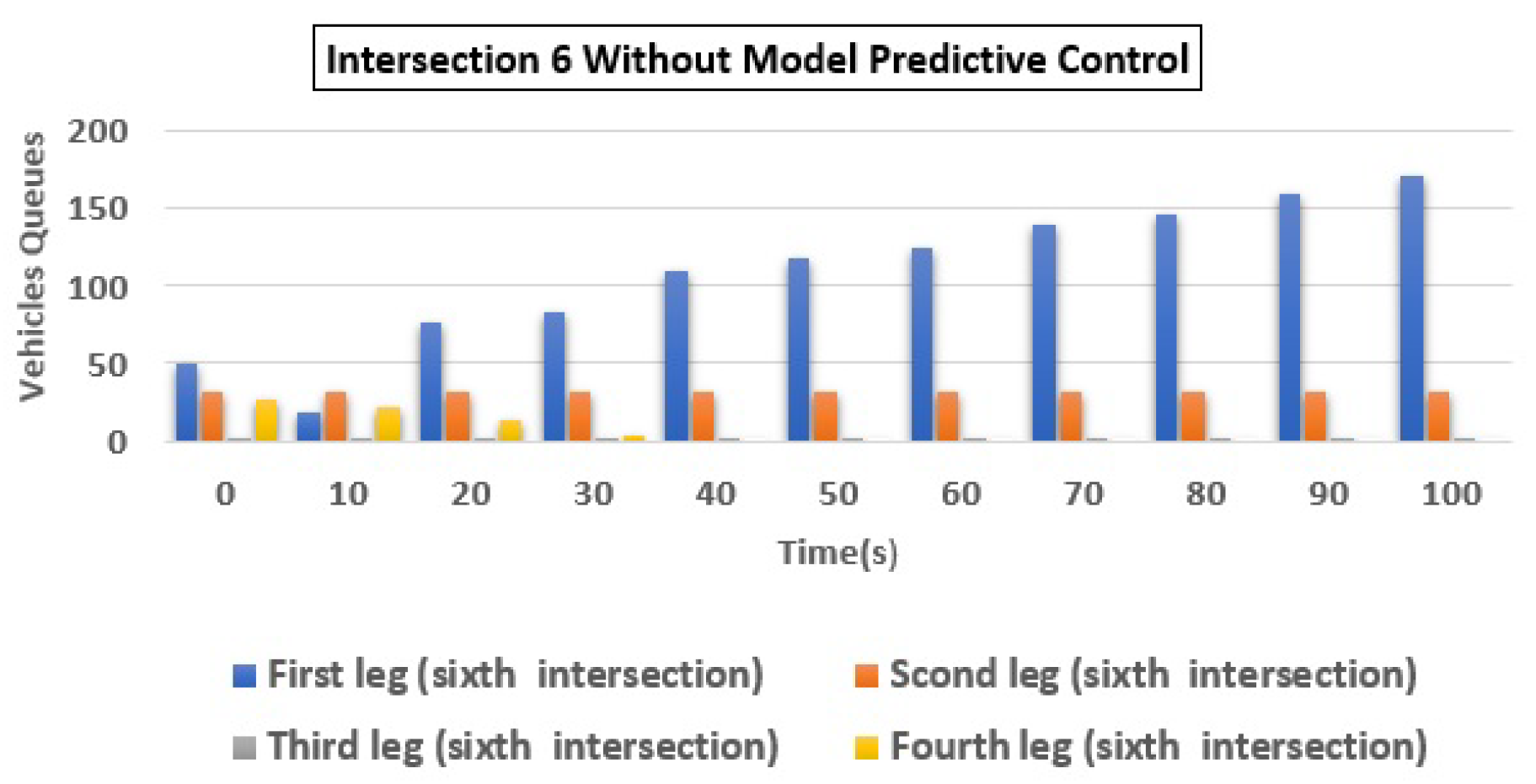
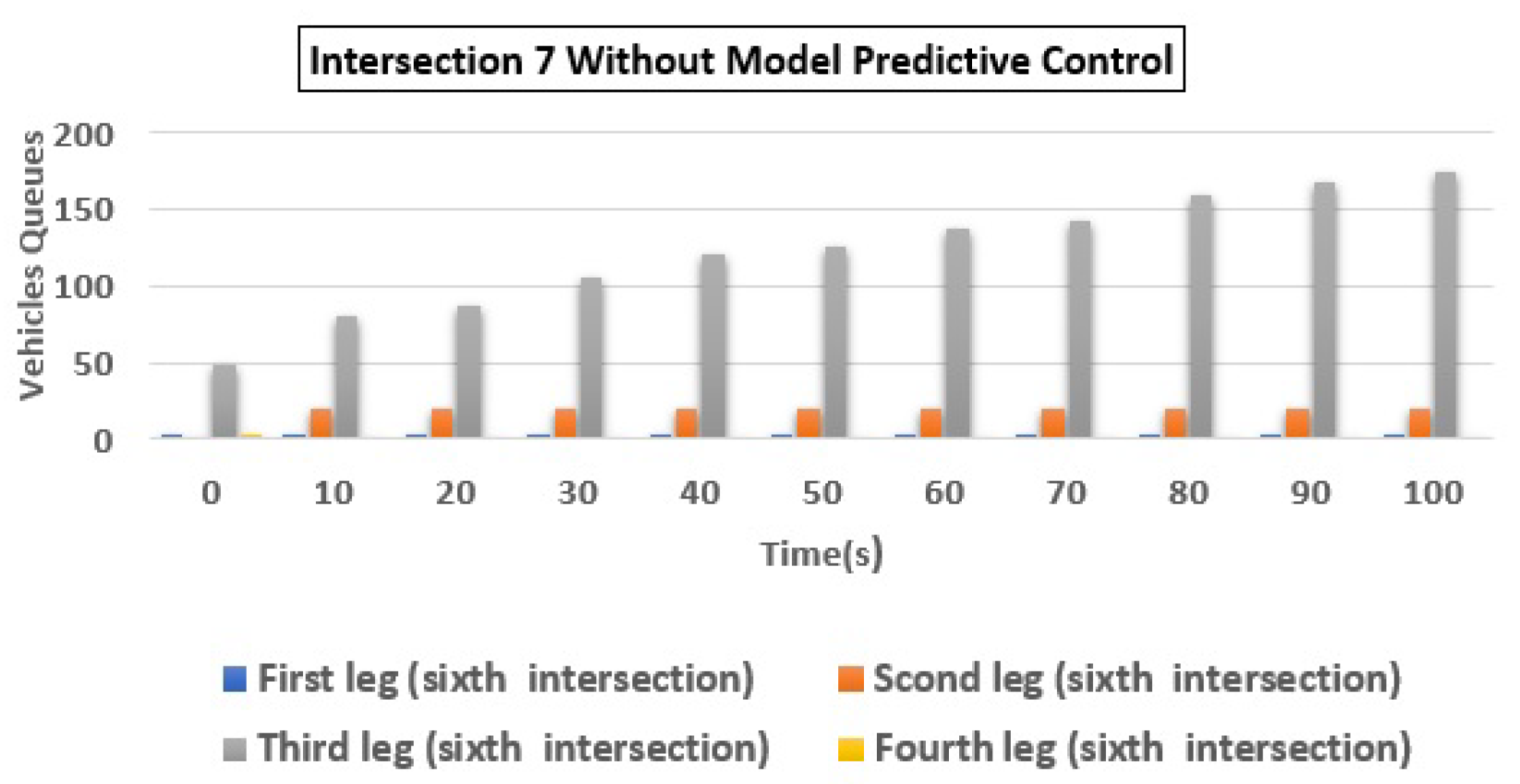
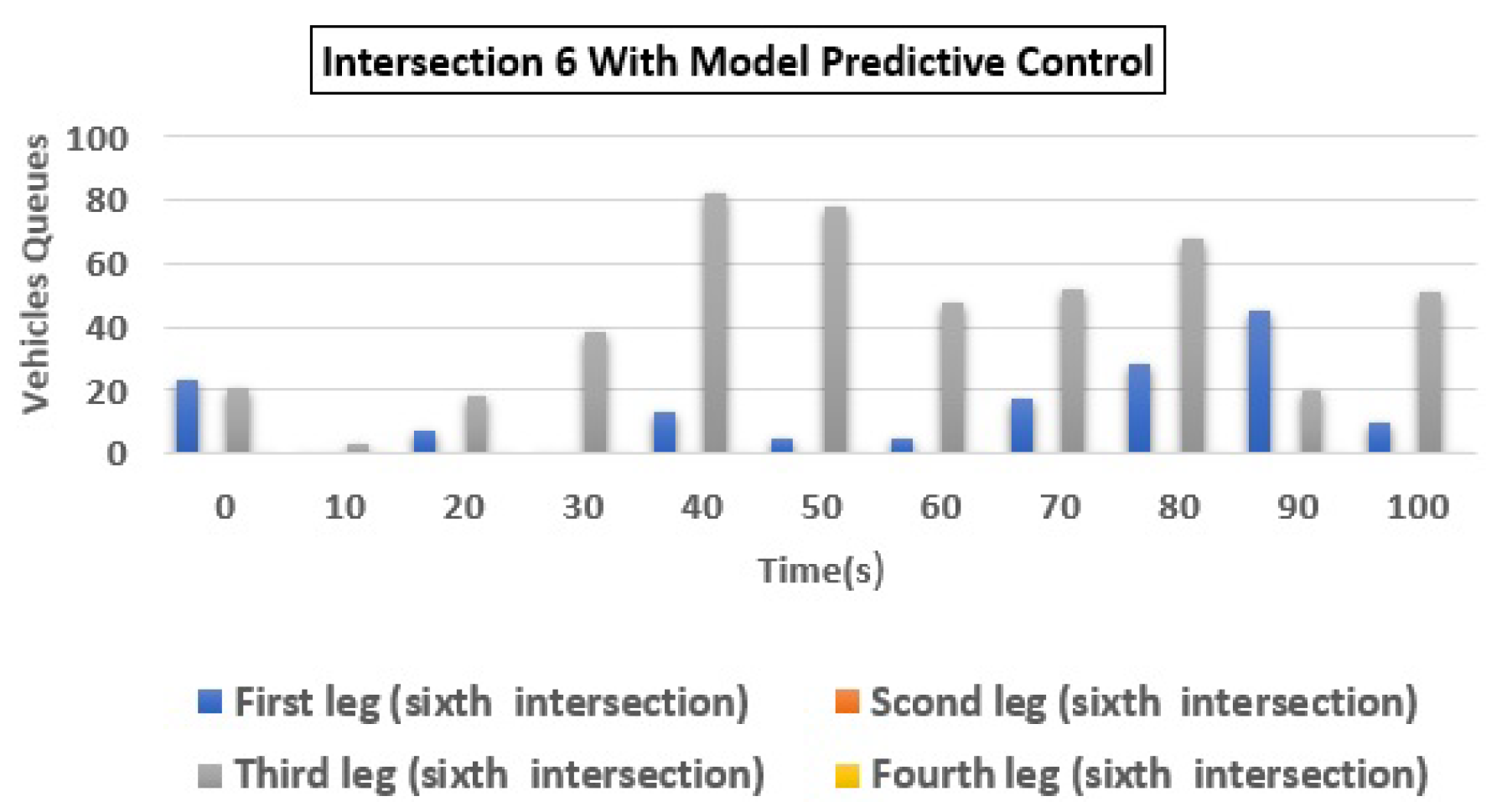
6	(a) Q1	175	12	93.14
	(b) Q2	32	3	90.63
	(c) Q3	2	3	−50.00
	(d) Q4	28	3	89.29
Total		237	21	91.14
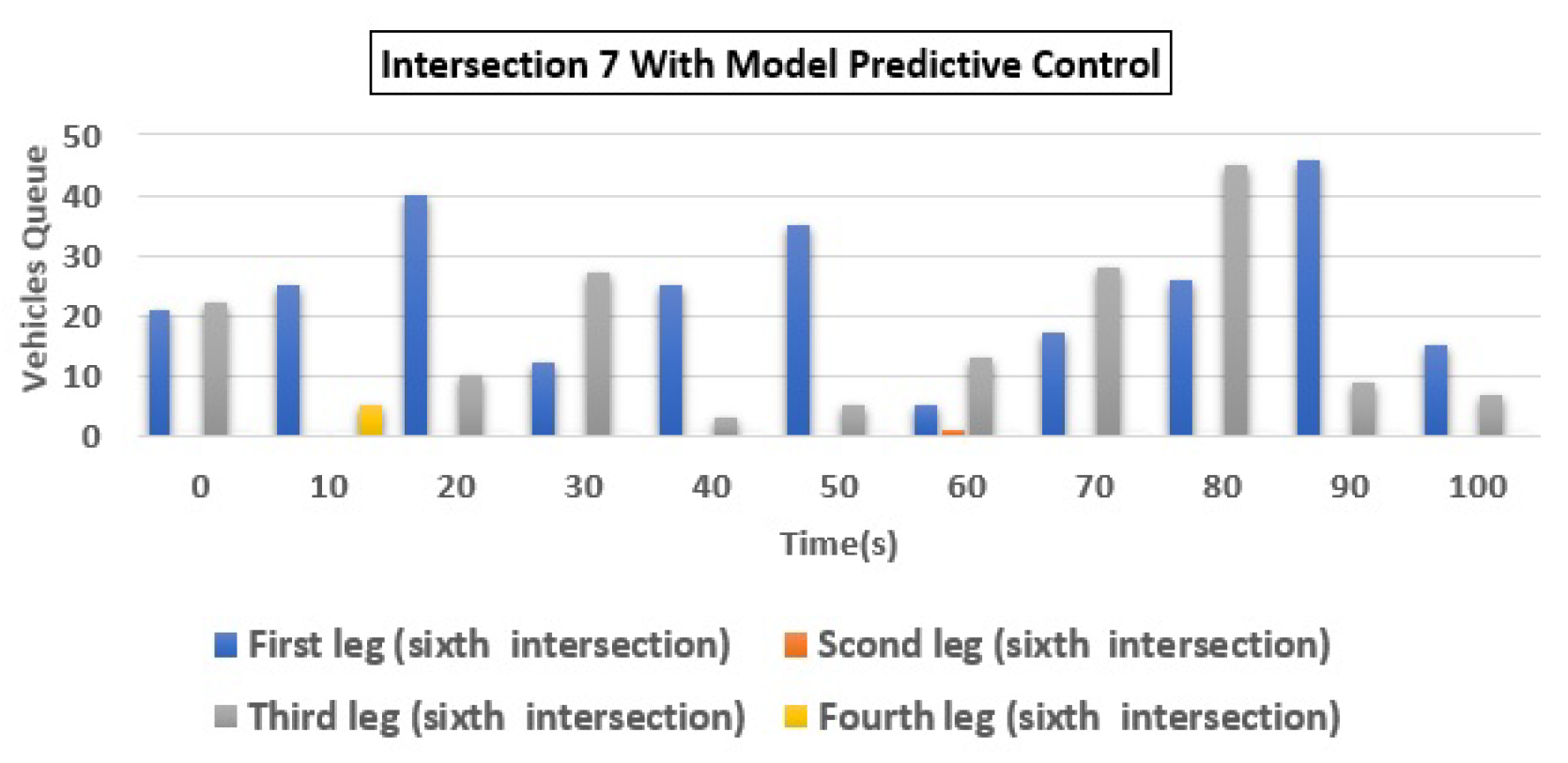
7	(a) Q1	3	0	100.00
	(b) Q2	20	3	85.00
	9c) Q3	175	7	96.00
	(d) Q4	3	1	66.67
Total		201	11	94.53
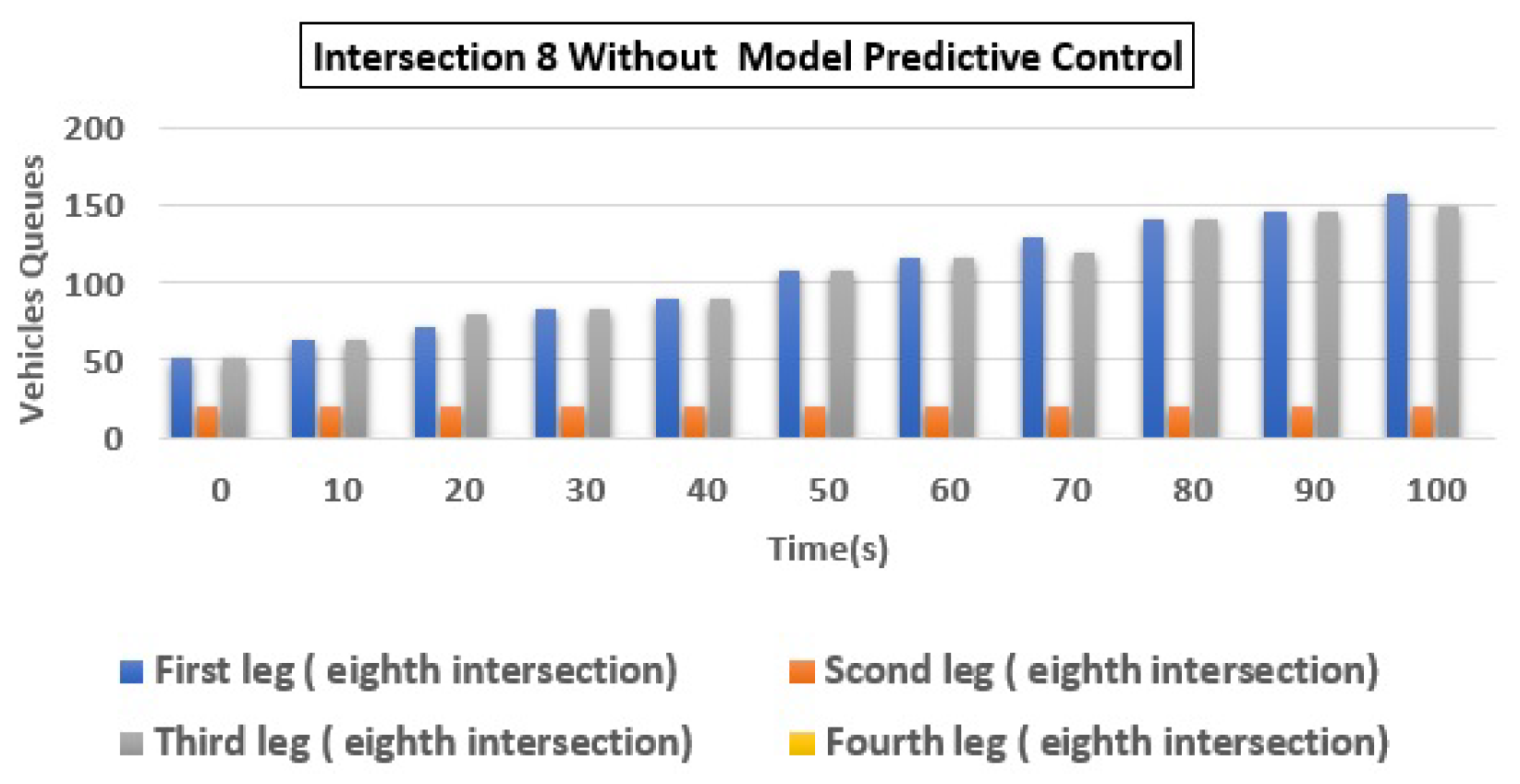
8	(a) Q1	175	7	96.00
	(b) Q2	20	3	85.00
	(c) Q3	150	12	92.00
	(d) Q4	3	0	100.00
Total		348	22	93.68

and Figure 21, which has been given below. Table 3 and Figure 21 below show the proposed model’s performance at eight intersections by comparing the fixed time control. The number of vehicles has been prepared with sample times equal to $0.1$ s. At the first intersection, a total of $97\%$ vehicles in the 4-line fixed model, 4 intersection was reduced to 13 while using the controller. Furthermore, the improvement measure is $86.60\%$. Using model predictive control, the second intersection has reduced the number of vehicles from 159 to 52. As can be seen, the queue length in Leg 4 has been reduced from 162 to 33 in the third intersection. The measure of improvement in these four roads was $79.63\%$. The number of vehicles has been minimized in the fourth intersection, clearly seen in Figure 21 and

Table 4. Comparison of intersections the proposed method with other existing studies.

Existing Work	Approach	Benefit	Applied Model
Azimirad et al. [35]	Single intersection	Minimal waiting time and length of queue	Fuzzy Logic
Jafari et al. [53]	Single intersection	Optimal traffic and reducing queue length	Model Predictive Control
Jiachen Yang et al. [54]	3 intersection	Significant reduction in delay or various traffic conditions.	Multi-Agent Deep Reinforcement Learning
Hyunjin et al. [55]	9 intersection	Maximize the throughput and efficiently distribute the signals	Deep Q-Network
Hongwei Ge et al. [56]	4 intersection	Adaptive multi intersection signal control	Cooperative deep Q-network
Proposed	8 intersection	Optimal traffic and reducing queue length	Model Predictive Control

. Similarly, the improvement percentage is $91.43\%$, which has resulted in optimization. In other intersections such as eighth, sixth, and seventh, respectively, using the model predictive control, a percentage of improvement has been seen compared to the fixed time, which indicates the excellent performance of the controller. In the simulation, an improvement has been seen in the intersection by using model predictive control as shown in Figure 21. The queue length at each intersection has been reduced compared to the fixed time controller using a model-based predictive model.

The Comparison of the Proposed Method with Other Existing Studies

This section has compared different models and intersections with the proposed model, such as fuzzy logic, model predictive control, and machine learning methods shown in the table. Additionally, each model has been applied on different intersections, including single intersections, four intersections, six intersections, and nine intersections. This paper [35] has been used as a fuzzy logic control for traffic flows under both normal and exceptional traffic conditions. Still, the dynamic model is not stable on a single intersection. Here, [53] has been considered at only one intersection for reducing queue length of the vehicle. Algorithms derived from RL techniques operate based on biological principles. Developed creatures can change their behavior based on their environment and optimize their efforts to improve, getting better compensations. In RL algorithms, this ability is made achievable by making agents. This paper [54] considered the speed of vehicles and the iteration number by using Multi-Agent Deep Reinforcement Learning to reduce traffic. The traffic signal control system used in intelligent transportation analyzes and controls traffic flow in real-time. This article [55] presented a Deep Q-Network model, which is determined by the optimal demand of a green signal. Another study on the multi intersection has [56] shown a cooperative deep Q-network for signal control modeled as a multiagent reinforcement learning system. At the proposed model, we expanded one intersection to several intersections. However, in the model predictive control, in addition to having all the advantages of all intelligent methods, the superiority of the model-based predictive control over the rest of the fuzzy control is inherent predictive property. It does not depend on anything. Model predictive control also has the intrinsic ability to compensate for dead time, while in fuzzy, it depends on the expert. Additionally, our proposed method results show the proposed model’s good performance. In the other existing studies, these types of learning systems are not present. Available traffic control methods do not consider the latest multiagent deep reinforcement learning progress. In addition, current traffic congestion management explanations based on deep reinforcement learning (DRL) do not consider vehicles cooperating with traffic lights but only controlling traffic lights signals. Therefore, traffic control in cities does not achieve a general effect. A comparison of the proposed method has been presented in Table 4 in one intersection. The advantages and disadvantages of the proposed model compared with other existing works are summarized as below:

Advantages:

• Model predictive control is updated every minute, and this update applies controls based on what will happen in the future to the system.
• They can be used for delayed systems and multidimensional systems.
• Can be added to that constraint. For example: control the traffic load behind the crossroads for one h a day.
• Being bound by model predictive control.
• All controllers are unpredictable, including advanced controllers such as slip model control (a nonlinear controller is resistant). Nonlinear resistors mean that they do their job against system uncertainties. For example, in the math model from the real world, we do not know the name of a parameter.
• Unlike all controllers, the $\left(u\right)$ predictor signal drops at $(t+1)$ to $(t+np)$. ($np:Predictivehorizon)$.

Disadvantages:

• Model predictive control has several models. Any situation that is based on step response and impact response must be stable. The system must have no integral behavior. Integral behavior means that there should be no necessities in the system model.
• In the basic model, the conversion function is noise-sensitive.

7. Conclusions

In this paper, a model predictive control was first developed to generate and control traffic signals for multiagent intersections linking to each other; then, their stability was proved. The model predictive control is designed based on the theory of multi-functional systems, and the effect of adjacent intersections on their behavior is considered. In each phase, two basic parameters are the length of the queue and signal traffic to reduce them. A model predictive control, which is designed based on the state space equations, showed that the queue of vehicles in each phase decreased compared to the constant time mode and maximized the volume of traffic. Simulation results depicted the efficiency of the method proposed for the intersections.

Discussion and Future Direction

Table 5. Comparison of the proposed model with other works.

Author	Model	Queue Length	Sample Time	Limitations	Solution
Elvira et al. [57]	Macroscopic model	Exit	250 s	Large scale urban traffic network	Determining queue length, flow crossing and routing decisions
Rasool et al. [58]	Integrated formulation and adistributed solution technique	-	6 s	Urban streetnetworks	Cooperative signal controland perimeter traffic metering
Yunp eng et al. [59]	Mutual coordination traffic organization method	-	40 s	Multiintersection road networks	Traffic organization method method for CAVs road networks
Azzedine et al. [60]	Reinforcement Learning based Cooperative	-	5 s	Traffic signalsystem	Real time and delaytraffic conditions
Xiancheng et al. [61]	Model based on swarm intelligence algorithm	-	90 s	Trafficflow at intersections	Relieving trafficcongestion
Proposed Model	Model predictive control with multi-agent	Reducing length queue	0.1 s	Urban traffic	Relieving traffic congestion and optimization model of intersection traffic signal timing

compares the proposed model with modern technology in terms of sampling time and limits of the queue length; this article is a new way to discuss traffic lights at intersections. The traffic control system was designed to improve traffic light scheduling processes. This article is a new method of discussing traffic lights in intersections. We intend to expand the proposed method for future work to engage with different cities for better performance. Examples of things that can be done to continue working on the issue of traffic control are:

• Provide a comprehensive model of traffic behavior at several adjacent intersections by considering parking lots and side streets near the adjacent intersection and parking lots and side roads near intersections in the model.
• Hybrid systems are used to design suitable transmission systems by designing several models.
• We impose traffic restrictions on pedestrians, weather conditions, etc.